Уклон кровли из профлиста – полезная информация Металлобаза Новосаратовка
Стальной профилированный лист с защитным цинковым покрытием или цинковым+полимерным слоем – популярный материал для покрытия кровель. Одна из задач, которую решают перед строительством крыши с покрытием из профнастила, – определение минимально допустимого угла уклона ската. Если сделать этот уклон слишком большим, то снизится устойчивость к ветровым нагрузкам и увеличатся расходы профлиста, если слишком маленьким – конструкция может не выдержать массы снеговых накоплений. Чем больше угол между основанием крыши и скатом, тем опаснее кровельные работы.
СНиП о необходимом уклоне ската кровли из профлиста
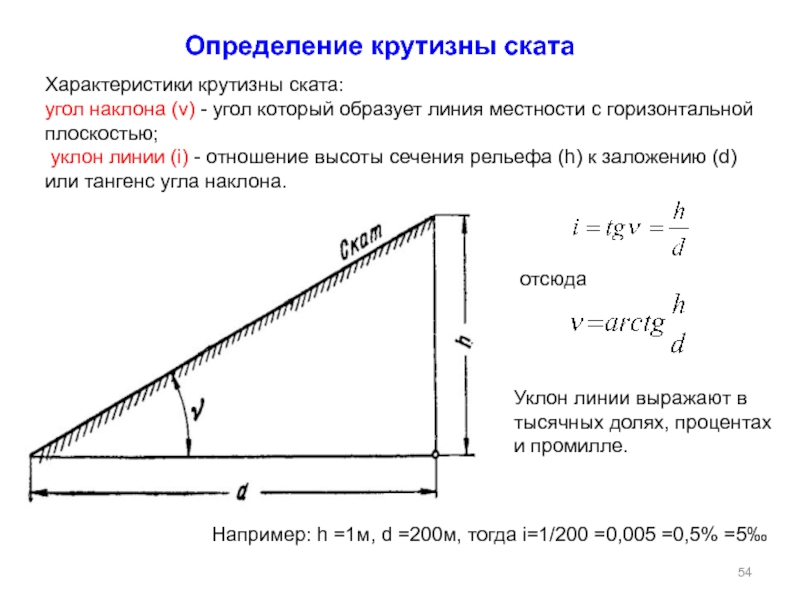
Определение! Углом уклона ската называют угол между ним и горизонтальной поверхностью. Эта величина может измеряться в градусах или в %. Параметр в % равен отношению вертикального катета прямоугольного треугольника, образованного одним скатом и горизонтальной поверхностью, к горизонтальному катету.
В СП 17.13330.2011, который является актуализированной редакцией СНиПа II-26-76, минимальный угол уклона скатов крыш из профнастила составляет 12°. Угол может быть и меньше, но в этом случае велика вероятность попадания осадков в стыки между листами профнастила из-за медленного стекания воды. Для решения проблемы необходимы дополнительные мероприятия по гидроизоляции с использованием специальных герметиков для кровель.
Для плоских кровель и крыш с малым уклоном ската подходит только профилированный лист с высоким профилем. Если на крышах с уклоном скатов 12-14° сделать увеличенный нахлест – на две волны, то дополнительные гидроизоляционные мероприятия не проводят. Минус такого варианта – значительное увеличение расхода материала.
Виды крыш, в зависимости от угла уклона кровли
В зависимости от угла уклона ската (скатов), крыши разделяют на:
- плоские – до 5°, профилированный лист для таких конструкций применять не рекомендуется;
- односкатные или многоскатные с небольшим уклоном – 20-40°, в многоскатных конструкциях крыш скаты могут быть наклонены под одинаковыми или разными углами;
- с крутыми скатами – более 40°, обычно такие кровли устраиваются в строениях с мансардным этажом.
Нормативных ограничений по максимальному углу уклона ската не существует, но обычно он не превышает 60°. Конструкции крыш с большим углом сооружаются только в регионах с низкими ветровыми нагрузками.
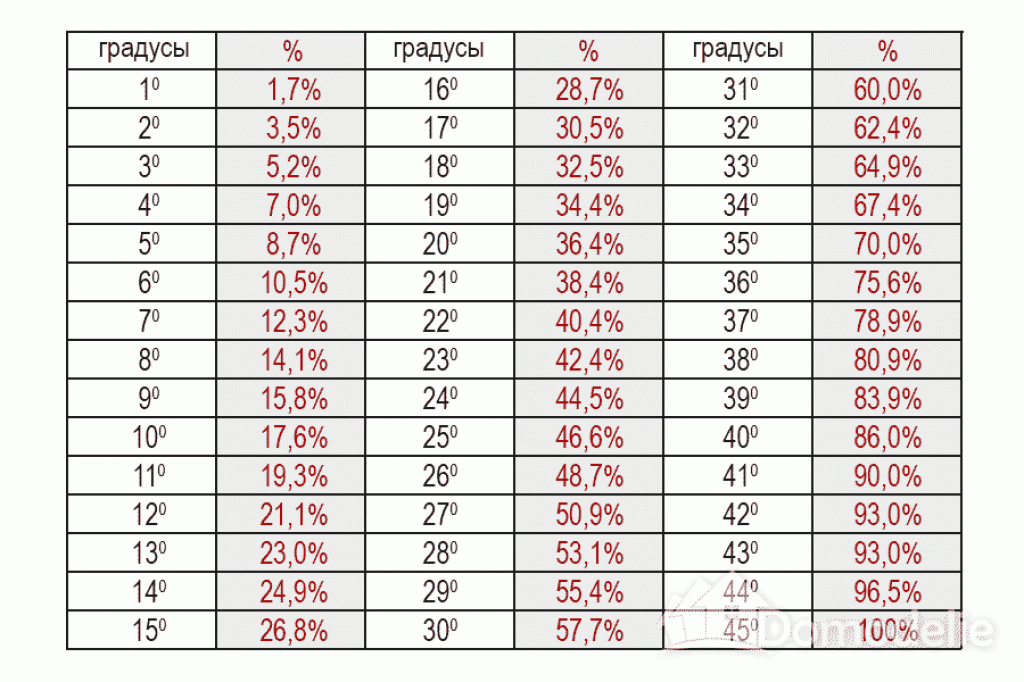
Таблица соответствия уклона ската кровли, изготовленной из профлиста, в градусах и процентах
| Градусы | % | Градусы | % | Градусы | % |
| 1 | 1,7 | 16 | 28,7 | 31 | 60,0 |
| 2 | 3,5 | 17 | 30,5 | 32 | 62,4 |
| 3 | 5,2 | 18 | 32,5 | 33 | 64,9 |
| 4 | 7,0 | 19 | 34,4 | 34 | 67,4 |
| 5 | 8,7 | 20 | 36,4 | 35 | 70,0 |
| 6 | 10,5 | 21 | 38,4 | 36 | 72,6 |
| 7 | 12,3 | 22 | 40,4 | 37 | 75,4 |
| 8 | 14,1 | 23 | 42,4 | 38 | 78,9 |
| 9 | 15,8 | 24 | 44,5 | 39 | 80,9 |
| 10 | 17,6 | 25 | 46,6 | 40 | 83,9 |
| 11 | 19,3 | 26 | 48,7 | 41 | 86,0 |
| 12 | 21,1 | 27 | 50,9 | 42 | 90,0 |
| 13 | 23,0 | 28 | 53,1 | 43 | 93,096,5 |
| 14 | 24,9 | 2 | 55,4 | 44 | 100 |
| 15 | 26,8 | 30 | 57,7 | 45 |
Сложность выбора правильного уклона ската заключается в том, что в этом вопросе необходимо учесть ряд параметров, среди которых:
- возможность быстрого схода осадков с поверхности кровли;
- способность сопротивляться ветровым нагрузкам;
- простота конструкции;
- экономия кровельных материалов;
- возможность использования подкровельного пространства.
Расчеты угла уклона кровли с учетом различных параметров
Предварительно угол уклона ската принимают в соответствии с общепринятыми в данном регионе и личными предпочтениями. А затем определяют допустимость выбранного наклона скатов кровли с учетом массы кровельного пирога, снеговых и ветровых нагрузок, характерных для конкретного региона.
Масса кровельного пирога
Примерную величину нагрузки на стропильную систему от самого кровельного пирога можно определить по представленной ниже таблице.
| Масса 1 м2 профнастила, кг |
Масса 1 м2 теплоизоляции, кг |
Масса 1 м2 обрешетки, кг | Прочие компоненты, кг | Суммарная нагрузка на 1 м2 стропильной системы, кг |
| 6 | 20 | 30 | 2 | 58 |
Определение снеговых нагрузок
Для определения этого параметра используют карту РФ, на которой отмечена средняя величина снеговых нагрузок на горизонтальную плоскость.
Для наших расчетов используется первое число дроби. В зависимости от запланированного угла, при расчетах используется поправочный коэффициент µ, который равен:
- до 25° – 1;
- 25°-60° – 0,7;
- выше 60° – не учитывается.
Пример: Строительство ведется в Московской области – регионе со средними снеговыми нагрузками 180 кг/м2, запланированный угол наклона ската – 30°, следовательно, коэффициент µ составляет 0,7. При умножении средней нагрузки на поправочный коэффициент получают 180х0,7 = 126 кг/м2. Если запланирован уклон ската более 60°, то величина снеговой нагрузки не учитывается, поскольку снег легко сходит с крыши.
Определение ветровых нагрузок
Ветровые нагрузки, как и снеговые, определяются по специальной карте.
Величину ветрового сопротивления умножают на поправочный коэффициент, зависящий от конкретного расположения здания.
Таблица поправочных коэффициентов
| Высота здания, м | Местоположение строения | ||
| Открытая местность – степь, пустыня | Лесная местность, города с домами, высота которых не превышает 10 м | Плотная городская застройка со строениями высотой более 25 м | |
| До 5 | 0,75 | 0,5 | 0,4 |
| 5…10 | 1,0 | 0,65 | 0,4 |
| 10…20 | 1,25 | 0,85 | 0,55 |
Для континентальной части России он в большинстве случаев составляет 32 кг/м2.
Предположим, мы строим дом в Московской области высотой до 5 м в городе с невысокими домами, поправочный коэффициент – 0,5. Это означает, что ветровая нагрузка для данного случая составляет 32х0,5 = 16 кг/м 2.
Для получения точного результата специалисты проводят расчеты по формулам, учитывающим аэродинамический коэффициент.
Суммарная нагрузка на стропильную систему
Суммарная нагрузка на среднюю стропильную систему не должна превышать 300 кг/м2. Сравним с ней нагрузку, полученную в результате расчетов. Она равна сумме массы кровельного пирога, снеговой и ветровой нагрузок.
М = 58 + 126 + 16 = 200 кг/м2. Это означает, что выбранный нами изначально угол уклона скатов 30°, является допустимым для дома высотой до 5 м, расположенного в Московской области в населенном пункте с малоэтажной застройкой.
Зависимость между углом наклона ската и типом профнастила
Марка профнастила, который может использоваться в качестве кровельного материала, во многом зависит от того, какой угол уклона имеет скат кровли.
Таблица популярных марок профнастила и допустимые углы уклона кровли
| Марка профилированного листа | Угол уклона ската, ° | Толщина листа, мм | Шаг обрешетки | Величина нахлеста |
| С-8 | Не менее 15 | 0,5 | Сплошная обрешетка | Оптимально – две гофры |
| С-10 | До 15 | 0,5 | Сплошная обрешетка | Оптимально – 2 гофры |
| Более 15 | До 300 мм | Одна гофра | ||
| С-20 | До 15 | 0,5…0,7 | Сплошная обрешетка | Одна гофра |
| Более 15 | До 500 мм | |||
| С-21 | До 15 | 0,5…0,7 | До 300 мм | Одна гофра |
| Более 15 | До 650 мм | |||
| НС-35 | До 15 | 0,5…0,7 | До 500 мм | Одна гофра |
| Более 15 | До 1000 мм |
как вы там ездите? — журнал За рулем
Когда-то эти районы заселялись от безысходности.
Сейчас они – объекты туристического паломничества. Но жить там по-прежнему – особое удовольствие.
Чтобы жить на «крутых улочках», нужна сноровка. Необходима хорошая физическая форма, чтобы ежедневно совершать восхождения. А если вы водите машину, то и специальные навыки. Например, если позволяет ширина дороги, парковаться лучше перпендикулярно, а не параллельно направлению дороги – будет проще трогаться с места. Если не позволяет, то рекомендуется ставить автомобиль на прикол с вывернутыми в сторону бордюра колесами – не укатится.
Ну и, конечно, к автомобилям тоже предъявляются повышенные требования. У машины должны быть особо эффективные и надежные тормоза. Второе важное требование – мощный мотор. С чахлым двигателем подниматься в такие кручи – сомнительное удовольствие. Кроме того, желательна хорошая автоматическая коробка передач. Вариаторы в таких условиях долго не живут. У робота с двумя сцеплениями, если остановиться посреди подъема, фрикционы зачастую размыкаются – и машина катится назад, как на нейтрали.
Опасно! С обычной механикой быстро выходит из строя сцепление. В общем, альтернативы классическому автомату в таких условиях, по сути, нет.
1. Ффордд Пен Лех, город Харлеч (Великобритания)
В 2019 году улица попала в Книгу рекордов Гиннесса – уклон составляет 37,5%. В самом крутом месте высота дороги повышается на один метр на каждые 2,67 м длины. А всего за 330 метров подъем составляет 50 м. Поскольку широким массам местечко стало известно только в прошлом году, туристов здесь пока не очень много. Но власти города уже готовятся к их наплыву. В частности, обустраивают поблизости парковку для автобусов и строят общественные туалеты.
2. Болдуин-стрит, город Данидин (Новая Зеландия)
Эта улица куда более густонаселенная. Кроме того, она уже давно – одна из главных достопримечательностей Новой Зеландии, поэтому здесь бывает множество туристов, которые желают себя запечатлеть на столь экзотическом фоне. Кроме того, на улице регулярно проводятся состязания по бегу: спортсмены сначала поднимаются наверх, а потом спускаются к финишу (общая длина дистанции составляет 359 м).
Лучшее показанное время – 1 минута 56 секунд.
3. Кантон-авеню, город Питтсбург (США)
Как и у Болдуин-стрит, уклон Кантон-авеню составляет 37%. Но мы поставили ее в нашем рейтинге на третье место, потому что улочка короче – всего 192 метра. Но смотрится она очень живописно – во многом благодаря мощению из брусчатки. Здесь проводится один из этапов велогонки «Грязная дюжина». Причем задачи прийти первым не стоит – главное просто добраться до финиша! Далеко не каждому это удается…
4. Элдрид-стрит, город Лос-Анджелес (США)
Уклон улицы равен 33% – в Калифорнии круче ничего нет. Почтовые службы отказались от адресной доставки местным жителям – все почтовые ящики находятся в начале улицы. Еще один интересный факт: стандартные мусоровозы не могли здесь работать – переворачивались при разворотах, поэтому властям города пришлось закупить партию с более низким центром тяжести. Асфальт на дороге неровный, весь в трещинах, а сама дорога выполнена в форме желобка. Выглядит все это дело не слишком презентабельно, поэтому соревнования или скопища туристов здесь не часты.
5. Фарго-стрит, город Лос-Анджелес (США)
Здесь крутизна тоже равна 33%. Однако выглядит эта улочка поприличнее, чем Элдрид-стрит: ровный и свежий асфальт, аккуратные бордюры. На Фарго-стрит ежегодно проводятся велосостязания. Их лозунг повторяет олимпийский: главное не победа, а участие. Однако среди выступающих особо котируются те, кто добрался до финиша без остановок. Наиболее упертые умудряются подняться наверх несколько раз за соревновательный день.
6. Бакстер-стрит, город Лос-Анджелес (США)
Улица идет под чуть менее крутой уклон (32%), чем у «земляки». Но она более протяженная (свыше километра). И идет лесенкой, отчего следующие по ней автобусы на перегибах скребут днищем – впечатляющее зрелище. Вообще, по этой улице в последнее время усилился автомобильный трафик, что вынудило власти города внедрить раздельный поток: по одной части улицы машины могут ехать только в одну сторону, по другой – в другую. Автомобилистам стало несподручно петлять, и они начали ездить по соседним улицам.
7. Ломбард-стрит, город Сан-Франциско (США)
Главная особенность улицы даже не уклон (32%), а извилистость – на коротком промежутке здесь восемь крутых поворотов. Этот факт позволил занести Ломбард-стрит в Книгу рекордов Гиннесса. Причем повороты сделаны искусственно – чтобы водители не гоняли. А чтобы уж было наверняка – сократили максимальную скорость движения до 8 км/ч. Впрочем, автомобилистов это не смущает – каждый из гостей города считает своим долгом проехаться здесь.
8. Вайпио Уолли, Гавайские острова (США)
Эта дорога может показаться несерьезной, поскольку средний показатель крутизны составляет 25%. Однако на ней есть отрезок, где уклон составляет 40% — взять его не каждому автомобилю будет по силам! Особенно, когда дорога мокрая. А мотоциклистам сюда и вовсе путь заказан – от греха подальше. Ну а основной поток здесь состоит из пешеходов-любителей. Многим по нраву тренировать тут кардиосистему.
9. Вэйл-стрит, город Бристоль (Великобритания)
Рекордов по уклону Вэйл-стрит не ставит – он всего 20% (хотя на фотографиях кажется гораздо круче).
Тем не менее жители Бристоля и окрестностей нашли ей применение: здесь проходит традиционный ежегодный Пасхальный фестиваль, на котором жители соревнуются в спуске с горы раскрашенных яиц. Побеждает тот, чье укатится дальше.
10. Кальсада ду Лавра, город Лиссабон (Португалия)
Португальская столица стоит на холмистой местности, поэтому большинство дорог там имеют уклон. Одна из самых живописных – Кальсада ду Лавра (23%), которая застроена милыми сердцу туристов историческими домиками. Ее особенность, впрочем, в другом – привычной дороги здесь нет. Вместо асфальта проложены рельсы, по которым передвигается фуникулер, запущенный в 1884 году. Национальный памятник, однако.
- О нестандартных методах для дорожной безопасности читайте тут.
Фото: из архива автора
Уклон | математика | Британика
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы. - Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Связанный контент
Нулевой наклон – определение, типы, графики, уравнения, примеры, факты
Что такое нулевой наклон в математике?
Наклон — это показатель скорости изменения.
Вы когда-нибудь задумывались, что означает термин «нулевой наклон»? В этом случае вы пришли в нужное место. В этой статье мы определяем нулевой наклон и обсуждаем, что это значит в геометрии. Чтобы помочь вам понять, как работает эта идея, мы также приведем несколько примеров уравнений нулевого наклона и прямых линий. 9{\circ}$ с положительной осью x. Значение координаты y является постоянным на линии с нулевым наклоном. Меняются только значения x.
Пример: Красная линия параллельна оси x и имеет нулевой наклон.
Родственные игры
Что означает нулевой наклон в математике?
Линия с нулевым наклоном — это горизонтальная линия, параллельная оси x.
На графике наклон линии рассчитывается по формуле «подъем над пробегом» или $\frac{Rise}{Run}$.
Таким образом, если прямая проходит через точки $(x_1,\;y_1)$ и $(x_2,\;y_2)$, наклон определяется как
наклон $= m = \frac{y_2\;-\; y_1}{x_2\;-\;x_1} = \frac{\Delta y}{\Delta x}$
Для горизонтальной линии нет «подъема».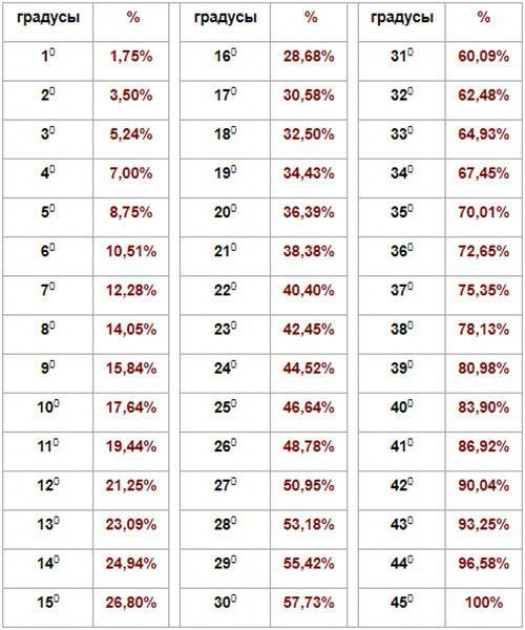
Если вы укажете любые две точки на горизонтальной линии, их координата y будет одинаковой. Итак, мы получаем $\Delta y = 0$.
Таким образом, наклон горизонтальной линии $= 0$
Связанные рабочие листы
Типы наклона линии
Существует четыре основных типа графиков наклона:
Положительный уклон
Положительный уклон линии можно представить как идущую в гору. Значение y увеличивается по мере увеличения значения x.
Отрицательный уклон
Это можно сравнить с бегом под уклон. Здесь значение у уменьшается по мере увеличения значения х.
Нулевой наклон
Наклон равен нулю , когда линия не имеет подъема по вертикали. Это будет прямая горизонтальная линия. Он останется таким же слева направо. См. рисунок ниже.
Неопределенный наклон
Неопределенный наклон относится к наклону вертикальной линии. Координата x остается прежней. Итак, в формуле «подъем над пробегом» знаменатель становится равным нулю.
Уравнение линии с неопределенным наклоном имеет вид $x = b$, где b — константа.
Форма с нулевым уклоном
Формула для формы точки наклона прямой линии: $y = mx + b$, где
y: координата y точки на линии
m: уклон
x: x-координата точки на прямой
b: точка пересечения с y
Теперь мы можем подставить наклон «0» для m и посмотреть, как это изменит формулу:
$y = 0x + b$
$y = 0 + b$
0 можно убрать из формулы, получим:
$y = b$
Это форма нулевого наклона.
Линия нулевого наклона
Как выглядит линия нулевого наклона? Это линия, параллельная оси x. Это горизонтальная линия.
Некоторые примеры уравнений для линии нулевого наклона:
$y = 5$
$y = 8,7$
$y = -\;19$
b может быть равно любому числу, положительному или отрицательному, целому или рациональному, или любому другому действительному числу.
Уравнение нулевого наклона
Уравнение нулевого наклона или уравнение линии с нулевым наклоном можно записать как
$y = b$.
Это также записывается как $y = c$.
График с нулевым наклоном
График линии с нулевым наклоном дает линию, параллельную оси x. На следующем графике показаны примеры линий с нулевым наклоном.
Нулевой наклон против неопределенного наклона
Наклон линии может быть положительным, отрицательным, нулевым или неопределенным.
| Нулевой наклон | Неопределенный наклон |
| Наклон горизонтальной линии равен нулю, поскольку она не поднимается вертикально $(y_1 \;−\; y _2 = 0)$. | Наклон вертикальной линии не определен, поскольку она не проходит горизонтально $(x_1 \;-\; x_2 = 0)$. |
Как рассчитать нулевой уклон
Нулевой наклон линии можно рассчитать с помощью трех простых методов. Нулевой наклон линии можно рассчитать по точкам на линии, углу, который линия образует с положительной осью x, или по производной уравнения линии/кривой.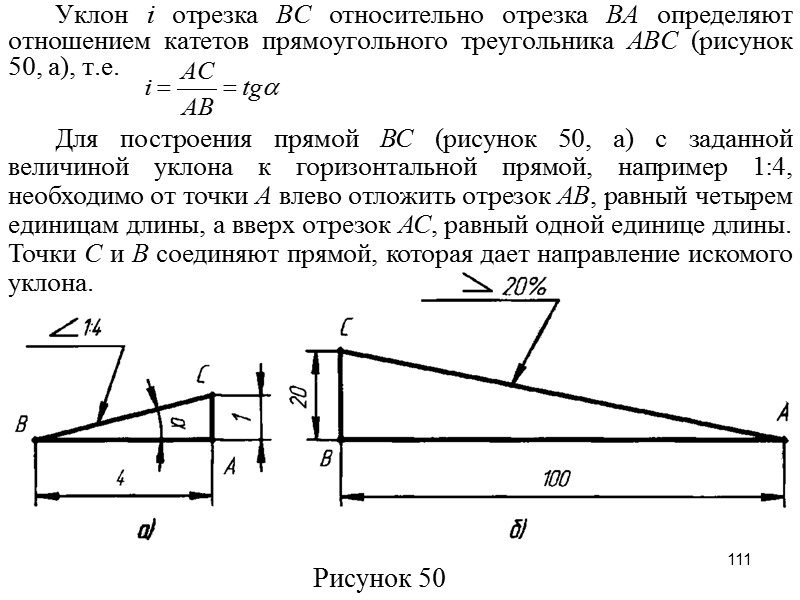
{\circ} = 0$.
Для заданного уравнения для кривой f(x) наклон кривой представляет собой наклон касательной к точке на кривой, вычисленный путем дифференцирования функции. $m = f'(x) = dy/dx$.
Почему горизонтальные линии имеют нулевой наклон?
Наклон линии определяется как
$Slope = \frac{(Rise)}{(Run)}$
Наклон горизонтальной линии равен нулю, поскольку координата y постоянна.
Таким образом, наклон равен нулю.
Какие линии имеют нулевой наклон?
Наклон оси X или горизонтальной оси равен 0.
Кроме того, как упоминалось выше, все горизонтальные линии или линии, параллельные оси X, имеют 0 наклон.
Интересные факты!
- Линия с нулевым уклоном идеально плоская в горизонтальном направлении.
- Горизонтальная линия имеет нулевой наклон, поскольку она не поднимается вертикально.
- Мы не можем делить на ноль, мы говорим, что наклон вертикальной линии бесконечен.
Заключение
В этой статье мы узнали о линиях с нулевым наклоном.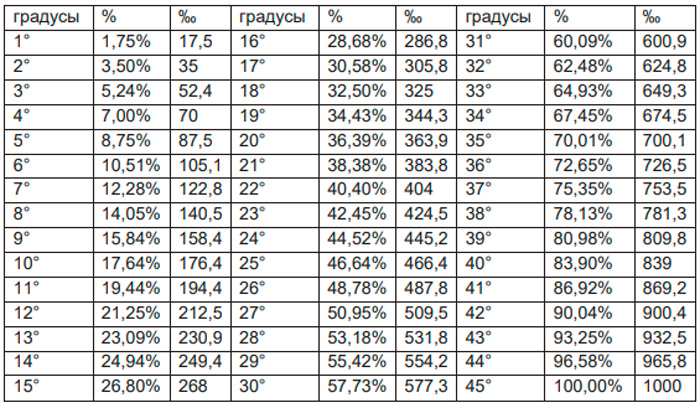
Мы также обсудили график, уравнение и факты. Давайте решим несколько примеров и попрактикуемся в решении задач, чтобы лучше понять концепцию.
1. Рассмотрим прямую с нулевым наклоном. Найдите точку на той же прямой, которая находится на расстоянии 6 единиц от точки (5, 8).
Решение:
Учитывая, что наклон данной линии равен нулю, значение «y» не изменится. Таким образом, любая дополнительная точка на прямой будет иметь вид $(x,\; 8)$.
Поскольку направление не указано, точка, удаленная на шесть единиц от $(5,8)$, может быть либо $(5 + 6,\; 8)$, либо $(5\;-\;6,\ ; 8)$.
Таким образом, точка может быть либо $(11,\; 8)$, либо $(\;-\;1,\;8)$ для указанной линии.
2. Найдите наклон данной прямой.
Решение:
Линия на графике горизонтальна. Его наклон равен нулю.
Как мы видим, на прямой есть две точки $(\;-\;2,\;5)$ и $(6,\;5)$.
Мы будем использовать эти две точки для определения наклона.
$Slope = m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$ [формула наклона]
$\Rightarrow m = \frac{5 \;–\; 5}{6 \;-\; (\;−\;2)}$
$\Rightarrow m = \frac{0}{8}$
$\Rightarrow m = 0$
3. Как найти наклон кривой ось х?
Решение:
$y = 0$ — уравнение оси x.
Уравнение можно переписать в виде $y = 0.x + 0$.
Сравните его с общим уравнением $y = mx + c$
Получаем, $m = наклон = 0$
Наклон оси x равен 0
4. Определить наклон данной прямой.
Решение:
Линия на графике вертикальная. Поэтому его наклон не определен.
Давайте посчитаем наклон, используя формулу наклона, чтобы проверить наш вывод.
На графике две точки (1, 5) и (14) соответственно (1, -3). Итак,
$Slope = m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$ [формула уклона]
$\Rightarrow m = \frac{(\;−\;3)\;−\;5}{1\;–\;1}$
$\Rightarrow m = \frac{−8}{0 }$
$m = undefined$
Следовательно, наклон графика не определен.
5. Определите точку на горизонтальной линии, которая должна быть удалена от этой точки на 5 единиц (2,6).
Решение:
Учитывая горизонтальную линию, мы можем сделать вывод, что она имеет нулевой наклон, а это означает, что значение «y» останется постоянным. Следовательно, любая дополнительная точка на прямой будет иметь вид $(x,\;6)$.
Поскольку направление не указано, точка может быть либо $(2 + 5,\; 6)$, либо $(2\;-\;5,\; 6)$.
Таким образом, точка может быть либо $(7,\;6)$, либо $(\;-\;3,\;6)$ для данной прямой.
Практические задачи на нулевом наклоне
1Определите линии с нулевым наклоном.
строки a и $y = 2$
строки b и $y = 2$
строки a и $x = \;-\;5$
строки e и $x = \;-\;5$
Правильный ответ: строки a и $y = 2$
Линия a и линия $y = 2$ — горизонтальные линии на графике. В результате наклон линии a и линии $y = 2$ равен нулю.
Линия b и линия $x = \;-\;5$ образуют на графике вертикальную линию.
В результате наклон «линий b и $x = \;-\;5$» не определен.
Каким будет наклон линии, параллельной оси Y?
Ноль
$1$
Не определено
$-\;1$
Правильный ответ: Не определено
Неопределенный наклон относится к наклону вертикальных линий.
Найдите расстояние от оси x, если она имеет нулевой наклон и проходит через точку $(4,\; 5)$.
5 единиц
7 единиц
2 единицы
4 единицы
Правильный ответ: 5 единиц
Линия с нулевым наклоном параллельна оси x. Таким образом, расстояние прямой от оси x $=$ координаты y $=$ 5 единиц
Линия, образующая угол 90 градусов с положительным направлением оси x, имеет _____________.
нулевой наклон
положительный наклон
неопределенный наклон
отрицательный наклон
Правильный ответ: неопределенный наклон
Линия, образующая угол 90 градусов с положительным направлением оси x, имеет неопределенный наклон.