Измерение вертикальных углов
Вертикальный угол – это плоский угол, лежащий в вертикальной плоскости. К вертикальным углам относятся угол наклона и зенитное расстояние. Угол между горизонтальной плоскостью и направлением линии местности называется углом наклона и обозначается буквой ν. Углы наклона бывают положительные и отрицательные.
Угол между вертикальным направлением и направлением линии местности называется зенитным расстоянием и обозначается буквой Z. Зенитные расстояния всегда положительные (рис.4.20).
Рис.4.20
Угол наклона и зенитное расстояние одного направления связаны соотношением:
Z + ν = 90 , (4.22)
или
ν = 90 – Z , (4.23)
или
Z = 90 – ν . (4.24)
Вертикальный круг теодолита. Вертикальный круг теодолита предназначен для измерения вертикальных углов, то-есть, углов наклона или зенитных расстояний.
Вертикальный круг большинства теодолитов устроен следующим образом: лимб вертикального круга жестко соединен с трубой (насажен на один из концов оси трубы), центр лимба совмещен с геометрической осью вращения трубы, а его плоскость перпендикулярна этой оси. Деления на лимбе наносят по разному: либо от 0 до 360, либо от 0 до 180 в обе стороны со знаками “плюс” и “минус” или без знаков и т.д. Для отсчета по лимбу имеется алидада. Основные части алидады: отсчетное приспособление, цилиндрический уровень (или компенсатор) и микрометренный винт.
Деления на лимбе наносят по разному: либо от 0 до 360, либо от 0 до 180 в обе стороны со знаками “плюс” и “минус” или без знаков и т.д. Для отсчета по лимбу имеется алидада. Основные части алидады: отсчетное приспособление, цилиндрический уровень (или компенсатор) и микрометренный винт.
Пузырек уровня в момент отсчета приводится в нуль-пункт, то есть, ось уровня служит указателем горизонтального направления. Отсчетным индексом является нулевой штрих отсчетного приспособления. Ось уровня и линия отсчетного индекса (линия, соединяющая отсчетный индекс с центром лимба) должны быть параллельны; при выполнении этого условия линия отсчетного индекса будет горизонтальна в момент взятия отсчета по вертикальному кругу.
Взаимное положение лимба и зрительной трубы должно удовлетворять условию: визирная линия трубы и нулевой диаметр лимба должны быть параллельны.
Оба условия вместе составляют так называемое главное условие вертикального круга теодолита; оно читается так: визирная линия трубы должна занимать горизонтальное положение, когда отсчет по лимбу равен нулю и пузырек уровня находится в нульпункте. На практике оба эти условия могут не выполняться и имеет место случай, изображенный на рис.4.21-а.
На практике оба эти условия могут не выполняться и имеет место случай, изображенный на рис.4.21-а.
Во-первых, при насаживании лимба на ось трубы между нулевым диаметром лимба и визирной линией трубы остается малый угол x. Во-вторых, линия отсчетного индекса может быть непараллельна оси уровня и между ними существует малый угол y. Таким образом, хотя отсчет по лимбу равен нулю, визирная линия трубы занимает наклонное положение, и угол наклона ее равен:
ν = x + y.
Рис.4.21
Если установить визирную линию горизонтально (рис.4.21-б), то отсчет по лимбу станет равным:
N = 360 – (x + y). (4.25)
Этот отсчет называется местом нуля вертикального круга и обозначается М0.
Таким образом, место нуля вертикального круга теодолита – это отсчет по лимбу вертикального круга при горизонтальном положении визирной линии трубы и оси уровня вертикального круга.
Для конкретного теодолита формулы для вычисления угла наклона и места нуля приводятся в паспорте. Например, для теодолитов 2Т30 и Т15 эти формулы имеют вид:
Например, для теодолитов 2Т30 и Т15 эти формулы имеют вид:
М0 = 0.5 . (NL + NR), (4.26)
ν = 0.5 . (NL – NR),
ν = NL – M0,
ν = M0 – NR.
Положение вертикального круга, при котором отсчет по лимбу вертикального круга равен (с точностью до M0) углу наклона, считается основным; у большинства современных теодолитов основным положением является КЛ.
Для измерения углов наклона удобно иметь М0 близким к нулю, поэтому нужно регулярно выполнять поверку места нуля, которая предусматривает следующие действия:
наведение трубы на точку при КЛ, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,
перевод трубы через зенит, наведение трубы на точку при КП, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,
вычисление по соответствующим формулам места нуля М0 и угла наклона ν.
Если М0 получается большим, то при основном положении круга нужно навести трубу на точку и микрометренным винтом алидады установить отсчет, равный углу наклона; при этом пузырек уровня отклонится от нульпункта.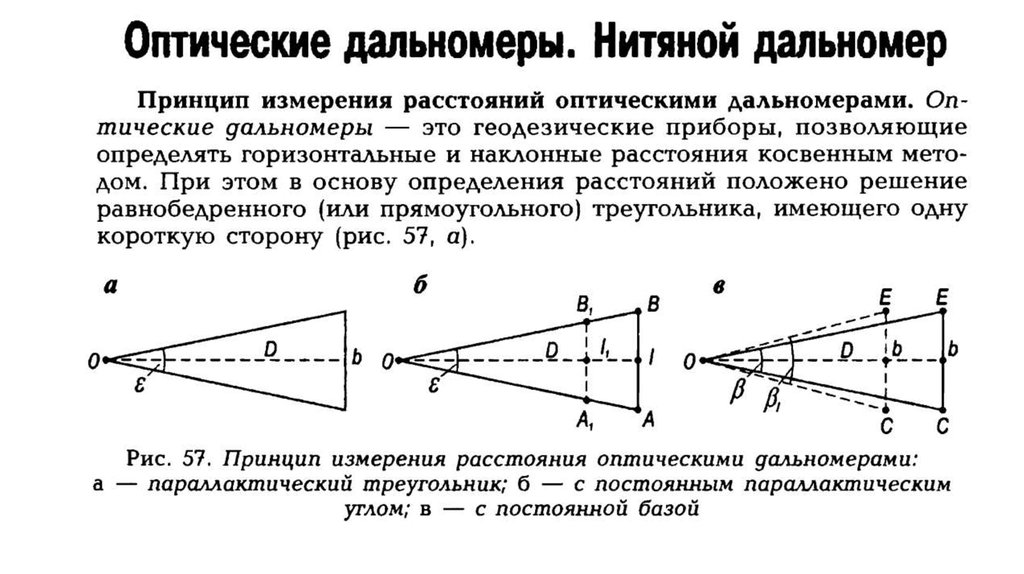 Исправительными винтами уровня привести пузырек в нульпункт.
Исправительными винтами уровня привести пузырек в нульпункт.
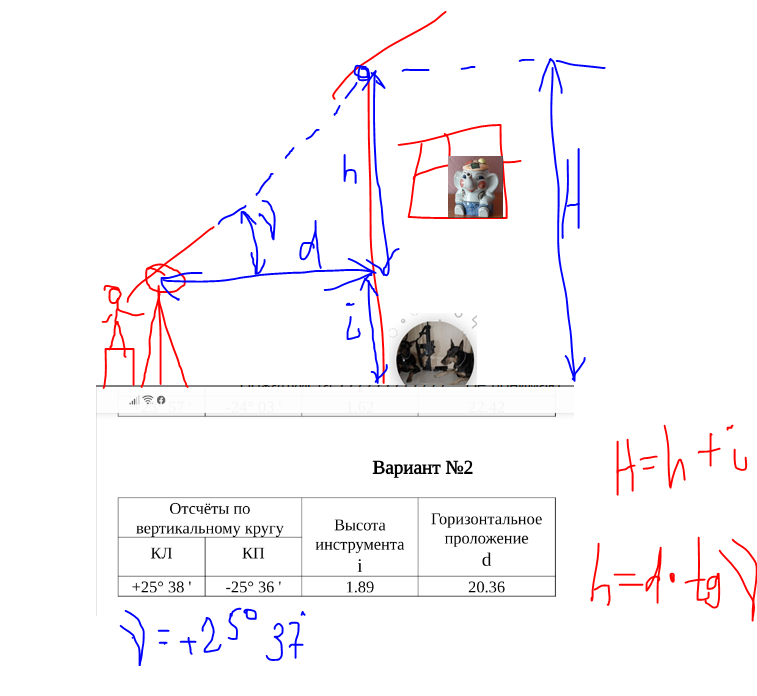
7.2. Измерение углов наклона линий
7.2.1. Определение
Угол наклона линии – угол, отсчитываемый от горизонтальной плоскости, проходящей через центр лимба вертикального угломерного круга до направления линии визирования.
Углы наклона бывают положительные (+ν), отрицательные (–ν), могут изменяться от 0 до 90° (рис. 52).
Для измерения углов наклона у теодолитов служит вертикальный угломерный круг (ВУК), у которого имеются два конструктивных отличия от круга горизонтального:
Перед каждым
отсчётом алидаду необходимо установить
в горизонтальное положение. Это положение
обеспечивается тогда, когда пузырёк
цилиндрического уровня при алидаде ВУК
находится на середине.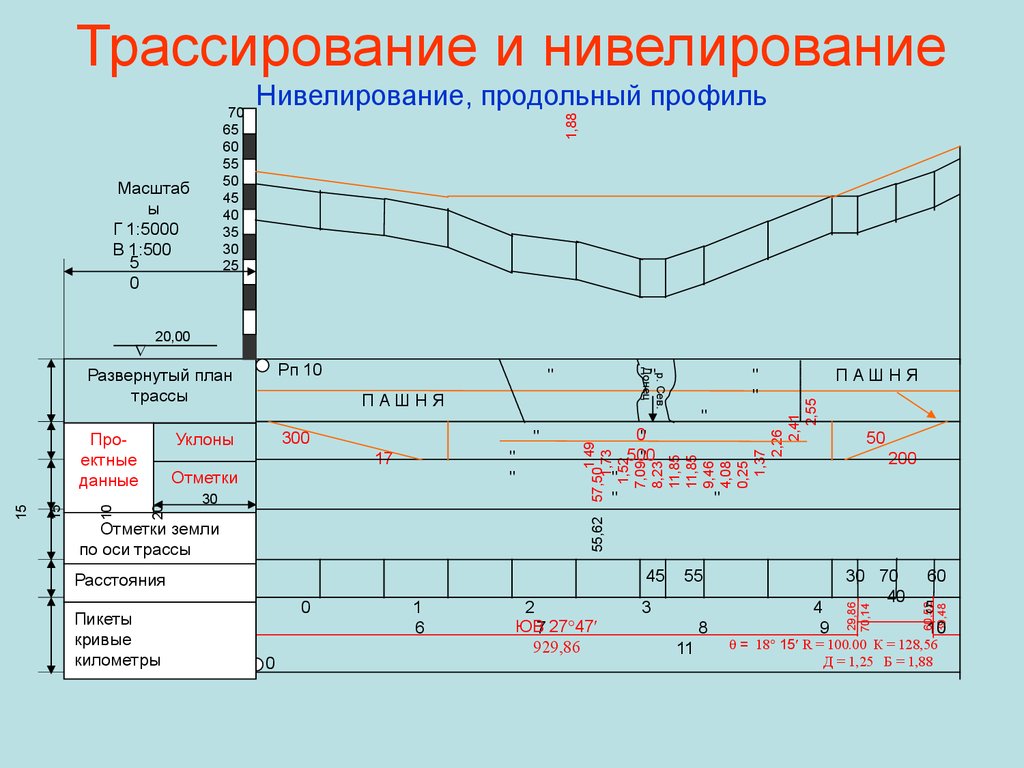
Рис. 52. Измерение вертикальных углов
7.2.2. Место нуля вертикального круга
Место нуля –
отсчет по вертикальному кругу, когда
пузырёк уровня при алидаде находится
в нульпункте, а визирная ось зрительной
трубы занимает горизонтальное положение.
Микрометренный винт алидады ВУК
Рис. 53. Цилиндрический уровень при алидаде вертикального круга (TT-50, TT-5)
7.2.3. Расчётные формулы места нуля для теодолитов с металлическими кругами
Если МО≠0, то для приведённой на рис. 51 оцифровки лимба получаем расчётные формулы, исходя из следующего.
При визировании на точку М обозначим отсчёт по вертикальному кругу при круге право – КП (рис. 54 а), при круге лево – КЛ (рис. 54 б). Тогда
и , (28, 29)
соответственно
, (30)
. (31)
Решая систему, получаем:
, . (32, 33)
Итак, визируя на какую-то достаточно удалённую и высоко расположенную точку при двух положениях вертикального круга, взяв отсчёты КП и КЛ для определения МО и для вычисления угла наклона, можем пользоваться расчётными формулами:
, (34)
,
, (35)
. (36)
(36)
При использовании этих формул к отсчётам, меньшим 90°,следует прибавить 360° .
7.2.4. Расчётные формулы места нуля для оптических теодолитов
Приведённые выше расчётные формулы для определения угла наклона получены для теодолитов с металлическими кругами (ТТ-50; ТТ-5 и др.). Конструктивные особенности оптических теодолитов определяют отличие в расчётных формулах и в способах приведения М0 к нулю. Так, для Т30 будет:
,
,,
.
При значениях КП и КЛ меньшим 90°, прибавить 360°.
Рис. 54. Определение места нуля вертикального угломерного круга
GS6777 – Спутниковая геодезия
|
[ Основной ] [Расписание занятий] [Учебный план] [ Электронная почта ] [ Домашнее задание ] [Полезное Ссылки и ссылки ]
Весна 2013
GS6777 Расписание занятий по спутниковой геодезии
http://geodesy. geology.ohio-state.edu/course/gs6777
geology.ohio-state.edu/course/gs6777
29 сентября (четверг , 13:00
4 октября (вторник) : Раздаточный материал: Yoder et al. [1983] Бумага Nature. Еще примеры по приложениям
Законы Кеплера и законы Кеплера
Уравнение. Использование «измерений» из Проводника
27 для оценки ГМ Земли. Вывод уравнения Кеплера . Вывод
задача двух тел в относительной системе координат. Его решение, начиная с Ньютона
Закон тяготения и использование относительной системы координат. Обратите внимание на все
предположения в выводе. Орбита в космосе (3D). Физический смысл шести кеплеровских орбит
элементы. Сохранение углового момента – его физ.
значение: инвариант плоскости орбиты. Интеграл энергии. (1) Проверить
и узнайте об эксперименте по восстановлению гравитации и климату (GRACE)
двухспутниковая миссия, спутниковая миссия TOPEX/POSEIDON.
6 октября (четверг) : Раздаточные материалы: (1) Обзор программы двух тел и Орбиты в космосе (лекция примечания), (2) Орбиты в 3D, Отношения между элементами орбиты и декартовыми координатами. Вывод из Программа двух тел в полярных координатах. Просмотрите сделанные предположения (инерционные координаты, точечная масса или тела с постоянными плотностями). Объяснение так называемого термина центрального тела. Обсуждение термина «несферическое геопотенциальное или гравитационное поле». Земли: связанные с приложениями GRACE (последнее исследование вопрос). Орбита в космосе, обзор физического значения шести элементов орбиты Келпера, продвижение и ретроградные орбиты. Преобразование между орбитой элементов и декартовых векторов положения и скорости (раздаточный материал, Relationship между элементами орбиты и декартовыми координатами, не подробно обсуждалось на уроке). Иллюстрация топлива,
 Самый большой срок
когда изменение наклона Delta-i равно 60 0 , требуется Delta-v=v~= 7 км/сек ,
что почти невозможно. Учебный вопрос :
что такое точки Лагранжа (системы Земля-Солнце)?
Самый большой срок
когда изменение наклона Delta-i равно 60 0 , требуется Delta-v=v~= 7 км/сек ,
что почти невозможно. Учебный вопрос :
что такое точки Лагранжа (системы Земля-Солнце)?6 октября (четверг, 13:00) : лаборатория Сессия. Продолжение обсуждения Lab. № 1.
11 октября (вторник): Больше дискуссий о Кеплере.
3 rd Закон: T=2*pi*SQRT(a 3 /G(M 1 +M 2 )) Is
это уравнение объясняет эллиптические орбиты? Если ГМ (или плотность) тела на меньше ден, например, вода вместо
камень. Орбитальный период, T, увеличивается на . Краткое описание
обсуждение инновационного использования GPS (затенение GPS, уровень воды GPS
измерения над океаном, реками, GPS-альтиметрия или рефлектометрия).
Связь между широтой места запуска спутника и
азимутальный угол и наклонение орбиты запускаемых спутников.
Вывод уравнения движения, энергии и угла N тел
интегралы импульса.

Учебный вопрос Ответы : (1) Существуют варианты
наклон (наклон орбиты Земли вокруг Солнца, 23,4 0 ),
эксцентриситет, гравитационное притяжение Солнца и Луны на Земле
экваториальная выпуклость (сплющенная Земля) вызывает медленное изменение
в ориентации вращения Земли (прецессия, с периодом 26000
лет), колебания Земли (полярное движение), вращение ~ 24 часа в сутки и скорость вращения
замедляется из-за приливной диссипации Луны и нутации (периодической
изменения наклона или наклона 23,4 0 . Лунная орбита
вокруг Земли: эксцентриситет 0,05, колебания от 0,03 до 0,06 из-за
Возмущение Солнца, большая полуось колеблется примерно от 5 000 до 10 000 км о
средняя большая полуось, наклон варьируется примерно от 5
Лунная орбита
вокруг Земли: эксцентриситет 0,05, колебания от 0,03 до 0,06 из-за
Возмущение Солнца, большая полуось колеблется примерно от 5 000 до 10 000 км о
средняя большая полуось, наклон варьируется примерно от 5  , 1976]. Исследования ледяных кернов относятся к числу других
инструменты изучения палеоклимата. Обсуждения использования N-Body
уравнения движения, основанные на планетарных эфемеридах JPL , , которые
обеспечивает положение и скорость планет как функцию времени, а
ГМ планет, к интегрировать в обратном порядке
орбите Земли вокруг Солнца, чтобы получить орбиту как функцию времени, скажем
на 1 миллион лет. Спектральный
анализ, при условии, что моделирование адекватно, а эфемерида JPL достаточно точна, может выявить различные
периодичности орбиты и идентифицировать Миланковича
Периодичность циклов.
, 1976]. Исследования ледяных кернов относятся к числу других
инструменты изучения палеоклимата. Обсуждения использования N-Body
уравнения движения, основанные на планетарных эфемеридах JPL , , которые
обеспечивает положение и скорость планет как функцию времени, а
ГМ планет, к интегрировать в обратном порядке
орбите Земли вокруг Солнца, чтобы получить орбиту как функцию времени, скажем
на 1 миллион лет. Спектральный
анализ, при условии, что моделирование адекватно, а эфемерида JPL достаточно точна, может выявить различные
периодичности орбиты и идентифицировать Миланковича
Периодичность циклов.
13 октября (четверг): Практические соображения о Земле-Солнце
система координат. Система Земля-Луна-Солнце. Движение
луна. Орбита Земля-Луна (возмущенная Солнцем): прецессия (20 000
лет), нутация, 18,6-летняя регрессия лунного узла (т.
Цикл Сароса, или Античность). Общая теория возмущений.
возмущенное уравнение орбитального движения. Обсуждение оскуляции
(орбитальные) элементы, предположение о прецессирующем эллипсе,
и вариации методов параметров, а также основные допущения (возмущение
мал по сравнению с членом центрального тела, а истинная скорость равна соприкасающейся скорость), что дает скобки Лагранжа и планетарные уравнения Лагранжа
(итало-французский математик Жозеф Луи Лагранж, 1736-1813). Цель состоит в том, чтобы вывести уравнение Лагранжа.
Уравнение. Классовые вопросы : (1) Что такое сидерический и синодический
периоды (орбитальные периоды)? (2) Рассмотрим систему Земля-Луна, где
центр масс системы? (3) Рассмотрим уравнение Лапласа, вникнем в его
решение и предположения. Обсуждать
возможный метод проверки модели геопотенциала U,
из уравнения Лапласа и определяется по данным. Например, оцените U с помощью функции Лапласа.
уравнение глобально и как функция радиального расстояния.
Цель состоит в том, чтобы вывести уравнение Лагранжа.
Уравнение. Классовые вопросы : (1) Что такое сидерический и синодический
периоды (орбитальные периоды)? (2) Рассмотрим систему Земля-Луна, где
центр масс системы? (3) Рассмотрим уравнение Лапласа, вникнем в его
решение и предположения. Обсуждать
возможный метод проверки модели геопотенциала U,
из уравнения Лапласа и определяется по данным. Например, оцените U с помощью функции Лапласа.
уравнение глобально и как функция радиального расстояния.
13 октября (четверг, 13:00): Лаб. Опубликовано № 2. Нет лаборатории.
Учебный вопрос Ответы : (1) Синодический период – это временной интервал, который требуется для
объекта вновь появиться в той же точке по отношению к двум другим объектам (линейная
узлы), т. е. Луна относительно Солнца при наблюдении с Земли. Расчет «фазы Луны»
(лунный синодический период, 29,53087 дней) = (1/27,32166 дней – 1/365,256363
дней) -1 . (2) Центр масс системы Земля-Луна находится внутри
Земля. (3) Решение Лапласа
уравнение, U или геопотенциал могут быть выражены в
термины сферических гармоник.
(2) Центр масс системы Земля-Луна находится внутри
Земля. (3) Решение Лапласа
уравнение, U или геопотенциал могут быть выражены в
термины сферических гармоник.
Поддерживается Lei Wang & C.K. Shum
Страница геодезии Джеймса К. Джейкобса
СТРАНИЦА ГЕОДЕЗИИ Джеймс К. Джейкобс ОПРЕДЕЛЕНИЯ — КООРДИНАТ СИСТЕМЫ — ФИГУРА ЗЕМЛИ |
|
| ОПРЕДЕЛЕНИЯ: |
Геодезия – это дисциплина, которая занимается
измерение и представление земли, ее гравитационного поля и
геодинамические явления (движение полюсов, земные приливы и движение земной коры)
в трехмерном изменяющемся во времени пространстве. Геоид – это, по сути, реальная форма земли без учета топографических особенностей. Это идеализированная поверхность равновесия. Геоид, в отличие от эллипсоида, слишком сложно служить вычислительной поверхностью для решения геометрические задачи, такие как положение точки. Система координат. Справочная система для определения точек в пространстве или на плоскостях и поверхностях с отношением к заданным осям, плоскостям или поверхностям. При съемке и картографировании трех используются общие типы: (1.) Плоскополярный, при котором точки на плоскости определяются расстояние от указанной точки по лучу, имеющему заданное направление относительно базовой линии; Геоцентрическая широта (Ø’) определяется углом между плоскостью экватора и линией от локальное положение до пересечения оси вращения с экваториальная плоскость. Определение, основанное на сферической земле, также называется аутентичной широтой. Геодезическая широта (Ø) определяется углом между плоскостью геодезического экватора и местное направление геодезической вертикали. Геодезическая широта и географическая широта практически одинаковый. Географическая широта определяется на поверхности
наблюдение за угловой высотой видимого полюса. Угол к вертикали разница между геоцентрическим радиусом и астрономической вертикалью. Максимум составляет 0,1924167° при 45,0962222°. Это также называется сокращение широты, потому что геоцентрическая широта никогда не бывает больше чем географический. Стандартные эллипсоиды обычно выражаются
по величине большой полуоси (а) и уплощения (е). Количество
f является чисто математическим. Эквипотенциальный эллипсоид или эллипсоид уровня
представляет собой эллипсоид, который определяется как эквипотенциальная поверхность. Прецессия это эффект
внешнего крутящего момента, действующего на геоид, заставляющего ось вращения описывать
круглый конус. Это движение вызвано гравитационным притяжением
других небесных масс, особенно Солнца, Луны и планет. Прецессия
возникает из-за эллиптичности геоида, с крутящим моментом, оказывающим
на экваториальной выпуклости, в сочетании с наклоном оси
вращения относительно плоскости вращения (эклиптики и
неподвижное, гелиоцентрическое пространство). Для 2009 года IAU количественно оценил ошибку в
предыдущую формулировку и рекомендует новую параметризацию прецессии.
МАС рекомендует заменить термины лунно-солнечная прецессия и
планетарная прецессия с терминами прецессия экватора и
прецессия эклиптики соответственно, принятие новой прецессии
формулировках, а метод параметризации прецессии оставить
к
пользователь. Узловая линия является пересечением плоскости лунной орбиты с эклиптикой (солнечной орбитой) самолет. Линия пересечения вращается в пространстве каждые 18,6133 года (NU). Это ретроградное движение, лунный узел цикл прецессии, соответствует большому лунному циклу. лунный плоскость орбиты наклонена в среднем на 5,1453964 ° (IL) и равна изменяется под действием солнечной гравитации. Наклон и поворот узловой линии возмущает прецессию и приводит к другому движению земного вращения ось, называемая нутацией в наклонности. Нутация земной оси в конусе наклона составляет 0,00511666°. Polar Motion — это
изменение положения оси вращения относительно поверхности
геоида. Правильное движение — это движение звезд. Point Позиционирование — это определение
координат точки на суше, на море или в космосе относительно
к системе координат. Положение точки определяется путем вычисления из измерений
связывая известные положения внеземных объектов с земными
позиция. Обычно это включает преобразование астрономических и
наземные системы координат. Зенит — вектор силы тяжести точки вытянут вверх, чтобы пересечь небесную сферу, с противоположной точка, называемая надиром. Астрономический меридиан — любая плоскость, перпендикулярная к небесному экватору и содержащий полюса. Северный полюс небес является расширением мгновенной оси вращения Земли (прецессирующей и нутирующей) к пересекаются с небесной сферой. Небесный горизонт — плоскость, перпендикулярная к вектору силы тяжести точки. Географическая миля определяется как одна минута дуги на экваторе ( = 1855,32571922 м). Морская миля — это одна минута астрономического
широта. Радиус кривизны эллипсоида зависит от широты,
будучи самым длинным на полюсе и самым коротким на экваторе, как и морской
миля.
Международная система единиц определяет морскую милю как 1852 метра. Нулевое прямое восхождение — это позиция Солнце в момент весеннего равноденствия. Полюс эклиптики, по рекомендации МАС, должен быть явно определен как плоскость перпендикулярно вектору среднего орбитального углового момента барицентра Земля-Луна в инерциальной системе отсчета. |
| ОПРЕДЕЛЕНИЯ — КООРДИНАТ СИСТЕМЫ — РИСУНОК ЗЕМЛИ |
| КООРДИНАТ СИСТЕМЫ: |
Система прямого восхождения (RA) является гелиоцентрической
и весенне относится к цвету равноденствия (ось прямого восхождения
указывает на точку весны) и против часовой стрелки, если смотреть с
Северный небесный полюс (NCP). Эпохальная экспликация координат варьируется
прецессией, нутацией и мгновенными возмущениями оси вращения, соответствующими
к геодезическим координатам. Звездные координаты публикуются в РА и, в связи с
изменение во времени, относятся к эпохе. Когда РА принимает во внимание
прецессии, но не нутации, это называется системой среднего прямого восхождения (MRA). Эпохальная экспликация координат варьируется
прецессией, нутацией и мгновенными возмущениями оси вращения, соответствующими
к геодезическим координатам. Звездные координаты публикуются в РА и, в связи с
изменение во времени, относятся к эпохе. Когда РА принимает во внимание
прецессии, но не нутации, это называется системой среднего прямого восхождения (MRA).Возникновение местной астрономической системы (ЛА) в точке наблюдения на топографической поверхности (топоцентрическая). Продолжением оси вращения является небесный полюс и плоскость пересечение географического экватора является небесным экватором. астрономический вертикаль определяется местной гравитацией, с протянутой отвесной линией как астрономическая вертикаль. Астрономическая широта взята от экватора и положительный в северном полушарии. Обычная наземная система (CT)
является геоцентрическим и указывает на север до 1900-1905 средний полюс и 0° долготы
до Гринвичской обсерватории. Земные системы координат привязаны к земле и
вращаться и вращаться вместе с землей. Наземная система отсчета (TRS) представляет собой пространственную привязку система, вращающаяся вместе с Землей в космосе, с положениями точек, прикрепленных к твердой поверхности Земли, имеющих координаты которые со временем претерпевают лишь небольшие изменения из-за геофизических, тектонических или приливные деформации. Международная наземная система отсчета (ITRS)
был определен IUGG в 1991 как геоцентрическая невращающаяся система идентична
к геоцентрической системе отсчета, определенной IAU, с геоцентрическим временем координат
(ТКГ). Эволюция ориентации во времени обеспечивается отсутствием глобальных
остаточное вращение по отношению к горизонтальным движениям у поверхности Земли.
Единицей длины является метр.
Резолюция Международного союза геодезии и геофизики (IUGG) 1991 г.
Наземная система отсчета (CTRS), учитывая необходимость однозначного определения CTRS.
на миллиметровом уровне и с учетом относительности и деформации Земли, одобрено
МАС определил эталонную систему и рекомендовал
CTRS, 1) определяться из геоцентрической невращающейся системы пространственным вращением
приводящее к квазидекартовой системе, 2) геоцентрическая невращающаяся система должна быть
идентична Геоцентрической системе отсчета (GRS), определенной в резолюциях МАС,
3) координаты-время CTRS, а также GRS должны быть геоцентрическими координатами. Мгновенные ссылки на наземные системы (IT) ось в эпохальное положение, что привело к преобразованиям нескольких десятых долях угловой секунды относительно КТ. IT геодезически варьируется с время и меридиональная ось смещается из-за сдвига полюсов. Инерциальная система координат аппроксимирует Эклиптическая система, считает систему неподвижных объектов гелиоцентрически. Теоретически это лучшая система для звездных координат. это инерционно за исключением планетарной прецессии и очень медленного движения галактика. Он неподвижен относительно галактик. гелиоцентрический ось совпадает с земной осью прецессии. Система геодезических координат (B, L, H) экспресс
широта (B) как угол, образованный нормалью к эллипсоиду и
экваториальная плоскость. Геодезическая долгота L и высота над
эллипсоид – H. Геоцентрические координаты (X, Y, Z) относятся к пересечению оси и экваториальной плоскости. Разность между геодезической и геоцентрической широтой называется углом к вертикали. Геоцентрическая и геодезическая долготы равны. |
| ОПРЕДЕЛЕНИЯ — КООРДИНАТ СИСТЕМЫ — РИСУНОК ЗЕМЛИ |
| РИСУНОК ЗЕМЛИ: |
Опорный эллипсоид определен (получен из Геодезическая система отсчета 1980 IUGG константы): Определение констант. a = большая полуось = экваториальный радиус = 6 378 137,0 мУравнение меридионального эллипса (при условии Земля представляет собой сплюснутый сфероид, а географические и геодезические широты равны) равно (x 2 / a 2 ) + (у 2 / б 2 ) = 1 Геометрия меридионального сечения эталона эллипсоид. Локальный радиус (p) на геоцентрическом расстоянии определяется по формуле приравнивая экваториальный радиус к единице. где:Чтобы приблизиться к размеру 1 градуса широты или долготы с центром в данном геодезическая широта:Ø = геодезическая широтаp sin Ø’ = S sin Ø 1° широты = (111,13297955 – 0,5598 cos 2 Ø + 0,0012 cos 4 Ø) кмУменьшение широты (r) можно найти для любого значения географической широты по следующим формулам: r = Ø – Ø’ = 0,198353703703 sin 2 Ø – 0,0003222 sin 4 ØДлина морской мили в широта Ø = а / 3438 [1 – с / 2 (1 + 3 cos 2 Ø)] Кроме того, более общее выражение — (6,077 – 31
cos 2 Ø) футов. Формула расстояния между двумя точками на сфере с заданной широтой и долготой. На этой странице есть ссылка в небольшую электронную таблицу Excel для выполнения формул сферической тригонометрии. Вам нужно только ввести переменные. |
Международный Служба вращения Земли и систем отсчета, числовая Стандарты (2003) Precession (IAU 1976 исправлено
значение при J2000.0) = 5038,47875″ t – 1,07259″ t2 – 0,001147″ t3,
где t измеряется в юлианских столетиях единиц TDB. (Эта формула была
устарело в 2009 году, заменено более точными определениями. См. Хилтон и др.
др. 2006, Доклад Международного
Рабочая группа Отдела I астрономического союза по
Прецессия и эклиптика , Селеста. Наклон эклиптики в J2000,0 = 84381,4059″ Экваториальный радиус Земли = 6378136,60м Коэффициент выравнивания Земли = 298,256420 |
| ОПРЕДЕЛЕНИЯ — КООРДИНАТ СИСТЕМЫ — ФИГУРА ЗЕМЛИ |
ИСТОЧНИКИ и ВНЕШНИЕ ССЫЛКИ: Международный союз Геодезия и геофизика (IUGG) Международная ассоциация геодезии Международный Служба вращения Земли и системы отсчета Географические названия
Информационная система (ГНИС) — официальный репозиторий с 2 млн. ГЕОНет Сервер имен (GNS) обеспечивает национальную геопространственную разведку Агентства (NGA) и Совета США по географическим названиям (US BGN). база данных названий зарубежных географических объектов. База данных – это официальный репозиторий иностранных топонимических решений. На сайте Nearby.org.uk есть большой Конвертер координат и многие другие картографические инструменты. Национальная океаническая служба NOAA Образование: геодезия: GPS, CORS и ГИС. Ньюарк
Археогеодезия Фотогалерея строителей курганов |
Астрономические формулы – – –
Астрономические константы- – – Космографические
Значения  |

 Геодезия занимается в первую очередь
с позиционированием, гравитационным полем и геометрическими аспектами их
временные вариации.
Геодезия занимается в первую очередь
с позиционированием, гравитационным полем и геометрическими аспектами их
временные вариации. ) Прямоугольная, точки определяются расстоянием от двух перпендикулярных
ось или три взаимно перпендикулярные плоскости;
) Прямоугольная, точки определяются расстоянием от двух перпендикулярных
ось или три взаимно перпендикулярные плоскости; Из-за уплощения
геоэллипсоида местное отвесное отклонение от геоцентрического относительно
расстоянию от экватора и полюсов и длине геофракционной
меридиональная линия будет меняться по длине в зависимости от широты, увеличиваясь к
полюс. На любой конкретной широте географическая и геодезическая широта
значения больше, чем эквивалентная геоцентрическая широта. Географический
Широта также называется астрономической
Широта.
Из-за уплощения
геоэллипсоида местное отвесное отклонение от геоцентрического относительно
расстоянию от экватора и полюсов и длине геофракционной
меридиональная линия будет меняться по длине в зависимости от широты, увеличиваясь к
полюс. На любой конкретной широте географическая и геодезическая широта
значения больше, чем эквивалентная геоцентрическая широта. Географический
Широта также называется астрономической
Широта.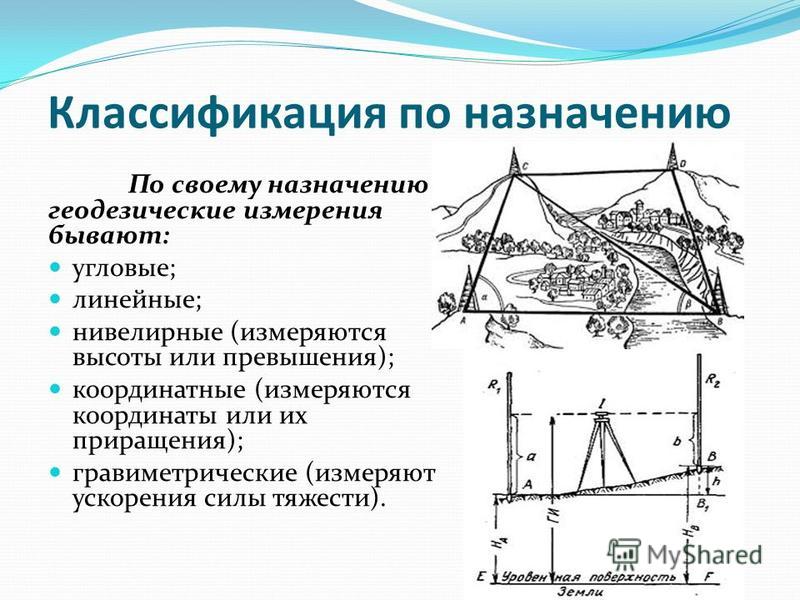 Механическая эллиптичность Земли
(динамическое уплощение) определяется наблюдением и отличается от
геометрическая, потому что земля не имеет однородной плотности. 1967
Геодезическая система отсчета установила большую полуось 6 378 160 м и
1 : 298,247 уплощение. Геодезическая система отсчета 1980 г.
6 378 137 м по большой полуоси и 1 : 298,257 уплощения. Эта система
был принят на XVII Генеральной Ассамблее Международного Союза
геодезии и геофизики (IUGG). Геодезическая система отсчета 1980 г.
система используется для данных Рисунок Земли
следовать ниже. Многочисленные другие системы использовались в разных странах.
для их карт и диаграмм. 1979 Международный астрономический союз (МАС)
значения равны 6 378 140 м и 1 : 298,257. Всемирная геодезическая система (WGS84),
используются GPS, значения составляют 6 378 137,0 м и 1: 298,257223563 (6 356 752,3141
м).
Механическая эллиптичность Земли
(динамическое уплощение) определяется наблюдением и отличается от
геометрическая, потому что земля не имеет однородной плотности. 1967
Геодезическая система отсчета установила большую полуось 6 378 160 м и
1 : 298,247 уплощение. Геодезическая система отсчета 1980 г.
6 378 137 м по большой полуоси и 1 : 298,257 уплощения. Эта система
был принят на XVII Генеральной Ассамблее Международного Союза
геодезии и геофизики (IUGG). Геодезическая система отсчета 1980 г.
система используется для данных Рисунок Земли
следовать ниже. Многочисленные другие системы использовались в разных странах.
для их карт и диаграмм. 1979 Международный астрономический союз (МАС)
значения равны 6 378 140 м и 1 : 298,257. Всемирная геодезическая система (WGS84),
используются GPS, значения составляют 6 378 137,0 м и 1: 298,257223563 (6 356 752,3141
м). Когда
эллипсоид вращения (большая полуось a, малая полуось b)
определено, его можно сделать эквипотенциальной поверхностью нормального гравитационного потенциала,
определяется с помощью эллипсоидальной поверхности, заключенной массы и
угловая скорость (независимо от распределения внутренней плотности).
Эквипотенциальный эллипсоид обеспечивает простую, непротиворечивую и однородную
система отсчета для всех целей геодезии и не вычисляет
атмосфера.
Когда
эллипсоид вращения (большая полуось a, малая полуось b)
определено, его можно сделать эквипотенциальной поверхностью нормального гравитационного потенциала,
определяется с помощью эллипсоидальной поверхности, заключенной массы и
угловая скорость (независимо от распределения внутренней плотности).
Эквипотенциальный эллипсоид обеспечивает простую, непротиворечивую и однородную
система отсчета для всех целей геодезии и не вычисляет
атмосфера. Период прецессии в настоящее время около
25 780 лет. Поскольку Земля вращается, крутящий момент не может измениться
наклон оси относительно эклиптики. Вместо этого угол
витков, вписывая конус в фиксированное пространство перпендикулярно плоскости
крутящий момент (эклиптика). Юлианская дата 2000,0 Скорость общей прецессии
до 2003 г. определялся как 5029″0,0906 по юлиану
Столетие, затем скорректированное до 5028″.797. Измененная во времени скорость была
ранее определяемый в тропических веках (T) с 1900 г. как 1 / (0,0000387858796397
+ (0,0000000171682098765*T)) лет.
Период прецессии в настоящее время около
25 780 лет. Поскольку Земля вращается, крутящий момент не может измениться
наклон оси относительно эклиптики. Вместо этого угол
витков, вписывая конус в фиксированное пространство перпендикулярно плоскости
крутящий момент (эклиптика). Юлианская дата 2000,0 Скорость общей прецессии
до 2003 г. определялся как 5029″0,0906 по юлиану
Столетие, затем скорректированное до 5028″.797. Измененная во времени скорость была
ранее определяемый в тропических веках (T) с 1900 г. как 1 / (0,0000387858796397
+ (0,0000000171682098765*T)) лет. Они предоставили параметры для четырех
возможные параметризации.
Термин «прецессия» имеет общее значение, охватывающее любое изменение
ось вращения, включая полярный блуждание, нутации и
Чендлер качается.
Они предоставили параметры для четырех
возможные параметризации.
Термин «прецессия» имеет общее значение, охватывающее любое изменение
ось вращения, включая полярный блуждание, нутации и
Чендлер качается. Пять станций на широте около 39,1333 ° северной широты начала широты
наблюдения в 1899 году. Общепринятое международное происхождение
определяется как среднее положение мгновенного полюса в течение
период 1900-1905 гг. Вечное полярное движение
дрейф положения полюса, как полагают, произошел из-за тектонического движения.
Сезонное полярное движение — это флуктуация
с годовым периодом со значительными колебаниями амплитуды в пределах
от 1°.111 х 10 -5 до 3°.333 x 10 -5 (от 1,3 до 3,7 м).
Пять станций на широте около 39,1333 ° северной широты начала широты
наблюдения в 1899 году. Общепринятое международное происхождение
определяется как среднее положение мгновенного полюса в течение
период 1900-1905 гг. Вечное полярное движение
дрейф положения полюса, как полагают, произошел из-за тектонического движения.
Сезонное полярное движение — это флуктуация
с годовым периодом со значительными колебаниями амплитуды в пределах
от 1°.111 х 10 -5 до 3°.333 x 10 -5 (от 1,3 до 3,7 м).


 Время (TCG), 4) начало системы, чтобы быть геоцентром масс Земли
включая океаны и атмосферу, и, 5) система не имеет глобального остаточного вращения
по отношению к горизонтальным движениям земной поверхности.
Время (TCG), 4) начало системы, чтобы быть геоцентром масс Земли
включая океаны и атмосферу, и, 5) система не имеет глобального остаточного вращения
по отношению к горизонтальным движениям земной поверхности. Земля имеет форму, близкую к сплюснутому сфероиду,
эллипс в поперечном сечении. Ось вращения дает геодезические полюса.
Плоскость вращения большой оси – экватор. Направление
геодезическая вертикаль – это локальная внешняя нормаль к поверхности эллипса и
не зависит от числовых параметров эллипса.
Земля имеет форму, близкую к сплюснутому сфероиду,
эллипс в поперечном сечении. Ось вращения дает геодезические полюса.
Плоскость вращения большой оси – экватор. Направление
геодезическая вертикаль – это локальная внешняя нормаль к поверхности эллипса и
не зависит от числовых параметров эллипса.
 в
в  — Это
на основе эллипсоида Кларка 1880 г. длиной 6 378 236 м.
— Это
на основе эллипсоида Кларка 1880 г. длиной 6 378 236 м. мех., 94; 351-367. J2000.0
годовая ставка 0,0000388024397761°)
мех., 94; 351-367. J2000.0
годовая ставка 0,0000388024397761°) физические и культурные географические особенности в Соединенных Штатах.
Распознанные имена идентифицируются, а местоположение объекта по штатам,
уезд и географические координаты.
физические и культурные географические особенности в Соединенных Штатах.
Распознанные имена идентифицируются, а местоположение объекта по штатам,
уезд и географические координаты.