1.4. Систематические погрешности
Систематическая погрешность измерения – это составляющая погрешности результата измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же ФВ. В зависимости от характера изменения систематические погрешности подразделяются на постоянные, прогрессивные и погрешности, изменяющиеся по более сложным законам, например, периодические.
Постоянные систематические погрешности в течение длительного времени сохраняют свое значение, например, в течение заданного временного интервала. Они встречаются наиболее часто. Например, погрешность, возникающая из-за того, что вольтамперная характеристика детектора считается квадратичной во всем диапазоне входных напряжений, в то время как показатель степени зависит от амплитуды входного напряжения.
Прогрессивные погрешности
 Например, погрешности,
связанные с систематическим износом
узлов средства измерений, с прогревом
измерительных приборов и т.п. Простейший
бытовой пример – это определение
момента времени при помощи часов с
постоянной систематической погрешностью
хода. В этом случае с каждым днем
погрешность определения времени
возрастает.
Например, погрешности,
связанные с систематическим износом
узлов средства измерений, с прогревом
измерительных приборов и т.п. Простейший
бытовой пример – это определение
момента времени при помощи часов с
постоянной систематической погрешностью
хода. В этом случае с каждым днем
погрешность определения времени
возрастает.Периодические погрешности чаще всего проявляются при наличии внешних циклических воздействий или при измерении циклических величин (измерения разности фаз синусоидальных колебаний). Простейший пример – башенные часы с люфтом стрелок. Очевидно, что под воздействием силы тяжести, действующей на стрелки, при наличии люфта возникает периодическая систематическая погрешность отсчета времени. Другой пример – измерение распределения поля в раскрыве антенны. При движении зонда и измерении при его помощи интенсивности поля возникает периодическая интерференционная погрешность, обусловленная переотражением сигнала между антенной и зондом.
В
зависимости от причин появления
систематические погрешности подразделяют
на погрешности метода измерений
(методические), погрешности из-за
отклонений внешних условий от
установленных, инструментальные
погрешности (погрешности средства
измерений), субъективные погрешности.
По
возможностям учета и исключения
(уменьшения) систематические погрешности
разделяют на три группы. Первая группа
– это погрешности, природа которых
известна и численное значение также
известно. В этом случае в результат
измерения обычно можно внести поправку. Поправка –
это значение ФВ, одноименной с измеряемой,
вводимое в неисправленный результат
измерения с целью исключения одной из
систематических составляющих погрешности.
Например, при измерении мощности и
энергии оптического квантового генератора
(лазера) приемником излучения (например,
фотодиодом) часть энергии, падающей на
вход приемника, отражается. Измерив
коэффициент отражения приемника, можно
ввести поправку на значение отраженной
энергии и учесть таким способом
составляющую систематической погрешности
из-за отражения. Поправка равна абсолютной
систематической погрешности с обратным
знаком. Другой способ исправления
результата измерений – это умножение
результата измерения на поправочный
множитель.
– имеются априорные сведения об объекте измерения, принципе и методе измерения, средстве измерения, достаточные для построения модели;
– проведен теоретический расчет составляющих систематической погрешности на модели и определены численные значения поправок;
– проведены эксперименты по определению численных значений поправок (поправочных множителей).
Вторую
группу систематических погрешностей
составляют такие, природа которых
известна, однако их значение и (или) знак
неизвестны, так что поправка не может
быть введена. Эти погрешности называют
неисключенными систематическими. Они
остаются неисключенными до тех пор,
пока не придуманы и не реализованы
способы их учета, то есть пока не выполнены
необходимые процедуры, перечисленные
выше. Указывают обычно границы
неисключенной систематической погрешности
как значение суммы всех отдельных ее
составляющих.
Эти погрешности называют
неисключенными систематическими. Они
остаются неисключенными до тех пор,
пока не придуманы и не реализованы
способы их учета, то есть пока не выполнены
необходимые процедуры, перечисленные
выше. Указывают обычно границы
неисключенной систематической погрешности
как значение суммы всех отдельных ее
составляющих.
Третью группу составляют систематические погрешности, природа которых неизвестна, то есть мы не подозреваем об их существовании в силу ограниченности наших знаний о процессах, происходящих в измерительных средствах, о характере взаимодействия средства измерений и объекта измерений.
Изучение
и исключение систематических погрешностей
измерения является одной из наиболее
сложных научных задач при измерениях,
поскольку требует глубокого понимания
не только принципа работы средств
измерений, но и физических явлений,
происходящих в объекте измерения, а
также при взаимодействии объекта и
средства измерений. Поэтому весьма
желательный перевод систематических
погрешностей из третьей группы в первую
сопряжен с постоянной инженерной и
исследовательской творческой работой.
ГОСТ 8.381-80 Государственная система обеспечения единства измерений. Эталоны. Способы выражения погрешностей / ГСИ ГСОЕИ / 8 381 80
ГОСТ 8.381-80
(СТ СЭВ 403-76)
Группа Т80
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ
ЕДИНСТВА ИЗМЕРЕНИЙ
ЭТАЛОНЫ
Способы выражения погрешностей
State system for ensuring the uniformity of measurements.
Standards. The ways of expressing the errors
Дата введения 1981-01-01
РАЗРАБОТАН Государственным комитетом СССР по стандартам
ИСПОЛНИТЕЛИ
М.Н.Селиванов, канд. техн. наук; Б.Ф.Лосев, канд. техн. наук
ВНЕСЕН Государственным комитетом СССР по стандартам
Член Госстандарта Л.К.Исаев
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ постановлением Государственного комитета СССР по стандартам от 13 мая 1980 г.
ВНЕСЕНА поправка, опубликованная в ИУС N 3, 1981 год
Поправка внесена изготовителем базы данных
Настоящий стандарт распространяется на эталоны СЭВ, государственные первичные (специальные) и вторичные эталоны и устанавливает способы выражения их погрешностей в нормативно-технической документации в области метрологии.
Стандарт соответствует СТ СЭВ 403-76 в части установления общих положений, способов выражения погрешностей эталонов и обозначений (см. справочное приложение 5).
1.1. Погрешность эталонов СЭВ и государственных первичных (специальных) эталонов (далее – первичных эталонов) характеризуется:
неисключенной систематической погрешностью;случайной погрешностью;
нестабильностью.
Допускается указывать случайную погрешность воспроизведения единицы с учетом передачи ее размера или последнюю указывать отдельно.
1.2. Оценку неисключенной систематической погрешности первичного эталона находят на основании экспериментальных данных исследований эталона, анализа погрешностей метода воспроизведения единицы и погрешностей от действия влияющих величин, а также на основании международных сличений эталона с эталонами других стран и с эталоном СЭВ, если он имеется.
1.3. Оценку случайной погрешности первичного эталона находят на основании экспериментальных данных, полученных при исследовании эталона, и на основе анализа влияющих величин.
1.5. В оценку погрешности передачи размера единицы должны входить как неисключенные систематические, так и случайные погрешности метода и средств передачи.
1. 6. Оценки погрешности вторичных эталонов должны характеризовать отклонения размеров хранимых ими единиц от размера единицы, воспроизводимой при помощи первичного эталона.
6. Оценки погрешности вторичных эталонов должны характеризовать отклонения размеров хранимых ими единиц от размера единицы, воспроизводимой при помощи первичного эталона.
Для вторичного эталона указывают суммарную погрешность, включающую случайные погрешности сличаемых эталонов и погрешность передачи размера единицы от первичного (или более точного вторичного) эталона, а также нестабильность вторичного эталона.
Допускается суммарную погрешность вторичного эталона определять с учетом его неисключенной систематической погрешности.
Допускается указывать отдельно неисключенную систематическую погрешность вторичного эталона, а также его нестабильность.
По требованию заказчика могут быть указаны отдельно и другие составляющие погрешности вторичного эталона.
1.7. Нестабильность вторичного эталона должна определяться на основании сличений с первичным эталоном в начале и конце периода, для которого она определяется.
1.8. Оценку погрешности эталонов следует указывать либо в абсолютной форме в единицах измеряемой величины, либо в относительной форме.
Примечание. Если зависимость погрешности от значения воспроизводимой величины сложнее, чем линейная, погрешность может быть указана в виде таблицы по выбранным диапазонам (в абсолютной или относительной форме) или в виде функции зависимости этой погрешности.
1.9. Определения нестандартизованных терминов, употребляемых в данном стандарте, приведены в справочном приложении 1.
Примеры формул для вычисления погрешностей приведены в справочном приложении 2. Обозначения погрешностей приведены в справочном приложении 3. Примеры вычисления погрешностей приведены в справочном приложении 4.
2.1. Неисключенная систематическая погрешность (НСП) первичного эталона, лежащая в границах ±, характеризуется границей без указания знака.
2.2. Случайная погрешность характеризуется средним квадратическим отклонением (СКО) результата измерений при воспроизведении единицы (или при воспроизведении единицы и передаче ее размера) с указанием числа независимых наблюдений.
2.3. Нестабильность эталона следует характеризовать изменением размера единицы за определенный промежуток времени, который указывается.
2.4. Погрешность передачи размера единицы характеризуют указанием среднего квадратического отклонения результата измерений , обусловленного влиянием случайных и неисключенных систематических погрешностей метода и средств измерений, примененных при передаче размера единицы.
3.1. Суммарная погрешность вторичного эталона характеризуется средним квадратическим отклонением результата измерений () при его сличении с первичным эталоном или вышестоящим по поверочной схеме вторичным эталоном или же в виде доверительной границы погрешности с доверительной вероятностью 0,99.
При учете неисключенной систематической погрешности через следует выражать среднее квадратическое отклонение суммы неисключенных систематических и случайных погрешностей эталона.
Если неисключенную систематическую погрешность и нестабильность вторичного эталона указывают отдельно, то их выражают в виде, принятом для первичного эталона (пп.2.1, 2.3).
ПРИЛОЖЕНИЕ 1
Справочное
Термин |
Определение |
|
|
2. Нестабильность эталона |
Изменение размера единицы, воспроизводимой или хранимой эталоном, в установленный промежуток времени |
3. |
Погрешность результата измерений, выполняемых при воспроизведении единицы |
4. Погрешность передачи размера единицы |
Погрешность результата измерений, выполняемых при передаче размера единицы |
5. Неисключенная систематическая погрешность |
Систематическая погрешность, оставшаяся после введения поправки |
6. Оценка погрешности средства измерений |
Погрешность данного средства измерений, полученная из ограниченного числа данных |
ПРИЛОЖЕНИЕ 2
Справочное
Доверительную вероятность при определении доверительных границ погрешности эталона (как для случайной, так и для неисключенной систематической) принимают равной 0,99.
1. Границу неисключенной систематической погрешности эталона вычисляют по формуле
. (1)
При числе слагаемых
, (2)
где – граница -й составляющей неисключенной систематической погрешности эталона;
– коэффициент зависимости неисключенных систематических погрешностей от выбранной доверительной вероятности при их равномерном распределении при доверительной вероятности 0,99 =1,4.
2. Среднее квадратическое отклонение результата прямых измерений с многократными наблюдениями выражают по формуле
, (3)
где – среднее квадратическое отклонение результата наблюдений, вычисляемое по формуле
, (4)
где
;
– число наблюдений;
– результат -го наблюдения;
– результат измерений, вычисленный как среднее арифметическое результатов наблюдений.
Примечание. При многократных наблюдениях должна быть обеспечена практическая независимость отдельных наблюдений.
3. Среднее квадратическое отклонение результата косвенных измерений величины, являющейся функцией
вычисляют по формуле
, (5)
где – средние квадратические отклонения результатов измерений величин .
4. Границу неисключенной систематической погрешности при косвенном измерении в зависимости от числа слагаемых вычисляют по формулам (1) или (2), в которых
, (6)
где – неисключенная систематическая погрешность измерения величины .
5. Среднее .квадратическое отклонение суммы неисключенных систематических и случайных погрешностей вычисляют по формуле
, (7)
где – среднее квадратическое отклонение суммы неисключенных систематических погрешностей.
6. При определении доверительной границы погрешности вторичного эталона коэффициент вычисляют по формуле
, (8)
где – коэффициент для нахождения доверительных границ погрешности результата измерений.
7. Погрешность передачи размера единицы состоит из суммы случайных и неисключенных систематических погрешностей метода и средств измерений, применяемых для передачи размера единицы. Оценку суммы неисключенных систематических и случайных погрешностей указывают в виде среднего квадратического отклонения , которое вычисляют по формуле
, (9)
где – среднее квадратическое отклонение случайной погрешности метода и средства передачи размера единицы;
– среднее квадратическое отклонение неисключенной систематической погрешности метода и средств передачи размера единицы.
ПРИЛОЖЕНИЕ 3
Справочное
, – граница -й составляющей неисключенной систематической погрешности эталона в абсолютной и относительной форме
, – граница неисключенной систематической погрешности эталона в абсолютной и относительной форме
– результат -го наблюдения
– результат измерений
, – среднее квадратическое отклонение -го результата наблюдения в абсолютной и относительной форме
, – среднее квадратическое отклонение результата измерения в абсолютной и относительной форме
– среднее квадратическое отклонение суммы неисключенных систематических погрешностей, рассматриваемых как случайные величины
– среднее квадратическое отклонение суммы случайных погрешностей (или суммы случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины)
– коэффициент для нахождения доверительных границ погрешности результата измерения
– доверительная граница случайной погрешности результата измерений
– коэффициент для нахождения доверительных границ суммы случайных погрешностей и неисключенных систематических погрешностей
– доверительная граница суммы случайных погрешностей (или суммы случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины)
– коэффициент для нахождения границ неисключенных систематических погрешностей
– нестабильность эталона
– среднее квадратическое отклонение результата измерений при передаче размера единицы от первичного эталона вторичному эталону
– среднее квадратическое отклонение случайной погрешности средства и метода передачи размера единицы
– граница неисключенной систематической погрешности средства и метода передачи размера единицы
– доверительная вероятность
ПРИЛОЖЕНИЕ 4
Справочное
Погрешности рабочего эталона единицы длины – штрихового метра при сличении с первичным эталоном интерференционным методом определены на основании десяти наблюдений (n=10):
1. Результат измерений =1 м+1,47 мкм.
Результат измерений =1 м+1,47 мкм.
2. Среднее квадратическое отклонение результата измерений при сличении рабочего эталона с первичным =0,023 мкм.
Вычислены неисключенные систематические погрешности:
из-за неточного определения показателя преломления воздуха = 0,030 мкм
из-за неточного значения длин волн = 0,016 мкм
из-за неточного значения температуры = 0,026 мкм
из-за неточного определения поправок на размер коллиматорной щели = 0,002 мкм
Требуется определить доверительные границы суммарной погрешности рабочего эталона.
Решение: 1. По формуле (2) определяют границы неисключенных систематических погрешностей
мкм.
= 0,06 мкм; = 0,99. Принимается, что составляющие имеют равномерное распределение =4.
Принимается, что составляющие имеют равномерное распределение =4.
2. По формуле (7) вычисляют среднее квадратическое отклонение суммы неисключенных систематических и случайных погрешностей
мкм.
3. Вычисляют доверительные границы суммарной погрешности , полагая распределение случайных погрешностей нормальным. Для этого предварительно вычисляют коэффициент по формуле (8), выбрав из таблиц Стъюдента =3,25 (=0,99; =10):
.
Доверительные границы суммарной погрешности:
= ±2,81 · 0,034 мкм = ±0,096 мкм ±0,10 мкм.
4. Из исследований платино-иридиевой штриховой меры (рабочий эталон) за ряд лет установлено, что его максимальная нестабильность не превышает 0,10 мкм в год, т.e. =0,10 мкм/гoд.
Следовательно, результат измерений, полученный из 10 наблюдений, равен 1 м+1,47 мкм. При этом суммарная погрешность, состоящая из неисключенных систематических погрешностей при равномерном распределении и случайной погрешности при нормальном распределении и доверительной вероятности 0,99 составляет ±0,10 мкм.
При этом суммарная погрешность, состоящая из неисключенных систематических погрешностей при равномерном распределении и случайной погрешности при нормальном распределении и доверительной вероятности 0,99 составляет ±0,10 мкм.
Форма представления результата может быть следующей:
= 1 м + 1,47 мкм;
= ±0,10 мкм при =0,99, нормальной =10 и равномерном распределении =4.
Нестабильность эталона =0,10 мкм/год.
ПРИЛОЖЕНИЕ 5
Справочное
1. Разд. 1, 2, 3 ГОСТ 8.381-80 соответствуют разд.1, 2, 3 СТ СЭВ 403-76.
2. Справочное приложение 1 ГОСТ 8.381-80 соответствует пп.6, 8, 9 информационного приложения 1 СТ СЭВ 403-76.
3. Справочные приложения 2, 3, 4 ГОСТ 8.381-80 соответствуют информационным приложениям 2, 3, 4 СТ СЭВ 403-76.
Классификация погрешностей • Метрология и стандартизация
Погрешности измерения классифицируются:
1) По способу выражения
– абсолютные
– относительные
2) По источнику возникновения
– инструментальные – составляющая погрешности, которая зависит от свойств СИТ (класс точности, цена деления и т. д.). Этот вид погрешности легко предсказуем и заранее просчитываемый, и как следствие можно его учесть при помощи ввода поправок, либо другим способом.
д.). Этот вид погрешности легко предсказуем и заранее просчитываемый, и как следствие можно его учесть при помощи ввода поправок, либо другим способом.
– методические – составляющая общей погрешности измерения, которая обусловлена несовершенством метода измерения. Так, например, при измерении сопротивления на участке цепи при помощи омметра, величина измеренного сопротивления будет иметь методическую погрешность, за счет входного сопротивления самого омметра.
– личные, или субъективные – погрешность оператора
3) По закономерностям возникновения и проявления
– ситематические – составляющие общей погрешности измерения, которая остается постоянной, либо закономерно изменяется при повторных измерениях одной и той же величины. Систематическую погрешность можно учесть при большом количестве повторный измерений (?50) одной величины, произведенных при одинаковых условиях. Существует много методов снизить систематическую погрешность, если это нужно.
– случайные – составляющая общей погрешности измерения, которая изменяется случайным образом как по величине и по знаку при повторных измерениях одной и той же величины.
Причины возникновения случайных погрешностей могут быть самые различные: конструктивные недостатки и неточности приборов, случайные внешние колебания случайных величин (к примеру, колебания температуры окружающей среды), ошибки оператора, шумы, вибрации, нестабильность питания приборов, внешние колебания электро – магнитных полей и много др. Учесть появление случайных погрешностей невозможно, но они (согласно теории вероятностей) имеют пару очень полезных особенностей:
а) чаще возникают маленькие случайные погрешности, чем большие
б) одинаково часто возникают одинаковые по модулю, но противоположные по знаку случайные погрешности
Из этих свойств можно сделать вывод, что при количестве измерений n?? случайную погрешность можно исключить:
– среднее арифметическое всех результатов измерений
однако, поскольку не возможно чтобы количество измерений было бесконечным, то при большом количестве измерений
– грубая погрешность – это погрешность, которая существенно превышает ожидаемую в данных условиях погрешность.
Причинами возникновения грубой погрешности может быть:
– скрытый метрологический отказ прибора (или эталона, или прибора, при помощи которого производится измерение) – именно с целью выявления скрытых метрологических отказов приборов производятся периодические поверки и калибровки (об этом также говорится и в п.5.9 ДСТУ ISO/IEC 17025:2006)
– ошибка оператора
– резкое внезапное изменение внешних факторов.
Результаты измерений, которые получены с грубой погрешностью называются промахом, и должны быть исключены из результатов измерений.
СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ ХИМИЧЕСКОГО АНАЛИЗА – Справочник химика 21
ОЦЕНКА ЗНАЧИМОСТИ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ ХИМИЧЕСКОГО АНАЛИЗА. [c.110]
В целях последовательного устранения систематических погрешностей химического анализа удобно рассмотреть их в рамках следующей классификации [c.37]
Классификация погрешностей на систематические, случайные и грубые (промахи) с указанием некоторых причин их возникновения дана в разделе 1. 5. Инструментальные ошибки в химическом анализе связаны с точностью взвешивания на аналитических весах и точностью измерения объемов мерной посудой. Методические ошибки обусловлены особенностями реакции, лежащей в основе метода, и неправильно составленной методикой анализа. В терминах теории информации случайные погрешности соответствуют шумам в канале передачи информации, систематические погрешности — помехам, а грубые — нарушениям канала связи. [c.129]
5. Инструментальные ошибки в химическом анализе связаны с точностью взвешивания на аналитических весах и точностью измерения объемов мерной посудой. Методические ошибки обусловлены особенностями реакции, лежащей в основе метода, и неправильно составленной методикой анализа. В терминах теории информации случайные погрешности соответствуют шумам в канале передачи информации, систематические погрешности — помехам, а грубые — нарушениям канала связи. [c.129]
СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ ХИМИЧЕСКОГО АНАЛИЗА [c.30]
Сопоставим погрешности разной природы с основными метрологическими характеристиками воспроизводимостью и правильностью результатов анализа. Отсутствие в Химическом анализе систематических погрешностей обеспечивает его правильность. Кучность отдельных результатов, степень их. близости к среднему значению характеризует воспроизводимость анализа. Воспроизводимость-характеристика случайных погрешностей химического анализа. Ее численной мерой является абсолютное 3 или относительное Зг стандартное отклонение, вычисляемое из результатов нескольких параллельных определений. Количественной оценкой систематической погрешности анализа или правильности служит разность между средним арифметическим результата многократных анализов и истинным значением определяемой величины [c.31]
Количественной оценкой систематической погрешности анализа или правильности служит разность между средним арифметическим результата многократных анализов и истинным значением определяемой величины [c.31]
Методическая ошибка — одна из наиболее трудно поддающихся учету систематических погрешностей химического анализа, которая складывается из погрешностей отдельных химических операций. Ни процессы разложения, ни процессы синтеза химических соединений, равно как и процессы разделения компонентов, которые всегда связаны с образованием новых фаз, никогда не проходят до конца. Стремление любой физико-химической системы к максимуму энтропии и минимуму энергии Гиббса всегда как бы- противодействует стремлению аналитика-экспериментатора выделить полностью определяемый компонент и нацело превратить его в аналитически активное соединение. По той же причине даже условие практической полноты образования и выделения соединений определяемого компонента никогда не гарантирует его чистоты от примесей других компонентов. [c.46]
[c.46]
К систематическим ошибкам И типа относятся инструментальная, реактивная, методическая ошибки (включая индикаторную), эталонная ошибка и некоторые другие. Инструментальная ошибка. Каждый прибор, используемый для измерения, вносит в результаты измерения погрешности, часть из кото рых имеет характер случайных, а часть — систематических ошибок. Поскольку случайные ошибки рассматриваются и учитываются в совокупности, имеет смысл попытаться вычленить систематическую составляющую инструментальной ошибки химического анализа. Систематический характер носят ошибки калибровки приборов. Так, например, истинный объем мерной посуды (бюреток, пипеток, мерных колб) никогда в точности не соответствует номиналу, указанному на заводском клейме или в паспорте. Разница между истинным значением и номиналом тем меньше, чем выше класс точности измерительного прибора и обычно не превышает цены наименьшего деления на измерительной шкале.
 В частности, каждый конкретный экземпляр мерной посуды содержит свою персональную систематическую ошибку, завышающую или занижающую измеряемый объем в сравнении с номиналом. Для того чтобы оценить величину этой ошибки, следует провести калибровку посуды — найти достаточно точный вес точно отмеренного объема чистой жидкости (например, дистиллированной воды), а затем вычислить объем, используя точное справочное значение плотности жидкости при заданной температуре рн[c.25]
В частности, каждый конкретный экземпляр мерной посуды содержит свою персональную систематическую ошибку, завышающую или занижающую измеряемый объем в сравнении с номиналом. Для того чтобы оценить величину этой ошибки, следует провести калибровку посуды — найти достаточно точный вес точно отмеренного объема чистой жидкости (например, дистиллированной воды), а затем вычислить объем, используя точное справочное значение плотности жидкости при заданной температуре рн[c.25] Закон нормального распределения Гаусса. Определяя понятие случайных погрещностей химического анализа, мы подчеркивали, что в отличие от систематических погрещностей они не имеют видимых причин. Точнее говоря, ввиду многочисленности отдельных случайных погрешностей и ничтожных значений каждой из них химик-аналитик сознательно отказывается от выяснения их причин и оценки значений. Ценой этого отказа он получает право изучать и описывать общую случайную погрешность и оценивать результаты анализа методами математической статистики, рассматривая их как случайные величины. Аналогичным образом поступает исследователь-физик, который ценой отказа от измерения скоростей и направления движения отдельных молекул газа приобретает возможность статистического описания огромного макроскопического ансамбля молекул —газа как физического тела с помощью усредненных параметров температуры, давления, теплоемкости, энтропии и т. д. [c.77]
Аналогичным образом поступает исследователь-физик, который ценой отказа от измерения скоростей и направления движения отдельных молекул газа приобретает возможность статистического описания огромного макроскопического ансамбля молекул —газа как физического тела с помощью усредненных параметров температуры, давления, теплоемкости, энтропии и т. д. [c.77]
При обработке результатов химического анализа систематические погрешности должны быть выявлены и устранены или, по возможности, оценены. [c.64]
Оценка результатов измерения, следовательно, и результатов анализа — заключительная аналитическая стадия. Ее осуществляют, рассчитывая случайные и систематические погрешности (ошибки). Установление химического состава вещества относится к метрологическим процедурам (метрология —наука об измерениях). Его особенность по сравнению с физическими измерениями заключается в том, что в аналитической химии измерение носит не прямой, а косвенный характер, так как измеряется не число химических частиц, а, например, их общая масса, физические параметры (свойства), расход реагента и т. д. Кроме того, в отличие от большинства физических величин, непосредственно не влияющих друг на друга, компоненты химической системы оказывают взаимное влияние, и часто очень сильное, что приводит к искажениям аналитических сигналов. Все это вызывает появление погрешностей при каждом аналитическом определении. [c.17]
д. Кроме того, в отличие от большинства физических величин, непосредственно не влияющих друг на друга, компоненты химической системы оказывают взаимное влияние, и часто очень сильное, что приводит к искажениям аналитических сигналов. Все это вызывает появление погрешностей при каждом аналитическом определении. [c.17]
Иными словами, информация о систематической погрешности химического анализа может быть получена лишь на фоне случайных погрешностей, а точность ее оценки в принципе не превышает точности оценок воспроизводимости анализа. Отсюда вытекает очевидный принцип уменьшение систематических погрешностей имеет смысл только в том случае, когда они больше или соизмеримы со случайными. Вместе с тем улучшение воспроизводимости, например за счет увеличения числа параллельных анализов, позволяет обнаруживать систематические погрешности, ранее недоступные для определения. [c.111]
К стандартным образцам предъявляется ряд требований. Наиболее важными для них являются следующие. Содержание эталонированных элементов в пределах регламентированных и указанных погрешностей не должно отличаться от истинного. Состав стандартного образца по некоторым компонентам удостоверяется официальным свидетельством (паспортом). При хранении в течение длительного времени состав стандартного образца не должен меняться. Он должен обладать высокой однородностью химического состава по всей массе, чтобы обеспечивать тождественность отбора проб для анализа, поэтому обычно изготовляется в виде монолитного образца, мелкой металлической стружки, порошка и т. д. Содержание эталонируемых элементов в стандартных образцах устанавливается с точностью, заведомо превышающей точность определения этих элементов в производственных образцах. Идеальные эталоны должны отличаться от проб лишь содержанием определяемого компонента. Это требование практически невыполнимо, поэтому обычно ограничиваются требованием, чтобы колебания в составе проб и эталонов не вызывали систематических погрешностей, превышающих случайные.
Содержание эталонированных элементов в пределах регламентированных и указанных погрешностей не должно отличаться от истинного. Состав стандартного образца по некоторым компонентам удостоверяется официальным свидетельством (паспортом). При хранении в течение длительного времени состав стандартного образца не должен меняться. Он должен обладать высокой однородностью химического состава по всей массе, чтобы обеспечивать тождественность отбора проб для анализа, поэтому обычно изготовляется в виде монолитного образца, мелкой металлической стружки, порошка и т. д. Содержание эталонируемых элементов в стандартных образцах устанавливается с точностью, заведомо превышающей точность определения этих элементов в производственных образцах. Идеальные эталоны должны отличаться от проб лишь содержанием определяемого компонента. Это требование практически невыполнимо, поэтому обычно ограничиваются требованием, чтобы колебания в составе проб и эталонов не вызывали систематических погрешностей, превышающих случайные. [c.124]
[c.124]
Систематические погрешности — это погрешности, вызываемые известными причинами, или причины которых можно установить при детальном рассмотрении процедуры химического анализа. Другими словами, причины систематических погрешностей значимы для аналитика. Каждая из систематических погрешностей анализа однозначна и постоянна по значению (при повторных анализах). Однако, поскольку систематические погрешности, как правило, не единичны, результат анализа может включать как положительную, так и отрицательную суммарную систематическую погрешность, причем значение ее может быть большим. [c.30]
В рассмотренных примерах причина систематических погрешностей заключалась в химических свойствах используемых в анализе соединений. В других случаях источником погрешностей является примесь посторонних веществ в растворах и в реагентах. Так, хлороводородная кислота нередко содержит примеси железа (П1), При фотометрическом определении последнего в виде роданидного комплекса необходимо пользоваться только химически чистой кислотой, иначе железа будет найдено больше, чем его в действительности было в анализируемом материале. [c.56]
[c.56]
Если установлено, что тангенс угла наклона и свободный член незначимо отличаются от 1 и О соответственно, можно заключить, что систематические погрешности отсутствуют. Наличие пропорциональной систематической погрешности приведет к значимому отличию 61 от единицы, а наличие постоянной погрешности — к значимому отличию бо от нуля. Разумеется, оба этих типа погрешностей могут присутствовать и одновременно. Могут возникнуть и еще более сложные ситуации, особенно при анализе распределения вещества по химическим формам. [c.446]
Расчет и оценка надежности результатов анализа. Корректное решение задачи химического анализа, помимо основного результата, обязано содержать оценку надежности полученного результата с помощью статистического критерия — доверительного-интервала (интервал возможных вариаций искомой величины) при заданной надежности (доверительная вероятность). Кроме этого, необходимо указывать кратность (повторность) определений и характер оценки погрешности (погрешность в оценке единичного анализа, погрешность определения среднего значения, погрешность метода). И, наконец, если имеется возможность объективной оценки систематической погрешности (см. гл. П), необходимо оценить правильность выполненного анализа. [c.21]
И, наконец, если имеется возможность объективной оценки систематической погрешности (см. гл. П), необходимо оценить правильность выполненного анализа. [c.21]
Погрешности химических эталонов и стандартных образцов кроются не только в несоответствии истинного и номинального содержаний компонента, но и в неполной химической идентичности стандартного и анализируемого образцов, которая обусловлена большим или меньшим различием их химического состава и структуры. Несовпадение составов на различных этапах анализа приводит к различию условий выделения и определения искомого компонента и в конечном счете к систематической эталонной погрешности. Так, в методах эмиссионного спектрального анализа несовпадение химического состава эталона и образца приводит к разнице в условиях возбуждения компонента и разной степени затенения его аналитической спектральной линии на фотопластинке ближними линиями сопутствующих элементов. [c.54]
Физические и физико-химические методы анализа имеют в значительной степени общие виды погрешностей с химическими методами, так как включают такие операции, как взвешивание, измерение объема, разделение компонентов перед конечным определением, концентрирование и т. д., однако им присущи и собственные виды случайных и систематических погрешностей. Особенности погрешностей физических и физико-химических методов анализа определяются, с одной стороны, большим разнообразием природы используемых в них аналитических сигналов, а с другой — широким применением измерительной аппаратуры. Они будут рассмотрены во втором томе учебника. [c.107]
д., однако им присущи и собственные виды случайных и систематических погрешностей. Особенности погрешностей физических и физико-химических методов анализа определяются, с одной стороны, большим разнообразием природы используемых в них аналитических сигналов, а с другой — широким применением измерительной аппаратуры. Они будут рассмотрены во втором томе учебника. [c.107]
К началу обработки результатов химического анализа методами математической статистики систематические погрешности должны быть выявлены и устранены или переведены в разряд случайных. При этом данные анализа — случайные величины с определенным распределением вероятности. Прежде чем рассматривать оценку случайных погрешностей, остановимся на двух понятиях генеральная совокупность — гипотетическая совокупность всех мыслимых результатов от -да до + выборочная совокупность (выборка) — реальное число (л) результатов, которое имеет исследователь. [c.42]
Стандартное отклонение имеет ту же размерность что и х. Чаще других характеристик воспроизводимости используют относительное стандартное отклонение, выраженное в долях определяемой величины. Обычно при обработке данных химического анализа определяют также интервал, в кото-. ром при заданной вероятности (и при отсутствии систематических погрешностей) лежит истинное значение. Этот интервал можно рассчитать, пользуясь выражением (2.7), откуда [c.48]
Чаще других характеристик воспроизводимости используют относительное стандартное отклонение, выраженное в долях определяемой величины. Обычно при обработке данных химического анализа определяют также интервал, в кото-. ром при заданной вероятности (и при отсутствии систематических погрешностей) лежит истинное значение. Этот интервал можно рассчитать, пользуясь выражением (2.7), откуда [c.48]
Правильность — это качество химического анализа, отражающее близость к нулю систематической погрешности. Правильность характеризует отклонение полученного результата анализа от истинного значения измеряемой величины (см. рис. 9.2). [c.268]
К началу обработки результатов химического анализа методами математической статистики систематические погрешности должны быть выявлены и устранены или переведены в разряд случайных. При этом данные анализа — случайные величины с определенным распределением вероятности. [c.268]
Перед расчетом основных метрологических характеристик результата химического анализа методами математической статистики систематические погрешности должны [c. 66]
66]
Полученное значение /р сравнивают с теоретическим значением и (см. табл. 5.2) для выбранного уровня доверительной вероятности Р. Если 1 расхождение между и Х-2 вызвано случайными погрешностями, обусловленными воспроизводимостью при условиях сравниваемых выборок и, следовательно, систематическая погрешность отсутствует. Если необходимо оценить отклонение X от теоретического содержания ц (анализ химически чистого вещества или стандартного образца), то вычисление /р упрощается [c.99]
Методом выявления основных источников систематических погрешностей хроматографического анализа является изучение физической модели МКХА, включающее как экспериментальные исследования, так и расчетные оценки. Как правило, методика состоит из ряда операций, таких, как поглощение определяемых компонентов в различных ловушках и их последующее выделение, экстракция, проведение химических реакций, концентрирование и др., и лишь как заключительный этап — хроматографическое разделение, детектирование и измерение аналитического сигнала. [c.433]
[c.433]
При анализе сложных образцов, содержащих преимущественно соединения близкой химической природы, допускается принимать все значения равными единице, что приводит, однако, к некоторому снижению точности анализа за счет возрастания вклада систематической погрешности. Наиболее распространенный способ экспериментального определения /, состоит в хроматографическом анализе серии искусственных смесей необходимых компонентов с выбранным стандартным веществом и последующем расчете по формуле [c.97]
Объективное условие возможности исключения значительной систематической погрешности в методе газовой хроматографии следующее компоненты смеси перед количественным определением в детекторе должны быть полностью разделены в хроматографической колонке, тогда взаимное влияние компонентов смеси, являющееся, как известно, одним из основных источников систематической погрешности в физико-химических методах анализа, в принципе, может быть исключено. При выполнении этого условия источником систематических погрешностей является в основном изменение чувствительности детектора. Контроль чувствительности можно проводить по чистым компонентам, поскольку как при контроле, так и при анализе детектор работает на бинарной смеси газа-носителя и чистого компонента. Сравнительная простота контроля позволяет сделать его регулярным, и тем самым практически исключить значительную по величине систематическую погрешность. [c.157]
При выполнении этого условия источником систематических погрешностей является в основном изменение чувствительности детектора. Контроль чувствительности можно проводить по чистым компонентам, поскольку как при контроле, так и при анализе детектор работает на бинарной смеси газа-носителя и чистого компонента. Сравнительная простота контроля позволяет сделать его регулярным, и тем самым практически исключить значительную по величине систематическую погрешность. [c.157]
Твердый носитель оказывает существенное влияние на количественные результаты хроматографического анализа. Как известно, в процессе газохроматографического разделения, за исключением специальных случаев применения методов аналитической реакционной газовой хроматографии [101], качественный и количественный состав анализируемой смеси должен оставаться постоянным. В противном случае корректная интерпретация результатов опыта резко усложняется, а часто становится вообще невозможной. Основной причиной изменения состава смеси, приводящей к систематическим погрешностям в анализе, является адсорбционная и каталитическая активность ТН. В результате необратимой или квазинеобратимой адсорбции некоторых компонентов анализируемой смеси на поверхности ТН, химических превращений хроматографируемых соединений или неподвижн1з1х жидких фаз (НЖФ) происходит резкое изменение состава смеси, что приводит к грубым погрешностям в результатах количественного анализа. В настоящей главе рассматриваются именно эти аспекты влияния ТН на результаты количественного анализа, хотя, вообще говоря, влияние ТН может проявляться и в асимметричности хроматографических зон и в понижении эффективности хроматографического разделения, что также влияет на получаемые результаты количественного анализа. [c.80]
В результате необратимой или квазинеобратимой адсорбции некоторых компонентов анализируемой смеси на поверхности ТН, химических превращений хроматографируемых соединений или неподвижн1з1х жидких фаз (НЖФ) происходит резкое изменение состава смеси, что приводит к грубым погрешностям в результатах количественного анализа. В настоящей главе рассматриваются именно эти аспекты влияния ТН на результаты количественного анализа, хотя, вообще говоря, влияние ТН может проявляться и в асимметричности хроматографических зон и в понижении эффективности хроматографического разделения, что также влияет на получаемые результаты количественного анализа. [c.80]
Химический и фазовый состав стандартов должен соответ-ствова1ь составу проб. Погрешность в содержании определяемого элемента в стандартах не должна быть больше 1/3—1/4 слу-чайпо11 погрешности применяемого. метода анализа. Так, если наз-работанный метод характеризуется относительным стандартным отклонением 5г 0,02, то систематическая погрешность за счет приготовления стандарта не должна превышать 0,005—0,007. Таким образом определяются требования к чистоте исходных веществ и к точности операций при приготовлении стандартов. Это особенно важно при определении малых содержаний примесей, например при анализе веществ высоко чистоты. [c.90]
Таким образом определяются требования к чистоте исходных веществ и к точности операций при приготовлении стандартов. Это особенно важно при определении малых содержаний примесей, например при анализе веществ высоко чистоты. [c.90]
В этом отношении воспроизводимость результатов гораздо важнее, чем сходимость, т. е. случайная погрешность результатов, полученных одним и тем же аналитиком в одной и той же лаборатории в серии параллельных измерений (см. разд. 2.4). Хорошая сходимость — теобходимое, ио не достаточное условие для полного контроля качества работы химической лаборатории. Международные соглашения, особенно в сфере торговли, требуют, чтобы результаты анализов не содержали систематической погрешности и ьюгли быть проверены вне зависимости от того, кем, где и когда оии ыли получены. Результат химического измерения должен представлять собой истинное утверждение, и должна существовать возможность доказательства его истинности (см. гл.З). [c.45]
Правильность анализа характеризуется систематическими погрешностями. Их выявление, учет и устранение осуществляются в рамках конкретных методов на основании детального анализа всех этапов и общей схемы аналитического определения при постановке специальных экспериментов с использованием стандартных образцов. Воспроизводимость результатов анализа — характеристика случайных погрешностей, теория которых (математическая статистика) к настоящему времени разработана достаточно полно. В приложении к задачам аналитической химии, химическим и инструментальным методам анализа систематический и детальный обзор применения методов и идей математической статистики можно найти в монографиях В. В. Налимова и К. Доерфеля, приводимых в перечне рекомендуемой литературы. В книге А. Н. Зайделя, выдержавшей четыре издания, в доступной и одновременно лаконичной форме рассмотрены узловые вопросы статистической оценки погрешностей измерения физических величин. [c.6]
Их выявление, учет и устранение осуществляются в рамках конкретных методов на основании детального анализа всех этапов и общей схемы аналитического определения при постановке специальных экспериментов с использованием стандартных образцов. Воспроизводимость результатов анализа — характеристика случайных погрешностей, теория которых (математическая статистика) к настоящему времени разработана достаточно полно. В приложении к задачам аналитической химии, химическим и инструментальным методам анализа систематический и детальный обзор применения методов и идей математической статистики можно найти в монографиях В. В. Налимова и К. Доерфеля, приводимых в перечне рекомендуемой литературы. В книге А. Н. Зайделя, выдержавшей четыре издания, в доступной и одновременно лаконичной форме рассмотрены узловые вопросы статистической оценки погрешностей измерения физических величин. [c.6]
По-видимому, есть основания считать, что реальные случаи химического анализа отягощены разнородными систематическими погрешностями, которые имеют черты обеих предельных разновидностей — коррелированных и некоррелированных погрешностей. Это позволяет считать, что в суммарной систематической погрешности анализа отдельные составляющие группируются по двум главным слагаемым. Исходя из этого, можно предположить, что между суммарной систематической погрешностью Ахс и истинным содержанием Хист, а также между средним результатом многократного (из п параллельных) анализа х и истинным содержанием Хист имеют место линейные зависимости [c.35]
Это позволяет считать, что в суммарной систематической погрешности анализа отдельные составляющие группируются по двум главным слагаемым. Исходя из этого, можно предположить, что между суммарной систематической погрешностью Ахс и истинным содержанием Хист, а также между средним результатом многократного (из п параллельных) анализа х и истинным содержанием Хист имеют место линейные зависимости [c.35]
При обработке результатов химического анализа систематические погрешности должны быть выявлены и устранены или, по крайней мере, охге-нены. Один из способов выявления систематической погрешности (проверка правильности) — варьирование величины пробы. Удваивая (способ удвоения) или увеличивая размер пробы в кратное число раз, можно обнаружить по изменению найденного содержания определяемого компонента (см. рис. 2.6) постоянную систематическую погрешность. [c.38]
Чтобы найти причину и источник таких погрешностей, следует кропотливо и придирчиво, шаг за шагом пересмотреть все детали и операции химического анализа реактивы, эталоны, мерную посуду, весы, способы отбора средней пробы, операции осаждения, фильтрования и промывания осадков, отбора аликвотных проб и т. д. В ходе такого пересмотра отдельные операции и детали анализа следует последовательно переоснастить , заменяя реактивы, посуду и т. д. Кроме того, следует попытаться установить связь погрешности с такими внешними условиями, как время (время приготовления растворов, сроки хранения реактивов), температура, состав атмосферы (в отдельных заводских и лабораторных помещениях состав атмосферы может сильно отличаться от среднего), влажность и т. д. В результате тщательного расследования находят источник, а вслед за этим и Т1ричину систематической погрешности, которая может быть устранена или по крайней мере оценена. [c.58]
д. В ходе такого пересмотра отдельные операции и детали анализа следует последовательно переоснастить , заменяя реактивы, посуду и т. д. Кроме того, следует попытаться установить связь погрешности с такими внешними условиями, как время (время приготовления растворов, сроки хранения реактивов), температура, состав атмосферы (в отдельных заводских и лабораторных помещениях состав атмосферы может сильно отличаться от среднего), влажность и т. д. В результате тщательного расследования находят источник, а вслед за этим и Т1ричину систематической погрешности, которая может быть устранена или по крайней мере оценена. [c.58]
Естественным способом обнаружения и оценки систематических погрешностей в химическом анализе является сравнение среднего результата многократного анализа стандартного образца х с паспортным содержанием Хст определяемого компонента. Разность значений Лхс = х — Хст значима, т. е. методика анализа содержит систематическую цогрешность, если /л, критерий, рав ный отношению [c. 110]
110]
Погрешности метода, или инструментальные погрешности, связаны с методом и прежде всего с инструментом для измерения аналитического сиг-йала. Самый простой пример ошибок такого типа — погрешность взвешивания на аналитических весах, обусловливающая систематическую погрешность гравиметрического метода анализа. Так, если погрешность взвешивания составляет 0,2 мг, то минимальная относительная погрешность гравиметрического определения (при навеске 1 г) составит 0,02%. Периодическая проверка аналитических приборов (спектрофотометры, иономеры, поляро-графы, хроматографы и т. д.) сводит к минимуму систематическую составляющую инструментальных погрешностей. Так как в большинстве методов анализа используют образцы сравнения, то к погрешностям метода часто относят погрешности образцов сравнения, в частности стандартных образцов, обусловленные несоответствием истшшого и номинального содержания в них компонента, различием общего химического состава и структуры анализируемого образца и образца сравнения. Инструментальная погрешность обычно составляет лишь небольшую долю общей погрешности результата химического анализа. [c.37]
Инструментальная погрешность обычно составляет лишь небольшую долю общей погрешности результата химического анализа. [c.37]
Общепринятый прием оценки правильности — анализ стандартного образца. Это самый надежный способ выявления систематической погрешности, аттестации на правильность метода анализа, аналитической методики, инструменга дпя измерения аналитического сигнала. Стандартные образцы готовят из материала, состав и свойства которого надежно установлены и официально удостоверены. Обычно стандартные образцы (на один или более компонентов) анализируют многими методами в нескольких лабораториях, поэтому содержание компонентов, указанное в свидетельстве о составе образца, можно принимать за истинное значение. Непременное условие применения стандартного образца в химическом анализе — максимальная близость состава и свойств стандартного образца и анализируемой пробы. При использовании стандартного образца для оценки правильности метода или методики проводят многократный химический анализ образца и сравнивают найденное содержание с истинным (паспортным) содержанием определяемого компонента. [c.39]
[c.39]
Оценка правильности метода или методики должна проводиться дпя нескольких разных содержаний определяемого компонента, т. е. с использованием двух или нескольких стандартных образцов. Стандартные образцы применяют не только дпя проверки правильности конечного результата определения компонента, но и на отдельных стадиях химического анализа в целях выявления систематических погрешностей. Например, стацдартные образцы часто используют для выявления погрешностей пробоотбора и пробоподготовки, систематической инструментальной погрешности на стадии измерения аналитического сигнала. [c.39]
Правильность (a ura y). Степень близости между полученным результатом и истинным значением. Правильность является качественной характеристикой и включает комбинацию компонентов случайных погрешностей и обычную систематическую погрешность. Это качество измерений, отражающее близость к нулю систематических погрешностей. Отсутствие в химическом анализе систематических погрешностей обеспечивает его правильность (рис. 2.3). Количественной оценкой правильности результата анализа (оценкой систематической погрешности) служит разность между средним (средним арифметическим результатов наблюдений) и истинным значением оп-peдeJ яeмoй величины. [c.62]
2.3). Количественной оценкой правильности результата анализа (оценкой систематической погрешности) служит разность между средним (средним арифметическим результатов наблюдений) и истинным значением оп-peдeJ яeмoй величины. [c.62]
Переменная систематическая погрешность – Большая Энциклопедия Нефти и Газа, статья, страница 1
Переменная систематическая погрешность
Cтраница 1
Переменные систематические погрешности изменяются в процессе измерений. Если при измерениях погрешность монотонно убывает или возрастает, то она называется прогрессирующей. Например, монотонно меняется погрешность из-за разряда источника питания прибора, если результат измерений зависит от напряжения питания. [1]
Переменные систематические погрешности разделяются на прогрессирующие и периодические. Прогрессирующие систематические погрешности возрастают или убывают в функции некоторого аргумента ( влияющей величины), их вызывающего. Периодические – изменяются в интервале времени наблюдения с определенным периодом. Для уменьшения переменных систематических погрешностей необходимо выявить закон их изменения и вычислить поправки. Иногда это удается сделать путем поверки и тогда поправки составляются в виде графиков или таблиц, но чаще поправки находят аналитически и тогда они выражаются математическими уравнениями.
[2]
Периодические – изменяются в интервале времени наблюдения с определенным периодом. Для уменьшения переменных систематических погрешностей необходимо выявить закон их изменения и вычислить поправки. Иногда это удается сделать путем поверки и тогда поправки составляются в виде графиков или таблиц, но чаще поправки находят аналитически и тогда они выражаются математическими уравнениями.
[2]
Переменная систематическая погрешность ( например, обусловленная износом инструмента) при описанном методе построения кривой распределения оказывает влияние на ее форму. [3]
Переменные систематические погрешности изменяются в процессе измерений. Если при измерениях погрешность монотонно убывает или возрастает, то она называется прогрессирующей. Например, монотонно меняется погрешность из-за разряда источника питания прибора, если результат измерений зависит от напряжения питания. [4]
[4]
Переменными систематическими погрешностями называют составляющие погрешности измерения, изменяющиеся в процессе измерений. [5]
Примером переменной систематической погрешности может быть погрешность от закономерного изменения напряжения вспомогательного источника питания ( разряд аккумулятора), если результат измерения зависит от значения этого напряжения. [6]
Среди переменных систематических погрешностей принято выделять прогрессивные, монотонно возрастающие или убывающие в процессе своего изменения ( в функции времени, значения измеряемой величины или параметров внешних условий), и периодические. [7]
Примером переменной систематической погрешности может служить погрешность, обусловленная изменениями напряжения вспомогательного источника питания, если результат измерения зависит от этого напряжения. [8]
[8]
Примером переменной систематической погрешности могут служить: погрешность от износа режущего инструмента, величина радиального биения, вызываемого эксцентриситетом, погрешность измерения углов с помощью синусной линейки, у которой действительные значения расстояний между осями роликов отличаются от расчетных. [9]
При переменной систематической погрешности последовательность неисправленных отклонений результатов наблюдений обнаруживает тенденцию к возрастанию или убыванию, что легко устанавливается по графику зависимости погрешностей от номера измерения. [10]
Наличие переменных систематических погрешностей при многократных измерениях может быть обнаружено статистическими методами. Предполагая нормальное распределение результатов N измерений, разделенных на п серий, находят оценки дисперсий – внутрисерийную S. Если данные не содержат систематических погрешностей, то Sf и S должны иметь / – распределение для числа степеней свободы N – п и п – 1 соответственно.
[11]
Если данные не содержат систематических погрешностей, то Sf и S должны иметь / – распределение для числа степеней свободы N – п и п – 1 соответственно.
[11]
К переменным систематическим погрешностям, как указывалось выше, относятся, в основном, погрешности, обусловленные тепловыми деформациями звеньев технологической системы и размерным износом режущего инструмента. [12]
Известно, что переменные систематические погрешности измерений малы. Необходимо получить оценку массы тела по данным всех трех групп и оценить СКО полученной оценки. [13]
В качестве примера переменной систематической погрешности приводим изменение размера в функции от длины или времени обработки, обусловленное износом инструмента или температурными деформациями технологической системы. Здесь размер закономерно изменяется при переходе к обработке каждой последующей детали. [14]
[14]
Количественная оценка влияния переменных систематических погрешностей на точность обработки наиболее наглядно выявляется путем анализа точечных диаграмм, полученных экспериментальным путем для конкретных условий производства. [15]
Страницы: 1 2 3 4
Погрешность измерений при помощи штангенинструментов.
Погрешность измерений штангенинструментами
Погрешности линейных измерений
Как и при измерениях любыми инструментами, штангенинструментом можно измерить линейные размеры детали с некоторой предельной степенью точности, которая зависит не только от качества и точности изготовления измерительного средства, но и от некоторых других факторов.
Погрешностью средств измерений называется отклонение его показания (выходного сигнала) от воздействующей на его вход измеряемой величины (входного сигнала).
Погрешности, возникающие в процессе измерений, можно разделить на систематические и случайные.
Кроме этого, в процессе измерения могут появиться грубые (очень большие) погрешности, а также могут быть допущены промахи.
К систематическим погрешностям относят составляющую погрешности измерений, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины.
Как правило, систематические погрешности могут быть в большинстве случаев изучены и учтены до начала измерений, а результат измерения может быть уточнен за счет внесения поправок, если их числовые значения определены, или за счет использования таких способов измерений, которые дают возможность исключить влияние систематических погрешностей без их определения.
К случайным погрешностям измерения относят составляющие погрешности измерений, которые изменяются случайным образом при повторных измерениях одной и той же величины.
Эти погрешности, в отличие от систематических, нельзя предвидеть заранее, поскольку их появление носит случайный характер.
Основными причинами грубых погрешностей и промахов могут являться ошибки экспериментатора, резкое и неожиданное изменение условий измерения, неисправность прибора и т. п.
Суммарная погрешность измерения с помощью штангенинструментов состоит из следующих составляющих:
- погрешность Δ1,возникающая от ошибок нанесения штрихов шкалы на штанге и на нониусе. Это систематическая погрешность, но она не известна и не может быть учтена и компенсирована, поэтому ее учитываю как случайную;
- погрешность Δ2, возникающая из-за нарушения принципа Аббе. Это случайная погрешность первого порядка, зависящая от длины губок, зазоров в направляющей ползуна и усилия прижима губки к измеряемой детали;
Эрнст Аббе (1840-1905) – немецкий физик-оптик. Является автором теории микроскопа, конструктор многих оптических приборов. Руководитель оптических заводов К. Цейса в Йене.
Руководитель оптических заводов К. Цейса в Йене.
Принцип Аббе (компараторный принцип, принцип последовательного расположения) заключается в следующем: линия измерения должна являться продолжением линии рабочих (снимающих размер) элементов измерительного прибора, т. е. необходимо, чтобы ось шкалы прибора располагалась на одной прямой с контролируемым размером проверяемой детали.
В случае расположения измерителя и измеряемого предмета не на одной прямой при измерении возникает ошибка первого порядка, величина которой будет тем больше, чем больше при одних и тех же условиях было расстояние между предметом и измерителем.
При уменьшении этого расстояния уменьшается и возможная ошибка, которая сделается равной нулю, когда измеряемый предмет и измеритель, с которыми производится сравнение, будут расположены на одной прямой.
Это положение было впервые высказано Э. Аббе в 1890 г. на съезде в Бремене. Оно легло в основу устройства ряда измерительных приборов, сконструированных фирмой К. Цейса в Йене и получило название принцип Аббе.
Цейса в Йене и получило название принцип Аббе.
Если этот принцип не выдерживается, то перекос и не параллельность направляющих измерительного прибора вызывают значительные погрешности измерения.
При соблюдении принципа Аббе погрешностями, вызываемыми перекосами, можно пренебречь, так как они являются ошибками второго порядка малости.
- погрешность Δ3, возникающая из-за ошибок отсчета по штриховой шкале и нониусу. Это случайная погрешность;
- погрешность Δ4, возникающая из-за неодинакового усилия прижима губки к измеряемой детали. Это случайная погрешность, возникающая из-за деформации контролируемой поверхности измерительными губками;
- погрешность Δ5,возникающая из-за отклонений температуры изделия и штангенинструмента от нормальной температуры. В процессе измерения штангенинструмент, а иногда и контролируемую деталь держат в руках. Поэтому температура измеряемой детали и штангенинструмента переменная, что вызывает случайную погрешность;
- погрешность Δ6, возникающая от перекосов губок штангенинструмента относительно измеряемой детали.

***
Суммарная погрешность определяется суммой квадратов всех перечисленных погрешностей:
ΔΣ = ±2σ = √(∆12 + ∆22 + ∆32 + ∆42 + ∆52 + ∆62).
У электронного штангенциркуля дополнительно возникает погрешность Δ7 из-за ошибок инкрементного емкостного преобразователя, но зато отсутствует погрешность штриховых шкал Δ1 и отсчета по ним Δ3.
Таким образом, погрешность электронного штангенциркуля может быть определена по формуле:
ΔΣ = ±2σ = √(∆22 + ∆42 + ∆52 + ∆62 + ∆72).
Из этих формул видно, что основные и наиболее значимые составляющие погрешности механического и электронного штангенинструмента – погрешности, обусловленные нарушением принципа Аббе (перекосами инструмента при измерениях) и отклонением температуры. Поэтому наличие инкрементного преобразователя и цифрового отсчета не повышает точность электронного штангенинструмента, несмотря на меньшую дискретность отсчета (0,01 мм) и более удобное считывание показаний.
Фирмы-изготовители часто приводят эмпирические формулы для расчета погрешности измерения собственных инструментов.
Так, фирма “Tesa” (Швейцария) приводит следующие формулы для ориентировочного расчета предельно допустимой погрешности измерения штангенциркулем:
– с нониусом или циферблатом с ценой деления нониуса 0,1 или 0,05 мм: Δlim = (20 + ℓ/10 мм) мкм;
– для штангенциркулей с ценой деления нониуса 0,02 мм: Δlim = (22 + ℓ/50 мм) мкм.
Однако во всех случаях практически предельно допустимая погрешность измерения штангенинструментов будет более 50 мкм.
Штангенциркули, штангенглубиномеры и штангенрейсмасы так же, как и другие средства измере-ния, подлежат обязательной поверке и калибровке. Поверку и калибровку штангенинструментов проводят в соответствии с ГОСТ 8.113-85.
Поверку погрешностей показаний штангенинструментов производят с помощью концевых мер длины в нескольких точках диапазона измерений.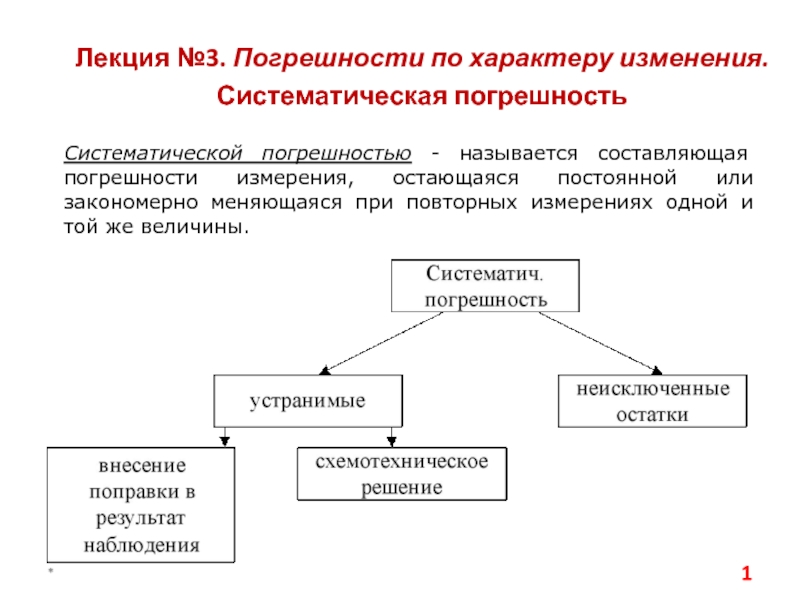
При поверке губки штангенинструмента должны быть перпендикулярны широким нерабочим плоскостям мер.
Поверка показаний производится при свободной и закрепленной рамке для двух положений блока мер на ближнем и дальнем расстоянии от штанги.
Губки штангенинструмента должны прижиматься к мерам с усилием, обеспечивающим нормальное скольжение по рабочим поверхностям мер.
***
Допуски, посадки, квалитеты
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Измерения и их погрешности
ПРЯМЫЕ ОДНОКРАТНЫЕ ИЗМЕРЕНИЯ И ИХ ПОГРЕШНОСТИ.
1. КЛАССИФИКАЦИЯ ПРИЧИН ВОЗНИКНОВЕНИЯ ПОГРЕШНОСТЕЙ.
В соответствии с причиной их возникновения погрешности измерений физических величин классифицируются:
– случайные
– систематические
– промахи
1. 1. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ.
1. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ.
Результаты измерения одной и той же физической величины, проведённые в одинаковых условиях и с одинаковой тщательностью, всегда несколько отличаются друг от друга. Причины этих различий могут быть самыми разнообразными, но главное – нельзя обеспечить полную одинаковость условий при повторных испытаниях.
В теории погрешностей показано, что при повторении опытов наиболее близким к неизвестному истинному значению величины будет среднее арифметическое измерений, полученных в неизменных условиях.
При использовании одного и того же прибора можно получить разные результаты измерений, а тем более, когда используется поочерёдно два однотипных прибора.
ПРИМЕР. При взвешивании одного и того же тела на одних и тех же весах обычно получают несколько отличающихся друг от друга значений массы, т.к. нельзя устранить трение в осях, влияния воздушных потоков, горизонтальность коромысла определяется визуально и т.д.
Погрешности, возникающие из-за случайных факторов, называют случайными.
1.2. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ.
Погрешности, возникающие из-за влияния измерительных приборов на исследуемые процессы или неверного анализа процессов при теоретическом рассмотрении явлений, называются систематическими.
Систематические погрешности бывают разных видов. К ним относят, например, погрешности, причины которых неизвестны экспериментатору. Часто причиной систематических погрешностей является отклонение равновесного положения указателя прибора от нулевой отметки шкалы. К систематическим можно отнести и неизбежные погрешности средств измерения. У каждого прибора эту погрешность можно найти, но на заводе-изготовителе определяют максимальную погрешность для всех приборов данного типа и обозначают её ∆пр.
ПРИМЕР. В электрической цепи измеряют амперметром силу тока. Амперметр не является идеальным прибором и обладает собственным сопротивлением. Понятно, что до включения амперметра в цепь сила тока была несколько больше. Разница между силой тока в цепи до включения амперметра и его показаниями и есть систематическая погрешность. Она практически неустранима.
Она практически неустранима.
1.3. ПРОМАХИ.
Погрешности, которые существенно превышают систематические и случайные погрешности, называют промахами.
Причиной промахов являются ошибки экспериментатора при снятии показаний прибора, неисправность средств измерения, эксплуатация прибора не по инструкции.
Промах обычно возникает при проведении первого опыта. Для избежания промахов следует тщательно готовиться к измерениям, внимательно считывать и записывать показания. Если условия проведения опытов позволяют, никогда не следует ограничиваться одним измерением.
2. ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ.
2.1 . ПОВЕРКА.
Погрешность прямых измерений (инструментальная погрешность) связана прежде всего с основными погрешностями мер и измерительных приборов. Процедура определения её называется поверкой. Поверка состоит в сравнении показаний рабочего прибора с показаниями образцового прибора на заводе – изготовителе.
ПРИМЕР. На заводе – изготовителе можно определить массу гирь с помощью точных весов и гарантировать, что истинное значение массы гири отличается от номинального значения m н не более, чем на ∆m. Это значение ∆m и называется погрешностью меры. Истинное значение массы гирь находится в интервале:
[ m – ∆m; m + ∆m]
2.2. КЛАСС ТОЧНОСТИ.
Класс точности – это число, которое показывает в процентах соотношение основной погрешности и предела измерения.
Класс точности показывается на шкале прибора число в кружке. Зная класс точности прибора, легко найти границу абсолютной основной погрешности прибора ∆пр.
предел измерения · класс точности
∆ пр = ————————————————- (1)
100
ПРИМЕР № 1. На шкале прибора в кружке проставлено число 2,5. Это и есть класс точности. Число показывает: основная погрешность прибора не превышает 2,5 % предела измерения.
ПРИМЕР № 2.
Название позиции \ прибор | Амперметр | Вольтметр |
Предел измерения | 2 А | 6 В |
Класс точности | 2,5 | 4 |
Граница абсолютной основной погрешности прибора
| 2 А ·2,5 ∆ А = ———— = 0,05 А 100 | 6 В · 4% ∆ В = ———- = 0,24 В 100 |
3. СЧИТЫВАНИЕ ПОКАЗАНИЙ ПО ШКАЛЕ ПРИБОРА.
СЧИТЫВАНИЕ ПОКАЗАНИЙ ПО ШКАЛЕ ПРИБОРА.
Считывание показаний по шкале прибора осуществляется с учетом цены деления шкалы. Обязательным является эксплуатация прибора согласно инструкции.
3.1. СОВПАДЕНИЕ УКАЗАТЕЛЯ СО ШТРИХОМ ШКАЛЫ.
В этом случае наиболее просто находится граница погрешности прямого измерения: она не превосходит основную погрешность прибора ∆ пр.
3.2. НЕСОВПАДЕНИЕ УКАЗАТЕЛЯ СО ШТРИХОМ ШКАЛЫ.
Граница погрешности прямого измерения возрастает, если указатель не совпадает со штрихом шкалы, потому что визуально невозможно точно определить расстояние от штриха до указателя. Это и есть так называемая погрешность отсчета. Специальные исследования показали, что при ширине деления не менее 1 – 2 мм границу погрешности отсчета можно принять равной половине деления. Принято считать, что граница погрешности отсчета не превосходит половины цены деления:
Цена деления
∆ отсчета = ———————– (2)
2
В соответствии с арифметическим сложением погрешностей можно утверждать, что при несовпадении указателя со штрихом шкалы граница абсолютной погрешности прямого измерения ∆ не превосходит значение суммы основной погрешности прибора и границы погрешности отсчета:
∆ = ∆ прибора + ∆ отсчета (3)
3. 3. ПАРАЛЛАКС.
3. ПАРАЛЛАКС.
Параллакс – кажущееся смещение объекта, вызванное изменением точки наблюдения.
Отсчет всегда надо проводить тщательно:
– располагать глаз наблюдателя на прямой, перпендикулярной шкале,
– располагать предмет как можно ближе к шкале прибора,
Крайне важно, что бы стрелка прибора имела малую толщину и
перекрывала как можно меньшую часть шкалы.
Для уменьшения параллакса шкала прибора может быть зеркальной.
3.4. СОВМЕСТНЫЙ УЧЕТ ∆ прибора И ∆ отсчета
Совместный учет границы абсолютной основной погрешности прибора ∆ пр. и границы погрешности отсчета ∆ отсчета целесообразен, если половина цены деления близка к основной погрешности прибора.
В случае, когда погрешность прибора превышает половину цены деления прибора в 4 и более раз (∆ пр. > 4 · С/2), то погрешностью отсчета можно пренебречь.
Если же выполняется неравенство (4 ∆ пр. < С/2), то можно пренебречь основной погрешностью прибора.
< С/2), то можно пренебречь основной погрешностью прибора.
4. ВЫБОР СРЕДСТВ ИЗМЕРЕНИЯ.
При планировании прямых измерений очень важно правильно выбрать средства измерения. Не всегда прибором с меньшей инструментальной погрешностью можно получить более точный результат.
ПРИМЕР. Для измерения расстояния 6 м используют рулетку с пределом 10 м и с основной погрешностью ∆ р = 1,0 см, а затем линейку длиной 30 см и основной погрешностью ∆ л = 1 мм. Длина рулетки сравнима с измеряемым расстоянием, а линейка значительно короче: для измерения расстояния рулетку нужно приложить один раз, а линейку – двадцать раз. Прикладывание линейки требует в данном случае нанесение меток, ширина которых больше или сравнима с шириной штриха и ценой деления. Это приведет к увеличению погрешности. Она станет много больше суммы (∆ л + С/ 2 ) и больше основной погрешности рулетки.
5. ПОГРЕШНОСТЬ ПРИ ИСПОЛЬЗОВАНИИ ВЕСОВ.
Несколько сложнее определить погрешность при использовании весов. Для них необходимо учитывать основную погрешность весов, основную погрешность гирь и основную погрешность подбора гирь. При прямом измерении массы на весах граница погрешности измерений равна:
Для них необходимо учитывать основную погрешность весов, основную погрешность гирь и основную погрешность подбора гирь. При прямом измерении массы на весах граница погрешности измерений равна:
∆ = ∆ весов + ∆ подбора гирь + ∆ всех гирь. (5)
5.1. ПОГРЕШНОСТЬ ВЕСОВ | 5.3. ПОГРЕШНОСТЬ ГИРЬ | ||||||||||||||||||||||||
Зависимость погрешности весов ВТ – 200 от нагрузки представляется графически. | Границы погрешности гирь набора Г4 – 210 приведены в таблице. | ||||||||||||||||||||||||
|
|
Систематическая ошибка / Случайная ошибка: определение и примеры
Что такое систематическая ошибка?
Систематическая ошибка (также называемая систематической погрешностью ) – это последовательная повторяемая ошибка, связанная с неисправным оборудованием или неправильным планом эксперимента.
Что такое случайная ошибка?
Случайная ошибка (также называемая несистематической ошибкой, системным шумом или случайной вариацией) не имеет шаблона. Через минуту ваши показания могут быть слишком маленькими. В следующий раз они могут оказаться слишком большими.Невозможно предсказать случайную ошибку, и эти ошибки обычно неизбежны.
Посмотрите видео для обзора или прочтите ниже:
Систематические и случайные ошибки
Систематические ошибки обычно вызваны измерительными приборами, которые неправильно откалиброваны или используются неправильно. Однако они могут проникнуть в ваш эксперимент из многих источников, включая:
- Изношенный инструмент .
 Например, пластиковая рулетка с годами слегка растягивается, в результате чего размеры становятся немного завышенными,
Например, пластиковая рулетка с годами слегка растягивается, в результате чего размеры становятся немного завышенными, - Неправильно откалиброванный или тарированный инструмент, как весы, которые не показывают ноль, когда на них ничего нет,
- Человек постоянно измеряет неверно. Например, они могут подумать, что отметка 3/4 ″ на линейке – это отметка 2/3 ″.
Основные различия между этими двумя типами ошибок:
- Случайные ошибки (как следует из названия) являются полностью случайными.Это непредсказуемые и , которые невозможно воспроизвести , повторив эксперимент еще раз.
- Систематические ошибки приводят к постоянным ошибкам , фиксированной величине (например, 1 фунт) или пропорциональной (например, 105% от истинного значения). Если вы повторите эксперимент, вы получите ту же ошибку .

Систематические ошибки всегда в одном направлении (например, они всегда на 50 г, на 1% или 99 мм больше или меньше). Напротив, случайных ошибки производят разные значения в случайных направлениях.Например, вы используете весы, чтобы взвесить себя и получить 148 фунтов, 153 фунтов и 132 фунта.
Типы систематических ошибок
1. Ошибка смещения – это тип систематической ошибки, при которой прибор не обнуляется, когда вы начинаете взвешивать предметы. Например, кухонные весы включают кнопку «тара», которая устанавливает весы и емкость на ноль перед тем, как содержимое помещается в емкость. Это значит, что вес контейнера не входит в показания. Если тара установлена неправильно, все показания будут иметь ошибку смещения.
Ошибки смещения приводят к постоянно неправильным показаниям.
2. Ошибки масштабного коэффициента. Это ошибки, пропорциональные истинному измерению. Например, измерительная лента, растянутая до 101% от исходного размера, будет постоянно давать результаты, которые составляют 101% от истинного значения.
Ошибки масштабного коэффициента увеличивают (или уменьшают) истинное значение на пропорцию или процент.
Сравните два вышеуказанных шаблона ошибок с случайными ошибками , у которых нет шаблона:
Случайные ошибки не соответствуют шаблону.
Предотвращение ошибок
Случайная ошибка может быть уменьшена на:
- Использование среднего измерения из набора измерений, или
- Увеличение размера выборки.
Систематическую ошибку трудно обнаружить и, следовательно, предотвратить. Чтобы избежать подобных ошибок, знайте ограничения вашего оборудования и понимайте, как работает эксперимент. Это может помочь вам определить области, которые могут быть подвержены систематическим ошибкам.
Список литературы
Гоник, Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Everitt, B. S .; Скрондал, А. (2010), Кембриджский статистический словарь, Cambridge University Press.
Kotz, S .; и др., ред. (2006), Энциклопедия статистических наук, Wiley.
Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Версия для печати
Когда мы что-то измеряем или собираем информацию, есть много причин, по которым наши выводы могут быть неверными. Самая очевидная причина в том, что мы могли просто сделать ошибку, записав что-то. Такого рода ошибка – вот как мы обычно думаем об ошибке.Однако есть и другие виды ошибок, которые мы могли бы не увидеть, если бы не научились их искать. Эти ошибки не являются ошибками в том смысле, что мы сделали что-то не так. Ошибки такого типа могут снизить надежность или точность того, что мы делаем, но часто из-за вещей, которые мы не можем контролировать.
Одна из них называется случайной ошибкой. Ошибка считается случайной, если значение того, что измеряется, иногда повышается, а иногда понижается.Очень простой пример – наше кровяное давление. Даже если кто-то здоров, это нормально, что его кровяное давление не остается неизменным каждый раз при его измерении. Если с течением времени было проведено несколько измерений артериального давления, некоторые из них были бы выше, а некоторые – ниже. Причину этой случайной ошибки следует ожидать из-за различий в нормальных процессах в организме и в том, как работает измерительное устройство. Если ошибка действительно случайна, и если мы сделаем достаточно измерений, то еще можно получить хорошую оценку того, что мы измеряем.Однако, если случайная ошибка велика, наши измерения будут непредсказуемыми, непоследовательными и не будут отражать истинное значение того, что мы измеряем.
Второй тип ошибок называется систематической ошибкой. Ошибка считается систематической, если она постоянно изменяется в одном и том же направлении. Например, это могло произойти с измерением артериального давления, если непосредственно перед измерением что-то всегда или часто приводило к повышению артериального давления. Или это могло произойти из-за того, что наш прибор для измерения артериального давления был неисправен, поэтому всегда давал результат выше или всегда давал результат ниже истинного значения.В этих случаях, даже если бы наши измерения были предсказуемыми и последовательными, результаты все равно не были бы точными.
Определение: Ошибка в исследовании – это все, что мешает сделать уверенный вывод об исследовании.
Примеры систематической и случайной ошибки
Систематическая ошибка
В исследовании потери веса исследователи определили в конце исследования, что весы, которые использовались для измерения веса участников, были неточными. Весы добавляли к фактическому весу человека 10 фунтов каждый раз, когда их использовали.Поскольку исследователь понял, что весы постоянно увеличивают вес каждого участника на десять фунтов, они скорректировали эту проблему при анализе результатов.
Раздел 2.3: Вопросы для обсуждения
- Если бы вы были исследователем, как бы вы справились с этой проблемой, если бы узнали о ней в конце исследования?
- Что исследователь должен был сделать в первую очередь, чтобы избежать этой проблемы?
- Является ли систематическая ошибка проблемой в исследованиях в целом, если ее можно исправить? Что делать, если исследователь не знает о систематической ошибке?
Случайная ошибка
В исследовании по снижению веса использовались весы, которые добавляли на несколько фунтов больше или несколько фунтов меньше каждый раз, когда использовались весы.Исследователь не знал, что весы не измеряли точный вес участника. Поскольку исследователь этого не осознавал, он не мог приспособиться к этой проблеме при анализе результатов. Это привело к тому, что в результаты исследования были включены некоторые ошибки.
Раздел 2.3: Вопросы для обсуждения
- Точны ли результаты этого исследования? Почему или почему нет?
- Вызывает ли использование немного неточной шкалы серьезных проблем с результатами исследования?
- Есть ли что-нибудь, что исследователь должен был сделать, чтобы избежать этой проблемы?
- Что, по вашему мнению, является более серьезной проблемой в исследовании – систематическая или случайная ошибка?
- Какой тип ошибки – случайный или систематический – легче контролировать?
Ошибки
ОшибкиОшибки
Неопределенность
Многие единичные коэффициенты основаны на определениях.В миле ровно 5280 футов и Например, 2,54 сантиметра в дюйме. Единичные коэффициенты, основанные на определениях, известны как полная уверенность. С этими числами нет никакой ошибки или неопределенности. Однако измерения всегда сопровождаются конечной ошибкой или неопределенностью. что отражает ограничения в методах их изготовления.
Есть два источника погрешности измерения: (1) ограничения чувствительности используемые инструменты и (2) несовершенство методов, используемых для измерения.Эти ошибки можно разделить на два класса: систематические и случайные.
Систематические ошибки
Систематическая ошибка может быть вызвана несовершенством используемого оборудования или ошибки, которые делает человек при измерении. Баланс неверный калибровка приведет к систематической ошибке. Неправильное чтение бюретки будет приводят к систематической ошибке.
Случайные ошибки
Случайные ошибки чаще всего возникают из-за ограничений оборудования или методов, используемых для сделайте замер. Предположим, например, что вы хотите собрать 25 мл раствора. Вы можете использовать стакан, мерный цилиндр или бюретку. Измерения объема с Стакан на 50 мл имеет точность до 5 мл. Другими словами, вы с большей вероятностью получите 20 мл раствора (на 5 мл меньше) как 30 мл (на 5 мл больше).Вы можете уменьшить количество погрешности при использовании градуированного цилиндра, позволяющего проводить измерения до в пределах 1 мл. Погрешность может быть уменьшена еще больше, если использовать бюретку, которая с точностью до 1 капли или 0,05 мл.
| Практическая задача 6 Что из следующего процедуры могут привести к систематическим ошибкам, а какие – к случайным? (a) Использование 1-литрового пакета молока для измерения 1-литровых проб молока. (b) Использование весов с чувствительностью до 0,1 грамма для получения 250 миллиграммов витамина. С. (c) Отмерить 2,5 миллилитра раствора с помощью градуированного цилиндра на 100 миллилитров. Нажмите здесь, чтобы проверьте свой ответ на практическую задачу 6 |
шт. | Ошибки | Значимые цифры | Научная запись
Вернуться к общей теме химии Отзыв
Разница между систематическими и случайными ошибками
Независимо от того, насколько осторожны вы при проведении экспериментов, вероятно, будет экспериментальная ошибка.Будь то проблемы, связанные с точным измерением, или проблемы с вашим оборудованием, полностью избежать ошибок практически невозможно. Чтобы противодействовать этой проблеме, ученые делают все возможное, чтобы классифицировать ошибки и количественно оценить любую неопределенность в измерениях, которые они делают. Выявление разницы между систематическими и случайными ошибками – ключевая часть обучения планированию более эффективных экспериментов и минимизации любых ошибок, которые действительно появляются.
TL; DR (слишком долго; не читал)
Систематические ошибки обычно возникают из-за неправильной калибровки оборудования.Каждое выполненное вами измерение будет ошибочным на одну и ту же величину, потому что есть проблема с вашим измерительным прибором. Случайные ошибки неизбежны и возникают в результате трудностей при проведении измерений или попытках измерения величин, которые меняются со временем. Эти ошибки будут колебаться, но обычно группируются вокруг истинного значения.
Что такое случайная ошибка?
Случайная ошибка описывает ошибки, которые колеблются из-за непредсказуемости или неопределенности, присущей вашему процессу измерения, или из-за изменения величины, которую вы пытаетесь измерить.
Ученый, измеряющий насекомое, например, попытался бы поместить насекомое в нулевую точку линейки или мерной линейки и прочитать значение на другом конце. Сама линейка, вероятно, будет измерять только до ближайшего миллиметра, и считывание с точностью может быть затруднено. Вы можете недооценить истинный размер насекомого или переоценить его, исходя из того, насколько хорошо вы читаете шкалу, и своего суждения о том, где останавливается голова насекомого. Насекомое также может немного сдвинуться с нулевого положения, даже если вы этого не заметите.Многократное повторение измерения из-за этого дает много разных результатов, но они, скорее всего, будут группироваться вокруг истинного значения.
Точно так же измерение величины, которая меняется от момента к моменту, приводит к случайной ошибке. Например, скорость ветра может увеличиваться и уменьшаться в разные моменты времени. Если вы сделаете измерение в течение одной минуты, вероятно, через минуту оно изменится. Опять же, повторные измерения приведут к результатам, которые колеблются, но группируются вокруг истинного значения.
Что такое систематическая ошибка?
Систематическая ошибка – это ошибка, которая возникает в результате постоянной проблемы и приводит к постоянной ошибке в ваших измерениях. Например, если ваша измерительная лента была растянута, ваши результаты всегда будут ниже истинного значения. Точно так же, если вы используете весы, которые не были установлены на ноль заранее, будет систематическая ошибка в результате ошибки в калибровке (например, если истинный вес 0 читается как 5 граммов, 10 граммов будут читаться как 15 и 15 граммов будут читаться как 20).
Другие различия между систематическими и случайными ошибками
Основное различие между систематическими и случайными ошибками состоит в том, что случайные ошибки приводят к колебаниям вокруг истинного значения в результате трудностей при проведении измерений, тогда как систематические ошибки приводят к предсказуемым и последовательным отклонениям от истинного значения. значение из-за проблем с калибровкой вашего оборудования. Это приводит к двум дополнительным отличиям, которые стоит отметить.
Случайные ошибки по существу неизбежны, а систематические – нет.Ученые не могут проводить точные измерения, независимо от того, насколько они квалифицированы. Если величина, которую вы измеряете, меняется от момента к моменту, вы не можете заставить ее перестать меняться во время измерения, и независимо от того, насколько детальна ваша шкала, ее точное считывание все равно представляет проблему. Хорошая новость заключается в том, что многократное повторение измерения и усреднение эффективно сводят к минимуму эту проблему.
Иногда бывает трудно обнаружить систематические ошибки. Это потому, что все, что вы измеряете, будет неверным на ту же (или аналогичную) сумму, и вы можете вообще не осознавать, что существует проблема.Однако, в отличие от случайных ошибок, их часто можно вообще избежать. Правильно откалибруйте свое оборудование перед его использованием, и систематические ошибки будут намного меньше.
Систематическая ошибка – обзор
Смещение или систематическая ошибка
Если говорить о смещении или систематической ошибке, есть также компонент выборки. Во-первых, основа выборки (т.е. список или перечисление элементов в генеральной совокупности) может либо не включать, либо дважды подсчитывать единицы. Например, при переписи населения США не учитываются люди (особенно афроамериканцы и иммигранты), а остальные учитываются дважды (особенно люди с более чем одним местом жительства), а выборки, основанные на переписи, отражают эти ограничения.Во-вторых, некоторые жилые единицы, такие как новые дома, второстепенные квартиры (например, квартиры в подвале в том, что кажется односемейным домом) и удаленные жилища, как правило, упускаются из виду в поле. Аналогичным образом, в жилищных единицах определенные лица, такие как постояльцы, как правило, недопредставлены, и некоторые методы отбора респондентов не работают беспристрастно (например, метод последнего / следующего дня рождения превышает представительство тех, кто отвечает на вопросы выборочного отбора). В-третьих, возникают различные статистические ошибки выборки.Обычно мощность образцов переоценивается, поскольку не принимаются во внимание эффекты дизайна. Кроме того, систематическая выборка может коррелировать с различными атрибутами целевой группы населения. Например, в одном исследовании экспериментальная форма и выбор респондентов были связаны посредством систематической выборки таким образом, что старшие члены домохозяйства были непропорционально отнесены к одной экспериментальной версии вопросника, что не позволило рандомизировать респондентов для обеих экспериментальных форм.
Ошибка отсутствия выборки возникает как из-за ошибок ненаблюдения, так и из-за ошибок наблюдения. Первый тип ошибки, не связанной с наблюдениями, – это ошибка охвата, при которой отдельный сегмент целевой группы не включается в выборку. Например, в Соединенных Штатах опросы с произвольным набором номеров перед выборами (RDD) хотят обобщить на голосующее население, но систематически исключить всех избирателей, не проживающих в домохозяйствах с телефонами. Точно так же в выборке предприятий часто недостаточно представлены более мелкие фирмы.Второй тип ошибок, не связанных с наблюдениями, состоит в отсутствии ответа (единицы включаются в выборку, но не опрашиваются). Отсутствие ответа имеет три основные причины: отказ от участия, невозможность связаться с людьми из-за отсутствия дома (например, на работе или в отпуске) и все другие причины (такие как болезнь и умственные и / или физические недостатки).
Ошибка наблюдения включает ошибки сбора, обработки и анализа. Как и в случае с переменной ошибкой, ошибка сбора связана с методом, инструментом, интервьюером и респондентом.Режим влияет на охват населения. Недопредставленность глухих и бедных наблюдается в телефонных опросах, а слепых и неграмотных – в опросах по почте. Режим также влияет на объем и качество собираемой информации. Открытые вопросы в телефонных опросах дают более короткие и менее полные ответы по сравнению с личными интервью. Смещение также связано с инструментом. Контент или диапазон охватываемой информации, очевидно, определяет то, что собирается. Одним из примеров ошибки содержания является включение вопросов, представляющих только одну сторону проблемы, что обычно делается в так называемом адвокационном опросе.Второй пример – это ошибка спецификации, при которой одна или несколько существенных переменных опускаются, поэтому модели не могут быть адекватно построены и, следовательно, указаны неверно.
Различные проблемные аспекты формулировки вопросов могут исказить вопросы. К ним относятся вопросы, которые слишком длинные и сложные, двусмысленные, включают двойное отрицание, используют нагруженные термины и содержат слова, которые не являются широко понятными. Например, следующий пункт о Холокосте является одновременно сложным и использует двойное отрицание: «Как вы знаете, термин« холокост »обычно относится к убийству миллионов евреев в нацистских лагерях смерти во время Второй мировой войны.Вам кажется возможным или невозможным, чтобы нацистское истребление евреев никогда не происходило? » После того, как в 1992 году 22% респондентов представили это утверждение в ходе национального опроса RDD в США, они заявили, что возможно, что Холокоста не было, 65% заявили, что это невозможно, а 12% не уверены. Однако последующие исследования показали, что многие люди были сбиты с толку этой формулировкой и что сомневающиеся в Холокосте на самом деле составляли около 2% населения, а не 22%.Ошибка из-за формулировки вопроса также возникает, когда термины понимаются непоследовательно.
Предлагаемые шкалы отклика также создают проблемы. Некоторым форматам, таким как шкала измерения звездных величин, трудно следовать, в результате чего многие, особенно наименее образованные, не могут выразить свое мнение. Даже широко используемые и простые весы могут вызвать ошибку. У 10-точечного скалометра нет четкой средней точки, и многие люди ошибочно выбирают точку 5 по шкале от 1 до 10 в безуспешной попытке поместить себя в середину.Контекст или порядок пунктов в опросе также влияет на ответы по-разному. Предыдущие вопросы могут активизировать определенные темы и сделать их более доступными (и, следовательно, более влиятельными), когда будут заданы более поздние вопросы. Или они могут создать эффект контраста, при котором предыдущий контент исключается из последующего рассмотрения в соответствии с правилом неповторения. Может быть создана норма беспристрастности, которая заставит людей отвечать на более поздние вопросы в манере, совместимой с более ранними вопросами.Например, во время холодной войны американцы, после того как их спросили, следует ли разрешить американским репортерам сообщать новости в России, с гораздо большей вероятностью ответили, что российским репортерам следует разрешить освещать статьи в Соединенных Штатах, чем когда Сначала задавались вопросы о российских репортерах. Даже введение в опрос может повлиять на качество данных последующих вопросов.
Хотя ученые-обществоведы надеются, что интервьюеры просто собирают информацию, в действительности интервьюеры также влияют на то, какая информация передается.Во-первых, простое присутствие интервьюера обычно усиливает эффект социальной желательности, так что интервьюеры чаще занижают информацию о чувствительном поведении, чем когда используется самозаполнение. Во-вторых, на ответы влияют основные характеристики интервьюеров. Например, белые выражают больше поддержки расовому равенству и интеграции, когда опрашивают чернокожие, чем белые. В-третьих, интервьюеры могут иметь точку зрения, которую они передают респондентам, побуждая интервьюеров интерпретировать ответы, особенно на открытые вопросы, в свете своих убеждений.
Значительная часть ошибок сбора исходит от респондентов. Некоторые проблемы когнитивные. Даже при самых лучших намерениях люди могут ошибаться. Сообщения о прошлом поведении могут быть искажены из-за того, что инциденты забываются или неправильно датируются. О незначительных событиях часто забывают, а о крупных событиях часто вспоминают как о произошедших позже, чем это было на самом деле. Конечно, у респондентов не всегда самые лучшие намерения. Люди склонны занижать сведения о поведении, которое плохо отражается на них самих (например,g., употребление наркотиков и судимость) и завышение сведений о позитивном поведении (например, голосование и благотворительность).
При обработке данных возникает систематическая ошибка. Один из источников ошибок связан с различными способами кодирования данных. Исследование социальных изменений в Детройте первоначально обнаружило большие изменения в ответах респондентов на один и тот же открытый вопрос, заданный и закодированный с разницей в несколько десятилетий. Однако, когда исходные открытые ответы из более раннего опроса были перекодированы теми же кодировщиками, которые кодировали последний опрос, различия практически исчезли, указывая на то, что изменение коснулось протоколов кодирования и выполнения, а не взглядов жителей Детройта.Хотя ошибки при вводе данных чаще бывают случайными, они могут серьезно исказить результаты. Например, в какой-то момент ни один из жителей Хартфорда, штат Коннектикут, не был вызван для исполнения обязанностей присяжных; Было обнаружено, что новая база данных жителей была отформатирована таким образом, что буква «d» в слове «Хартфорд» упала в поле, указывающее на то, что подопечный мертв. Ошибки также могут возникать при передаче данных. Примеры включают неправильное перекодирование, неверно названные переменные и неправильное расположение полей данных. Иногда потеря может произойти без внесения каких-либо ошибок.Например, в 1950-х годах в опросе Gallup было задано 20 словарных статей, и была создана сводная шкала. Данные сводной шкалы все еще сохранились, но 20 индивидуальных переменных были потеряны. Более поздние опросы включали 10 словарных пунктов, но их нельзя сравнивать с итоговой шкалой из 20 пунктов.
Неправильная или неполная документация может привести к ошибке. Например, в документации по исследованию политического участия (PPS) 1967 года указано, что одним из членов группы, о котором спрашивали, были «группы, связанные с церковью.Таким образом, когда позже в Общих социальных исследованиях (ОСО) была использована батарея членства в группах, религиозные группы были одной из 16 групп, представленных респондентам. Однако позже выяснилось, что церковным группам не задавали явных вопросов в предыдущем опросе, но что это обозначение было вычеркнуто из пункта «указать другое». Поскольку СОБ прямо спрашивал о религиозных группах, оно получило гораздо больше упоминаний, чем было в СПБ; это было всего лишь артефактом различных процедур сбора данных, возникшим в результате нечеткой документации.
Большинство обсуждений общей погрешности опроса останавливается на стадии обработки данных. Но данные не говорят сами за себя. Данные «говорят», когда они анализируются, и исследователи сообщают об анализе. На этом заключительном этапе часто вносятся значительные ошибки. Модели могут быть указаны неправильно, не только из-за исключения важных переменных из обследования, но также из-за исключения таких переменных из анализа, даже если они собираются. Во время анализа возникают всевозможные статистические и вычислительные ошибки.Например, в одном анализе модели, объясняющей уровни насилия с применением огнестрельного оружия, увеличение на 1 процентный пункт от базового уровня заболеваемости около 1% было неверно описано как увеличение на 1%, а не как увеличение на 100%. Даже когда количественный анализ выполнен безупречно, в описании могут возникнуть искажения. Общие проблемы включают использование жаргона, нечеткое письмо, чрезмерный акцент и преувеличение результатов, неточные описания и неполную документацию. Хотя каждый из множества источников общей ошибки опроса можно обсуждать индивидуально, они постоянно сложным образом взаимодействуют друг с другом.Например, плохо обученные интервьюеры с большей вероятностью ошибаются при составлении сложных вопросников, раса интервьюеров может взаимодействовать с расой респондентов, создавая эффекты ответа, длинные и обременительные вопросники с большей вероятностью вызовут усталость у пожилых респондентов, а шкалы ответов использовать полные рейтинги труднее по телефону, чем лично. Фактически, ни один этап опроса не отделен от других этапов, и большая часть ошибок опроса возникает в результате или формируется в результате взаимодействия между различными компонентами опроса.
Систематическая ошибка | Психология вики
Оценка |
Биопсихология |
Сравнительный |
Познавательный |
Развивающий |
Язык |
Индивидуальные различия |
Личность |
Философия |
Социальные |
Методы |
Статистика |
Клиническая |
Образовательная |
Промышленное |
Профессиональные товары |
Мировая психология |
Статистика : Научный метод · Методы исследования · Экспериментальная конструкция · Курсы бакалавриата по статистике · Статистические тесты · Теория игры · Теория принятия решений
Систематические ошибки – это смещения в измерениях, которые приводят к систематически завышенным или заниженным измеренным значениям.См. Также систематические ошибки (статистика) и ошибки и остатки в статистике. Все измерения подвержены систематической ошибке. Систематическая ошибка – это любой эффект смещения в окружающей среде, методах наблюдения или используемых инструментах, который вносит ошибку в эксперимент и всегда влияет на результаты эксперимента в одном и том же направлении. Расстояние, измеренное радаром, будет ошибочным, если не учитывать небольшое замедление волн в воздухе. Частота колебаний маятника будет ошибочной, если не учитывать небольшое движение опоры.Неправильная установка нуля прибора, приводящая к ошибке нуля, является примером систематической ошибки прибора. Так что часы идут быстро или медленно. См. Также ошибки наблюдений и ошибки и остатки в статистике.
Постоянные систематические ошибки очень трудно исправить, потому что их влияние можно наблюдать только в том случае, если их можно устранить. Такие ошибки невозможно устранить повторением измерений или усреднением большого количества результатов. Обычным средством устранения систематической ошибки является наблюдение за известным процессом, т.е.е. через калибровку. Еще один способ устранения систематической ошибки – это последующее измерение с помощью более сложного экспериментального оборудования.
Систематические ошибки, которые изменяются во время эксперимента (дрейф), легче обнаружить. Измерения показывают тенденции во времени, а не случайные колебания относительно среднего значения.
Дрейф очевиден, если измерение повторяется несколько раз и измерения смещаются в одну сторону во время эксперимента, например, если каждое измерение выше, чем предыдущее измерение, что может произойти, если во время эксперимента прибор станет теплее.Еще одним признаком систематической ошибки при использовании измерительного прибора является проверка нулевого показания во время эксперимента, а также в начале эксперимента. Если нулевое показание постоянно выше или ниже нуля после каждого сброса на ноль, присутствует систематическая ошибка. Если это не может быть устранено, это необходимо учесть, вычтя его из показаний и принимая во внимание при оценке точности измерения.
Если закономерность в серии повторных измерений не очевидна, наличие фиксированных систематических ошибок может быть обнаружено только в том случае, если измерения проверены либо путем измерения известной величины, либо путем сравнения показаний с показаниями, полученными с использованием другого известного, точный.Например, предположим, что измерение времени маятника с использованием точного секундомера несколько раз дает показания, случайно распределенные относительно среднего значения. Систематическая ошибка присутствует, если секундомер сравнивается с «часами разговора» телефонной системы и обнаруживается, что он работает медленно или быстро. Ясно, что время маятника необходимо корректировать в зависимости от того, насколько быстро или медленно работает секундомер. Измерительные приборы, такие как амперметры и вольтметры, необходимо периодически проверять на соответствие известным стандартам.
Систематические ошибки также можно обнаружить путем измерения уже известных величин. Например, спектрометр, снабженный дифракционной решеткой, можно проверить, используя его для измерения длины волны D-линий электромагнитного спектра натрия, которые находятся на 589,0 и 589,6 нм. Измерения могут использоваться для определения количества линий на миллиметр дифракционной решетки, которые затем могут использоваться для измерения длины волны любой другой спектральной линии. lt: Sisteminė paklaida
Ошибка измерения | Безграничная статистика
Смещение
Систематические или предвзятые ошибки – это ошибки, которые постоянно приводят к результатам, которые либо выше, либо ниже правильного измерения.
Цели обучения
Контрастность случайных и систематических ошибок
Основные выводы
Ключевые моменты
- Систематические ошибки – это смещения в измерениях, которые приводят к ситуации, когда среднее значение многих отдельных измерений значительно отличается от фактического значения измеряемого атрибута в одном направлении.
- Систематическая ошибка делает измеренное значение всегда меньше или больше истинного значения, но не одновременно. Эксперимент может включать более одной систематической ошибки, и эти ошибки могут аннулировать друг друга, но каждая изменяет истинное значение только одним способом.
- Точность (или достоверность) – это мера систематической ошибки. Если эксперимент точен или действителен, то систематическая ошибка очень мала.
- К систематическим ошибкам относятся личные ошибки, инструментальные ошибки и ошибки метода.
Ключевые термины
- систематическая ошибка : ошибка, которая постоянно дает результаты выше или ниже правильного измерения; погрешность
- случайная ошибка : ошибка, которая представляет собой комбинацию результатов как выше, так и ниже желаемого измерения; ошибка точности
- Точность : степень близости измерений величины к ее фактическому (истинному) значению
Два типа ошибок
При проведении измерений в эксперименте обычно встречаются два разных типа ошибок: случайные (или случайные) ошибки и систематические (или смещенные) ошибки.
Каждому измерению присуща погрешность. Поэтому нам необходимо дать некоторое представление о надежности измерений и неопределенности результатов, рассчитанных на основе этих измерений. Чтобы лучше понять результат экспериментальных данных, следует рассмотреть оценку размера систематических ошибок по сравнению со случайными ошибками. Случайные ошибки связаны с точностью оборудования, а систематические ошибки связаны с тем, насколько хорошо было использовано оборудование или насколько хорошо контролировался эксперимент.
Низкая точность, высокая точность : эта цель демонстрирует пример низкой точности (точки не находятся близко к центру цели), но высокой точности (точки расположены близко друг к другу). В этом случае систематической ошибки больше, чем случайной ошибки.
Высокая точность, низкая точность : эта цель демонстрирует пример высокой точности (все точки находятся близко к центральной цели), но низкой точности (точки не расположены близко друг к другу). В этом случае случайной ошибки больше, чем систематической.
Предвзятые или систематические ошибки
Систематические ошибки – это смещения в измерениях, которые приводят к ситуации, когда среднее многих отдельных измерений значительно отличается от фактического значения измеряемого атрибута. Все измерения подвержены систематическим ошибкам, часто нескольких разных типов. Источниками систематических ошибок могут быть несовершенная калибровка измерительных приборов, изменения в окружающей среде, мешающие процессу измерения, и несовершенные методы наблюдения.
Систематическая ошибка делает измеренное значение всегда меньше или больше истинного значения, но не то и другое вместе. Эксперимент может включать более одной систематической ошибки, и эти ошибки могут аннулировать друг друга, но каждая изменяет истинное значение только одним способом. Точность (или достоверность) – это мера систематической ошибки. Если эксперимент точен или действителен, то систематическая ошибка очень мала. Точность – это мера того, насколько хорошо эксперимент измеряет то, что он пытался измерить.Это трудно оценить, если у вас нет представления об ожидаемой стоимости (например, значение из учебника или рассчитанное значение из книги данных). Сравните ваше экспериментальное значение с литературным значением. Если он находится в пределах погрешности для случайных ошибок, то наиболее вероятно, что систематические ошибки меньше, чем случайные ошибки. Если он больше, то нужно определить, где произошли ошибки. Когда приемлемое значение доступно для результата, определенного экспериментально, можно рассчитать процентную ошибку.
Например, представьте, что экспериментатор измеряет период полного раскачивания маятника. Если их секундомер или таймер запускаются с 1 секундой на часах, то все их результаты будут отключены на 1 секунду. Если экспериментатор повторяет этот эксперимент двадцать раз (начиная с 1 секунды каждый раз), тогда будет процентная ошибка в вычисленном среднем значении их результатов; конечный результат будет немного больше истинного периода.
Категории систематических ошибок и способы их устранения
- Персональные ошибки : Эти ошибки являются результатом незнания, небрежности, предрассудков или физических ограничений экспериментатора.Ошибки этого типа можно значительно уменьшить, если вы знакомы с экспериментом, который проводите.
- Инструментальные ошибки : Инструментальные ошибки связаны с несовершенством инструментов, с которыми работает аналитик. Например, мерное оборудование, такое как бюретки, пипетки и мерные колбы, часто доставляют или содержат объемы, немного отличающиеся от тех, которые указаны по их градуировке. Калибровка может устранить этот тип ошибки.
- Ошибки метода : Этот тип ошибки возникает много раз, когда вы не думаете, как управлять экспериментом.Для любого эксперимента в идеале у вас должна быть только одна управляемая (независимая) переменная. Часто это очень сложно сделать. Чем больше переменных вы можете контролировать в эксперименте, тем меньше у вас будет ошибок метода.
Случайная ошибка
Случайные или случайные ошибки – это ошибки, которые представляют собой комбинацию результатов как выше, так и ниже желаемого измерения.
Цели обучения
Объясните, как в эксперименте возникают случайные ошибки
Основные выводы
Ключевые моменты
- Из-за случайной ошибки измеренное значение становится как меньше, так и больше истинного значения; это ошибки точности.
- Случайные ошибки возникают случайно, и их невозможно избежать.
- Случайная ошибка возникает из-за факторов, которые мы не контролируем или не можем контролировать.
Ключевые термины
- систематическая ошибка : ошибка, которая постоянно дает результаты выше или ниже правильного измерения; погрешность
- случайная ошибка : ошибка, которая представляет собой комбинацию результатов как выше, так и ниже желаемого измерения; ошибка точности
- Precision : возможность единообразного воспроизведения измерения
Два типа ошибок
При проведении измерений в эксперименте обычно встречаются два разных типа ошибок: случайные (или случайные) ошибки и систематические (или смещенные) ошибки.
Каждому измерению присуща погрешность. Поэтому нам необходимо дать некоторое представление о надежности измерений и неопределенности результатов, рассчитанных на основе этих измерений. Чтобы лучше понять результат экспериментальных данных, следует рассмотреть оценку размера систематических ошибок по сравнению со случайными ошибками. Случайные ошибки связаны с точностью оборудования, а систематические ошибки связаны с тем, насколько хорошо было использовано оборудование или насколько хорошо контролировался эксперимент.
Низкая точность, высокая точность : эта цель демонстрирует пример низкой точности (точки не находятся близко к центру цели), но высокой точности (точки расположены близко друг к другу). В этом случае систематической ошибки больше, чем случайной ошибки.
Высокая точность, низкая точность : эта цель демонстрирует пример высокой точности (все точки находятся близко к центральной цели), но низкой точности (точки не расположены близко друг к другу). В этом случае случайной ошибки больше, чем систематической.
Случайные или случайные ошибки
Из-за случайной ошибки измеренное значение становится меньше и больше истинного значения; это ошибки точности. Только случай определяет, больше или меньше значение. Считывание шкал весов, градуированного цилиндра, термометра и т. Д. Приводит к случайным ошибкам. Другими словами, вы можете взвесить блюдо на весах и каждый раз получать разный ответ просто из-за случайных ошибок. Их нельзя избежать; они являются частью процесса измерения.Неопределенности – это меры случайных ошибок. Это ошибки, возникающие в результате выполнения измерений на несовершенных инструментах, которые могут иметь только определенную степень точности.
Случайная ошибка возникает из-за факторов, которые мы не можем (или не контролируем) контролировать. Это может быть слишком дорого, или мы можем слишком игнорировать эти факторы, чтобы контролировать их каждый раз, когда проводим измерения. Возможно даже, что все, что мы пытаемся измерить, меняется во времени или является фундаментально вероятностным. Случайная ошибка часто возникает, когда инструменты работают на пределе своих возможностей.Например, цифровые весы часто показывают случайную ошибку в младшем разряде. Три измерения одного объекта могут показывать что-то вроде 0,9111 г, 0,9110 г и 0,9112 г.
Выбросы
В статистике выброс – это наблюдение, которое численно отличается от остальных данных.
Цели обучения
Объясните, как определять выбросы в распределении
Основные выводы
Ключевые моменты
- Отклонения могут возникать случайно, в результате человеческой ошибки или неисправности оборудования.Они могут указывать на ненормальное распределение или могут быть просто естественными отклонениями, возникающими в большой выборке.
- Если не будет установлено, что отклонение не является значительным, не стоит игнорировать наличие выбросов.
- Не существует строгого математического определения того, что является выбросом. Однако часто мы используем практическое правило, согласно которому любая точка, расположенная дальше, чем на два стандартных отклонения выше или ниже линии наилучшего соответствия, является выбросом.
Ключевые термины
- выброс : значение в статистической выборке, которое не соответствует шаблону, описывающему большинство других точек данных; в частности, значение, которое на 1,5 IQR превышает верхний или нижний квартиль
- Линия наилучшего соответствия : Линия на графике, показывающая общее направление, в котором группа точек, кажется, движется.
- линия регрессии : гладкая кривая, подобранная для набора парных данных в регрессионном анализе; для линейной регрессии кривая представляет собой прямую линию.
- межквартильный размах : разница между первым и третьим квартилями; надежная мера дисперсии выборки.
Выбросы
В статистике выброс – это наблюдение, которое численно отличается от остальных данных. Выбросы могут возникать случайно в любом распределении, но они часто указывают либо на ошибку измерения, либо на то, что популяция имеет распределение с тяжелыми хвостами. В первом случае их желают отбросить или использовать статистику, устойчивую к выбросам, в то время как во втором случае они указывают на то, что распределение искажено и что следует быть очень осторожными при использовании инструментов или интуиции, предполагающих нормальное распределение.
Если смотреть на линии регрессии, которые показывают, где попадают точки данных, выбросы далеки от линии наилучшего соответствия. У них есть большие «ошибки», где «ошибка» или невязка – это расстояние по вертикали от линии до точки.
Выбросы требуют внимательного изучения. Иногда по тем или иным причинам их не следует включать в анализ данных. Возможно, выброс является результатом ошибочных данных. В других случаях выброс может содержать ценную информацию об исследуемой популяции и должен оставаться включенным в данные.Ключ состоит в том, чтобы тщательно изучить, почему точка данных является выбросом.
Выявление выбросов
Мы могли угадывать выбросы, глядя на диаграмму рассеяния и линию наилучшего соответствия. Тем не менее, мы хотели бы получить некоторые рекомендации относительно того, как далеко должна находиться точка, чтобы считаться выбросом. В качестве приблизительного практического правила мы можем пометить любую точку, которая расположена дальше, чем на два стандартных отклонения выше или ниже линии наилучшего соответствия, как выброс , как показано ниже.Используемое стандартное отклонение – это стандартное отклонение остатков или ошибок.
Статистические выбросы : На этом графике показана линия наилучшего соответствия (сплошная синяя), соответствующая точкам данных, а также две дополнительные линии (синяя пунктирная линия), которые представляют собой два стандартных отклонения выше и ниже линии наилучшего соответствия. Оранжевым цветом выделены все точки, которые иногда называются «выпадающими», которые лежат в этом диапазоне; все, что находится за пределами этих линий – синие точки – можно считать выбросом.
Примечание. Не существует строгого математического определения того, что является выбросом; Определение того, является ли наблюдение выбросом, в конечном итоге является субъективным делом.Приведенное выше правило – лишь одно из многих используемых правил. Другой часто используемый метод основан на межквартильном размахе (IQR). Например, некоторые люди используют правило [latex] 1.5 \ cdot \ text {IQR} [/ latex]. Это определяет выброс как любое наблюдение, которое падает [latex] на 1,5 \ cdot \ text {IQR} [/ latex] ниже первого квартиля, или любое наблюдение, которое падает [latex] на 1,5 \ cdot \ text {IQR} [/ latex] выше третий квартиль.
Если мы собираемся использовать правило стандартного отклонения, мы можем сделать это визуально на диаграмме рассеяния, нарисовав дополнительную пару линий, которые на два стандартных отклонения выше и ниже линии наилучшего соответствия.Любые точки данных, которые находятся за пределами этой дополнительной пары линий, помечаются как потенциальные выбросы. Или мы можем сделать это численно, вычислив каждый остаток и сравнив его с удвоенным стандартным отклонением. Графические калькуляторы делают этот процесс довольно простым.
Причины выбросов
Выбросы могут иметь множество аномальных причин. Физическое устройство для проведения измерений могло иметь временную неисправность. Возможно, произошла ошибка при передаче или транскрипции данных.Выбросы возникают из-за изменений в поведении системы, мошенничества, ошибки человека, ошибки прибора или просто из-за естественных отклонений в популяциях. Образец мог быть загрязнен элементами, не относящимися к исследуемой популяции. В качестве альтернативы, выброс может быть результатом ошибки в предполагаемой теории, требующей дальнейшего исследования исследователем.
Если не будет установлено, что отклонение не является значительным, не рекомендуется игнорировать наличие выбросов.

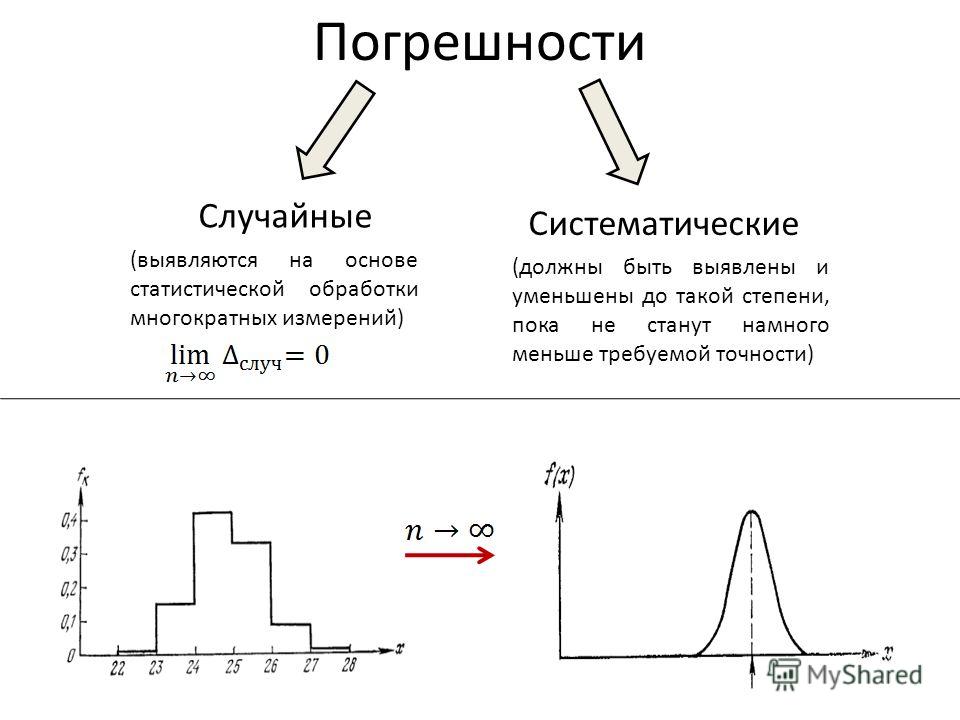 Погрешность воспроизведения единицы
Погрешность воспроизведения единицы


 Например, пластиковая рулетка с годами слегка растягивается, в результате чего размеры становятся немного завышенными,
Например, пластиковая рулетка с годами слегка растягивается, в результате чего размеры становятся немного завышенными,