Как строить сечения 🚩 что такое сечение в геометрии 🚩 Математика
Автор КакПросто!
Сечением многогранника является плоскость, которая пересекает её грани. В зависимости от исходных данных существует множество методов построения сечения. Рассмотрим случай, когда даны три точки сечения, лежащие на разных рёбрах многогранника. В этом случае для построения сечения проводятся прямые через точки, лежащие на одной прямой, после чего ищутся прямые пересечения граней с плоскостью сечения.
Статьи по теме:
Инструкция
Пусть дан куб ABCDA1B1C1D1. Необходимо провести сечение через точки M, N и L, лежащие на его рёбрах.Соединим точки L и M. Прямая ML и ребро A1D1 лежат в одной плоскости ADA1D1. Пересечём их, получим точку X1. Отрезок ML – пересечение плоскости сечения с гранью AA1D1D.
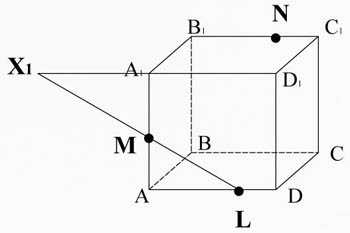
Точка X1 принадлежит плоскости A1B1C1D1, т.к. лежит на прямой A1D1. Прямая X1N пересекает ребро A1B1 в точке K. Отрезок KM – пересечение плоскости сечения с гранью AA1B1B.
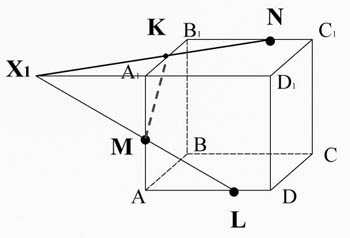
Прямая ML и ребро D1D лежат в одной плоскости AA1D1D. Пересечём их, получим точку X2. Прямая KN и ребро D1C1 так же лежат в одной плоскости A1B1C1D1. Пересечём их, получим точку X3.
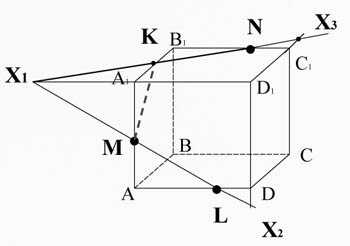
Построим прямую X2X3. Эта прямая лежит на плоскости CC1D1D и пересекает ребро DC в точке P, ребро СС1 в точке T.
Соединив точки L, P, T и N получим сечение MKNTPL.
Таким способом можно построить сечение любого многогранника.
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Учимся строить сечения многогранников. Часть 2.
Учимся строить сечения многогранников. Часть 2.
Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.
Вспомним, что сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат сторонам, а ребра – граням многогранника. Две соседние вершины принадлежат одной грани многогранника.
Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.
В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.
Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.
Постройте сечения, проходящие через точки .
Задание 1:
Подсказка. показать
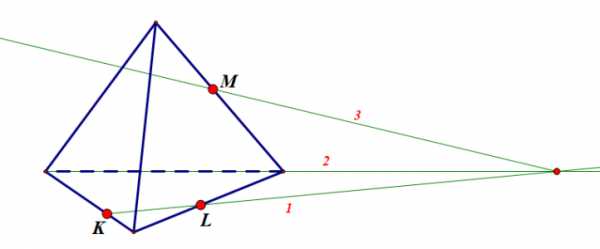
Ответ. показать
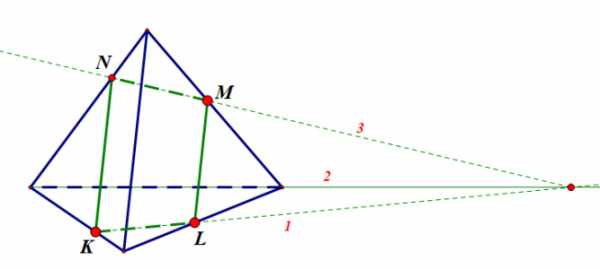
Задание 2:
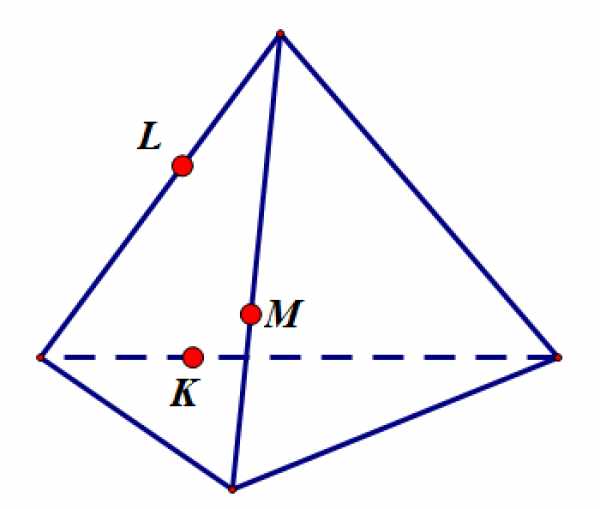
Подсказка: показать
Ответ: показать
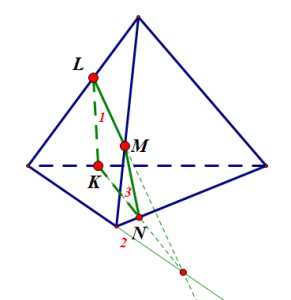
Задание 3:
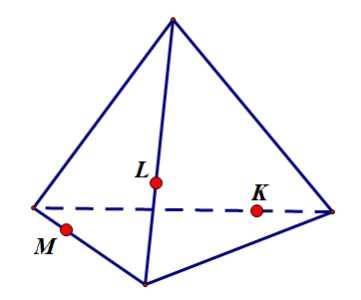
Подсказка: показать
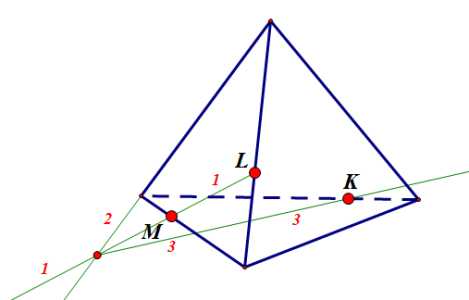
Ответ: показать
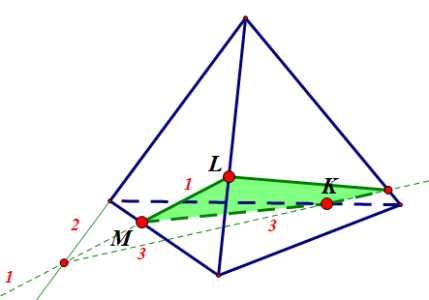
Задание 4:
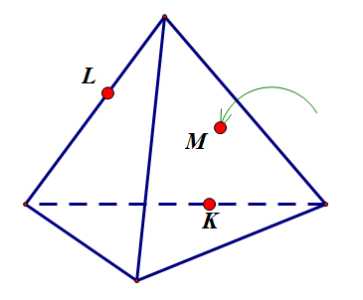
Подсказка: показать
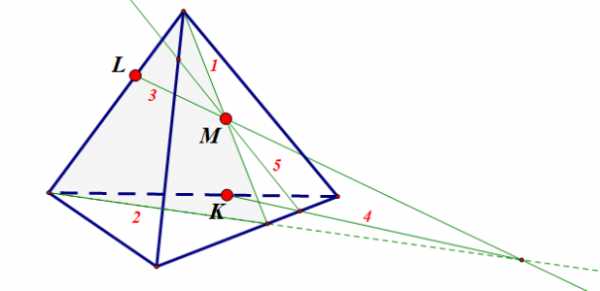
Ответ: показать
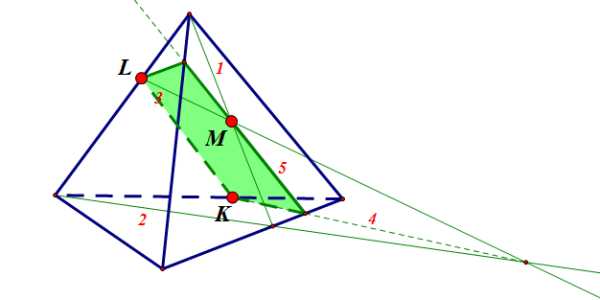
Задание 5:
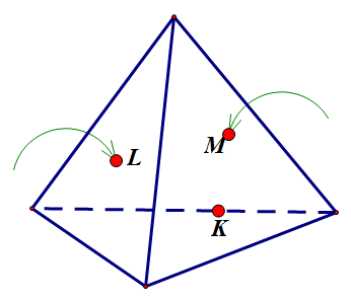
Подсказка: показать
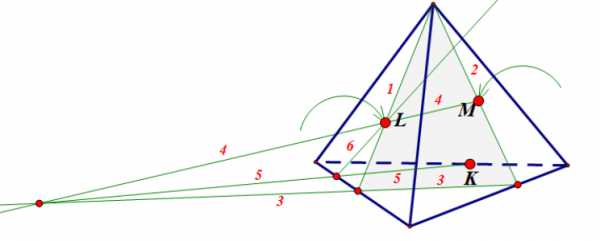
Ответ: показать
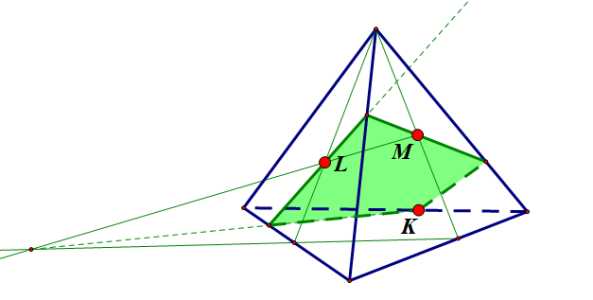
Задание 6:
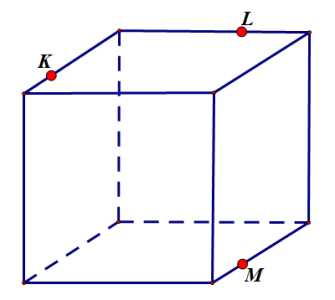
Подсказка: показать
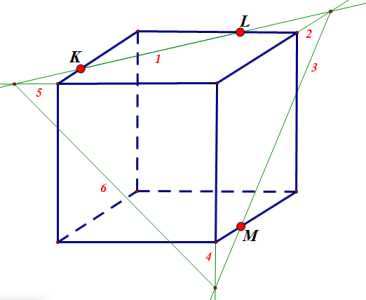
Ответ: показать
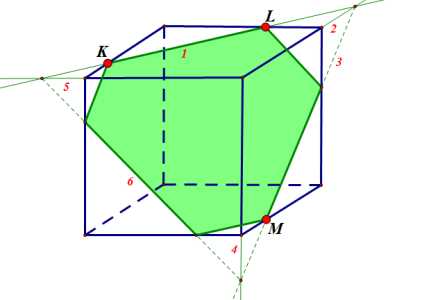
Задание 7:
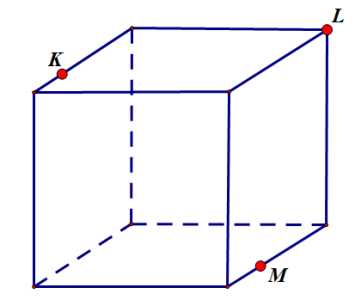
Подсказка: показать
Ответ: показать
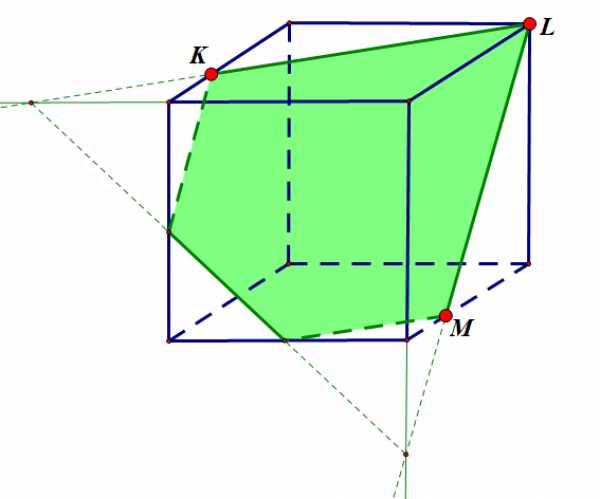
Задание 8:
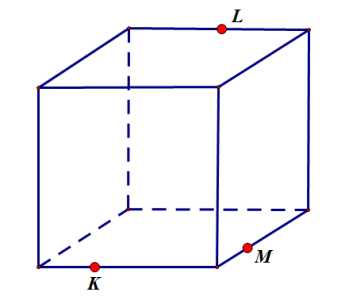
Подсказка: показать
Ответ: показать
Задание 9:
Подсказка: показать
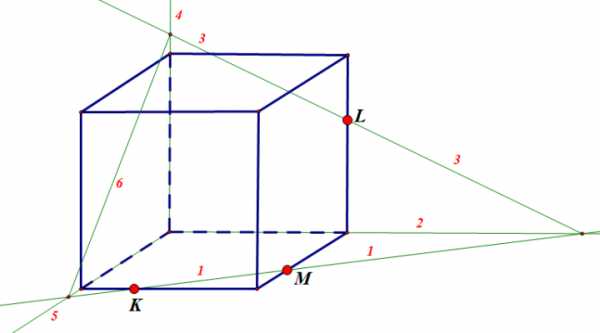
Ответ: показать
Задание 10:
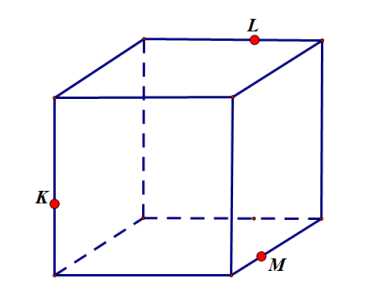
Подсказка: показать
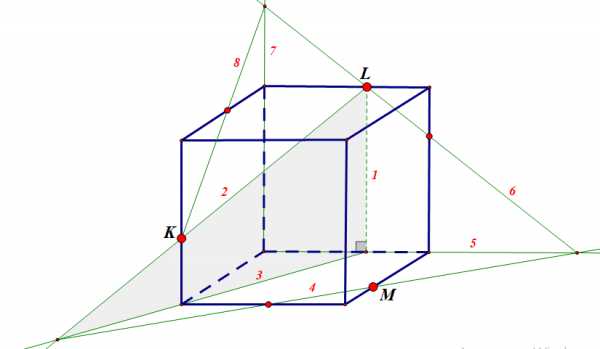
Ответ: показать
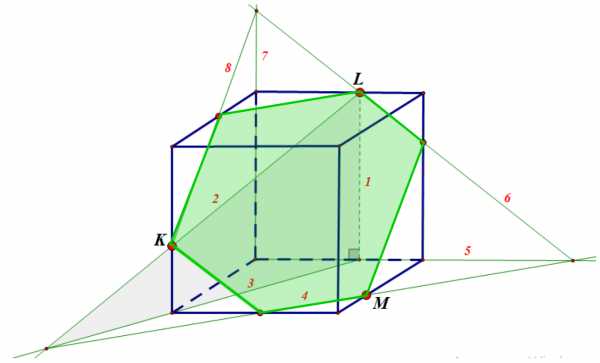
Задание 11:
Подсказка: показать
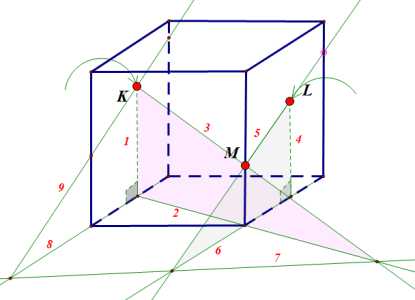
Ответ: показать
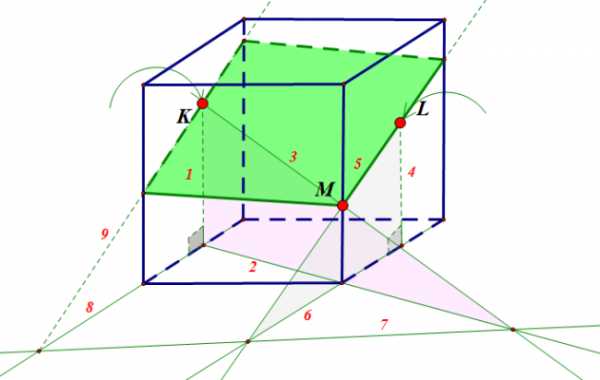
И. В. Фельдман, репетитор по математике.
ege-ok.ru
Построение сечений
Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.
Важные определения
1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.
3. Прямая и плоскость параллельны, если они не имеют общих точек.
4. Две плоскости параллельны, если они не имеют общих точек.
5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен \(90^\circ\).
6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
7. Две плоскости называются перпендикулярными, если угол между ними равен \(90^\circ\).
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая \(a\), не лежащая в плоскости \(\pi\), параллельна некоторой прямой \(p\), лежащей в плоскости \(\pi\), то она параллельна данной плоскости.
2. Пусть прямая \(p\) параллельна плоскости \(\mu\). Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\), то линия пересечения плоскостей \(\pi\) и \(\mu\) — прямая \(m\) — параллельна прямой \(p\).
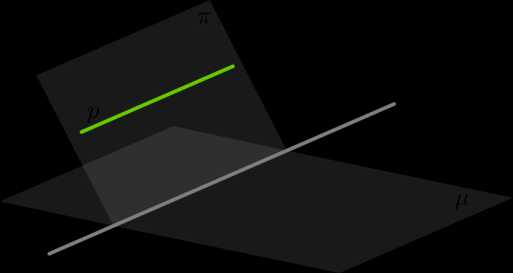
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\), то линии пересечения плоскостей также параллельны:
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]
5. Пусть прямая \(l\) лежит в плоскости \(\lambda\). Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\), не лежащей на прямой \(l\), то прямые \(l\) и \(s\) скрещиваются.
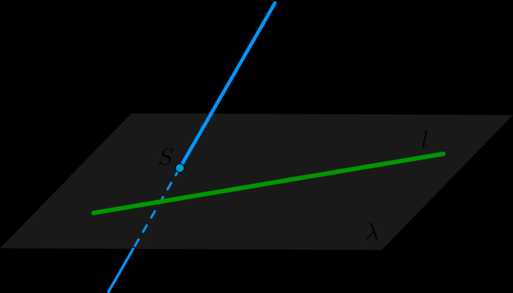
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
7. Теорема о трех перпендикулярах.
Пусть \(AH\) – перпендикуляр к плоскости \(\beta\). Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\). Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.
Для этого из двух произвольных точек \(A\) и \(B\) прямой \(a\) проведем перпендикуляры на плоскость \(\mu\) – \(AA’\) и \(BB’\) (точки \(A’, B’\) называются проекциями точек \(A,B\) на плоскость). Тогда прямая \(A’B’\) – проекция прямой \(a\) на плоскость \(\mu\). Точка \(M=a\cap A’B’\) и есть точка пересечения прямой \(a\) и плоскости \(\mu\).
Причем заметим, что все точки \(A, B, A’, B’, M\) лежат в одной плоскости.
Пример 1.
Дан куб \(ABCDA’B’C’D’\). \(A’P=\dfrac 14AA’, \ KC=\dfrac15 CC’\). Найдите точку пересечения прямой \(PK\) и плоскости \(ABC\).
Решение
1) Т.к. ребра куба \(AA’, CC’\) перпендикулярны \((ABC)\), то точки \(A\) и \(C\) — проекции точек \(P\) и \(K\). Тогда прямая \(AC\) – проекция прямой \(PK\) на плоскость \(ABC\). Продлим отрезки \(PK\) и \(AC\) за точки \(K\) и \(C\) соответственно и получим точку пересечения прямых – точку \(E\).
2) Найдем отношение \(AC:EC\). \(\triangle PAE\sim \triangle KCE\) по двум углам (\(\angle A=\angle C=90^\circ, \angle E\) – общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
Если обозначить ребро куба за \(a\), то \(PA=\dfrac34a, \ KC=\dfrac15a, \ AC=a\sqrt2\). Тогда:
\[\dfrac{\frac34a}{\frac15a}=\dfrac{a\sqrt2+EC}{EC} \Rightarrow EC=\dfrac{4\sqrt2}{11}a \Rightarrow AC:EC=4:11\]
Пример 2.
Дана правильная треугольная пирамида \(DABC\) с основанием \(ABC\), высота которой равна стороне основания. Пусть точка \(M\) делит боковое ребро пирамиды в отношении \(1:4\), считая от вершины пирамиды, а \(N\) – высоту пирамиды в отношении \(1:2\), считая от вершины пирамиды. Найдите точку пересечения прямой \(MN\) с плоскостью \(ABC\).
Решение
1) Пусть \(DM:MA=1:4, \ DN:NO=1:2\) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку \(O\) пересечения медиан основания. Найдем проекцию прямой \(MN\) на плоскость \(ABC\). Т.к. \(DO\perp (ABC)\), то и \(NO\perp (ABC)\). Значит, \(O\) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр \(MQ\) из точки \(M\) на плоскость \(ABC\). Точка \(Q\) будет лежать на медиане \(AK\).
Действительно, т.к. \(MQ\) и \(NO\) перпендикулярны \((ABC)\), то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки \(M, N, O\) лежат в одной плоскости \(ADK\), то и точка \(Q\) будет лежать в этой плоскости. Но еще (по построению) точка \(Q\) должна лежать в плоскости \(ABC\), следовательно, она лежит на линии пересечения этих плоскостей, а это – \(AK\).
Значит, прямая \(AK\) и есть проекция прямой \(MN\) на плоскость \(ABC\). \(L\) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки \(L\) (например, на нашем чертеже точка \(L\) лежит вне отрезка \(OK\), хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим \(AB=DO=a\). Тогда медиана \(AK=\dfrac{\sqrt3}2a\). Значит, \(OK=\dfrac13AK=\dfrac 1{2\sqrt3}a\). Найдем длину отрезка \(OL\) (тогда мы сможем понять, внутри или вне отрезка \(OK\) находится точка \(L\): если \(OL>OK\) – то вне, иначе – внутри).
а) \(\triangle AMQ\sim \triangle ADO\) по двум углам (\(\angle Q=\angle O=90^\circ, \ \angle A\) – общий). Значит,
\[\dfrac{MQ}{DO}=\dfrac{AQ}{AO}=\dfrac{MA}{DA}=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \ AQ=\dfrac 45\cdot \dfrac 1{\sqrt3}a\]
Значит, \(QK=\dfrac{\sqrt3}2a-\dfrac 45\cdot \dfrac 1{\sqrt3}a=\dfrac7{10\sqrt3}a\).
б) Обозначим \(KL=x\).
\(\triangle LMQ\sim \triangle LNO\) по двум углам (\(\angle Q=\angle O=90^\circ, \ \angle L\) – общий). Значит,
\[\dfrac{MQ}{NO}=\dfrac{QL}{OL} \Rightarrow \dfrac{\frac45 a}{\frac 23a} =\dfrac{\frac{7}{10\sqrt3}a+x}{\frac1{2\sqrt3}a+x} \Rightarrow x=\dfrac a{2\sqrt3} \Rightarrow OL=\dfrac a{\sqrt3}\]
Следовательно, \(OL>OK\), значит, точка \(L\) действительно лежит вне отрезка \(AK\).
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\)).
Пример 3
Дана правильная четырехугольная пирамида \(SABCD\). Найдите сечение пирамиды плоскостью \(\alpha\), проходящей через точку \(C\) и середину ребра \(SA\) и параллельной прямой \(BD\).
Решение
1) Обозначим середину ребра \(SA\) за \(M\). Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\). Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\).
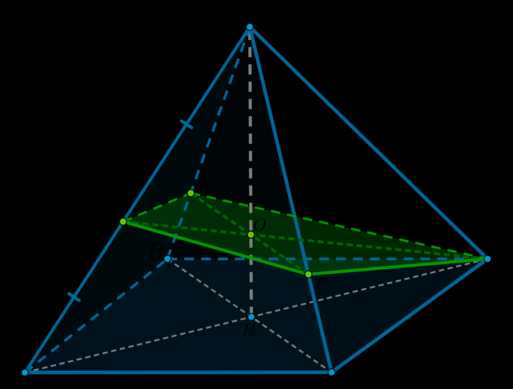
Для того, чтобы плоскость \(\alpha\) была параллельна прямой \(BD\), она должна содержать некоторую прямую, параллельную \(BD\). Точка \(O\) находится вместе с прямой \(BD\) в одной плоскости – в плоскости \(BSD\). Проведем в этой плоскости через точку \(O\) прямую \(KP\parallel BD\) (\(K\in SB, P\in SD\)). Тогда, соединив точки \(C, P, M, K\), получим сечение пирамиды плоскостью \(\alpha\).
2) Найдем отношение, в котором делят точки \(K\) и \(P\) ребра \(SB\) и \(SD\). Таким образом мы полностью определим построенное сечение.
Заметим, что так как \(KP\parallel BD\), то по теореме Фалеса \(\dfrac{SB}{SK}=\dfrac{SD}{SP}\). Но \(SB=SD\), значит и \(SK=SP\). Таким образом, можно найти только \(SP:PD\).
Рассмотрим \(\triangle ASC\). \(CM, SH\) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении \(2:1\), считая от вершины, то есть \(SO:OH=2:1\).
Теперь по теореме Фалеса из \(\triangle BSD\): \(\dfrac{SP}{PD}=\dfrac{SO}{OH}=\dfrac21\).
3) Заметим, что по теореме о трех перпендикулярах \(CO\perp BD\) как наклонная (\(OH\) – перпендикуляр на плоскость \(ABC\), \(CH\perp BD\) – проекция). Значит, \(CO\perp KP\). Таким образом, сечением является четырехугольник \(CPMK\), диагонали которого взаимно перпендикулярны.
Пример 4
Дана прямоугольная пирамида \(DABC\) с ребром \(DB\), перпендикулярным плоскости \(ABC\). В основании лежит прямоугольный треугольник с \(\angle B=90^\circ\), причем \(AB=DB=CB\). Проведите через прямую \(AB\) плоскость, перпендикулярную грани \(DAC\), и найдите сечение пирамиды этой плоскостью.
Решение
1) Плоскость \(\alpha\) будет перпендикулярна грани \(DAC\), если она будет содержать прямую, перпендикулярную \(DAC\). Проведем из точки \(B\) перпендикуляр на плоскость \(DAC\) — \(BH\), \(H\in DAC\).
Проведем вспомогательные \(BK\) – медиану в \(\triangle ABC\) и \(DK\) – медиану в \(\triangle DAC\).
Т.к. \(AB=BC\), то \(\triangle ABC\) – равнобедренный, значит, \(BK\) – высота, то есть \(BK\perp AC\).
Т.к. \(AB=DB=CB\) и \(\angle ABD=\angle CBD=90^\circ\), то \(\triangle
ABD=\triangle CBD\), следовательно, \(AD=CD\), следовательно, \(\triangle DAC\) – тоже равнобедренный и \(DK\perp AC\).
Применим теорему о трех перпендикулярах: \(BH\) – перпендикуляр на \(DAC\); наклонная \(BK\perp AC\), значит и проекция \(HK\perp AC\). Но мы уже определили, что \(DK\perp AC\). Таким образом, точка \(H\) лежит на отрезке \(DK\).
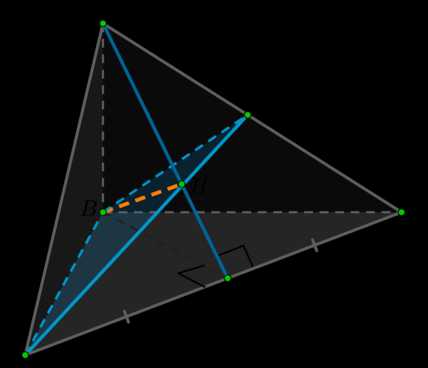
Соединив точки \(A\) и \(H\), получим отрезок \(AN\), по которому плоскость \(\alpha\) пересекается с гранью \(DAC\). Тогда \(\triangle ABN\) – искомое сечение пирамиды плоскостью \(\alpha\).
2) Определим точное положение точки \(N\) на ребре \(DC\).
Обозначим \(AB=CB=DB=x\). Тогда \(BK\), как медиана, опущенная из вершины прямого угла в \(\triangle ABC\), равна \(\frac12 AC\), следовательно, \(BK=\frac12 \cdot \sqrt2 x\).
Рассмотрим \(\triangle BKD\). Найдем отношение \(DH:HK\).
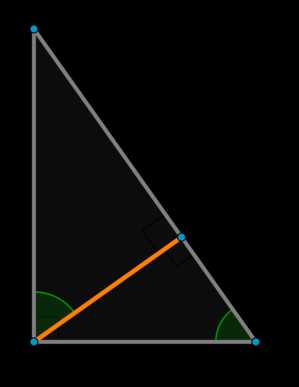
Заметим, что т.к. \(BH\perp (DAC)\), то \(BH\) перпендикулярно любой прямой из этой плоскости, значит, \(BH\) – высота в \(\triangle DBK\). Тогда \(\triangle DBH\sim \triangle DBK\), следовательно
\[\dfrac{DH}{DB}=\dfrac{DB}{DK} \Rightarrow DH=\dfrac{\sqrt6}3x \Rightarrow HK=\dfrac{\sqrt6}6x \Rightarrow DH:HK=2:1\]
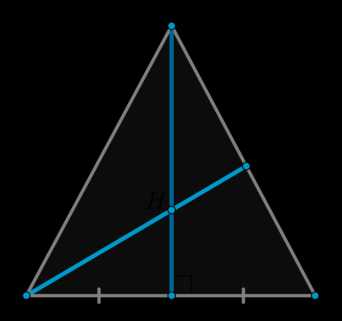
Рассмотрим теперь \(\triangle ADC\). Медианы треугольника точной пересечения делятся в отношении \(2:1\), считая от вершины. Значит, \(H\) – точка пересечения медиан в \(\triangle ADC\) (т.к. \(DK\) – медиана). То есть \(AN\) – тоже медиана, значит, \(DN=NC\).
shkolkovo.net
Пошаговое построение сечения параллелепипеда
Построение сечения методом следов – это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.
Задача 1. Построить сечение параллелепипеда плоскостью, проходящей через точки .
Задача 1. Дано
Шаг 1. Чезез точки и , которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой , которая также принадлежала бы основанию. Для этого проводим прямую , и находим точку ее пересечения с прямой – .
Задача 1. Шаг 1.
Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра – .
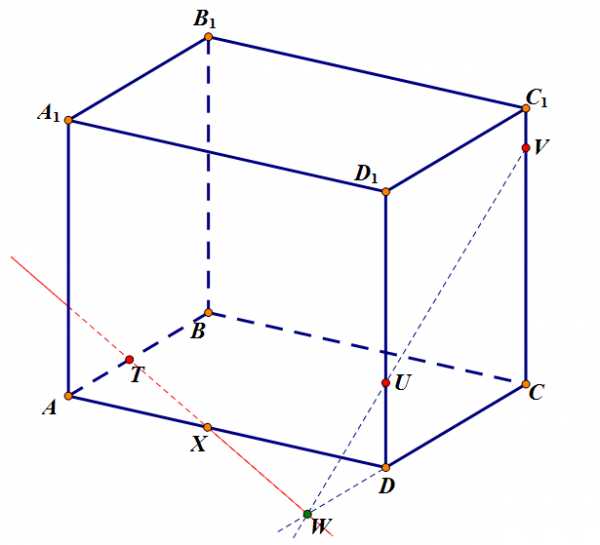
Задача 1. Шаг 2.
Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой , которая принадлежала бы плоскости задней грани. Для этого проведем прямую , которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой – . Через две точки задней грани проводим прямую , и находим место пересечения этой прямой с ребром – .
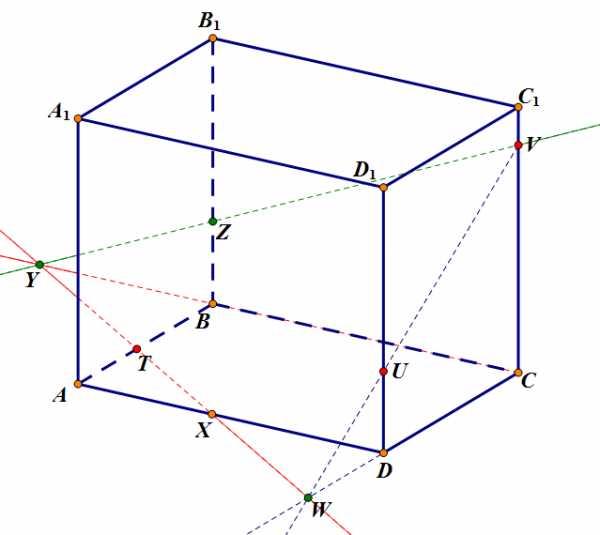
Задача 1. Шаг 3.
Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.
Задача 1. Шаг 4.
Задача 2. Построить сечение параллелепипеда плоскостью, проходящей через точки
Задача 2. Дано.
Шаг 1. Точки и лежат в одной плоскости, можно соединить их прямой. Прямая пересечет ребро в точке .
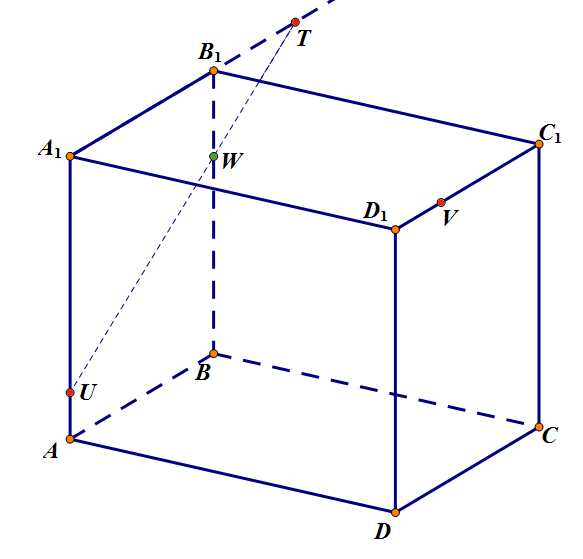
Задача 2. Шаг 1.
Шаг 2. Точки и также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра – .
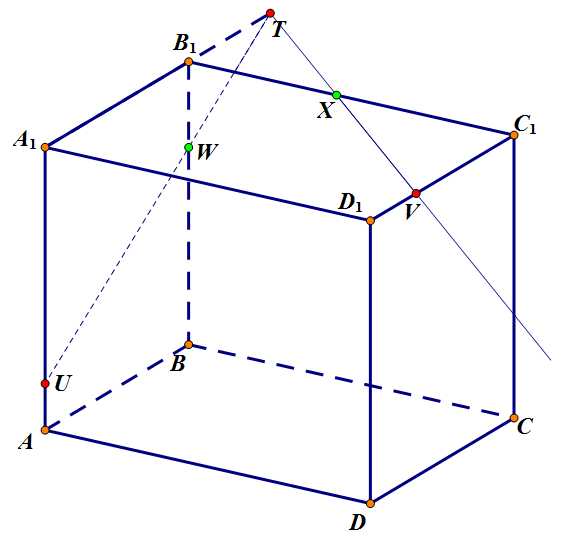
Задача 2. Шаг 2
Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч и найдем его пересечение с прямой – ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения – точка . Точки и можно соединить отрезком.
Задача 2. Шаг 3.
Шаг 4. Находим точку пересечения отрезком ребра – точку .
Задача 2. Шаг 4
Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.
Задача 2. Шаг 5
Задача 3. Построить сечение параллелепипеда плоскостью, проходящей через точки
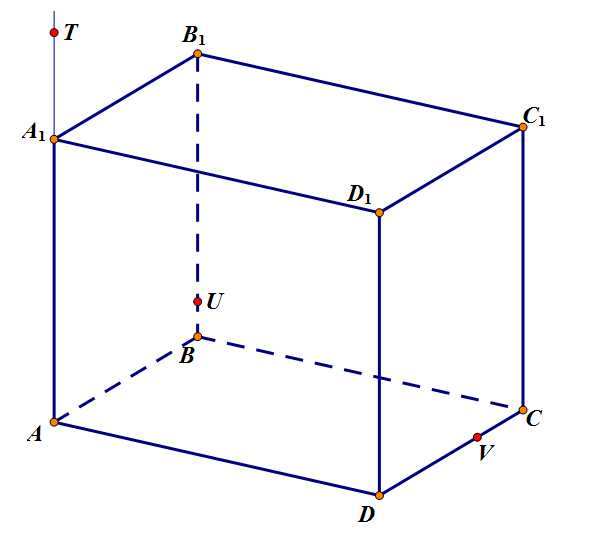
Задача 3. Дано.
Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка принадлежит грани основания, поэтому нужна точка в этой плоскости.
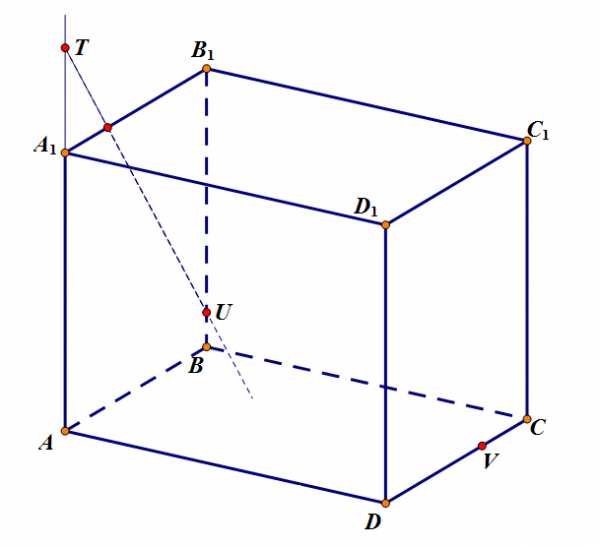
Задача 3. Шаг 1
Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой – .
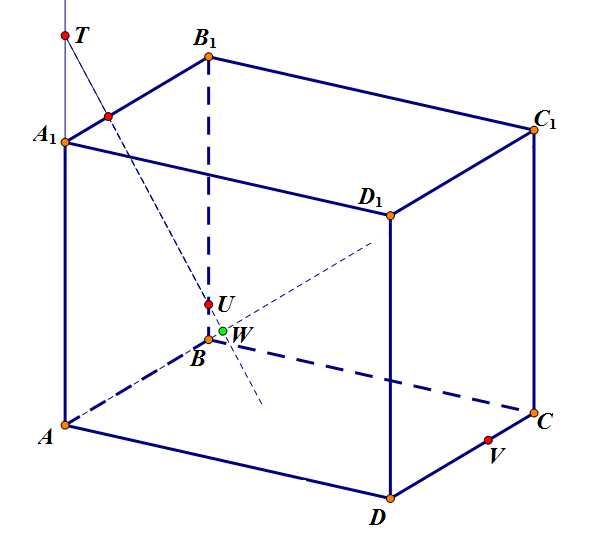
Задача 3. Шаг 2.
Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром – точка .
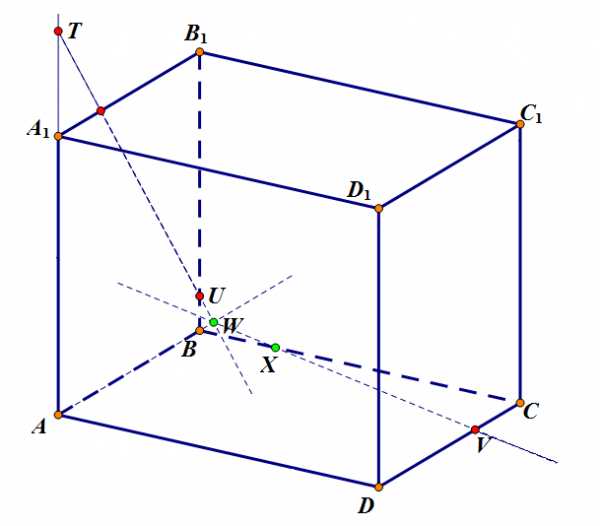
Задача 3. Шаг 3.
Шаг 4. Теперь надо найти точку в плоскости передней грани, потому что в этой плоскости у нас уже есть точка – точка . Для того, чтобы найти такую точку, продлим прямую и найдем пересечение этой прямой с прямой – точка .
Задача 3. Шаг 4
Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер – точку , и ребра – точку .
Задача 3. Шаг 5.
Шаг 6. Соединяем точки и получаем многоугольник сечения.
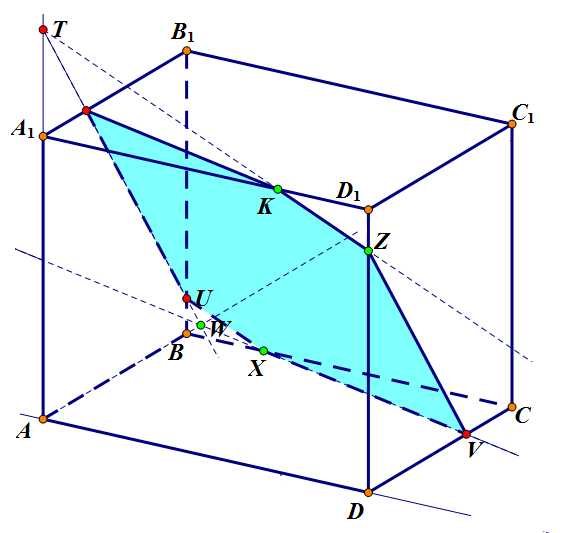
Задача 3. Шаг 6
Окончательный вид сечения с другого ракурса:
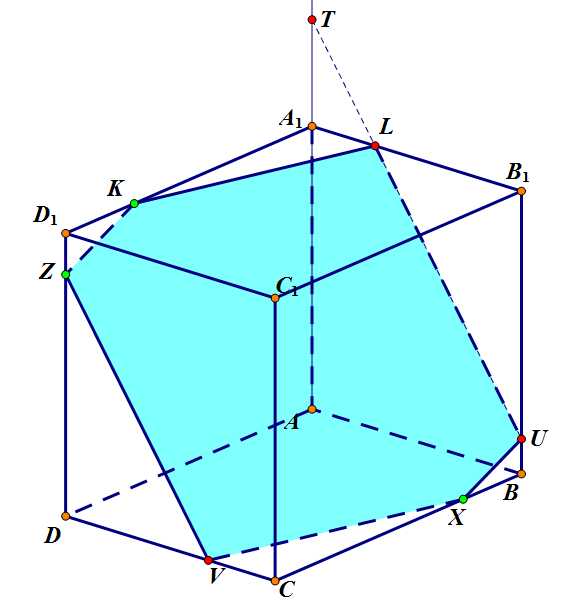
Окончательный вид
Задача 4. Построить сечение параллелепипеда плоскостью, проходящей через точки . Точка в задней грани.
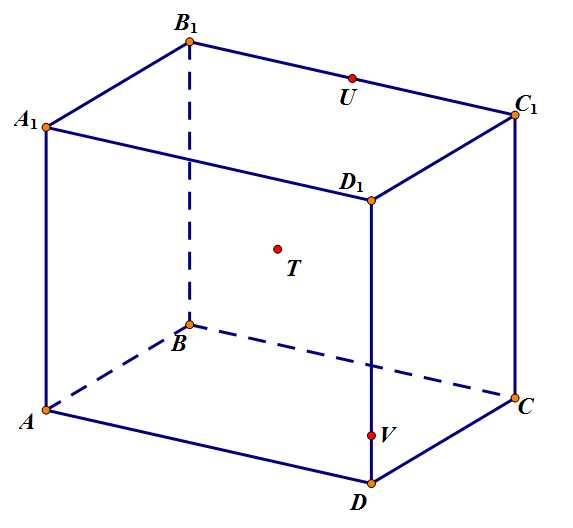
Задача 4. Дано
Шаг 1. Проводим прямую через две точки одной плоскости – и . Определяем точку пересечения данной прямой ребра – .
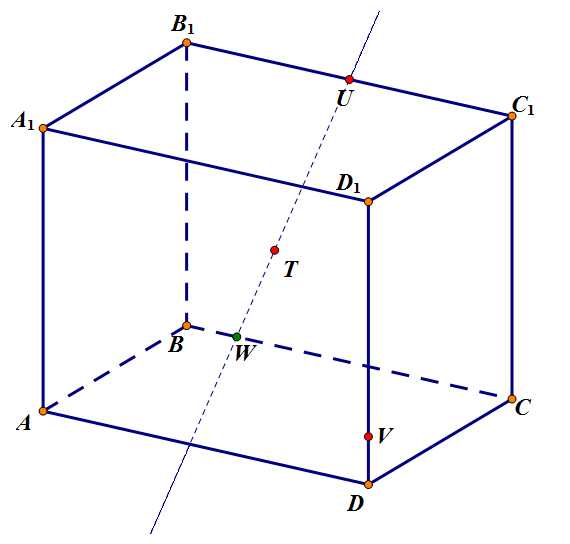
Задача 4. Шаг 1.
Шаг 2. Продолжение прямой пересечется с продолжением прямой – так как обе прямые принадлежат плоскости задней грани. Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .
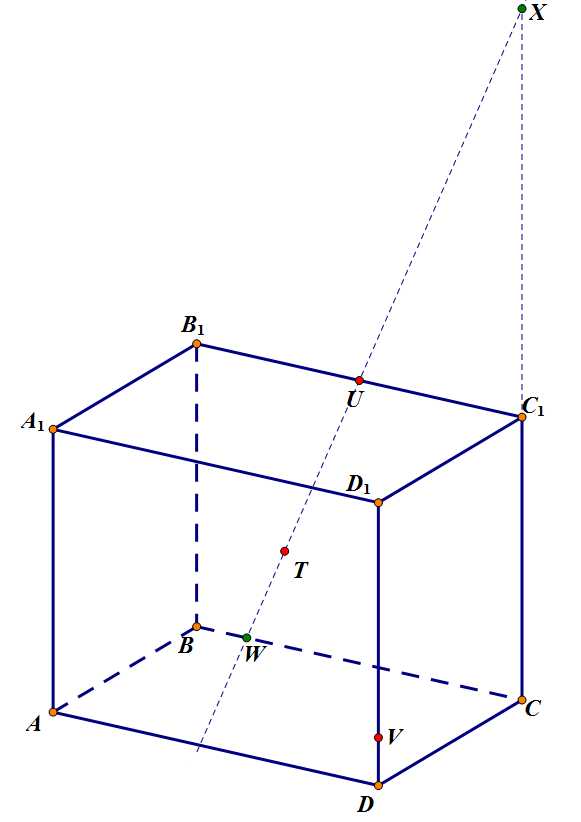
Задача 4. Шаг 2.
Шаг 3. Точка – точка пересечения прямой ребра . Продлим также ребро и найдем пересечение прямой и прямой – точку , которая принадлежит плоскости основания.
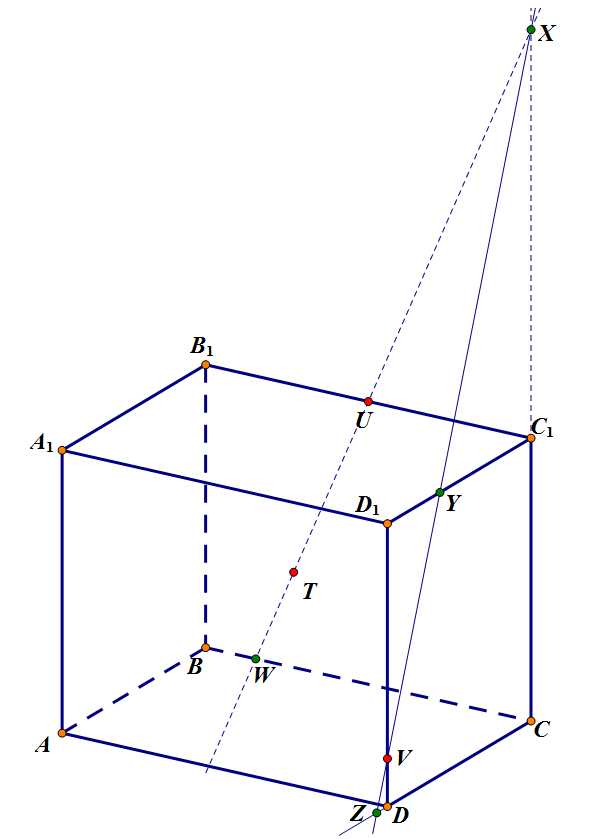
Задача 4. Шаг 3
Шаг 4. Соединяем Точки и плоскости основания, определяем точку пересечения данной прямой с ребром – точку . Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.
Задача 4. Шаг 4.
Окончательный вид сечения с другого ракурса:
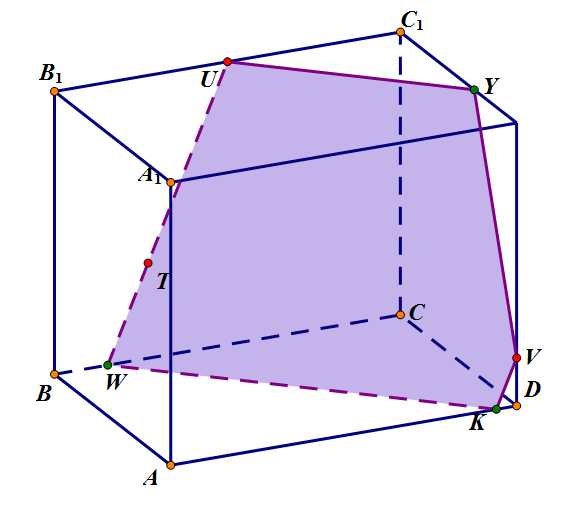
Окончание построения
easy-physic.ru
Примеры построения сечений многогранников
Как известно, любой экзамен по математике содержит в качестве основной части решение задач. Умение решать задачи – основной показатель уровня математического развития.
Достаточно часто на школьных экзаменах, а так же на экзаменах, проводимых в ВУЗах и техникумах, встречаются случаи, когда ученики, показывающие хорошие результаты в области теории, знающие все необходимые определения и теоремы, запутываются при решении весьма простых задач.
За годы обучения в школе каждый ученик решает большое число задач, но при этом для всех учеников задачи предлагаются одни и те же. И если некоторые ученики усваивают общие правила и методы решения задач, то другие, встретившись с задачей незнакомого вида, даже не знают, как к ней подступиться.
Одной из причин такого положения является то, что если одни ученики вникают в ход решения задачи и стараются осознать и понять общие приёмы и методы их решения, то другие не задумываются над этим, стараются как можно быстрее решить предложенные задачи.
Многие учащиеся не анализируют решаемые задачи, не выделяют для себя общие приёмы и способы решения. В таких случаях задачи решаются только ради получения нужного ответа.
Так, например, многие учащиеся даже не знают, в чём суть решения задач на построение. А ведь задачи на построение являются обязательными задачами в курсе стереометрии. Эти задачи не только красивы и оригинальны в методах своего решения, но и имеют большую практическую ценность.
Благодаря задачам на построение развивается способность мысленно представлять себе ту или иную геометрическую фигуру, развивается пространственное мышление, логическое мышление, а так же геометрическая интуиция. Задачи на построение развивают навыки решения проблем практического характера.
Задачи на построения не являются простыми, так как единого правила или алгоритма для их решения не существует. Каждая новая задача уникальна и требует индивидуального подхода к решению.
Процесс решения любой задачи на построение – это последовательность некоторых промежуточных построений, приводящих к цели.
Построение сечений многогранников базируется на следующих аксиомах:
1) Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в данной плоскости;
2) Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Теорема: если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны.
Примеры построения сечений многогранников
Построить сечение многогранника плоскостью, проходящей через точки А, В и С. Рассмотрим следующие примеры.
Метод следов
I. Построить сечение призмы плоскостью, проходящей через данную прямую g (след) на плоскости одного из оснований призмы и точку А.
Случай 1.
Точка А принадлежит другому основанию призмы (или грани, параллельной прямой g) – секущая плоскость пересекает это основание (грань) по отрезку ВС, параллельному следу g.
Случай 2.
Точка А принадлежит боковой грани призмы:
1) строится точка D, в которой плоскость грани пересекает данный след g;
2) проводится прямая через точки А и D.
Отрезок ВС прямой AD и есть пересечение данной грани с секущей плоскостью.
Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. И т. д.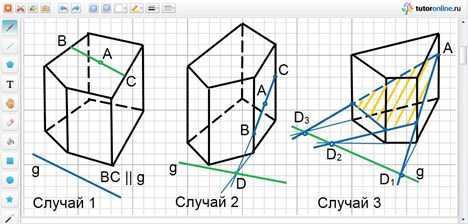
Случай 3.
Построение сечения четырехугольной призмы плоскостью, проходящей через прямую g в плоскости нижнего основания призмы и точку А на одном из боковых ребер.
II. Построить сечение пирамиды плоскостью, проходящей через данную прямую g (след) на плоскости основания пирамиды и точку А.
Для построения сечения пирамиды плоскостью достаточно построить пересечения ее боковых граней с секущей плоскостью.
Случай 1.
Если точка А принадлежит грани, параллельной прямой g, то секущая плоскость пересекает эту грань по отрезку ВС, параллельному следу g.
Случай 2.
Если точка А, принадлежащая сечению, расположена на грани, не параллельной грани следу g, то:
1) строится точка D, в которой плоскость грани пересекает данный след g;
2) проводится прямая через точки А и D.
Отрезок ВС прямой АD и есть пересечение данной грани с секущей плоскостью.
Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. И т. д.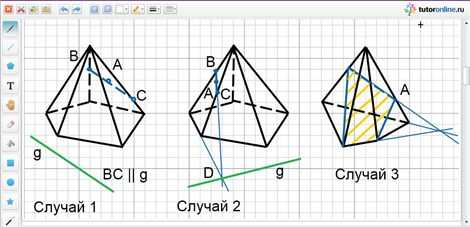
Случай 3.
Построение сечения четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку А на одном из боковых ребер.
Задачи на построение сечений через точку на грани
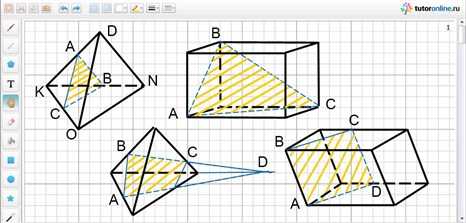
1. Построить сечение тетраэдра АВСD плоскостью, проходящей через вершину С и точки М и N на гранях АСD и АВС соответственно.
Точки С и М лежат на грани АСD, значит, и прямая СМ лежит в плоскости этой грани (рис. 1).
Пусть Р – точка пересечения прямых СМ и АD. Аналогично, точки С и N лежат в грани АСВ, значит прямая СN лежит в плоскости этой грани. Пусть Q – точка пересечения прямых СN и АВ. Точки Р и Q принадлежат и плоскости сечения, и грани АВD. Поэтому отрезок РQ – сторона сечения. Итак, треугольник СРQ – искомое сечение.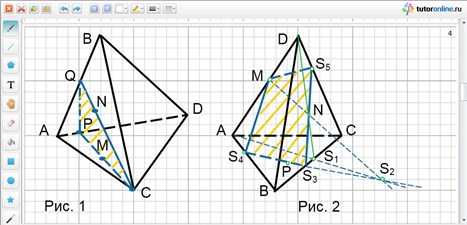
2. Построить сечение тетраэдра АВСD плоскостью MPN, где точки M, N, P лежат соответственно на ребре АD, в грани ВСD и в грани АВС, причем MN не параллельно плоскости грани АВС (рис. 2).
Остались вопросы? Не знаете, как построить сечение многогранника?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Учимся строить сечения многогранников.
Учимся строить сечения многогранников.
В этой статье я предлагаю вам самостоятельно построить сечения многогранника, проходящее через точки . Каждое задание сопровождается видео с пошаговым построением сечения. Продолжение статьи читайте здесь.
Задание 1.
Построение. показать
Задание 2.
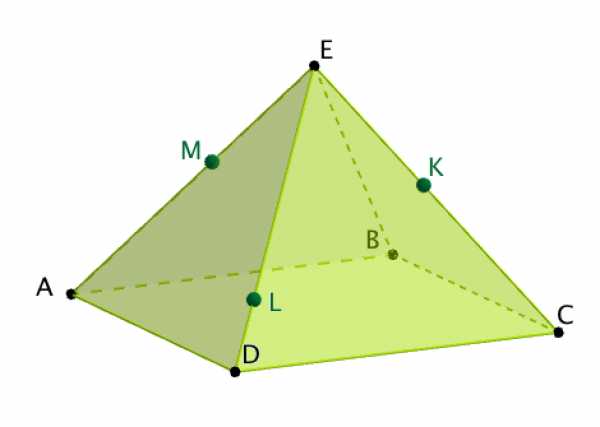
Построение. показать
Задание 3.
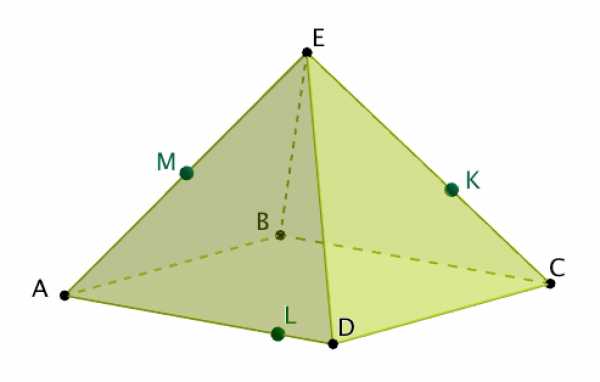
Построение. показать
Задание 4.
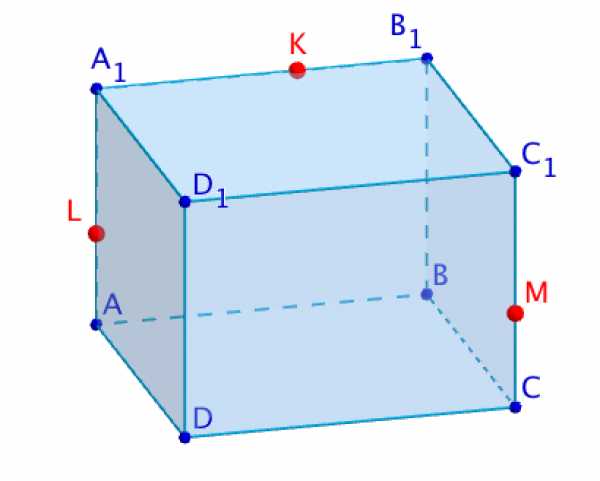
Построение. показать
Задание 5.
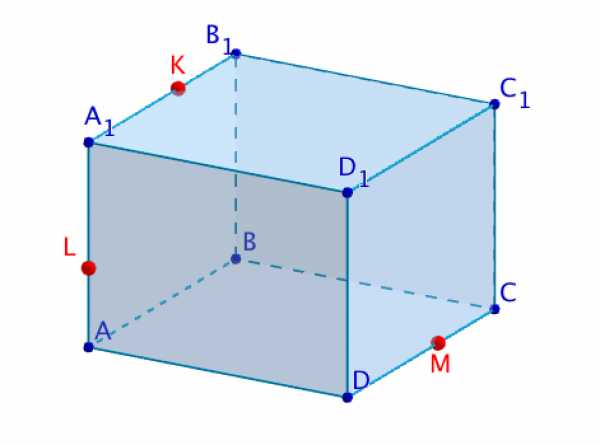
Построение. показать
Задание 6.
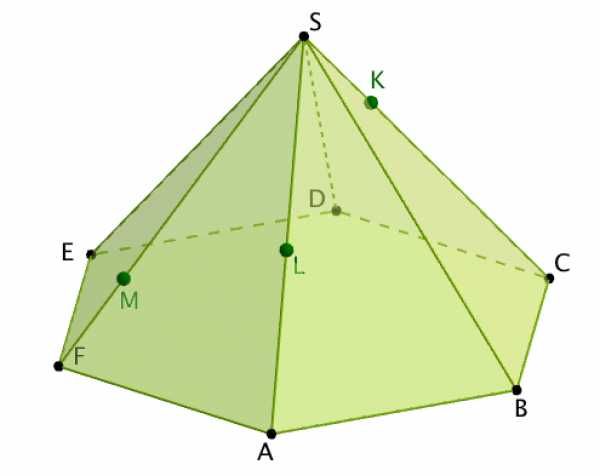
Построение. показать
И. В. Фельдман, репетитор по математике.
ege-ok.ru
Построение сечений многогранников
А вы знаете, что называется сечением многогранников плоскостью? Если вы пока сомневаетесь в правильности своего ответа на этот вопрос, то можете довольно просто себя проверить. Предлагаем пройти небольшой тест, представленный ниже.
Вопрос. Назовите номер рисунка, на котором изображено сечение параллелепипеда плоскостью?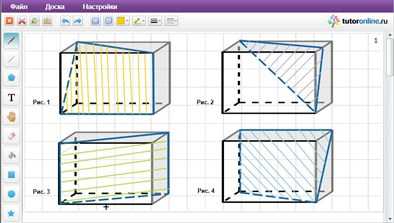
Итак, правильный ответ – на рисунке 3.
Если вы ответите правильно, это подтверждает то, что вы понимаете, с чем имеете дело. Но, к сожалению, даже правильный ответ на вопрос-тест не гарантирует вам наивысших отметок на уроках по теме «Сечения многогранников». Ведь самым сложным является не распознавание сечений на готовых чертежах, хотя это тоже очень важно, а их построении.
Для начала сформулируем определение сечения многогранника. Итак, сечением многогранника называют многоугольник, вершины которого лежат на ребрах многогранника, а стороны – на его гранях.
Теперь потренируемся быстро и безошибочно строить точки пересечения данной прямой с заданной плоскостью. Для этого решим следующую задачу.
Построить точки пересечения прямой MN с плоскостями нижнего и верхнего оснований треугольной призмы ABCA1B1C1, при условии, что точка M принадлежит боковому ребру CC1, а точка N – ребру BB1.
Начнем с того, что продлим на чертеже прямую MN в обе стороны (рис. 1). Затем, чтобы получить необходимые по уловию задачи точки пересечения, продлеваем и прямые, лежащие в верхнем и нижнем основаниях. И вот наступает самый сложный момент в решении задачи: какие именно прямые в обоих основаниях необходимо продлить, так как в каждом из них имеется по три прямые.
Чтобы правильно сделать заключительный шаг построения, необходимо определить, какие из прямых оснований находятся в той же плоскости, что и интересующая нас прямая MN. В нашем случае – это прямая CB в нижнем и C1B1 в верхнем основаниях. И именно их и продлеваем до пересечения с прямой NM (рис. 2).
Полученные точки P и P1 и есть точки пересечения прямой MN с плоскостями верхнего и нижнего оснований треугольной призмы ABCA1B1C1.
После разбора представленной задачи можно перейти непосредственно к построению сечений многогранников. Ключевым моментом здесь будут рассуждения, которые и помогут прийти к нужному результату. В итоге постараемся в итоге составить шаблон, который будет отражать последовательность действий при решении задач данного типа.
Итак, рассмотрим следующую задачу. Построить сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через точки X, Y, Z, принадлежащие ребрам AA1, AC и BB1 соответственно.
Решение: Выполним чертеж и определим, какие пары точек лежат в одной плоскости.
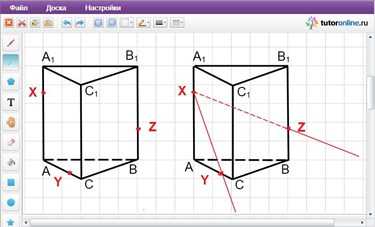Пары точек X и Y, X и Z можно соединить, т.к. они лежат в одной плоскости.
Построим дополнительную точку, которая будет лежать в той же грани, что и точка Z. Для этого продлим прямые XY и СС1, т.к. они лежат в плоскости грани AA1C1C. Назовем полученную точку P.
Точки P и Z лежат в одной плоскости – в плоскости грани CC1B1B. Поэтому можем их соединить. Прямая PZ пересекает ребро CB в некоторой точке, назовем ее T. Точки Y и T лежат в нижней плоскости призмы, соединяем их. Таким образом, образовался четырехугольник YXZT, а это и есть искомое сечение. 
Подведем итог. Чтобы построить сечение многогранника плоскостью, необходимо:
1) провести прямые через пары точек, лежащих в одной плоскости.
2) найти прямые, по которым пересекаются плоскости сечения и грани многогранника. Для этого нужно найти точки пересечения прямой, принадлежащей плоскости сечения, с прямой, лежащей в одной из граней.
Процесс построения сечений многогранников сложен тем, что в каждом конкретном случае он различен. И никакая теория не описывает его от начала и до конца. На самом деле есть только один верный способ научиться быстро и безошибочно строить сечения любых многогранников – это постоянная практика. Чем больше сечений вы построите, тем легче в дальнейшем вам будет это делать.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru