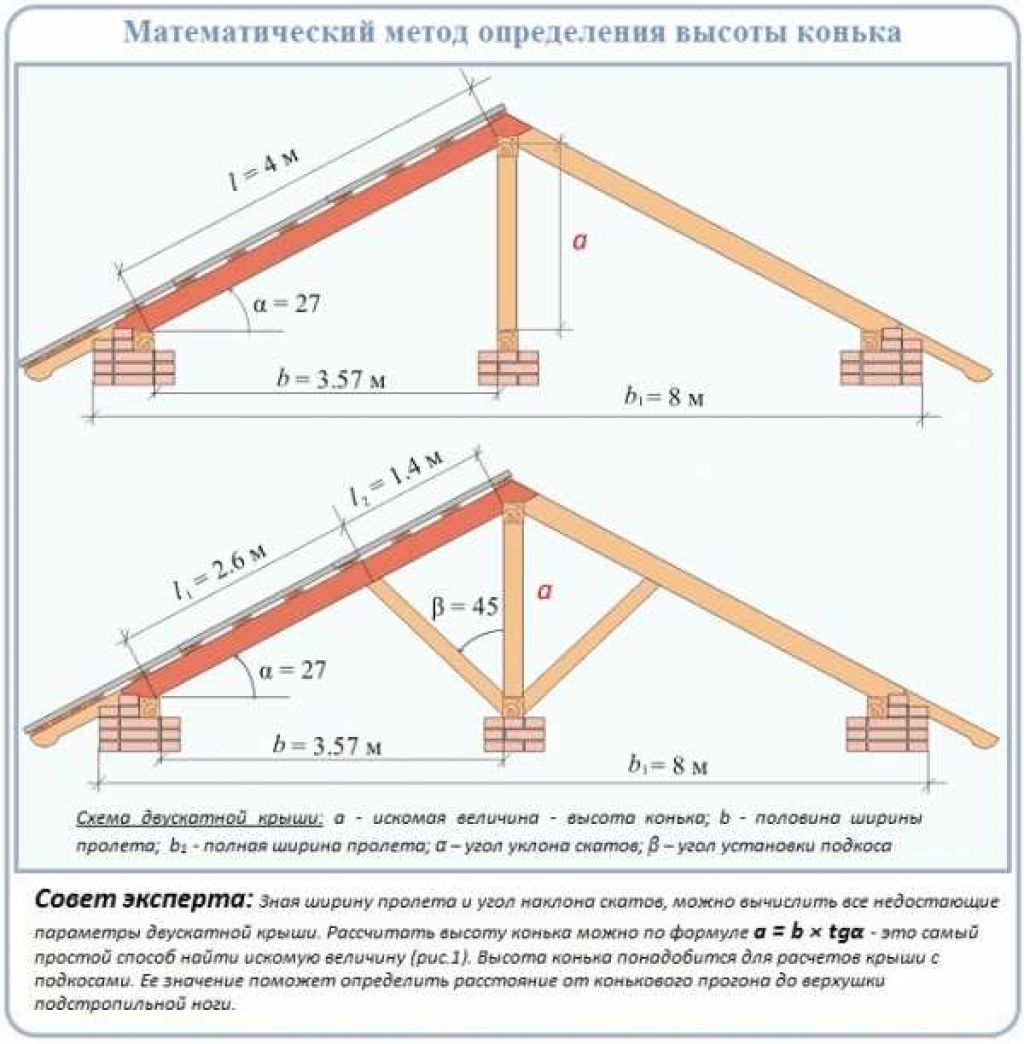
Как определить уклон: Как посчитать уклон в процентах. Угол уклона кровли для различных условий и кровельных материалов

Как определить уклон кровли своими руками

Сложно представить себе любое здание без крыши. Кровля должна защищать здание от воздействия природных осадков, обладать огнестойкими и водонепроницаемыми свойствами, обеспечивать эффективный отвод атмосферных осадков. Долговечность эксплуатации здания и его отдельных элементов во многом зависит от качественной крыши. Для достижения лучших результатов стоит использовать более простые виды скатных крыш: односкатные, двухскатные, вальмовые, полувальмовые, мансардные.

Минимальный угол наклона крыши из металлочерепицы должен составлять 14 градусов.

Основные данные

График выбора кровельного материала в зависимости от уклона крыши.

Допустимый угол наклона металлической крыши обычно измеряют своими руками исходя из климатических условий того района, в котором ведется строительство, и кровельного материала. Минимально угол наклона должен составлять 110°, максимальный угол наклона можно определить путем анализа погодных условий, его значение может быть 45°.

и больше. Для более теплого и сухого климата используется менее пологая крыша. Более крутой угол наклона дает возможность минимально скапливать снег и, соответственно, снижать снеговую нагрузку. Например, уклон 45° позволяет почти не учитывать вес снежного покрова.

Наряду с этим, увеличенный угол наклона резко повышает давление ветра на крышу. При уклоне в 45° давление ветра больше в 5 раз по сравнению с показателем в 11°. Следовательно, для большего угла наклона возникает необходимость в большем количестве реек для усиления обрешетки и стропил. От угла уклона крыши прямо зависит и ее стоимость.

Для кровли с углом наклона около 40-45° необходимо больше материалов (примерно в 1,5 раза), нежели для плоской крыши, а для 60° требуется в 2 раза больше кровельных материалов. При выборе конфигурации важно помнить, что от угла наклона напрямую зависит выбор кровельных материалов. Учет угла наклона позволяет определить материалы для кровли, а также произвести расчет слоев крыши и ее площади.

Зависимость полезной площади мансарды от уклона крыши.

Материалы для кровли по своим свойствам (технические, экономические, физические) объединились в группе 1-11.

На графике они показаны дугообразными стрелками. Линии наклона показывают уклон ската. Выделенная (жирным) линия на графике обозначает отношение полной высоты данного конька h к половине его обычного заложения ½. Отношение 1/2 указывает, что вертикальный отрезок h располагается на горизонтальном отрезке ½ два раза. Наклонная линия на полукруглой шкале обозначает угол наклона в градусах, а шкала, расположенная вертикально, – уклон крыши в %.

Так рассчитывают минимальный уклон для тех или иных кровельных материалов. В качестве примера, с помощью данного графика проведем расчет нужного угла наклона для данной крыши с использованием металлической черепицы.

Вернуться к оглавлению

Как измерить уклон

Таблица соотношения градус/процент уклона кровли.

На графике ищем наклонную линию, с которой стыкуется дугообразная стрела 2. Пересечение наклонной линии c вертикальной шкалой определяет уклон, минимально допустимый для данной крыши, который равен 50%. Нам известно, что уклон ската определяется отношением высоты конька к половине его заложения. Произведем расчет таким образом:

i = 10 метров (заложение)

h = 4 метра (высота конька)

получаем

i= h / (1/2) = 4 / (10/2) = 0,8

Для того чтобы измерить уклон в %, это отношение умножают на 100

0,8х100 = 80.

Схема расчета угла кровли.

Таким образом, уклон в 80% при соблюдении норм строительства обеспечит достаточный сброс дождевой воды со всей площади. Для кровли из рулонных полимерно-битумных, битумных и мастичных материалов с уклоном 10° необходим защитный слой для основного водоизоляционного покрова из гравия либо каменной крошки, у которой марка морозостойкости не меньше 100. Такой же защитный слой применяется для кровли крыши с помощью пленочных рулонных материалов с углом до 2,5%. Слой для защиты из гравия должен быть толщиной 1-1,6 см, а слой крупнозернистой посыпки – 0,3-0,5 см.

Причем на крышах с уклоном примерно до 2,5% с использованием эластомерных пленочных материалов в рулонах, выполненных свободной кладкой, необходим утяжеляющий слой гравия из расчета 50 кгс/кв.м.

На крышах из битумно-полимерных или битумных покрытий в рулонах с углом наклона выше 10% верхний слой гидроизоляционного покрова выполняется из крупнозернистой посыпки. На крышах из мастичных материалов с углом больше 10% предусматривается защитный слой из красочных составов.

При создании крыши из асбестоцементных листов, а также профнастила и металлической черепицы с наклоном до 20% по всей площади необходимо производить герметизацию стыков. Не более чем на 5% можно допустить отклонение уклона кровли из мелкоштучных материалов. Производя эти расчеты, можно узнать площадь помещения мансарды или чердака.

Вернуться к оглавлению

Единицы измерения и инструменты

В основание металлической конструкции встроены цифровой дисплей с элементами управления.  

Величина уклона на всех чертежах может обозначаться в градусах или в процентах, а сам он обозначается буквой «i». В настоящий момент нет строгих правил, как обозначать данную величину. Единицей измерения считают градусы или проценты (%).

Угол уклона измеряется двумя способами:

1. Специальным уклономером.
2. Математическим способом, с помощью вычислений.

Уклономер – это специальная рейка с рамкой, у которой между планками есть ось, на которой закреплен маятник, и своя шкала деления. Когда эта рейка расположена в горизонтальном положении, то маятник на ее шкале отклонен на ноль градусов. Для произведения измерения уклона ската рейку прибора располагают перпендикулярно коньку, в вертикальном положении.

По шкале определяют угол отклонения маятника, который указывает уклон этого ската данной крыши в градусах. Этот метод определения применяется очень и очень редко. На данный момент разработано множество геодезических приборов для определения этих величин и специальные уровни-уклономеры, как капельные, так и электронные.

Математический расчет

Расчет уклона кровли.

Можно спокойно рассчитать наклон данной крыши, не прибегая к использованию специальных геодезических, механических и других видов приборов для замеров уклона. Необходимо просто измерить некоторые параметры крыши:

1. Вертикальная высота (обозначается как H) – высота от верхней точки данного ската (обычно считают от конька) до самой нижней точки (так называемого карниза).
2. Заложение – горизонтальный промежуток от самой нижней точки данного ската до самой верхней его точки.

Уклон крыши (его величину) с применением математического расчета находят так.

Угол наклона отдельного ската i выражается через отношение измеренной высоты крыши Н к расстоянию заложения L. Таким образом

i = Н:L

Для точного определения этого значения в процентах отношение i умножают на 100. Затем, для определения его значения в градусах, мы производим перевод процентов в градусы.

Для полного понимания этого метода приведем наглядный расчет:

высота равна 3,0 м,

длина заложения равна 5 м.

По формуле вычисляем i:

i = 3:5 = 0,6

Проводим расчет процентов

i × 100 = 60%.

Переводим в градусы. Получаем 31 градус.

Калькулятор Уклонов найти наклон линии

Может быть, вы знакомы с вопросом «как рассчитать уклон»! Наклон является важной концепцией в математике, которая обычно используется в базовом или расширенном графике, таком как линейная регрессия; говорят, что наклон является одним из основных чисел в линейной формуле.

Ну что ж, самое главное – команда онлайн-калькуляторов предлагает еще один образовательный инструмент, известный как «калькулятор уклонов», который помогает найти неопределенный уклон с помощью простой формулы уклона. В этом посте мы решили обсудить расчет уклона, как найти уклон, что такое формула уклона, и все, что вам нужно знать о уклоне!

Итак, начнем с «определения уклона».

Что такое склон?

Определение уклона очень просто; говорят, что это мера разницы в положении между двумя точками на линии.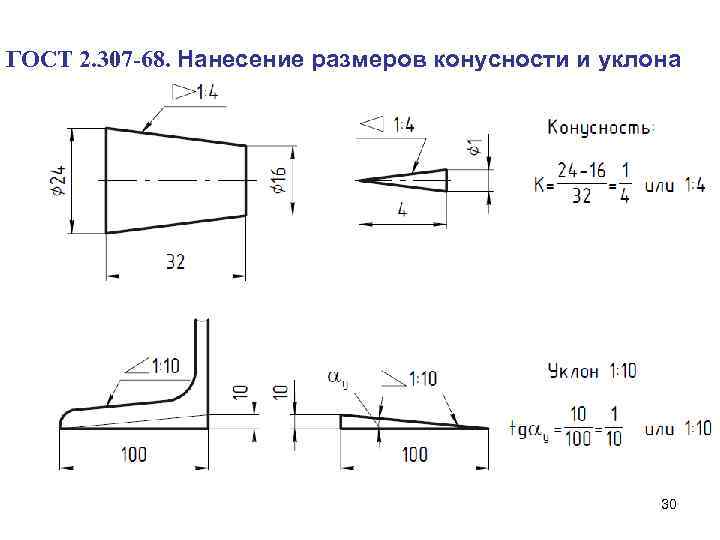 Согласно математике, если линия построена на двухмерном графике, то наклон – это то, что показывает, насколько линия движется вдоль оси x и оси y между этими двумя точками. Да, найти уклон становится легко с помощью нашего надежного калькулятора уклонов – этот инструмент использует простое уравнение уклона, чтобы найти уклон.

Формула уклона:

Наклон (м) = ΔY / ΔX

В этом уравнении наклона;

M = уклон

ΔY = (y₂ – y₁)

ΔX = (x₂ – x₁)

Kалькулятор Yклонов По калькулятору онлайн:

К счастью, вы можете найти наклон или градиент между двумя точками в декартовой системе координат с помощью нашей точки расчет уклона. Да, это калькулятор уклонов помогает вычислить уклон (из точек) для данного ввода. Проще говоря, эта точка онлайн калькулятор уклонов r работает как «искатель склона». Хорошо, заполните поля вышеупомянутой находки калькулятор наклона, чтобы найти наклон линии.

Наш Pасчет Yклона работает:

Калькулятор формулы наклона очень удобен в использовании; он использует простую формулу для наклона в поиске наклона линии.

Вы должны придерживаться указанных шагов для наклона между двумя точками:

• В приведенном выше калькуляторе вы можете видеть поля для X1, Y1, X2 и Y2 соответственно!
• Прежде всего, вы должны ввести значения четырех координат
• Сразу после этого вы должны нажать кнопку расчета
• После этого вы получите пять выходных значений, включая наклон, угол наклона, расстояние, изменение X и изменение Y

К счастью, вы узнали, как найти уклон, используя простой уклон линейной формулы.

Как найти наклон линии?

Вы можете найти наклон линии, сравнивая любые 2 точки на линии. Точка называется значением X и Y декартовой координаты на сетке. Склон; представленный как m, его можно найти, используя формулу наклона:

Формула уклона: m = ((y2 – y1)) / ((x2 – x1))

Например:

Линия проходит через точки (3, 2) и (7, 5), как найти наклон линии?

Решение:

m = ((5 – 2)) / ((7 – 3))

m = ((3)) / ((4))

Как найти расстояние между 2 точками?

Формула для определения расстояния (D) между двумя разными точками:

Расстояние (d) = √ (〖ΔX〗 ^ 2 + 〖ΔY〗 ^ 2)

Где – 〖ΔX〗 ^ 2 = 〖(x₂ – x₁)〗 ^ 2 и 〖ΔY〗 ^ 2 = 〖(у₂ – у₁)〗 ^ 2

Как конвертировать наклон в угол?

Вы можете найти угол наклона линии в градусах от обратного тангенса наклона (м). Кроме того, вы можете использовать простой калькулятор касательной линии, чтобы скрыть наклон к ангелу.

Формула это:

θ = загар-1 (м)

ИЛИ θ = арктан (ΔY / ΔX)

Куда;

м = уклон

θ = угол наклона

Например:

Если наклон равен 5, угол наклона в градусах равен tan-1 (5).

Как конвертировать угол в наклон?

Вы также можете преобразовать угол в градусах в уклон. Просто все, что вы должны помнить, это то, что наклон равен тангенсу угла.

Уравнение:

m = tan (θ)

Например: если угол = 90, то наклон равен tan (90).

Слова по калькулятору онлайн:

К счастью, вы узнали, как найти склон. Удивительно то, что вам не нужно запоминать эти формулы, вам просто нужно ввести четыре координаты в калькуляторе выше, чтобы найти наклон, угол наклона, расстояние, изменение в X и изменение в Y, соответственно!

Other Languages: Slope Calculator, Steigung Berechnen, 勾配計算, Calcul Pente, Calculo De Inclinação, Calcular Pendiente, Calcolo Pendenza, Výpočet Sklonu, Kattokaltevuus Laskuri, Eğim Hesaplama, Kalkulator Nachylenia, Kalkulator Kemiringan.

Algebra 1 Help

Студенты, нуждающиеся в помощи по алгебре 1, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Алгебре 1. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите много помощи по Алгебре 1. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по алгебре 1.

• Алгебра 1

• Распределительная собственность

• Как использовать FOIL в дистрибутивной собственности

• Как использовать метод сетки для FOIL

• Уравнения / Неравенства

• Системы уравнений

• Уравнения/наборы решений

• Как разложить уравнение на множители

• Как найти решение set

• Как найти решение системы уравнений

• Линейные/рациональные уравнения/уравнения с переменными

• Как узнать, когда уравнение не имеет решения

• Как найти решение рационального уравнения с LCD

• Как найти решение уравнения

• Квадратные уравнения

• Как разложить на множители квадратное уравнение

• Как найти решение квадратного уравнения

• Системы неравенств

• Как найти решение неравенства со сложением

• Как найти решение неравенства с делением

• Как найти решение неравенства с умножением

• Как найти решение неравенства с вычитанием

• Функции и линии

• Алгебраические функции

• Как найти прямой вариант

• Как найти f(x)

• Как найти обратную вариацию

• Как найти домен функции

• Как использовать квадратичную функцию

• Уравнения прямых

• Формула средней точки

• Как найти концы отрезка

• Как найти середину отрезка

• Параллельные линии

• Как узнать, параллельны ли прямые

• Как найти уравнение параллельной прямой

• Как найти наклон параллельных прямых

• Перпендикулярные линии

• Как узнать, перпендикулярны ли прямые

• Как найти уравнение перпендикулярной прямой

• Как найти наклон перпендикулярных линий

• Точки и формула расстояния

• Как узнать, находится ли точка на прямой с уравнением

• Как найти длину линии по формуле расстояния

• Уравнения наклона и линии

• Как найти наклон линии

• Как найти уравнение прямой

• Графика

• Как построить график функции

• Как построить линию

• Как нарисовать точку

• Как построить график квадратичной функции

• Как построить график двухшагового неравенства

• Как построить график функции абсолютного значения

• Как построить график экспоненциальной функции

• Как построить график упорядоченной пары

• последовательности

• Как найти последовательные целые числа

• Как найти ответ на арифметическую прогрессию

• Как найти общую разницу в последовательностях

• Как найти следующий член арифметической прогрессии

• Как найти n-й член арифметической прогрессии

• Линейные уравнения

• Преобразование измерений

• Как решать уравнения абсолютного значения

• Как решить одношаговые уравнения

• Как решать двухшаговые уравнения

• Как писать выражения и уравнения

• Проценты

• Пропорции

• Линейные неравенства

• Неравенства абсолютного значения

• Графические неравенства

• Запись неравенств

• Проценты

• Десятичные числа и проценты

• Как найти десятичный эквивалент процента

• Как найти процент эквивалентный десятичной дроби

• Дроби и проценты

• Как найти дробь от процента

• Как найти дробные проценты

• Как найти процент от дроби

• Денежный процент

• Как найти размер прибыли

• Как найти простые проценты

• Как найти сумму налога с продаж

• Как узнать цену продажи

• Процент изменения

• Как найти процент уменьшения

• Как найти процент увеличения

• Целое и часть

• Как найти часть от целого в процентах

• Как найти целое из части с процентами

• Реальные числа

• Подсчет/наборы

• Как найти недостающее число в наборе

• Как найти количество целых чисел между двумя другими целыми числами

• Целочисленные операции

• Как складывать целые числа

• Как делить целые числа

• Как умножать целые числа

• Как вычитать целые числа

• Количество линий и абсолютное значение

• Как найти абсолютное значение

• Как найти значение с числовой строкой

• Как построить график неравенства с числовой прямой

• Как построить дроби на числовой прямой

• Статистика и вероятность

• Как найти межквартильный размах

• Как найти среднее

• Как найти медиану

• Как найти режим

• Как найти диапазон

• Как найти стандартное отклонение

• Переменные

• мономы

• Как делить одночленные частные

• Как умножить одночлен на многочлен

• Как умножать одночленные частные

• Многочлены

• Биномы

• Как найти решение рационального уравнения с биномиальным знаменателем

• Как найти решение биномиальной задачи

• Как найти значение коэффициента

• Как умножать биномы с распределительным свойством

• Как упростить биномы

• Факторные полиномы

• Как разложить многочлен на множители

• Как факторизовать переменную

• Полиномиальные операции

• Как складывать многочлены

• Как делить многочлены

• Как найти степень многочлена

• Как умножать многочлены

• Как вычитать многочлены

• Трехчлены

• Как складывать трехчлены

• Как делить трехчлены

• Как разложить трехчлен на множители

• Как умножать трехчлены

• Как вычитать трехчлены

Алгебра I часто впервые знакомит учащихся с процессами вычисления переменных, понимания неравенств и использования порядка операций для упрощения выражений.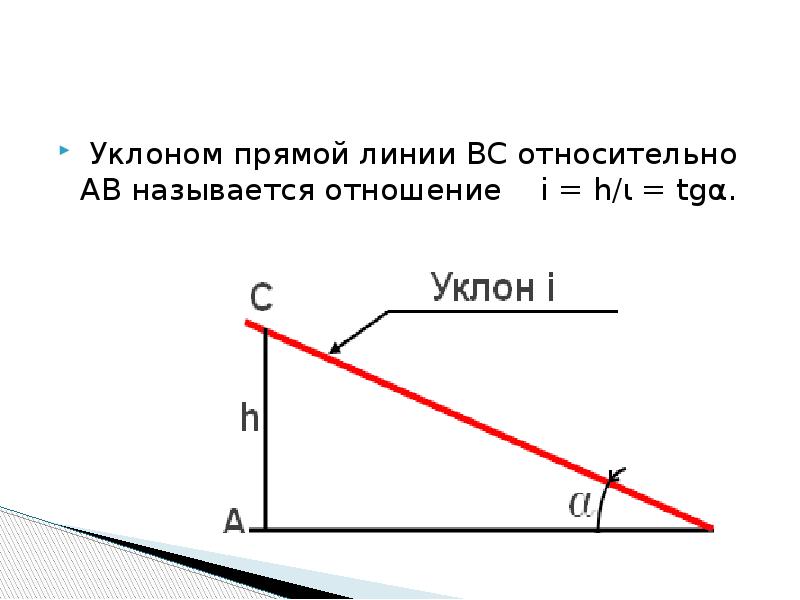 Некоторым учащимся часто бывает трудно освоить эти новые навыки; однако усердная практика основных алгебраических принципов жизненно важна для успеха в дальнейших курсах математики. Понимание геометрии, предварительного исчисления, исчисления и высшей математики, физики и химии требует фундаментального понимания того, как упростить выражения и манипулировать переменными. Нужны ли вам лучшие репетиторы по алгебре 1 в Бостоне, репетиторы по алгебре 1 в Детройте или лучшие репетиторы по алгебре 1 в Далласе, Форт-Уэрт, работа с профессионалом может вывести ваше обучение на новый уровень.

В общем, Алгебра I фокусируется на основах понимания и упрощения задач. Учащиеся работают над тем, чтобы логически продумать этапы решения проблемы, не делая немедленных выводов или решений. Кроме того, учащихся учат объяснять отношения между уравнениями, давать словесные описания графиков, таблиц и диаграмм и предсказывать форму фигур на основе математических соотношений. Репетиторы Varsity Tutors предлагают такие ресурсы, как бесплатные практические тесты по алгебре 1, которые помогут вам в самостоятельном обучении.

Общие темы по алгебре I включают:

• Арифметика с полиномиальными и рациональными выражениями: учащимся предлагается упростить числовые выражения с помощью порядка операций, разложить переменные в числовые уравнения и упростить сложные выражения с помощью различных комбинаций чисел и переменных.

• Создание выражений: используя графики и таблицы в качестве руководства, учащимся предлагается определить взаимосвязь между двумя или более переменными. Например, учащимся может быть предоставлена ​​таблица пройденного расстояния и времени, необходимого для преодоления этого расстояния. Ожидается, что учащиеся определят, как пройденное расстояние влияет на затраченное время (удвоение пройденного расстояния требует удвоения времени при той же скорости).

• Рассуждения с помощью уравнений и неравенств: учащиеся, изучающие алгебру I, должны найти значение переменных, упрощая числовые выражения. Кроме того, студентов учат, как графически отображать эти решения в системах координатной плоскости. Также рассматриваются неравенства и определение того, как будет затеняться график системы координат на основе численного решения.

• Видение структуры в выражении: использование рассуждений с помощью уравнений и неравенств в качестве основы, учащихся учат писать алгебраические выражения и неравенства на основе графиков, а иногда и таблиц данных.

Ключом к успеху в алгебре I является постоянная практика. В то время как некоторые учащиеся будут иметь опыт упрощения выражений, добавление графиков, диаграмм, неравенств и факторизации будет новым для других. Общие стратегии достижения успеха включают просмотр кратких резюме в учебниках перед выполнением домашних заданий и отработку дополнительных 10–15 заданий после выполнения назначенных отрывков домашнего задания. Часто учащиеся изучают шаблоны, необходимые для решения задач, путем постоянного повторения вместо того, чтобы читать разделы книги.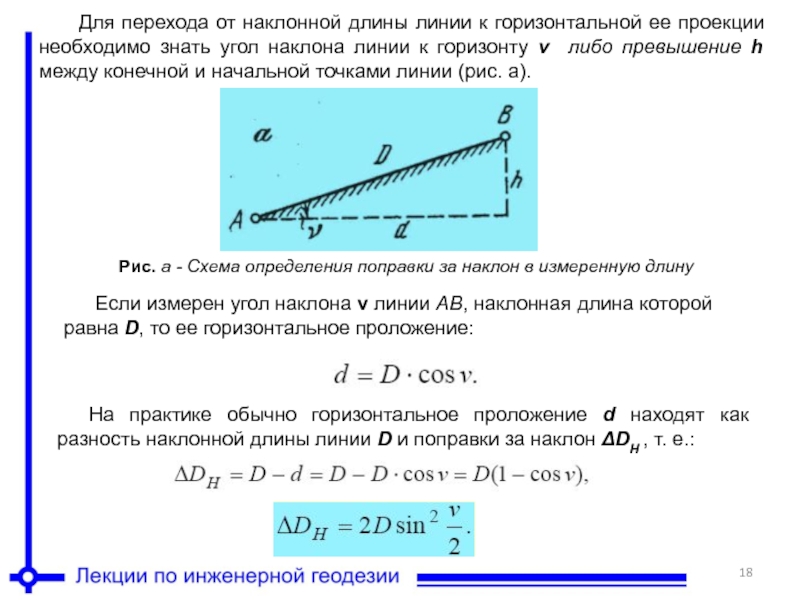 Наличие другого метода материального подкрепления в дополнение к обучению в классе и домашнему заданию обычно полезно для большинства учащихся. В дополнение к справочному разделу по алгебре 1 и урокам по алгебре 1 вы также можете рассмотреть некоторые из наших карточек по алгебре 1.

Если вы хотите укрепить свои знания по алгебре I, решая практические задачи, ознакомьтесь с бесплатными ресурсами по алгебре I от Varsity Tutors. Каждая практическая задача сопровождается подробным пошаговым ответом, поэтому, если вы пропустите какой-либо из них, вы сможете точно определить, где в своих расчетах или рассуждениях вы ошиблись, и избежать повторения этой ошибки позже. Практические задачи также организованы по понятиям, поэтому, если у вас возникают трудности с графическим отображением линейных функций или порядком операций, вы можете отвечать на вопросы только по этим темам, не перебирая материал, который будет полезен для ваших конкретных учебных потребностей. Бесплатные практические задачи по алгебре I от Varsity Tutors помогут вам получить дополнительную практику, которая вам нужна при сдаче или повторении алгебры I!

 

Как найти уклон | Albert Resources

Как найти наклон линейного уравнения? Давайте погрузимся и узнаем!

Хотя математику часто относят к естественным наукам, в некоторых отношениях математика — прекрасный язык. Например, сравнивая, как что-то растет, можно сказать, что оно растет медленно, умеренно или быстро. Но как медленно? Как быстро? Используя математику, мы можем описать рост функций, используя наклон .

В этом обзоре мы объясним, как найти наклон, сосредоточившись на линейных функциях. К концу вы будете знать, как найти наклон линии. Это включает в себя, как найти наклон с двумя точками, как найти наклон с помощью графика и как найти наклон уравнения.

Что мы рассматриваем

Что такое уклон?

  Наклон  описывает скорость изменения или «крутизну» линии. 

Линейная функция на графике выглядит как прямая линия. Вот несколько примеров линейных уравнений и их наклонов (щелкните изображения, чтобы развернуть):

y=2x+1

Наклон: 2

y=7x-2

Наклон: 7

y=-x+2

Наклон: -1

Какова формула для уклона?

Для двух точек с координатами (x_1, y_1) и (x_2, y_2) формула для уклона:

Начните заниматься алгеброй 1 на Альберте прямо сейчас!

«Подъем над бегом»

  Наклон  линии можно описать как  рост  над  пробег  .  

Подъем — вертикальное изменение y, прогон — горизонтальное изменение x.

В приведенной выше формуле наклона буква m обозначает уклон.

Ниже показано, что мы подразумеваем под «подъемом» (изменение по вертикали показано синей пунктирной линией) и «бегом» (изменение по горизонтали показано зеленой пунктирной линией):

Отрицательный и положительный наклон линейных уравнений

Положительный наклон

Когда функция имеет положительный наклон , линия движется вверх слева направо. Другими словами, при увеличении значения x значение y также увеличивается. Чем больше наклон линии с положительным наклоном, тем она круче.

Например, наклон 7 создаст более крутую линию, чем наклон 2.

Вот несколько примеров линий с положительными наклонами (щелкните изображения, чтобы развернуть):

y=\frac{ 1}{4 }x+1

Наклон: \frac{ 1}{4 }

y=2x+1

Наклон: 2

y=7x-2

Наклон: 7

Отрицательный наклон

Когда функция имеет отрицательный наклон , линия движется вниз слева направо. Другими словами, при увеличении значения x значение y уменьшается. Чем меньше наклон линии с отрицательным наклоном, тем она круче.

Например, наклон -10 создаст более крутую линию, чем наклон -2.

Вот несколько примеров линий с отрицательным наклоном (щелкните изображения, чтобы развернуть):

y=- \frac{ 1}{4 }x+1

Наклон: – \frac{ 1}{4 }

y=-x+2

Наклон: -1

y=-10x+2

Наклон: -10

Нахождение уклона по двум точкам (пример)

Теперь мы поговорим о том, как найти уклон по двум точкам.

Начнем с простого примера. Мы будем использовать точку A, (5,8) и точку B (1,4) .

Помните, мы можем начать с формулы для уклона:

Формула уклона m=\dfrac{y_2-y_1}{x_2-x_1}

Прежде чем мы сможем подставить значения в уравнение, мы должны пометить точки.

Теперь мы можем заменить x_1 на 5, y_1 на 8, x_2 на 1 и y_2 на 4.

\dfrac{y_2-y_1}{x_2-x_1}

\dfrac{4-8}{1-5}

Далее упростим нахождение наклона линии.

\dfrac{-4}{-4} = 1

Таким образом, наклон линии, проходящей через точку A, (5,8) и точку B (1,4), будет равен 1. Это был пример того, как найти наклон по двум точкам.

Ознакомьтесь с лицензиями школы Альберта !

Если полезно, вот короткое видео, объясняющее, как рассчитать наклон по двум точкам:

Найти наклон на графике (пример)

Чтобы вычислить наклон линии на графике, мы используем график для определить подъем (изменение по вертикали) и прогон (изменение по горизонтали)

Для начала выберем две точки на графике, которые легко идентифицировать. В качестве примера можно рассмотреть линию y=2x-1.

На приведенном ниже графике красная линия представляет y=2x-1. Мы можем определить точки (1,1) и (2,3) на этой прямой.

y=2x-1

Теперь мы можем подсчитать вертикальное расстояние между точками, чтобы определить рост . На следующем изображении вертикальное расстояние {2} выделено синим цветом, как показано ниже: 

«Подъем» синим цветом

Мы также должны подсчитать горизонтальное расстояние между точками, чтобы определить прогон . На следующем изображении горизонтальное расстояние {1} выделено зеленым цветом.

«Бег» зеленым

Следовательно, подъем равен {2}, а пробег равен {1}. Уклон — это подъем над трассой или \dfrac{2}{1}, что упрощается до 2.

Теперь мы знаем, как найти уклон с помощью графика!

Начните заниматься алгеброй 1 на Альберте прямо сейчас!

Для тех, кто предпочитает видео, вот короткий ролик, демонстрирующий этот метод определения наклона по графику:

Поиск наклона по уравнению (пример)

уравнение, вы должны сначала знать, что линейные уравнения часто записываются в форме пересечения наклона.

В форме пересечения наклона записывается уравнение:

Форма пересечения наклона y=mx+b

перехват.

Чтобы определить, как найти наклон , необходимо определить коэффициент перед x.

Например, рассмотрим уравнение:

y=7x+10

Коэффициент перед x равен 7. Следовательно, мы знаем, что наклон линии y=7x+10 равен 7,

Если вы столкнулись с уравнением в другой форме, просто решите уравнение для y и запишите уравнение в форме пересечения наклона. Затем вы можете использовать этот метод для определения наклона.

Кроме того, в этой статье есть несколько замечательных приложений уклона в реальной жизни.

А вот короткое видео о том, как найти наклон линии по заданному уравнению:

---

Наклон горизонтальных и вертикальных линий

При обучении вычислению наклона есть два необычных случая, требующих особого внимания. внимание: по горизонтали и по вертикали строк.

Горизонтальные линии

Если вы нашли наклон по двум точкам и в числителе оказался ноль, вы нашли наклон горизонтальной линии.

 Этот наклон горизонтальной линии   всегда равен 0. 

Уравнение горизонтальной линии: y=a, где a — действительное число.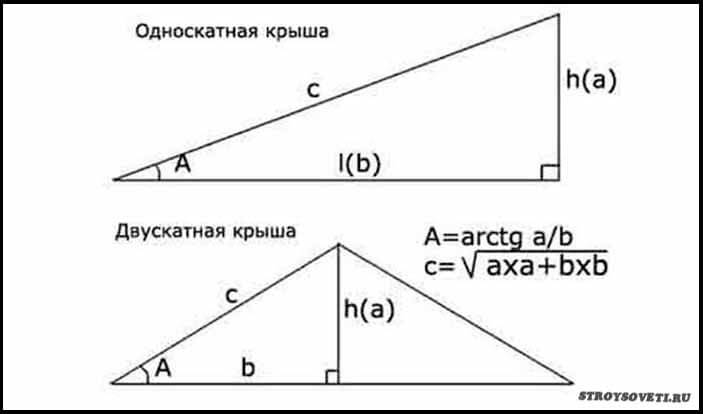 Вот два примера горизонтальных линий, выделенных красным цветом (щелкните изображения, чтобы развернуть):

y=-1

Наклон: 0

у=2

Наклон: 0

Вертикальные линии

Если вы нашли наклон по двум точкам и получили ноль в знаменателе, вы нашли наклон вертикальной линии.

 Этот наклон вертикальной линии   всегда не определен. 

Уравнение вертикальной линии: x=a, где a — действительное число. Вот два примера вертикальных линий, выделенных красным цветом (щелкните изображения, чтобы развернуть):

x=-1

Наклон: не определено

x=2

Наклон: не определено

Резюме: Наклон линейных уравнений

• Понимание того, как найти уклон, может помочь объяснить мир вокруг нас!
• Наклон линейного уравнения — это «подъем над пробегом», или изменение y по сравнению с изменением x.
• Уравнение, чтобы найти наклон линии:

641414144144141414141414144141414141414141414146464141464141414141414141414141414141414141414141 4164.

Формула наклона M = \ DFRAC {Y_2-Y_1} {x_2-x_1}