Геодезическая разбивка осей фундамента
Цены на услуги
Разбивка осей фундамента является одним из самых важных этапов начала строительных работ по возведению зданий. И неудивительно. Ведь от качества подобных работ будет зависеть устойчивость объекта и безопасность его эксплуатации в целом.Геодезическая разбивка осей фундаментов состоит из трёх этапов:
- определение главных осей;
- нанесение габаритных осей;
- обноска.
Цена:
от 2 000 руб
1 ось
Выезд в течение суток с момента подачи заявки
Выезжаем в любой день недели
Главные оси
Под главными осями подразумевают две линии, расположенные перпендикулярно друг другу. Точка их пересечения должна совпасть с точкой, в которой пересекаются диагонали будущего здания, тогда разбивка произведена правильно. Некоторые строители считают, что главные оси небольших объектов можно не проводить, однако профессионалы рекомендуют выполнять данные работы, хотя бы для самоконтроля.
Габаритные оси
Габаритными осями называют линии, которые указывают общие плановые размеры здания. Для того чтобы их найти в натуру выносят две крайние точки, которые определяют расположение самой длинной продольной оси здания. А после этого на чертеже разбивки осей фундамента отмечают все расстояния между ними и осями, а также привязку фундамента к ним.
Обноска
Данный этап предполагает создание конструкции из двух деревянных столбов, с прибитой между ними горизонтальной доской. Устанавливают её, учитывая естественный откос будущего котлована, соблюдая определённое расстояние (не менее 1,5 м) от его стен. Затем на доску переносятся все данные размеров котлована и обноску выверяют по уровню. После этого можно приступать непосредственно к рытью котлована.
Из всего сказанного напрашивается логический вывод, что разбивка осей фундамента является процессом достаточно сложным, трудоёмким и ответственным. Именно поэтому доверять его проведение следует исключительно специалистам, например, ООО «Лимб».
При проведении работ по геодезической разбивке осей фундаментов следует учесть два важных момента:
- если дом прямоугольно типа, то его стены должны примыкать друг к другу исключительно под прямым углом;
- фундамент здания с крупно-пустотными панелями обязательно должен соответствовать размерам стандартных панелей.
А ведь для того чтобы выполнить эти важные условия, необходимо специализированное оборудование. И если «шабашники» орудуют подручными самодельными приборами, то в распоряжении сотрудников компании «Лимб» имеется высокоточное и качественное оборудование. К тому же все специалисты фирмы обладают многолетним опытом и необходимой квалификацией для проведения подобных работ.
Доверьте работу профессионалам компании «Лимб» и вы гарантированно получите профессиональную консультацию, высокое качество выполненных работ и надёжные эксплуатационные характеристики возводимого здания в будущем.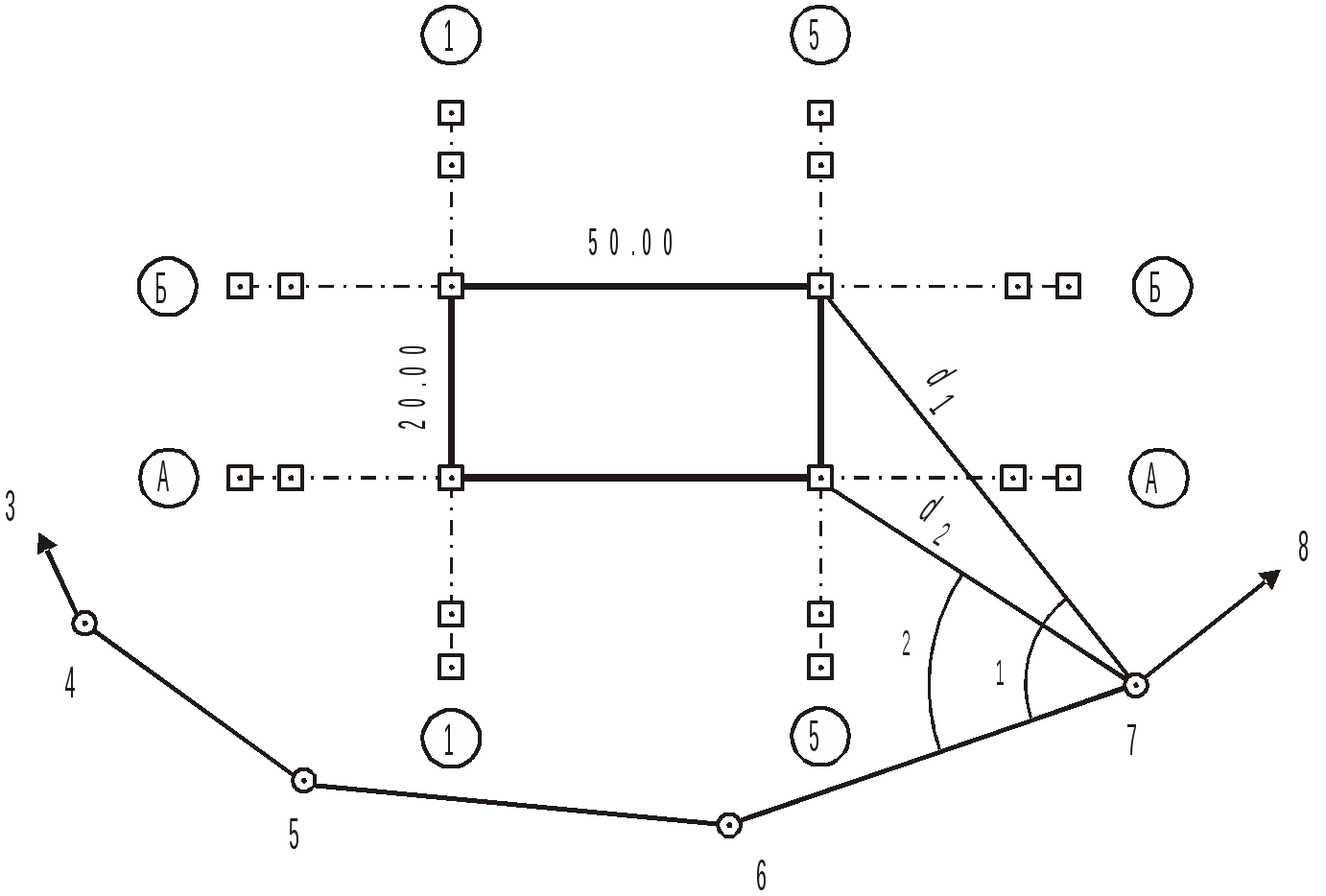
- Разбивка осей трассы
Геодезическая разбивка осей зданий – разбивки осей объекта капитального строительства на местности в Москве и МО
Для получения надежного, безопасного, функционального и долговечного здания, необходимо обеспечить грамотную геодезическую разбивку осей здания на местности. Процедура является элементом геодезии участка, предназначенного под капитальное строительство, и заключается в переносе на местность и закреплении данных о расположении строения, указанных в проектной документации. То есть, фиксация на поверхности земли точек с указанными координатами и высотами, на которые дальше будут ориентироваться специалисты в процессе перенесения полного плана постройки.
Необходимые документы
Для возможности заказать проведение разбивочных работ, заказчик должен предоставить пакет документов, который включает следующие бумаги:
- топографический план для рассмотрения ситуации на участке;
- строительные акты, схематическое изображение фундамента и нулевого этажа, что необходимо для получения информации о будущем сооружении;
- чертежи с указанием красных линий для перенесения их на местность;
- генплан с привязкой к существующим объектам;
- разбивочный проект здания;
- техническое задание по геодезии участка, в котором указана необходимость проведения разбивки с закреплением реперов на стройплощадке, а также материалы для строительства всех элементов сооружения.

Этапы разбивки
- Подготовительный. Рассматривается документация. Определяется способ выноса точек и линий в натуру и место для станции. Устанавливается прибор (тахеометр, теодолит, нивелир), выполняется центрирование по лазерному или оптическому уровню.
- Основной.
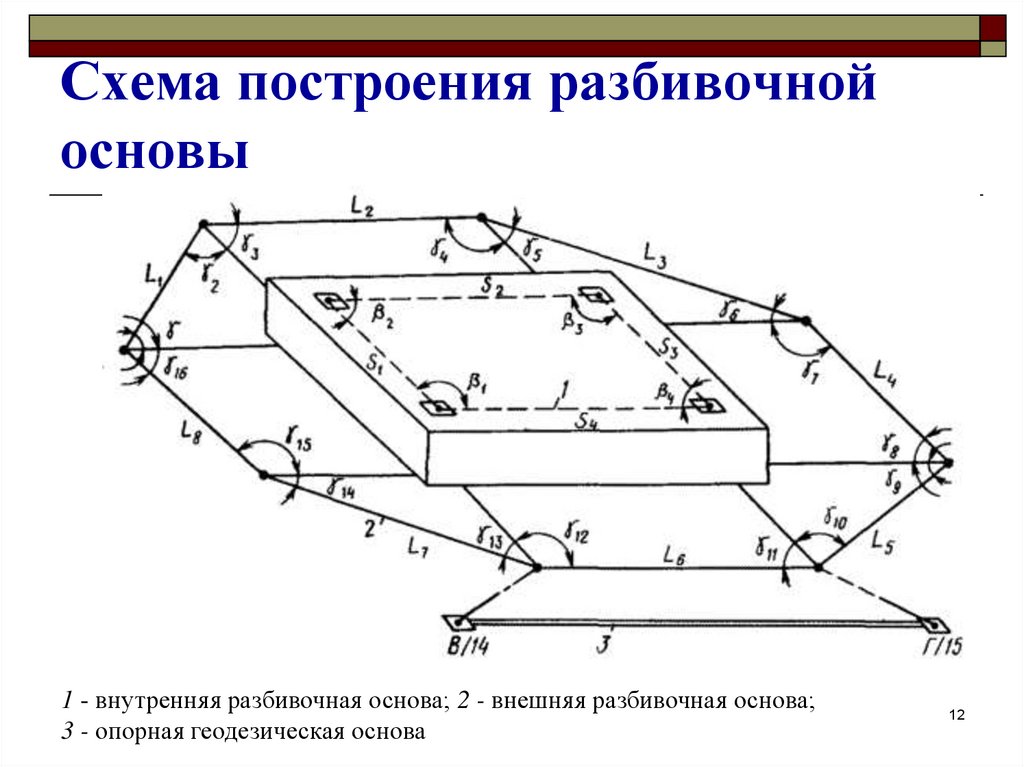
- Выявляется геодезическая разметка главных и промежуточных осей, что определяется в соответствии с координатами объектов геоподосновы. Съемными и стационарными реперами фиксируется местоположение линий. Проводится построение разбивочной сети.
- Детальная разбивка осей – вынос проектных точек в натуру с установкой двух опорных знаков на каждый исходный и монтажный горизонт, что в дальнейшем послужит основой для высотной разбивки.
- Рулеточное построение с замерами и выносом проектного расстояния между точками.
- Заключительный. Проведение исполнительной геодезической съемки для выявления согласованности сделанных построений с исходными данными, указанными в проектной документации.
 Вся информация, полученная в результате разбивочных работ, обрабатывается специальным программным обеспечением. Составляется технический отчет по разбивке строительных осей, который включает схему осей, акт о приемке работ.
Вся информация, полученная в результате разбивочных работ, обрабатывается специальным программным обеспечением. Составляется технический отчет по разбивке строительных осей, который включает схему осей, акт о приемке работ.
Способы разбивки
В зависимости от ситуации на участке, габаритов и типа объекта, вида геодезической основы, основные линии и точки выносятся в натуру разными методами:
- прямоугольных координат – применяется, если на площадке имеется строительная сетка или красные линии застройки;
- полярных координат – для открытой местности, если точки трасс находятся в удалении от строительной сетки;
- угловой засечки – способ актуален при строительстве мостов и гидротехнических сооружений, если проектные точки располагаются на большом удалении от опорных пунктов, либо территории имеются препятствия в виде оврага или водоема;
- линейной засечки – для линейных объектов;
- створной засечки – используется для детальной разбивки сооружений по отношению к створам главных и основных осей;
- разбивка основных осей относительно существующих объектов – при строительстве новых зданий на уже застроенной территории.

К чему приводят ошибки при разбивочных работах?
Если точки и оси здания были вынесены неправильно или со значительными погрешностями, то это может привести к неравномерной осадке строения и нарушению гидроизоляции, снижению несущей способности фундамента и стен, обрушению строения. Обеспечить качественную разбивку могут только профессионалы, поэтому экономить на этом процессе не следует.
Компания «GeologyLab» выполняет геодезические изыскания в Москве и МО. У нас можно заказать комплексные услуги или поставить перед специалистами отдельные задачи. Гарантируется отличное качество работ, сжатые сроки выдачи результата, выгодные цены. Задать вопросы, уточнить стоимость, оформить заявку будет удобно по телефону +7-495-135-15-75.
Об аэрокосмических системах координат – MATLAB & Simulink
Об аэрокосмических системах координат
Основные концепции системы координат
Системы координат позволяют отслеживать положение самолета или космического корабля и
ориентация в пространстве. Системы координат Aerospace Blockset™ основаны на этих основных концепциях из
геодезии, астрономии и физики.
Системы координат Aerospace Blockset™ основаны на этих основных концепциях из
геодезии, астрономии и физики.
Определения
В наборе блоков используется правосторонний (RH) Декартово системы координат. Правило правой руки устанавливает x – y – z последовательность координатные оси.
Инерциальная система отсчета представляет собой неускоряющуюся систему отсчета движения. В В инерциальной системе отсчета выполняется второй закон Ньютона: сила = масса x ускорение. свободно говоря, ускорение определяется по отношению к далекому космосу, а инерциальную систему отсчета часто называют неускоренной относительно фиксированной звезды. Поскольку Земля и звезды движутся так медленно относительно друг друга, это предположение является очень точным приближением.
Строго определенная, инерциальная система отсчета является членом множества всех неускоряющихся отсчетов
относительно друг друга. Неинерциальная система отсчета — это любая система отсчета, ускоряющаяся относительно
к инерциальной системе отсчета. Его ускорение, вообще говоря, включает в себя как поступательное
и вращательные компоненты, в результате чего
Его ускорение, вообще говоря, включает в себя как поступательное
и вращательные компоненты, в результате чего
Набор блоков моделирует форму Земли ( геоид ) в виде сплюснутого сфероида, особый тип эллипсоида с двумя равными длинными осями (определяющий экваториальная плоскость ) и третья, немного короче ( геополярный ) ось симметрии. Экватор – это пересечение экваториальной плоскости и земной поверхности. Географические полюса являются пересечением земной поверхности и геополярной оси. В целом, Геополярная ось и ось вращения Земли не идентичны.
Широты параллельны экватору. Долготы параллельны геополярной оси. ноль долгота или начальный меридиан проходит через Гринвич, Англия.
Приближения
Набор блоков делает три стандартных приближения при определении
системы координат относительно Земли.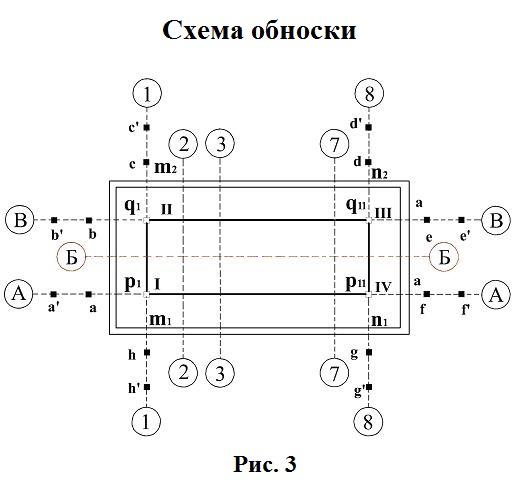
Поверхность Земли или геоид представляет собой сплюснутый сфероид, определяемый более длинная экваториальная и более короткая геополярная оси. В действительности Земля является слегка деформирован по отношению к стандартному геоиду.
Ось вращения Земли и экваториальная плоскость перпендикулярны, поэтому что оси вращения и геополярные оси идентичны. В действительности эти оси немного смещены, а экваториальная плоскость качается, когда Земля вращается. В большинстве приложений этот эффект незначителен.
Единственный неинерционный эффект в земных координатах связан с Вращение Земли вокруг своей оси. Это вращающийся, геоцентрическая система . Блокчейн игнорирует Землю ускорение вокруг Солнца, ускорение Солнца в Галактике и Ускорение галактики через космос. В большинстве приложений только Вращение Земли имеет значение.
Это приближение должно быть изменено для космического корабля, отправленного в глубокое космос, например, за пределами системы Земля-Луна, и гелиоцентрическая система является предпочтительным.

Пассивные преобразования
Все кватернионы в Aerospace Blockset являются пассивными преобразованиями. При пассивном преобразовании вектор не меняется, а система координат, в которой он определен, поворачивается. Для большего информацию о преобразованиях см. в разделе Активные и пассивные преобразования.
Движение относительно других планет
Набор блоков использует стандартный геоид WGS-84 для моделирования Земли. Вы можете изменить длину экваториальной оси, сглаживание и скорость вращения.
Вы можете изобразить движение космического корабля относительно любой небесное тело, которое хорошо аппроксимируется сплюснутым сфероидом изменение размера сфероида, сглаживания и скорости вращения. Если небесное тело вращается на запад (ретроградно), сделайте вращение оценка отрицательная.
Системы координат для моделирования
Моделирование самолетов и космических аппаратов проще всего, если использовать систему координат, закрепленную в теле
сам. В случае самолета направление вперед изменяется наличием
ветра, и движение корабля по воздуху не совпадает с его движением относительно
на землю.
В случае самолета направление вперед изменяется наличием
ветра, и движение корабля по воздуху не совпадает с его движением относительно
на землю.
См. уравнения движения для получения дополнительной информации о том, как набор блоков реализует тело и ветер координаты.
Координаты тела
Неинерциальная система координат тела фиксируется как в начале координат, так и в ориентации движущееся судно. Судно считается жестким.
Ориентация осей координат тела зафиксирована в форме тела.
Ось x указывает через нос корабля.
Ось y указывает справа от x -ось (лицом в направлении взгляда пилота), перпендикулярно
Ось z указывает вниз через дно корабля, перпендикулярно плоскости xy и удовлетворяющей RH правило.
Поступательные степени свободы
Поступательные движения определяются перемещением вдоль этих осей на расстояния x , y и z от
Происхождение.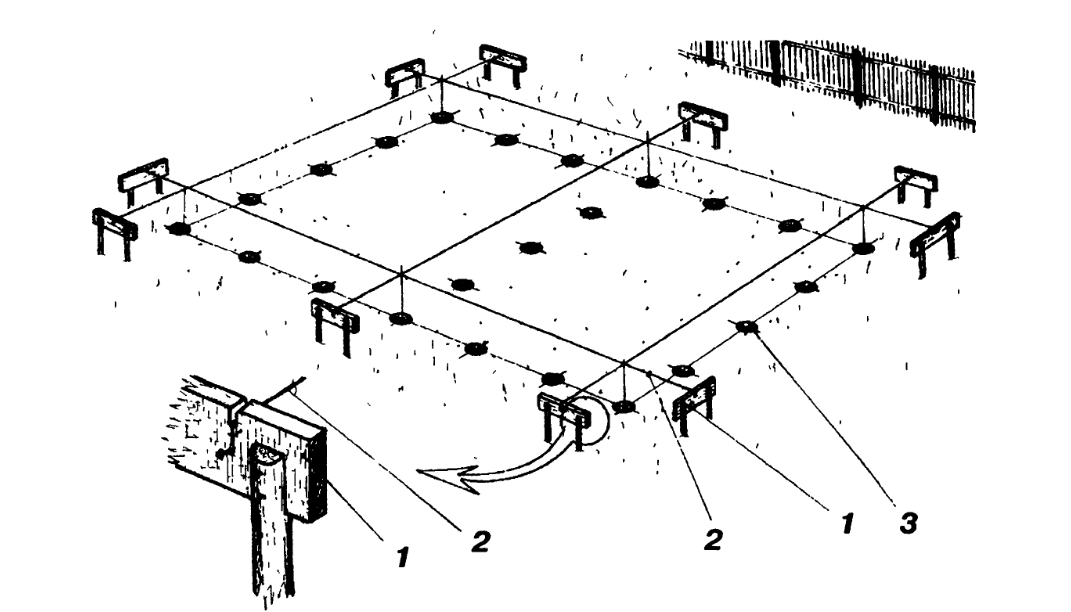
Степени свободы вращения
Вращения определяются углами Эйлера Р , Q , R или Φ, Θ, Ψ. К ним относятся:
| P или Φ | Ролик вокруг оси x |
| Q или Θ | Шаг относительно оси y |
| R или Ψ | Рыскание относительно оси z |
Если не указано иное, по умолчанию программа использует порядок вращения ZYX для углов Эйлера.
Координаты ветра
Начало неинерциальной системы координат ветра зафиксировано в твердом самолете. Ориентация системы координат определяется относительно скорости корабля V .
Ориентация осей координат ветра фиксируется скоростью V .
Ось x указывает направление В .

Ось y указывает справа от x – ось (обращенная в направлении V ), перпендикулярная x – ось.
Ось z указывает перпендикулярно xy плоскость любым способом, необходимым для удовлетворения RH правило относительно x – и и -оси.
Поступательные степени свободы
Поступательные движения определяются перемещением вдоль этих осей на расстояния
Степени свободы вращения
Вращения определяются углами Эйлера Φ, γ, χ:
| Φ | Угол крена относительно оси x |
| γ | Траектория полета вокруг оси y |
| χ | Курсовой угол относительно оси z |
Если не указано иное, по умолчанию программа использует порядок ротации ZYX. для углов Эйлера.
для углов Эйлера.
Системы координат для навигации
Моделирование аэрокосмических траекторий требует позиционирования и ориентации самолета или космического корабля относительно вращающейся Земли. Навигация координаты определяются относительно центра и поверхности Земля.
Геоцентрическая и геодезическая широта
геоцентрическая широта λ на поверхности Земли определяется углом стягивается радиус-вектором от центра Земли к точке поверхности с экваториальная плоскость.
геодезическая широта µ на поверхности Земли определяется углом опирается на вектор нормали к поверхности n и экваториальную плоскость.
Координаты NED
Система северо-восток-вниз (NED) представляет собой неинерциальную систему, начало которой зафиксировано на самолете. или центр тяжести космического корабля. Его оси ориентированы по геодезической направления, определяемые земной поверхностью.
Ось x указывает на север параллельно геоиду поверхности в полярном направлении.

Ось y указывает на восток параллельно геоиду поверхность, вдоль кривой широты.
Ось z направлена вниз, к Земле поверхность, антипараллельная внешней нормали к поверхности n .
Полет на постоянной высоте означает полет на постоянной z над поверхностью Земли.
Координаты ECI
Геоцентрическая инерциальная система (ECI) не вращается. Для большинства приложений предположим, что это система инерциальна, хотя плоскости равноденствия и экватора очень сильно смещаются. немного со временем. Система ЭКИ считается истинно инерционной для высокоточные расчеты орбиты, когда экватор и равноденствие определены в конкретная эпоха (например, J2000). Аэрокосмические функции и блоки, использующие конкретная реализация системы координат ECI обеспечивает эту информацию в их документация. Начало системы ECI зафиксировано в центре Земли. (см. рисунок).
Ось x указывает на точку весеннего равноденствия (первая Точка Овна ♈).

Ось y указывает на 90 градусов к востоку от x – ось в экваториальной плоскости.
Ось z указывает на север вдоль Земли ось вращения.
Система координат с центром на Земле
Координаты ECEF
Система координат с центром на Земле и с привязкой к Земле (ECEF) неинерциальна и вращается вместе с Землей. Его начало координат зафиксировано в центре Земли (см. предыдущий рисунок).
Ось x ′ указывает на пересечение Экваториальная плоскость Земли и Гринвичский меридиан.
Ось y ′ указывает на 90 градусов к востоку от x ’-ось в экваториальной плоскости.
Ось z ′ указывает на север вдоль Земли. ось вращения.
Системы координат для отображения
Несколько инструментов отображения доступны для использования с продуктом Aerospace Blockset.
У каждого есть определенная система координат для рендеринга движения.
Графические координаты MATLAB
См. Внешний вид осей для получения дополнительной информации о MATLAB ® Graphics координатные оси.
MATLAB Graphics использует эту ориентацию оси координат по умолчанию:
Ось x указывает за пределы экрана.
Ось y указывает вправо.
Ось z направлена вверх.
Координаты FlightGear
FlightGear — это сторонний симулятор полета с открытым исходным кодом. интерфейс, поддерживаемый набором блоков.
Работа с интерфейсом симулятора полета обсуждает интерфейс blockset для FlightGear.
Полную информацию см. в документации FlightGear по адресу
www.flightgear.org. об этом авиасимуляторе.
Координаты FlightGear образуют специальную фиксированную систему, повернута от стандартной системы координат тела относительно г -ось на -180 градусов:
Ось x положительна к задней части транспортное средство.

Ось y положительна вправо от транспортное средство.
Ось z направлена вверх, например, колеса обычно имеют самые низкие значения z .
Координаты AC3D
AC3D — недорогой, широко используемый редактор геометрии, доступный на https://www.inivis.com . Его фиксированные координаты тела
образована инвертированием трех стандартных осей координат тела:
Ось x положительна к задней части транспортное средство.
Ось y направлена вверх, например, колеса обычно имеют самые низкие значения y .
Ось z положительна слева от транспортное средство.
Каталожные номера
[1] Рекомендуется Практика координат атмосферных и космических летательных аппаратов Systems , R-004-1992, ANSI/AIAA, февраль 1992 г.
[2] Rogers, R. M., Прикладная математика в интегрированных навигационных системах, AIAA,
Рестон, Вирджиния, 2000.
[3] Собел, Д., Долгота , Walker & Company, Нью-Йорк, 1995.
[4] Стивенс Б.Л. и Ф.Л. Льюис, Управление воздушным судном и моделирование, 2-е изд., Управление самолетом и моделирование, Wiley-Interscience, новый York, 2003.
[5] Thomson, W. T., Введение в космическую динамику, John Wiley & Sons, New Йорк, 1961/Dover Publications, Минеола, Нью-Йорк, 1986.
Внешние веб-сайты
- Управление геоматики
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в Окно команд MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Обратитесь в местный офис
Урок 5: Геодезические данные
Здравствуйте! И добро пожаловать на пятый урок курса. Этот урок будет посвящен геодезическим системам отсчета (датумам), потому что невозможно использовать GPS/GNSS, не занимаясь геодезией.
Этот урок будет посвящен геодезическим системам отсчета (датумам), потому что невозможно использовать GPS/GNSS, не занимаясь геодезией.
Поэтому необходимо понимать исходный формат координат GPS/GNSS и то, как элементы геодезии влияют на эти координаты. Геодезия — сложный предмет, но мы будем говорить лишь о нескольких элементах науки.
Трехмерные декартовы координаты (ECEF)
Источник: GPS для геодезистов
GPS/GNSS и геодезия
Сегодня GPS/GNSS толкает нас в самую гущу геодезии, которая больше не является исключительной областью далеких эксперты. К счастью, в эпоху микрокомпьютеров с вычислительной рутиной можно справиться с помощью пакетов программного обеспечения. Тем не менее, неразумно браться за GPS/GNSS, полагая, что знание основ геодезии не нужно. Это правда, что GPS/GNSS были бы невозможны без компьютеров, но слепое доверие к данным, которые они генерируют, в конечном итоге приводит к катастрофе.
Некоторые геодезические системы координат
Трехмерные (3-D) декартовы координаты
Пространственная декартова система с тремя осями подходит для описания наземных координат, полученных с помощью космической геодезии. Используя три прямоугольные координаты вместо двух, можно однозначно определить любое положение на Земле или над ней, если уж на то пошло. Трехмерные декартовы координаты (x, y, z), полученные из этой системы, известны как координаты, ориентированные на Землю и зафиксированные на Земле (ECEF). Это правосторонняя ортогональная система, которая вращается вместе с Землей и связана с ней, поэтому она называется 9.0011 Земля зафиксирована .
Используя три прямоугольные координаты вместо двух, можно однозначно определить любое положение на Земле или над ней, если уж на то пошло. Трехмерные декартовы координаты (x, y, z), полученные из этой системы, известны как координаты, ориентированные на Землю и зафиксированные на Земле (ECEF). Это правосторонняя ортогональная система, которая вращается вместе с Землей и связана с ней, поэтому она называется 9.0011 Земля зафиксирована .
Трехмерная декартова система координат является правосторонней, если ее можно описать следующей моделью: вытянутый указательный палец правой руки символизирует положительное направление оси x. Средний палец той же руки, вытянутый под прямым углом к указательному, символизирует положительное направление оси у. Вытянутый большой палец правой руки, перпендикулярный им обоим, символизирует положительное направление оси Z.
Правосторонняя система
Источник: GPS для землемеров. сделанный.
На этом рисунке показана трехмерная декартова система координат. Можно выразить точку на поверхности Земли с помощью этих координат x, y и z в этой системе, ориентированной на Землю, фиксированной на Земле или ECEF. Это собственная система, в которой выражаются координаты GPS/GNSS; очевидно, что жизненно важными элементами этой системы являются плоскость экватора, средняя экваториальная плоскость и нулевой меридиан (он же нулевой меридиан). Обычное расположение известно как Обычная наземная система отсчета (CTRS), и Обычная наземная система (CTS) . Здесь будет использоваться последнее название. Началом является центр масс всей Земли, включая океаны и атмосферу, геоцентр . Поскольку спутники вращаются вокруг центра масс Земли, разумно иметь систему координат, полученную от спутников с ее началом в центре масс. Его можно использовать для определения положения на поверхности Земли или, если уж на то пошло, положения над поверхностью Земли. В этой системе орбитального спутника можно иметь координату XYZ. Ось X — это линия, проходящая от этого геоцентра через его пересечение на нулевом меридиане, также известном как 9-й0011 Международный эталонный меридиан (IRM), с общепринятым международным экватором.
Можно выразить точку на поверхности Земли с помощью этих координат x, y и z в этой системе, ориентированной на Землю, фиксированной на Земле или ECEF. Это собственная система, в которой выражаются координаты GPS/GNSS; очевидно, что жизненно важными элементами этой системы являются плоскость экватора, средняя экваториальная плоскость и нулевой меридиан (он же нулевой меридиан). Обычное расположение известно как Обычная наземная система отсчета (CTRS), и Обычная наземная система (CTS) . Здесь будет использоваться последнее название. Началом является центр масс всей Земли, включая океаны и атмосферу, геоцентр . Поскольку спутники вращаются вокруг центра масс Земли, разумно иметь систему координат, полученную от спутников с ее началом в центре масс. Его можно использовать для определения положения на поверхности Земли или, если уж на то пошло, положения над поверхностью Земли. В этой системе орбитального спутника можно иметь координату XYZ. Ось X — это линия, проходящая от этого геоцентра через его пересечение на нулевом меридиане, также известном как 9-й0011 Международный эталонный меридиан (IRM), с общепринятым международным экватором.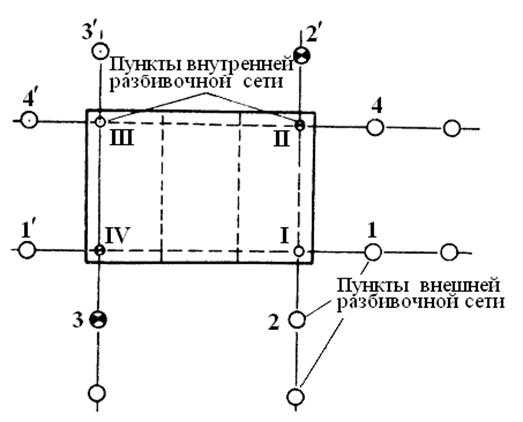 Ось у продолжается от геоцентра вдоль линии, перпендикулярной оси абсцисс, в той же средней экваториальной плоскости к 90° восточной долготы. Это означает, что положительный конец оси Y пересекает настоящую Землю в Индийском океане. В любом случае, они оба вращаются вместе с Землей вокруг оси z, линии от геоцентра до полюса, определенного на международном уровне, известного как Международный опорный полюс (IRP).
Ось у продолжается от геоцентра вдоль линии, перпендикулярной оси абсцисс, в той же средней экваториальной плоскости к 90° восточной долготы. Это означает, что положительный конец оси Y пересекает настоящую Землю в Индийском океане. В любом случае, они оба вращаются вместе с Землей вокруг оси z, линии от геоцентра до полюса, определенного на международном уровне, известного как Международный опорный полюс (IRP).
Полярное движение
Полярное движение
Источник: GPS для геодезистов
Абстрактная идея трехмерной системы координат совершенна в теоретическом смысле, но когда вы привязываете ее к реальной, физической Земле, возникают трудности. . Например, ось вращения Земли просто не будет стоять на месте. Земля качается, поэтому ось z этой трехмерной декартовой системы, центрированной на Земле и привязанной к Земле, зафиксирована в соответствии с международным соглашением. Земля, конечно же, постоянно движется. Хотя можно сказать, что Земля имеет определенную ось вращения, экватор и нулевой меридиан на мгновение, все они немного меняются в следующее мгновение.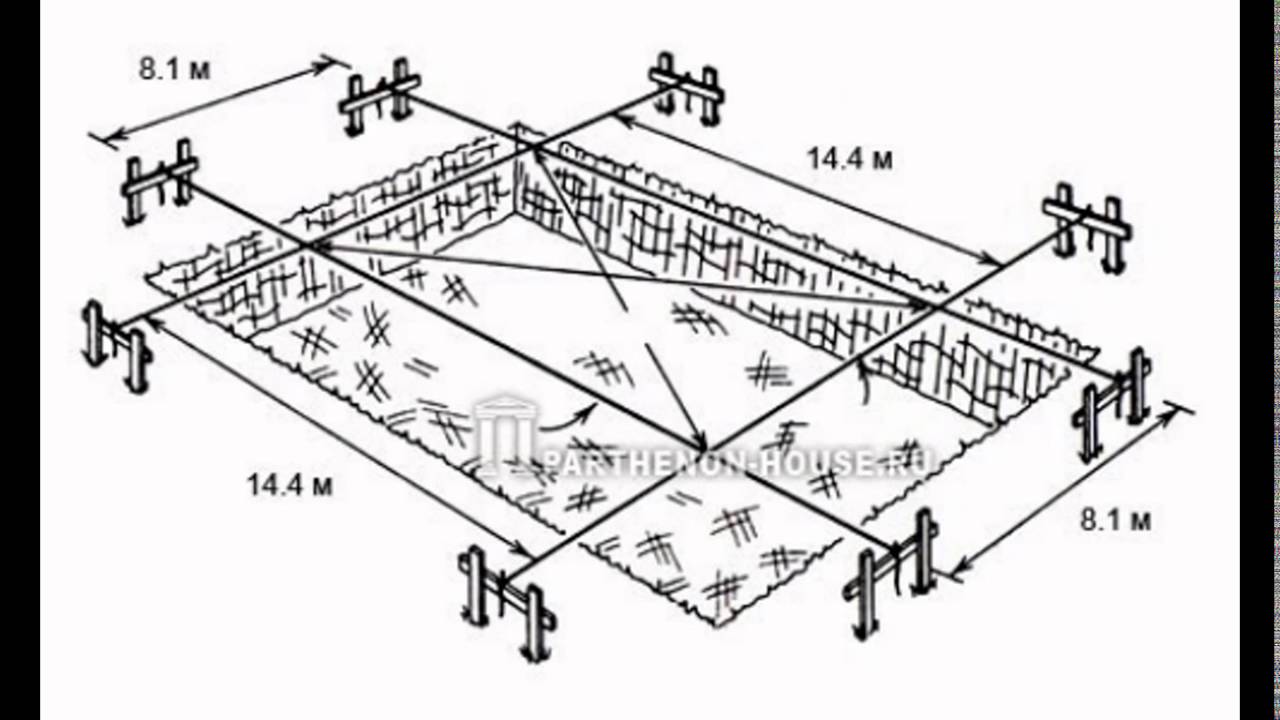 Во всем этом движении, как вы стабилизируете начало и направление трех осей в долгосрочной перспективе? Один из способов — выбрать момент времени и считать их прикрепленными к Земле такими, какие они есть в этот момент.
Во всем этом движении, как вы стабилизируете начало и направление трех осей в долгосрочной перспективе? Один из способов — выбрать момент времени и считать их прикрепленными к Земле такими, какие они есть в этот момент.
Вот пример процесса определения. Ось вращения Земли слегка отклоняется относительно твердой Земли в виде очень медленных колебаний, называемых полярным движением . Самая большая составляющая движения относительно земной коры имеет 430-дневный цикл, известный как Чандлеровский период . Он был назван в честь американского астронома Сета К. Чандлера, который описал его в статьях в Astronomical Journal в 1891 году. Другой аспект движения полюсов иногда называют полярное странствие. Обычная земная система координат была бы бесполезна, если бы ее третья ось постоянно качалась. Первоначально для положения шеста было выбрано среднее устойчивое положение. Между 1900 и 1905 годами среднее положение полюса вращения Земли обозначалось как условное международное происхождение (CIO) и ось z . Это было определено Bureau International de l’Heure (BIH) . С тех пор он был усовершенствован Международной службы вращения Земли (IERS) с использованием интерферометрии со сверхдлинной базой (VLBI) и спутниковой лазерной локации (SLR). Теперь он расположен так, как это было в полночь в канун Нового 1983 года или 1 января 1984 года (UTC). Этот момент известен как эпоха и может быть записан как 1984.0. Итак, теперь мы используем показанные оси. Название оси z было изменено на Международный опорный полюс, эпоха IRP 1984, но остается в пределах 0,005 дюйма от предыдущего определения. Он обеспечивает геометрически стабильное и четкое определение земной поверхности для z -ось.
Это было определено Bureau International de l’Heure (BIH) . С тех пор он был усовершенствован Международной службы вращения Земли (IERS) с использованием интерферометрии со сверхдлинной базой (VLBI) и спутниковой лазерной локации (SLR). Теперь он расположен так, как это было в полночь в канун Нового 1983 года или 1 января 1984 года (UTC). Этот момент известен как эпоха и может быть записан как 1984.0. Итак, теперь мы используем показанные оси. Название оси z было изменено на Международный опорный полюс, эпоха IRP 1984, но остается в пределах 0,005 дюйма от предыдущего определения. Он обеспечивает геометрически стабильное и четкое определение земной поверхности для z -ось.
Станция CTMC
Источник: GPS для геодезистов
В этой трехмерной правосторонней системе координат координата x представляет собой расстояние от плоскости y-z, измеренное параллельно оси x. Она всегда положительна от нулевого меридиана до 90° западной долготы и от нулевого меридиана до 90° восточной долготы.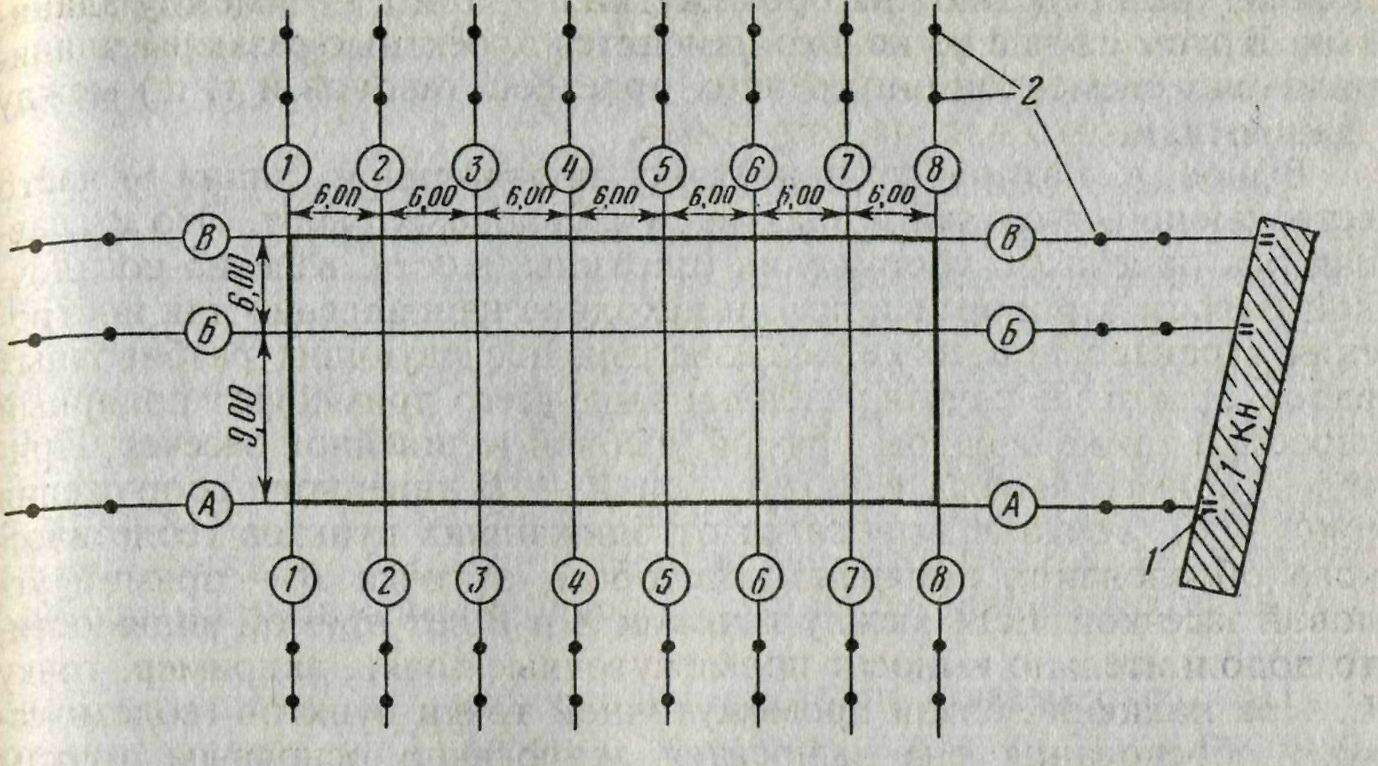 В остальных 180º координата X отрицательна. Координата Y представляет собой перпендикулярное расстояние от плоскости нулевого меридиана. В восточном полушарии он всегда положительный, а в западном полушарии отрицательный. Координата z представляет собой перпендикулярное расстояние от плоскости экватора. В Северном полушарии он всегда положительный, а в Южном полушарии отрицательный. Вот, выше, пример — положение станции CTMC, выраженное в трехмерных декартовых координатах этого типа, выраженное в метрах, родная единица системы:
В остальных 180º координата X отрицательна. Координата Y представляет собой перпендикулярное расстояние от плоскости нулевого меридиана. В восточном полушарии он всегда положительный, а в западном полушарии отрицательный. Координата z представляет собой перпендикулярное расстояние от плоскости экватора. В Северном полушарии он всегда положительный, а в Южном полушарии отрицательный. Вот, выше, пример — положение станции CTMC, выраженное в трехмерных декартовых координатах этого типа, выраженное в метрах, родная единица системы:
Различия в ECEF X, Y и Z
Источник: GPS для геодезистов
Важно отметить, что сегмент управления GPS/GNSS генерирует положение и скорость самих спутников в координатах ECEF. Из этого следует, что большинство современных программ GPS/GNSS также обеспечивают координаты GPS/GNSS в ECEF. Кроме того, концы базовых линий, определенные с помощью GPS/GNSS-наблюдений, обычно задаются в координатах ECEF, так что сами векторы становятся разницей между этими 9 точками. 0011 x , y и z координаты. Отображение этих различий как DX , DY и DZ является обычным результатом этих вычислений с последующей обработкой. Именно так GPS/GNSS определяет векторы. Из этих координат можно получить любое количество других координат, т. е. координаты системы Universal Transfers Mercater, координаты State Plane, широту и долготу. Все это может быть получено из координат XYZ в трехмерной декартовой системе, ориентированной на Землю и зафиксированной на Земле.
0011 x , y и z координаты. Отображение этих различий как DX , DY и DZ является обычным результатом этих вычислений с последующей обработкой. Именно так GPS/GNSS определяет векторы. Из этих координат можно получить любое количество других координат, т. е. координаты системы Universal Transfers Mercater, координаты State Plane, широту и долготу. Все это может быть получено из координат XYZ в трехмерной декартовой системе, ориентированной на Землю и зафиксированной на Земле.
Широта и долгота
Широта и долгота
Источник: GPS для геодезистов
Несмотря на свою полезность, такие трехмерные декартовы координаты не являются наиболее распространенным методом выражения геодезического положения. Широта и долгота были координатами выбора на протяжении веков. Их обозначение основано на тех же двух стандартных линиях, что и трехмерные декартовы координаты: средний экватор и нулевой меридиан. Однако, в отличие от них, они требуют некоторого четкого представления земной поверхности.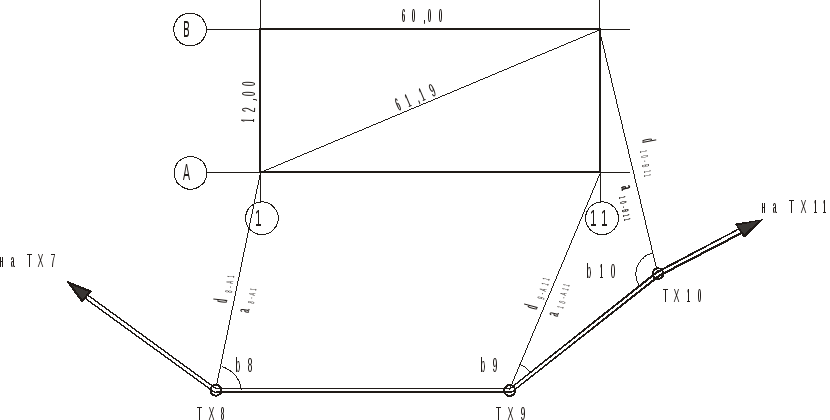

 Вся информация, полученная в результате разбивочных работ, обрабатывается специальным программным обеспечением. Составляется технический отчет по разбивке строительных осей, который включает схему осей, акт о приемке работ.
Вся информация, полученная в результате разбивочных работ, обрабатывается специальным программным обеспечением. Составляется технический отчет по разбивке строительных осей, который включает схему осей, акт о приемке работ.