Экспликация зданий и сооружений размеры таблицы: Размеры граф таблицы устанавливает разработчик

1.1: Введение в структурный анализ

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 17606

Феликс Удойо
Университет Темпл

Глава 1

Введение в структурный анализ

1.1 Структурный анализ Определение

Конструкция, применительно к гражданскому строительству, представляет собой систему взаимосвязанных элементов, используемых для поддержки внешних нагрузок. Структурный анализ – это прогноз реакции конструкций на заданные произвольные внешние нагрузки. На этапе предварительного проектирования конструкции оценивается возможная внешняя нагрузка конструкции, и на основе расчетных нагрузок определяются размеры взаимосвязанных элементов конструкции.

Структурный анализ устанавливает взаимосвязь между ожидаемой внешней нагрузкой элемента конструкции и соответствующими развитыми внутренними напряжениями и смещениями конструкции, которые возникают внутри элемента во время эксплуатации. Это необходимо для обеспечения того, чтобы элементы конструкции удовлетворяли требованиям безопасности и эксплуатационной пригодности местных строительных норм и правил и спецификаций района, где расположена конструкция.

1.2 Типы конструкций и элементов конструкции

Существует несколько типов гражданских инженерных сооружений, включая здания, мосты, башни, арки и тросы. Члены или компоненты, составляющие структуру, могут иметь различные формы или формы в зависимости от их функциональных требований. Конструктивные элементы могут быть классифицированы как балки, колонны и натяжные конструкции, рамы и фермы. Особенности этих форм будут кратко рассмотрены в этом разделе.

1.2.1 Балки

Балки – это элементы конструкции, продольные размеры которых значительно больше их поперечных размеров. Например, длина балки, как показано на рис. 1.1, значительно больше ее ширины и глубины. Поперечное сечение балки может быть прямоугольным, круглым или треугольным, или оно может иметь так называемые стандартные сечения, такие как швеллеры, тройники, уголки и двутавры. Балки всегда нагружены в продольном направлении.

Рис. 1.1. Луч.

1.2.2 Колонны и натяжные конструкции

Колонны представляют собой вертикальные элементы конструкции, подвергающиеся осевому сжатию, как показано на рис. 1.2а. Их также называют стойками или стойками. Колонны могут быть круглыми, квадратными или прямоугольными в поперечном сечении, а также стандартного сечения. В некоторых инженерных приложениях, где прочности одного элемента может быть недостаточно для выдерживания заданной нагрузки, используются составные колонны. Сборная колонна состоит из двух или более стандартных секций, как показано на рис. 1.2b. Натяжные конструкции аналогичны колоннам, за исключением того, что они подвергаются осевому растяжению.

Рис. 1.2. Колонны.

1.2.3 Рамки

Рамы представляют собой конструкции, состоящие из вертикальных и горизонтальных элементов, как показано на рис. 1.3а. Вертикальные элементы называются колоннами, а горизонтальные — балками. Рамы классифицируются как качающиеся и не качающиеся. Качающаяся рама допускает боковое или боковое движение, а некачающаяся рама не допускает движения в горизонтальном направлении. При их анализе учитываются боковые перемещения качающихся рам. Каркасы также можно разделить на жесткие и гибкие. Соединения жесткого каркаса неподвижны, а шарниры гибкого каркаса подвижны, как показано на рис. 1.3б.

Рис. 1.3. Рамка.

1.2.4 Фермы

Фермы — это несущие конструкции, состоящие из прямых элементов, соединенных в узлах, как показано на рис. 1.4. При расчете ферм нагрузки прикладывают к стыкам, и предполагается, что элементы соединяются в стыках с помощью штифтов без трения.

Рис. 1.4. Ферма.

1.3 Основные понятия и принципы структурного анализа

1.3.1 Условия равновесия

Гражданские инженерные конструкции должны находиться в состоянии покоя при воздействии внешних сил. Конструкция в состоянии покоя должна удовлетворять условиям равновесия, которые требуют, чтобы результирующая сила и результирующий момент, действующие на конструкцию, были равны нулю. Условия равновесия конструкции могут быть выражены математически следующим образом:

1.3.2 Совместимость рабочего объема

Концепция совместимости перемещений подразумевает, что когда конструкция деформируется, элементы конструкции, которые соединены в одной точке, остаются соединенными в этой точке без пустот или отверстий. Другими словами, говорят, что две части конструкции совместимы по смещениям, если части остаются соединенными вместе, когда конструкция деформируется из-за приложенной нагрузки. Совместимость перемещений — мощная концепция, используемая при анализе неопределенных конструкций с неизвестными избыточными силами, превышающими три уравнения равновесия.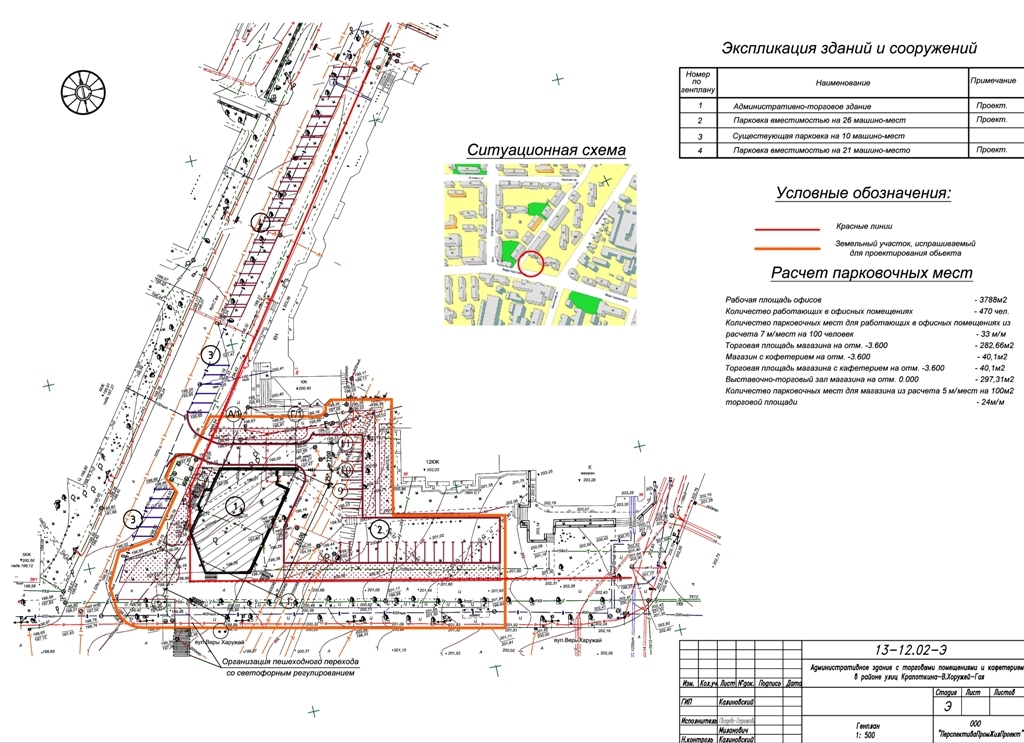 Для иллюстрации концепции рассмотрим подпертую консольную балку, показанную на рис. 1.5а. В балке имеются четыре неизвестные реакции: реактивный момент, вертикальная и горизонтальная реакции на закрепленном конце и еще одна вертикальная реакция на подпорке в точке 9.0086 Б

. Для определения неизвестных реакций в балке к трем уравнениям равновесия необходимо добавить еще одно. Дополнительное уравнение можно получить следующим образом, учитывая совместимость структуры:

В этом уравнении ∆ _BP — перемещение в точке B конструкции под действием приложенной нагрузки P (рис. 1.5b), а ∆ _BR — перемещение в точке 6 B

за счет реакции на проп R (рис. 1.5в). Студенты всегда должны помнить, что первый нижний индекс смещения указывает на место, где происходит смещение, а второй нижний индекс указывает на нагрузку, вызывающую смещение.

Рис. 1.5. Подпертая консольная балка.

1. 3.3 Принцип суперпозиции

Принцип суперпозиции — еще один очень важный принцип, используемый в структурном анализе. Принцип гласит, что эффекты нагрузки, вызванные двумя или более нагрузками в линейно-упругой конструкции, равны сумме эффектов нагрузки, вызванных отдельной нагрузкой. Для иллюстрации рассмотрим консольную балку, несущую две сосредоточенные нагрузки 9.0086 P

₁ и P ₂ на рис. 1.6а. На рисунках 1.6b и 1.6c представлены реакции конструкции на смещение свободного конца балки при воздействии отдельных нагрузок. По принципу суперпозиции перемещение на свободном конце балки представляет собой алгебраическую сумму перемещений, вызванных отдельными нагрузками. Эта банка записывается следующим образом:

В этом уравнении ∆ _B — это смещение на Б ; ∆ _{BP ₁} и ∆ _{BP ₂} являются смещениями при B , вызванные нагрузками P ₁ и P.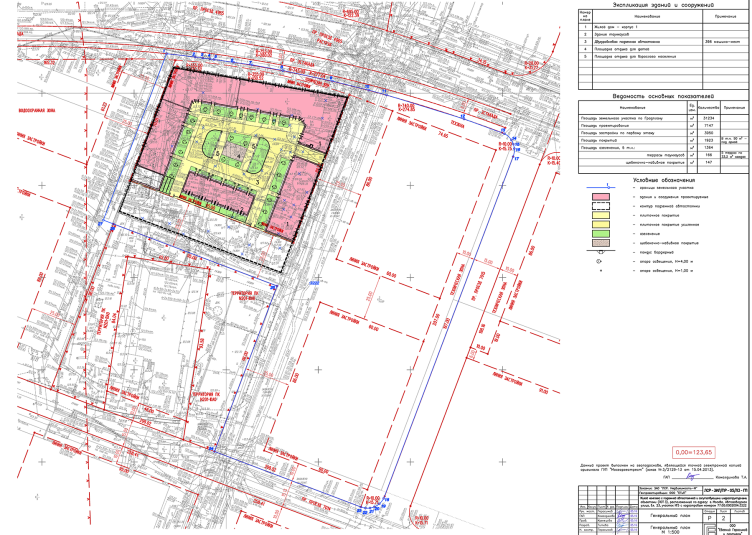 P ₁ и P.

2 _{.
Рис. 1.6. Применение принципа суперпозиции.
1.3.4 Принцип работы-энергии
Принцип работы-энергии является очень мощным инструментом в структурном анализе. Работа определяется как произведение силы на расстояние, пройденное силой, а энергия определяется как способность совершать работу. Работа может быть преобразована в различную энергию, включая кинетическую энергию, потенциальную энергию и энергию деформации. В случае структурной системы, основанной на законе сохранения энергии, работа совершается Вт равно энергии деформации U запасенной при деформации системы. Это выражается математически следующим образом:
Рассмотрим случай, когда сила F постепенно прикладывается к деформируемой структурной системе. Построив зависимость приложенной силы от деформации ∆ конструкции, можно построить график нагрузки-деформации, показанный на рис. 1.7а. В случае линейно-упругой конструкции диаграмма нагрузка-деформация будет такой, как показано на рис.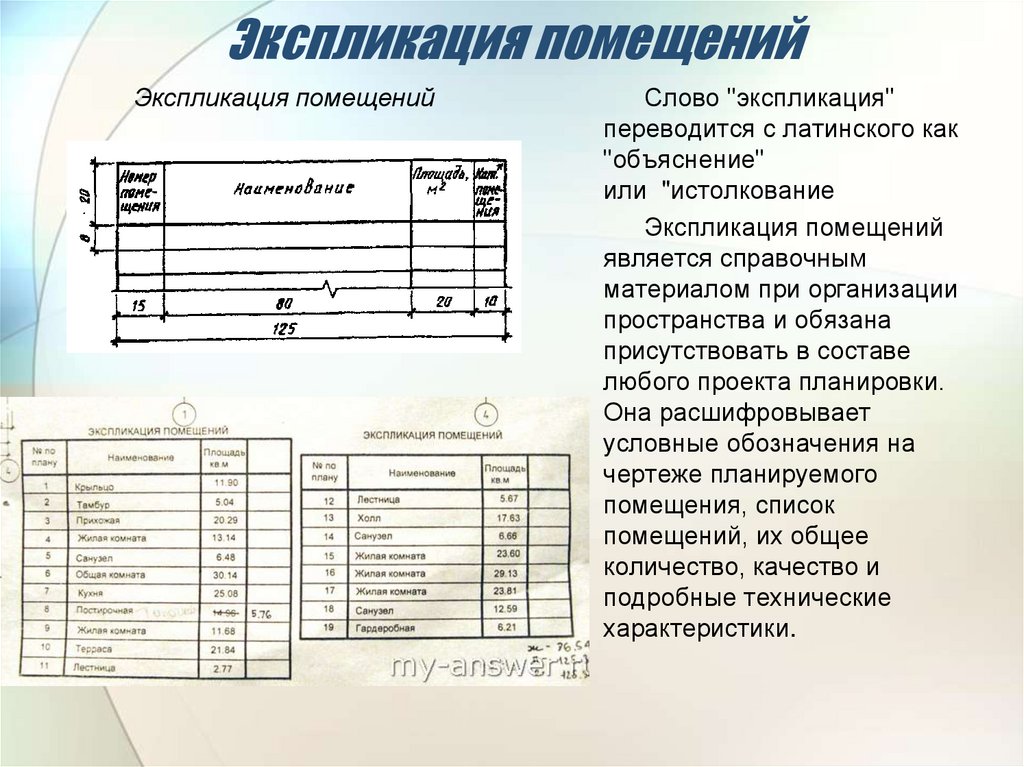
1.7б. Проделанная дополнительная работа dW силой при деформации конструкции на пошаговое перемещение d ∆ выражается следующим образом:
Общая проделанная работа представлена следующим образом:
Таким образом, энергия деформации записывается следующим образом:
Энергия деформации в случае линейно-упругой деформации может быть получена путем вычисления площади под диаграммой нагрузка-деформация на рис. 1.7b. Это выражается следующим образом:
Рис. 1.7. Диаграмма нагрузка-деформация.
1.3.5 Принцип виртуальной работы
Принцип виртуальной работы — еще один мощный и полезный аналитический инструмент в структурном анализе. Он был разработан в 1717 году Иоганном Бернулли. Виртуальная работа определяется как работа, совершаемая виртуальной или воображаемой силой, действующей на деформируемое тело через реальное расстояние, или работа, совершаемая реальной силой, действующей на твердое тело посредством виртуального или фиктивного перемещения.
Чтобы сформулировать этот принцип в случае виртуальных перемещений через твердое тело, рассмотрим подпертую консольную балку, на которую действует сосредоточенная нагрузка P на расстоянии x от фиксированного конца, как показано на рис. 1.8а. Предположим, что балка претерпевает элементарное виртуальное перемещение δu на подпираемом конце, как показано на рис. 1.8b. Суммарная выполненная виртуальная работа выражается следующим образом:
Поскольку балка находится в равновесии, δW = 0 (по определению принципа виртуальной работы тела).
Принцип виртуальной работы твердого тела гласит, что если твердое тело находится в равновесии, то суммарная виртуальная работа всех внешних сил, действующих на тело, равна нулю при любом виртуальном перемещении.

Рис. 1.8. Подпертая консольная балка.
1.3.6 Структурная идеализация
Структурная идеализация — это процесс, при котором реальная конструкция и действующие на нее нагрузки заменяются более простыми моделями для целей анализа. Строительные конструкции и их нагрузки чаще всего сложны и поэтому требуют тщательного анализа. Чтобы сделать анализ менее громоздким, структуры представлены в упрощенном виде. Выбор подходящей упрощенной модели является очень важным аспектом процесса анализа, поскольку прогностическая реакция такой идеализации должна быть такой же, как у реальной структуры. Рисунок 1.9а показывает свободно опертую балочную конструкцию с широкими полками и ее нагрузку. План той же балки показан на рис. 1.9б, а идеализация балки показана на рис. 1.9в. В идеализированном виде балка представлена линией, проходящей вдоль нейтральной оси балки, а нагрузка, действующая на балку, показана точечной или сосредоточенной нагрузкой, поскольку нагрузка занимает площадь, значительно меньшую, чем общая площадь конструкции. поверхности в плоскости ее приложения. На рисунках 1.10а и 1.10б изображен кадр и его идеализация соответственно. В идеализированной форме две колонны и балка рамы представлены линиями, проходящими через их соответствующие нейтральные оси. На рисунках 1.11а и 1.11б показана ферма и ее идеализация. Элементы фермы представлены линиями, проходящими через их соответствующие нейтральные оси, а соединение элементов в узлах предполагается без трения.
Рис. 1.9. Идеализация широкополочной балки.
Рис. 1.10. Идеализация кадра.
Рис. 1.11. Идеализация фермы.
1.3.7 Метод секций
Метод сечений полезен при определении внутренних сил в элементах конструкции, находящихся в равновесии. Метод заключается в прохождении воображаемого сечения через конструктивный элемент таким образом, что он делит конструкцию на две части. Силы стержня определяются с учетом равновесия любой части. Для балки, находящейся в равновесии и подвергаемой поперечной нагрузке, как показано на рис. 1.12, внутренние силы включают осевую или нормальную силу, Н , поперечная сила, В , и изгибающие моменты, М .
Рис. 1.12. Балка в равновесии под действием поперечной нагрузки.
1.3.8 Схема свободного тела
Диаграмма свободного тела — это диаграмма, показывающая все силы и моменты, действующие на всю конструкцию или ее часть. Диаграмма свободного тела также должна быть в равновесии с фактической структурой. Диаграмма свободного тела всей балки, показанная на рисунке 1.13а, изображена на рисунке 1.13b. Если требуется диаграмма свободного тела сегмента балки, сегмент будет изолирован от всей балки с использованием метода сечений. Тогда к изолированной части будут приложены все внешние силы на сегмент и внутренние силы от примыкающей части конструкции.
Рис. 1.13 Схема свободного тела балки.
1.4 Единицы измерения
Двумя наиболее часто используемыми системами в науке и технике являются Международная система единиц (единицы СИ) и обычная система США (USCS).
1.4.1 Международная система единиц
В единицах СИ произвольно определенные базовые единицы включают метр (м) для длины, килограмм (кг) для массы и секунду (с) для времени. Единица силы, ньютон (Н), получена из второго закона Ньютона. Один ньютон — это сила, необходимая для того, чтобы придать килограмму массы ускорение 1 м/с ² . Величина в ньютонах веса тела массой м записывается следующим образом:
Вт (Н) = м (кг) × г (м/с ² )
где
г = 9,81 м/с ²
1.4.2 Система обычного права США
В традиционной системе Соединенных Штатов базовые единицы включают фут (фут) для длины, секунду (с) для времени и фунт (фунт) для силы. Слизняк для массы является производной единицей. Одна порция – это масса, ускоренная со скоростью 1 фут/с ² силой 1 фунт. Масса тела в порции определяется следующим образом:
Эти две системы единиц суммированы в таблице 1.1 ниже.
Таблица 1.1. Сравнение систем единиц измерения.
Таблица 1.2. Преобразование единиц.
1.4.3 Префиксы SI
Префиксы используются в Международной системе единиц, когда числовые величины являются достаточно большими или малыми. Некоторые из этих префиксов представлены в таблице 1.3.
Таблица 1.3. префиксы СИ.
Резюме главы
Введение в структурный анализ: Структурный анализ определяется как прогнозирование поведения конструкций при воздействии заданных произвольных внешних нагрузок.
Типы конструкций : Конструктивные элементы могут быть классифицированы как балки, колонны и натяжные конструкции, рамы и фермы.
Основные понятия структурного анализа: Фундаментальная концепция и принципы структурного анализа, обсуждаемые в главе, включают условия равновесия, совместимость перемещений, принцип суперпозиции, принцип работы-энергии, принцип виртуальной работы, структурную идеализацию, метод сечений и диаграмму свободного тела.
Эта страница под названием 1.1: Введение в структурный анализ распространяется под лицензией CC BY-NC-ND 4.0 и была создана, изменена и/или курирована Феликсом Удойо посредством исходного контента, отредактированного в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Автор
Феликс Удоэйо
Лицензия
CC BY-NC-ND
Версия лицензии
4,0
Теги
источник@https://temple.manifoldapp.org/projects/structural-analysis
Совет штата Калифорния по контролю за водными ресурсами
Страница, которую вы просматриваете
поскольку, возможно, был перемещен.}