Виды сечений в геометрии: Сечение многогранников – презентация по Геометрии

9.3. Сечения

Форму отдельных элементов детали на чертежах наглядно демонстрируют сечения, которые показывают только то, что расположено в секущей плоскости.

Сечения подразделяются на вынесенные и наложенные. Вынесенные сечения обводятся сплошной основной линией толщиной S и вычерчиваются на свободном поле чертежа (рис. 9.8).

Рис. 9.8. Вынесенные сечения.

Они имеют такое же обозначение, как сложные и наклонные разрезы, при этом они могут быть вычерчены с изменением масштаба и повернуты. Если сечение повернуто относительно заданной секущей плоскости, то после присвоения имени ставится знак “повернуто” в виде окружности диаметром 3 – 5 мм и стрелкой, расположенной на ней. Внутри контура сечение штрихуется тонкими линиями под углом 45⁰.

Наложенные сечения обводятся сплошной тонкой линией S/2 и располагаются непосредственно на изображении.

Ось симметрии наложенного и вынесенного сечения указывают штрих-пунктирной тонкой линией.

9.4. Условности и упрощения

При изображении видов, разрезов, сечений надо стремиться к тому, чтобы их количество было минимальным, но достаточным для полного представления о предмете или конструкции при применении условных обозначений и надписей. Для этого предусмотрен ряд условностей:

• В случае симметрии изображения детали относительно какой-либо оси допускается совмещение половины вида с половиной разреза по штрих-пунктирной осевой линии.

• Если при совмещении половины вида с половиной разреза на осевую линию попадает ребро призматической поверхности, то допускается соединение части вида с частью разреза с использованием тонкой волнистой линии, с таким расчетом, чтобы была видна линия видимого контура.

• Сплошные тонкие тела, типа ребер жесткости, спиц маховиков и пр.

  в продольных разрезах принято не штриховать; в поперечных разрезах, при построении сечений и аксонометрических проекций, эти элементы штрихуются.

• Если длинные предметы имеют участки с постоянным или равномерно изменяющимся поперечным сечением, допускается изображать их с разрывами, выполненными на этих участках. Контуры разрыва выполняются сплошной тонкой линией (рис. 9.9).

Рис. 9.9. Изображение контурных разрывов на чертеже.

• В разрезе допускается изображать отверстия, расположенные в цилиндрической поверхности, когда они не попадают в секущую плоскость, используя метод “выкатывания”.

• Для выделения на чертеже плоских поверхностей предмета проводят перекрещивающиеся диагонали сплошными тонкими линиями.

Список использованных источников

1. Соломонов К.Н., Бусыгина Е. Б., Чиченева О.Н., Щеглов С.В. Основы начертательной геометрии: уч. пособие. — М.: Вузовская книга, 2003. — 108 с..

2. Соломонов К.Н., Бусыгина Е.Б., Чиченева О.Н. Начертательная геометрия: учебник. — М.: МИСиС, 2004. — 160 с.

3. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. — М.: Наука, 1968. —368 с.

4. Чекмарев А.А. Инженерная графика: учебник. — М.: Высшая школа, 1998. — 365 с.

5. Инженерная графика / Под ред. В.Г. Бурова — М.: Логос, 2006. — 232 с.

6. ГОСТ 2.301 – 68 — Форматы.

7. ГОСТ 2.302 – 68 — Масштабы.

8. ГОСТ 2.303 – 68 — Линии.

9. ГОСТ 2.304 – 81 — Шрифты чертежные.

10. ГОСТ 2.305 – 68 — Изображения — виды, разрезы, сечения.

11. ГОСТ 2.307 – 68 — Нанесение размеров и предельных отклонений.

12. ГОСТ 2.317 – 69 — Аксонометрические проекции.

124

Сечение тел плоскостью. (11 класс)

Похожие презентации:

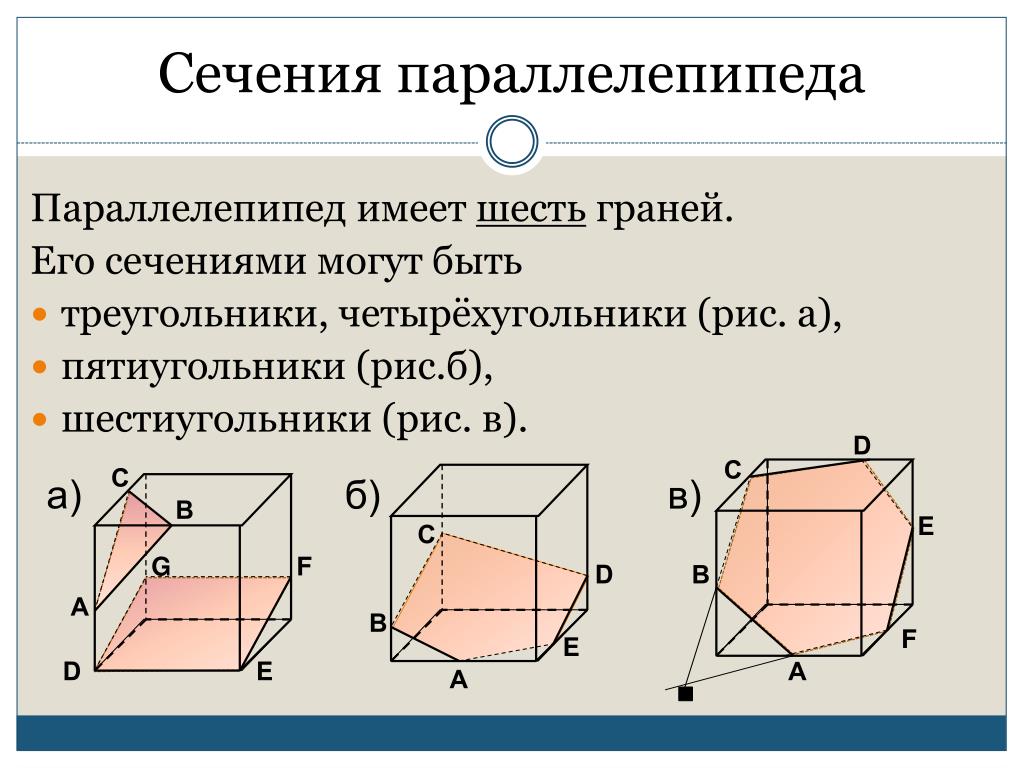
Сечение многогранников

Построение сечений многогранников

Сечение многогранников

Построение сечений многогранников

Построение сечения многогранника плоскостью

Параллелепипед. Тетраэдр. Виды многогранников

Сечение тел плоскостью

Построение сечений многогранников

Построение сечений многогранников

Построение сечений многогранников

1. СЕЧЕНИЕ ТЕЛ ПЛОСКОСТЬЮ

Урок геометрии в
11 классе.
Рахмеева Л.А.
Тема: Построение сечений
призмы и пирамиды
Цели:
Знакомство с методами построения сечений многогранников плоскостью,
видов сечений.
Формирование умений и навыков при решении задач на построение.
Изучение методов и основных понятий, систематизация заданий и
упражнений на построение.
Практическое применение умений и навыков при решении задач на
построение.
1.
2.
3.
4.
Методы:
1.
2.
3.
Демонстрация наглядных и электронных пособий.
Выполнение практических работ.
Устный рассказ.
Содержание урока
I. Сообщение учащимся темы, целей и задач урока.
II. Рассказ учителя о значении задач на построение сечений
многогранников в курсе геометрии.
III. Разбор и объяснение темы.
а) Виды сечений и их использование в различных областях науки.
(использование мультимедийной презентации)
б) Основные методы построения сечений в курсе геометрии 10-го
класса.
в) Разбор примера построения сечения пирамиды с использованием
наглядного пособия.
IV. Первичное закрепление.
а) Разбор задачи, выполненной учащимся в качестве
дополнительного задания.
б) Решение и разбор задачи на доске.
V. Подведение итогов урока. Объяснение домашнего задания.

4. Примеры сечения

Продольное сечение
детали.

5. Примеры сечения

Линкор ‘’Джулио Чезаре’ и его поперечное сечение

6. Примеры сечения

Трос биметаллический. Поперечное сечение.

7. Примеры сечения

Вид внутринности дома в
сечении.

8. Примеры сечения

План крепости.
Сечение по первому этажу.

9. Примеры сечения

Пропорции тела по Золотому сечению, в шаре
‘Золотого сечения’.
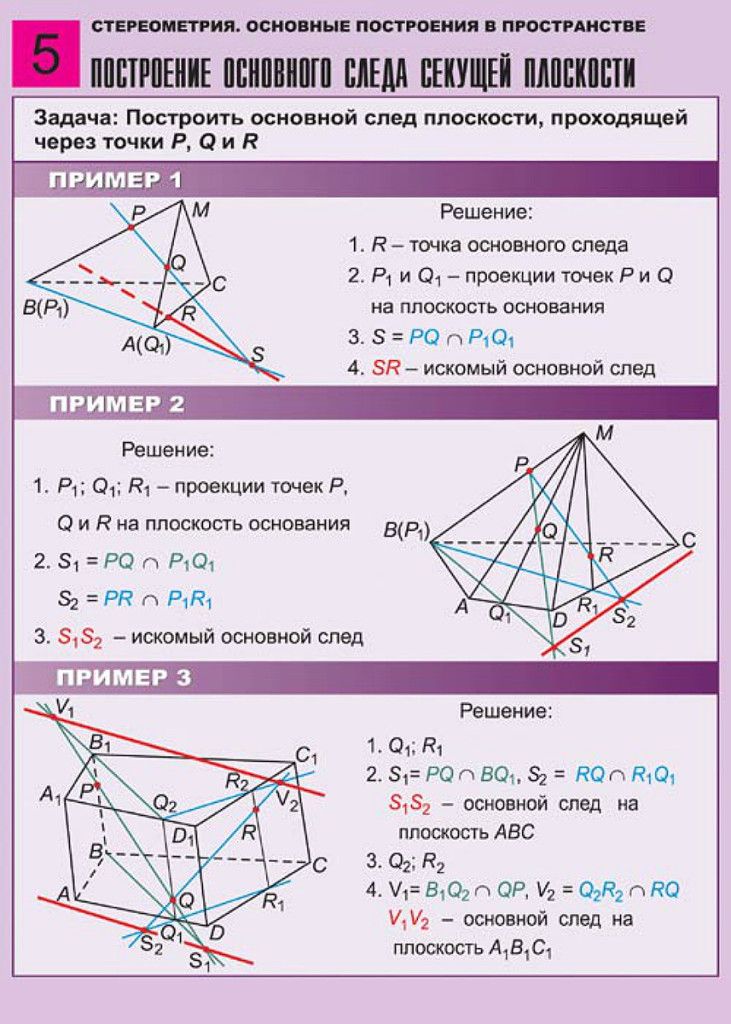
Методы построения сечений
1. Метод следов.
2. Метод внутреннего проектирования.
3. Комбинированный метод.
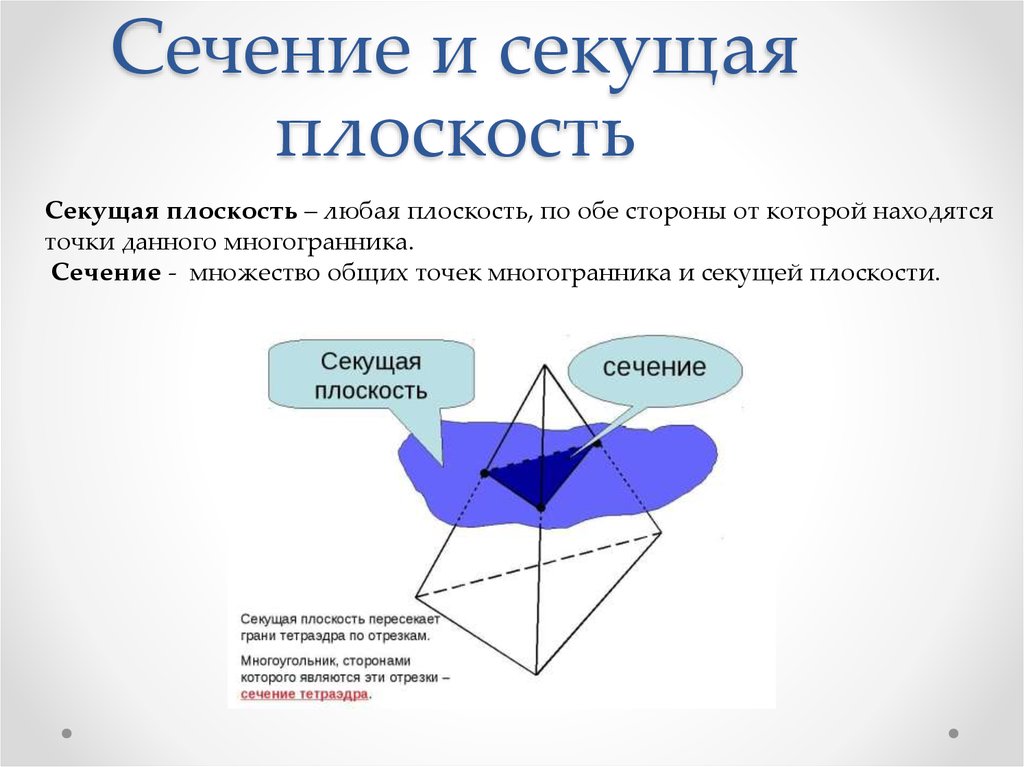
ОПРЕДЕЛЕНИЕ
Сечением поверхности геометрических
тел плоскостью называется плоская
фигура,
полученная
в
результате
пересечения
тела
плоскостью
и
содержащая точки, принадлежащие как
поверхности тела, так и секущей
плоскости.

12. Пример След секущей плоскости пересекает нижнюю грань многогранника

Сечение по трем точкам
Пример
След секущей плоскости
пересекает нижнюю грань
многогранника
Демо – эскиз
Призма
Три
данные
точки на
боковых
ребрах
Сечение
Плоскость основания
•Секущая плоскость
пересекает грани
многогранника по
прямым, а точнее по
отрезкам – разрезам.
•Так как секущая
плоскость идет
непрерывно, то разрезы
образуют замкнутую
фигуру-многоугольник.
•Полученный таким
образом многоугольник и
будет сечением тела.
Шаг 1: Разрезаем грани KLBA и
L
LMCB
• Проводим через
точки F и O прямую
FO.
F
K
• Отрезок FO есть
разрез грани KLBA
секущей плоскостью.
•Аналогичным образом
отрезок FG есть разрез
грани LMCB.
M
N
G
B
O
A
C
D
Шаг2: Ищем след секущей плоскости на плоскости
основания
L
F
• Проводим прямую АВ до
пересечения с прямой FO.
• Получим точку H, которая
принадлежит и секущей
плоскости, и плоскости
основания.
• Аналогичным образом
получим точку R.
• Через точки H и R
проводим прямую HR –
след секущей плоскости
H
M
K
N
G
B
O
A
C
R
D
Шаг3: Делаем разрезы на других гранях
• Так как прямая HR
пересекает нижнюю грань
многогранника, то
получаем точку E на входе
и точку S на выходе.
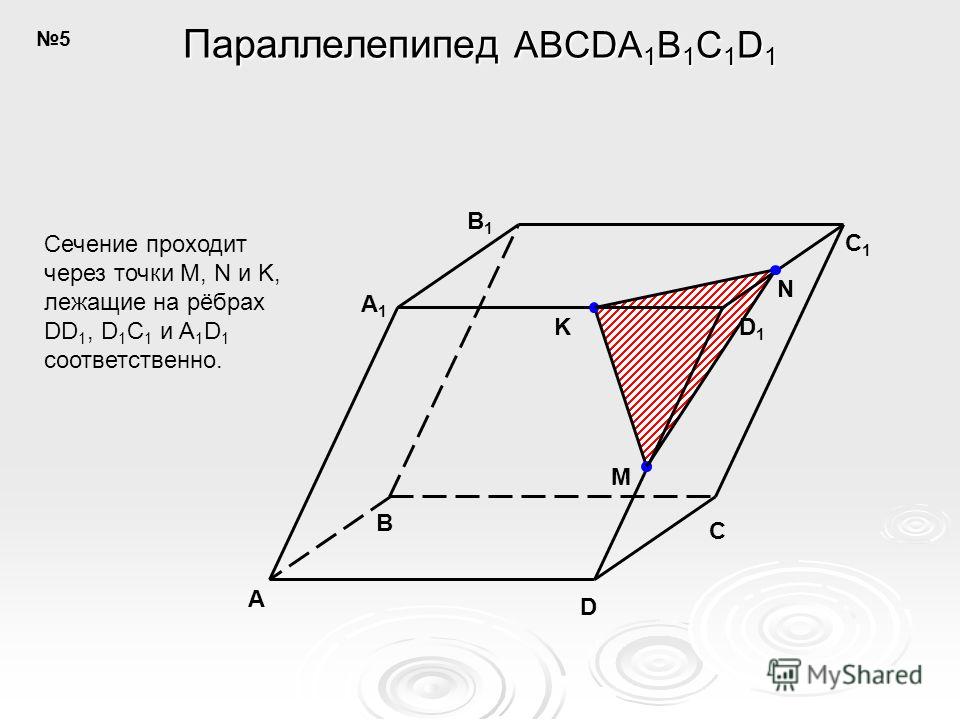
• Таким образом отрезок ES
есть разрез грани ABCD.
L
M
F
K
N
• Проводим отрезки ОЕ
(разрез грани KNDA) и GS
(разрез грани MNDC).
G
B
O
C
R
S
H
A
E
D
Шаг4: Выделяем сечение многогранника
L
•Все разрезы
образовали
пятиугольник OFGSE,
который и является
сечением призмы

плоскостью,
проходящей через
точки O, F, G.
M
F
K
N
G
B
O
C
S
A
E
D
Решение задачи.
Построение:
Дано: точки M, N, K
B
C
Рассмотрим случай: MN BB1,
N CC1DD1, K AA1E1.
В данном случае очевидно, что M1=B1.
А
M
E
D
C2
A2 K
N
B1 = M1
s
D2
А1
K1
Y
C1
E2
E1
N1
А0
D0
X
Построение.
1. MN M1N1= X.
2. MK M1K1 = Y.
3. XY = s – след секущей плоскости.
4. A1K s = A.
5. A0K A1A = A, A0K EE 1 = E.
6. D1N1 s = D0.
7. D0N DD1 = D, D0N CC1 = C2.
8. Пятиугольник A2MC2D2E –
искомое сечение данной
призмы.
Карточки с задачами для cамостоятельной работы
учащихся с доской
Итог урока
а) Обобщение темы урока.
б) Вопросы по ведению урока.
в) Домашнее задание:
§ 4, пункт 14, задачи: 79, 81

English     Русский Правила

Поперечное сечение геометрических фигур – Mechamath

Поперечное сечение представляет собой пересечение плоскости с трехмерным объектом. Сечением называют двумерную фигуру, полученную пересечением плоскости с трехмерной фигурой. Например, при разрезании цилиндра плоскостью, параллельной одному из его оснований, полученное поперечное сечение представляет собой круг. В зависимости от ориентации плоскости мы можем получить несколько сечений одного и того же объекта.

Здесь мы узнаем больше о поперечных сечениях и изучим поперечные сечения наиболее важных фигур.

ГЕОМЕТРИЯ

Актуально для …

Изучение сечений геометрических фигур.

См. сечения

Содержание

ГЕОМЕТРИЯ

Актуально для …

Изучение сечений геометрических фигур.

См. поперечные сечения

Типы поперечных сечений

В зависимости от ориентации плоскости, которая разрезает объект, мы можем иметь три типа поперечных сечений:

• Горизонтальное поперечное сечение
• Вертикальное поперечное сечение
• Наклонное поперечное сечение

Горизонтальное или параллельное поперечное сечение

Это поперечное сечение образуется, когда плоскость пересекает объект в направлении, параллельном основанию объекта.

Вертикальное или перпендикулярное поперечное сечение

Вертикальное поперечное сечение образуется при разрезании предмета плоскостью, перпендикулярной его основанию, то есть под углом 90°.

Наклонное поперечное сечение

Это поперечное сечение образуется, когда угол наклона плоскости, пересекающей объект, больше 0° и меньше 90°.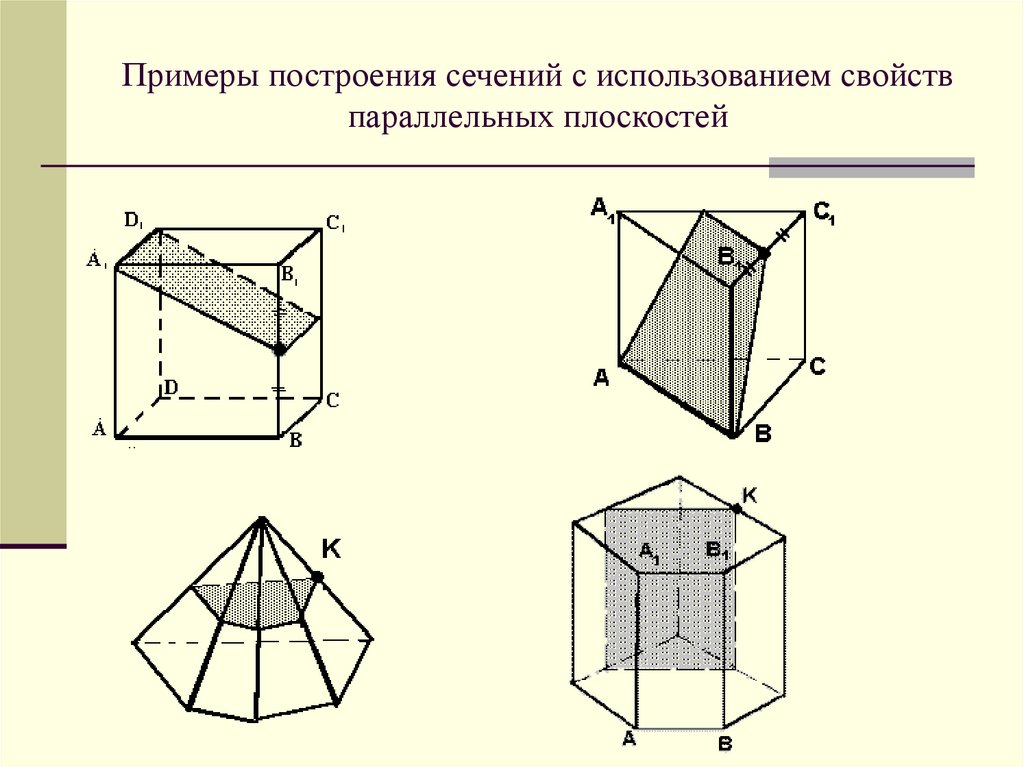

---

Площадь поперечного сечения

Когда плоскость пересекает твердый объект, площадь проецируется на плоскость. Если плоскость ориентирована горизонтально, то она будет перпендикулярна оси симметрии. В зависимости от фигуры мы можем рассчитать площадь поперечного сечения, признав, что поперечное сечение равно основаниям фигуры. 92}$, поэтому площадь поперечного сечения равна $латексу A=25$.

---

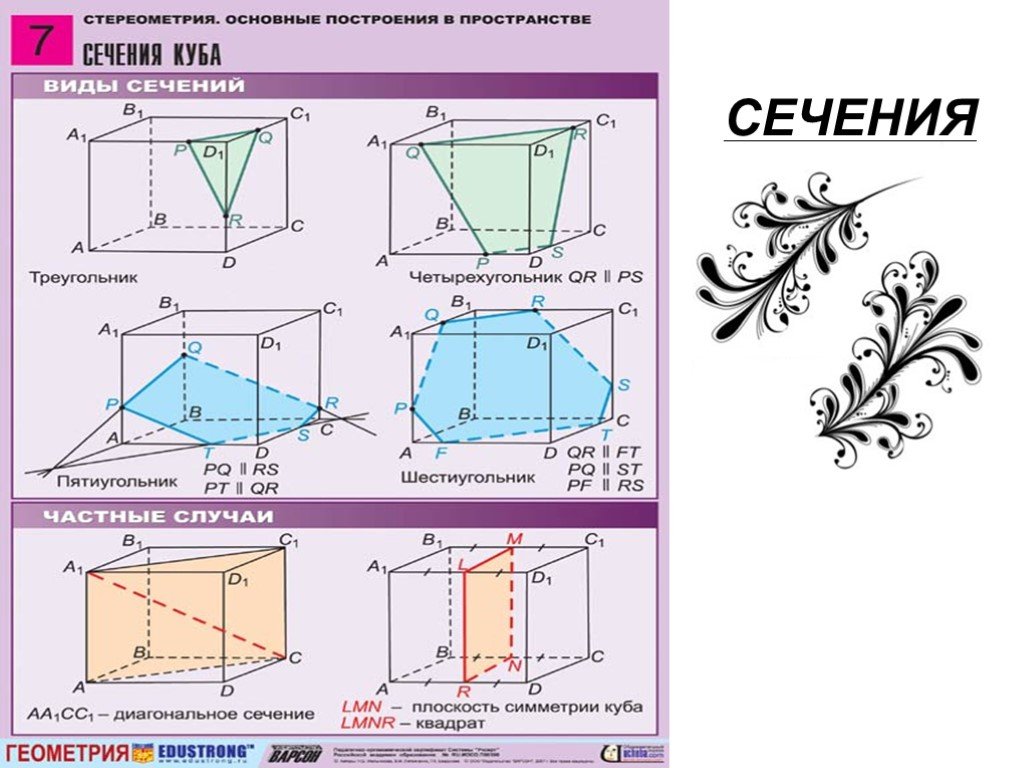
Сечения куба

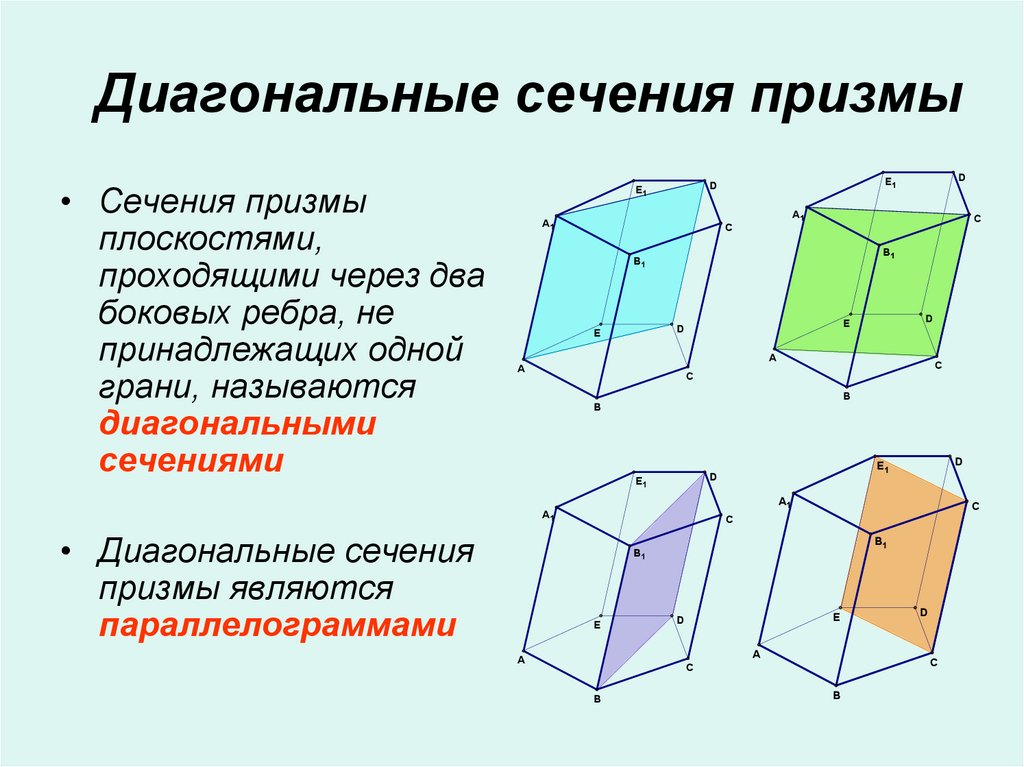
Куб — это трехмерная фигура, все стороны которой имеют одинаковую длину. Всего у куба шесть квадратных граней. Это означает, что когда плоскость пересекает куб в направлении, параллельном одной из его граней, поперечное сечение всегда будет квадратным.

Однако также возможно получение различных сечений путем разрезания куба с наклоном относительно его основания. Если плоскость пересекает три ребра куба, ее поперечное сечение будет треугольником.

Если секущая плоскость пересекает куб таким образом, что он пересекает диагонали граней, мы получим прямоугольное сечение:

Кроме того, мы также можем образовать шестиугольное сечение, пересекая куб наклонной плоскостью. следующим образом:

---

Сечения цилиндра

Цилиндр — это трехмерная фигура, имеющая круглые основания, соединенные боковой поверхностью. В зависимости от того, как он вырезан, поперечное сечение цилиндра может быть кругом, прямоугольником или овалом. Если цилиндр разрезать плоскостью, параллельной одному из его оснований, поперечное сечение будет кругом.

Овальное поперечное сечение получается, когда плоскость пересекает цилиндр под углом больше 0° и меньше 90° по отношению к основанию.

Если плоскость разрезает цилиндр в направлении, перпендикулярном основаниям, поперечное сечение будет прямоугольником.

---

Сечения конуса

Конус можно рассматривать как пирамиду с круглым поперечным сечением. В зависимости от соотношения между плоскостью и секущей поверхностью, поперечные сечения конуса могут быть окружностями, эллипсами, параболами и гиперболами.

Круг образуется при разрезании конуса плоскостью, параллельной его основанию.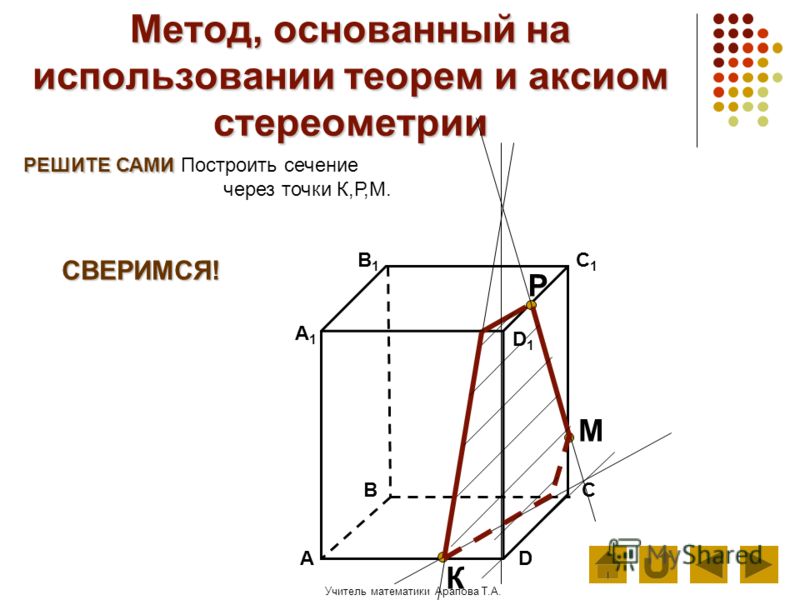

Эллипс образуется при разрезании конуса плоскостью, наклоненной под небольшим углом (меньше угла боковых сторон) по отношению к основанию конуса.

Парабола образуется, когда плоскость, пересекающая конус, параллельна одной боковой стороне конуса.

Гипербола образуется, когда плоскость, пересекающая конус, имеет больший угол (больше, чем угол боковых сторон) по отношению к основанию конуса.

---

Поперечное сечение сферы

Сфера — это идеально круглая трехмерная фигура. Поперечное сечение сферы всегда является окружностью, независимо от ориентации плоскости.

---

См. также

Хотите узнать больше о геометрических фигурах? Взгляните на эти страницы:

• Периметр и площадь – формулы и примеры
• Площадь геометрических фигур – формулы и диаграммы
• Объем геометрических фигур – формулы и примеры

Изучите определение поперечного сечения и способы его нахождения на примерах

В математике и геометрии поперечное сечение — это форма, возникающая при разрезании объекта плоскостью. Если форма и размер поперечного сечения одинаковы в каждой точке по всей длине/ширине/высоте тела, то поперечное сечение всегда будет однородным.

Например, когда спиливают дерево, оно имеет форму кольца по всей поверхности. Это реальный пример поперечных сечений. С помощью этой статьи вы узнаете значение сечения, его вид и площадь сечения геометрических фигур на примерах.

Поперечное сечение

Поперечное сечение в математике — это иллюстрация пересечения объекта плоскостью. Для твердого тела сечение, полученное в результате разреза, реального или воображаемого, перпендикулярного, диагонального или вертикального к длине, ширине или высоте твердого тела, называется его поперечным сечением.

Например, если у нас есть прямоугольный торт, нарезанный на квадратную грань, каждый его кусочек имеет квадратную форму. Однако, если торт разрезать с прямоугольной стороны, каждый ломтик будет прямоугольным. Теперь, если мы возьмем математический пример, если цилиндр разрезать по вертикали, его поперечное сечение будет прямоугольником. С другой стороны, если его разрезать по горизонтали, поперечное сечение будет кругом.

Типы поперечного сечения

Поперечное сечение в целом символизирует пересечение плоскости с трехмерным объектом или формой. В предыдущем заголовке мы прочитали, что в зависимости от ориентации плоскости мы можем получить несколько сечений от одного и того же объекта или объекта. Три распространенных типа ориентации:

• Вертикальное сечение
• Горизонтальное сечение
• Наклонное сечение

Изучите различные свойства прямоугольников.

Вертикальное поперечное сечение

В вертикальном или перпендикулярном поперечном сечении данная плоскость разрезает твердое тело в вертикальной ориентации, т. е. перпендикулярно основанию твердого тела, таким образом, что образует перпендикулярное поперечное сечение.

ИЛИ

При разрезании предмета плоскостью, перпендикулярной основанию предмета, то есть под углом 90 градусов, мы получаем вертикальное сечение предмета.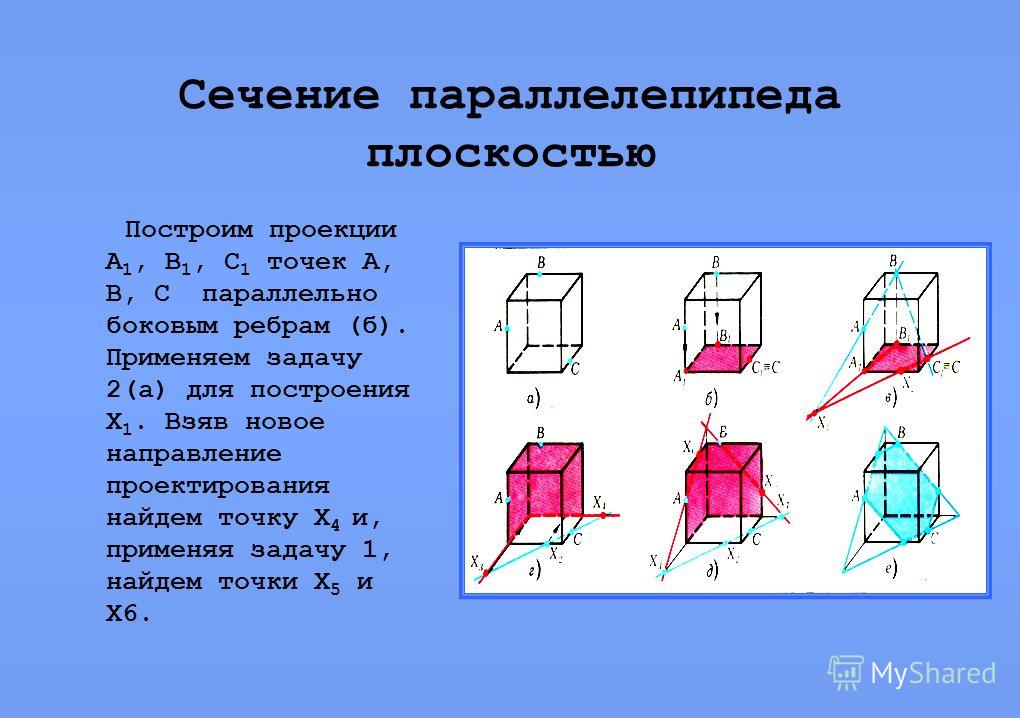

Например, если мы рассмотрим цилиндрический стержень. Вертикальное или перпендикулярное поперечное сечение цилиндрического стержня будет прямоугольником.

Горизонтальное поперечное сечение

В горизонтальном или параллельном поперечном сечении данная плоскость разрезает твердое тело в горизонтальной ориентации, т. е. параллельно основанию твердого тела, таким образом, что образует параллельное поперечное сечение.

ИЛИ

При разрезании объекта плоскостью, параллельной основанию объекта, то есть под углом 0 градусов, мы получаем горизонтальное сечение объекта.

Например, если мы рассмотрим цилиндрический стержень. Горизонтальное или параллельное сечение цилиндрического стержня будет кругом.

Наклонное поперечное сечение

Кроме вертикального и горизонтального, когда создается поперечное сечение и плоскость пересекает или пересекает объект под углом больше 0 градусов и меньше 90 градусов; такое сечение называется наклонным сечением.

Поперечное сечение геометрических фигур

Теперь, когда мы знаем определение поперечного сечения, а также его различные типы, давайте разберемся с понятиями площади поперечного сечения различных геометрических фигур.

Поперечные сечения конусов

Конус представляет собой тип пирамиды, но с круглым поперечным сечением, или представляет собой структуру, подобную пирамиде, имеющую круглое основание и треугольную вершину. В зависимости от положения плоскости, встречающейся с конусом, и угла пересечения образуются различные типы конических сечений, а именно; круг, эллипс, парабола и гипербола.

• Круг получается, когда режущая грань параллельна основанию конуса. Другими словами, если плоскость перпендикулярна оси вращения, полученное коническое сечение представляет собой окружность.
• Эллипс образуется, когда плоскость касается конуса под определенным углом. Другими словами, при разрезании конуса плоскостью, наклоненной под небольшим углом к ​​основанию конуса, образуется эллипс. Угол наклона менее 90 градусов для образования эллипса.
• Если плоскость параллельна образующей, то образующееся поперечное сечение называется параболой. Другими словами, парабола образуется, когда плоскость, пересекающая конус, параллельна одной боковой стороне конуса.
• Гипербола образуется, когда интересующая плоскость параллельна оси конуса и соединяет обе стороны двустороннего конуса.

Узнайте больше о Mesuration 2D здесь.

Посмотрите на рисунок ниже, чтобы понять различные поперечные сечения конуса.

Прочтите эту статью о Параболе, Эллипсе и Гиперболе .

Поперечные сечения куба

Куб — это трехмерная фигура, имеющая шесть граней, каждая из которых связана с четырьмя другими гранями. Кроме того, все стороны куба имеют одинаковую длину. Давайте разберемся с различными поперечными сечениями куба.

• Когда пересекающая плоскость пересекает данный куб так, что он параллелен одной из его 6 граней, то полученное поперечное сечение будет квадратом.
• Далее, если плоскость сечения пересекает любые три ребра куба, то полученное поперечное сечение будет треугольником.
• Если плоскость разрезает куб таким образом, что пересекает диагонали граней, полученное поперечное сечение будет прямоугольным.
• Когда плоскость разрезает куб таким образом, что она встречается со всеми гранями куба, получается шестиугольное поперечное сечение.
• Точно так же другие поперечные сечения, такие как параллелограмм, трапеция и пятиугольник, также могут быть получены путем выравнивания плоскости сечения.

На рисунке ниже показаны различные поперечные сечения куба.

Узнайте о площади поверхности куба здесь.

Сечения прямоугольного параллелепипеда

Прямоугольный параллелепипед — это трехмерная фигура. В кубоиде стороны имеют разную длину и называются длиной, шириной и высотой. Давайте разберемся в различном поперечном сечении прямоугольного параллелепипеда.

• Если данный прямоугольный параллелепипед разрезать вдоль более длинной стороны, то есть стороны с меньшим основанием, получится квадратное поперечное сечение.
• Если данный прямоугольный параллелепипед разрезать вдоль меньшей стороны, имеющей большее основание, получится прямоугольное поперечное сечение.

Рассмотрим приведенную ниже диаграмму, чтобы понять то же самое.

Узнайте больше о Mesuration 3D .

Поперечные сечения цилиндра

Цилиндр представляет собой трехмерную трубчатую структуру, включающую два параллельных круглых основания, соединенных изогнутой поверхностью на определенном расстоянии от центра.

По линии разреза поперечное сечение цилиндра может быть кругом, прямоугольником или овалом. Давайте разберемся в них один за другим.

• Если плоскость разрезает цилиндр таким образом, что он параллелен одному из его оснований (плоскость сечения перпендикулярна оси вращения), полученное поперечное сечение будет окружностью.
• Если эта же плоскость разрезает цилиндр таким образом, что он перпендикулярен основаниям (плоскость сечения параллельна оси вращения), полученное поперечное сечение будет прямоугольником.
• Если плоскость разрезает цилиндр под углом больше 0° и меньше 90° относительно основания, полученное поперечное сечение будет овальным. В общем, плоскость, которая параллельна или перпендикулярна основанию с небольшим изменением угла при заданной овальной форме.

Ниже представлены все поперечные сечения, сформированные таким образом в цилиндре.

Сечения сферы

Сфера представляет собой идеально круглое трехмерное образование, каждая точка на поверхности которого находится на одинаковом расстоянии от центра. Мы можем рассматривать нашу землю как пример того же самого. Кроме того, он имеет наименьшую площадь поверхности для своего объема.

Давайте поймем поперечное сечение сферы. Любое поперечное сечение сферы всегда будет окружностью, независимо от ориентации плоскости. На рисунке ниже показано то же самое.

Площадь поперечного сечения геометрических фигур

В предыдущем разделе мы читали о различных поперечных сечениях, образованных различными фигурами в соответствии с ориентацией линии разреза.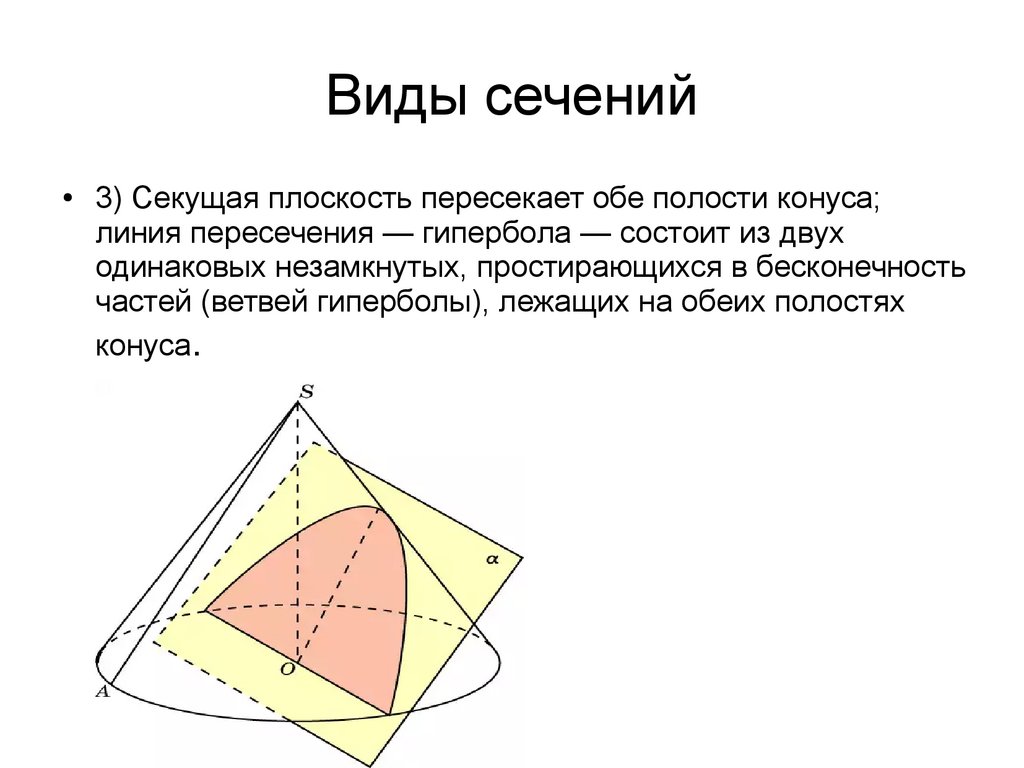 Двигаясь вперед, узнайте о формуле площади поперечного сечения для различных форм. 9{2}\).

Далее рассмотрим случай цилиндра, в котором секущая плоскость разрезает цилиндр таким образом, что он перпендикулярен основаниям, полученное поперечное сечение будет прямоугольником.

Площадь поперечного сечения прямоугольника = длина × ширина.

Изучите концепции трехмерной геометрии здесь.

Решенные примеры поперечного сечения

Теперь, когда мы знаем, что такое площадь поперечного сечения? как найти то же самое с подробными изображениями. Давайте рассмотрим несколько решенных примеров, связанных с этой темой, для большей практики.

Решено Пример 1: Определить площадь поперечного сечения цилиндра высотой 20 см и диаметром 6 см. При условии, что плоскость, пересекающая цилиндр, параллельна одному из его оснований.

Решение: Дано;

Высота цилиндра = 20 см

Диаметр цилиндра = 6 см

Радиус = 3 см

Плоскость при разрезании цилиндра, параллельная любому из его оснований, даст окружность.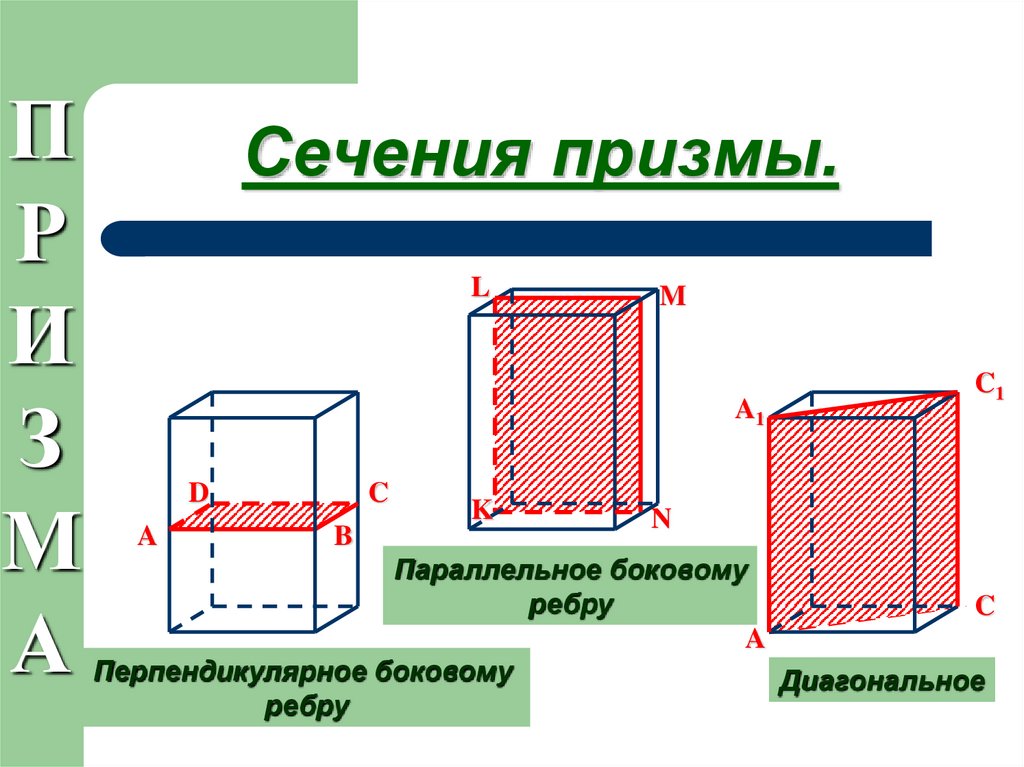 {2}\), где r — радиус круга. 92\).

Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы о поперечном сечении

В.1 Что вы понимаете под поперечным сечением?

Ans.1 Поперечное сечение образуется, когда плоскость пересекает объект в направлении, параллельном, диагональном или перпендикулярном к основанию объекта.

Q.2 Что такое площадь поперечного сечения?

Ответ 2 Когда плоскость пересекает твердый объект, на данную плоскость проецируется площадь. Эта площадь проекции называется площадью поперечного сечения.

В.3 Как найти поперечное сечение?

Ответ 3 Чтобы найти поперечное сечение любой заданной твердой формы, мы проверяем совмещение линии разреза с данной формой.