Ломаная линия / Виды линий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Ломаная линия
Ломаная линия состоит из отрезков – звеньев.
Конец одного отрезка – начало другого. Никакие два соседние звена не лежат на одной прямой.
Концы каждого звена – это вершины. Их можно обозначать буквами.
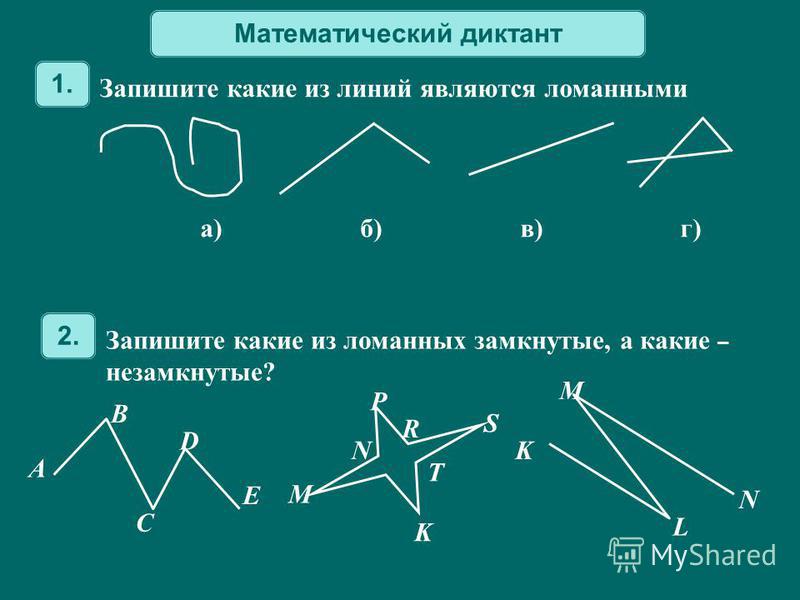
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Например,
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точка. Кривая. Прямая линия
Отрезок. Луч
Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Виды линий
Правило встречается в следующих упражнениях:
1 класс
Страница 43, Моро, Волкова, Степанова, Учебник, часть 1
Страница 93, Моро, Волкова, Степанова, Учебник, часть 1
Страница 12. Вариант 1. № 3, Волкова, Проверочные работы
Страница 13.
Страница 5, Моро, Волкова, Степанова, Учебник, часть 2
Страница 25, Моро, Волкова, Степанова, Учебник, часть 2
Страница 41, Моро, Волкова, Степанова, Учебник, часть 2
Страница 84, Моро, Волкова, Степанова, Учебник, часть 2
Страница 89, Моро, Волкова, Степанова, Учебник, часть 2
Страница 36, Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 50. Вариант 1. Тест,
Моро, Волкова, Проверочные работы
Вариант 1. Тест,
Моро, Волкова, Проверочные работы
Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 10. Урок 3, Петерсон, Учебник, часть 3
3 класс
Страница 14, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1
Страница 41, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1
Страница 5, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 14, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 61, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 15, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67. Урок 22,
Петерсон, Учебник, часть 1
Урок 22,
Петерсон, Учебник, часть 1
Страница 33. Урок 13, Петерсон, Учебник, часть 2
4 класс
Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 77, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Ломаная. Виды ломаных. Многоугольники
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с nn вершинами называется n−n−угольником.
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют A1A2A3A4A5A6A1A2A3A4A5A6 или A6A5A4A3A2A1A6A5A4A3A2A1.
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
На рисунке 2 вершины A2A2 и A3A3 являются соседними, так как они являются концами стороны A2A3.A2A3.
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны A4A5A4A5 и A5A6A5A6 являются смежными, так как они имеют общую вершину A5.A5.
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны A1A4A1A4 и A2A3A2A3 пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
На рисунке 5 многоугольник лежит по одну сторону от прямых m, n, l, p, q, rm, n, l, p, q, r проходящих через стороны многоугольника.
На рисунке 6 прямая mm делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой mm. Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу.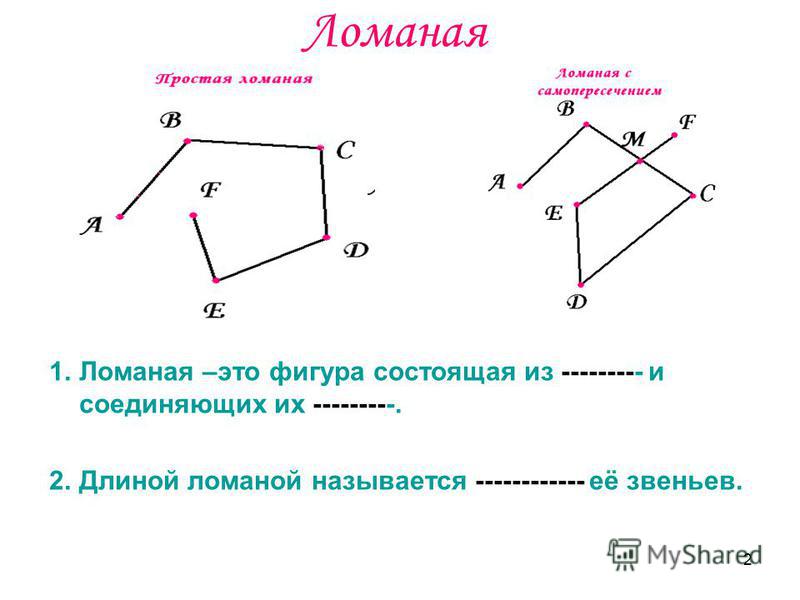 Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы A1, A2, A3, A4, A5A1, A2, A3, A4, A5 равны и равны все стороны: A1A2=A2A3=A3A4=A4A5=A5A1.A1A2=A2A3=A3A4=A4A5=A5A1.
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника A1A2…An−1AnA1A2…An−1An периметр вычисляется из формулы:
| P=A1A2+A2A3+…+An−1An+AnA1P=A1A2+A2A3+…+An−1An+AnA1 |
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине.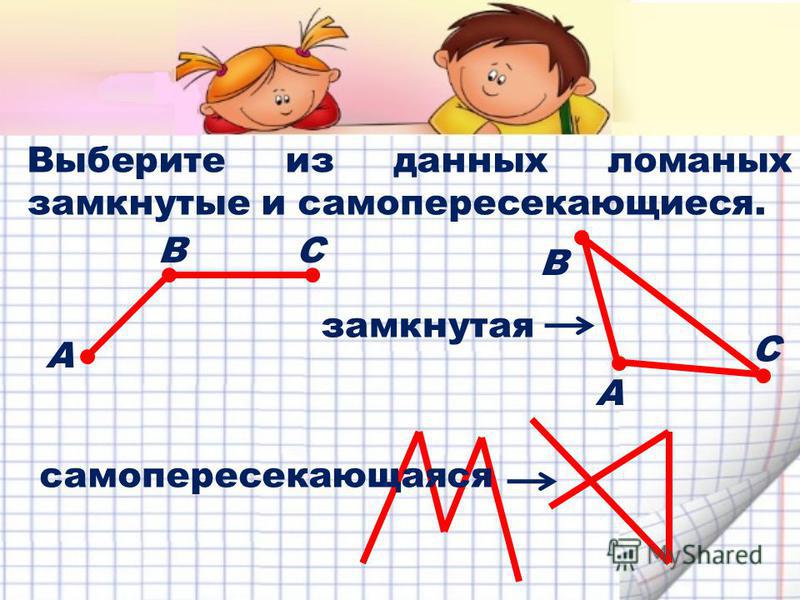 Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол A3A3 на рисунке 2).
Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол A3A3 на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
| Рис.10 |
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине E.E.
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан nn-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим n−1n−1 отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из n−1n−1 вычтем 2. Получим n−3n−3. Всего nn вершин. Следовательно количество вычисленных диагоналей будет n(n−3).n(n−3). Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей n−n−мерного многоугольника:
Получим n−3n−3. Всего nn вершин. Следовательно количество вычисленных диагоналей будет n(n−3).n(n−3). Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей n−n−мерного многоугольника:
| . |
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины A1A1 все диагноали многоугольника A1A2…An−1AnA1A2…An−1An (Рис.11):
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно n−3n−3. Следовательно, эти диагонали разделяют многоугольник на n−3+1=n−2n−3+1=n−2 треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: 180°(n−2).180°(n−2).
| 180°(n−2),180°(n−2), | (1) |
где nn −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
| αi=n−2n⋅180°,αi=n−2n⋅180°, |
где nn −количество сторон (вершин) правильного многоугольника
Просмотр содержимого документа
«Ломаная. Виды ломаных. Многоугольники»
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.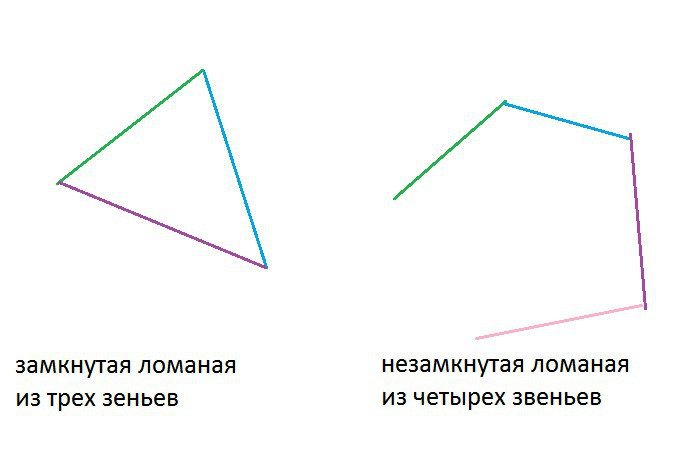
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с nn вершинами называется n−n−угольником.
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют A1A2A3A4A5A6A1A2A3A4A5A6 или A6A5A4A3A2A1A6A5A4A3A2A1.
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.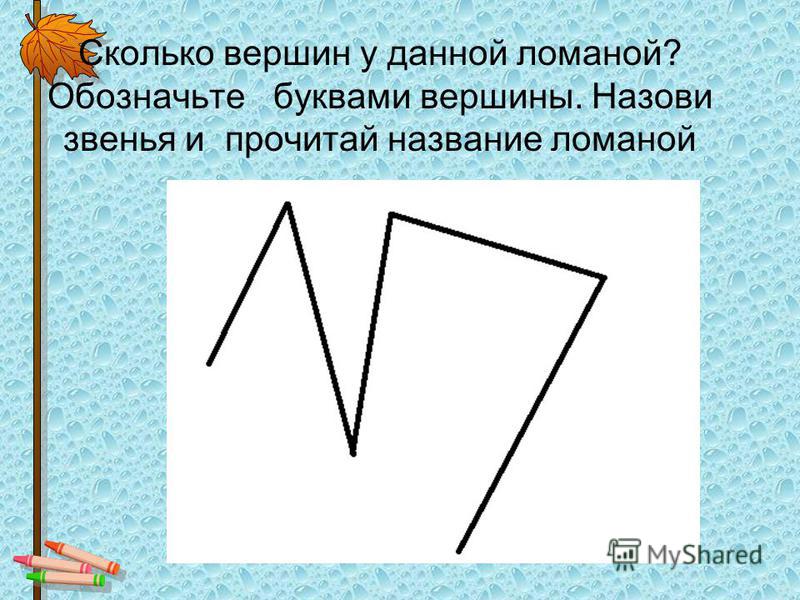
На рисунке 2 вершины A2A2 и A3A3 являются соседними, так как они являются концами стороны A2A3.A2A3.
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны A4A5A4A5 и A5A6A5A6 являются смежными, так как они имеют общую вершину A5.A5.
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны A1A4A1A4 и A2A3A2A3 пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
На рисунке 5 многоугольник лежит по одну сторону от прямых m, n, l, p, q, rm, n, l, p, q, r проходящих через стороны многоугольника.
На рисунке 6 прямая mm делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой mm. Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.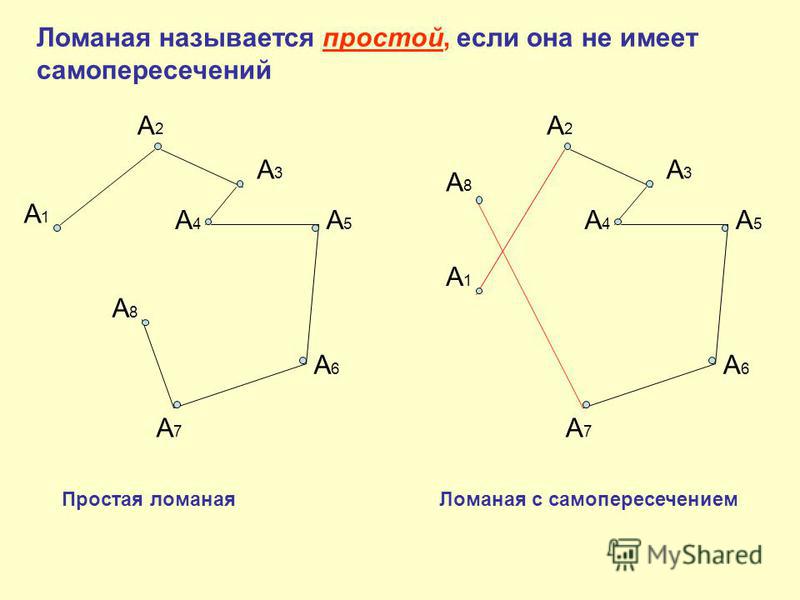
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы A1, A2, A3, A4, A5A1, A2, A3, A4, A5 равны и равны все стороны: A1A2=A2A3=A3A4=A4A5=A5A1.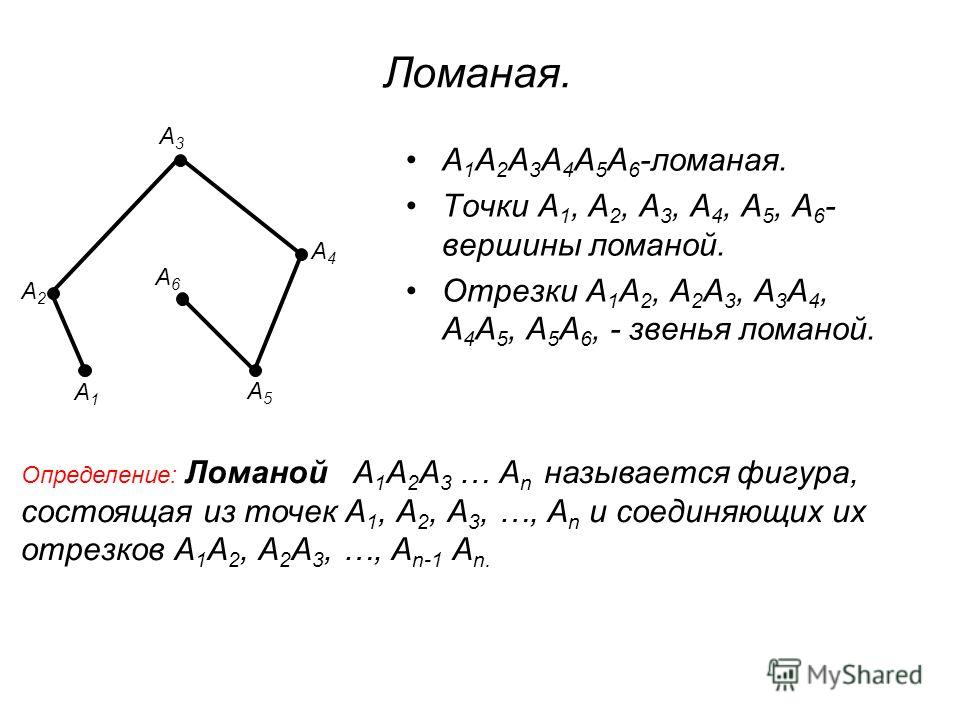 A1A2=A2A3=A3A4=A4A5=A5A1.
A1A2=A2A3=A3A4=A4A5=A5A1.
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника A1A2…An−1AnA1A2…An−1An периметр вычисляется из формулы:
P=A1A2+A2A3+…+An−1An+AnA1P=A1A2+A2A3+…+An−1An+AnA1 |
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол A3A3 на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
Рис. |
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине E.E.
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан nn-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим n−1n−1 отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из n−1n−1 вычтем 2. Получим n−3n−3. Всего nn вершин. Следовательно количество вычисленных диагоналей будет n(n−3).n(n−3). Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей n−n−мерного многоугольника:
. |
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины A1A1 все диагноали многоугольника A1A2…An−1AnA1A2…An−1An (Рис.11):
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно n−3n−3. Следовательно, эти диагонали разделяют многоугольник на n−3+1=n−2n−3+1=n−2 треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: 180°(n−2).180°(n−2).
180°(n−2),180°(n−2), | (1) |
где nn −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
αi=n−2n⋅180°,αi=n−2n⋅180°, |
где nn −количество сторон (вершин) правильного многоугольника.
Дорожная разметка | Справочник водителя
Для безопасного вождения во Флориде вы должны понимать, что означают различные линии на дороге. Их цвет и то, являются ли они цельными или сломанными, говорят вам, как вести машину в этой ситуации и что вы можете и чего не можете делать. Например, двойная желтая линия означает, что вы не можете пройти.
Рассматриваемые темы включают: Разметка дорожного покрытия
Справочник водителя во Флориде — Разметка дорожного покрытия
Линии, символы и слова часто наносятся на проезжую часть, чтобы помочь водителям направлять водителей и контролировать транспортный поток. Вы должны знать, что означают различные линии и цвета, и подчиняться им, как дорожным знакам или сигналам.
Белые и желтые линии используются вдоль краев тротуара и между полосами движения, чтобы удерживать транспортные средства на одной линии. Эти линии могут быть сплошными или прерывистыми (длинные штрихи), одинарными или двойными.
Желтые полосы движения
Желтые полосы движения разделяют полосы движения в противоположных направлениях. Одиночные желтые линии могут также обозначать левый край тротуара на разделенных автомагистралях и улицах с односторонним движением. Желтая прерывистая линия
Желтая прерывистая линия
Желтая прерывистая линия разделяет полосы движения, движущиеся в противоположных направлениях. Оставайтесь справа от линии, если только вы не обгоняете впереди идущее транспортное средство. При прохождении вы можете временно пересечь эту линию, когда это будет безопасно.
Двойные желтые линии: одна сплошная, одна прерывистая
Сплошная желтая линия справа от прерывистой желтой центральной линии означает, что движение по этой полосе запрещено, за исключением поворота налево. Если ломаная линия находится ближе к вам, вы можете пересечь ломаную линию только для того, чтобы обогнать другое транспортное средство, и только тогда, когда это безопасно.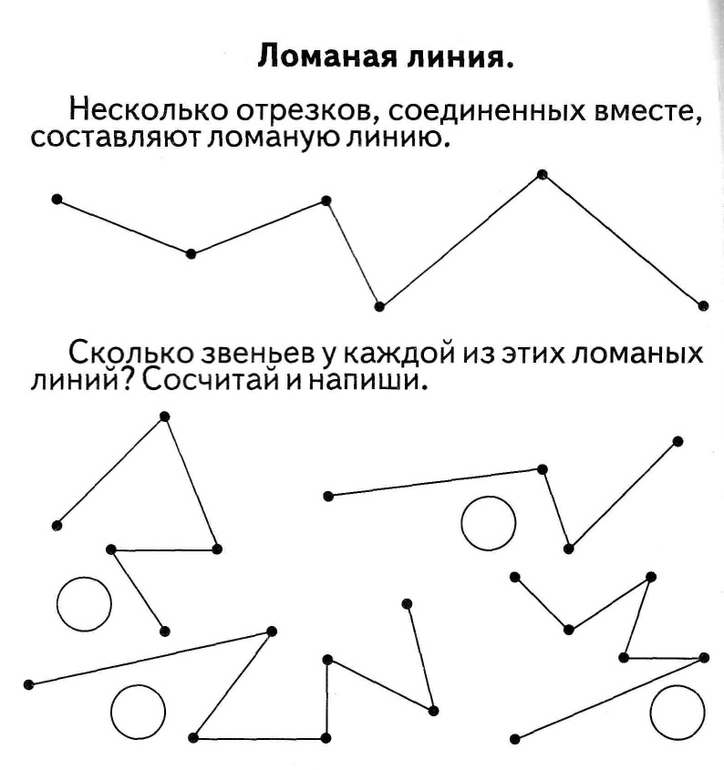
Двойные желтые линии
Двойные сплошные желтые линии запрещают транспортным средствам, движущимся в любом направлении, пересекать линии. Вы не можете пересекать эти линии, если только не повернете налево, когда это безопасно.
Белые полосы движения
Белые полосы движения разделяют полосы движения в одном направлении. Одиночные белые линии могут также обозначать правый край тротуара.
Белая ломаная линия
Белая ломаная линия разделяет две полосы движения в одном направлении. После того, как вы подали сигнал и если это безопасно, вы можете пересекать эту линию при перестроении.
Сплошная белая линия
Сплошная белая линия отмечает правый край проезжей части или разделяет полосы движения в одном направлении. Вы можете двигаться в одном и том же направлении по обеим сторонам этой линии, но вы не должны пересекать линию, если только вы не должны сделать это, чтобы избежать опасности.
Двойная сплошная белая линия
Двойная сплошная белая линия разделяет две полосы движения в одном направлении. Пересечение двойной сплошной линии запрещено. полоса только для поворота налево
сплошная полоса со стрелкой 9 для поворота0004
Сплошные белые линии используются для обозначения поворотных полос и предотвращения перестроений вблизи перекрестков. Стрелки часто используются с белыми линиями, чтобы показать, какой поворот можно сделать с полосы движения.
Если вы находитесь на полосе, отмеченной изогнутой стрелкой и словом ТОЛЬКО, вы должны повернуть в направлении стрелки. Если ваша полоса отмечена как изогнутой, так и прямой стрелкой, вы можете либо повернуть, либо ехать прямо.
Реверсивные полосы
На некоторых автомагистралях есть реверсивные полосы движения, чтобы облегчить движение в час пик. Направление движения обычно меняется в определенное время каждый день. Эта разметка тротуара используется вместе со специальными сигналами полосы движения и другими знаками и символами.
Сплошная белая линия отмечает край тротуара на большинстве дорог. Стоп-линии, пешеходные переходы и парковочные места также отмечены белыми линиями. Такие символы, как стрелки, также окрашены в белый цвет. Одна желтая линия отмечает левый край всех разделенных дорог или дорог с односторонним движением. Бордюры часто отмечены желтым цветом в зонах, где нет парковки, возле пожарных гидрантов или перекрестков. Запрещается парковаться или проезжать через участки, на тротуаре которых есть разметка, указывающая на противопожарные полосы или зоны безопасности.
Стрелка разметки полосы в центральной полосе на приведенной ниже диаграмме указывает на то, что движение по этой полосе может быть изменено в соответствии с местными правилами дорожного движения из-за движения в «час пик» или других особых условий движения.
Водители с любого направления могут использовать центральную полосу для левых поворотов.
Проезжая часть с двусторонним движением и центральной полосой
Проезжая часть с двусторонним движением и центральной полосой для левых поворотов в любом направлении движения. Специально обозначенная центральная полоса поворота предназначена для замедления и укрытия поворачивающих транспортных средств и не может использоваться для обгона.
Специально обозначенная центральная полоса поворота предназначена для замедления и укрытия поворачивающих транспортных средств и не может использоваться для обгона.
Водители с любого направления могут использовать центральную полосу для левых поворотов. Водители, движущиеся в любом направлении, могут использовать центральную полосу только для поворотов налево.
Back to Florida Drivers Handbook Table of Contents
Road Markings: What to do in Yellow, White or Double Road Lines
Help Center
- Alabama
- Alaska
- Arizona
- Arkansas
- California
- Колорадо
- Коннектикут
- Делавэр
- Флорида
- Джорджия
- Гавайи
- Айдахо
- Иллинойс Индиан
- a16
- Iowa
- Kansas
- Kentucky
- Louisiana
- Maine
- Maryland
- Massachusetts
- Michigan
- Minnesota
- Mississippi
- Missouri
- Montana
- Nebraska
- Nevada
- New Hampshire
- New Jersey
- Нью-Мексико
- Нью-Йорк
- Северная Каролина
- Северная Дакота
- Огайо
- Оклахома
- Oregon
- Pennsylvania
- Rhode Island
- South Carolina
- South Dakota
- Tennessee
- Texas
- Utah
- Vermont
- Virginia
- Washington
- Washington D.
 C.
C. - West Virginia
- Wisconsin
- Wyoming
Добро пожаловать в наш быстрый и простой информационный справочник по вождению
Полезная информация для вождения
Онлайн-драйверы, выпуск
Курсы доступны для всех уровней квалификации. Выберите свой штат, чтобы начать.
Тест на получение разрешения
Подготовьтесь к тесту на получение разрешения на сайте DriversEd.com
БЕЛЫЕ ЛИНИИ , нанесенные на тротуаре, указывают на движение транспорта в вашем направлении.
Прерывистая белая линия: вы можете перестроиться, если это безопасно.
Сплошная белая линия: требует, чтобы вы оставались в пределах полосы, а также отмечает обочину проезжей части.
ЖЕЛТЫЕ ЛИНИИ обозначают центр дороги с двусторонним движением, используемой для двустороннего движения.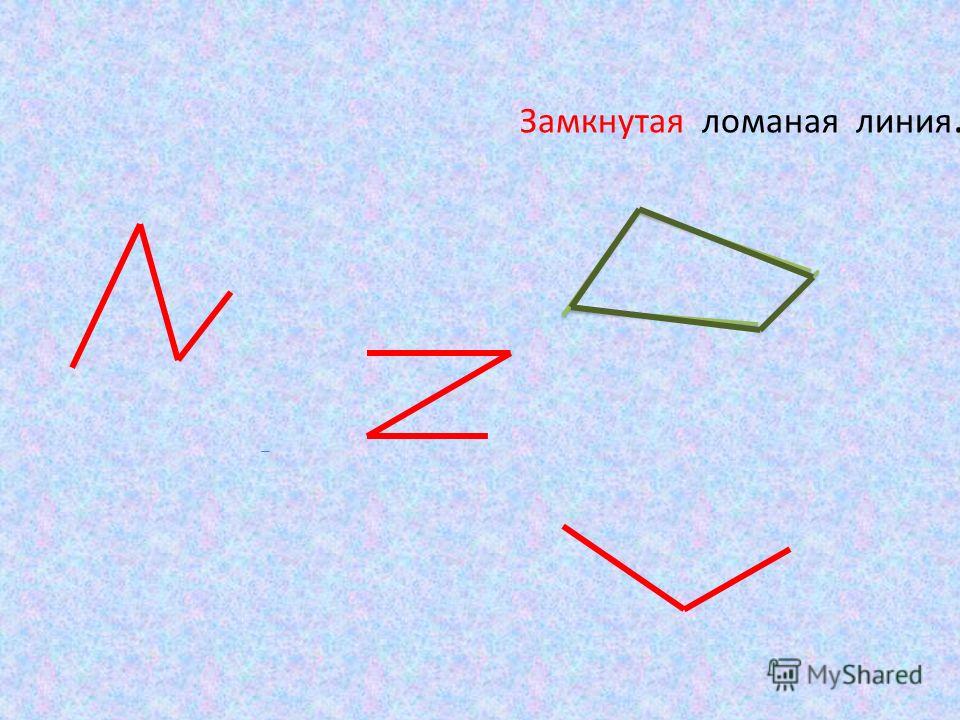

 10
10
 C.
C.