Ломаная линия / Виды линий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Ломаная линия
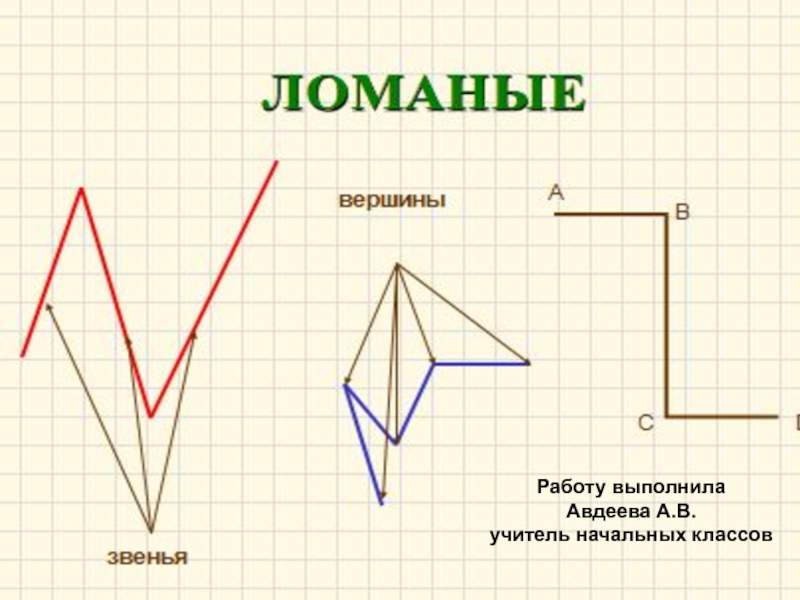
Ломаная линия состоит из отрезков – звеньев.
Конец одного отрезка – начало другого. Никакие два соседние звена не лежат на одной прямой.
Концы каждого звена – это вершины. Их можно обозначать буквами.
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Например,
Советуем посмотреть:
Точка. Кривая. Прямая линия
Отрезок. Луч
Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Виды линий
Правило встречается в следующих упражнениях:
1 класс
Страница 45, Моро, Волкова, Степанова, Учебник, часть 1
Страница 71, Моро, Волкова, Степанова, Учебник, часть 1
Страница 93, Моро, Волкова, Степанова, Учебник, часть 1
Страница 124, Моро, Волкова, Степанова, Учебник, часть 1
Страница 17, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 37, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 13.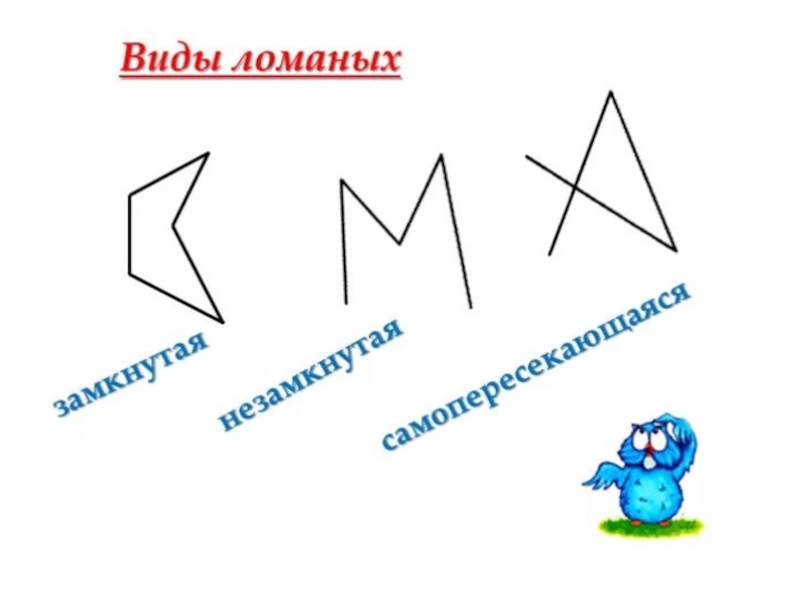 ПР 3. Вариант 2,
Волкова, Проверочные работы
ПР 3. Вариант 2,
Волкова, Проверочные работы
Страница 5, Моро, Волкова, Степанова, Учебник, часть 2
Страница 41, Моро, Волкова, Степанова, Учебник, часть 2
Страница 89, Моро, Волкова, Степанова, Учебник, часть 2
2 класс
Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 20. ПР 3. Вариант 1, Моро, Волкова, Проверочные работы
Страница 24. Тест 1. Вариант 1, Моро, Волкова, Проверочные работы
Страница 25.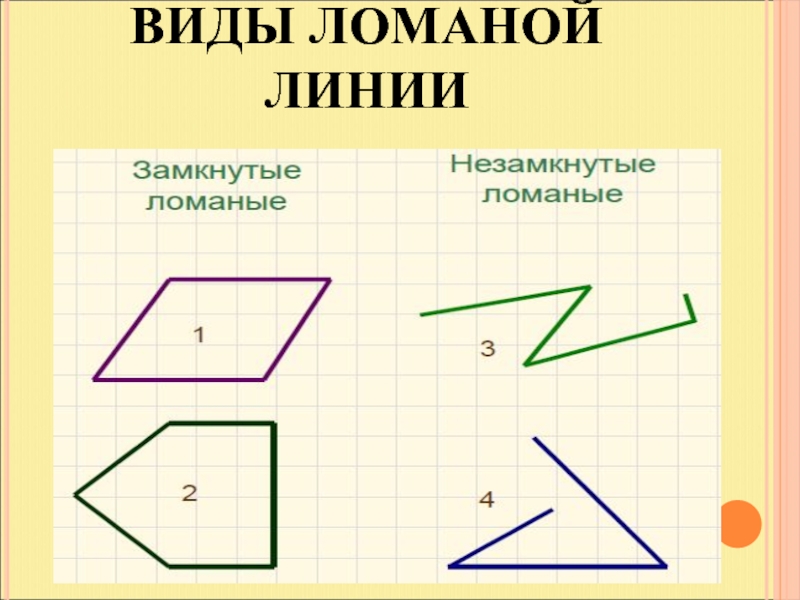 Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 33. ПР 3. Вариант 2, Моро, Волкова, Проверочные работы
Страница 51. Тест. Вариант 2, Моро, Волкова, Проверочные работы
Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 68, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
3 класс
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 108, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 5, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 14, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 61, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 67. Урок 22,
Петерсон, Учебник, часть 1
Урок 22,
Петерсон, Учебник, часть 1
Страница 33. Урок 13, Петерсон, Учебник, часть 2
4 класс
Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 77, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27. Урок 9, Петерсон, Учебник, часть 1
Ломаная. Виды ломаных. Многоугольники
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с nn вершинами называется n−n−угольником.
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют A1A2A3A4A5A6A1A2A3A4A5A6 или A6A5A4A3A2A1A6A5A4A3A2A1.
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
На рисунке 2 вершины A2A2 и A3A3 являются соседними, так как они являются концами стороны A2A3.A2A3.
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны A4A5A4A5 и A5A6A5A6 являются смежными, так как они имеют общую вершину A5.A5.
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны A1A4A1A4 и A2A3A2A3 пересекаются.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
На рисунке 5 многоугольник лежит по одну сторону от прямых m, n, l, p, q, rm, n, l, p, q, r проходящих через стороны многоугольника.
На рисунке 6 прямая mm делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой mm. Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы A1, A2, A3, A4, A5A1, A2, A3, A4, A5 равны и равны все стороны: A1A2=A2A3=A3A4=A4A5=A5A1.A1A2=A2A3=A3A4=A4A5=A5A1.
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника A1A2…An−1AnA1A2…An−1An периметр вычисляется из формулы:
Для многоугольника A1A2…An−1AnA1A2…An−1An периметр вычисляется из формулы:
| P=A1A2+A2A3+…+An−1An+AnA1P=A1A2+A2A3+…+An−1An+AnA1 |
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол A3A3 на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
| Рис.10 |
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине E.E.
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.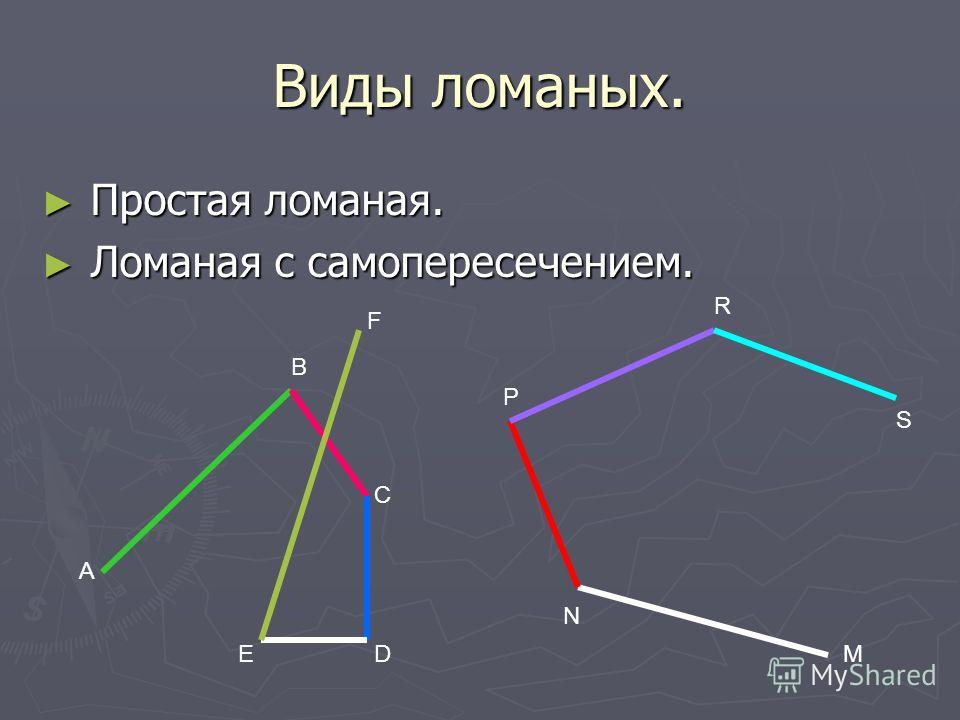
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан nn-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим n−1n−1 отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из n−1n−1 вычтем 2. Получим n−3n−3. Всего nn вершин. Следовательно количество вычисленных диагоналей будет n(n−3).n(n−3). Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей n−n−мерного многоугольника:
| . |
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины A1A1 все диагноали многоугольника A1A2…An−1AnA1A2…An−1An (Рис.11):
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно n−3n−3. Следовательно, эти диагонали разделяют многоугольник на n−3+1=n−2n−3+1=n−2 треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: 180°(n−2).180°(n−2).
Следовательно, эти диагонали разделяют многоугольник на n−3+1=n−2n−3+1=n−2 треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: 180°(n−2).180°(n−2).
| 180°(n−2),180°(n−2), | (1) |
где nn −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
| αi=n−2n⋅180°,αi=n−2n⋅180°, |
где nn −количество сторон (вершин) правильного многоугольника
Просмотр содержимого документа
«Ломаная. Виды ломаных. Многоугольники» Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольниковМногоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с nn вершинами называется n−n−угольником.
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника Обозначают многоугольник буквами, стоящих при его вершинах.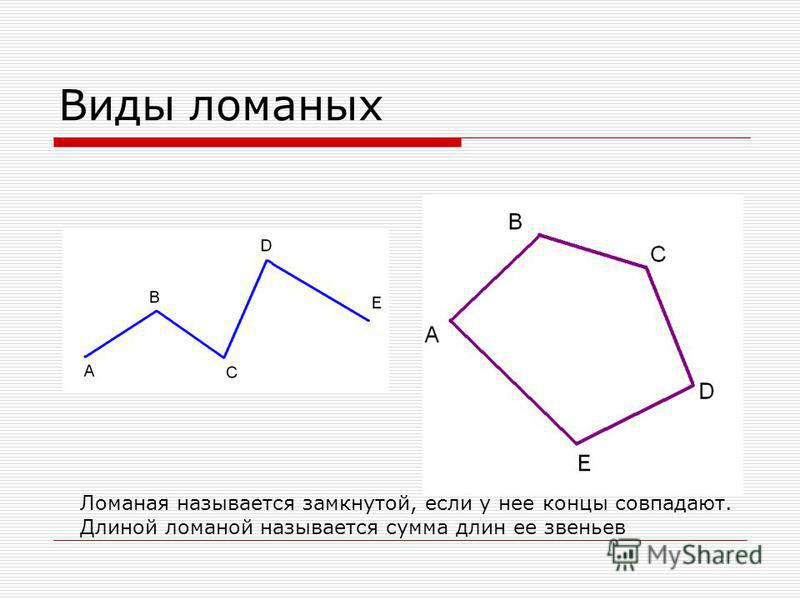 Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют A1A2A3A4A5A6A1A2A3A4A5A6 или A6A5A4A3A2A1A6A5A4A3A2A1.
Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют A1A2A3A4A5A6A1A2A3A4A5A6 или A6A5A4A3A2A1A6A5A4A3A2A1.
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
На рисунке 2 вершины A2A2 и A3A3 являются соседними, так как они являются концами стороны A2A3.A2A3.
Смежные стороны многоугольникаСтороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны A4A5A4A5 и A5A6A5A6 являются смежными, так как они имеют общую вершину A5.A5.
Простой многоугольник. Самопересекающийся многоугольникМногоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны A1A4A1A4 и A2A3A2A3 пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
А на рисунке 4 многоугольник не является простым, так как стороны A1A4A1A4 и A2A3A2A3 пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
На рисунке 5 многоугольник лежит по одну сторону от прямых m, n, l, p, q, rm, n, l, p, q, r проходящих через стороны многоугольника.
На рисунке 6 прямая mm делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой mm. Следовательно многоугольник не является выпуклым.
Правильный многоугольник Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольникСамопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы A1, A2, A3, A4, A5A1, A2, A3, A4, A5 равны и равны все стороны: A1A2=A2A3=A3A4=A4A5=A5A1.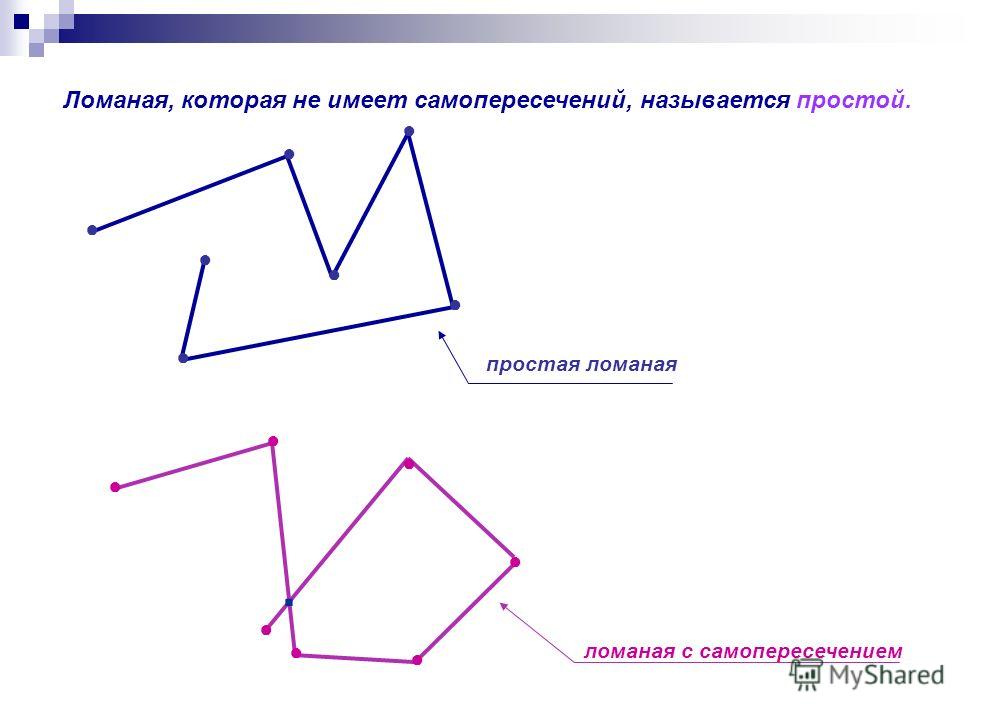 A1A2=A2A3=A3A4=A4A5=A5A1.
A1A2=A2A3=A3A4=A4A5=A5A1.
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника A1A2…An−1AnA1A2…An−1An периметр вычисляется из формулы:
P=A1A2+A2A3+…+An−1An+AnA1P=A1A2+A2A3+…+An−1An+AnA1 |
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол A3A3 на рисунке 2).
Внешний угол многоугольникаВнешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
Рис. |
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине E.E.
Диагональ многоугольника. Количество диагоналейДиагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан nn-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим n−1n−1 отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из n−1n−1 вычтем 2. Получим n−3n−3. Всего nn вершин. Следовательно количество вычисленных диагоналей будет n(n−3).n(n−3). Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей n−n−мерного многоугольника:
. |
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины A1A1 все диагноали многоугольника A1A2…An−1AnA1A2…An−1An (Рис.11):
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно n−3n−3. Следовательно, эти диагонали разделяют многоугольник на n−3+1=n−2n−3+1=n−2 треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: 180°(n−2).180°(n−2).
180°(n−2),180°(n−2), | (1) |
где nn −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
αi=n−2n⋅180°,αi=n−2n⋅180°, |
где nn −количество сторон (вершин) правильного многоугольника.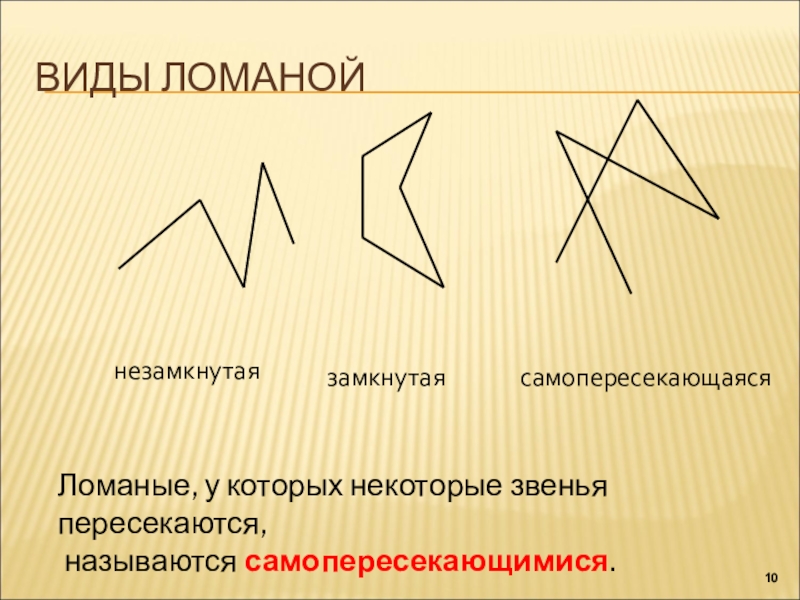
США Разметка дорожного покрытия: разметка для двустороннего движения Подробное описание
Услуги > Публикации > Разметка дорожного покрытия
Двухполосные проезжие части
На рисунке «Двухполосные проезжие части» показано, что Обгон разрешен — это двусторонняя разметка, обгон которой разрешен в обоих направлениях. показано с обозначением осевой линии пунктирной желтой линией Стрелки показывают, что направление движения – одна полоса в каждом направлении.
Запрещенные зоны и граничные линии — двусторонняя маркировка с запретными зонами. Двухполосная проезжая часть показана осевой линией (сверху вниз на рисунке): одинарной прерывистой желтой линией; сплошная желтая линия, примыкающая к левой полосе движения, и желтая прерывистая линия, примыкающая к правой полосе движения; двойная сплошная желтая линия; желтая прерывистая линия, примыкающая к левой полосе движения, и сплошная желтая линия, примыкающая к правой полосе движения; и одна прерывистая желтая линия. В середине рисунка каждый участок сплошной желтой линии накладывается на участок, имеющий двойную сплошную желтую линию. Сплошная белая линия отмечена на внешнем краю каждой дорожки. Стрелки показывают, что направление движения — по одной полосе в каждом направлении.
В середине рисунка каждый участок сплошной желтой линии накладывается на участок, имеющий двойную сплошную желтую линию. Сплошная белая линия отмечена на внешнем краю каждой дорожки. Стрелки показывают, что направление движения — по одной полосе в каждом направлении.
Легенда показывает черную стрелку, указывающую направление движения по полосам.
Многополосные дороги
На рисунке “Многополосные дороги” показана Без полос для левого поворота показана четырехполосная дорога. Стрелки показывают, что направление движения составляет две полосы в каждом направлении. Проезжая часть имеет осевую разметку сплошной двойной желтой линией. Белая прерывистая линия разделяет полосы движения в одном направлении.
Разрезанные полосы для левого поворота — пятиполосная проезжая часть, где пятая, центральная полоса используется для левых поворотов. Стрелки показывают, что направление движения – две сквозные полосы в каждом направлении и повороты налево от центральной полосы. Проезжая часть имеет разметку в виде сплошной двойной желтой линии и чередующихся каналов левого поворота, отмеченных сплошной белой линией, чтобы отделить полосу поворота от полос движения, движущихся в том же направлении. Полосы поворота имеют необязательные белые стрелки для левого поворота, отмеченные на тротуаре. Ломаная белая линия разделяет полосы движения в одном направлении.
Проезжая часть имеет разметку в виде сплошной двойной желтой линии и чередующихся каналов левого поворота, отмеченных сплошной белой линией, чтобы отделить полосу поворота от полос движения, движущихся в том же направлении. Полосы поворота имеют необязательные белые стрелки для левого поворота, отмеченные на тротуаре. Ломаная белая линия разделяет полосы движения в одном направлении.
Полоса поворота налево с двусторонним движением В центре показана вертикальная пятиполосная проезжая часть. Черные стрелки показывают, что направление движения направлено на юг по двум левым полосам и на север по двум правым полосам. Пятая полоса находится в центре. Сплошная белая линия отмечена на правом краю каждой стороны проезжей части. По всей длине рисунка (за исключением перекрестков) прерывистая белая линия разделяет две сквозные полосы движения на юг, а прерывистая белая линия разделяет две сквозные полосы движения на север.
В верхней части рисунка самая внутренняя сквозная полоса движения на юг отделена от центральной полосы сплошной желтой линией. Ломаная желтая линия проходит к востоку от него прямо внутри центральной полосы. Еще одна прерывистая желтая линия находится на восточной стороне центральной полосы, рядом со сплошной желтой линией, отделяющей ее от самой внутренней сквозной полосы движения в северном направлении.
Ломаная желтая линия проходит к востоку от него прямо внутри центральной полосы. Еще одна прерывистая желтая линия находится на восточной стороне центральной полосы, рядом со сплошной желтой линией, отделяющей ее от самой внутренней сквозной полосы движения в северном направлении.
Горизонтальная улица пересекает вертикальную проезжую часть. К югу от этого перекрестка разметка, разделяющая каждую из полос движения, продолжается по той же схеме, что и к северу от перекрестка. На центральной полосе показана белая стрелка левого поворота, изгибающаяся на юг и восток. Сразу за ним показана еще одна белая стрелка левого поворота, изгибающаяся на север и запад.
К югу от этих стрелок желтые прерывистые линии на центральной полосе не показаны. После небольшого расстояния вторая сплошная желтая линия показана рядом со сплошной желтой линией, разделяющей центральную полосу и самую внутреннюю сквозную полосу движения на север. За этой точкой показана сплошная белая линия, разделяющая центральную и самую внутреннюю полосу движения на юг, а на центральной полосе показана белая стрелка левого поворота, изгибающаяся на юг и восток.
Прямо под стрелкой левого поворота показано пересечение вертикальной проезжей части с горизонтальной улицей. К югу от этого перекрестка на центральной полосе показана еще одна белая стрелка левого поворота, изгибающаяся на север и запад. К югу от перекрестка сплошная двойная желтая линия отделяет центр и самую внутреннюю полосу движения на юг, а сплошная одиночная белая линия разделяет центр и самую внутреннюю полосу движения на север.
Легенда показывает черную стрелку, указывающую направление движения по полосам.
Трехполосные проезжие части
На рисунке «Трехполосные проезжие части» показано Разрешено движение в направлении с одной полосой представляет собой двустороннюю разметку, разрешенное движение в направлении с одной полосой движения. Трехполосная дорога показана стрелками, указывающими направление движения: одна полоса движется на юг, а две полосы – на север. Ломаная желтая линия показана рядом с полосой движения на юг, а сплошная желтая линия показана рядом с крайней левой из двух полос движения на север.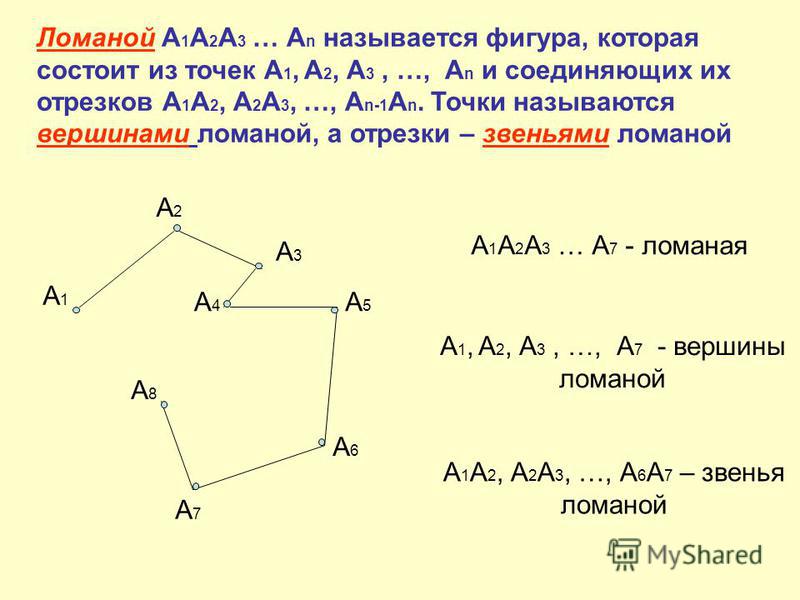 Показана прерывистая белая линия, разделяющая две полосы движения на север. Сплошная белая линия показана на внешнем краю полосы движения в южном направлении и самой правой полосы движения в северном направлении.
Показана прерывистая белая линия, разделяющая две полосы движения на север. Сплошная белая линия показана на внешнем краю полосы движения в южном направлении и самой правой полосы движения в северном направлении.
Обгон запрещен в направлении с одной полосой — это двусторонняя разметка с запретом обгона в однополосном направлении». две полосы, ведущие на север. Показана сплошная двойная желтая линия, отделяющая полосу движения на юг от крайней левой полосы движения на север. Показана прерывистая белая линия, разделяющая две полосы движения на север. Сплошная белая линия показана на внешнем краю полосы движения на юг и на крайний правый северный переулок
Изменение направления движения на центральной полосе показана вертикальная трехполосная дорога. Показана сплошная двойная желтая линия, отделяющая каждую полосу движения от других. Две полосы движения в южном направлении показаны переходящими в одну полосу. Показана сплошная двойная желтая линия, отделяющая каждую полосу движения от других. Сплошная двойная желтая линия показана рядом с полосой движения в южном направлении. Снизу рисунка показаны две полосы движения на север, переходящие в одну полосу. Сплошная желтая линия показана рядом с полосой движения в северном направлении на этом конусе. На конусе показана буферная зона в конце полосы движения на юг и на север.
Сплошная двойная желтая линия показана рядом с полосой движения в южном направлении. Снизу рисунка показаны две полосы движения на север, переходящие в одну полосу. Сплошная желтая линия показана рядом с полосой движения в северном направлении на этом конусе. На конусе показана буферная зона в конце полосы движения на юг и на север.
Реверсивная центральная полоса представляет собой вертикальную трехполосную дорогу с двусторонним движением. Стрелки показывают, что направление движения по левой полосе — на юг, по правой полосе — на север, а по центральной полосе может быть любое направление. Показаны прерывистые двойные желтые линии, отделяющие полосы друг от друга. Легенда показывает черную стрелку, указывающую направление движения по полосам.
Назад к разметке для двустороннего движения
Разметка дорожного покрытия США — FHWA MUTCD
Услуги > Публикации
Для получения дополнительной информации: https://www.mutcd.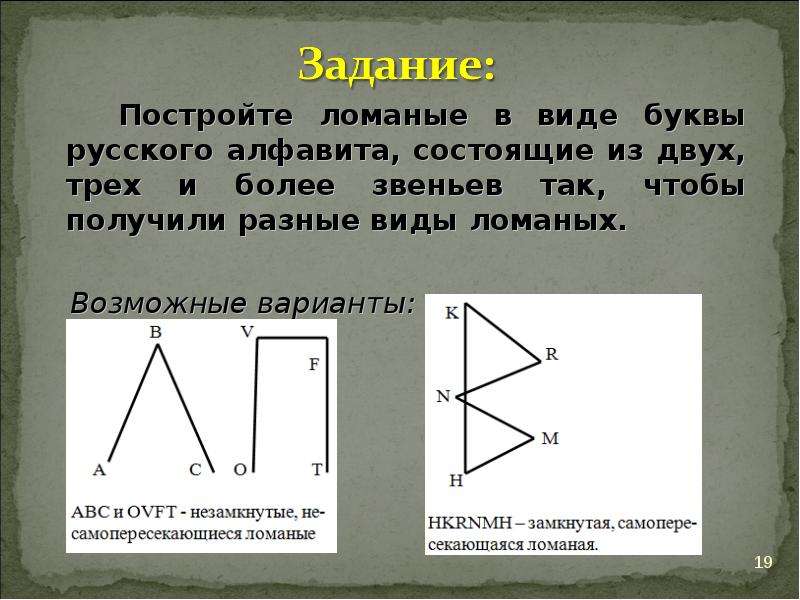 fhwa.dot.gov
fhwa.dot.gov
Контактная информация: Кевин Сильвестр, [email protected]
Эта публикация является архивной и может содержать датированную техническую информацию, контактную информацию и информацию о ссылках.
PDF-версия, 18 МБ
PDF-файлы можно просматривать с помощью Acrobat® Reader®
Предисловие
Разметка дорожного покрытия используется для передачи сообщений пользователям проезжей части. Они указывают, какой участок дороги следует использовать, предоставляют информацию об условиях впереди и указывают, где разрешен обгон. Желтые линии разделяют транспортные потоки, движущиеся в противоположных направлениях. Водители должны оставаться справа от желтых линий. Сплошная желтая линия означает, что проезд запрещен. Желтая пунктирная линия означает, что проход разрешен. Белые линии разделяют полосы, движение по которым осуществляется в одном направлении. Двойная белая линия означает, что смена полосы движения запрещена. Одна белая линия указывает на то, что смена полосы движения не рекомендуется. Белая пунктирная линия указывает на то, что смена полосы движения разрешена.
Одна белая линия указывает на то, что смена полосы движения не рекомендуется. Белая пунктирная линия указывает на то, что смена полосы движения разрешена.
Символы используются для обозначения разрешенного использования полосы движения. Ромб указывает на полосу, зарезервированную для использования транспортными средствами с высокой вместимостью. Велосипед указывает на полосу, предназначенную для велосипедистов. Стрелки показывают обязательные или разрешенные движения на перекрестках. Ряд сплошных треугольников указывает на то, что участник дорожного движения должен уступить дорогу.
Дорожная разметка также используется для предупреждения пользователей о потенциально опасных условиях впереди. Буква X с буквой R с каждой стороны указывает на пересечение шоссе и железной дороги впереди. Пустой треугольник указывает на доход впереди. Ряд постепенно расширяющихся линий, пересекающих полосу движения, указывает на лежащий впереди «лежачий полицейский».
Стандарты для проектирования и нанесения дорожной разметки можно найти в Руководстве по унифицированным устройствам управления дорожным движением (MUTCD) .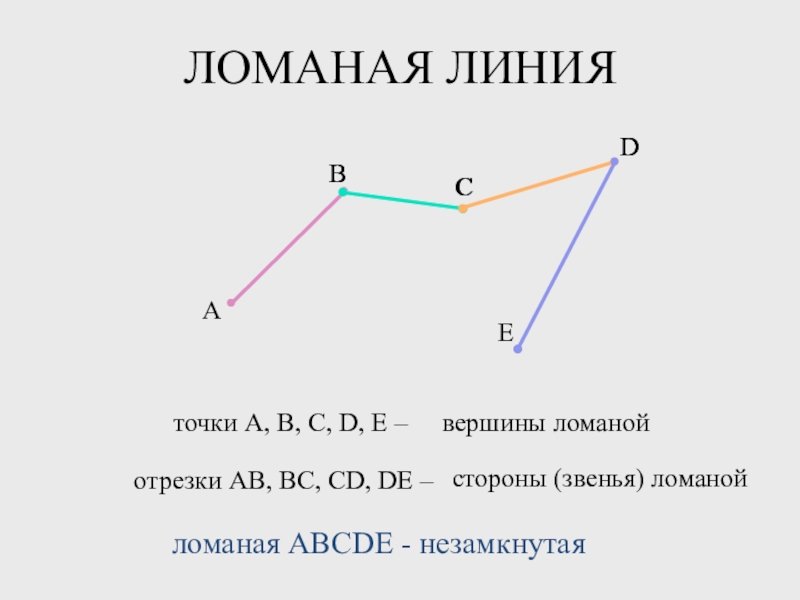

 10
10