Ветровая нагрузка на решетчатые конструкции: Расчет ветровой нагрузки металлических конструкций, решетчатой башни (мачты). Пульсационная составляющая ветровой нагрузки

Определение коэффициента давления от ветровой нагрузки для результирующих нагрузок на стержни плоских решетчатых конструкций

В этой статье представлен простой пример решетчатой конструкции, который объясняет, как задать ветровое нагружение в качестве функции сплошности решетки.

Ветер, перпендикулярный конструкции

Базовая скорость v_b = 25,0 м/с
Базовое скоростное давление q_b = 0,39 кН/м²
Пиковый скоростной напор

Формула 1

qp(z) = 1,7 · qb · z100,37 = 1,7 · 0,39 · 7,5100,37 = 0,596 kN/m²

Коэффициент силы cf для решетчатых конструкций:

Формула 2

cf = cf,0 · Ψλ

Определение коэффициента силы c

_{f, 0} для решетчатых конструкций без торцевого воздействия с использованием коэффициента твердости φ

Коэффициент твердости:

Формула 3

φ = AAC

где
A = сумма предполагаемых площадей стержней
A_C = l ⋅ b = замкнутая площадь рассматриваемой грани

Соотношение площадей решетки:

Формула 4

A = 2,828 m · 0,1 m · 5  2,0 m · 0,05 m · 4  2,0 m · 0,1 m · 2  10 m · 0,2 m · 2 = 6,214 m²AC = 10 m · 2 m = 20 m²

Коэффициент твердости:

Формула 5

φ = 6,214 m²20 m² = 0,3107

После того, как коэффициент прочности получен, коэффициент силы c_{f, 0,} равный 1,6, может быть определен, например, по стандарту EN 1991‑1‑4, рисунок 7.

33 [1] .

• Базовый коэффициент силы cf, 0

Также необходимо определить эффективную гибкость конструктивного элемента, чтобы определить коэффициент концевого эффекта Ψ_λ .

Эффективная гибкость λ (Таблица 7.16 → BS EN 1991‑1‑4 [2] )

Формула 6

λ = 2 · 10 m2 m = 10 < 70 → 10 ist maßgebend

Используя ранее рассчитанные значения, коэффициент конечного эффекта Ψ_λ , равный 0,95, можно определить по диаграмме на рисунке 7.36 стандарта.

• Понижающий коэффициент Ψλ

Используя этот коэффициент, получается следующий коэффициент силы:

Формула 7

cf = cf,0 · Ψλ = 1,6 · 0,95 = 1,52

Расчет результирующей ветровой нагрузки на решетчатую конструкцию

Вариант 1: Эквивалентная статическая нагрузка F_w

Формула 8

Fw = cf · qp(z) · Aref

где
A_ref = проектируемая площадь

Формула 9

Fw = 1,52 · 0,596 kN/m² · 6,214 m² = 5,63 kN

Вариант 2: нагрузка на стержень из нагрузки на площадь

Формула 10

Fw1 = 1,52 · 0,596 kN/m² = 0,91 kN/m²

Чтобы распределить нагрузку на эту область в RFEM/RSTAB только на стержни, необходимо выбрать опцию «Пусто, только на стержнях» в разделе «Область приложения нагрузки».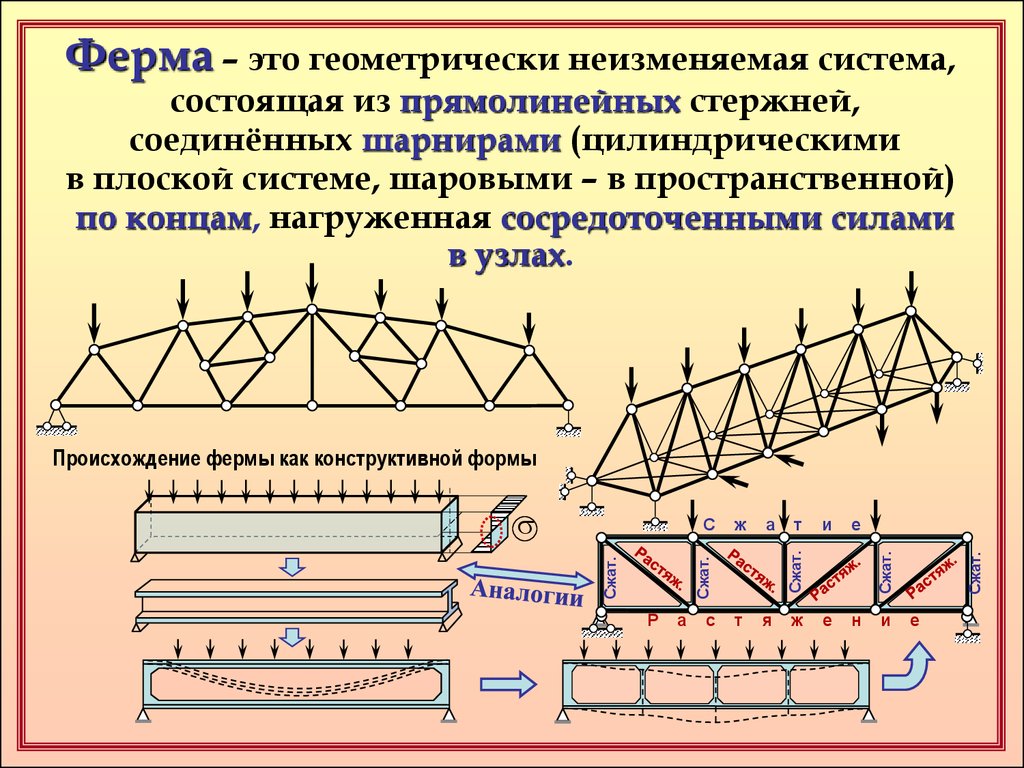 После ввода нагрузки и нажатия [OK] сумма нагрузки, которую необходимо приложить, снова отображается в информационном окне.

[1]	Eurocode 1: Actions on structures – Part 1-4: General actions – Wind actions; German version EN 1991-1-4:2005 + A1:2010 + AC:2010
[2]	National Annex – Nationally determined parameters – Eurocode 1: Actions on structures – Part 1-4: General actions – Wind actions; EN 1991-1-4/NA:2010-12

Нагрузки и воздействия | SELENATEL

Главная>Расчет>Нагрузки и воздействия

Основным сочетанием нагрузок по СНиП 2.01.07-85 «Нагрузки и воздействия» для башен и мачт является ветровой напор на конструкции ствола и оборудования с собственным весом конструкций и оборудования. Также данным СНиПом предусмотрен учет гололедной, температурной и сейсмической нагрузки.

Расчет производится по двум предельным состояниям: 1) по прочности и устойчивости 2) по деформативности.

Согласно п.1.3 СНиП расчетное значение нагрузки следует определять как произведение ее нормативного значения на коэффициент надежности по нагрузке y_f, соответствующий рассматриваемому предельному состоянию и принимаемый при расчете на прочность и устойчивость:

– для весовой нагрузки γ_f — 1.05

– для ветровой нагрузки γ_f — 1.4

– для гололедной нагрузки γ_f — 1.3

При расчете по деформациям γ_f =1

Ветровая нагрузка

Согласно СНиП 2.01.07-85* ветровая нагрузка определяется как сумма средней и пульсационной составляющей W=W_m+W_p. Чтобы определить среднюю составляющую ветровой нагрузки Wm на сооружение и оборудование надо знать ветровое давление в районе установки, а также наветренную площадь сооружения с оборудованием. Если выразить это формулой то получается следующее:

Среднее значение ветровой нагрузки (кгс) = ветровое давление(кгс/м) х высотный коэффициент х наветренная площадь(м²)

или

W_m = w₀ k Fc_x

– высотный коэффициент k определяется по таблице 6, промежуточные значения определяются интерполяцией.

Данная формула является аналогом ф-лы (6) СНиП с той разницей, что вместо одного аэродинамического коэффициента с у нас введено Fc_x — наветренная площадь, это произведение площади проекции какого-либо элемента конструкции на его аэродинамический коэффициент лобового сопротивления. В практике расчета антенно-мачтовых сооружений удобнее чтобы эти два параметра шли неотделимо друг от друга. Отметим, что для антенно-мачтовых сооружений и их элементов используется именно аэродинамический коэффициент лобового сопротивления с_х.

Для примера если взять уголок 50х5 длиной 2м, то его проекцией будет прямоугольник 0.05х2м => площадь проекции F=0.1м², аэродинамический коэффициент для профилей по СНиП равен 1.4, т.о. наветренная площадь уголка Fc_x будет равна 0.14м².

Для цилиндрических элементов (трубы, круглая сталь, тросы) аэродинамический коэффициент с_х варьируется от 0.4 до 1.2 и определяется по схеме 14 приложения 4 СНиП.

Для плоской решетчатой конструкции (фермы) очевидно, что ее наветренная площадь будет равна сумме наветренных площадей ее элементов. Но башни и мачты являются пространственными фермами, где есть наветренная грань и следующая за ней затеняемая грань. Для этого случая СНиПом предусмотрена схема 17 приложения 4. Строго следуя указаниям несложно определить аэродинамический коэффициент с_t секции. Помножив его на контурную площадь секции А_к, получаем наветренную площадь секции.

Нормативное значение ветрового давления w₀ определяется согласно пункту 6.4: по карте 3 определяется ветровой район и по таблице 5 определяется w₀. Если район строительства по карте 3 относится к малоизученным, то скорость ветра следует принимать по данным районной метеостанции, причем берется значение скорости, превышаемой раз в 5 лет, и по ф-ле (7) определяется ветровое давление w₀.

Помимо средней составляющей ветровой нагрузки СНиП требует учитывать пульсационную составляющую Wp. Для упрощенного ручного расчета, можно воспользоваться формулой (9) пункта 6.7б в которой антенно-мачтовое сооружение рассматривается как система с одной степенью свободы и учитывается только первая форма собственных колебаний, а период собственных колебаний может быть определен энергетическим методом. В современных расчетных комплексах определение пульсационной составляющей автоматизировано, и определяется она для каждой формы колебаний, учитывая s первых форм. Количество учитываемых форм s определяется из условия f_s < f_lim < f_s+1, где f_lim по СНиП берется из таблицы 8.

Гололедная нагрузка

Гололедную нагрузку следует учитывать при проектировании антенно-мачтовых сооружений по п.7 СНиП. Для этого необходимо учесть увеличение наветренной площади элементов конструкции и увеличение их веса за счет гололедных образований, а затем произвести расчет на ветровое воздействие в сочетании с собственным весом.

При учете гололедной нагрузки согласно пункту 7.4 СНиПа давление ветра на элементы покрытые гололедом следует принимать равным 25%. Данная цифра, видимо, взята из тех соображений, что по наблюдениям период образования гололеда (в основном это начало или конец зимы) сопровождается слабым ветром. Заранее можно предположить, что такое сочетание нагрузок оказывает более слабое воздействие, чем 100% ветровая нагрузка. Правда есть примечание 1 к пункту 7.4 «В отдельных районах, где наблюдаются сочетания значительных скоростей ветра с большими размерами гололедно-изморозевых отложений, толщину стенки гололеда и его плотность, а также давление ветра следует принимать в соответствии с фактическими данными». Поэтому данный вопрос требует рассмотрения в отдельных случаях, особенно когда сооружение состоит из большого количества тонких элементов (в таком случае прирост наветренной площади от гололеда будет значительным).

Сейсмические воздействия

При определении сейсмических воздействий на опоры необходимо руководствоваться СНиП II-7-81* (СП 14.13330.2011) Строительство в сейсмических районах. Согласно п.2.1 данного СНиП (п.5.1. СП), при расчете конструкций и оснований на сейсмическое воздействие, температурные климатические воздействия и ветровые нагрузки не учитываются.

 

 

Thermal Science – научный журнал [статья: Определение коэффициента аэродинамического сопротивления решетчатых конструкций под действием ветровой нагрузки с использованием метода пористых сред]

АННОТАЦИЯ

Силовые передатчики, мачты с оттяжками и другие решетчатые конструкции подвергаются воздействию ветра. Аэродинамические силы, действующие на конструкции высоких башен, имеют решающее значение для устойчивости конструкции. Определение коэффициента сопротивления решетчатой ​​конструкции регулируется международными стандартами ЕСДУ 81027 и 81028 и Еврокодом 3, часть 3.1, но его также можно определить численными методами. Для этой цели моделирование с использованием CFD оказалось точным и надежным. В этом исследовании поток жидкости вокруг сегмента передатчика мощности моделировался с помощью трехмерной модели, где геометрия сегмента аппроксимируется пористой структурой, имеющей соответствующий коэффициент пористости, для упрощения геометрии. Мы использовали три репрезентативные модели турбулентности, стандартную модель k-ε, модель RNG k-ε и модель напряжения Рейнольдса. Значения коэффициента лобового сопротивления извлекаются из поля течения и сравниваются для всех изученных случаев и с имеющимися экспериментальными результатами в аэродинамической трубе. Моделирование проводилось для четырех скоростей ветра от 10 м/с до 30 м/с.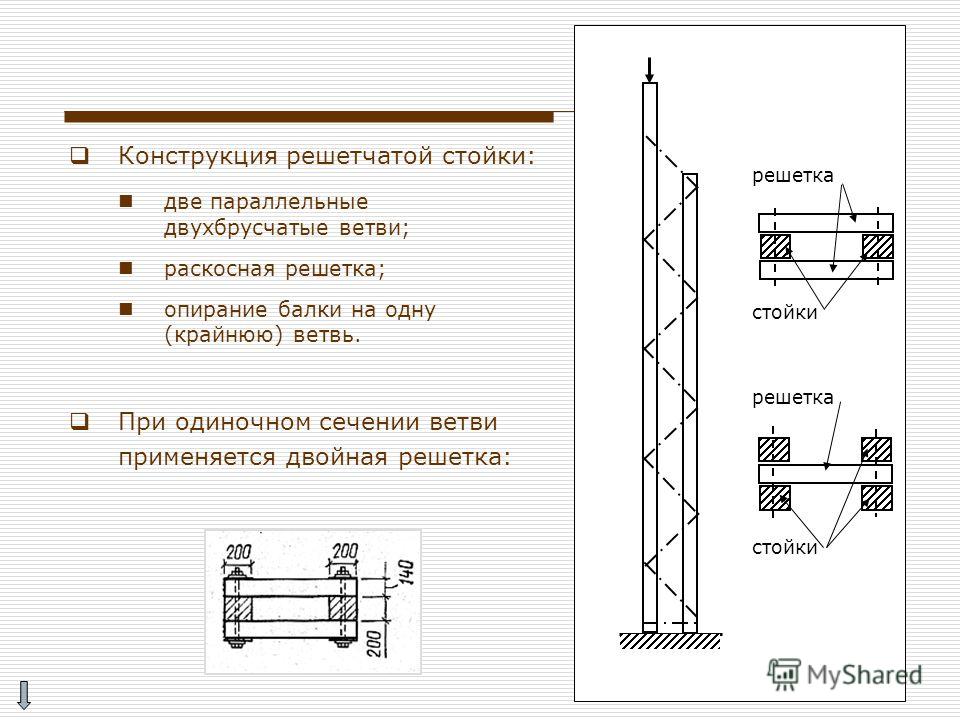 Результаты дополнены результатами, полученными искусственной нейронной сетью. Цель этого исследования — показать, как простая модель турбулентности в сочетании с аппроксимированной геометрией может быть использована для анализа аэродинамических сил, действующих на решетчатую структуру.

КЛЮЧЕВЫЕ СЛОВА

ветровая нагрузка, решетчатая конструкция, коэффициент аэродинамического сопротивления, пористый материал -11

ОПУБЛИКОВАН В ИНТЕРНЕТЕ: 10.07.2021

DOI REFERENCE: https://doi.org/10.2298/TSCI210511233P

ЭКСПОРТ ЦИТАТОВ: просмотреть в браузере или загрузить в виде текстового файла ТОМ 26 , ВЫПУСК Выпуск 1 , СТРАНИЦЫ [309 – 317]

ССЫЛКИ

1. Денг, Х., Ли, Ф., Цай, К., Донг, Дж., Фу, П., Экспериментальный и численный анализ изменения наклона стык четверки опор ЛЭП из стальных труб и колонн, Тонкостенные конструкции 119 (2017), стр. 572-585, doi.org/10.1016/j.tws.2017.07.006
2. Fu, X., Li, H.N. , Анализ неопределенностей прочности и пути разрушения опоры ЛЭП под действием ветровой нагрузки, Journal of Wind Engineering & Industrial Aerodynamics 173 (2018), стр. 147-155, doi.org/10.1016/j.jweia.2017.12.009
3. Фу, X., Ли, Х. Н., Динамический анализ системы опора-линия электропередачи, подверженной ветровым и дождевым нагрузкам, Journal of Wind Engineering & Industrial Aerodynamics 157 (2016), стр. 95-103, doi.org/10.1016/ j.jweia.2016.08.010
4. Пезо, М., Бакич, В., Маркович, З., Структурный анализ мачты с оттяжками, подверженной воздействию ветра, Теплотехника 20(5) (2016), стр. S1473-S1483, doi.org/10.2298/TSCI16S5473P
5. Ченг, Н., Сравнение формул для коэффициента сопротивления и скорости осаждения сферических частиц, Технология порошков 189(2009), стр. 395-398, doi.org/10.1016/j.powtec.2008.07.006
6. Guo, X., Lin, J., Nie, D., Новая формула для коэффициента сопротивления цилиндрических частиц, Particuology 9 (2011), стр. 114-120, doi.org/10.1016/j.partic.2010.07.027
7. Хёльцер А., Зоммерфельд М., Новая формула простой корреляции для коэффициента сопротивления несферических частиц, Powder Technology 184 (2008), стр. 361-365, doi.org/10.1016/j.powtec.2007.08.021
8. Гао, В., Нелиас, Д., Лю, Ю., Буассон, Н., Численные исследования о коэффициенте лобового сопротивления круглого цилиндра с двумя свободными концами в роликовых подшипниках, Tribology International 123 (2018), стр. 43-49., doi.org/10.1016/j.triboint.2018.02.044
9. Хан, Ю., Чен, Х., Цай, К.С., Сюй, Г., Шен, Л., Ху, П., Численный анализ разницы коэффициентов силы сопротивления секций настила моста между методами распределения глобальной силы и давления, Journal of Wind Engineering & Industrial Aerodynamics 159 (2016), стр. 65-79, doi.org/10.1016/j.jweia.2016.10.004
10. Пезо, М., Бакич, В., Численное определение коэффициента лобового сопротивления мачты с оттяжками, подверженной воздействию ветра, Инженерные конструкции 62-63 (2014), стр. 98-104, doi.org/10.1016/j.engstruct.2014.01.025
11. Balczo, M., Lajos, T., Kovacs, T., Sebestyen, P., Прогнозирование ветровой нагрузки, действующей на телекоммуникационные мачты, IABSE 2006 Ежегодные собрания и симпозиум, Будапешт, Венгрия, 2006 г.
12. Лю, Х., Левитан, М., Никитопулос, Д., Испытания в аэродинамической трубе для определения средних коэффициентов сопротивления и подъемной силы на нескольких круглых цилиндрах, расположенных в линию, Journal of Wind Engineering and Промышленная аэродинамика 96 (2008), стр. 831-839, doi.org/10.1016/j.jweia.2007.06.011
13. Бакич, В., Экспериментальное исследование турбулентных течений вокруг сферы, докторская диссертация, Технический университет Гамбург-Харбург, Германия, 2002
14. Георгакис, К. , Косс, Х. Х., Коэффициенты лобового сопротивления решетчатых мачт по результатам полномасштабных испытаний в аэродинамической трубе, EACWE 5, Флоренция, Италия, 19–23 июля 2009 г.
15. Чжу, Н., Испытание в аэродинамической трубе динамических характеристик мачты с оттяжками при ветровых нагрузках , Диссертация, представленная в Колледж аспирантуры и исследований при частичном выполнении требований для получения степени магистра наук на факультете гражданского и геологического строительства Университета Саскачевана, 2007 г. , Саскатун
16. ***, Стандарт Канадской ассоциации стандартов S37 2001 для антенн, башен и антенно-несущих конструкций, 2001
17. Аллегрини, Дж., Маесшалк, Дж., Алесси, Г., Глабеке, Г., Кристоф, Д., ван Бек, Дж., CFD-моделирование пористости и геометрического разрешения решетчатой ​​опоры ЛЭП, подтвержденное измерениями силы сопротивления и поля потока, Engineering Structures 168 (2018), стр. 462-472, doi.org/10.1016/j.engstruct. 2018.05.007
18. Маесшалк, Дж., Глабеке, Г., Ван Бек, Дж., Аллегрини, Дж., Концепция очень высоких башен для пересечения реки Шельды. Международный совет по большим электрическим системам, СИГРЭ, документ B2-213. Париж, Франция, 2018
19. Гуань, Д., Чжан, Ю., Чжу, Т., Исследование аэродинамической трубы сопротивления ветра, Сельскохозяйственная и лесная метеорология 118 (2003), стр. 75-84, doi.org/10.1016/S0168-1923 (03)00069-8
20. Маникатан Л., Дефрайе Т., Аллегрини Дж., Дером Д., Кармелиет Дж., Параметрическое исследование влияния факторов окружающей среды и трех свойств на транспиративное охлаждающее действие деревья, Сельскохозяйственная и лесная метеорология 248 (2018), стр. 259-274, doi.org/10.1016/j.agrformet.2017.10.014
21. Wilcox, D.C., Моделирование турбулентности для CFD, DCW Industries, 2006
22. Patankar, S.V. Численный теплообмен и поток жидкости, Hemisphere Publishing Corporation, 1980
23. Kollo, T., von Rosen, D., Расширенная многомерная статистика с матрицами, Springer , Дордрехт, 2005
24. Тураньи Т., Томлин А.С. «Анализ кинетических механизмов реакции» (Springer, Berlin Heidelberg), 2014.

Ветроустойчивая оптимизация размеров геометрически нелинейных решетчатых конструкций с использованием модифицированного метода критерия оптимальности

Оптимизация ветрозащитных размеров геометрически нелинейных решетчатых конструкций с использованием модифицированного метода критерия оптимальности

• Фу Цзи-Ян
;
• Ву, Бен-Ганг
;
• Ву, Джиу-Ронг
;
• Дэн, Тин
;
• Пи, Юн-Лин
;
• Се, Чжуан-Нин

Аннотация

Решетчатые конструкции обычно имеют тонкие элементы и малый вес, высокую гибкость и малые коэффициенты демпфирования.

Следовательно, на их структурное поведение может повлиять геометрическая нелинейность, и они подвержены большим смещениям и проблемам безопасности из-за ветровых нагрузок. Оптимальное проектирование таких нелинейных и гибких структур сложно и сложно. В данной статье представлен автоматический алгоритм оптимизации интегрированного анализа отклика на воздействие ветра и оптимального проектирования ветроустойчивых линейных и нелинейных решетчатых конструкций на основе модифицированного алгоритма критерия оптимальности (ОК). Метод структурно-динамического анализа и реакции решетчатой ​​конструкции на воздействие ветра разработан путем объединения правильной ортогональной декомпозиции (POD) с векторным методом Ритца, зависящим от нагрузки (LDR), вместе с методом гармонического возбуждения (HEM) и корреляцией отклика нагрузки (LRC). метод. При этом метод квадратичного программирования используется для оценки множителей Лагранжа в модифицированном методе критерия оптимальности. На основе полученных результатов анализа чувствительности конструкции для узловых смещений, напряжений элементов и коэффициента нелинейной критической нагрузки линейных и нелинейных пространственных рамных конструкций в сопроводительном документе затем устанавливается автоматический поток оптимизации путем принятия интерфейса прикладного программирования (API) SAP2000. интегрировать реакцию, вызванную ветром, анализ чувствительности конструкции и ветроустойчивую оптимальную конструкцию структурной системы пространственного каркаса. Предложенный автоматический оптимизирующий поток затем применяется к оптимизированному процессу решетчатой ​​конструкции при динамической ветровой нагрузке. Обнаружено, что для решетчатой ​​конструкции при их оптимизации необходимо учитывать геометрический нелинейный анализ и ограничение нелинейного коэффициента критической нагрузки, в то время как обновление временной истории ветровых нагрузок и эквивалентных статических ветровых нагрузок (ESWL) является обязательным. необходимо в результате изменений в размере элемента конструкции в процессе оптимизации. Также установлено, что ограничение максимального смещения является наиболее важным фактором в оптимизации решетчатой ​​конструкции, а максимальное напряжение элементов конструкции обычно оказывается неактивным ограничением во время процедуры оптимизации. В случае, когда предварительно установлен нижний предел максимального смещения, нелинейный коэффициент критической нагрузки становится важным ограничением.