Уклон в геодезии: Уклон (геодезия) | это… Что такое Уклон (геодезия)?

Уклон местности – определение термина

Термин и определение

тангенс угла наклона линии местности к горизонтальной плоскости в данной точке.

Еще термины по предмету «Геодезия»

Автоматизированная картография

раздел картографии, охватывающий теорию, методологию и практику создания, обновления и использования карт, атласов и других пространственно-временных картографических произведений в графической, цифровой и электронной формах с помощью автоматических картографических систем и прочих технических и аппаратнопрограммных средств.

Государственная нивелирная сеть

единая система высот на территории всей страны, она является высотной основой всех топографических съемок и инженерногеодезических работ, выполняемых для удовлетворения потребностей экономики, науки и обороны страны.

Граница землевладения, землепользования

линия, точно проложенная техническими средствами и обозначенная на местности, представляющая собой территориальный предел прав собственника, владельца или пользователя земли.

Похожие

• Уклон
• Местность
• Руководящий уклон
• Уклон кровли
• Уклон поперечный
• Уклон продольный
• Уклон реки
• Уклонный конвейер
• Гидравлический уклон
• Критический уклон
• Пьезометрический уклон
• Защита уклоном
• Проектный уклон
• Уклон линии
• Сельская местность
• Справка о местности
• Необороняемая местность
• Безлюдная местность
• Труднодоступная местность
• Профиль местности

Смотреть больше терминов

Научные статьи на тему «Уклон местности»

Третья составляющая анализа рельефа связана с определением уклона – в геодезии это показатель крутизны. ..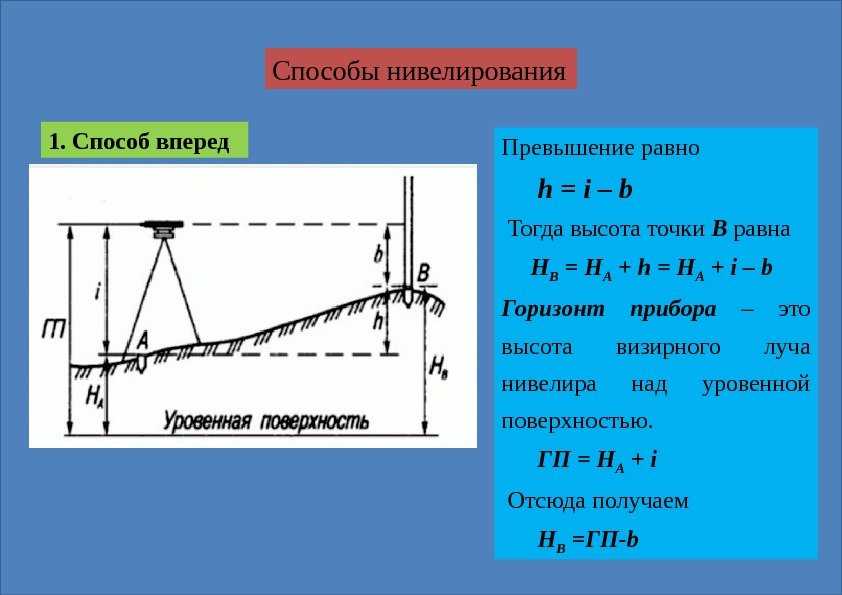
Уклон представляет собой отношение превышения местности к горизонтальной прямой, на которой идет наблюдение…
Например, подъему 12 м на 100 м перемещения будет соответствовать уклон, равный 0,12….
Уклоны обязательно указываются на дорожных знаках – «крутой спуск», «крутой подъем» и т.д….
На топографических картах уклоны определяются по графику заложений уклонов.

Статья от экспертов

Приводятся фактические скорости движения воды при поливе по бороздам при различных уклонах и расходах воды в борозду при поливе постоянной и переменной струей. Фактические скорости движения воды сравниваются со скоростями, вычисленными по формулам Шези, Ляпиха. Даются рекомендации по применению элементов техники полива на различных уклонах.

Научный журнал

Creative Commons

Проектирование плана трассы Горная местность характеризуется сложными условиями рельефа, климата, геологии. ..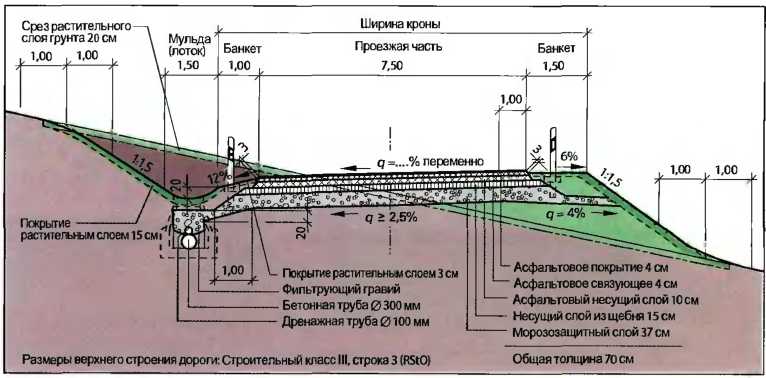
Между вершиной и переводом на склоне, трассу ведут зигзагами, при этом отрезки имеют максимальный уклон…
понижающаяся боковая часть возвышенности Проектирование продольного профиля автомобильных дорог в горной местности…
В зависимости от разницы рабочих отметок и уклона

могут потребоваться подпорные стены….
Продольный профиль дополняется поперечными планами местности, и на них проектируется земляное плотно.

Статья от экспертов

Рельеф поля во многом определяет водно-воздушный, а также питательный режим почвы, от рельефа зависит также микроклимат поля. Целью работы разработка способа возделывания озимого пивоваренного ячменя на склоновых землях, включающий посев культуры поперек склона узкорядным способом, отличающийся тем, что на склонах крутизной в пределах 2-12° высевают озимый ячмень. Исследования проводились в предгорной зоне КБР на ЗАО НП «Чегем» Чегемского района КБР и ООО «МЭЛТ» Урванского района КБР. В работ…

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

• 📝 Напиши термин
• ✍️ Выбери определение из предложенных или загрузи свое
• 🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Возможность создать свои термины в разработке

Еще чуть-чуть и ты сможешь писать определения на платформе Автор24. Укажи почту и мы пришлем уведомление с обновлением ☺️

Как работает инструмент Уклон—ArcMap | Документация

Доступно с лицензией Spatial Analyst.

Доступно с лицензией 3D Analyst.

• Методы вычисления и эффект ребер
• Плоскостной метод
• Геодезический метод
• Использование графического процессора (GPU)
• Справочная информация

Инструмент Уклон определяет крутизну в каждой ячейке растровой поверхности. Чем меньше значение уклона, тем более плоской является земная поверхность; чем больше значение уклона, тем более крутые склоны расположены на поверхности.

Выходной растр уклонов может быть вычислен в двух различных единицах измерения, в градусах или в процентах (‘процент подъема’). Процент подъема можно лучше понять, если вы рассматриваете его как подъем, деленный на пробег (спуск), умноженный на 100. Рассмотрим треугольник B на рисунке внизу. Когда угол равен 45 градусам, подъем равен пробегу (спуску), а процент подъема равен 100 процентам. По мере того, как угол наклона приближается к вертикальному (90 градусов), как в треугольнике C, процент подъема стремится к бесконечности.

Сравнение значений уклонов в градусах и процентах.

Инструмент Уклон чаще всего работает с набором данных высот, как показано на следующих рисунках. Более крутые уклоны заштрихованы красным на выходном растре уклона.

Инструмент также может использоваться с другими типами непрерывных данных, например, численность населения, для выявления резких изменений значения.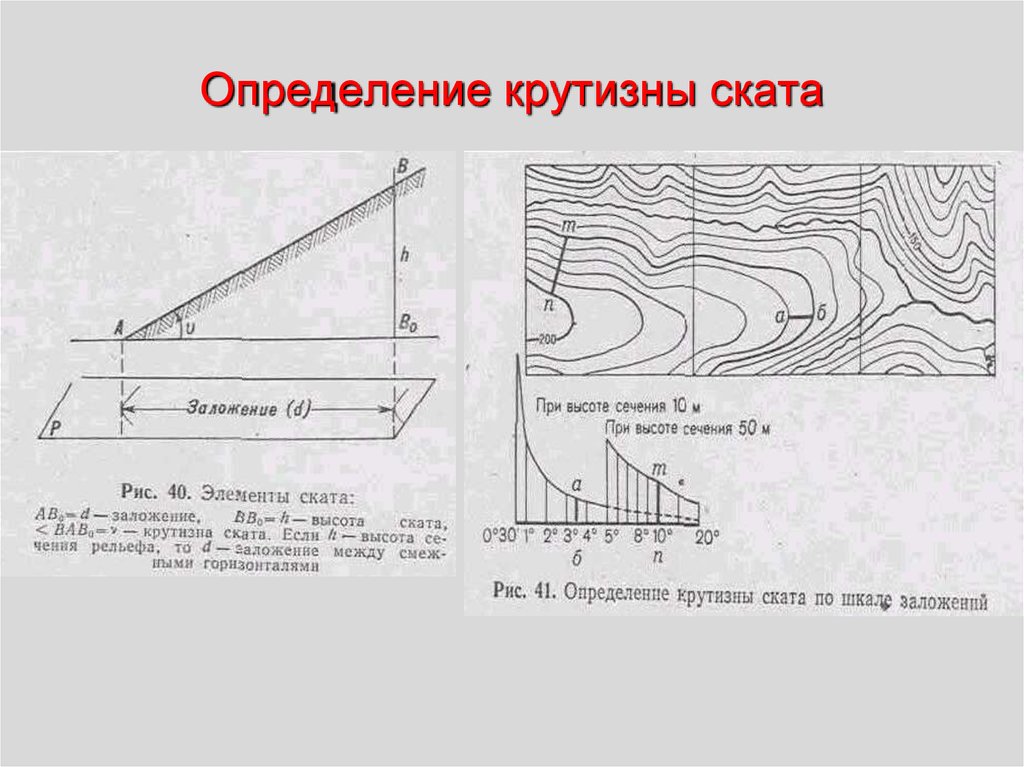

Методы вычисления и эффект ребер

Для вычисления уклона доступно два метода. Вы можете выбрать метод вычисления Плоскостной или Геодезический, используя параметр Метод.

Для плоскостного метода, уклон измеряется как максимальное соотношение изменения значений ячейки и ее непосредственного окружения. Расчет выполняется на проецированной плоскости при использовании декартовой системы координат 2D. Значение уклона вычисляется с использованием методики усредненного максимума (Burrough, 1998).

По геодезическому методу вычисления будут выполняться в декартовой системе координат 3D учетом формы земной поверхности в виде эллипсоида. Значение уклона вычисляется измерением угла между топографической поверхностью и базовым датумом.

Плоскостные и геодезические вычисления выполняются с помощью окрестности размером 3 на 3 ячейки (плавающее окно). Для каждой окрестности, если обрабатываемая (центральная) ячейка имеет значение NoData, выходное значение будет NoData. Для вычислений также необходимо, чтобы не менее семи окрестных ячеек имели допустимые значения.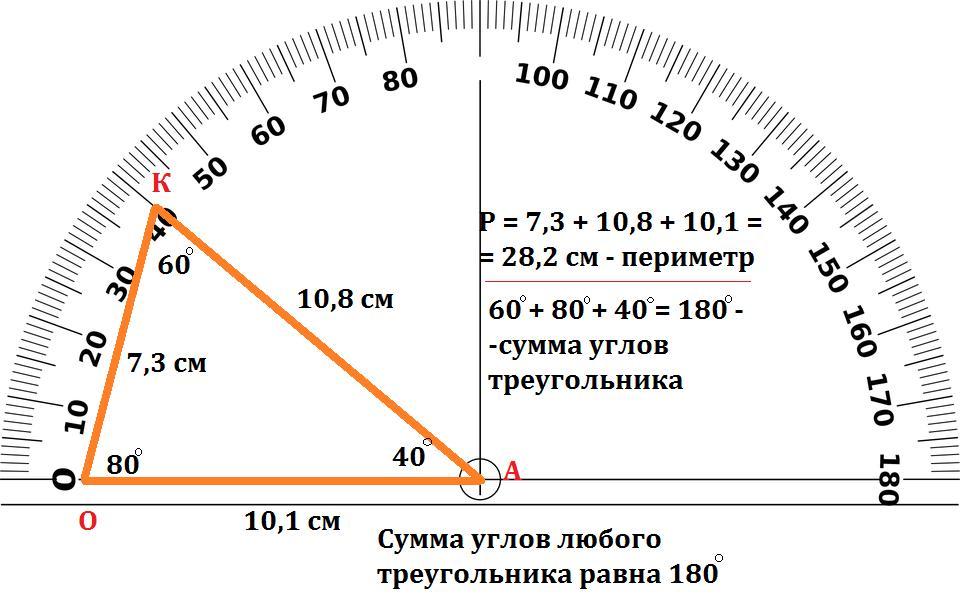 Если менее семи ячеек имеют корректные значения, вычисление не производится, а выходным значением обрабатываемой ячейки будет NoData.

Ячейки в наиболее удаленных строках и столбцах выходного растра получат значение NoData. Это происходит потому, что вдоль границы входного набора данных у ячеек нет достаточного количества соседей.

Плоскостной метод

Для каждой ячейки инструмент вычисляет максимальную степень изменения в значении z между конкретной ячейкой и соседними с ней ячейками. По сути, максимальная степень изменения в значениях высоты на единицу расстояния между ячейкой и восемью соседними с ней ячейками определяет самый крутой спуск вниз по склону из ячейки.

Алгоритм вычисления плоскостного уклона

Уклон определяет степень изменения (дельту) поверхности в горизонтальном (dz/dx) и вертикальном (dz/dy) направлениях из центральной ячейки. Базовый алгоритм, используемый для вычисления уклона, выглядит так:

 slope_radians = ATAN ( √ ([dz/dx]2 + [dz/dy]2) )

Уклон обычно измеряется в градусах с использованием следующего алгоритма:

 slope_degrees = ATAN ( √ ([dz/dx]2 + [dz/dy]2) ) * 57. 29578

Примечание:

Показанное здесь значение 57,29578 – это сокращенная версия результата операции 180/pi.

Алгоритм уклона может быть проинтерпретирован также следующим образом:

 slope_degrees = ATAN (rise_run) * 57.29578

Горизонтальную и вертикальную дельты определяют значения центральной ячейки и восьми соседних с ней ячеек. Соседние ячейки обозначаются буквами от a до i, при этом буква e обозначает ячейку, для которой вычисляется уклон.

Окно сканирования поверхности

Степень изменения по направлению x для ячейки ‘e‘ вычисляется с помощью следующего алгоритма:

  [dz/dx] = ((с + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize)

• где:

  wght1 и wght2 являются горизонтально взвешенным числом корректных ячеек.

  Например, если:

  • c, f и i имеют корректные значения, wght1 = (1+2*1+1) = 4.
  • i является NoData, wght1 = (1+2*1+0) = 3.
  • f является NoData, wght1 = (1+2*0+1) = 2.

  Аналогичная логика применяется к wght2, за исключением того, что соседними местоположениями являются a, d и g.

Степень изменения по направлению y для ячейки ‘e‘ вычисляется с помощью следующего алгоритма:

  [dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + с)*4/wght4) / (8 * y_cellsize)

Пример вычисления плоскостного уклона

В качестве примера будет вычислено значение уклона центральной ячейки скользящего окна.

Пример входных данных Уклона

Степень изменения для центральной ячейки ‘e‘ по направлению x:

  [dz/dx] = ((с + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize)          = ((50 + 60 + 10)*4/(1+2+1) - (50 + 60 + 8)*4/(1+2+1)) / (8 * 5)          = (120 - 118) / 40          = 0. 05

Степень изменения для центральной ячейки ‘e‘ по направлению y:

  [dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + с)*4/wght4) / (8 * y_cellsize)          = ((8 + 20 + 10)*4/(1+2+1) - (50 + 90 + 50)*4/(1+2+1)) / (8 * 5)          = (38 - 190 ) / 40          = -3.8

Учитывая степень изменения в направлении x и y, уклон для центральной ячейки e вычисляется с использованием следующего алгоритма:

  rise_run = √ ([dz/dx]2 + [dz/dy]2)           = √ ((0.05)2 + (-3.8)2)           = √ (0.0025 + 14.44)           = 3.80032

  slope_degrees = ATAN (rise_run) * 57.29578                = ATAN (3.80032) * 57.29578                = 1.31349 * 57.29578                = 75.25762

Целочисленное значение уклона для ячейки ‘e‘ составляет 75 градусов.

Пример выходных данных Уклона

Геодезический метод

При геодезическом методе уклон поверхности измеряется в геоцентрической 3D системе координат – также называющейся системой координат Earth Centered, Earth Fixed (ECEF) – с учетом эллипсоидной формы земли. Проекция набора данных на результаты вычислений не влияет. При этом используются единицы измерения z входного растра, если они заданы в пространственной привязке. Если в пространственной привязке входных данных не заданы единицы измерения z, необходимо сделать это с помощью параметра задания z-единиц. Геодезический метод дает более точный результат, чем плоскостной.

Преобразование геодезических координат

Система координат ECEF является 3D правосторонней Декартовой системой координат с центром земли в качестве начальной точки, в которой любое местоположение представлено координатами X, Y и Z. На следующем рисунке приводится пример целевого местоположения T, выраженного в геоцентрических координатах.

Растр поверхности трансформируются из входной системы координат в 3D геоцентрическую систему координат.

В геодезических вычислениях используются координаты X, Y, Z, которые вычисляются на основе геодезических координат(широта φ, долгота λ, высота h). Если система координат входного растра поверхности является системой координат проекции, растр сначала перепроецируется в географическую систему координат, в которой каждое местоположение имеет геодезические координаты, затем он преобразуется в систему координат ECEF. Высота h (z-значение) является эллипсоидной высотой, основанной на поверхности эллипсоида. См. иллюстрацию ниже.

Эллипсоидальная высота

Для преобразования геодезических координат (широта φ, долгота λ, высота h) в координаты ECEF используются следующие формулы:

X = (N(φ)+h)cosφcosλ

Y = (N(φ)+h)cosφsinλ

Z = (b2/a2*N(φ)+h)sinφ

• , где:
  • N( φ ) = a²/ √(a²cosφ²+b²sinφ²)
  • φ = широта
  • λ = долгота
  • h = эллипсоидальная высота
  • a = большая полуось эллипсоида
  • b = малая полуось эллипсоида

Эллипсоидная высота h в следующих формулах дается в метрах. Если z-значения входного растра даны в других единицах измерения, они будут преобразованы в метры.

Вычисление уклона

Геодезический уклон является углом между топографической поверхностью и поверхностью эллипсоида. Любая поверхность, параллельная поверхности эллипсоида, имеет уклон 0. Чтобы вычислить уклон в каждом местоположении, вокруг обрабатываемой ячейки создается плоскость окрестности размером 3 x 3 ячейки, по методу наименьших квадратов. Наилучшее соответствие по методу наименьших квадратов минимизирует сумму квадратов разницы (dz_i) между реальным и подобранным z-значением. Пример приведен на рисунке ниже.

Пример использования метода наименьших квадратов

Здесь плоскость представлена в виде z = Ax + By + C. Для каждого центра ячейки, dz_i является разницей между реальным z-значением и подобранным.

Наилучшее соответствие плоскости достигается, когда ∑⁹_i=1dz_i² минимальна.

После подгонки плоскости, в местоположении ячейки вычисляется нормаль к поверхности. В том же местоположении вычисляется нормаль эллипсоида, перпендикулярная плоскости, проходящей по касательной к поверхности эллипсоида.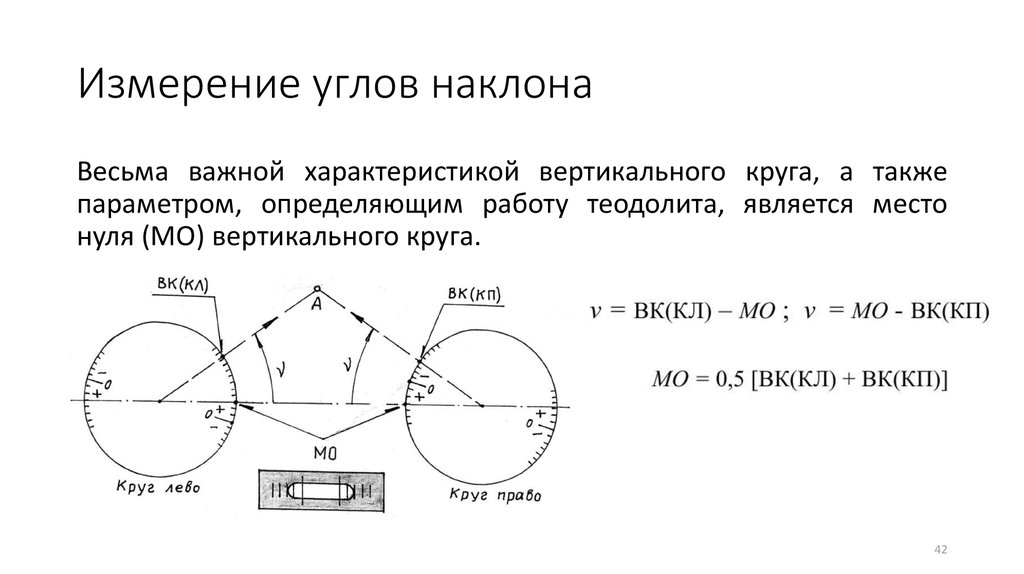

Вычисление геодезического уклона

Уклон, в градусах, вычисляется по углу между нормалью к эллипсоиду и нормалью к топографической поверхности, который здесь обозначается как β. Согласно рисунку выше, угол α является геодезическим уклоном, что соответствует углу β, согласно закону подобной геометрии.

Для вычисления уклона в процентах используется следующая формула:

Slope_PercentRise = ATAN(β) * 100%

Использование графического процессора (GPU)

При использовании геодезического метода, производительность инструмента значительно повышается если используются GPU определенных моделей. Дополнительные сведения о поддержке этого механизма, его настройке и включении см. в разделе Работа GPU с Spatial Analyst.

Справочная информация

Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.

Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159

B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS – theory and practice. Section 10.2.1. p. 282.

David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.

Связанные разделы

Временные погрешности в наблюдениях лазерной локации: Актуальный вопрос космической геодезии

• Эксертье, Пьер
;
• Белли, А.
;
• Лемуан, Дж. М.

Аннотация

Передача времени с помощью лазерной локации (LR) недавно продемонстрировала замечательную стабильность (несколько пс в течение ∼1000 с) и точность (<1 нс) при синхронизации космических и наземных часов на расстояниях от нескольких тысяч до десятков тысяч километров. Учитывая его потенциальную роль в навигации, фундаментальной физике и метрологии, крайне важно, чтобы синергия между технологиями лазерной локации и технологий времени и частоты (T/F) улучшалась для удовлетворения нынешних и будущих требований космической геодезии. В этой статье мы исследуем поведение систем T/F, которые используются в станциях слежения LR международной службы лазерной локации. Подход, который мы исследуем, заключается в вычислении синхронизации времени между часами, используемыми на станциях LR, с использованием точных данных эксперимента Time Transfer by Laser Link (T2L2) на борту спутника Jason-2 (Samain et al., 2014). Систематические смещения времени оцениваются по шкале времени UTC для набора из 22 станций наблюдения в 2013 г. в диапазоне от нуля до нескольких мкс. Наши результаты показывают, что сеть ILRS страдает от проблем с точностью из-за временных погрешностей в наблюдениях лазерной локации. Мы обсуждаем, как эти систематические эффекты влияют на точное определение орбиты геодезических спутников LAGEOS в течение 1 года, и дополнительно даем меру локального эффекта в координатах станции, в частности, в отношении эффекта в компоненте восток-запад, который составляет 2 -6 мм для типичного систематического смещения времени в один мкс.

Публикация:

Достижения в области космических исследований

Дата публикации:

Сентябрь 2017

DOI:

10.1016/ж.аср.2017.05.016

Биб-код:

2017AdSpR..60..948E

Ключевые слова:

• Передача времени;
• Лазерный дальномер;
• Временная погрешность;
• Космическая геодезия

Временные погрешности в измерениях лазерной локации; воздействие на геодезические продукты (система отсчета и орбитография)

NASA/ADS

Погрешности времени в измерениях лазерной локации; воздействия на геодезические продукты (система отсчета и орбитография)

• Белли, А.
;
• Эксертье, П.
;
• Лемуан, Ф. Г.
;
• Чинн, Д. С.
;
• Зеленский Н.П.

Аннотация

Задачи GGOS заключаются в поддержании геодезической сети с точностью до 1 мм и стабильностью 0,1 мм в год. В течение многих лет метод лазерной локации, который обеспечивает очень точные абсолютные расстояния до геодезических целей, позволяет определять масштабный коэффициент, а также координаты геоцентра. Для достижения этой цели необходимо учитывать и устранять систематические ошибки, возникающие при измерениях лазерной локации. В дополнение к смещению по дальности (RB), которое является основным источником неопределенности метода, смещение по времени (TB) было недавно обнаружено с помощью космического прибора Time Transfer by Laser Link (T2L2) на борту спутника Jason- 2. Вместо определения TB с помощью точного определения орбиты, которое применяется к широко используемым геодезическим целям, таким как LAGEOS, для оценки глобальных геодезических продуктов, мы независимо друг от друга разработали специальный метод для передачи времени между удаленными спутниковыми станциями лазерной локации. В результате эволюционирующий фазовый сдвиг часов к UTC около 30 станций был определен в виде временных рядов смещения времени на станцию ​​с 2008 по 2016 год с точностью 3-4 нс. Он продемонстрировал сложность, с точки зрения используемых технологий времени и частоты, локального поддержания точности и долгосрочной стабильности, по крайней мере, в диапазоне 100 нс, что является текущим требованием для измерения времени (UTC) для метода лазерной локации. Поскольку некоторые станции лазерной локации часто превышают этот предел (от 100 нс до нескольких мкс), мы изучали эти эффекты сначала на самом точном определении орбиты, а затем на позиционировании станции. Мы обсуждаем влияние TB на орбиты LAGEOS и Jason-2, которое, по-видимому, существенно влияет на продольную составляющую.