|
Random converter |
Калькулятор остановочного пути автомобиляКалькулятор определяет остановочный путь автомобиля с момента обнаружения водителем опасности до момента полной остановки автомобиля, а также другие параметры, связанные с этим событием, в частности, время восприятия водителем сигнала о необходимости торможения, время реакции водителя, а также расстояние, которое прошел автомобиль во время этих событий. Калькулятор также определяет начальную скорость (скорость до начала торможения) по известной длине торможения (длины тормозного пути) с учетом дорожных условий. Как и все остальные калькуляторы, этот калькулятор не следует использовать в судебных процессах и при необходимости получения высокой точности. Пример 1: Рассчитать расстояние, необходимое для остановки автомобиля, движущегося со скоростью 90 км/ч по мокрой горизонтальной дороге с асфальтобетонным покрытием (коэффициент трения μ = 0,4) если время восприятия водителя 0,5 с и время реакции водителя 0,7 с. Пример 2: Рассчитать начальную скорость автомобиля, движущегося по дороге с мокрым асфальтобетонным покрытием (μ = 0.4), если длина тормозного пути равна 100 м. Автомобиль движется на спуске с уклоном 10%. Калькулятор остановочного путиВходные данные Начальная скорость v0м/скм/чфут/смиля/ч Время восприятия опасности водителем thp с Время реакции водителя thr с Уклон σградус% Движение вверх Движение вниз Состояние дороги —Сухой асфальтМокрый асфальтПокрытый снегом асфальтПокрытый льдом асфальт или Коэффициент трения μ Тип привода тормозов —ПневматическийГидравлический или Время срабатывания тормозной системы tbrl с Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Угол крутизны уклона θ= ° Замедление a= м/с² Время торможения tbr= с Расстояние, которое проедет автомобиль во время восприятия водителем опасности Shp= м Расстояние, которое проедет автомобиль во время реакции водителя на опасность Shr= м Расстояние, которое проедет автомобиль за время задержки срабатывания тормоза Sbrl= м Тормозной путь Sbr= м Остановочный путь Sstop= м Критический угол наклона для заданного коэффициента трения θcrit= ° Критический уклон для заданного коэффициента трения σcrit= % Калькулятор определения скорости по тормозному путиВходные данные Длина тормозного следа Sbrметр (м)футярд Уклон σградус% Движение вверх Движение вниз Состояние дороги —Сухой асфальтМокрый асфальтПокрытый снегом асфальтПокрытый льдом асфальт или Коэффициент трения μ Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Скорость перед началом торможения v0 м/с км/ч Определения и формулы Остановочный путь Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуации Расстояние, которое пройдет автомобиль во время реакции водителя Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы Замедление Тормозной путь автомобиля Вывод зависимости тормозного пути от скорости и трения с использованием второго закона Ньютона Вывод зависимости тормозного пути от скорости и трения с помощью энергетического метода Время торможения Движение вверх и вниз по уклону Уклон Критический угол Определения и формулыОстановочный путьОстановочный путь — это расстояние, которое проходит автомобиль с момента, когда водитель видит опасность, оценивает ее, принимает решение остановиться и нажимает на педаль тормоза и до момента полной остановки автомобиля. где shr — расстояние, которое проедет автомобиль во время восприятия и оценки водителем ситуации, shr — расстояние, которое проедет автомобиль во время во время реакции водителя на ситуацию, sbrl — расстояние, которое проедет автомобиль во время задержки срабатывания тормозов, и sbr — тормозной путь. Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуацииРасстояние человеческого восприятия ситуации — это расстояние, которое пройдет автомобиль в то время, пока водитель оценивает опасность и принимает решение уменьшить скорость и остановиться. Оно определяется по формуле где shp расстояние человеческого восприятия в метрах, v скорость автомобиля в км/ч, thp — время человеческого восприятия в секундах и 1000/3600 — коэффициент преобразования километров в час в метры в секунду (1 километр равен 1000 метров и 1 час равен 3600 секундам). Расстояние, которое пройдет автомобиль во время реакции водителяРасстояние реакции водителя — это расстояние, которое пройдет автомобиль пока водитель выполняет решение остановить автомобиль после оценки опасности и принятия решения об остановке. Оно определяется по формуле где shp — расстояние реакции водителя с метрах, v — скорость автомобиля в км/ч и thr — время реакции водителя в секундах. Расстояние, которое пройдет автомобиль во время срабатывания тормозной системыРасстояние, которое пройдет автомобиль во время срабатывания тормозной системы, зависит от типа тормозной системы, установленной на автомобиле. Почти на всех легковых автомобилях и малотоннажных грузовых автомобилях используются гидравлическая тормозная система. На большинстве большегрузных автомобилей используются тормоза с пневматическим приводом. Задержка срабатывания пневматических тормозов приблизительно равна 0,4 с, а гидравлических (жидкость несжимаема!) 0,1–0,2 с. Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, определяется по формуле где sbrl — расстояние в метрах, которое пройдет автомобиль во время срабатывания тормозной системы, v — скорость движения автомобиля в км/ч, tbrl — время срабатывания тормозной системы в секундах. ЗамедлениеДля упрощения расчетов предположим, что автомобиль движется с постоянным ускорением или замедлением, которое определяется по известной из курса элементарной физики формуле равноускоренного или равнозамедленного движения где a — ускорение, v — начальная скорость, v0 — конечная скорость и t — время. Тормозной путь автомобиляТормозной путь автомобиля — это расстояние, которое проходит автомобиль с момента полного нажатия на педаль тормоза до момента полной остановки. Это расстояние зависит от скорости автомобиля перед началом торможения и от коэффициента трения между шинами и дорожным покрытием. В этом калькуляторе мы не учитываем другие факторы, влияющие на тормозной путь, например, сопротивление качению шин или лобовое сопротивление воздуха В результатах исследования1, в котором коэффициент трения определялся путем измерения замедления, определено, что антиблокировочная тормозная система (АБС) влияла на коэффициент трения таким образом: он увеличивается с увеличением скорости при использовании АБС и уменьшается, если АБС не используется. В этом исследовании также подтверждается, что на коэффициент трения между шинами и дорожным покрытием влияет температура и интенсивность дождя. Вывод зависимости тормозного пути от скорости и трения с использованием второго закона НьютонаКоэффициент трения определяется как отношения силы трения к силе нормального давления, прижимающей тело к опоре: или где Ffr — сила трения, μ коэффициент трения и Fnorm — сила реакции опоры. Действующая на тело нормальная сила реакции опоры определяется как составляющая силы реакции, перпендикулярная к поверхности опоры тела. В простейшем случае, когда тело находится на плоской горизонтальной поверхности, нормальная сила равна весу этого тела: где m — масса тела и g — ускорение свободного падения. Эта формула выведена из второго закона Ньютона: В более сложном случае, если тело расположено на наклонной плоскости, нормальная сила рассчитывается как где θ — угол наклона между плоскостью поверхности и горизонтальной плоскостью. В этом случае нормальная сила меньше веса тела. Случай наклонной поверхности мы рассмотрим чуть позже. В случае же горизонтальной поверхности, если коэффициент трения между телом и поверхностью равен μ, то сила трения равна В соответствии со вторым законом Ньютона, эта сила трения, приложенная к движущемуся телу (автомобилю) приводит к возникновению пропорционального ей замедления: или Теперь, в соответствии с уравнением ускоренного (замедленного) движения имеем Из курса элементарной физики известно, что при равнозамедленном движении с постоянным замедлением, если конечная скорость равна нулю, то тормозной путь определяется уравнением Это уравнение можно переписать в более удобной форме с использованием преобразования скорости в км/час в м/с: Подставляя в это уравнение a = μg, получаем формулу тормозного пути: где скорость v задается в км/час, а ускорение силы тяжести g в м/с². Решая это уравнение относительно v, получаем: Аналогичную формулу для определения тормозного пути можно получить с помощью энергетического метода. Вывод зависимости тормозного пути от скорости и трения с помощью энергетического методаТеоретическое значение тормозного пути можно найти, если определить работу по рассеиванию кинетической энергии автомобиля. Если автомобиль, движущийся со скоростью v, замедляет движение до полной остановки, работа тормозной системы Wb, требуемая для полного рассеяния кинетической энергии автомобиля Ek, равна этой энергии: Кинетическая энергия движущегося автомобиля Ek определяется формулой где m — масса автомобиля и v — скорость движения автомобиля перед началом торможения. Работа Wb, выполненная тормозной системой, определяется как где m — масса автомобиля, μ — коэффициент трения между шинами и дорожным покрытием, g — ускорение силы тяжести и sbr — тормозной путь, то есть расстояние, которое прошел автомобиль от начала торможения до полной остановки. Теперь, с учетом того, что Ek = Wb, имеем: или Скорость автомобиля до начала торможения является наиболее важным фактором, влияющим на величину остановочного пути. Другими, менее важными, факторами, влияющими на остановочный путь, являются время оценки водителем ситуации, время реакции водителя, скорость работы тормозной системы автомобиля и состояние дороги. Время торможенияИз курса элементарной физики известно, что средняя скорость при равноускоренном движении равна полусумме начальной и конечной скорости: С учетом, что конечная скорость равна нулю, время торможения определяется в калькуляторе как Движение вверх и вниз по уклонуСилы, действующие на автомобиль на уклоне: Fg — сила тяжести (вес автомобиля), Fgd — скатывающая вниз составляющая веса автомобиля, Ffr — сила трения, действующая параллельно поверхности дорожного полотна с уклоном, Fgn — нормальная составляющая веса автомобиля, направленная перпендикулярно поверхности дороги, и Fnr — сила реакции опоры, равная нормальной составляющей веса автомобиля. Когда водитель нажимает на педаль тормоза, замедляющий движение автомобиль может быть представлен в виде тела на поверхности с углом наклона θ (см. рисунок выше). Для простоты мы будем рассматривать только две силы, действующие на автомобиль, находящийся на уклоне. Это вес автомобиля и сила трения. Автомобиль, движущийся с начальной скоростью, замедляет движение, если сила трения, действующая параллельно дорожному полотну, больше, чем скатывающая сила, являющаяся составляющей силы тяжести, которая также параллельна дорожному полотну. Если начальная скорость автомобиля равна нулю, он в этой ситуации остается на месте при условии, что угол уклона меньше критического (об этом — ниже). В то время, как сила тяжести Fg стремится скатывать автомобиль вниз, сила трения Ffr сопротивляется этому движению. Чтобы автомобиль мог в этой ситуации остановиться, сила трения должна превышать скатывающую составляющую силы тяжести Fgd. В то же время, если сила трения превышает скатывающую составляющую силы тяжести, автомобиль будет двигаться вниз с постоянным ускорением и его тормозная система будет неспособна его остановить. Это может произойти, если угол наклона (уклон) дорожного полотна слишком велик или коэффициент трения слишком мал (вспомним как ведет себя автомобиль с обычными шинами на уклоне, если он покрыт коркой льда!). По определению коэффициента трения, можно записать уравнение для силы трения: или Скатывающая составляющая силы тяжести: Результирующая сила Ftotal, действующая на автомобиль на уклоне: или Как мы уже отмечали, сила Ftotal должна быть направлена вверх, иначе автомобиль при движении вниз остановить невозможно. В соответствии со вторым законом Ньютона, ускорение (точнее, замедление) автомобиля, движущегося под действием силы Ftotal, определяется как Подставляя ускорение в выведенную выше формулу тормозного пути, получаем: Решая это уравнение для vpre-braking, получим: Отметим еще раз, что в этих формулах g задается в м/с, v в км/ч и s в метрах. Припаркованные и движущиеся по ул. Дивисадеро в Сан-Франциско (Калифорния) автомобили. Уклон дорожного полотна в этом месте равен 31% или 17°. УклонВеличина уклона дороги (показателя крутизны склона) равна тангенсу угла плоскости дорожного покрытия к горизонтали. Он рассчитывается как отношение перпендикуляра, опущенного из точки на поверхность (превышения местности) к длине горизонтальной поверхности от начала склона до перпендикуляра (горизонтальному расстоянию). По определению уклона считается, что при движении вверх уклон является положительным, а при движении вниз уклон является отрицательным, когда превышение в действительности является понижением дороги. Уклон дороги σ выражают как угол наклона к горизонтали в градусах или как отношение в процентах. Например, подъёму 15 метров на 100 метров перемещения по горизонтали соответствует уклон, равный 0,15 или 15%. В этом калькуляторе мы используем уклон в процентах, определяемый по формуле где Δh — превышение местности и d — проекция уклона на горизонталь (см. Критический уголПри увеличении угла наклона дорожного полотна выше определенного значения, называемого критическим углом, движущийся вниз автомобиль затормозить невозможно, так как действующая на него сила трения становится меньше скатывающей силы. Этот критический угол находится из условия или или Из этой формулы можно найти критический угол для данного коэффициента трения, при котором автомобиль не сможет затормозить: Уклон, выраженный в процентах, определяется по известному углу наклона таким образом: ПримерВ этом примере мы покажем, как использовать формулу для определения тормозного пути. Пусть автомобиль движется с начальной скоростью vpre-braking = 90 км/ч вниз по уклону σ = 5% по мокрому асфальту (коэффициент трения μ = 0,4). Нужно определить тормозной путь. Для расчетов используем выведенные выше формулы. Особые случаиНажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:
Литература
Автор статьи: Анатолий Золотков Вас могут заинтересовать и другие калькуляторы из группы «Механика»:Калькулятор скорости, времени и расстояния при свободном падении Калькулятор выигрыша в силе Калькуляторы рычага Калькулятор выигрыша в силе, даваемого воротом Калькулятор выигрыша в силе, даваемого полиспастом Калькулятор выигрыша в силе наклонной плоскости Калькулятор выигрыша в силе винта Калькулятор выигрыша в силе, даваемого клином Калькулятор давления Калькулятор импульса (количества движения) и импульса силы Калькулятор закона сохранения импульса: столкновения и взрывы при условии, что два тела находятся на прямой линии Калькуляторы Механика |
Калькулятор Уклона – Mathcracker.
 Com
ComИнструкции: Используйте этот калькулятор, чтобы получить наклон линии со всеми показанными вычислениями, шаг за шагом. Для этого вам необходимо указать линию, для которой вам нужно вычислить наклон.
Укажите либо корректное линейное уравнение, либо две точки \((x_1, y_1)\) и \((x_2, y_2)\), через которые проходит прямая.
Как использовать этот калькулятор уклона с шагами
Используйте этот калькулятор, чтобы найти наклон линии, которую вы предоставили, со всеми показанными шагами.
Наклон — это мера наклона линии относительно координированных осей.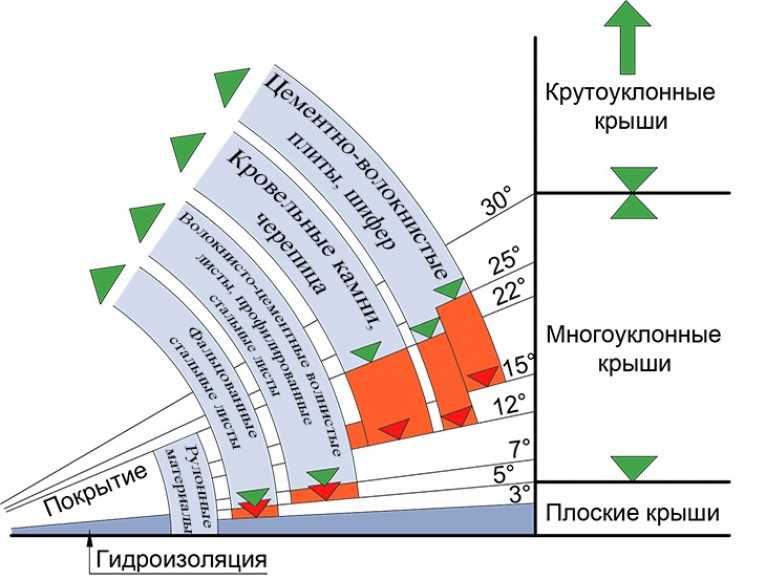 Положительный наклон указывает на то, что линия имеет восходящий наклон, тогда как отрицательный наклон указывает на то, что линия имеет нисходящий наклон.
Положительный наклон указывает на то, что линия имеет восходящий наклон, тогда как отрицательный наклон указывает на то, что линия имеет нисходящий наклон.
Наклон, равный нулю, указывает на то, что линия является горизонтальной, тогда как вертикальная линия не имеет четко определенного наклона.
Калькулятор уклона из уравнения
Этот калькулятор покажет вам, как вычислить наклон предоставленной вами линии, и у вас будут различные способы обозначения и определения вашей линии.
Например, одним из распространенных способов является определение вашей линии с помощью уравнения, а затем у вас будет этот калькулятор для вычисления наклона из уравнения.
Общая стратегия для этого состоит в том, чтобы представить уравнение прямой в форме наклона-пересечения , откуда легко распознать наклон по структуре уравнения \(y = mx + n\).
Это тоже наклон из двухточечного калькулятора.
Возможно, один из наиболее распространенных способов вычисления наклона — это когда вы определите уравнение, предоставив две точки as\((x_1, y_1)\), \((x_2, y_2)\), где наклон вычисляется как
\[m = \frac{y_2-y_1}{x_2-x_1}\]
как найти наклон по двум точкам.
В конечном счете, как найти наклон линии, будет зависеть от того, как определена линия. Этот калькулятор поможет вам во всех случаях, даже если в расчетах есть дроби.
Пример: расчет уклона
Предположим, что у вас есть строка, имеющая следующую стандартную форму \( \frac{3}{4} x + 2y = 6\). Найдите наклон линии.
Отвечать: Расчет наклона линии
Нам было предложено следующее уравнение:
\[\displaystyle \frac{3}{4}x+2y=6\]
Помещая \(y\) в левую часть и \(x\) и константу в правую часть, мы получаем
\[\displaystyle 2y = -\frac{3}{4}x +6\]
Теперь, находя \(y\) путем деления обеих частей уравнения на \(2\), получается следующее
\[\displaystyle y=-\frac{\frac{3}{4}}{2}x+\frac{6}{2}\]
и упрощая окончательно получаем следующее
\[\displaystyle y=-\frac{3}{8}x+3\]
Вывод
: На основании предоставленных данных делаем вывод, что наклон линии равен \(\displaystyle m = -\frac{3}{8}\).
Пример: расчет уклона по двум точкам
Предположим, что у вас есть линия, которая проходит через 2 точки: \( (1, 2)\) и \( (4, 11/3)\). Найдите наклон линии.
Решение:
Расчет наклона линии
Информация о линии заключается в том, что линия проходит через точки \(\displaystyle \left( 1, 2\right)\) и \(\displaystyle \left( 4, \frac{11}{3}\right)\).
Поэтому первый шаг состоит в вычислении наклона. Формула наклона: \[\displaystyle m = \frac{y_2 – y_1}{x_2 – x_1} \]
Формула наклона: \[\displaystyle m = \frac{y_2 – y_1}{x_2 – x_1} \]
Теперь, подставив соответствующие числа , получим, что наклон равен: \[\displaystyle m = \frac{y_2 – y_1}{x_2 – x_1} = \frac{ \displaystyle \frac{11}{3} – 2}{ \displaystyle 4 – 1} = \frac{ \displaystyle \frac{11}{3}-2}{ \displaystyle 4-1} = \frac{5}{9}\]
Итак, мы находим, что наклон равен \(\displaystyle m = \frac{5}{9}\) и что линия проходит через точку \(\displaystyle \left( 1, 2\right)\).
Вывод
: На основании предоставленных данных делаем вывод, что наклон линии равен \(\displaystyle m = \frac{5}{9}\).
Наклон линии — одно из важнейших ее свойств, наряду с Y-перехват а также x-перехват , потому что они по существу определяют линию.
Калькулятор уклона
Как пользоваться калькулятором уклона?
Калькулятор уклона — это простой в использовании инструмент. Вам нужно будет
- Выберите метод, чтобы найти наклон линии.

- В случае двух точек введите X 1 , Y 1 , X 2 и Y 2 .
- Если вы выбрали метод Line Equation, введите коэффициенты.
- Нажмите Вычислите , чтобы получить наклон линии.
точка Х 1
Точка Д 1
Точка Х 2
Точка Да 2
Уклон (м)
Уклон Пересечение
\(y = mx + b\)
путем подстановки значений
Решение:
Имеем
\(X_1 = \)
\(Y_1 = \) \(Y_1 = \) \(Y_1 = \) \(Y_1 = \) 90_004\(X_2 = \)
\(Y_2 = \)
Формула для нахождения
| Балл | Значения |
|---|---|
| Процентное содержание | |
| Угол \(θ\) | град |
| Расстояние | |
| \(Δx\) | |
| \(Δy\) | |
| Y – Перехват | |
| Х – Перехват |
Что такое калькулятор уклона?
Калькулятор формулы уклона имеет большое значение как в математике, так и в физике. Это помогает найти градиент (наклон) линии, взяв в качестве входных данных две точки или линейные уравнения.
Это помогает найти градиент (наклон) линии, взяв в качестве входных данных две точки или линейные уравнения.
Помимо нахождения простого уклона, он также находит множество других характеристик наклона и линии. К ним относятся:
- Форма пересечения уклона
- Процент уклона, расстояния и угла
- 𝚫X и 𝚫Y
- График наклона
Что такое наклон линии?
Уклон в математике имеет то же значение, что и в английском, а именно « Крутизна ». За исключением математики, мы используем слово «наклон» для обозначения крутизны линий и кривых.
Также известен как градиент, уклон и уклон. Примеры наклона в повседневной жизни включают крыши, горки и крутые горы.
Наклон может быть положительным, отрицательным, нулевым или неопределенным. Типы наклона зависят от их значений и знака со значением. Для быстрого обзора склон, который имеет
- A положительный знак , затем положительный
- A отрицательный знак , тогда, конечно, отрицательный
- Горизонтальное значение означает, что оно равно нулю
Как найти наклон линии?
Если вам нужно найти склон быстро и без ошибок, вы можете использовать для этой цели искатель уклона. Но если вы хотите рассчитать это самостоятельно, продолжайте читать пример ниже.
Но если вы хотите рассчитать это самостоятельно, продолжайте читать пример ниже.
1. Наклон по двум точкам
Пример:
Найдите наклон линии, проходящей через точки (3,6) и (8,2).
Решение:
Шаг 1: Определите значения.
x 1 = 3
x 2 = 8
Y 1 = 6
Y 2 = 2
Шаг 2: Найдите разницу между точками.
𝚫Х = Х 2 – x 1
= 8 – 3
= 5
𝚫y = Y 2 – Y 1
= 2 – 6
= – 4
Шаг 3: . дробь 𝚫Y / 𝚫X.
м = 𝚫Y / 𝚫X
= -4 / 5
= -0,8
Следовательно, наклон линии равен -0,8 и имеет отрицательный характер.
2. Наклон с помощью линейного уравнения
Наклон также можно найти, если у вас есть уравнение прямой. Найдем наклон, используя линейное уравнение.
Найдем наклон, используя линейное уравнение.
Пример:
Найдите наклон линии в следующем уравнении прямой.
4y – 2x + 5 = 0
Решение:
Шаг 1: Оформите уравнение в виде y = mx + c
4y = 2x – 5
5 90 (2x – 5
5 90) /4
Шаг 2: Упростите правую часть уравнения.
y = 2x/4 – 5/4
y = 0,5x – 1,25
Теперь, когда у нас есть уравнение прямой линии, можно найти наклон, сравнив его с исходным уравнением, где м представляет уклон.
Y = MX + C
Y = 0,5x – 1,25
Slope (M) = 0,5
Список литературы- Khan Academy. (н.д.). Что такое наклон линии? Академия Хана.
- Обучение, Л. (без даты). Как найти наклон линии? Люмен.
Формула уклона
Формула уклона: «подъем над уклоном». Математически это можно записать как:
Математически это можно записать как:
м = (Y2 – Y1) / (X2 – X1)
м = 𝚫Y / 𝚫X
Это могут быть любые две точки прямой на декартовой плоскости.
Как это работает
Нажмите здесь, чтобы узнать подробности
Сопутствующие инструменты
Блоги
2 месяца назад
ПОДРОБНЕЕ
Калькулятор уклона
Поделиться в PinterestPinterestПоделиться в FacebookFacebookПоделиться в PocketPocketПоделиться в TwitterTwitterПоделиться в электронной почтеПоделиться в FlipboardFlipboardРабочие листы
Печатные формы
Футболки с пазлами
Рабочие листы по математике
Go Ad Free!
Core Math Worksheets
Fraction Worksheets
Word Problems
Algebra
Other Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Рабочие листы по математике для 9 класса0060
Рабочий лист Новости
В вашем веб-браузере должен быть включен JavaScript
для того, чтобы калькулятор наклона работал.
Использование калькулятора уклона
Этот калькулятор уклона берет две точки, а затем использует формулу наклона для расчета наклона линии, определяемой этими двумя точками, а затем точку пересечения по оси Y. Затем наклон и точка пересечения объединяются, чтобы получить уравнение линии в форме точки пересечения наклона (“y=mx+b”). График линии рисуется на координатной плоскости вместе с уравнением пересечения наклона.
Калькулятор уклона автоматически обновляет график и уравнение при вводе новых значений точек. Калькулятор также позволяет напрямую вводить значения роста или пробега или десятичное значение m. Калькулятор автоматически создаст правильные десятичные или дробные компоненты для всего, что вы вводите.
Вы также можете вычислить уравнение для линии, независимо изменив наклон (либо в виде доли наклона, либо в виде десятичной дроби) или введя новую точку пересечения по оси y. Если введен новый уклон, калькулятор уклона переместит одну из точек, чтобы уравнение соответствовало новой линии. Если введена новая точка пересечения по оси y, наклон останется прежним, но калькулятор переместит две точки, чтобы сместить линию, чтобы она соответствовала новой точке пересечения по оси y.
Если введена новая точка пересечения по оси y, наклон останется прежним, но калькулятор переместит две точки, чтобы сместить линию, чтобы она соответствовала новой точке пересечения по оси y.
Что такое наклон линии?
Наклон линии — это математическое измерение того, насколько крутой выглядит линия, нарисованная на графике, и это значение обычно отображается как переменная m в уравнении в форме пересечения наклона, y=mx+b.
Наклон определяется как отношение изменения по вертикали (по оси Y) к заданной величине изменения по горизонтали (по оси X), часто более просто запоминается как дробь, описывающая рост по отношению к пробегу или скорость изменения . Этот калькулятор наклона предоставляет это отношение как в виде дроби, так и в виде десятичной дроби, но показывает наклон в виде дроби на графике калькулятора.
Если линия наклонена вверх и вправо, она поднимается, когда вы смотрите слева направо по оси x. Подъем в этом случае положительный, и такая линия будет иметь положительный наклон .
Если линия наклонена вниз и вправо, она падает, если смотреть слева направо по оси x. Подъем в этом случае отрицательный (линия «падает»), и такая линия будет иметь отрицательный наклон .
Форма пересечения наклона
Когда мы имеем дело с уравнением, описывающим линии (т. е. линейным уравнением ), мы обычно помещаем уравнения в форму, называемую формой пересечения наклона , которая выглядит следующим образом…
y = mx + b
Уравнение в этой форме описывает, как вычисляется координата y для точки на прямой при заданной координате x. Калькулятор наклона берет указанные вами точки, а затем вычисляет наклон и точку пересечения по оси y, как описано ниже. Эти значения объединяются, и уравнение линии отображается в области графика калькулятора.
Как найти наклон линии
Если у вас есть две точки, они определяют линию в декартовой координатной плоскости, и вы можете использовать эти точки для вычисления наклона линии. Этот калькулятор склона делает именно то, что использует формулу ниже…
Этот калькулятор склона делает именно то, что использует формулу ниже…
M =
Rise
Run
=
Y 2 -Y 1
x 2 -x 1
2 -x 1
. с двумя точками (x 1 ,y 1 ) и (x 2 ,y 2 ), калькулятор уклона подставляет значения в это уравнение, чтобы рассчитать «подъем» вверху и «пробег» внизу. При выборе между двумя точками не имеет значения, какая точка используется как (x 1 ,y 1 ) или (x 2 ,y 2 ), но очень важно, чтобы вы последовательно использовать соответствующие индивидуальные координаты в пределах каждой точки. Например, если вы выбираете одну точку, такую как (5, 6), обязательно используйте 6 (координата y) в качестве первого члена вычитания «подъема» в верхней части уравнения и 6 в качестве первого члена вычитание «бег» в нижней части уравнения. Смешивая отдельные координаты между точками или думая, что есть какая-то конкретная причина выбрать одну точку как (x 1 ,y 1 ) являются распространенными ошибками при расчете уклона. Если вы сомневаетесь, проверьте свой ответ с помощью этого калькулятора наклона, и вы увидите, что это намного проще, чем кажется.
Смешивая отдельные координаты между точками или думая, что есть какая-то конкретная причина выбрать одну точку как (x 1 ,y 1 ) являются распространенными ошибками при расчете уклона. Если вы сомневаетесь, проверьте свой ответ с помощью этого калькулятора наклона, и вы увидите, что это намного проще, чем кажется.
Что такое наклон горизонтальной линии?
Наклон горизонтальной линии равен нулю. В приведенной выше формуле наклона верхний компонент коэффициента наклона показывает вертикальное изменение между двумя точками на линии. Поскольку каждая точка на горизонтальной линии будет иметь одну и ту же координату по оси Y, числитель этой доли наклона всегда будет равен нулю, и, следовательно, вычисленный наклон также всегда будет равен нулю.
Калькулятор наклона рассчитает уравнение прямой без первого члена, эффективно приведя уравнение y=mx+b к форме y=b, отражая, что вычисленная координата y постоянна для любой заданной координаты x.
Каков наклон вертикальной линии?
Как и наклон горизонтальной линии, наклон вертикальной линии особенный. Опять же, обращаясь к уравнению наклона, рассмотрим, как меняются координаты при движении вверх и вниз по вертикальной линии. В случае вертикальной линии координата оси x никогда не изменится для любой заданной координаты оси y. Из-за этого изменение по оси x, представленное как нижний компонент коэффициента наклона, равно нулю.
Опять же, обращаясь к уравнению наклона, рассмотрим, как меняются координаты при движении вверх и вниз по вертикальной линии. В случае вертикальной линии координата оси x никогда не изменится для любой заданной координаты оси y. Из-за этого изменение по оси x, представленное как нижний компонент коэффициента наклона, равно нулю.
Здесь проблема. Уравнение наклона делится на это изменение результата значения x, и деление на ноль не допускается. В результате наклон вертикальной линии не определен, и вы можете легко видеть, что вы не можете вычислить значения y через значения x, используя уравнение в форме пересечения наклона y=mx+b, потому что значение m для наклона не определено, делая все уравнение неопределенным.
Проще говоря, не существует эквивалентного уравнения формы пересечения наклона для вертикальной линии, поэтому нам нужно что-то еще.
Уравнение для вертикальной линии преобразуется калькулятором наклона в форму x=c, где c представляет постоянное значение x, определяющее линию для каждой возможной координаты y.
Как найти точку пересечения линии по оси Y
Если у вас есть уравнение линии в форме точки пересечения наклона, найти точку пересечения по оси Y несложно, но понимание того, почему уравнение выделяет точку пересечения, так же важно, как и умение читать это из последнего члена уравнения.
Точка пересечения y — это точка пересечения прямой с осью y. Поскольку каждая точка на оси y имеет нулевое значение координаты x, уравнение пересечения наклона линии можно использовать для решения для y при нулевом значении x. Это рассчитает значение, в котором линия пересекает ось Y.
Точка пересечения y формально представляет собой пару координат, но поскольку координата x по определению равна нулю, точка пересечения y часто идентифицируется только одним значением (координатой y).
Кроме того, это значение по оси Y является единственным в качестве переменной b в уравнении пересечения наклона y=mx+b. На самом деле, когда линия описывается как уравнение пересечения наклона, значение пересечения y можно считать из последнего члена уравнения.
Но что, если у вас нет уравнения прямой и вы только начинаете с точек? Вы можете перетасовать уравнение пересечения наклона, чтобы оно приняло следующую форму…
b = y – mx
Эта формула вычисляет пересечение от наклона и одной точки на линии. Калькулятор уклона использует эту же формулу для нахождения точки пересечения после определения фактического уклона, как описано выше.
Как найти уравнение линии
Существует два сценария нахождения уравнения линии, оба из которых используются внутри этого калькулятора наклона в зависимости от того, какие значения вы изменяете.
Вышеприведенное обсуждение показывает, как калькулятор находит уклон, используя две точки, используя формулу уклона (расчет «нарастания по пробегу»).
Учитывая наклон и хотя бы одну точку, уравнение b=y-mx используется для нахождения точки пересечения.
После вычисления точки пересечения и наклона имеются все части, необходимые для создания уравнения в форме точки пересечения наклона.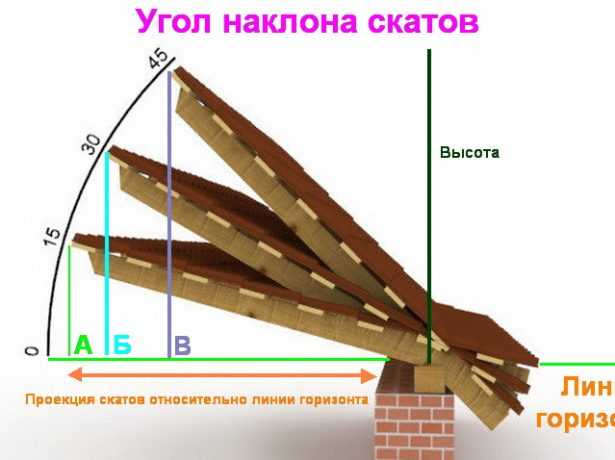


 Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки.
Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки.
 Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический.
Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический.


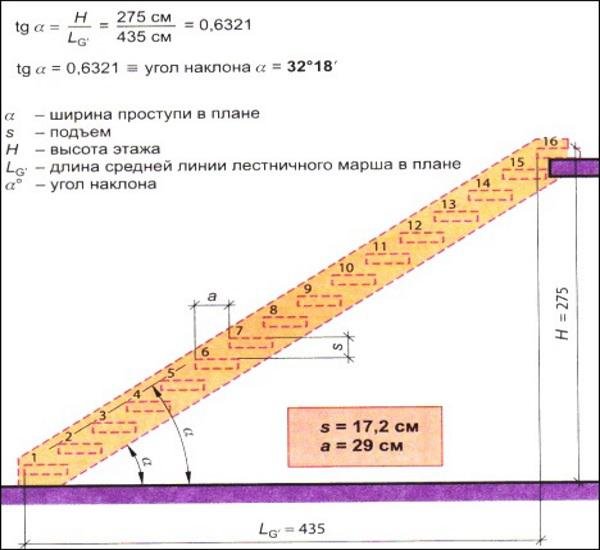

 В нашем калькуляторе используются две последние формулы.
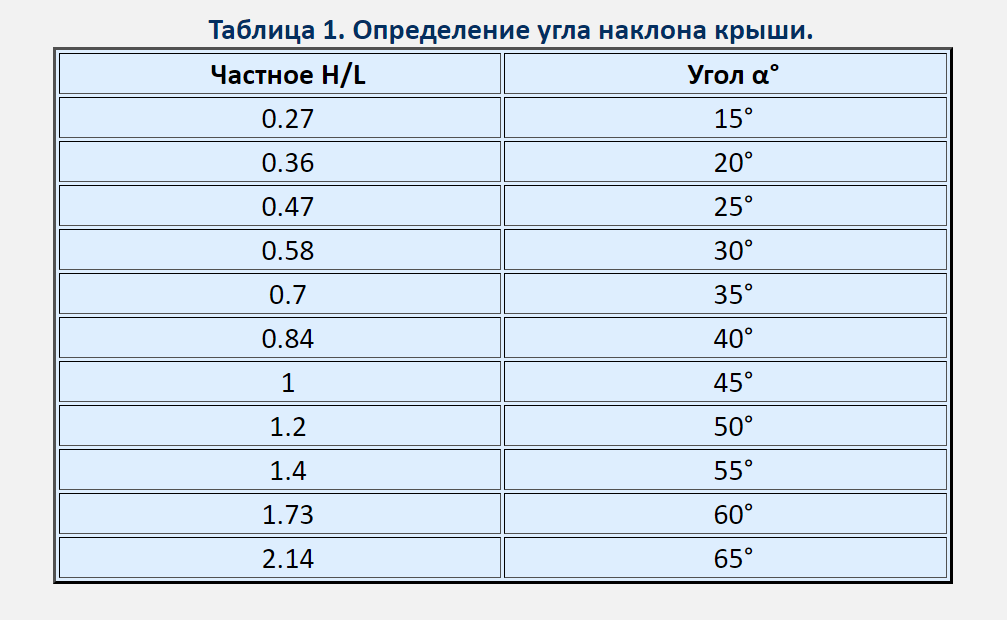
В нашем калькуляторе используются две последние формулы. рисунок выше). Если известен уклон, то угол наклона можно определить по формуле
рисунок выше). Если известен уклон, то угол наклона можно определить по формуле
 Движущийся вниз автомобиль не может быть остановлен и будет двигаться вниз с постоянным ускорением.
Движущийся вниз автомобиль не может быть остановлен и будет двигаться вниз с постоянным ускорением.