Уклон канализации на 1 метр СНиП для монтажа внутренней и наружной инженерной системы
Содержание:
- Что такое угол наклона трубопровода?
- Ошибки при выборе угла наклона труб
- Как рассчитать степень наполненности трубопровода
- Формула для расчета уклона труб
- Угол уклона для наружной инженерной сети
Грамотный монтаж канализационной системы невозможен без предварительных расчетов. Необходимо определить диаметр труб, скорость движения стоков и уклон канализации на 1 метр СНиП. Ошибки при выборе последнего параметра могут вызвать существенные проблемы в работе автономной канализации.
Что такое угол наклона трубопровода?
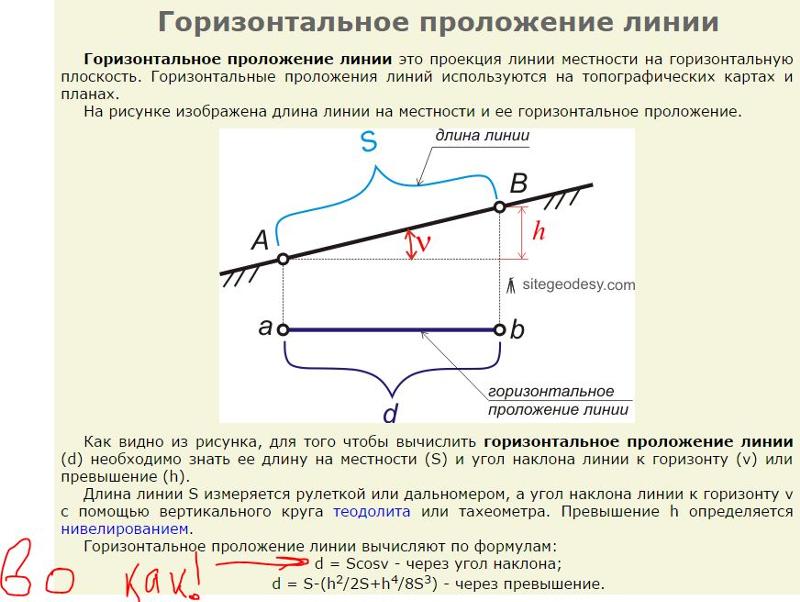
Монтаж труб канализации не должен выполняться по горизонту, а находится к нему под небольшим углом, значение которого определяют специальные нормативы. Для обозначения уклона трубы используется не привычная система градусов, здесь коэффициент определяется в сантиметрах на метр. Такая размерность позволяет избежать больших погрешностей при монтаже магистрали к септику. Длина такой ветки может составлять 10-12 метров и выдержать заданный угол очень сложно. Предложенное обозначение показывает – насколько один конец трубы длиной в 1 метр должен быть выше другого.
Такая размерность позволяет избежать больших погрешностей при монтаже магистрали к септику. Длина такой ветки может составлять 10-12 метров и выдержать заданный угол очень сложно. Предложенное обозначение показывает – насколько один конец трубы длиной в 1 метр должен быть выше другого.
Внимание. В справочной литературе уклон трубы обозначается простой или десятичной дробью. Например, коэффициент 0,03 означает уклон 3 см на 1 метр.
Соотношение диаметров труб и рекомендуемого уклона
Кроме рекомендованного уклона канализации на 1 метр, норматив определяет максимальный и минимальный показатель.
Максимальный уклон
Верхняя граница допустимого значения не должна превышать 0,15, это означает наклон погонного метра трубы на 15 см. Больший коэффициент может использоваться на коротких участках, примыкающих к сантехническим приборам. Необходимо учитывать скорость потока, она не может быть больше 1,4 м/с, иначе твердые фракции осядут на стенках магистрали.
Минимальный уклон
Минимальный показатель определен для каждого сечения трубы:
- 50 мм – 0,025;
- 100 мм – 0,012;
- 150 мм – 0,007;
- 200 мм – 0,005.
При несоблюдении этих показателей трубопровод быстро забьется. На отдельных участках, протяженностью не более 1 метра, допускается коэффициент 0,01.
Ошибки при выборе угла наклона труб
Нормальное функционирование системы отведения загрязненных вод обеспечивает сила тяжести, жидкость движется по трубам самотеком. При неверном выборе угла наклона возникают следующие сбои:
- Недостаточный уклон канализации – сточные воды двигаются медленно и застаиваются в трубе, что приводит к образованию засора. Особенно губительно такое явление для чугунных магистралей, которые подвергаются усиленной коррозии, возникают порывы и протечки.

- Большой угол наклона – ускорение потока приводит к недостаточной очистке труб, вода быстро уходит, а крупные фракции остаются на стенках. Работа такой магистрали сопровождается шумом и срывом водных затворов на сифонах.
Рекомендуемый коэффициент уменьшается с возрастанием диаметра трубы:
- 40-50 мм – 0,03;
- 100 мм – 0,02;
- 150 мм – 0,008;
- 200 мм – 0,007.
Ошибки при монтаже трубопровода
Как рассчитать степень наполненности трубопровода
Для стабильной работы канализации важны такие показатели:
- скорость течения стоков V;
- наполнение канализационной системы K.
K=H/D,
H – высота уровня сточных вод;
D – сечение канализации.
Рассчитав уровень наполненности магистрали, можно определить оптимальную скорость потока, при которой система будет функционировать без заиливания и мусорных засоров. Полная наполненность тубы составляет 1, при этом нарушается вентиляция системы, и могут сорваться гидрозатворы.
Совет. Описание последовательности расчетов и необходимые формулы берутся из СНиП 2.04.01-85.
Формула для расчета уклона труб
Скорость течения сливаемых отходов является ключевым параметром при вычислении оптимального уклона канализационной трубы. Ее минимальное значение составляет 0,7 м/с. Выполнить расчет для индивидуальной системы можно по формуле:
K – наполнение трубы, для полимерных материалов коэффициент – 0,5, для чугуна – 0,6;
d – сечение трубы;
V – скорость потока.
Из формулы следует, что соотношение скорости движения канализационных стоков к наполненности магистрали не должна быть меньше коэффициента K. В случае H/d=0 – канализация пуста, и скорость потока рассчитать невозможно.
Рекомендации по монтажу внутренней системы канализации
В квартирах и внутренней разводке частного дома используются трубы небольшого диаметра, кроме подключения унитаза. Уклон канализационной трубы 50 мм, используемой для ванны, раковины и душа, составляет 3 см на каждый метр. При монтаже магистрали длиной в 10 метров, ее самая высокая точка должна находиться в 30 см от самой низкой. Устраивая самостоятельно разводку, необходимо действовать согласно правилам:
- для горизонтальных труб не допускаются повороты в 90º, нужно устанавливать два фасонных элемента по 45º;
- соединение вертикальных участков под прямым углом допускается нормативами;
- исключаются изменения в типе канализационной разводки на ее различных участках, это приведет к выходу из строя всей системы в результате возникновения гидроударов;
- на отдельных частях магистрали, имеющих небольшое расстояние, возможно увеличение уклона больше максимальной нормы.
Схема размещения сантехники с уклоном труб
Угол уклона для наружной инженерной сети
Наружные сети монтируются из труб большего сечения, чем внутридомовая разводка. Материалом для них служит:
Материалом для них служит:
- полиэтиленовая труба с верхним гофрированным слоем;
- пластик;
- чугун;
- асбестоцемент.
Их установка согласно нормам СНиП должна учитывать уровень промерзания почвы. Глубина траншеи может составлять от 70 см в средней полосе до 2 метров в холодных регионах. В местах поворота трубопровода и при длине магистрали более 12 метров, необходимо устанавливать ревизионные колодцы, эти элементы позволят прочистить засоры в системе.
Для загородного дома с двумя санузлами используется трубами диаметром 110 мм, если в доме три туалета и более, рекомендуется прокладка трубопровода сечением 160 мм. При выкапывании траншеи оставляется запас до 20 см для выравнивания трубы до рекомендуемого угла уклона. Каждый размер магистрали имеет свой рекомендованный коэффициент уклона:
- 110 мм – 0,02 или 2 см на 1 метр;
- 160 мм – 0,008 или 8 мм на 1 метр.
Совет. При монтаже наружной магистрали следует ограничить число поворотов, увеличивающих угол наклона.
Из-за рельефа могут возникнуть сложности с обеспечением необходимого уклона.
Прокладывание наружной магистрали
Соблюдение нормативов позволяет сохранять работоспособность магистрали при движении нечистот самотеком. Оптимальным прибором для определения правильного уклона является нивелир, используя его можно добиться высокой точности. Но такое устройство есть не у всех, поэтому найдены способы проверки с помощью подручных средств. Для измерения понадобится:
- шнур или веревка;
- два колышка;
- строительный уровень.
В прокопанной траншее забиваются колышки – один в начале, а второй в конце. Между ними натягивается шнур и с помощью строительного уровня выставляется по горизонту. Затем измеряется глубина траншеи до шнура в начальной точке и в конечной. Разница между этими значениями, деленная на длину трубопровода должна составить искомую величину наклона канализационной трубы на 1 погонный метр. Подогнать значение под нужный показатель, можно углубив или подсыпав песок на дно.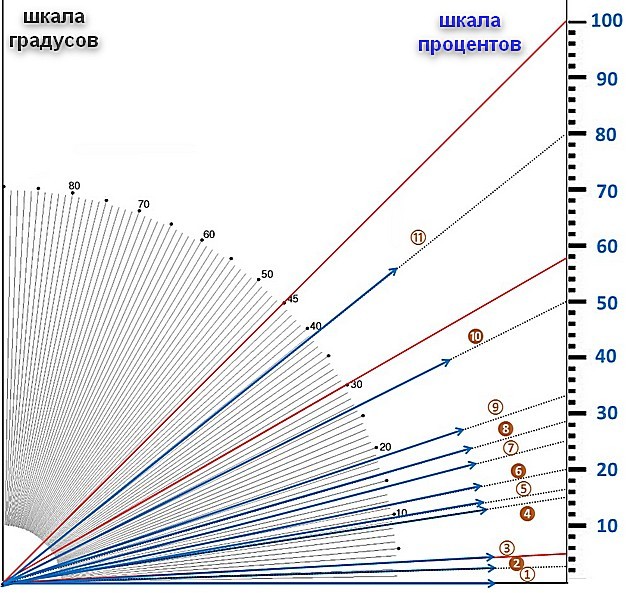
Если природный рельеф участка существенно превышает нормативный показатель, можно смонтировать магистраль двумя способами:
- создать систему, включающую несколько вертикальных переходов и горизонтальных участков, уложенных с рекомендованным уклоном;
- выкопать глубокую траншею, в которой разместится один вертикальный отрезок в начале трубопровода, остальная часть будет уложена по нормативному уклону.
Соблюдение правильного уклона при монтаже трубопровода внутри и снаружи частного дома обеспечит бесперебойную работу автономной канализации.
Не забудьте оценить статью:
2020_07_ДФ_Каталог_Уклон
%PDF-1.6
%
1 0 obj
>]/Pages 3 0 R/Type/Catalog>>
endobj
2 0 obj
>stream
2020-07-21T10:32:46+04:00Adobe Illustrator 24.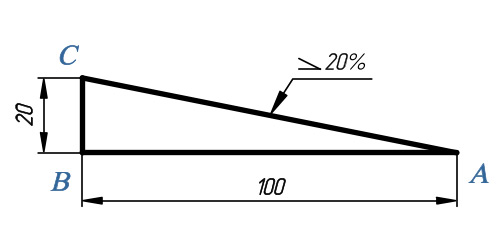 1 (Windows)2020-07-21T10:32:46+03:002020-07-21T10:32:46+03:00
1 (Windows)2020-07-21T10:32:46+03:002020-07-21T10:32:46+03:00
 00Falseapplication/pdf
00Falseapplication/pdf 062;PS 2.000;hotconv 1.0.57;makeotf.lib2.0.21895FalseMyriadPro-Bold.otf
062;PS 2.000;hotconv 1.0.57;makeotf.lib2.0.21895FalseMyriadPro-Bold.otf 0 0.0 595.276 841.89]/Type/Page>>
endobj
32 0 obj
>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
33 0 obj
>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
34 0 obj
>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
35 0 obj
>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
36 0 obj
>/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
58 0 obj
>stream
HWMo%I_G,j+3 NāA -H =mm
_WGfdddV=ܾ?n?~ψbxz8~ٶҢwoQỴ>߾l.uG?2םG1,Ρj/s/}c4XZXomea_Vwl{34sE%*7+7vhɼLwVڂ.ʜ~Zw?_k
r/5s”ཊM[٭Vnw{;asŋ’f6`(6?UKEp8x?”:uFtw%j2#V[no,Yfao|Ǣ%>]t>3-8
0 0.0 595.276 841.89]/Type/Page>>
endobj
32 0 obj
>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
33 0 obj
>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
34 0 obj
>/Font>/ProcSet[/PDF/Text/ImageC]/XObject>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
35 0 obj
>>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
36 0 obj
>/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 595.276 841.89]/Type/Page>>
endobj
58 0 obj
>stream
HWMo%I_G,j+3 NāA -H =mm
_WGfdddV=ܾ?n?~ψbxz8~ٶҢwoQỴ>߾l.uG?2םG1,Ρj/s/}c4XZXomea_Vwl{34sE%*7+7vhɼLwVڂ.ʜ~Zw?_k
r/5s”ཊM[٭Vnw{;asŋ’f6`(6?UKEp8x?”:uFtw%j2#V[no,Yfao|Ǣ%>]t>3-813.
 2.1: Определение наклона линии
2.1: Определение наклона линии- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 70402
- Проект NROC
Цели обучения
- Найти наклон линии на графике.
- Найдите наклон прямой через две точки.
- Найдите наклон линий \(\ x=a\) и \(\ y=b\).
Введение
С понятием уклона часто приходится сталкиваться в повседневной жизни. Подумайте о том, чтобы скатить тележку по пандусу или подняться по лестнице. Пандус и лестница имеют уклон. Вы можете описать наклон или крутизну пандуса и лестницы, рассматривая горизонтальное и вертикальное перемещение по ним. В разговоре вы используете такие слова, как «постепенный» или «крутой», чтобы описать уклон.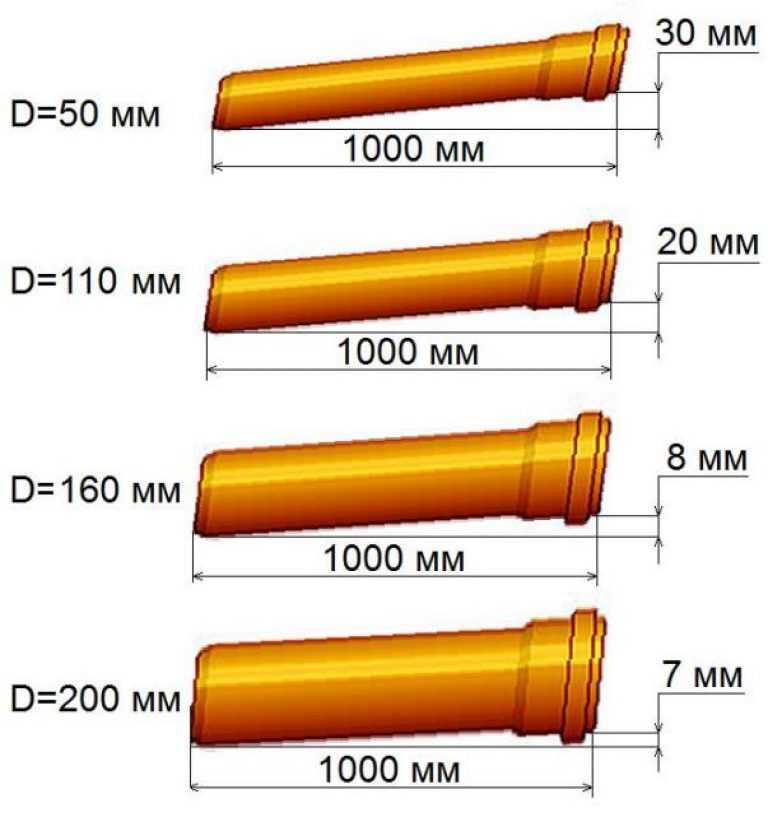 Вдоль постепенного склона большая часть движения горизонтальная. Вдоль крутого склона вертикальное перемещение больше.
Вдоль постепенного склона большая часть движения горизонтальная. Вдоль крутого склона вертикальное перемещение больше.
Определение уклона
Математическое определение уклона очень похоже на наше повседневное определение. В математике наклон используется для описания крутизны и направления линий. Просто взглянув на график линии, вы можете кое-что узнать о ее наклоне, особенно относительно других линий, построенных на той же координатной плоскости. Рассмотрим графики трех линий, показанных ниже:
Сначала давайте посмотрим на линии A и B. Если бы вы представили эти линии холмами, вы бы сказали, что линия B круче, чем линия A. Линия B имеет большую уклон, чем линия A.
Далее обратите внимание на то, что линии A и B наклоняются вверх при движении слева направо. Мы говорим, что эти две линии имеют положительный наклон. Линия C наклонена вниз слева направо. Линия C имеет отрицательный наклон. Используя две точки на линии, вы можете найти наклон линии, найдя подъем и бег. Вертикальное изменение между двумя точками называется подъемом , а горизонтальное изменение называется прогоном . Уклон равен подъёму, деленному на длину пробега: \(\ \text {Slope}=\frac{\text {rise}}{\text {run}}\).
Вертикальное изменение между двумя точками называется подъемом , а горизонтальное изменение называется прогоном . Уклон равен подъёму, деленному на длину пробега: \(\ \text {Slope}=\frac{\text {rise}}{\text {run}}\).
Определение наклона линии по графику
Вы можете определить наклон линии по графику, глядя на подъем и бег. Одной из характеристик линии является то, что ее наклон постоянен на всем ее протяжении. Таким образом, вы можете выбрать любые 2 точки на графике линии, чтобы вычислить наклон. Давайте посмотрим на пример.
Пример
Используйте график, чтобы найти наклон линии.
Решение
| \(\ \текст {рост}=2\) | Начните с точки на линии, например (2, 1), и двигайтесь вертикально, пока не совпадете с другой точкой на линии, например (6, 3). Подъем 2 единицы. Это положительно, поскольку вы продвинулись вверх. |
| \(\ \текст {выполнить}=4\) | Далее двигайтесь горизонтально к точке (6, 3). Подсчитайте количество единиц. Пробег 4 единицы. Это положительно, поскольку вы переместились вправо. |
| \(\ \text { Наклон }=\frac{2}{4}=\frac{1}{2}\) | \(\ \text {Наклон}=\frac{\text {подъем}}}{\text {бег}}\) |
Наклон равен \(\ \frac{1}{2}\).
Эта линия будет иметь наклон \(\ \frac{1}{2}\) независимо от того, какие две точки вы укажете на линии. Попробуйте измерить наклон от начала координат (0, 0) до точки (6, 3). Вы обнаружите, что \(\ \text {rise }=3\) и \(\ \text{run }=6\). Наклон равен \(\ \frac{ подъем }{r u n}=\frac{3}{6}=\frac{1}{2}\). Это то же самое!
Давайте рассмотрим другой пример.
Пример
Используйте график, чтобы найти наклон двух линий.
Решение
Обратите внимание, что обе эти линии имеют положительный наклон, поэтому вы ожидаете, что ваши ответы будут положительными. | |
| \(\ \текст { подъем }=4\) | Синяя линия 909:45 Начните с синей линии, идущей от точки (-2, 1) к точке (-1, 5). Эта линия имеет подъем на 4 единицы вверх, поэтому она положительна. |
| \(\ \text{run}=1\) | Пробег на 1 единицу вправо, поэтому он положительный. |
| \(\ \text {Наклон}=\frac{4}{1}=4\) | Подставьте значения подъема и пробега в формулу \(\ \text {Наклон}=\frac{\text {подъем}}{\text {бег}}\). |
| \(\ \текст {подъем}=1\) | Красная линия Красная линия, идущая от точки (-1, -2) к точке (3, -1), поднимается на 1 единицу. |
| \(\ \text{run}=4\) | Красная линия имеет пробег 4 единицы. |
| \(\ \text {Уклон }=\frac{1}{4}\) | Подставьте значения для подъема и спуска в формулу \(\ \text {Slope}=\frac{\text {rise}}{\text{run}}\). |
Наклон синей линии равен 4, а наклон красной линии равен \(\ \frac{1}{4}\).
Если вы посмотрите на две линии, вы увидите, что синяя линия круче, чем красная. Имеет смысл значение наклона синей линии, 4, больше, чем значение наклона красной линии, \(\ \frac{1}{4}\). Чем больше наклон, тем круче линия.
В следующем примере показана линия с отрицательным наклоном.
Пример
Найдите наклон линии на графике ниже.
Решение
| \(\ \text { подъем }=-3\) | Начните с точки А, (0, 4) и поднимитесь на -3. Это означает перемещение на 3 единицы в отрицательном направлении. |
| \(\ \text{run}=2\) | Оттуда пройдите 2 единицы в положительном направлении до точки B (2, 1). |
| \(\ \text { Наклон }=\frac{-3}{2}\) | \(\ \text {Наклон}=\frac{\text {подъем}}}{\text {бег}}\) |
Наклон линии равен \(\ -\frac{3}{2}\).
При определении уклона важно направление. Важно обращать внимание на то, двигаетесь ли вы вверх, вниз, влево или вправо; то есть, если вы движетесь в положительном или отрицательном направлении. Если вы идете вверх, чтобы добраться до второй точки, подъем положительный. Если вы спуститесь вниз, чтобы добраться до второй точки, подъем будет отрицательным. Если вы идете прямо, чтобы добраться до второй точки, пробег положительный. Если вы пойдете налево, чтобы добраться до второй точки, пробег будет отрицательным. В приведенном выше примере вы могли бы найти наклон, начав с точки B, пробежав -2, а затем поднявшись на +3, чтобы добраться до точки A. Результатом по-прежнему будет наклон \(\ \frac{r i s e}{r u n} =\frac{+3}{-2}=-\frac{3}{2}\).
Расширенный пример
Найдите наклон линии на графике ниже.
Решение
| \(\ \text {подъем}=4,5\) | Начните с (-3, -0,25) и поднимите 4,5. Это означает перемещение на 4,5 единицы в положительном направлении. Это означает перемещение на 4,5 единицы в положительном направлении. |
| \(\ \text {run}=6\) | Отсюда бегите 6 единиц в положительном направлении к (3, 4.25). |
| \(\ \text {Уклон }=\frac{4.5}{6}=0.75\) | \(\ \text {Наклон}=\frac{\text {подъем}}}{\text {бег}}\) |
Наклон линии 0,75.
Глядя на уравнения
Наклон линии иногда можно быстро определить из ее уравнения. Рассмотрим прямую, уравнение которой равно \(\ y=5 x\). Вы можете создать таблицу значений, чтобы найти три точки на линии.
| \(\ х\) | \(\у\) |
| -1 | -5 |
| 0 | 0 |
| 2 | 10 |
Нанеся эти точки на график, создайте график линии и определите наклон.
При движении от точки (-1, -5) к точке (2, 10) линия имеет подъем 15 и длину 3, поэтому наклон линии равен \(\ \ frac{15}{3}=5\). Обратите внимание, что число 5 также появляется в уравнении: \(\ y=5 x\).
Всякий раз, когда уравнение прямой записывается в форме \(\ y=m x+b\), оно называется формой уравнения с пересечением наклона. \(\ m\) – это наклон линии. И \(\ b\) – это \(\ b\) в точке, которая является y-пересечением \(\ (0, b)\).
Например, для уравнения \(\ y=3 x-7\) наклон равен 3, а точка пересечения с осью y равна (0, -7).
Что если уравнение будет записано в виде \(\ 2 y=5 x+1\)? Тогда вы должны переписать уравнение в виде \(\ y=m x+b\). Найдите \(\ у\).
\(\ 2 y=5 x+1\)
\(\ y=\frac{5}{2} x+\frac{1}{2}\) разделить обе части уравнения на 2.
Наклон равен \(\ \frac{5}{2}\), а точка пересечения по оси Y равна \(\ \left(0, \frac{1}{2}\right)\).
Упражнение
Каков наклон прямой, уравнение которой \(\ y=-2 x+7\)?
- 7
- 2
- -2
- \(\ -\frac{7}{2}\)
- Ответить
- Неверно.
 Наклон линии, записанной в \(\ y=m x+b\), определяется коэффициентом при \(\ x\). Правильный ответ -2.
Наклон линии, записанной в \(\ y=m x+b\), определяется коэффициентом при \(\ x\). Правильный ответ -2. - Неверно. Наклон линии, записанной в \(\ y=m x+b\), определяется коэффициентом при \(\ x\). Коэффициент равен -2. Правильный ответ -2.
- Правильно. Наклон линии, записанной в \(\ y=m x+b\), определяется коэффициентом при \(\ x\). Для этой линии коэффициент или \(\ m\), наклон равен -2.
- Неверно. Наклон линии, записанной в \(\ y=m x+b\), определяется коэффициентом при \(\ x\). Коэффициент равен -2. Правильный ответ -2.
- Неверно.
Нахождение наклона линии по двум точкам
Вы видели, что можно найти наклон линии на графике, измеряя подъем и спуск. Вы также можете найти наклон прямой линии без ее графика, если вам известны координаты любых двух точек на этой линии. Каждая точка имеет набор координат: значение x и значение y, записанные в виде упорядоченной пары (x, y). Значение x говорит вам, где точка находится по горизонтали. Значение y говорит вам, где точка находится по вертикали.
Значение x говорит вам, где точка находится по горизонтали. Значение y говорит вам, где точка находится по вертикали.
Рассмотрим две точки на прямой — точку 1 и точку 2. Точка 1 имеет координаты \(\ \left(x_{1}, y_{1}\right)\), а точка 2 имеет координаты \(\ \left( x_{2}, y_{2}\справа)\).
Высота — это расстояние по вертикали между двумя точками, представляющее собой разницу между их координатами Y. Это делает рост \(\ y_{2}-y_{1}\). Пробег между этими двумя точками — это разница координат x, или \(\ x_{2}=x_{1}\).
Итак, \(\ \text {Наклон}=\frac{\text {подъем}}{\text {бег}}\) или \(\ m=\frac{y_{2}-y_{1}} {х_{2}-х_{1}}\)
В приведенном ниже примере вы увидите, что на линии есть две точки, каждая из которых указана как упорядоченная пара. Точка (0, 2) обозначена как точка 1, а (-2, 6) — как точка 2. Таким образом, вы собираетесь двигаться из точки 1 в точку 2. Над линией нарисован треугольник, чтобы проиллюстрировать подъем. и беги.
На графике видно, что подъем из точки 1 в точку 2 равен 4, потому что вы двигаетесь на 4 единицы в положительном направлении (вверх).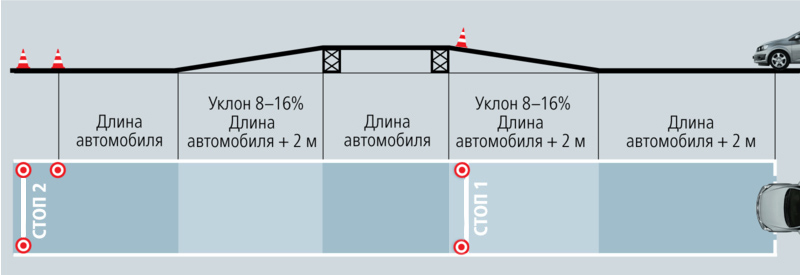 Пробег равен -2, потому что вы двигаетесь в отрицательном направлении (влево) на 2 единицы. Используя формулу наклона, \(\ \text {Slope}=\frac{r i s e}{r u n}=\frac{4}{-2}=-2\).
Пробег равен -2, потому что вы двигаетесь в отрицательном направлении (влево) на 2 единицы. Используя формулу наклона, \(\ \text {Slope}=\frac{r i s e}{r u n}=\frac{4}{-2}=-2\).
Вам не нужен график, чтобы найти наклон. Вы можете просто использовать координаты, тщательно отслеживая, какая точка является точкой 1, а какая точкой 2. Давайте систематизируем информацию о двух точках:
| Имя | Заказная пара | Координаты |
| Точка 1 | (0, 2) | \(\ \begin{array}{r} x_{1}=0 \\ y_{1}=2 \end{массив}\) |
| Точка 2 | (-2, 6) | \(\ \begin{выровнено} x_{2}&=-2 \\ y_{2}&=6 \end{выровнено}\) |
Наклон, \(\ m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{6-2}{-2-0} =\frac{4}{-2}=-2\).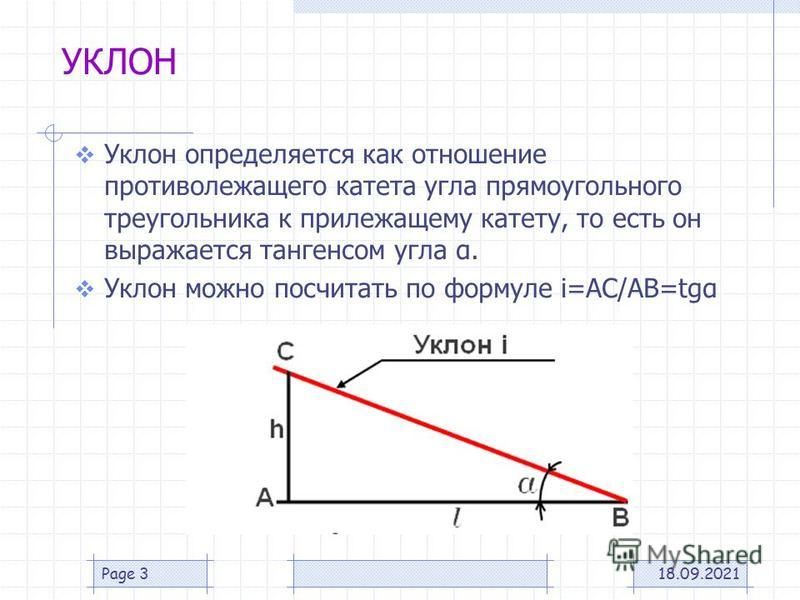 Наклон линии \(\ m\) равен -2.
Наклон линии \(\ m\) равен -2.
Не имеет значения, какая точка обозначена как Точка 1, а какая Точка 2. Вы могли бы назвать (-2, 6) Точку 1 и (0, 2) Точку 2. В этом случае, вводя координаты в формула наклона дает уравнение \(\ m=\frac{2-6}{0-(-2)}=\frac{-4}{2}=-2\). Еще раз наклон \(\m=-2\). Это тот же наклон, что и раньше. Важно соблюдать последовательность при вычитании: вы всегда должны вычитать в одном и том же порядке \(\ y_{2}-y_{1}\) и \(\ x_{2}-x_{1}\).
Пример
Каков наклон линии, содержащей точки (5, 5) и (4, 2)?
Решение
| \(\ \begin{align} x_{1}&=4 \\ y_{1}&=2 \end{align}\) | \(\ (4,2)=\текст {точка} 1,\влево(x_{1}, y_{1}\вправо)\) |
| \(\ \begin{выровнено} x_{2}&=5 \\ y_{2}&=5 \end{выровнено}\) | \(\ (5,5)=\text { Точка } 2,\left(x_{2}, y_{2}\right)\) |
| \(\ \begin{align} м&=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ м&=\frac{5-2} {5-4}=\frac{3}{1}\\ м&=3 \end{выровнено}\) | Подставьте значения в формулу наклона и упростите. |
Наклон равен 3.
В приведенном ниже примере показано решение, когда вы меняете порядок точек, называя (5, 5) точку 1 и (4, 2) точку 2.
Пример
Что наклон линии, содержащей точки (5, 5) и (4, 2)?
Решение
| \(\ \begin{align} x_{1}&=5 \\ y_{1}&=5 \end{align}\) | \(\ (5,5)=\текст {точка} 1,\влево(x_{1}, y_{1}\вправо)\) |
| \(\ \begin{выровнено} x_{2}=4 \\ y_{2}=2 \end{выровнено}\) | \(\ (4,2)=\текст {точка} 2,\влево(x_{2}, y_{2}\вправо)\) |
| \(\ \begin{align} м&=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ м&=\frac{2-5}{4-5}=\frac{-3}{-1}=3 \\ м&=3 \end{выровнено}\) | Подставьте значения в формулу наклона и упростите. |
Наклон равен 3.
Обратите внимание, что независимо от того, какая упорядоченная пара названа точкой 1, а какая — точкой 2, наклон по-прежнему равен 3.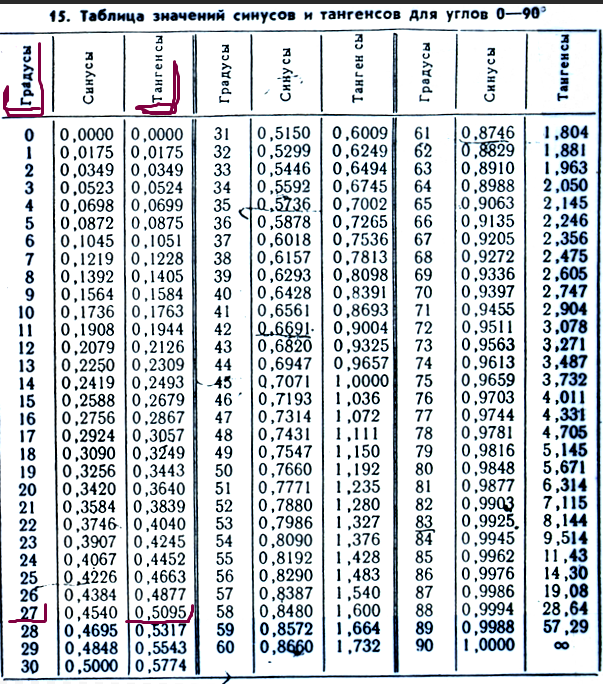
Расширенный пример
Каков наклон линии, содержит точки (3, -6,25) и (-1, 8,5)?
Решение
| \(\ \begin{align} x_{1}&=3 \\ y_{1}&=-6.25 \\ x_{2}&=-1 \\ у_{2}&=8,5 \конец{выровнено}\) | \(\ (3,-6.25)=\текст {точка} 1, (x_1, y_1)\) \(\ \begin{array}{l} |
| \(\ \begin{align} м&=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ м&=\frac{8.5-(-6.25)}{-1-3} \\ м&=\frac{14.75}{-4} \\ м&=-3.6875 \end{выровнено}\) | Подставьте значения в формулу наклона и упростите. |
Наклон равен -3,6875.
Упражнение
Каков наклон линии, включающей точки (-5, 1) и (-2, 3)
- \(\ \frac{2}{3}\)
- \(\ -\frac{2}{7}\)
- \(\ -\frac{2}{3}\)
- \(\ \frac{3}{2}\)
- Ответить
- Правильно.
 \(\ m=\frac{3-1}{-2-(-5)}=\frac{2}{3}\)
\(\ m=\frac{3-1}{-2-(-5)}=\frac{2}{3}\) - Неверно. Знаменатель равен \(\-2-(-5)\), \(\-2-5\). Правильный ответ
- Неверно. Подставьте координаты в формулу уклона последовательно: \(\ \frac{y_{2}-y_{1}}{x_{2}-x_{1}}\). Правильный ответ: \(\ m=\frac{3-1}{-2-(-5)}=\frac{2}{3}\).
- Неверно. Вы поменяли местами подъем и бег. Правильный ответ: \(\ m=\frac{3-1}{-2-(-5)}=\frac{2}{3}\).
- Правильно.
Расширенный вопрос
Каков наклон линии, включающей точки \(\ \left(5,-\frac{1}{5}\right)\) и \(\ \left(-3, \ frac{3}{5}\right)\)?
- \(\-10\)
- \(\ \фракция{8}{25}\)
- \(\ -\frac{1}{20}\)
- \(\ -\frac{1}{10}\)
- Ответить
- Неверно. Похоже, вы перепутали подъем и бег. Используйте формулу \(\ m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\), чтобы найти наклон. Правильный ответ: \(\ -\frac{1}{10}\).

- Неверно. Похоже, вы вычли координаты \(\y\) или \(\x\) в неправильном порядке. Убедитесь, что вы вычитаете \(\ y_{2}=y_{1}\), затем \(\ x_{2}-x_{1}\), а затем вычисляете наклон. Правильный ответ: \(\ -\frac{1}{10}\).
- Неверно. Похоже, вы вычли координаты \(\y\) или \(\x\) в неправильном порядке. Убедитесь, что вы вычитаете \(\ y_{2}=y_{1}\), затем \(\ x_{2}-x_{1}\), а затем вычисляете наклон. Правильный ответ: \(\ -\frac{1}{10}\).
- Правильно. Используя формулу для наклона \(\ m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\), вы обнаружили, что \(\ m=\frac{\ frac{3}{5}-\left(-\frac{1}{5}\right)}{-3-5}=\frac{\frac{4}{5}}{-8}=\frac {4}{5} \div(-8)=\frac{4}{5} \cdot \frac{1}{-8}=-\frac{4}{40}=-\frac{1}{ 10}\).
- Неверно. Похоже, вы перепутали подъем и бег. Используйте формулу \(\ m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\), чтобы найти наклон. Правильный ответ: \(\ -\frac{1}{10}\).
Нахождение наклонов горизонтальных и вертикальных линий
До сих пор вы рассматривали линии, которые проходят «в гору» или «вниз». Их склоны могут быть крутыми или пологими, но они всегда являются положительными или отрицательными числами. Но есть еще два вида линий, горизонтальные и вертикальные. Каков уклон плоской линии или ровной поверхности? Стены или вертикальной линии?
Но есть еще два вида линий, горизонтальные и вертикальные. Каков уклон плоской линии или ровной поверхности? Стены или вертикальной линии?
Рассмотрим горизонтальную линию на графике. Независимо от того, какие две точки вы выберете на линии, они всегда будут иметь одну и ту же координату y. Уравнение для этой линии \(\ y=3\). Уравнение также можно записать в виде \(\ y=(0) x+3\).
Используя форму \(\ y=0 x+3\), вы можете видеть, что наклон равен 0. Вы также можете использовать формулу наклона с двумя точками на этой горизонтальной линии, чтобы вычислить наклон этой горизонтальной линии . Используя \(\ (-3,3)\) в качестве точки 1 и \(\ (2,3)\) в качестве точки 2, вы получите:
\(\ \begin{array}{c}
м=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\
м=\frac{3- 3}{2-(-3)}=\frac{0}{5}=0
\end{array}\)
Наклон этой горизонтальной линии равен 0.
Рассмотрим любую горизонтальную линию. Независимо от того, какие две точки вы выберете на линии, они всегда будут иметь одну и ту же координату y. Таким образом, когда вы применяете формулу наклона, числитель всегда будет равен 0. Ноль, деленный на любое ненулевое число, равен 0, поэтому наклон любой горизонтальной линии всегда равен 0.
Таким образом, когда вы применяете формулу наклона, числитель всегда будет равен 0. Ноль, деленный на любое ненулевое число, равен 0, поэтому наклон любой горизонтальной линии всегда равен 0.
Уравнение для горизонтальной линии \(\ y=3\) говорит вам, что независимо от того, какие две точки вы выберете на этой линии, координата y всегда будет равна 3.
Как насчет вертикальных линий? В их случае, независимо от того, какие две точки вы выберете, они всегда будут иметь одну и ту же координату x. Уравнение для этой линии \(\ x=2\).
Невозможно представить это уравнение в виде точки наклона, поскольку коэффициент при \(\ y\) равен 0 \(\ (x=0 y+2)\).
Итак, что происходит, когда вы используете формулу уклона с двумя точками на этой вертикальной линии для расчета уклона? Используя \(\ (2,1)\) в качестве точки 1 и \(\ (2, 3)\) в качестве точки 2, вы получите:
\(\ \begin{array}{c}
м=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\
м=\frac{3- 1}{2-2}=\frac{2}{0}
\end{array}\)
Но деление на ноль не имеет смысла для множества действительных чисел.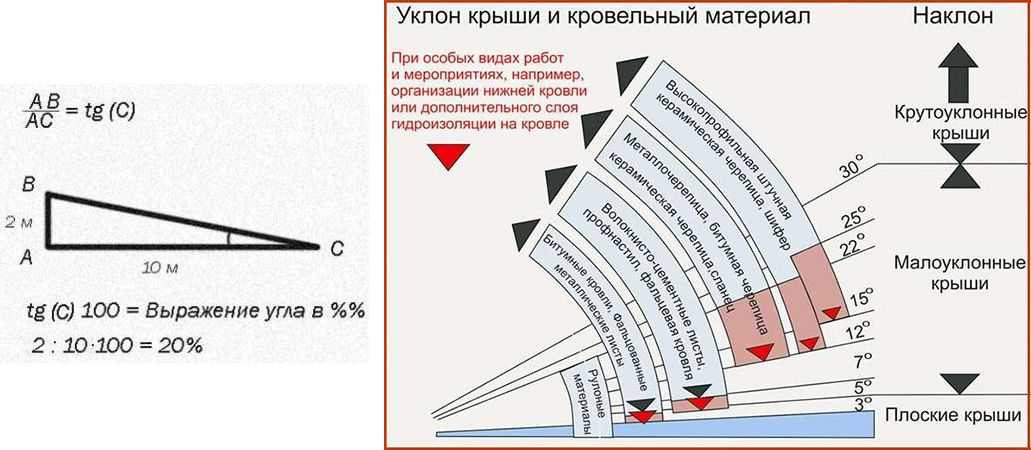 Из-за этого факта говорят, что наклон этой вертикальной линии не определен. Это верно для всех вертикальных линий — все они имеют неопределенный наклон.
Из-за этого факта говорят, что наклон этой вертикальной линии не определен. Это верно для всех вертикальных линий — все они имеют неопределенный наклон.
Пример
Каков наклон линии, содержащей точки (3, 2) и (-8, 2)?
Решение
| \(\ \begin{array}{l} x_{1}=3 \\ y_{1}=2 \end{array}\) | \(\ (3,2)=\текст {точка} 1,\влево(x_{1}, y_{1}\вправо)\) |
| \(\ \begin{array}{c} x_{2}=-8 \\ y_{2}=2 \end{массив}\) | \(\ (-8,2)=\текст {точка} 2,\влево(x_{2}, y_{2}\вправо)\) |
| \(\ \begin{array}{r} \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ \frac{(2)-(2)}{(-8)-(3)}=\frac{0}{-11}=0 \\ м=0 \end{массив}\) | Подставьте значения в формулу наклона и упростите. |
Наклон равен 0, поэтому линия горизонтальна.
Расширенный вопрос
Какая из следующих точек будет лежать на линии, образованной точками \(\ (-3,75,6,25)\) и \(\ (-3,75,0)\)?
- \(\ (0,-3,75)\)
- \(\ (-3,75,-14,55)\)
- \(\ (3,75,-6,25)\)
- \(\(0,6.
 25)\)
25)\)
- Ответить
- Неверно. Обратите внимание, что обе точки на линии имеют одинаковую координату x, но разные координаты y. Это делает ее вертикальной линией, поэтому любые другие точки на линии будут иметь x-координату -3,75. Правильный ответ: \(\ (-3,75,-14,55)\).
- Правильно. Точки \(\ (-3,75,6,25)\) и \(\ (-3,75,0)\) образуют вертикальную линию, поэтому любая другая точка на этой линии должна иметь координату x -3,75.
- Неверно. Попробуйте быстро нарисовать точки \(\ (-3,75,6,25)\) и \(\ (-3,75,0)\). Они образуют вертикальную линию, поэтому любые другие точки на линии будут иметь координату x -3,75. Правильный ответ: \(\ (-3,75,-14,55)\).
- Неверно. Обратите внимание, что обе точки на линии имеют одинаковую координату x, но разные координаты y. Это делает ее вертикальной линией, поэтому любые другие точки на линии будут иметь x-координату -3,75.
 Правильный ответ: (-3,75,-14,55).
Правильный ответ: (-3,75,-14,55).
Сводка
Наклон описывает крутизну линии. Наклон любой линии остается постоянным вдоль линии. Наклон также может сообщить вам информацию о направлении линии на координатной плоскости. Наклон можно рассчитать либо по графику линии, либо по координатам любых двух точек на линии. Есть две общие формулы для уклона: \(\ \text {Slope}=\frac{\text {rise}}{\text{run}}\) и \(\ m=\frac{y_{2}-y_ {1}}{x_{2}-x_{1}}\), где \(\ m=\text { наклон }\) и \(\ \left(x_{1}, y_{1}\right)\ ) и \(\ \left(x_{2}, y_{2}\right)\) — две точки на прямой.
На изображениях ниже показаны наклоны различных типов линий.
Эта страница под названием 13.2.1: Поиск наклона линии используется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована проектом NROC с помощью исходного контента, который был отредактирован в соответствии со стилем. и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

 Из-за рельефа могут возникнуть сложности с обеспечением необходимого уклона.
Из-за рельефа могут возникнуть сложности с обеспечением необходимого уклона. Наклон линии, записанной в \(\ y=m x+b\), определяется коэффициентом при \(\ x\). Правильный ответ -2.
Наклон линии, записанной в \(\ y=m x+b\), определяется коэффициентом при \(\ x\). Правильный ответ -2. \(\ m=\frac{3-1}{-2-(-5)}=\frac{2}{3}\)
\(\ m=\frac{3-1}{-2-(-5)}=\frac{2}{3}\)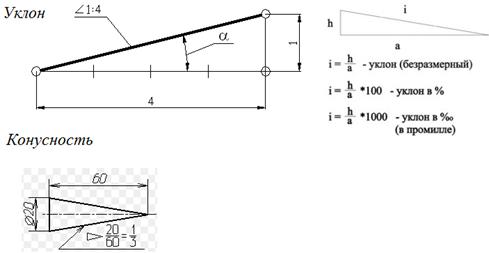
 25)\)
25)\) Правильный ответ: (-3,75,-14,55).
Правильный ответ: (-3,75,-14,55).