Уклон дороги в процентах как считать: Что означает уклон в процентах, и как перевести его в градусы

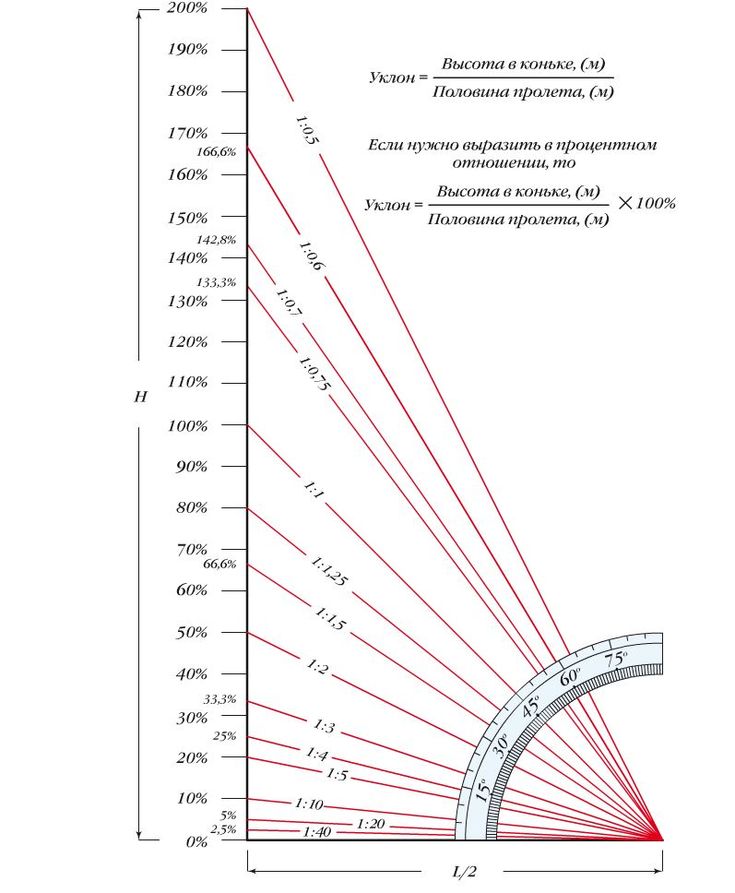
Что означает уклон в процентах, и как перевести его в градусы

Когда идет речь о кровле зданий, то под словом «уклон» подразумевают угол наклона оболочки крыши к горизонту. В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.

Расчет уклона в процентах

Попробуйте представить прямоугольный треугольник АВС, лежащей на одном из своих катетов АВ. Второй катет ВС будет направлен вертикально вверх, а гипотенуза АС образует с нижним катетом некий угол. Теперь нам предстоит немножко вспомнить тригонометрию и рассчитать его тангенс, который как раз и будет характеризовать уклон, образуемый гипотенузой треугольника с нижним катетом. Предположим, что катет АВ = 100 мм, а высота ВС = 36,4 мм. Тогда тангенс нашего угла будет равен 0,364, что по таблицам соответствует 20˚. Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.

Как понимать угол уклона в процентах?

Если дорожный знак показывает 12%, то это означает, что на каждом километре такого подъема или спуска дорога будет подыматься (опускаться) на 120 метров. Чтобы перевести процентное значение в градусы, нужно попросту вычислить арктангенс этого значения и при необходимости перевести его из радиан в привычные градусы. То же самое касается и строительных чертежей. Если, к примеру, указывается, что угол уклона в процентах равен 1, то это означает, что соотношение одного катета к другому равно 0,01.

Почему не в градусах?

Многих наверняка интересует вопрос: «Зачем для уклона использовать еще какие-то проценты?» Действительно, почему бы просто не обойтись одними градусами.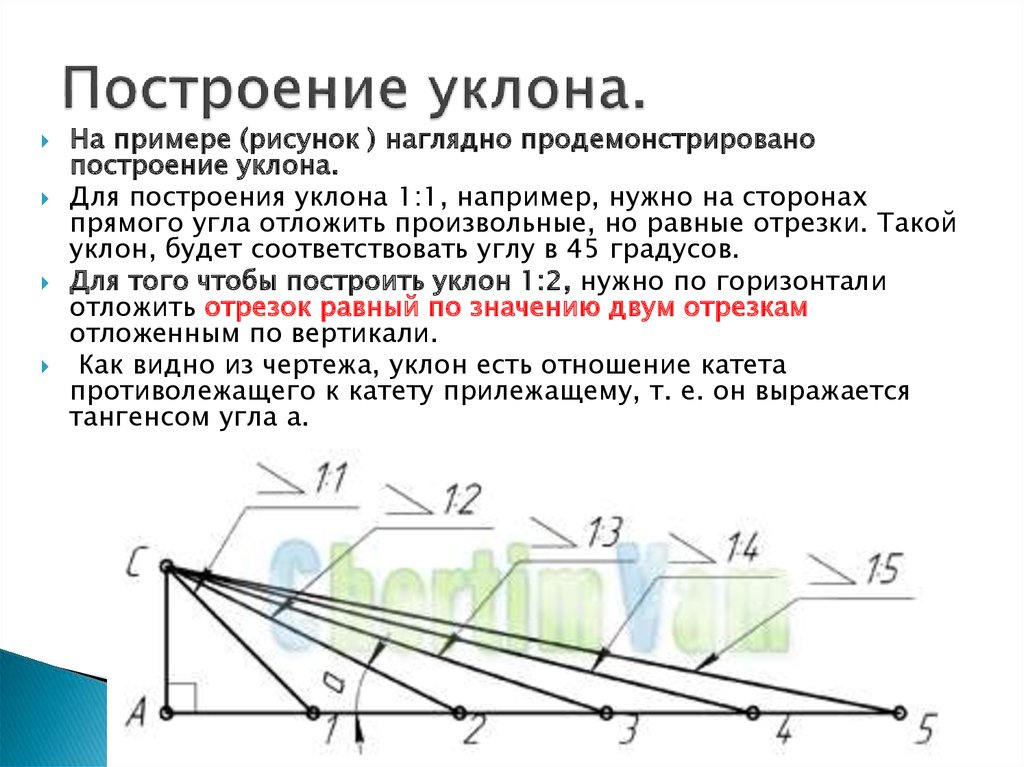 Дело в том, что при любых измерениях всегда имеет место некоторая погрешность. Если в проектной документации станут применять градусы, то неминуемо возникнут сложности с монтажом. Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.

Применение на практике

Предположим, что проект строительства загородного дома предполагает устройство скатной кровли. Требуется проверить ее уклон в процентах и градусах, если известно, что высота конька составляет 3.45 метра, а ширина будущего жилища равна 10 метрам. Так как спереди крыша представляет собой равносторонний треугольник, то ее можно разделить на два прямоугольных треугольника, в которых высота конька будет являться одним из катетов. Второй катет находим, разделив ширину дома пополам.

Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan^-1(0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.

Основные методы измерения геометрических параметров горной дороги

Цитировать:

Эшанбабаев А.А., Купайсинов Д. Основные методы измерения геометрических параметров горной дороги // Universum: технические науки : электрон. научн. журн. 2021. 2(83). URL: https://7universum.com/ru/tech/archive/item/11266 (дата обращения: 27.10.2022).

Прочитать статью:

 

DOI: 10.32743/UniTech.2021.83.2-2.22-24

 

АННОТАЦИЯ

В данной статье приведены сведения о работе по измерению вертикального уклона (высоты) дороги и радиуса кривизны в плане по геометрическим элементам продольного плана и профиля горной дороги простым методом и результаты исследований.

ABSTRACT

This article contains information about the work of measuring the vertical slope (height) of the road and the radius of curvature in the plan from the geometric elements of the longitudinal plan and profile of the mountain road by a simple method and the results of research.

 

Ключевые слова: горная дорога, транспортный поток, продольный и поперечный уклон дороги, радиус кривизны, плоская кривизна, элементы дороги, скорость, интервал, шоссе.

Keywords: mountain road, traffic flow, longitudinal and transverse road slope, curvature radius, plan curvature, road elements, speed, interval, highway.

Экспериментальное  изучение движения транспортных потоков в реальных горно-дорожных условиях весьма сложно и требует значительных затрат средств  и времени, так как связано с необходимостью изменения большого количества постоянно меняющихся (N, q, V и т.д) характеристик движения транспортного потока зависимо от изменяющих параметрам горным автомобильных дорог (уклон-i, радиус кривой-R).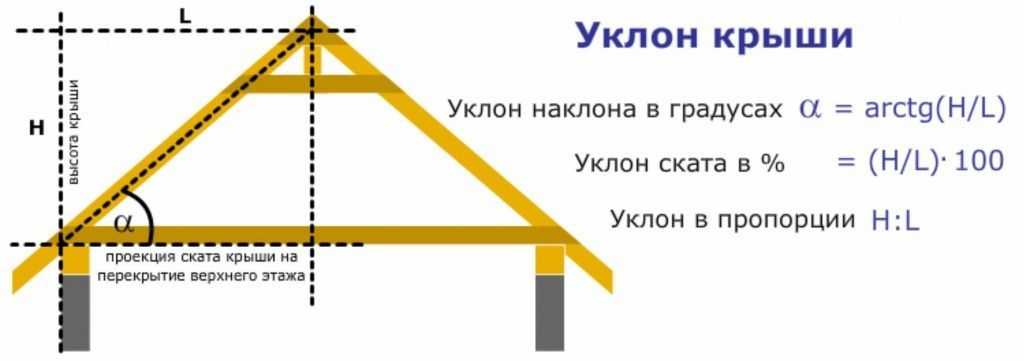

Результативность экспериментальных исследований в значительной степени зависит от правильности планирования экспериментов, суть которых заключается в выборе эффективной методики наблюдений и установлении оптимального числа замеров.

Исследования транспортного потока проводили в реальных горных дорожных условиях. В процессе экспериментальных исследований изучались основные характеристики транспортного потока – интенсивность, состав, скорость, интервал во времени между автомобилями, количество обгонов, плотность потока и другие.

Эксперименты проводились в течение 2005-2010 гг в летние и зимние периоды года, на горных участках автомобильных дорог. Ровность покрытия, план дороги не отражались на изменении режима движения, т.е. происходившие изменение режима движения были вызваны изменениями интенсивности и процентного соотношения автопоездов в общем потоке.

На подготовительном этапе было принято решение использовать для приборами и использованием ручного труда, причем некоторые из них уже применялись в СНГ и за рубежом.

Геометрические элементы плана и профиля дороги измеряют геодезическими инструментами (нивелиром, теодолитом, гониометром) или с помощью аэрофотосъемки, фотограмметрии и ходовых автомобильных лабораторий. Однако в первом приближении некоторые параметры, как уклон дороги, радиус закругления измерены упрощенным методам.

Уклон характеризует крутизну склона. Это высота подъема или спуска h, на котором образовался этот подъем (рис 1.1.)

Уклон в дорожном строительство определяет числом миллиметров подъема на каждый метр пройденного пути по горизонтали и выражают в промилях (‰).

Обычно уклоны проезжей части указывают в паспорте дороги, находящемся у дорожников. На их можно проверить с помощью рейки, линейки и уровня. (см.рис.1.2). Для этого рейку 1 с уровнем 2 кладут на дорогу вдоль направления линии измерения уклона. Поднимают нижний конец рейки до горизонтального показания уровня. Измеряют расстояние h между приподнятым концом рейки и дорогой. Делят это расстояние на длину рейки.

Чем длиннее рейка, тем точнее результат[1].

    

   

Рисунок 1.1. Натурные измерения для определения угла продольного или поперечного уклона дороги

   

Пример. Длина рейки  l=5 м. Нижний ее конец приподнят над поверхностью дороги до горизонтального положения по показанию уровня на 300 мм  (h).       

                                                                   (1.1.)

т.е. подъем 60 мм на 1 м дороги.

Для упрощения расчетов рейку обычно берут длиной 1 м, а еще лучше изготовить уровень такой длины. В этом случае показания линейки в миллиметрах будет соответствовать уклону дороги в промилях.

 

Рисунок 1.2. Схема определения угла продольного или поперечного уклона дороги:

l -длина линейка; h – высота; 1 – рейка;  2 – уровень;  3 – линейка;  4 – дорожное покрытие

 

Для определения радиуса закругления обычно используют метод хорды[1].

Измеряют расстояние АС (рис. 1.3). Находят срединную точку Д и определяют длину а (расстояние АД). Затем измеряют высоту b – расстояние ВД от этой точки до кромки проезжей части.

Радиус закругления подсчитывают по формуле R = (a² + b²)/2b (1.2.)

Мерный отрезок АС обычно берут 10…25…50 м в зависимости от величины радиуса закругления. Используют для этих целей обычную веревку, завязав на ее середине узел и измерив предварительно ее длину [2].

 

Рисунок 1.3. Схема определения радиуса кривой дороги:

АС – хорда;   ВД – расстояние от середины хорды до края дороги;  1 – проезжая часть дороги; 2 – линия, разделяющая потоки (осевая)

 

Таблица 1.

Основные параметры автомобильных дорог А-373 «Ташкент-Андижан-Ош» 164-184 километрах полученных при исследовательских работ на горных участках

Период измерения	Километр, км	Длина протяженности уклона, м	Уклон ‰	Радиус кривой     R, м
Зимой Летом	164 – 166	2200	86 – 90 ‰	–
Зимой Летом	166 – 168	1800	70%	200
Зимой Летом	168 – 170	1600	40%	–
Зимой Летом	170 – 171	800	60%	–
Зимой Летом	172 – 173	1000	50%	500
Зимой Летом	182 – 184	1800	20%	–

 

Список литературы:

1. Бочаров Е. В., Заметта М.Ю., Волошинов В.С. Безопасность дорожного движения – М.: Росагропромиздат ,1998.-284с.
2. Kholmurodova D.K., Negmatov. S.S., Boydadaev M.В.  Esearch influence of humidity of resined screw-polymer weight on parameters of physical and mechanical properties of composite wood and plastic plate materials. International Journal of Advanced Research in Science, Engineering and Technology, Vol.6, Issue 8
3. Г.И. Клинковiтейн, М.Б.Афанасьев «Организация дорожного движения» М.: Транспорт, 2002 – 247 с.

Калькулятор уровня строительства Австралия – Cody Corporation

Что такое уровень высоты?

Уровень физической характеристики объекта, формы рельефа или линии (плоскости) используется для обозначения наклона измеряемого объекта. Применение уклона включает в себя физические особенности, такие как холмы, берега рек и каньоны, а также аспекты строительства, такие как дороги, уклон крыши и ландшафтный дизайн. Другими словами, как найти уклон высоты является важным навыком во многих областях.

Марка также обычно называется наклон или подъем . В зависимости от метода, используемого для нахождения уровня высоты, он может выражаться по-разному, например, в десятичной дроби, процентах и ​​градусах.

Как рассчитать строительную марку

Прежде чем вычислить градус высот, необходимо взять отметки от начальной и конечной точек для сравнения, а также начальное и конечное расстояния. Имейте в виду, что пройденное расстояние — это не то же самое, что «бег» (рассматривается в следующем разделе). «Пройденное расстояние» — это расстояние, пройденное между начальной и конечной точками, а не обязательно «беговое» расстояние.

Также убедитесь, что все ваши юниты одинаковы.

В виде десятичной дроби

Легко запоминающееся уравнение для нахождения изменения высоты в виде десятичной дроби: «подъем над прогоном», означающий подъем (изменение расстояния по вертикали), деленный на прогон (изменение горизонтального расстояние).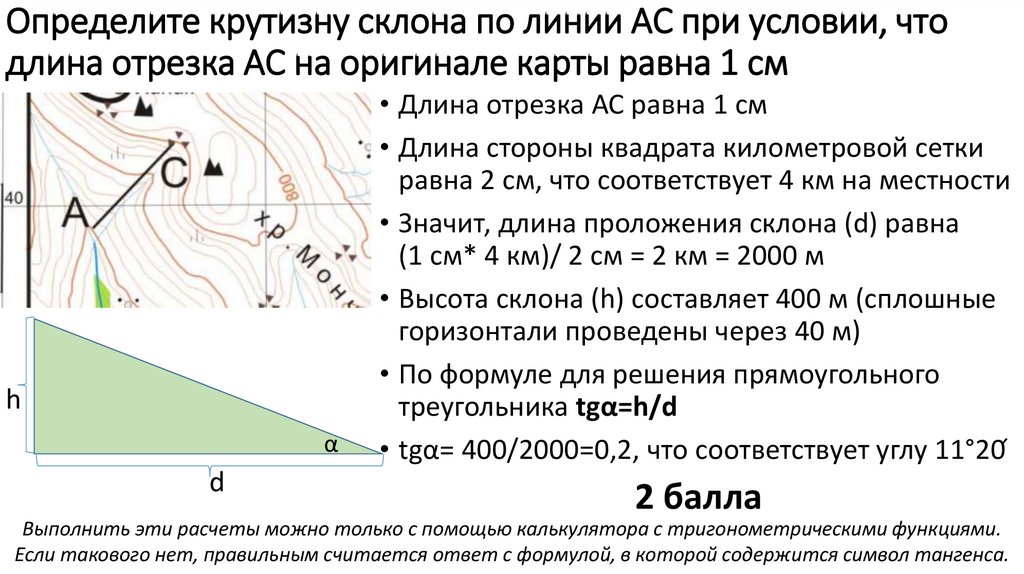 В качестве примера предположим, что подъем равен 2, а пробег — 6. Итак, вы должны взять 2 больше 6 (или 2/6), чтобы получить 0,33 — это ваша оценка в виде десятичной дроби.

В процентах

Процесс измерения высоты в процентах такой же, как и нахождение изменения высоты в виде десятичной дроби, но с одним дополнительным шагом. Итак, находим подъем над пробегом. В нашем примере это 2 на 6 (2/6) — это 0,33. Затем просто умножьте десятичную дробь на 100, чтобы найти процент. В данном случае 33%. Положительный процент указывает на восходящий наклон. Положительное число указывает на восходящий наклон, и наоборот.

В градусах

С точки зрения тригонометрии уклон представляет собой тангенс угла измеряемой поверхности к горизонтали. Чем больше число, тем больше степень (или «наклон»). В этом случае оценка выражается в градусах. Например, уклон улицы может составлять 6,2°, что означает, что улица наклонена вверх на 6,2° от горизонтали (горизонта).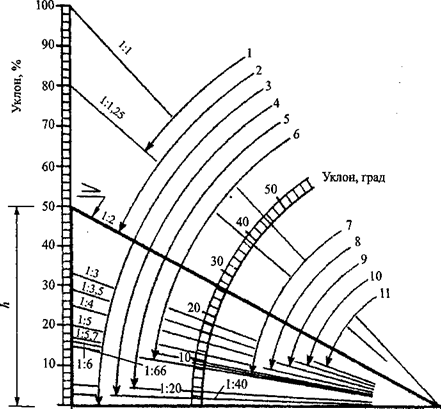 Другими словами, вы едете в гору.

При расчете уклона высоты в градусах полезно представлять задачу как прямоугольный треугольник. Используя базовую тригонометрию, вы можете быстро найти степень в градусах. На приведенной ниже диаграмме показаны три основных аспекта, которые вам понадобятся для получения оценки.

Просто возьмите «подъем над пробегом» и используйте арктангенс (тангенс ^-1 ), чтобы найти тета (θ) — это ваша оценка в градусах. Возвращаясь к нашему примеру, рост равен 2, а пробег равен 6. Таким образом, вы должны взять 2 больше 6 (или 2/6), чтобы получить 0,33. Возьмите арктангенс числа 0,33, что равно 18,26. Следовательно, ваша оценка 18,26°. Положительное число указывает на восходящий наклон, и наоборот.

 

Ниже приведен калькулятор для определения требуемого процента уклона для вашего следующего строительного проекта.

 

Практическое применение расчета и нахождения уровня высоты

Уравнение превышения высоты может быть применено для установки простого уровня для внутренних двориков, дорожек или проездов. Каждый проект уникален, и нет единого способа установить ставки для каждой рабочей площадки.

 

Мы надеемся, что вы нашли этот Калькулятор строительной марки полезным и используете его в своих повседневных задачах на строительной площадке. Следите за нашими сообщениями, чтобы в будущем появилось больше полезных инструментов, подобных этому.

Как измерить уклон дороги

Землемеры используют тригонометрию и свое причудливое оборудование для измерения таких вещей, как уклон участка земли (насколько он падает на определенном расстоянии). Вы когда-нибудь замечали рабочего на дороге, вглядывающегося в инструмент, смотрящего на коллегу по работе, держащего табличку или флаг?

Вы никогда не задумывались, что они делают? Вы тоже хотели выйти и посмотреть на инструмент? С помощью тригонометрии вы можете делать то же, что и эти рабочие — измерять расстояния и углы.

Вы можете заметить, что склон земли вниз похож на угол впадины. Наклоны, углы наклона и углы возвышения взаимосвязаны, поскольку они используют одни и те же триггерные функции.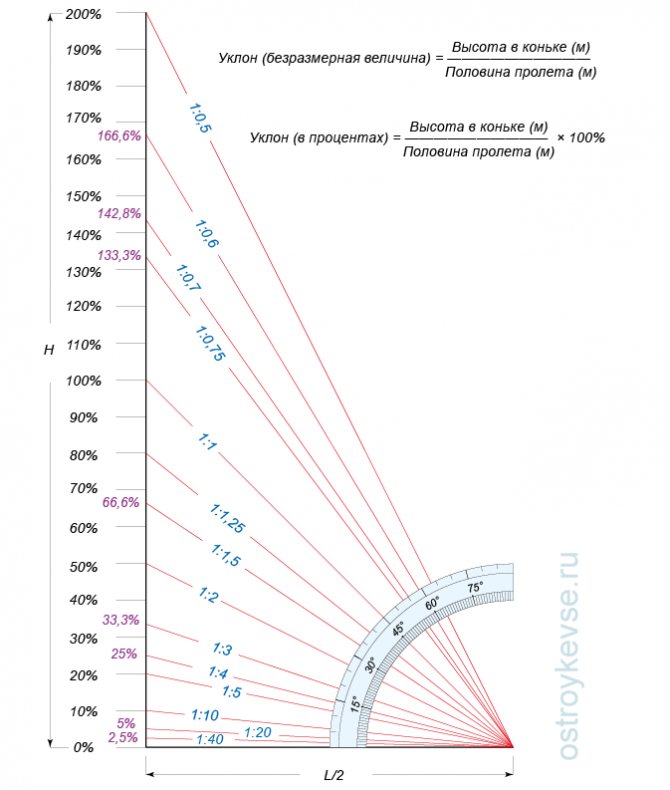

Просто в приложениях для наклона вы решаете угол, а не длину или расстояние.

Чтобы решить одну из этих геодезических задач, связанных с уклоном, вы можете использовать коэффициенты триггера и прямоугольные треугольники. Одна сторона треугольника — это расстояние от одного рабочего до другого; другая сторона – вертикальное расстояние от земли до точки на шесте. Вы составляете соотношение с этими мерами и определяете угол — вуаля!

Предположим, что Эллиот и Фред проводят измерения для дорожно-строительной бригады. Им нужно знать, насколько сильно уклон земли вдоль определенного участка дороги, чтобы обеспечить надлежащий дренаж.

Эллиот проходит 80 футов от Фреда и держит длинный шест, перпендикулярный земле, на каждом дюйме которого есть маркировка. Фред смотрит на столб через прицел. Глядя прямо, параллельно горизонту, Фред замечает точку на шесте на высоте 50 дюймов над землей — назовем ее точкой А. Затем Фред смотрит через инструмент на нижнюю часть шеста, создавая угол депрессии.

Каков угол углубления или наклона дороги к тому месту, где стоит Эллиот?

1. Определите части прямоугольного треугольника, которые вы можете использовать для решения задачи.

   Известные значения относятся к сторонам, прилегающим к углу депрессии и противоположным ему. Назовите меру угла x .

2. Определите, какую триггерную функцию использовать.

   Тангенс угла размером x использует деление противоположного на соседнее.

3. Напишите уравнение с триггерной функцией; затем вставьте значения, которые вы знаете.

   В этой задаче нужно написать уравнение с общепринятой единицей измерения — футами или дюймами. Замена 80 футов на дюймы дает большое число; изменение 50 дюймов на футы включает дробь или десятичную дробь. Какой блок вы выберете, зависит от вас. В этом примере конвертируйте футы в дюймы.

   80 футов = 80 x 12 дюймов = 960 дюймов

   Подставив значения, вы получите тангенс некоторого угла с мерой х градусов:

4. Найдите значение x .

   В приложении вы видите, что угол в 2,9 градуса имеет тангенс 0,0507, а угол в 3 градуса имеет тангенс 0,0524. Тангенс угла в 3 градуса ближе к 0,05208333, поэтому вы можете оценить, что дорога наклонена под углом в 3 градуса между Эллиоттом и Фредом.

Другой способ найти эту меру угла — использовать научный калькулятор и функцию арктангенса. Ваш калькулятор говорит, что угол, тангенс которого равен 0,05208333, равен 2,9.8146 градусов. Так что оценка в три градуса из таблицы верна.

Эта статья взята из книги:

• Тригонометрия для чайников,

Об авторе книги:

Мэри Джейн Стерлинг — автор книги Алгебра I для чайников и многих других книг для чайников 90. Она преподает математику в Университете Брэдли в Пеории, штат Иллинойс, уже более 30 лет, и ей нравилось работать с будущими руководителями предприятий, физиотерапевтами, учителями и многими другими.