Про высоту и уклон при движении на велосипеде
Когда я рассказываю кому-то про велопоходы, я часто замечаю, что собеседник вообще ничего не понимает про высоту.
— А это высокая гора?
— Не очень.
— Тяжело на нее въезжать?
— Тяжело.
— А сколько она метров?
— Пятьсот.
— Это как дом со сколькими этажами?
— …
На самом деле, я абсолютно уверен, что человек, ни разу не поднимавшийся в гору пешком или на велосипеде, просто не может представить себе, какие бывают степени у «высоко» и «тяжело». Нет у него такого опыта. Для него и 30 метров, и 300, и 3000 — это всё высоко и тяжело.
В то же время иногда меня спрашивают: «Ты за день проехал только 30 км? Почему так мало? Даже я больше могу». Спрашивают это городские велолюбители, которые спешиваются при подъеме на обычный виадук.
Чтобы каждый раз долго не объяснять одно и то же на словах, я решил нарисовать несколько схем с примерами высот, которые каждый может себе представить.
Буду давать ссылку на этот пост всем, кто спрашивает.
Вообще, сложность подъема для меня определяют четыре фактора:
1. Высота — абсолютная (над уровнем моря) и относительная (от начала подъема).
2. Уклон (то, что на знаках пишут в процентах).
3. Дорожное покрытие.
4. Погода.
С третьим и четвертым всё понятно, остановимся на первых двух.
Итак, высота.
Сначала представим себе обычный 10-этажный дом. Это высоко? Представим плавный подъем, идущий на эту высоту.
Теперь представим себе телевизионную башню. Питерцы — питерскую, москвичи — Останкинскую, остальные — кто какую хочет. Насколько она выше 10-этажного дома? Опять представляем себе подъем на эту высоту по серпантину.
Если это удалось, попробуем представить себе высоту перевала Лепоэдер, который я брал в первый день путешествия по Пути Св. Иакова.
Надеюсь, получилось достаточно наглядно. Длина пути от подножья до вершины при этом — около 20 км. Именно в этот день за 9 ходовых часов я преодолел всего 30 км.
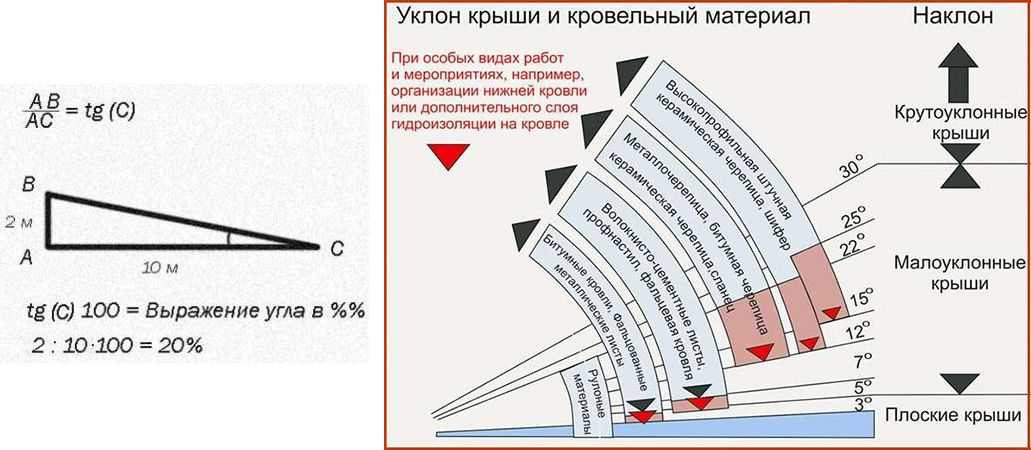
Далее — уклон. Почему-то многие считают, что уклон измеряется в градусах. Посмотрите на знаки. Уклон (как подъема, так и спуска) всегда измеряется в процентах:
Это необходимо, потому что уклон дороги всегда изменяется плавно, в каждый отдельный момент угол разный:
Понять запись в процентах очень просто: число на знаке — это то количество метров, на которое дорога опустится или поднимется на следующие 100 метров пути.
На фото выше изображен спуск, где на участок в 100 метров уровень дороги падает на 18% от длины этого участка, т. е. на 18 метров. Это очень крутой спуск с перевала. Фото взято из этого моего поста. Там дальше можно увидеть, насколько спуск крутой.
А вот схема 100-метрового участка подъема с уклоном 18%:
Попробуем представить подъем по такой дороге на высоту того же 10-этажного дома:
Естественно, в горах такая дорога не идет по прямой, а образует серпантин. Вот, например, как выглядит серпантин на перевале Кату-Ярык на Алтае, который мы брали в 2009 году:
Длина дороги на этом перевале 3,5 км, а набор высоты — около 600 м.
Т.е. приходится постоянно двигаться по подъему с уклоном в 17—18%. Ехать там, естественно, невозможно.
Почему мне смешно, когда кто-то говорит, что ехал по дороге с уклоном в 45 градусов? Потому что 45 градусов, если вспомнить школьную геометрию, это 100 метров подъема на 100 метров пути, то есть уклон в 100%. Таких дорог не бывает. 20-процентные подъемы — это уже очень и очень жестоко. В основном, дороги в горах делают с уклонами в диапазоне 7—14%. Средний уклон подъема на Лепоэдер — 6%. Т.е. там бывают ровные участки, и 16—18-процентные подъемы, но средний — шесть. И это то, что испанцы называют «mortal».
Вроде всё. Надеюсь, достаточно понятно получилось.
Tags: вело, мысли, путешествия
Школа жизни: проценты на дорожных знаках подъема и спуска | Живой Ангарск
Вы уже обращали внимание на предупреждающие дорожные знаки, обозначающие крутизну спуска или подъема, и, возможно, задавали себе вопрос – а, например, 12% – это сколько? И почему бы крутизну уклона не обозначать в градусах?
На знаках 1.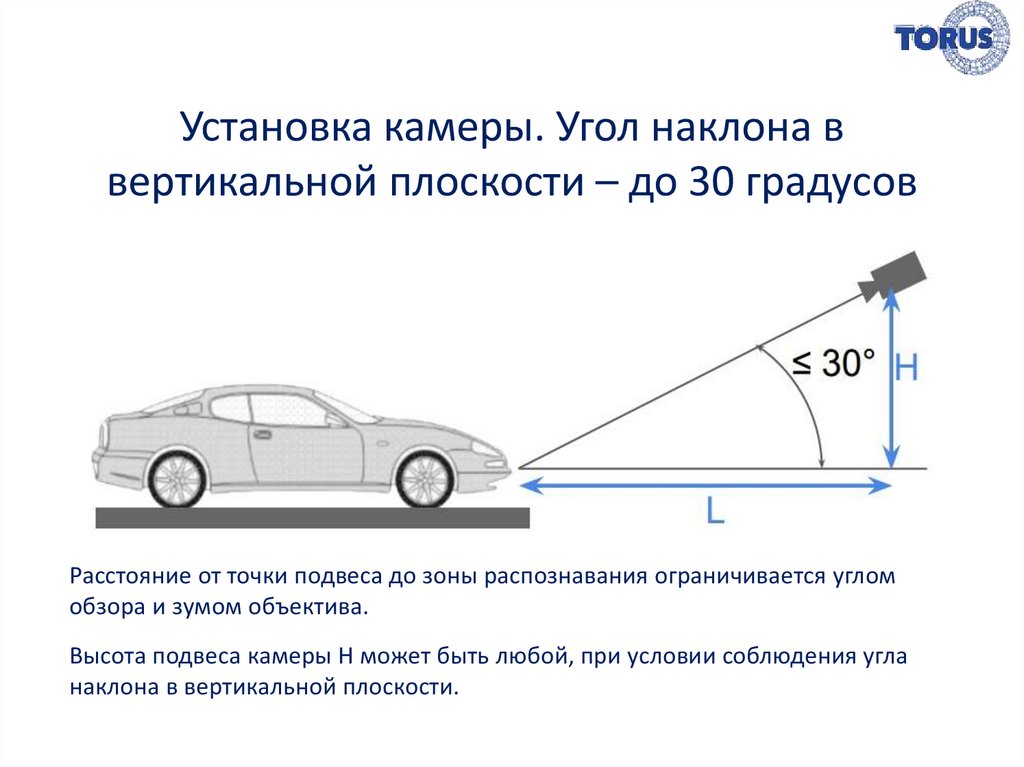
13 (Крутой спуск) и 1.14 (Крутой подъём) обозначен тангенс угла наклона, выраженный в процентах. Чтобы понять наглядно, что это такое, вспомним геометрию. Итак, прислоните лыжную палку под углом к стене напротив яркой лампы. Вы увидите две тени – одну на стене, другую на полу. Это проекции, соответственно, на вертикальную и горизонтальную плоскости. Та тень, что на стене, называется «синус», та, что на полу – «косинус». Чем ближе к стене вы придвинете низ палки, тем короче будет «косинус». Наоборот, отодвигая низ палки от стены, вы увидите, что «синус» становится все меньше, а «косинус» – больше. Отношение синуса к косинусу называется тангенсом. Если вы установите палку под углом 45 градусов от пола, синус и косинус будут совершенно одинаковы. В таком случае тангенс будет равен 1. Или, как говорили ваши учителя, тангенс 45 градусов равен 1. Если мы посмотрим сбоку на дорогу, в том месте, где она имеет уклон, то увидим, что угол этого уклона находится в пределах 8 градусов от горизонта.
Высота подъема, или «синус», гораздо меньше, чем длина проекции дороги на горизонтальную плоскость – «косинус». Разделив высоту подъема на длину горизонтальной проекции, обнаружим, что тангенс угла такого уклона не превышает 0,12. Его удобно выражать в процентах – например, 12 %. В таком случае тангенс угла 45 градусов равен 100 %.
Теперь вы уже смело можете использовать эту информацию. Так, проехав 1 километр по дороге с уклоном 12 %, вы подниметесь (или спуститесь) на 120 метров. (При таких небольших углах уклона длину горизонтальной проекции дороги можно считать равной длине дороги).
Из любопытства вы можете перевести угол уклона обратно в градусы с помощью калькулятора на сотовом телефоне, настроив его на «научный» режим, например: TAN-1(0,12)=7 градусов. В некоторых калькуляторах: ATAN(0,12)=7. Впрочем, для автолюбителей главное не это.
Отношение двух сил – силы, необходимой для сдвига машины с заблокированными колесами, и силы тяжести, прижимающей машину к дороге, называется коэффициентом сцепления.
Так мы легко можем получить коэффициенты сцепления для сухого асфальта – 7000/10000 = 0,7, для грязной дороги – 3000/10000 = 0,3, и для льда – 1000/10000 = 0,1. Эти значения приблизительно такие же и в том случае, если машину тянуть вбок. Зачем вам это знать?! Недостаточное внимание к коэффициенту сцепления или его неправильная оценка является основной причиной аварий на дорогах, особенно весной и осенью, когда из-за этого происходит до 70% аварий.
Оказывается, тангенс угла наклона равен коэффициенту сцепления. Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (Это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой.) Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы.
Так, при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину.
И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки 1.13 и 1.14. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае – не сможете сдвинуться с места. А уж если затормозите на спуске, машину может занести. Старайтесь тормозить двигателем на длительных спусках.
По материалам сайта “Школа жизни”
© Shkolazhizni.ru
qgis – Расчет реальной длины и уклона дорог
спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 435 раз
Я собрал точки вдоль дороги в виде CSV-файлов с z-значениями. При импорте в QGIS я использовал значение Set Z и Points to path, чтобы сделать линию.
Когда я использую правую кнопку в инструменте «Определить объекты», я вижу, что все вершины имеют соответствующие значения z.
Однако, когда я использую функцию $length в калькуляторе поля, я получаю точно такие же значения, как если бы у меня была линия рисования, но рука без значений z.
Кроме того, как я могу рассчитать средний наклон для той же линии?
- qgis
- z-значение
Встроенная функция $length даст вам только «горизонтальную» длину вдоль линии, а не истинную длину с учетом наклона. Чтобы вычислить это:
- Возьмите ваш векторный слой, который вы создали с помощью «Points to path» и используйте «Explode lines». Это разделит вашу одну строку на несколько строк с разрывами, расположенными в каждой вершине.
- На этом новом слое откройте калькулятор поля и создайте новое поле «h_length», используя функцию
$длина. Это «горизонтальная» длина каждого сегмента. - Также в калькуляторе полей создайте поле “z_start” с помощью функции
z(start_point($geometry))и другое поле “z_end” с помощью функцииz(end_point($geometry)).
Они обозначают высоту в начале и в конце каждого сегмента линии. - Вычислить разницу уровней между начальной и конечной точкой в новом поле “z_diff” с помощью функции
"z_start" - "z_end". 92)) . - Если вы хотите увидеть градиент каждого сегмента, создайте новое поле «градиент», используя функцию
«h_length» / «z_diff»(т. е. наклон 1 из 40 будет рассчитываться как 40, поменяйте местами этот раунд, если хотите) . - Используйте «Просмотр» > «Статистическая сводка», чтобы просмотреть статистику атрибута «s_length» в слое «Расчлененный». Статистика «сумма» даст вам общую наклонную длину всех сегментов.
Они обозначают высоту в начале и в конце каждого сегмента линии.Чтобы получить средний уклон всей линии, следуйте тем же принципам, рассчитав «горизонтальное» расстояние и разницу высот между первой и последней точками.
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
| | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
Это было бы эквивалентно дороге, идущей прямо на 9Угол 0 градусов. Таким образом, не реалистичное измерение для проезжей части.
Вы можете использовать наши вместо метрической версии .