Основные методы измерения геометрических параметров горной дороги
Цитировать:
Эшанбабаев А.А., Купайсинов Д. Основные методы измерения геометрических параметров горной дороги // Universum: технические науки : электрон. научн. журн. 2021. 2(83). URL: https://7universum.com/ru/tech/archive/item/11266 (дата обращения: 22.04.2023).
Прочитать статью:
DOI: 10.32743/UniTech.2021.83.2-2.22-24
АННОТАЦИЯ
В данной статье приведены сведения о работе по измерению вертикального уклона (высоты) дороги и радиуса кривизны в плане по геометрическим элементам продольного плана и профиля горной дороги простым методом и результаты исследований.
ABSTRACT
This article contains information about the work of measuring the vertical slope (height) of the road and the radius of curvature in the plan from the geometric elements of the longitudinal plan and profile of the mountain road by a simple method and the results of research.
Ключевые слова: горная дорога, транспортный поток, продольный и поперечный уклон дороги, радиус кривизны, плоская кривизна, элементы дороги, скорость, интервал, шоссе.
Keywords: mountain road, traffic flow, longitudinal and transverse road slope, curvature radius, plan curvature, road elements, speed, interval, highway.
Экспериментальное изучение движения транспортных потоков в реальных горно-дорожных условиях весьма сложно и требует значительных затрат средств и времени, так как связано с необходимостью изменения большого количества постоянно меняющихся (N, q, V и т.д) характеристик движения транспортного потока зависимо от изменяющих параметрам горным автомобильных дорог (уклон-i, радиус кривой-R). Результативность экспериментальных исследований в значительной степени зависит от правильности планирования экспериментов, суть которых заключается в выборе эффективной методики наблюдений и установлении оптимального числа замеров.
Исследования транспортного потока проводили в реальных горных дорожных условиях. В процессе экспериментальных исследований изучались основные характеристики транспортного потока – интенсивность, состав, скорость, интервал во времени между автомобилями, количество обгонов, плотность потока и другие.
Эксперименты проводились в течение 2005-2010 гг в летние и зимние периоды года, на горных участках автомобильных дорог. Ровность покрытия, план дороги не отражались на изменении режима движения, т.е. происходившие изменение режима движения были вызваны изменениями интенсивности и процентного соотношения автопоездов в общем потоке.
На подготовительном этапе было принято решение использовать для приборами и использованием ручного труда, причем некоторые из них уже применялись в СНГ и за рубежом.
Геометрические элементы плана и профиля дороги измеряют геодезическими инструментами (нивелиром, теодолитом, гониометром) или с помощью аэрофотосъемки, фотограмметрии и ходовых автомобильных лабораторий.
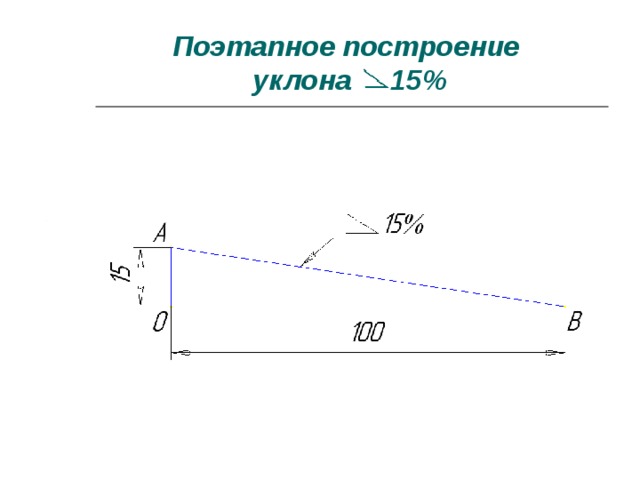
Уклон характеризует крутизну склона. Это высота подъема или спуска h, на котором образовался этот подъем (рис 1.1.)
Уклон в дорожном строительство определяет числом миллиметров подъема на каждый метр пройденного пути по горизонтали и выражают в промилях (‰).
Обычно уклоны проезжей части указывают в паспорте дороги, находящемся у дорожников. На их можно проверить с помощью рейки, линейки и уровня. (см.рис.1.2). Для этого рейку 1 с уровнем 2 кладут на дорогу вдоль направления линии измерения уклона. Поднимают нижний конец рейки до горизонтального показания уровня. Измеряют расстояние h между приподнятым концом рейки и дорогой. Делят это расстояние на длину рейки. Чем длиннее рейка, тем точнее результат[1].
Рисунок 1.1. Натурные измерения для определения угла продольного или поперечного уклона дороги
Пример.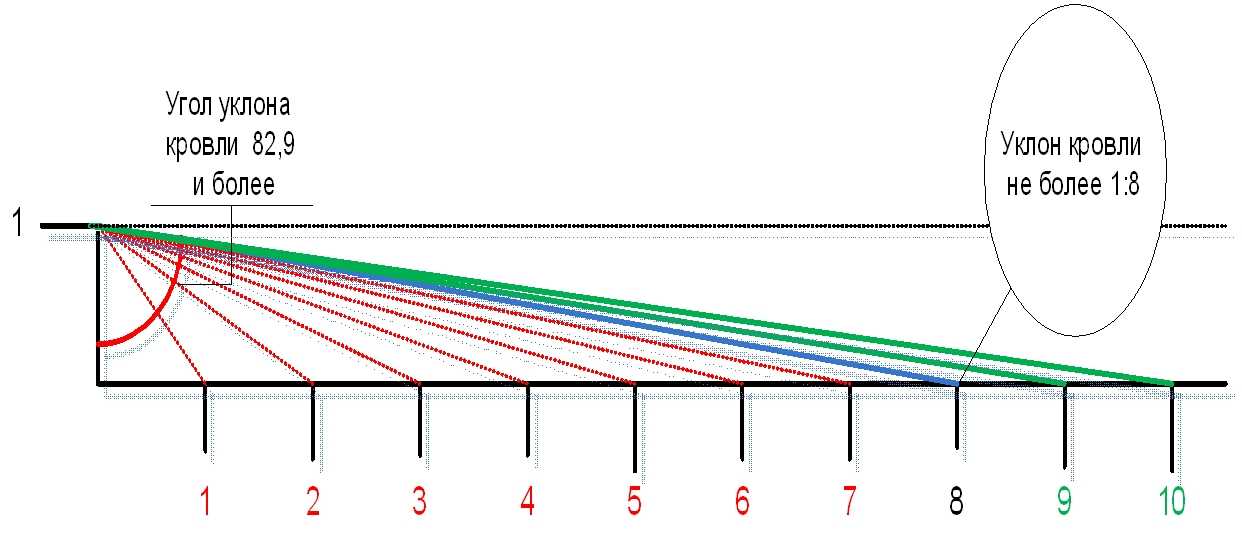
Длина рейки l=5 м. Нижний ее конец приподнят над поверхностью дороги до горизонтального положения по показанию уровня на 300 мм (h).
(1.1.)
т.е. подъем 60 мм на 1 м дороги.
Для упрощения расчетов рейку обычно берут длиной 1 м, а еще лучше изготовить уровень такой длины. В этом случае показания линейки в миллиметрах будет соответствовать уклону дороги в промилях.
Рисунок 1.2. Схема определения угла продольного или поперечного
l -длина линейка; h – высота; 1 – рейка; 2 – уровень; 3 – линейка; 4 – дорожное покрытие
Для определения радиуса закругления обычно используют метод хорды[1].
Измеряют расстояние АС (рис. 1.3). Находят срединную точку Д и определяют длину а (расстояние АД). Затем измеряют высоту b – расстояние ВД от этой точки до кромки проезжей части.
Радиус закругления подсчитывают по формуле R = (a2 + b2)/2b (1.2.)
Мерный отрезок АС обычно берут 10…25…50 м в зависимости от величины радиуса закругления. Используют для этих целей обычную веревку, завязав на ее середине узел и измерив предварительно ее длину [2].
Рисунок 1.3. Схема определения радиуса кривой дороги:
АС – хорда; ВД – расстояние от середины хорды до края дороги; 1 – проезжая часть дороги; 2 – линия, разделяющая потоки (осевая)
Таблица 1.
Основные параметры автомобильных дорог А-373 «Ташкент-Андижан-Ош» 164-184 километрах полученных при исследовательских работ на горных участках
|
Период измерения |
Километр, км |
Длина протяженности уклона, м |
Уклон ‰ |
Радиус кривой R, м |
|
Зимой Летом |
164 – 166 |
2200 |
86 – 90 ‰ |
– |
|
Зимой Летом |
166 – 168 |
1800 |
70% |
200 |
|
Зимой Летом |
168 – 170 |
1600 |
40% |
– |
|
Зимой Летом |
170 – 171 |
800 |
60% |
– |
|
Зимой
Летом |
172 – 173 |
1000 |
50% |
500 |
|
Зимой Летом |
182 – 184 |
1800 |
20% |
– |
Список литературы:
- Бочаров Е.
В., Заметта М.Ю., Волошинов В.С. Безопасность дорожного движения – М.: Росагропромиздат ,1998.-284с. - Kholmurodova D.K., Negmatov. S.S., Boydadaev M.В. Esearch influence of humidity of resined screw-polymer weight on parameters of physical and mechanical properties of composite wood and plastic plate materials. International Journal of Advanced Research in Science, Engineering and Technology, Vol.6, Issue 8
- Г.И. Клинковiтейн, М.Б.Афанасьев «Организация дорожного движения» М.: Транспорт, 2002 – 247 с.
В., Заметта М.Ю., Волошинов В.С. Безопасность дорожного движения – М.: Росагропромиздат ,1998.-284с.2125 – Стр 3
21
радиусы кривых в плане; радиусы кривых в продольном профиле: выпуклые, вогнутые:
длины кривых в продольном профиле: выпуклые, вогнутые.
Предельно допустимые нормы принимают согласно табл.1.6, исходя из расчетных скоростей движения по категориям дорог. Данные нормы распространяются на участки дорог вне населенных пунктов. Для населенных пунктов следует пользоваться нормами СНиП 2.07.01-89.
1.6.2 Оценка продольного уклона дороги
Под продольным уклоном понимается отклонение проектной линии от горизонтали в продольном направлении, наибольший (нормативный) продольный уклон предельно допустимый, принятый при проектировании продольного профиля, при котором обеспечивается рациональное сочетание строительной стоимости, транспортных расходов и безопасности движения.
Уклон дороги определяют с помощью простейшего приспособления (рис.1.7), состоящего из измерительной линейки 1 (длина 1 м), рейки 2 (длина не менее 1 м), строительного жидкостного уровня 3.
При определении продольного уклона рейку 2 с уровнем 3 располагают в середине полосы движения, параллельно оси дороги. Поднимая нижний конец рейки 2, пузырек уровня 4 устанавливают в центральное положение. Удерживая его в этом положении, линейкой 1 измеряют расстояние между приподнятым концом рейки 2 и поверхностью дороги (h).
Рис. 1.7 Измерение величины уклона дороги с помощью рейки и линейки: 1- линейка; 2 – рейка; 3 – уровень; 4 – пузырёк воздуха; b -длина рейки; h – отклонение поверхности дороги от горизонтали на длине рейки; a – угол наклона
22
Уклон дороги определяют как i = h/b. Угол уклона (в градусах) α =arctg(h/b).
При умножении i на 100 получаем уклон в процентах, на 1000 – в профи-
лях.
Наиболее точно величину уклона определяют с помощью нивелира и уклономеров различных конструкций.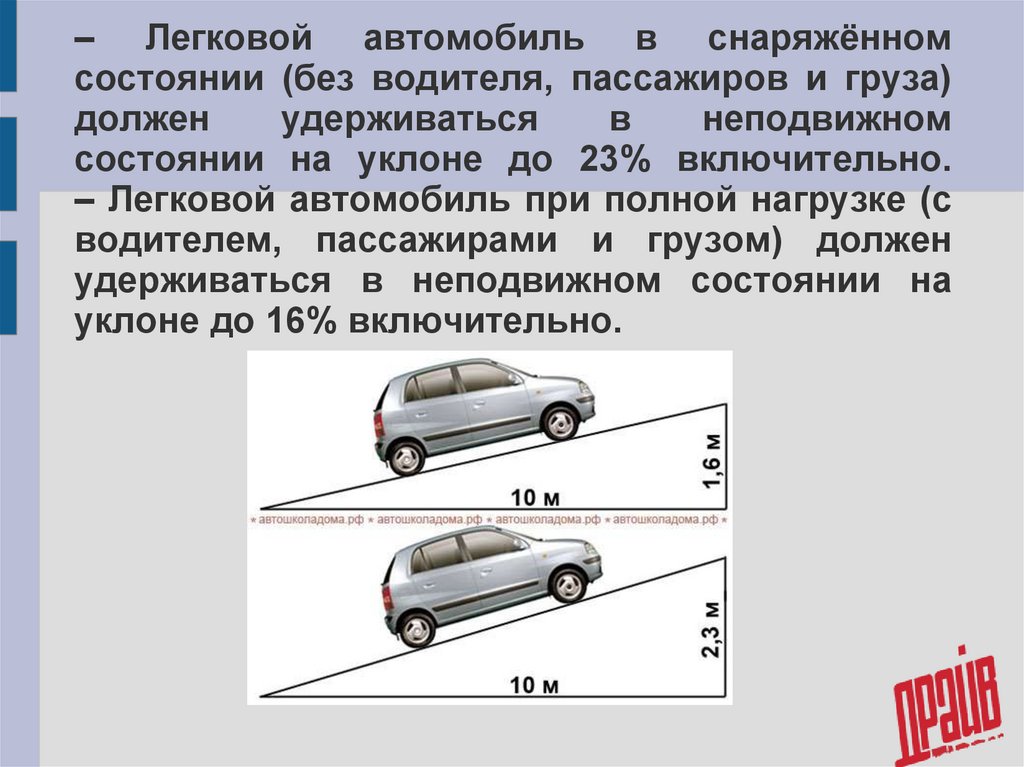
Нивелир широко используется при проведении строительных и дорожных работ.
При измерении уклона нивелир устанавливают на обочине дороги, а рейку, по которой снимают отсчеты, – в заданных точках, которыми могут быть начало и конец уклона. Разность отсчетов по рейке дает превышение одной точки над другой (h2-h3). Измерив расстояние между этими точками рулеткой, получаем величину l . Величину уклона определяют по формуле
i = | h2 − h3 | . | (1.6) |
| |||
| l |
| |
Для измерения уклонов (продольных и поперечных) используют уклономер КП-206 и линейку угломерную КП-135 (поставщик – ИТЦ “Доринжприбор”, г.Москва).
Уклономер КП 206 состоит из основания в виде рейки со встроенной ампулой уровня, которая с помощью специального устройства, снабженного ручкой и лимбом, имеет возможность изменять угол установки.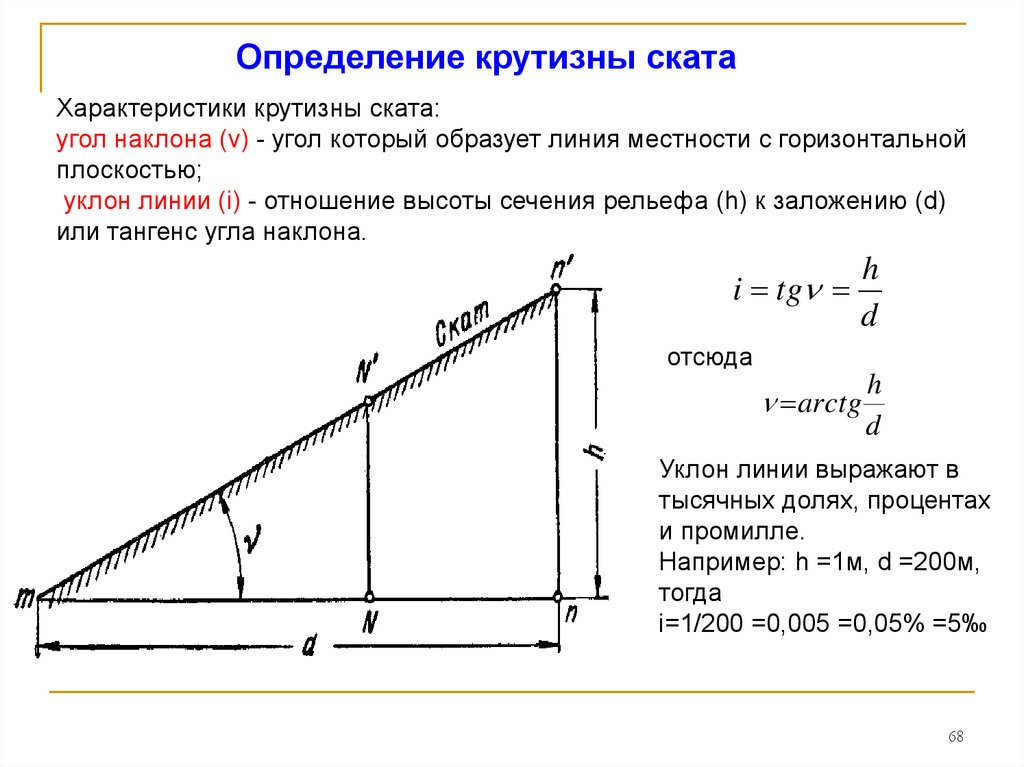
Принцип действия прибора основан на измерении уклона путем установки пузырька уровня в центральное положение вращением ручки и фиксированием величины уклона по указателю лимба. Габаритные размеры прибора – 1000 х 60 х 55, мм. Масса – 2 кг .
Рейка двутавровая КП-135 представляет собой планку в виде швеллера, соединенную с удлинителем. На ней шарнирно укреплена большая линейка для измерения малых углов и нанесена измерительная шкала, вдоль которой перемещается бегунок, показывающий величину угла в промилях. В торце планки расположен фиксатор для закрепления большой линейки в транспортном положении. На удлинителе шарнирно укреплена малая линейка для измерения больших углов, в верхней части которой помещена ампула уровня. Между удлинителем и малой линейкой находится транспортир с двумя шкалами, одна их которых проградуирована в градусах, другая – в промилях.
Принцип действия прибора основан на измерении уклона путем установки пузырька уровня в центральное положение перемещением бегунков вдоль линеек и фиксированием величины уклонов по соответствующим шкалам.
Габаритные размеры – 512 х 38 х 80 мм. Масса прибора – 6,5 кг.
Для определения соответствия уклона контролируемого участка дороги, полученного с помощью указанных устройств, требованиям нормативов определяют относительное содержание в % значений продольного уклона больших или меньших допуска, а также находящихся в пределах этого допуска по отношению ко всем измеренным. На участке дороги длиной 100 м проводят 10 измерений.
23
1.7 Определение радиуса кривой в плане и профиле
Кривая в плане – один из основных элементов автомобильной дороги, которая представляет собой криволинейный участок, сооруженный при изменении направления трассы.
Наименьший (нормативный) радиус кривой дороги в плане – радиус, при котором обеспечивается безопасное движение автомобилей с расчетной скоростью на чистом увлажненном и уширенном покрытии, имеющем нормативный вираж проезжей части.
Радиус закругления дороги по его протяженности, как правило, не одинаков. Средняя часть кривой имеет наименьший, но постоянный радиус закругления и называется круговой кривой.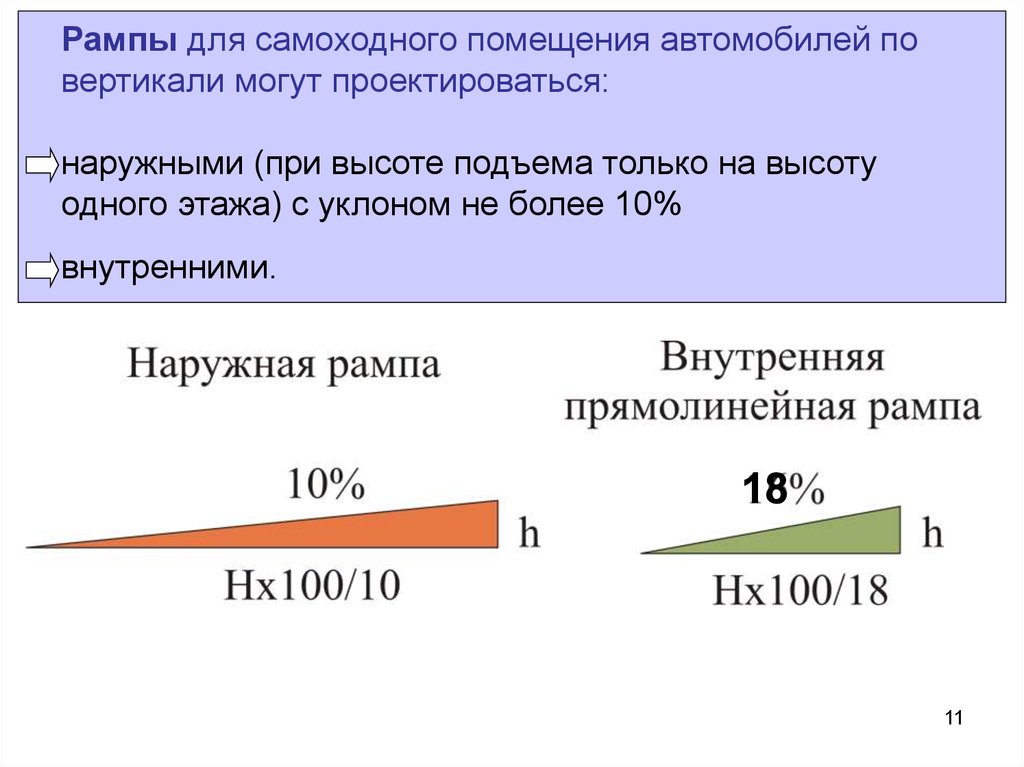
На сопряжении круговой кривой с прямым участком дороги, которое называется переходной кривой, кривизна закругления плавно изменяется. Тем самым обеспечивается плавное нарастание центробежной силы при входе в поворот, которая оказывает существенное влияние на условия и удобства движения транспортного средства в пределах закругления дороги (рис.1.8).
Рис. 1.8 Общий вид кривой на плане
Если необходимо определить величину радиуса кривой в плане на участках с постоянным радиусом или на небольшом участке переходной кривой, то можно воспользоваться известным простым способом.
Этот способ определения радиуса кривой в плане заключается в измерении длины хорды L (между двумя точками, находящимися на кромке проезжей части) и высоты сегмента f (перпендикуляра, восстановленного из середины хорды L до пересечения с кромкой проезжей части).
Измерив указанные на рис. 1.9 величины L и f , можно вычислить фактический радиус R по формуле
| f 2 + | L2 |
| ||
R = | 4 | , | |||
| |||||
2f |
| ||||
|
|
|
| ||
где f – высота сегмента; L – длина хорды.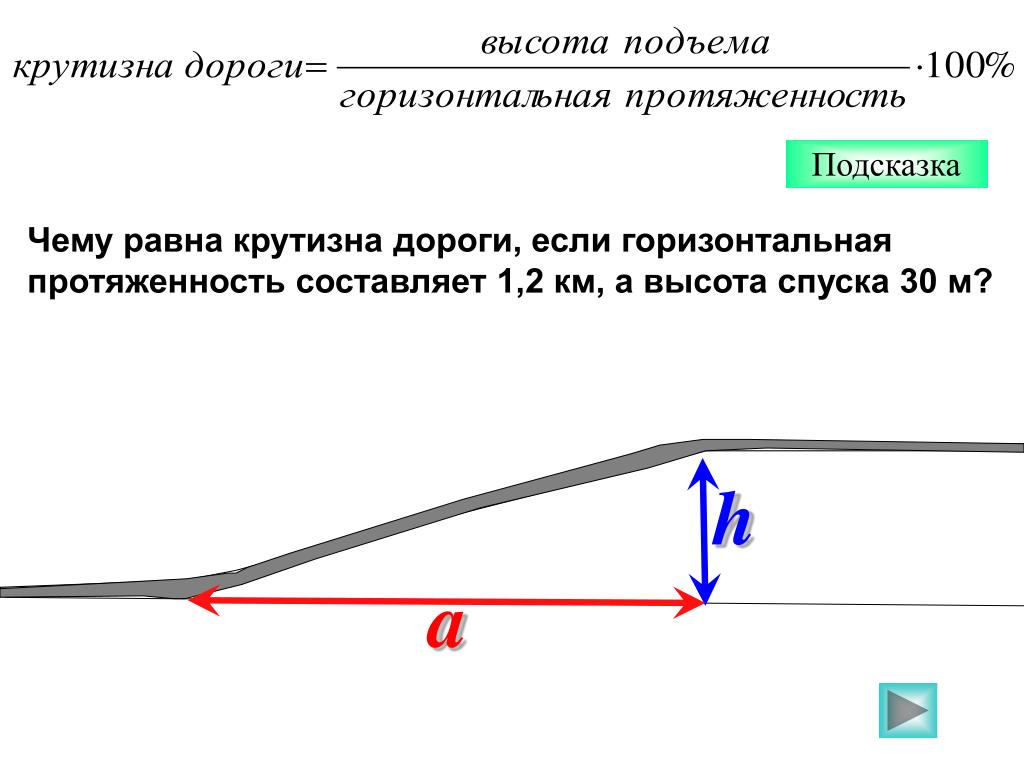
24
Для упрощения в полевых условиях можно воспользоваться заранее приготовленным приспособлением, которое состоит из двух мерных лент различной длины: 20 и 1,5 м. К середине 20-метровой ленты (в отметке 10 м) крепится полутораметровая лента. Натягивая 20-метровую ленту между двумя точками на кривой, измеряем высоту сегмента по полутораметровой ленте, которая также натягивается. Для удобства в работе можно использовать табл.1.9, составленную на основе заранее проведенных расчетов (для ленты длиной L = 20 м).
Рис. 1.9 Измерение кривой с помощью мерных лент
Таблица 1.9 Определение радиуса R кривой в плане по высоте f сегмента, м
f | 1,01 | 0,67 | 0,5 | 0,4 | 0,33 | 0,25 | 0,2 | 0,17 | 0,12 | 0,1 | 0,08 | 0,07 | 0,06 | 0,05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R | 50 | 75 | 100 | 125 | 150 | 200 | 250 | 300 | 400 | 500 | 600 | 700 | 800 | 1000 |
Примечание.
Перед проведением замеров фиксируют по всей длине участка, на котором проводятся измерения, внутреннюю и внешнюю кромки проезжей части. Если замеры необходимо провести по оси кривой, размечают середину проезжей части и проводят осевую линию.
При измерении на кривой переменного радиуса необходимо определить точку кривой, начиная от которой радиус начинает увеличиваться использованием способа, основанного на эффекте “наконечника стрелы”. Линия прямой видимости, проходящая через ось дороги, проведенная на определенном расстоянии от внешнего края, создает зрительный эффект стрелы, заканчивающейся на внешнем краю дороги (рис.1.10).
Направив ассистента в точку наконечника стрелы (рис.1.10а), наблюдатель может визуально выявить изменения радиуса кривой. Если наблюдатель и ассистент продвинулись вперед на одинаковое расстояние (3…5 м), а ассистент
25
остался в зоне наконечника стрелы, то радиус кривой на этом отрезке постоянный (рис.1.10б).
Этот радиус определяют по методу, изложенному выше.
Когда же при дальнейшем равномерном продвижении обоих участников будет обнаружено несовпадение стрелы, то, значит, на этом отрезке радиус кривой начал изменяться (рис.1.10в). Например, если расстояние 1 – 2, пройденное наблюдателем, меньше, чем вошедший в поле зрения участок внешнего края 1-3, то это свидетельствует об увеличении радиуса кривой, и наоборот.
Если по расстояниям 1 – 2 нельзя судить о том, начиная с какой точки на противоположном участке радиус увеличивается, мерные отрезки 1 – 2 принимают меньшие величины.
Рис. 1.10 Визирование изменения радиуса кривизны дороги в плане
Измеренное постоянное значение на участке наименьшего радиуса сравнивают с нормативным для данной категории дорог по табл. 1.8. Радиус кривой в плане соответствует требованиям нормативных документов, если полученное значение не менее нормативного.
Под радиусом кривой дороги в профиле понимается радиус кривой от дороги, спроецированной на вертикальную плоскость. Кривые в профиле (вертикальные кривые) подразделяются на выпуклые и вогнутые.
Выпуклые кривые устраивают для плавного перехода с одного уклона на другой и для улучшения видимости в продольном профиле. Наименьший нормативный радиус выпуклой кривой дороги в профиле – радиус выпуклой кривой, при котором обеспечивается при движении с расчетной скоростью расчетная видимость дороги на расстояние, необходимое для остановки в этих пределах транспортных средств путем экстренного торможения.
26
Вогнутые кривые устраивают для смягчения динамического вертикального воздействия на автомобиль на переломе продольного профиля. Наименьший нормативный радиус вогнутой кривой дороги в профиле – радиус вогнутой кривой, соответствующий допустимому для самочувствия пассажиров и перегрузки рессор значению центробежной силы в продольном профиле при движении с расчетными скоростями.
Радиус выпуклой кривой влияет на расстояние геометрической видимости дороги в продольном профиле, а радиус вогнутой кривой влияет на возможность пробоя подвески транспортного средства на перегоне продольного профиля.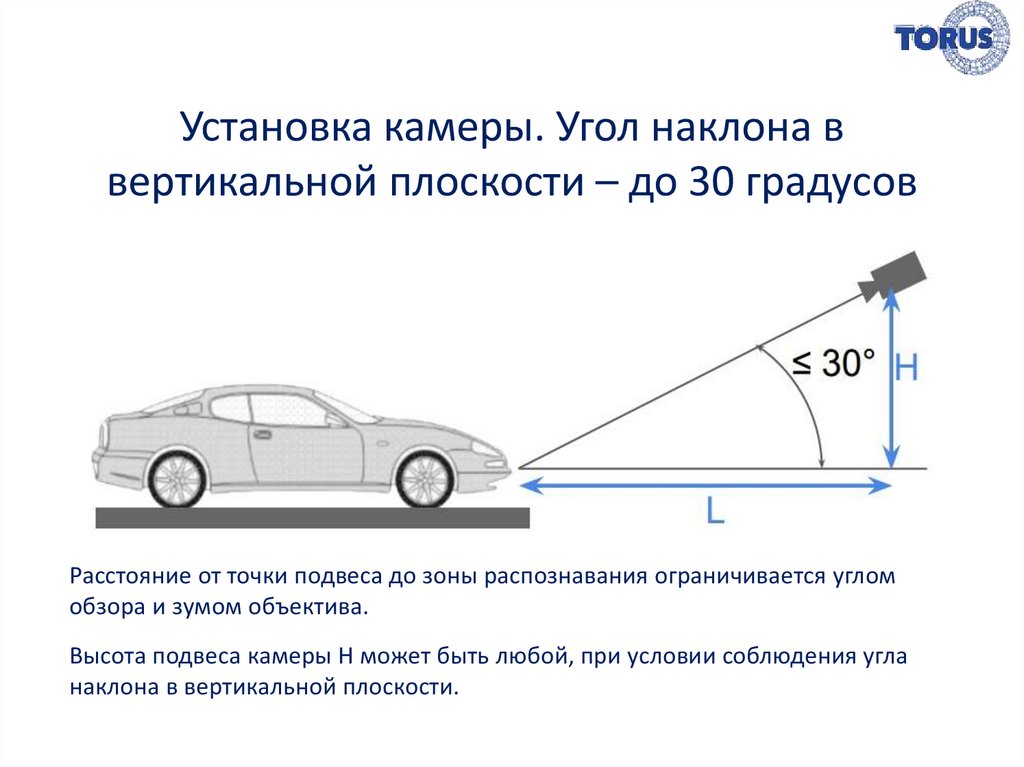
Радиус вертикальных кривых определяется одним из следующих спосо-
бов.
Способ 1. Радиус выпуклой кривой определяется расчетным путем как частное от деления квадрата измеренного расстояния геометрической видимости в продольном профиле (Sb) на удвоенное значение высоты глаз водителя над поверхностью дороги (h= 1,2 м)
S2 Rвып = 2hb .
Способ 2. Особенность способа заключается в подсчете вертикальной кривой по измеренной длине кривой и стрелки ее прогиба с помощью теодолита. С этой целью устанавливаем теодолит в точке А, а рейку – от теодолита на определенное расстояние (50, 100, 150, 200 м) в точке С. Визирную ось теодолита ориентируем на высоту инструмента по рейке в точке С (рис. 1.11).
Рис.1.11. Схема определения радиуса (а) и вогнутых (б) вертикальных кривых
Не меняя угол наклона визирной оси теодолита, устанавливаем рейку на середине расстояния между точками А и С в точке В и берем отсчет по рейке.
Алгебраическая разность h между высотой инструмента и отсчетом в точке С и составляет стрелку прогиба, соответствующую определенному радиусу.
27
1.8 Определение расстояния геометрической видимости
Под геометрической видимостью понимается видимость, обеспечиваемая геометрическими элементами дороги и притрассовыми объектами (посадки деревьев, застройки и т.д.). При этом различают геометрическую видимость:
дороги – расстояние, на протяжении которого наблюдатель (водитель автомобиля) может различать поверхность дороги и объекты, находящиеся на высоте до 20 см над поверхностью дороги;
встречного автомобиля – расстояние, с которого наблюдатель (водитель автомобиля) может обнаружить и различить движущееся навстречу транспортное средство.
Расстояние видимости оказывает существенное влияние на безопасный режим движения (выбор безопасной скорости движения, осуществление маневров обгона и опережения), тем самым определяет техническую возможность предотвращения ДТП и регламентирует предел безопасной скорости движения на участках с ограниченной видимостью.
Видимость дороги в плане, т.е. на закруглениях, а также в зоне примыканий и пересечений с автомобильными и железными дорогами, может быть ограничена посадками деревьев, застройкой, порослью, откосами выемки и поэтому зависит от состояния полосы отвода и прилегающей к ней местности.
Видимость дороги в профиле, т.е. на вертикальных переломах продольного профиля дороги (в местах перехода от подъема к спуску), также может быть ограничена и полностью зависит от конструктивных особенностей конкретного продольного профиля дороги.
Расстояние геометрической видимости дороги в продольном профиле измеряют методом удаления наблюдателя от объекта видимости на дискретные расстояния с равным интервалом и визуального проведения линии прямой видимости (1 – 0) с условной высоты глаз водителя (h = 1,2 м) (точки 1.2,3,4) к габаритной точке нахождения объекта высотой 0,2 м (точка 0) (рис. 1.12).
Рис. 1.12 Определение расстояния геометрической видимости дороги в продольном профиле
Максимальное расстояние, на котором эта линия еще не пересечется с профилем дороги, и будет расстоянием видимости (4-0).
Для определения расстояния геометрической видимости встречного автомобиля на вычерченном в масштабе продольном профиле дороги (рис. 1.13) в
28
заданном месте на высоте h = 1,2 м (условный уровень глаз водителя объекта 1) наносится точка А.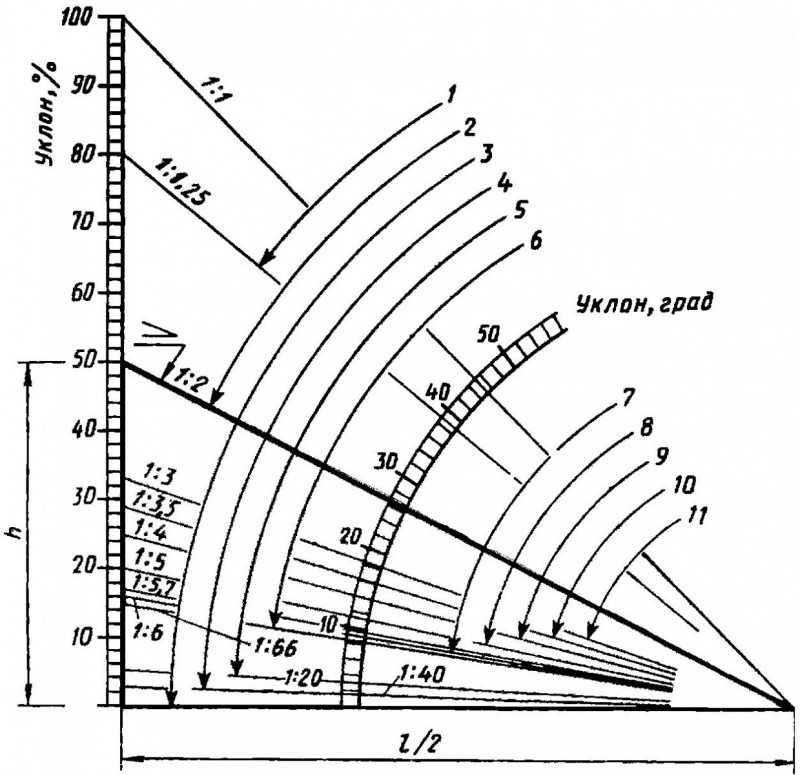
С противоположного конца перелома на высоте h = 1,2 м проводится дуга 2 – 2′, копирующая профиль дороги. Затем из точки А проводится луч зрения А-А’, касающийся перелома дороги и пересекающий в точке В дугу 2-2. Расстояние, измеренное от передней части объекта 1 до сечения В- В’, будет соответствовать расстоянию геометрической видимости из заданной точки А.
Рис. 1.13 Схема определения расстояния геометрической видимости встречного ТС в продольном профиле
Рис.1.14 Схема определения расстояния видимости в плане
Определение расстояния видимости дороги в плане (на криволинейном участке) (рис. 1.14) производят по полосе движения от проезжей части автомобиля до пересечения прямой АВ, проведенной через край непросматриваемой зоны из точки А (рабочее место водителя) с внешней границей проезжей части (точка В).
Расстояние видимости встречного автомобиля в плане (на криволинейном участке) (рис. 1.14) из заданной точки А (с места водителя объекта 1) равно расстоянию, измеренному по полосе движения объекта 1 от передней его части (точки А’)до точки В’, в которой препятствие (в данном случае объект 2) может быть четко опознано по его характерным признакам (в данном случае по точке В’).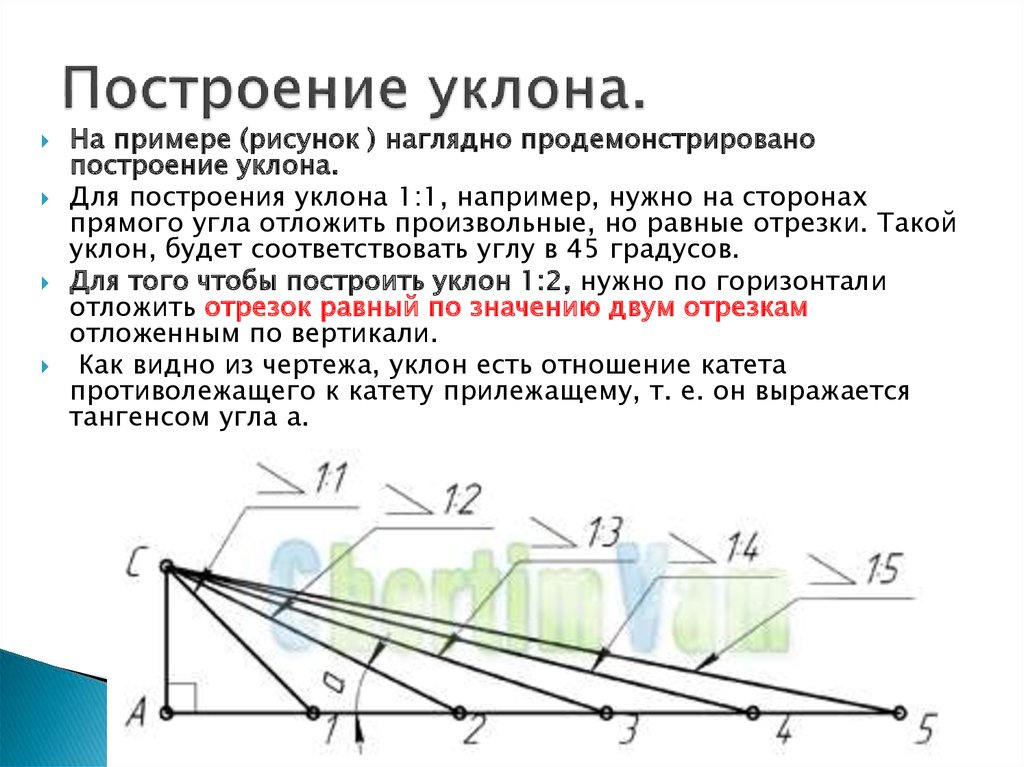
Полученные значения расстояния геометрической видимости сравнивают с нормативными для данной категории дорог или улиц. По этому параметру
29
участок дороги соответствует требованиям нормативных документов, если полученное расстояние не менее нормативного. Нормативные значения расстояний видимости как в плане, так и в профиле одинаковы и приведены в табл. 1.8.
Библиографический список
1.Курьянов В.К. Анализ расчетных и экспериментальных данных по допускаемым скоростям движения / В.К. Курьянов, О.Н. Бурмистрова, А.В. Скрыпников // Математическое моделирование, компьютерная оптимизация технологий, параметров оборудования и систем лесного комплекса: Межвуз. сб. науч. тр./ Под ред. проф. В.С. Петровского. – Воронеж: ВГЛТА, 2000.- С. 70.
2.Курьянов В.К. Повышение транспортно-эксплуатационных качеств автомобильных дорог лесопромывшленного комплекса: Монография / В.К. Курьянов, Д.Н. Афоничев, О.Н. Бурмистрова, А.В. Скрыпников; Воронеж. гос. Лесотехн. акад., Ухтинск.
гос. техн. ун-т. – Воронеж: Изд-во Воронеж. гос. унта, 2002. – 176 с.
3.Курьянов В.К. Лесотранспорт как система “водитель-автомобиль- дорога-среда”: Учеб. пособие для вузов. – Воронеж: Воронеж. гос. лесотехн. акад., 2002. – 251 с.
4.Ильин Б.А. Проектирование, строительство и эксплуатация лесовозных дорог. / Б.А. Ильин, Б.И. Кувалдин – М.: Лесн. промы-сть, 1982.- 384 с.
5.Зонов Ю.Б. Методика и приборы контроля транспортноэксплуатационного состояния автомобильных дорог: Методическое пособие для сотрудников дорожной инспекции ГАИ / Ю.Б. Зонов, В.С. Емышеев – М.: НИИСТ МВД России, 1996. – 65 с.
6.Бабков В.Ф. Дорожные условия и безопасность движения. – М.: Транспорт, 1982. – 280 с.
7.Алябьев В.И. Сухопутный транспорт леса / В.И. Алябьев, Б.А. Ильин, Б.И. Кувалдин, Г.В. Грехов – М.: Лесн. промы-сть, 1990.- 416 с.
8.Курьянов В.К. Воздействие дорожно-строительной отрасли на окружающую природную среду в воронежской области // Лесное хозяйство малолесной зоны России в условиях переходного периода к рынку: Мат.
регион. на- уч-практ. конф./ В.К. Курьянов, О.В. Рябова, А.В. Скрыпников. Под ред. проф. В.П. Бычкова Воронеж: Воронеж. гос. лесотехн. акад., 2000 – 115 с.
9.Курьянов В.К. Экологические требования к лесовозным автомобильным дорогам в лесных предприятиях Центрально-Черноземного района // Математическое моделирование, компьютерная оптимизация технологий, параметров оборудования и систем лесного комплекса: Межвуз. сб. науч. тр./ В.К. Курьянов, А.В. Скрыпников. Под ред. проф. В.С. Петровского. Воронеж: ВГЛТА, 2000, 255 с.
30
Гоптарев Сергей Михайлович Скрыпников Алексей Васильевич
ДОРОЖНЫЕ УСЛОВИЯ И БЕЗОПАСНОСТЬ ДВИЖЕНИЯ
Методические указания к выполнению лабораторно-практических работ для студентов специальности 240400 – Организация и безопасность движения
ЧАСТЬ 1
Редактор А.В. Гладких
Подписано в печать 11.12.03 Формат 60х841/16 Заказ № Объем 1,88 п.л. Тираж экз. Усл. п.л. 1,74 Уч-изд. л. 2,0 РИО ВГЛТА. УОП ВГЛТА. 394613, г. Воронеж, ул. Тимирязева, 8.
Что означают проценты на предупреждающих знаках крутой дороги?
Учитель математики Саймон Янг написал в Твиттере тему о процентах на дорожных знаках и дал мне разрешение опубликовать ее в блоге. Я остался верен оригинальной формулировке Саймона, с небольшими правками здесь и там, в основном на основе его собственных исправлений и некоторых разговоров, возникших в его ветке (исходная ветка связана в конце).
На дорожных знаках Великобритании крутизна дороги выражается в процентах: что это означает и откуда берутся цифры?
Вы когда-нибудь задумывались, что означают проценты в этих дорожных знаках о предстоящем изменении уклона? Я знаю, что у меня есть! Вот что я обнаружил…
Знак уклона 20% У дороги B836 на вершине холма к западу от Лох Стривен. © Авторское право Томаса Ньюджента и лицензия на повторное использование в соответствии с лицензией Creative Commons. |
У вас могут быть некоторые предположения о том, что означают проценты. Имеют ли они в виду…
а) процентное изменение градиента?
б) процент от угла?
c) что-то делать с тем, как вы должны регулировать скорость?
или
d) ничего из вышеперечисленного.
Вы выбрали d ? Конечно! Правильный!
Чтобы понять их происхождение, мы должны сначала вернуться в середину 19 века.70-е годы, когда знаки градиента показывали не проценты, а соотношения! Очевидно, некоторые из этих старых знаков все еще существуют, и я хотел бы их найти. Например, на знаках будет написано 1:3. Это означало, что каждые 3 единицы, пройденные по горизонтали, будут увеличивать/уменьшать 1 единицу по вертикали.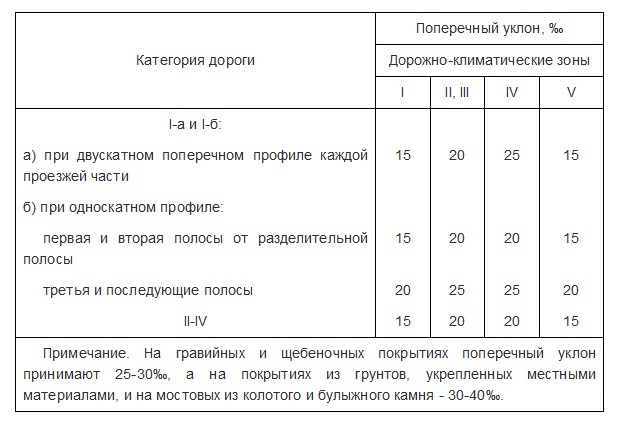
Неважно, какую единицу измерения вы используете (метры, футы и т. д.), потому что важно соотношение.
| Градиентный знак в старом стиле на Бишопс-роуд недалеко от Даунхилла, Северная Ирландия. Мост Альберта / CC BY-SA |
Пока все просто. Проблема в следующем: соотношение 1:5 (изменение на 1 единицу по вертикали на каждые 5 единиц, пройденных по горизонтали) является более крутым градиентом, чем соотношение 1:10 (1 по вертикали на каждые 10 единиц по горизонтали), и это на самом деле сбивает с толку некоторых людей. . Конечно, большее число ⟹ более крутое? Добавьте к этому, что большинство людей видят эти знаки за долю секунды, управляя транспортным средством на высокой скорости, и у вас есть еще большая проблема. Дорожный знак должен четко и мгновенно сообщать о предупреждении, а пропорциональная форма знака просто не делает этого: это сбивает с толку! Итак, степени, которые следует преобразовать из знаков отношения в знаки процентов.
Больший процент означает большую крутизну, и людям это легко понять. 20% в гору? Я бы лучше понизил передачу или две! 5% вниз по склону? Пора готовить мои тормоза!
Но я так и не ответил на поставленный вопрос… что на самом деле означают проценты? Ну, они получены из исходных соотношений. 1:5 означает, что изменение по вертикали составляет одну пятую от изменения по горизонтали… или 20%! (поэтому два примера на фотографиях выше показывают одинаковые градиенты). 1:10 станет 10%, 1:4 будет 25%
В общем, если знак говорит «𝓍%», это означает, что вертикальное изменение составляет 𝓍% горизонтального изменения: больший процент означает более крутой холм . Если на знаке написано 50%, это означает, что вертикальное изменение составляет только половину горизонтального изменения – это круто! Не для слабонервных!
Хотя поначалу проценты кажутся немного бессмысленными, на самом деле они основаны на правильной математике. Это всего лишь способ превратить что-то, что может сбить с толку некоторых, в более интуитивную систему (дорожный знак обязательно должен быть простым для понимания!)
Математика в подарок!
Задумывались ли вы, какому углу соответствуют проценты? Ну, теперь вы знаете, что они означают, вы можете использовать простую тригонометрию, чтобы вычислить это!
Trig Gradient TOA от T. Briggs лицензирован CC BY-SA 4.0 ” или “изменение в 𝓎, деленное на изменение в 𝓍”). Хороший ответ, когда ученик спрашивает, когда ему может понадобиться тригонометр в реальной жизни? Угол можно рассчитать, выполнив обратный тангенс изменения по вертикали, деленный на изменение по горизонтали.Несколько примеров со всеми углами, правильными до 3sf:
И так далее… (100% будет 4 тангенса ) = 1) Некоторые люди, отвечая на исходную ветку, указали, что в фактическая математика градиент, скорее всего, будет рассчитан путем сравнения изменения высоты с фактической длиной пройденного пути, и в этом случае мы получаем : Саймон подписан с :
Это меня конечно просветило! Вот твит, с которого началась ветка (нажмите, чтобы увидеть все):
| ||||||||||||||||||||||||||||||||||
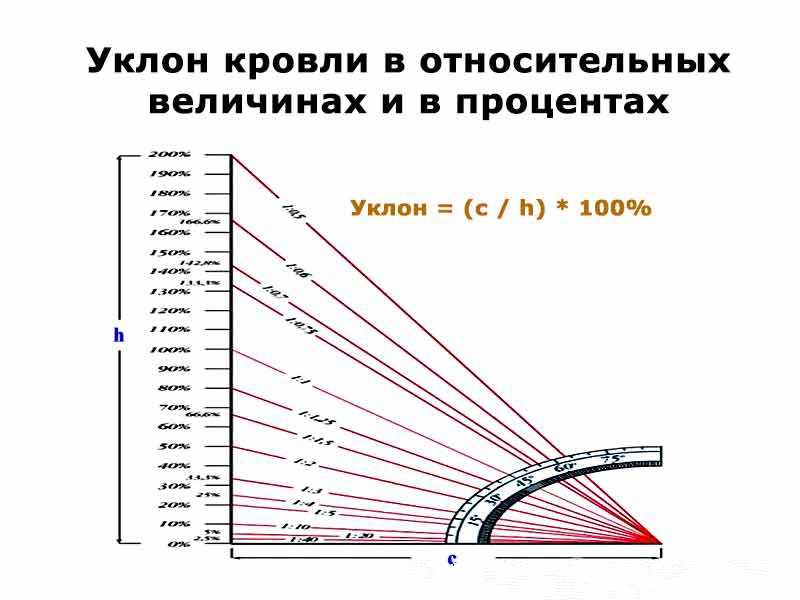Я не несу никакой ответственности, я просто рад поделиться знаниями!
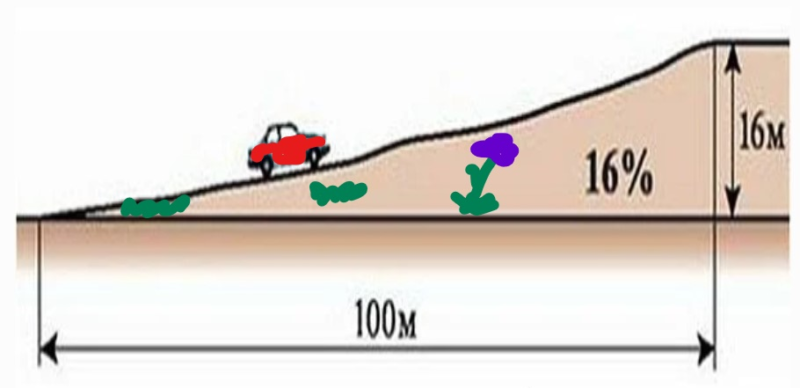1 в 1 по вертикали или 45 градусов? 
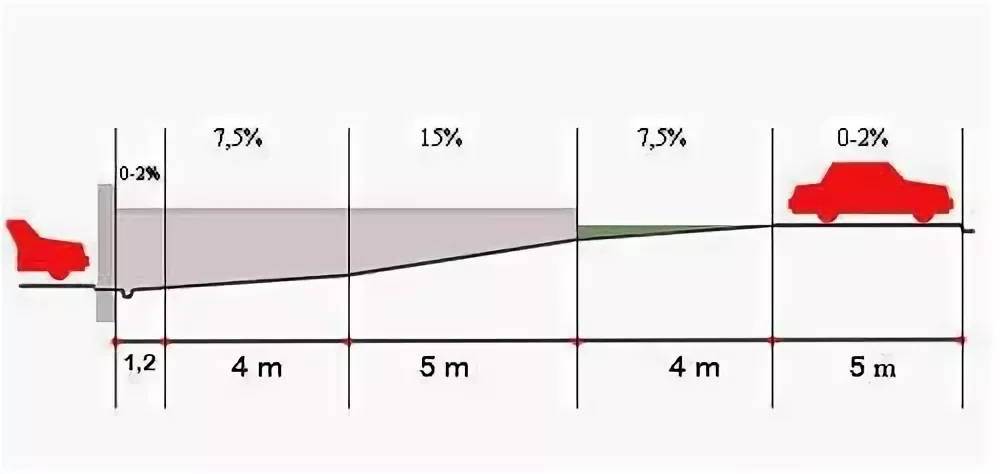А «1 в 3» делает одну единицу по вертикали на каждые три по горизонтали. 1 в 1 будет 45 градусов.