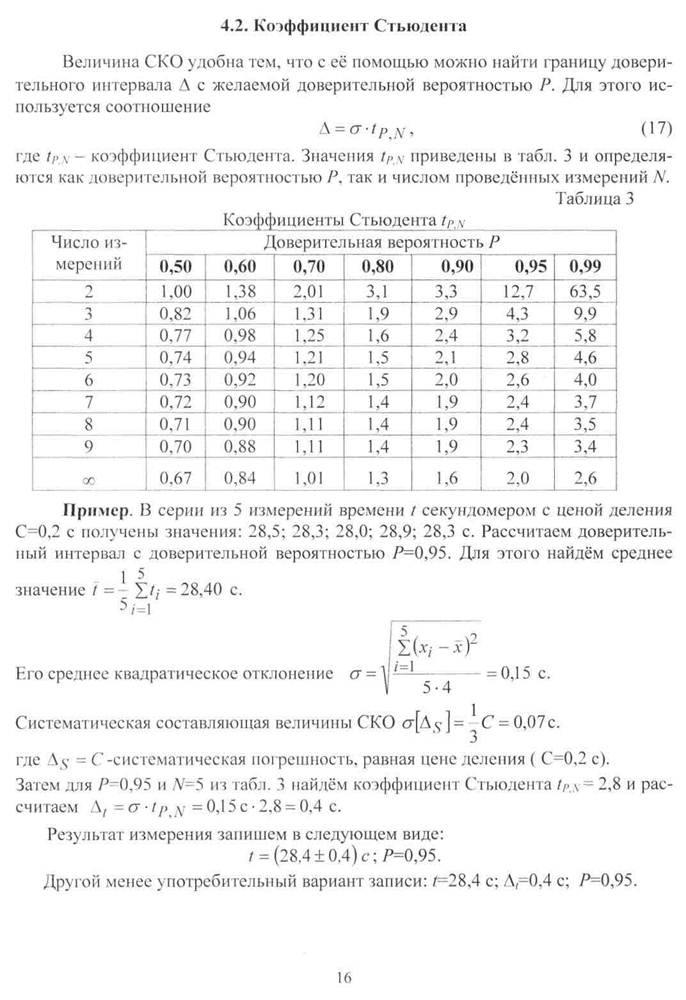
9.14 Средняя квадратическая погрешность результатов единичных измерений в ряду измерений;
средняя квадратическая погрешность измерений;
средняя квадратическая погрешность;
СКП
Оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле
, (9.6)
где xi – результат i-го единичного измерения;
–среднее арифметическое значение измеряемой величины из n единичных результатов.
П р и м е ч а н и е — На практике широко распространен термин среднее
квадратическое отклонение – (СКО). Под отклонением в соответствии
с формулой понимают отклонение единичных
результатов в ряду измерений от их
среднего арифметического значения. В
метрологии, как отмечено в 9.1, это
отклонение называется погрешностью
измерений. Если в результаты измерений
введены поправки на действие систематических
погрешностей, то отклонения представляют
собой случайные погрешности.
9.15 Средняя квадратическая погрешность результата измерений среднего арифметического;
средняя квадратическая погрешность среднего арифметического;
средняя квадратическая погрешность;
СКП
Оценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле
, (9.7)
где S средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; n число единичных измерений в ряду.
9.16 Доверительные границы погрешности результата измерений;
доверительные границы погрешности;
доверительные границы
Наибольше и
наименьшее значения погрешности
измерений, ограничивающие интервал,
внутри которого с заданной вероятностью
находится искомое (истинное) значение
погрешности результата измерений.
П р и м е ч а н и я
1) Доверительные границы в случае нормального закона распределения вычисляются как ,, где,– средние квадратические погрешности, соответственно, единичного и среднего арифметического результатов измерений;t – коэффициент, зависящий от доверительной вероятности P и числа измерений n.
2) При симметричных границах термин может применяться в единственном числе – доверительная граница.
3) Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности.
9.17 Поправка
П р и м е ч а н и е — Знак поправки противоположен знаку
погрешности. Поправку, прибавляемую к
номинальному значению меры, называют поправкой к
значению меры; поправку, вводимую в показание
измерительного прибора, называют поправкой к
показанию прибора.
Погрешности средств измерений. Средняя квадратическая погрешность результата измерений среднего арифметического;
⇐ Предыдущая1234
Средняя квадратическая погрешность результата измерений среднего арифметического;
Погрешностьметодаизмерений;
Погрешности измерений
Результаты измерений физических величин
8.1 результат измерения физической величины -Значение величины, полученное путем ее измерения
8.2 неисправленный результат измерения -Значение величины, полученное при измерении до введения в него поправок, учитывающих систематические погрешности
8.3 исправленный результат измерения – Полученное при измерении значение вели-
чины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей
8.
4 сходимость результатов измерений – Близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и
тем же методом в одинаковых условиях и с одинаковой тщательностью.
8.5 воспроизводимость результатов измерений -Близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений (температуре, давлению, влажности и др.).
8.6 ряд результатов измерений -Значения одной и той же величины, последовательно полученные из следующих друг за другом измерений
8.7 среднее взвешенное значение величины -Среднее значение величины из ряда неравноточных измерений, определенное с учетом веса каждого единичного измерения (см. 8.8).
Примечание — Среднее взвешенное значение иногда называют средним весовым
8.
8 вес результата измерений -Положительное число (р), служащее оценкой доверия к тому или иному отдельному результату измерения, входящему в ряд неравноточных измерений.
9.1 погрешность результата измерения -Отклонение результата измерения от истинного (действительного) значения измеряемой величины.
9.2 систематическая погрешность измерения -Составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.
9.3 инструментальная погрешность измерения -Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений
Составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.
9.5 погрешность (измерения) из-за изменений условий измерения -Составляющая систематической погрешности измерения, являющаяся следствием неучтенного
влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
9.6 субъективная погрешность измерения -Составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.
9.7 неисключенная систематическая погрешность -Составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
9.8 случайная погрешность измерения -Составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины
9.9 абсолютная погрешность измерения -Погрешность измерения, выраженная в единицах измеряемой величины
9.10 абсолютноезначениепогрешности – Значение погрешности без учета ее знака (модуль погрешности)
9.
11 относительная погрешность измерения -Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измерямой величины.
9.12 рассеяние результатов в ряду измерений -Несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
9.13 размах результатов измерений -рассеяния результатов единичныхизмерений физической величины, образующих ряд(или выборку из «измерений).
9.14 средняя квадратическая погрешность результатов единичных измерений в ряду измерений -Оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения
Примечание — На практике широко распространен термин среднее квадратическое отклонение— (СКО).
случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений
9.
16 доверительные границы погрешности результата измерений -Наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри
которого с заданной вероятностью находится искомое (истинное) значение погрешности результат аизмерений.
9.17 поправка -Значение величины, вводимое в неисправленный результат измерения с целью исключениясоставляющих систематической погрешности.
9.18 поправочный множитель -Числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
9.19 точность результата измерений -Одна из характеристик качества измерения,
отражающая близость к нулю погрешности результата измерения.
9.20 неопределенность измерений -Параметр, связанный с результатом измере-
ний и характеризующий рассеяние значений, которые можно приписать измеряемой величине.
9.21 погрешность метода поверки -Погрешность применяемого метода передачи
размера единицы при поверке
9.22 погрешность градуировки средства измерений -Погрешность действительного значения величины, приписанного той или иной отметке шкалысредства измерений в результате градуировки
9.23 погрешность воспроизведения единицы физической величины -Погрешность результата измерений, выполняемых при воспроизведении единицы физической
величины.
9.24 погрешность передачи размера единицы физической величины -Погрешность результата измерений, выполняемыхпри передаче размера единицы.
9.25 статическая погрешность измерений – Погрешность результатаизмерений, свойственная условиям статическогоизмерения
9.26 динамическая погрешность измерений -Погрешность результата измерений, свойственная условиям динамическогоизмерения
9.
27 промах -Погрешность результата отдельного измерения,входящего в ряд измерений, которая для данныхусловий резко отличается от остальных результатов
этого ряда.
9.28 предельная погрешность измерения в ряду измерений -Максимальная погрешность измерения (плюс,минус), допускаемая для данной измерительной
задачи.
9.29 погрешность результата однократного измеренгия -Погрешность одного измерения (не входящегов ряд измерений), оцениваемая на основанииизвестных погрешностей средства и метода измерений в данных условиях (измерений).
9.30 суммарная средняя квадратическая погрешность результата измерений Погрешность результата измерений (состоящая из суммы случайных и не исключенных систематических погрешностей, принимаемых за случайные),
10.1 погрешность средства измерений -Разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.
.
10.2 систематическая погрешность средства измерений – Составляющая погрешности
Средства измерений, принимаемая за постоянную или закономерную изменяющуюся.
10.3 случайная погрешность средства измерений – Составляющая погрешности средства измерений, изменяющаяся случайным образом
10.4 абсолютная погрешность средства измерений -Погрешность средства измерений, выраженная в единицах измеряемой физической величины
10.5 относительная погрешность средства измерений -Погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или к действительному значению измеренной физической величины
10.6 приведенная погрешность средства измерений -Относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в
части диапазона.
10.7 основная погрешность средства измерений -Погрешность средства измерений, применяемого в нормальных условиях
10.8 дополнительная погрешность средства измерений -Составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений
10.9 статическая погрешность средства измерений -Погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную
10.10 динамическая погрешность средства измерений -Погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины
10.11 погрешность меры -Разность между номинальным значением меры
и действительным значением воспроизводимой ею величины
10.
12 стабильность средства измерений -Качественная характеристика средства измерений, отражающая неизменность во времени его метрологических характеристик.
10.13 нестабильностьсредстваизмерений -Изменение метрологических характеристик
средства измерений за установленный интервал времени.
10.14 точность средства измерений -Характеристика качества средства измерений,
отражающая близость его погрешности к нулю.
Примечание — Считается, что чем меньше погрешность, тем точнее средство измерений
10.15 класс точности средств измерений -Обобщенная характеристика данного типа
средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.
10.16 предел допускаемой погрешности средства измерений -Наибольшее значение погрешности средств измерений, устанавливаемое нормативным документом для данного типа средств измерений, при котором оно еще признается годным к применению.
10.17 нормируемые метрологические характеристики типа средства измерений -Совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативными документами на средства измерений
10.18 точностные характеристики средства измерений – Совокупность метрологических характеристик средства измерений, влияющих на погрешность измерения.
⇐ Предыдущая1234 |
Дата добавления: 2015-04-30; Просмотров: 656; Нарушение авторских прав?; Мы поможем в написании вашей работы!
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Стандартное отклонение в статистике Объяснение
Что такое стандартная ошибка?
Стандартная ошибка (SE) статистики — это приблизительное стандартное отклонение совокупности статистических выборок.
Стандартная ошибка — это статистический термин, который измеряет точность, с которой выборочное распределение представляет совокупность, используя стандартное отклонение. В статистике выборочное среднее значение отклоняется от фактического среднего значения совокупности; это отклонение является стандартной ошибкой среднего.
Ключевые выводы
- Стандартная ошибка (SE) — это приблизительное стандартное отклонение статистической выборки.
- Стандартная ошибка описывает отклонение между рассчитанным средним значением генеральной совокупности и тем, которое считается известным или считается точным.
- Чем больше точек данных участвует в вычислении среднего значения, тем меньше стандартная ошибка.
Стандартная ошибка
Понимание стандартной ошибки
Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных выборочных статистических данных, таких как среднее значение или медиана.
Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности.
Соотношение между стандартной ошибкой и стандартным отклонением таково, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; чем больше размер выборки, тем меньше стандартная ошибка, потому что статистика будет приближаться к фактическому значению.
Стандартная ошибка считается частью статистики вывода. Он представляет собой стандартное отклонение среднего значения в наборе данных. Это служит мерой вариации случайных величин, обеспечивая измерение разброса. Чем меньше разброс, тем точнее набор данных.
Стандартная ошибка и стандартное отклонение являются показателями изменчивости, а показатели центральной тенденции включают среднее значение, медиану и т.
д.
Формула и расчет стандартной ошибки
Стандартную ошибку оценки можно рассчитать как стандартное отклонение, деленное на квадратный корень из размера выборки:
SE = σ / √n
где
- σ = стандартное отклонение генеральной совокупности
- √ n = квадратный корень из размера выборки
Если стандартное отклонение генеральной совокупности неизвестно, вы можете заменить стандартное отклонение выборки, s , в числителе, чтобы аппроксимировать стандартную ошибку.
Требования для стандартной ошибки
При выборке населения обычно рассчитывается среднее или среднее значение. Стандартная ошибка может включать отклонение между рассчитанным средним значением генеральной совокупности и тем значением, которое считается известным или считается точным. Это помогает компенсировать любые случайные неточности, связанные со сбором образца.
В случаях, когда собирается несколько выборок, среднее значение каждой выборки может немного отличаться от других, создавая разброс между переменными.
Этот разброс чаще всего измеряется как стандартная ошибка с учетом различий между средними значениями в наборах данных.
Чем больше точек данных участвует в расчетах среднего, тем меньше стандартная ошибка. Когда стандартная ошибка мала, говорят, что данные более репрезентативны для истинного среднего значения. В случаях, когда стандартная ошибка велика, данные могут иметь некоторые заметные отклонения.
Стандартное отклонение — это представление разброса каждой из точек данных. Стандартное отклонение используется для определения достоверности данных на основе количества точек данных, отображаемых на каждом уровне стандартного отклонения. Стандартные ошибки больше служат способом определения точности выборки или точности нескольких выборок путем анализа отклонений в пределах средних значений.
Стандартная ошибка и стандартное отклонение
Стандартная ошибка нормализует стандартное отклонение относительно размера выборки, используемой в анализе. Стандартное отклонение измеряет величину дисперсии или дисперсии данных, разбросанных вокруг среднего значения.
Стандартную ошибку можно рассматривать как дисперсию средних оценок выборки вокруг истинного среднего значения генеральной совокупности. По мере увеличения размера выборки стандартная ошибка будет уменьшаться, указывая на то, что оценочное среднее значение выборки лучше приближается к среднему значению генеральной совокупности.
Пример стандартной ошибки
Скажем, аналитик изучил случайную выборку из 50 компаний из S&P 500, чтобы понять связь между коэффициентом цена/прибыль акции и последующими 12-месячными результатами на рынке. Предположим, что полученная оценка равна -0,20, что указывает на то, что на каждый 1,0 пункт отношения P/E акции приносят на 0,2% более низкую относительную доходность. В выборке из 50 человек стандартное отклонение оказалось равным 1,0.
Таким образом, стандартная ошибка:
SE = 1,0/ √ 50 = 1/7,07 = 0,141
Таким образом, мы сообщаем оценку как -0,20% ± 0,14, что дает нам доверительный интервал (-0,34 – -0,06).
Таким образом, истинное среднее значение связи P/E с доходностью S&P 500 с высокой степенью вероятности попадет в этот диапазон.
Скажем теперь, что мы увеличиваем выборку акций до 100 и обнаруживаем, что оценка немного меняется с -0,20 до -0,25, а стандартное отклонение падает до 0,9.0. Таким образом, новая стандартная ошибка будет:
SE = 0,90/ √ ·100 = 0,90/10 = 0,09.
Результирующий доверительный интервал становится -0,25 ± 0,09 = (-0,34 – -0,16), что является более узким диапазоном значений.
Что подразумевается под стандартной ошибкой?
Стандартная ошибка интуитивно представляет собой стандартное отклонение выборочного распределения. Другими словами, он показывает, насколько вероятно расхождение в точечной оценке, полученной на основе выборки, по сравнению с истинным средним значением генеральной совокупности.
Что такое хорошая стандартная ошибка?
Стандартная ошибка измеряет величину ожидаемого расхождения выборочной оценки по сравнению с истинным значением генеральной совокупности.
Следовательно, чем меньше стандартная ошибка, тем лучше. На самом деле стандартная ошибка, равная нулю (или близкая к ней), указывает на то, что оценочное значение точно соответствует истинному значению.
Как найти стандартную ошибку?
Стандартная ошибка берет стандартное отклонение и делит его на квадратный корень из размера выборки. Многие статистические пакеты программного обеспечения автоматически вычисляют стандартные ошибки.
Итог
Стандартная ошибка (SE) измеряет разброс оценочных значений, полученных из выборки, относительно истинного значения, которое должно быть найдено в совокупности. Статистический анализ и вывод часто включают выборку и проведение статистических тестов для определения ассоциаций и корреляций между переменными. Таким образом, стандартная ошибка говорит нам, с какой степенью достоверности мы можем ожидать, что оценочное значение приблизится к значению генеральной совокупности.
Стандартная ошибка измерения – Human Kinetics
Это выдержка из 5-го издания «Статистика в кинезиологии с веб-ресурсом» Джозефа Вейра и Уильяма Винсента.
Коэффициент внутриклассовой корреляции дает оценку относительной погрешности измерения; то есть он безразмерный и чувствителен к изменчивости между субъектами. Поскольку общая форма коэффициента внутриклассовой корреляции представляет собой отношение изменчивости (см. уравнение 13.04), он отражает способность теста различать субъектов. Это полезно для оценки размера выборки и статистической мощности, а также для оценки степени затухания корреляции. Таким образом, коэффициент внутриклассовой корреляции полезен исследователям при оценке полезности теста для использования в исследовании с участием нескольких субъектов. Однако это не особенно информативно для практикующих врачей, таких как клиницисты, тренеры и преподаватели, которые хотят сделать выводы о людях на основе результатов теста.
Для практиков более полезным инструментом является стандартная ошибка измерения ( SEM ; не путать со стандартной ошибкой среднего). Стандартная ошибка измерения является абсолютной оценкой надежности теста, что означает, что он имеет оцениваемые единицы теста и не чувствителен к изменчивости данных между субъектами.
Кроме того, стандартная ошибка измерения является показателем точности теста или шумом теста от испытания к испытанию. Стандартную ошибку измерения можно оценить с помощью двух общих формул. Первая формула является наиболее распространенной и оценивает стандартную ошибку измерения как
(13.06)
где ICC — коэффициент внутриклассовой корреляции, как описано выше, а SD — стандартное отклонение всех оценок относительно общего среднего. Стандартное отклонение можно быстро рассчитать из повторных измерений ANOVA как
(13,07)
, где N — общее количество баллов.
Поскольку коэффициент внутриклассовой корреляции может быть рассчитан несколькими способами и чувствителен к изменчивости между субъектами, стандартная ошибка измерения, рассчитанная с использованием уравнения 13.06, будет варьироваться в зависимости от этих факторов. Для иллюстрации мы используем данные примера, представленные в таблице 13.5, и сводку ANOVA из таблицы 13.6.
Во-первых, стандартное отклонение рассчитывается из уравнения 13.07 как
Напомним, что мы рассчитали ICC (1,1) = 0,30, ICC (2,1) = 0,40 и ICC (3,1) = 0,73. Соответствующая стандартная ошибка значений измерений, рассчитанных с использованием уравнения 13.07, составляет
для ICC (1,1),
для ICC (2,1),
и
для ICC (3,1).
Обратите внимание, что стандартная ошибка значения измерения может заметно различаться в зависимости от величины используемого коэффициента внутриклассовой корреляции. Также обратите внимание, что чем выше коэффициент внутриклассовой корреляции, тем меньше стандартная ошибка измерения. Этого следует ожидать, потому что надежный тест должен иметь высокий коэффициент надежности, и мы также ожидаем, что надежный тест будет иметь небольшой шум от испытания к испытанию, и поэтому стандартная ошибка должна быть небольшой. Однако большие различия между стандартными ошибками оценок измерений в зависимости от того, какое значение коэффициента внутриклассовой корреляции используется, несколько неудовлетворительны.
Вместо этого мы рекомендуем использовать альтернативный подход к оценке стандартной ошибки измерения:
(13,08)
где MS E — член среднеквадратичной ошибки из повторных измерений ANOVA. Из таблицы 13.6, МС Е = 1044,54. Результирующая стандартная ошибка измерения рассчитывается как
Это значение стандартной ошибки измерения не меняется в зависимости от используемой модели внутриклассового коэффициента корреляции, поскольку среднеквадратическая ошибка постоянна для заданного набора данных. Кроме того, стандартная ошибка измерения по уравнению 13.08 не чувствительна к изменчивости между субъектами. Для иллюстрации вспомним, что данные в таблице 13.7 были созданы путем модификации данных в таблице 13.1 таким образом, что вариабельность между субъектами (большие стандартные отклонения) была увеличена, но средние значения не изменились. Среднеквадратическая ошибка для данных в таблице 13.
1 (см. таблицу 13.2, MS E = 1070,28) не изменились с добавлением межсубъектной изменчивости (см. таблицу 13.8). Следовательно, стандартная ошибка значений измерения для обоих наборов данных одинакова при использовании уравнения 13.08:
Интерпретация стандартной ошибки измерения
Как отмечалось ранее, стандартная ошибка измерения отличается от внутриклассового коэффициента корреляции тем, что стандартная ошибка измерения является абсолютным показателем надежности и указывает на прецизионность теста. Стандартная ошибка измерения отражает согласованность оценок по отдельным предметам. Кроме того, в отличие от коэффициента внутриклассовой корреляции, он в значительной степени не зависит от генеральной совокупности, по которой рассчитываются результаты. То есть утверждается, что он отражает неотъемлемую характеристику теста, независимо от испытуемых, от которых были получены данные.
Стандартная ошибка измерения также имеет некоторые применения, особенно полезные для практикующих врачей, таких как клиницисты и тренеры.
Во-первых, его можно использовать для построения доверительного интервала по результатам теста индивидуума. Этот доверительный интервал позволяет практикующему врачу оценить границы истинной оценки человека. Общая форма расчета этого доверительного интервала:
T = S ± Z крит ( SEM ), (13.09)
где T — истинный балл испытуемого, S — балл испытуемого за тест, Z крит — критический Z 9003 7 баллов за желаемый уровень достоверность (например, Z = 1,96 для 95% ДИ). Предположим, что наблюдаемая оценка испытуемого ( S ) в тесте Вингейта составляет 850 ватт. Поскольку все наблюдаемые оценки включают некоторую ошибку, мы знаем, что 850 ватт, скорее всего, не является истинной оценкой испытуемого. Предположим, что данные в таблице 13.7 и соответствующая сводка ANOVA в таблице 13.8 применимы, так что стандартная ошибка измерения для теста Вингейта составляет 32,72 Вт, как показано ранее.
Используя уравнение 13.09и желаемый 95% CI, результирующий доверительный интервал составляет
T = 850 Вт ± 1,96 (32,72 Вт) = 850 ± 64,13 Вт = от 785,87 до 914,13 Вт.
Таким образом, мы можем сделать вывод, что истинная оценка субъекта находится где-то между примерно 785,9 и 914,1 Вт (при 95% LOC). Этот процесс может быть повторен для любого последующего человека, который выполняет тест.
Следует отметить, что процесс, описанный с помощью уравнения 13.09, не совсем корректен, и более сложная процедура может дать более точный доверительный интервал. Для получения дополнительной информации см. Weir (2005). Однако для большинства приложений повышенная точность не стоит дополнительной вычислительной сложности.
Второе применение стандартной ошибки измерения, особенно полезное для практиков, которым необходимо делать выводы об отдельных спортсменах или пациентах, — это возможность оценить изменение результатов или минимальную разницу, которую необходимо считать реальной (иногда называемую минимальное обнаруживаемое изменение или минимальное обнаруживаемое различие).
Это типично в ситуациях, когда практикующий врач измеряет работоспособность человека, а затем выполняет какое-либо вмешательство (например, программу упражнений или терапевтическое лечение). Затем после вмешательства проводится тест, и практикующий врач хочет знать, действительно ли человеку стало лучше. Предположим, что спортсмен улучшил показатели теста Вингейта на 100 ватт после 8-недельной программы тренировок. Сообразительный тренер должен спросить, является ли улучшение на 100 ватт реальным улучшением анаэробной выносливости или изменение на 100 ватт находится в пределах того, что можно было бы ожидать просто из-за погрешности измерения теста Вингейта. Минимальную разницу можно оценить как
(13.10)
Опять же, используя предыдущее значение SEM = 32,72 Вт и 95% ДИ, минимальное значение разницы оценивается как быть не менее 90,7 Вт, чтобы практикующий врач был уверен при 95% LOC, что изменение индивидуальной производительности было реальным улучшением. В нашем примере мы были бы на 95% уверены, что улучшение на 100 Вт реально, потому что это больше, чем мы ожидали, только из-за ошибки измерения теста Вингейта.
Хопкинс (2000) утверждал, что 95% LOC является слишком строгим для таких ситуаций, и следует использовать менее строгий уровень достоверности. Это легко сделать, выбрав критическую оценку Z , соответствующую желаемому уровню достоверности.
Интуитивно не очевидно, почему необходимо использование термина в уравнении 13.10. То есть можно подумать, что простое использование уравнения 13.09 для построения доверительного интервала истинной оценки, связанного с оценкой до вмешательства, а затем проверка того, выходит ли оценка после вмешательства за пределы этой границы, даст ответ, который мы ищем. Однако этот аргумент игнорирует тот факт, что и оценка до вмешательства, и оценка после вмешательства измеряются с ошибкой, и этот подход учитывает только ошибку измерения в оценке до вмешательства. Поскольку обе наблюдаемые оценки были измерены с ошибкой, простое наблюдение за тем, выходит ли вторая оценка за пределы доверительного интервала первой оценки, не учитывает оба источника ошибки измерения.
Мы используем этот термин, потому что нам нужен индекс изменчивости оценок различий при вычислении минимальной разницы. Стандартное отклонение оценок различий ( SD d ) обеспечивает такой индекс, и когда есть только два измерения, как здесь, мы можем найти стандартное отклонение оценок различий, умножив стандартную ошибку измерение по . Уравнение 13.10 можно переосмыслить как
MD = SD d × Z крит .
Как и в уравнении 13.09, подход, описанный в уравнении 13.10, не является строго правильным, и несколько более сложная процедура может дать несколько более точный доверительный интервал. Однако для большинства приложений описанных процедур достаточно.
Дополнительным способом интерпретации размера стандартной ошибки измерения является преобразование его в тип коэффициента вариации ( CoV ). Вспомним из главы 5, что мы интерпретировали размер стандартного отклонения, разделив его на среднее значение, а затем умножив на 100, чтобы преобразовать значение в проценты (см.