Систематические погрешности — Студопедия
Классы точности средств измерений. Классификация погрешностей средств измерений
Погрешность средства измерений  – разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.
– разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.
Погрешность меры – разность между номинальным значением меры и действительным значением воспроизводимой ею величины. Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением, которое воспроизводится образцовым средством измерений или мерой. Для самой меры показанием является ее номинальное значение.
На рисунке 3.1 показана классификация погрешностей средств измерений, в которой они условно разбиты на пять групп в зависимости от природы их происхождения.
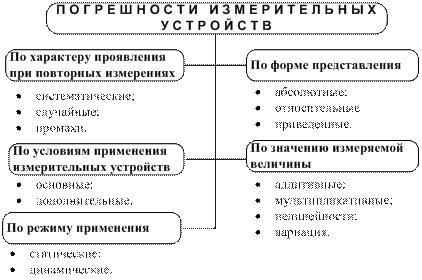
Рисунок 3.1 – Классификация погрешностей средств измерений
Систематическая погрешность средства измерений 
Систематическая погрешность конкретного средства измерений, как правило, будет отличаться от систематической погрешности другого экземпляра средства измерений этого же типа, вследствие чего для группы однотипных средств измерений систематическая погрешность может иногда рассматриваться как случайная погрешность. Причины возникновения систематических погрешностей и их классификация будут рассмотрены отдельно.
Случайная погрешность средства измерений  (случайная погрешность) – составляющая погрешности измерения, которая изменяется случайным образом. случайная погрешность может быть обнаружена при повторных измерениях одной и той же величины, когда получаются неодинаковые результаты. Её нельзя исключить, но их влияние на результата измерения может быть теоретически учтено методами теории вероятности и математической статистики.
(случайная погрешность) – составляющая погрешности измерения, которая изменяется случайным образом. случайная погрешность может быть обнаружена при повторных измерениях одной и той же величины, когда получаются неодинаковые результаты. Её нельзя исключить, но их влияние на результата измерения может быть теоретически учтено методами теории вероятности и математической статистики.
Промах – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Иногда вместо термина «промах» применяют термин грубая погрешность измерений.
Промахи связаны с резким нарушением условий испытаний при отдельном наблюдении: толчки, неисправности измерительной аппаратуры, неправильные действия наблюдателя. Результаты измерений, содержащие промахи, должны быть отброшены как недостоверные.
Основная погрешность средства измерений (основная погрешность) – погрешность средства измерений, применяемого в нормальных условиях.
Дополнительная погрешность средства измерений (дополнительная погрешность) – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.
Статическая погрешность средства измерений (статическая погрешность) – погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную.
Динамическая погрешность средства измерений (динамическая погрешность) – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины.
Абсолютная погрешность средства измерений (абсолютная погрешность) – погрешность средства измерений, выраженная в единицах измеряемой физической величины
D = хизм – х д , (3.1)
где хизм – измеренное значение, хд – действительное значение измеряемой величины.
Абсолютное значение погрешности – значение погрешности без учета ее знака (модуль погрешности). Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.
Относительная погрешность средства измерений (относительная погрешность) – погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или к действительному значению измеренной физической величины
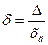 (3.2)
(3.2)
или
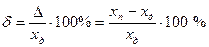 . (3.2*)
. (3.2*)
Приведенная погрешность средства измерения (приведенная погрешность) – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, по-
стоянному во всем диапазоне измерений или в части диапазона
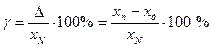 , (3.3)
, (3.3)
где 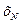 – нормирующее значение.Часто за нормирующее значение принимают верхний предел измерений.
– нормирующее значение.Часто за нормирующее значение принимают верхний предел измерений.
Аддитивная погрешность (по лат. – получаемая путем сложения) – погрешность, не зависящая от измеряемой величины. По закономерности проявления аддитивные погрешности могут быть случайными или систематическими.
Случайная аддитивная погрешность, например, вызываемая трением в опорах измерительного механизма, контактными сопротивлениями, дрейфом нуля и др., при изменении измеряемой величины принимать произвольное, но не зависящее от измеряемой величины значения. Её предельные значения образуют на характеристике полосу постоянной величины (рисунок 3.2,а). Точно такая же картина будет, если погрешность представляется как приведенная, поскольку знаменатель в выражении (3.3) не изменяется на протяжении всей шкалы независимо от значения измеряемой величины.
Примером систематической аддитивной погрешности является смещение нуля характеристики аналогового средства измерения (рисунок 3.2,б).
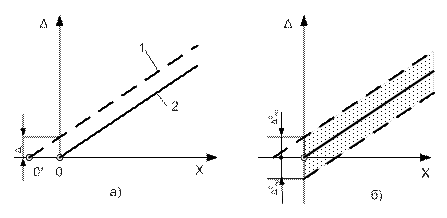
1 – фактическая характеристика, смещенная влево на длину О-О¢; 2 – номинальная характеристика прибора; Dс – значение систематической погрешности;
D0пр – предельное значение случайной погрешности
Рисунок 3.2 – Смещение характеристик аналогового измерительного прибора под влиянием аддитивных систематической (а) и случайной (б) погрешностей
Мультипликативная погрешность (по лат. – получаемая путем умножения
Пример – Источники мультипликативной погрешности – действие влияющих величин на параметры элементов и узлов СИ, например, изменение собственного сопротивления амперметра и встроенного в него шунта при изменении температуры окружающей среды.
В этом случае результат измерения определяется по формуле:
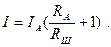
Поскольку при изменении температуры окружающей среды сопротивления 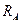 и
и 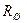 изменяются неодинаково, т.к. сделаны из разных материалов, погрешность измерения будет изменяться пропорционально соотношению этих сопротивлений.
изменяются неодинаково, т.к. сделаны из разных материалов, погрешность измерения будет изменяться пропорционально соотношению этих сопротивлений.
Погрешность нелинейности имеет нелинейную зависимость от измеряемой величины. Чаще всего возникает как систематическая погрешность, связанная с линеаризацией номинальной статической характеристики.
Вариация имеет нелинейную зависимость от измеряемой величины, появляется вследствие гистерезисных явлений, вариации, проявляющейся при подходе к измеряемой точке со стороны меньших и больших значений; проявляется как систематическая погрешность (рисунок 3.3).
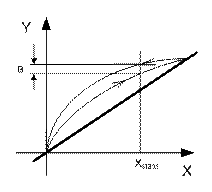
Рисунок 3.3 – Графическое представление вариации
Учёт всех нормируемых метрологических характеристик средств измерений является сложной и трудоёмкой процедурой. На практике такая точность не нужна. Поэтому для средств измерений, используемых в повседневной практике, принято деление на классы точности.
Класс точности средств измерений (класс точности) – обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая нормируемыми метрологическими характеристиками.
Класс точности дает возможность судить о том, в каких пределах находится погрешность средства измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Это важно при выборе средств измерений в зависимости от заданной точности измерений. Класс точности средств измерений конкретного типа устанавливают в стандартах технических требований (условий) или в других нормативных документах.
Нормируемые метрологические характеристики типа средства измерений (нормируемые метрологические характеристики) – совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативными документами на средства измерений
Требования к нормируемым метрологическим характеристикам устанавливаются в стандартах на средства измерений конкретного типа.
Например, для электроизмерительных приборов нормируют:
– пределы допускаемых погрешностей и соответствующие рабочие области влияющих величин;
– пределы допускаемых дополнительных погрешностей и соответствующие рабочие области влияющих величин;
– пределы допускаемой вариации показаний;
– невозвращение указателей к нулевой отметке.
Предел допускаемой погрешности средства измерений (предел допускаемой погрешности, предел погрешности) – наибольшее значение погрешности средств измерений, устанавливаемое нормативным документом для данного типа средств измерений, при котором оно еще признается годным к применению.
При превышении установленного предела погрешности средство измерений признается негодным для применения (в данном классе точности).
Обычно устанавливают пределы допускаемой погрешности, то есть границы зоны, за которую не должна выходить погрешность.
Пример –
Пределы допускаемой абсолютной основной погрешности устанавливают по формуле
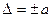 (3.4)
(3.4)
или
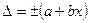 , (3.4*)
, (3.4*)
где 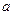 и
и 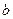 – положительные числа, не зависящие от
– положительные числа, не зависящие от 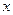 .
.
Пределы допускаемой приведенной погрешности
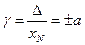 , (3.5)
, (3.5)
где 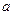 – положительное число, выбираемое из ряда
– положительное число, выбираемое из ряда
(1; 1,5; 2,0; 2,5; 4,0; 5,0; 6,0)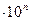 , при
, при 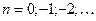 . (3.6)
. (3.6)
Пределы допускаемой относительной основной погрешности определяют из уравнения
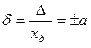 , (3.7)
, (3.7)
если 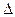 установлено по формуле (3.4).
установлено по формуле (3.4).
Если же D определено по формуле (3.4*), т.е. имеется мультипликативная составляющая погрешности, пределы допускаемой относительной основной погрешности определяют по формуле
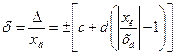 , (3.8)
, (3.8)
где 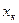 – больший по модулю из пределов измерений;
– больший по модулю из пределов измерений; 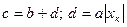 . Значения чисел
. Значения чисел 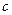 и
и 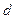 должны быть округлены до чисел из ряда (3.6).
должны быть округлены до чисел из ряда (3.6).
Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств. Классы точности присваиваются средствам измерений с учётом результатов государственных приёмочных испытаний.
Общие положения о делении средств измерений на классы точности и способы нормирования метрологических характеристик регламентированы ГОСТ 8.401—80. Однако этот стандарт не устанавливает классы точности средств измерения, для которых предусмотрены нормы отдельно для систематической и случайной составляющих погрешности, а также если необходимо учитывать динамические характеристики.
Если класс точности прибора установлен по пределу допускаемой относительной основной погрешности, т.е по значению погрешности чувствительности [см. формулу (3.7)] и форма полосы погрешности принята чисто мультипликативной, обозначаемое на шкале значение класса точности обводится кружком.
Пример – 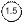 обозначает, что
обозначает, что 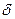 = 1,5 %.
= 1,5 %.
Если же полоса погрешности принята аддитивной и прибор нормируется по пределу допускаемой приведенной основной погрешности [см. формулу (3.5)], т.е. по значению погрешности нуля (таких приборов большинство), то класс точности указывается на шкале без каких-либо подчеркиваний.
Пример – 1,5 обозначает, что 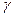 = 1,5 %.
= 1,5 %.
Если шкала прибора неравномерная (например, у омметров), предел допускаемой основной приведенной погрешности выражается формулой (3.5), а нормирующее значение принято равным длине шкалы или ее части, класс точности обозначается на шкале одним числом, помещенным между двумя линиями, расположенными под углом.
Пример – 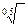 обозначает, что
обозначает, что 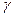 = 0,5 %.
= 0,5 %.
Если средство измерений обладает как аддитивной, так и мультипликативной полосой погрешности, а пределы допускаемой относительной погрешности в процентах устанавливаются формулой (3.8), классы точности обозначают числами с и d (в процентах), разделяя их косой чертой.
Пример – Если установлено, что для средства измерения 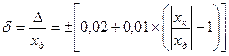 , где с = 0,02; d = 0,01, то обозначение в документации будет «класс точности 0,02/0,01», а на приборе 0,02/0,01.
, где с = 0,02; d = 0,01, то обозначение в документации будет «класс точности 0,02/0,01», а на приборе 0,02/0,01.
Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей по формуле (3.4), классы точности обозначают прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения.
Для всех рассмотренных случаев вместе с условным обозначением класса точности на шкале, щитке или корпусе средств измерений наносится номер стандарта или технических условий, устанавливающих технические требования на эти средства измерений. Таким образом, обозначение класса точности средства измерений дает достаточно полную информацию для вычисления приближенной оценки погрешностей результатов измерений.
Примеры обозначения классов точности на шкалах приборов приведены на рисунке 3.4.
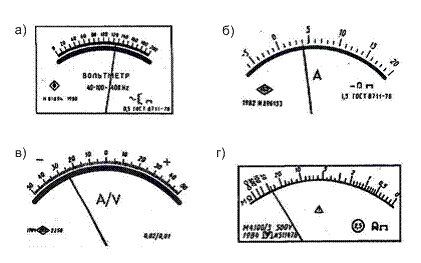
а – вольтметр класса точности 0,5 с равномерной шкалой;
б – амперметр класса точности 1,5 с равномерной шкалой; в – амперметр класса точности 0,02/0,01 с равномерной шкалой; г – мегаомметр класса точности 2,5 с неравномерной шкалой.
Рисунок 3.4 – Лицевые панели приборов

ТОП 10: |
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒ Говоря о погрешностях измерений, следует, прежде всего, упомянуть о грубых погрешностях (промахах), возникающих вследствие недосмотра экспериментатора или неисправности аппаратуры. Такие ошибки происходят, если, например, экспериментатор неправильно прочтет номер деления на шкале, если в электрической цепи произойдет замыкание и вследствие других подобных причин. Грубых ошибок следует избегать. Если установлено, что они произошли, соответствующие измерения нужно отбрасывать. Не связанные с грубыми ошибками погрешности опыта делятся на случайные и систематические. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего. Погрешности, меняющие величину и знак от опыта к опыту, называют случайными. Случайные погрешности могут быть связаны с сухим трением (из-за которого стрелка прибора вместо того, чтобы останавливаться в правильном положении, «застревает» вблизи него), с люфтами в механических приспособлениях, с тряской, которую в городских условиях трудно исключить, с несовершенством объекта измерений (например, при измерении диаметра проволоки, которая из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение) или с особенностями самой измеряемой величины. Рассмотрим последний случай. Пусть мы измеряем число космических частиц, проходящих в минуту через счетчик. При достаточно больших размерах счетчика это число может составлять несколько сот или даже тысяч. Пусть в первую минуту через счетчик прошло 345 частиц. Повторяя измерение, найдем, что в разных опытах получаются разные числа (вообще говоря, не слишком отличающиеся от 345). Это происходит потому, что в нашем случае число частиц, проходящих в минуту через счетчик, является случайной величиной. Космическое излучение правильно характеризовать не числом частиц, которые прошли через счетчик за выбранную минуту, а средним числом частиц, проходящих в минуту через счетчик, и средним отклонением чисел в различных опытах. Не следует думать, что, говоря о прохождении космических частиц через счетчик, мы выбрали исключительное явление. Подобный разброс результатов измерения наблюдается при изучении (с помощью счетчиков) числа распадов в радиоактивных источниках, при изучении очень слабых токов, когда через измерительный прибор за время измерения проходит не очень большое число электронов или ионов (например, в чувствительных масс-спектрометрах), и во многих других случаях. Случайные погрешности эксперимента исследуются путем сравнения результатов, полученных при нескольких опытах, поставленных в одинаковых условиях. Два-три измерения следует производить всегда. Если результаты совпали, то на этом следует остановиться. Если же они расходятся, нужно попытаться понять причину расхождения. Часто она связана с тем, что прибор неисправен, ненадежно закреплен или плохо смазан, что электрические контакты не пропаяны или недостаточно зажаты. В этом случае, прежде всего, нужно попытаться исправить аппаратуру. Если устранить причину не удается, нужно произвести несколько измерений и записать все полученные результаты. Ниже мы расскажем о том, как следует поступать с полученными числами. Систематические погрешности сохраняют свою величину. (и знак!) во время эксперимента. Они могут быть связаны с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического, винта, не равные плечи весов) и с самой постановкой опыта (определение скорости поезда по проходимому им расстоянию на участке, где движение происходит с небольшим ускорением, которое ускользнуло от внимания экспериментатора, влияние трения и т. д.). В результате систематических погрешностей разбросанные из-за случайных ошибок результаты опыта колеблются не вокруг истинного, а вокруг некоторого смещенного значения.
пренебрежимо мала. Измеренные значения отличаются от истинного вследствие случайных ошибок: опыта. На рис. 1, б изображены результаты опыта при наличии как случайных, так и систематических погрешностей. При желании систематические погрешности опыта могут быть изучены и скомпенсированы путем внесения поправок в результаты измерений. Неравноплечность весов можно исследовать, меняя местами грузы на чашках весов. Неточность шкал электроизмерительных приборов можно установить, сравнивая их показания с показаниями более точных приборов, и т. д. Как правило, этого не делают. Если систематическая погрешность опыта для выбранной цели слишком велика, то обычно оказывается проще поставить новые, более точные приборы, чем исследовать погрешности старых. Не следует думать, что различие между случайными и систематическими погрешностями является абсолютным. Оно связано с постановкой опыта. Производя измерения тока не одним, а несколькими разными амперметрами, мы превращаем систематическую ошибку, связанную с неточностью шкалы, в случайную ошибку, величина (и знак!) которой зависит от того, какой поставлен амперметр в данном опыте и т. д. Однако во всяком данном опыте – при заданной его постановке – различие между систематическими и случайными погрешностями всегда можно и нужно устанавливать с полной определенностью. Случайные погрешности Случайные величины, к которым относятся случайные погрешности, изучаются в теории вероятностей и в математической статистике. Мы здесь опишем – с пояснениями, но без доказательств – основные свойства и основные правила обращения с такими величинами в том объеме, который необходим для обработки результатов измерений, полученных в лаборатории. В этом параграфе мы будем предполагать, что систематические погрешности пренебрежимо малы и все ошибки сводятся к случайным. Позднее, в § 5, мы обсудим, как следует поступать в тех случаях, когда нужно принимать во внимание как случайные, так и систематические погрешности опыта. Рассмотрим для примера данные, полученные при измерении массы тела на весах, у которых имеется область застоя из-за трения призмы на подушке (разброс результатов для наглядности преувеличен). Пусть масса тела близка к 48 мг, результат измерений удается отсчитать по шкале с точностью до 0,1 мг. Имеем:
Вместо одного нужного нам результата мы получили одиннадцать. Что делать с полученными цифрами? Как найти из них достаточно близкое к истинному значение массы тела и как оценить погрешность полученного результата? Этот вопрос подробно изучается в математической статистике. Мы здесь изложим соответствующие правила без вывода. В качестве наилучшего значения для измеренной величины обычно принимают среднее арифметическое из всех полученных результатов:
В нашем случае получим mср = Этому результату следует приписать погрешность, определяемую формулой
В нашем случае Результат опыта записывается в виде х = xср ± σx.(5) В нашем случае m = (48,10± 0,10)мг. Рассмотрим формулы (3) и (4). Прежде всего, попытаемся понять, как зависит результат расчета от числа измерений. Формула (3) показывает, что xср от числа измерений зависит слабо. Все слагаемые, входящие в числитель, приблизительно равны друг другу. Их сумма пропорциональна числу слагаемых. После деления на знаменатель получается величина, мало зависящая от числа измерений. Так, конечно, и должно быть. Среднее измеренное значение – при правильной методике опыта – всегда лежит вблизи истинного значения и в разных независимых сериях измерений испытывает вокруг него небольшие случайные колебания. Погрешность опыта, определяемая формулой (4), с увеличением числа измерений п уменьшается как
(Число членов суммы в (4) растет как п, числитель (4) поэтому увеличивается как Формула (4) может быть записана в несколько ином виде
При такой записи множитель 1/
При обсуждении смысла величины σ следует помнить, что истинную величину погрешности невозможно узнать до тех пор, пока из каких-либо других опытов (или соображений) не удастся определить искомую величину с существенно лучшей точностью. Но тогда рассматриваемые опыты потеряют значение, и их погрешность никого не будет интересовать. Как уже отмечалось, погрешность результата не столько определяют, сколько оценивают. Оценка (4) подобрана так, что при проведении многочисленных серий измерений погрешность в 2/3 случаев оказывается меньше σx, а в 1/3 случаев больше, чем σx. Иначе говоря, если бы мы – в нашем случае – провели не одну серию из 11 взвешиваний, а десять таких серий, то мы могли бы ожидать, что в шести или семи из них усредненный результат будет отличаться от истинной массы тела меньше чем. на 0,1 мг. а в остальных случаях больше, чем, на 0,1 мг. Погрешность, определенную с достоверностью 2/3, обычно называют стандартной (или среднеквадратичной) погрешностью опытов, а ее квадрат – дисперсией. Можно показать, что, как правило, погрешность опыта только в 5% случаев превосходит ±2σ и почти всегда оказывается меньше ±3σ. На первый взгляд из сказанного можно сделать вывод, что, беспредельно увеличивая число измерений, можно даже с самой примитивной аппаратурой получить очень хорошие результаты. Это, конечно, не так. С увеличением числа измерений уменьшается только случайная погрешность опытов. Методические погрешности и погрешности, связанные с несовершенством приборов (например, с неправильностью их шкалы), при увеличении числа опытов не меняются. В приведенном выше примере результат взвешивания округлялся до десятых долей миллиграмма. Это-делалось потому, что сотых долей отсчитать было нельзя. Одна только ошибка отсчета составляет при этом около 0,1 мг. Поэтому погрешность результата ни при каком числе опытов не может быть сделана меньше. Число опытов в нашем случае было-выбрано разумно. Из приведенных в таблице цифр ясно, что при однократном измерении мы могли ошибиться на несколько десятых. Среди цифр встречаются результаты, отличающиеся на 0,3 и даже на 0,5 от среднего. После усреднения по 11 измерениям погрешность существенно уменьшилась. Но если окажется нужным узнать массу тела с лучшей, чем это мы сделали, точностью, то недостаточно просто увеличить число измерений. Придется взять более точные весы, позволяющие производить измерения не до десятых, а, скажем, до сотых долей миллиграмма. Скажем несколько слов о формуле (4). Эта формула позволяет хорошо оценивать величину стандартной погрешности в тех случаях, когда число опытов оказывается не меньше 4–5. При меньшем числе опытов лучше применять другие, более сложные оценки. Их мы, однако, рассматривать не будем, во-первых, чтобы не удлинять и не усложнять текста, а, во-вторых, по той причине, что надежность всех этих оценок при малом числе измерений оказывается невысокой. Систематические погрешности Оценку систематических погрешностей экспериментатор производит, анализируя особенности методики, паспортную точность приборов и производя контрольные опыты. Систематические погрешности электроизмерительных приборов, выпускаемых промышленностью (амперметров, вольтметров, мостов, потенциометров и т. д.), определяются их классом точности, который обычно выражают в процентах. Амперметр класса 0,2 (если он, конечно, исправен и проходит систематическую проверку) позволяет производить измерения с абсолютной погрешностью, не превосходящей 0,2% от тока, соответствующего полной шкале прибора. На всех участках шкалы – в ее начале, середине и конце – эта погрешность одна и та же. Отметим различие в правилах определения погрешностей и в определении класса точности. Погрешности принято характеризовать среднеквадратичными ошибками. При многочисленных измерениях реальная ошибка опытов только в 2/3 случаев меньше среднеквадратичной, а в 1/3 случаев превосходит ее. Класс точности определяет максимально возможное значение погрешности. Приборы, которые могут давать – хотя бы иногда – бóльшие погрешности, должны быть отнесены к другому классу. Такое различие в определениях очень неудобно. В научных публикациях принято приводить именно среднеквадратичную ошибку, а вовсе не максимальную. Строгих формул для перевода одних погрешностей в другие не существует. Можно пользоваться следующим простым правилом: чтобы оценить среднеквадратичную погрешность измерений электроизмерительными приборами, следует погрешность, определяемую классом .точности прибора, разделить на два. Как уже отмечалось, класс электроизмерительных приборов определяет максимальную погрешность, величина которой не меняется при переходе от начала к концу шкалы. Относительная ошибка при этом резко меняется, поэтому приборы обеспечивают хорошую точность при отклонении стрелки почти на всю шкалу и не дают ее при измерениях в начале шкалы. Отсюда следует рекомендация: выбирать прибор (или шкалу многошкального прибора) так, чтобы стрелка прибора при измерениях заходила за середину шкалы. Говоря о систематических погрешностях опыта, следует сказать несколько слов об ошибке отсчета «на глаз». Большинство приборов не имеет нониуспых шкал. При этом доли деления отсчитываются на глаз. Эта ошибка составляет 1–2 десятых доли деления. При отсчетах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для облегчения установки глаза на многих приборах устанавливается зеркало («зеркальные приборы»). Глаз экспериментатора установлен правильно, если стрелка прибора закрывает свое изображение в зеркале. При работе с электроизмерительными приборами отсчет должен включать число целых делений и число десятых долей деления, если отсчет может быть произведен с этой точностью (если стрелка или зайчик не ходят и не дрожат, что может сделать аккуратный отсчет невозможным). Поясним указанное правило. Шкалы электроизмерительных приборов обычно изготовляют так, что одно деление шкалы приблизительно равно максимальной погрешности прибора. Зачем же в этом случае отсчитывать десятые доли деления? Ответ на этот вопрос читатель найдет в § 7. Забегая вперед, отметим, что при измерениях, при расчетах и при записи результатов, кроме надежно известных значащих цифр, всегда указывается одна, лишняя. Такая процедура, среди прочих, имеет и то преимущество, что позволяет вовремя замечать мелкие нерегулярности исследуемых зависимостей. Если, например, стрелка прибора при измерениях отклонилась на полделения назад, этот результат является надежным и в том случае, когда погрешность прибора равна целому делению. Несколько слов о точности линеек. Металлические линейки очень точны: миллиметровые деления наносятся с погрешностью не более ±0,05 мм, а сантиметровые – не хуже, чем с точностью 0,1 мм. Погрешность измерений, производимых с помощью таких линеек, практически равна погрешности отсчета на глаз. Деревянными или пластиковыми линейками лучше не пользоваться: их погрешности неизвестны и могут оказаться неожиданно большими. Исправный микрометр обеспечивает точность 0,01 мм, а погрешность измерений штангенциркулем определяется точностью, с которой может быть сделан отсчет, т. е. точностью нониуса (у штангенциркулей цена делений нониуса составляет обычно 0,1 или 0,05 мм). |
Любая процедура измерения вне зависимости от условий, в которых она проводится, сопряжена с погрешностями. Они представляют собой отклонения, искажающие представление о реальном значении величины.

Источники погрешностей
Отклонения возникают по самым разным причинам. К основным следует отнести:
- Несовершенство конструкций измерительных средств или неточность их изготовления.
- Несоблюдение правил при проведении процедуры.
- Человеческий фактор.
- Несовершенство методов и пр.
Классификация отклонений
В процессе измерения могут возникать систематические и случайные погрешности.
Систематические отклонения классифицируют по разным основаниям. В частности, в зависимости от характера проявления, их разделяют на периодические, постоянные и прогрессивные погрешности.
Также могут появиться грубые погрешности или промахи. Они возникают вследствие:
- Ошибок специалиста.
- Внезапного изменения условий измерения.
- Неисправности оборудования и пр.
 Систематические погрешности
Систематические погрешности
Эти отклонения, как правило, можно изучить до начала измерения. Такие показатели остаются постоянными или изменяются закономерно при повторных измерениях одной величины. Результат исследования может корректироваться путем внесения поправок, если числовое значение отклонения известно, или с помощью таких измерительных средств, которые позволяют исключить влияние этих погрешностей без определения их значения.
При повторных измерениях действуют определенные законы, в соответствии с которыми изменяются значения систематических погрешностей. Эти отклонения можно иногда определить экспериментально. Соответственно, результат можно уточнить путем поправки.
Характер проявления
Как говорилось выше, по этому признаку выделяют три группы систематических погрешностей. Это:
- Постоянные отклонения. К ним относят такие погрешности, которые на протяжение всего процесса измерения сохраняют свою величину. К примеру, если для определения какого-то показателя специалист использует шкалу прибора, градуировка которой имеет погрешность, то ее величина переносится на все результаты эксперимента.
- Прогрессивные отклонения. Такие погрешности убывают или возрастают в ходе измерений. К ним относят, к примеру, отклонения, появляющиеся в результате износа контактирующих элементов измерительных средств, постепенное уменьшение напряжения токового источника, от которого питается измерительная цепь, и пр.
- Периодические погрешности. Их значения определяются периодической функцией времени либо функцией перемещения указателя на приборе, используемом для измерения. Они возникают в индикаторах с круговой шкалой и стрелками.

Показатели отклонений могут изменяться за счет одновременного влияния нескольких систематических погрешностей. Это проявляется, например, при измерении температуры.
Другие виды
К систематическим отклонения относят также:
- Теоретические погрешности. Их еще называют погрешностями измерительного метода.
- Инструментальные погрешности.
- Отклонения, возникающие вследствие неправильного расположения измерительного прибора.
- Личные погрешности.
- Отклонения, обусловленные влиянием внешних факторов.
Инструментальные погрешности
К ним относят отклонения, обусловленные свойствами используемых измерительных средств. К примеру, равноплечие весы идеально равноплечими быть не могут.
Отклонения возникают также вследствие трения сочленений подвижных элементов измерительных устройств. Они могут возникать из-за износа оборудования. Показатель износа, соответственно, будет зависеть от интенсивности эксплуатации прибора.
Погрешность результата
Правильность показаний некоторых измерительных средств зависит от положения их подвижных элементов относительно неподвижных. Речь, в частности, о таких приборах, как равноплечие весы, средства, частью конструкции которых является маятник или иные подвижные подвешенные детали. При отклонении прибора от правильного положения смещается точка отсчета и возникает погрешность результата. Для предупреждения ее появления при установке приборов используются специальные устройства: уровни, отвесы и пр.

Влияние внешних факторов
Температура, влажность, давление воздуха являются внешними условиями, влекущими появление погрешностей при изменении их величин. Если показатели тех или иных факторов выходят за рамки заданных границ, то могут возникнуть и дополнительные отклонения.
Погрешности измерительного метода
Они могут возникать в случае, когда между измеряемым свойством или явлением и принципом работы измерительного прибора отсутствует теоретически доказанная зависимость.
Погрешность метода обуславливается допущениями или упрощениями при применении эмпирических зависимостей и формул. Такая ситуация возникает, к примеру, при измерении твердости металлов разными способами: методами Бринелля, Роквелла, Виккерса и т. д. В каждом из них заданы свои условные единицы. Перевод результатов осуществляется приближенно.
Субъективные отклонения
Личные погрешности обусловливаются индивидуальными свойствами человека. Они, в свою очередь, связаны с особенностями организма, укоренившимися навыками (зачастую неправильными). К примеру, у всех людей разная скорость реакции на сигнал: на звук она варьируется в пределах 0,082-0,195 с., а на свет – 0,15-0,225 с.

Исключение погрешностей
Систематические отклонения влекут смещение результатов измерений. Наибольшую опасность в этих ситуациях представляют отклонения, которые остаются невыявленными и о наличии которых специалисты даже не подозревают. Такие погрешности становились причиной неверных научных выводов, установления ложных законов физики, несовершенных конструкций измерительных средств, брака в производстве.
Систематические погрешности необходимо выявить и исключить либо учесть при измерении. Способы исключения и учета отклонения разделяют на несколько групп:
- Устранение источников отклонений до начала процедуры измерения (профилактика).
- Исключение погрешностей в ходе процесса (экспериментальные методы).
- Внесение поправок в результаты измерения. В этом случае погрешности исключаются методом вычисления.
- Оценка пределов систематических погрешностей, если их исключение невозможно.
Устранение источников
Профилактические мероприятия перед началом измерения считаются наиболее рациональным способом исключения погрешностей. В этом случае специалист частично или полностью освобождается от необходимости выявлять и устранять отклонения в ходе измерения.
К наиболее эффективным профилактическим мероприятиям относятся:
- Регулирование или ремонт измерительных средств. Необходимость в проведении этих мероприятий определяется при поверке.
- Корректировка установки прибора. Для предотвращения смещения точки отсчета, перекосов и прочих негативных явлений используются отвесы и прочие приспособления.

Для устранения погрешностей, возникающих вследствие влияния внешних факторов, можно удалить непосредственный их источник или обеспечить защиту измерительного прибора от воздействия.
Исключение погрешностей в ходе экспериментов предполагает обычно проведение повторного измерения. В этой связи, описанные выше способы целесообразнее применять при работе со стабильными явлениями, показателями и пр.
Внесение поправок в результаты
Этот способ исключения систематических погрешностей предполагает исправление результата измерения путем вычисления.
Самым распространенным вариантом внесения поправок считается алгебраическое суммирование результата и самой поправки (с учетом знака). Ее числовое значение равно систематическому отклонению, а знак – противоположен. Таким способом исключается аддитивное отклонение.
В отдельных случаях систематическую погрешность можно исключить посредством умножения показателя, полученного в результате измерения, на поправочный коэффициент. Его значение приближается к единице (больше или меньше ее). Поправочным коэффициентом целесообразно пользоваться при необходимости исключить мультипликативную погрешность.
Оценка пределов отклонения
Она производится, когда исключить систематические погрешности на практике невозможно. Такое явление имеет место, если отклонения изучены недостаточно или изучены, но не могут использоваться для корректировки результата. Последнее характерно для интегрирующих измерительных средств (счетчиков).

Случайные погрешности
При повторном измерении постоянного физического показателя в одних и тех же условиях зачастую результаты незначительно отличаются. При этом отклонения между величинами не являются систематическими, не подчиняются каким-либо закономерностям. Такие погрешности принято именовать случайными.
Отклонения возникают при одновременном воздействии на процесс (объект, измерительное средство, специалиста и пр.) ряда факторов. Каждый источник может незначительно влиять на результат, но их совокупное воздействие приведет к значительному отклонению от действительного показателя измеряемого объекта.
Источники воздействия по-разному проявляют себя в тот или иной временной промежуток. При этом они действуют обособленно друг от друга, не имея какой-либо закономерной связи. Это приводит к различиям по знаку и размеру расхождений в результатах измерений. Они изменяются без какой-либо связи как с прежними, так и с последующими величинами. Соответственно, каким-либо образом их учесть невозможно.
В рамках теории вероятности используются математические методы, позволяющие изучать свойства случайных явлений в их больших совокупностях. В ходе развития измерительной техники и метрологии было установлено, что они полностью соответствуют задаче исследования случайных отклонений. Во многих случаях результаты, получаемые с их помощью, согласуются с данными, полученными опытным путем.
В теории вероятности случайным считается такое событие, наступление которого однозначно предугадать невозможно. Другими словами, в определенной совокупности условий это событие может наступить, а может и не наступить. При применении этого определения к сфере измерений можно говорить о том, что при выполнении повторных экспериментов с некоторым физическим показателем в одних и тех же условиях каждый из вероятных незначительных источников случайного изменения результатов может либо появиться, либо не появиться. Следовательно, отклонения становятся непредсказуемыми и по своей величине, и по знаку.
Учитывая вышесказанное, можно дать следующее определение случайным погрешностям: это такие отклонения, которые изменяются от одного измерения к другому, не поддаются непосредственному учету в связи с хаотическим изменением, обусловлены одновременным влиянием на результат нескольких факторов, обособленных друг от друга.
Наличие случайных погрешностей, в отличие от систематических, достаточно легко обнаруживается при повторном измерении.
Разновидности систематических погрешностей
Систематическая погрешность – это погрешность, остающаяся постоянной или изменяющаяся по определенному закону при повторных измерениях одной и той же величины при поддержании неизменных внешних условий. К постоянным систематическим погрешностям относят погрешности градуировки шкалы аналоговых приборов, калибровки цифровых приборов, погрешности, обусловленные неточностью подгонки резисторов, температурными изменениями параметров элементов в приборах и т.д.
По степени зависимости от измеряемой величины погрешности делятся на аддитивные, мультипликативные и нелинейные. При аддитивной (рис. 5.1а) абсолютная погрешность не зависит от измеряемой величины в заданном диапазоне изменений этой величины. Если погрешность мультипликативная (рис. 5.1б), то абсолютная погрешность пропорционально изменяется с изменением измеряемой величины. Относительная погрешность при этом остается постоянной. Нелинейная погрешность (рис. 5.1в) имеет нелинейную зависимость от измеряемой величины. Обычно числовая оценка погрешности известна в виде усредненного значения, которое может иметь как положительный, так и отрицательный знак.
В общем случае при повторных измерениях систематическая погрешность может меняться по сложному непериодическому закону. Но для упрощения анализа различают постоянные систематические погрешности и систематические погрешности, изменяющиеся по определенному закону. Последние разделяются на прогрессирующие, периодические и изменяющиеся по сложному закону.
Постоянная систематическая погрешность – это погрешность, остающаяся неизменной и присутствующая в результатах всех повторных наблюдений.
Пример – погрешность от неустановки указателя на начало шкалы перед измерением.
Прогрессирующие погрешности – это погрешности, постоянно возрастающие или убывающие при наблюдениях. Характерны для средств измерений, показания которых зависят от прогревания прибора после включения, или приборов, показания которых зависят от величины питающего напряжения с питанием их от аккумуляторов.
Периодические погрешности – это погрешности, меняющиеся с определенным периодом. Они характерны для измерительных приборов с круглой шкалой.
 |
а) б) в)
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Рис. 5.1. Зависимости погрешностей от измеряемой величины х:
а – аддитивная, б – мультипликативная, в – нелинейная
Погрешность, изменяющуюся по сложному закону в зависимости от тока нагрузки, имеет, например, индукционный счетчик электрической энергии.
Количественно оценить систематическую погрешность достаточно сложно. При этом необходимо иметь в виду, что именно систематические, а не случайные погрешности вызывают смещение результата измерения и могут приводить к ложным выводам о значениях измеряемой величины.
Экспериментальная оценка систематической погрешности состоит в сопоставлении результата измерения какой-либо величины с результатом измерения той же величины, но полученным другим методом или при использовании более точных средств измерений. Теоретически оценить некоторые составляющие систематической погрешности возможно путем тщательного анализа условий измерения, на основе известных свойств средств измерений.
Способы исключения и учета систематических погрешностей в зависимости от этапов проведения измерений можно разделить на четыре основные группы: устранение источников погрешностей до начала измерений, исключение погрешностей в процессе измерения, внесение известных поправок в результат измерения, оценка границ систематических погрешностей.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьСистематическая погрешность (или, на физическом жаргоне, систематика) характеризует неточность измерительного инструмента или метода обработки данных. Если точнее, то она показывает наше ограниченное знание этой неточности: ведь если инструмент «врет», но мы хорошо знаем, насколько именно, то мы сможем скорректировать его показания и устранить инструментальную неопределенность результата. Слово «систематическая» означает, что вы можете повторять какое-то измерение на этой установке миллионы раз, но если у нее «сбит прицел», то вы систематически будете получать значение, отличающееся от истинного.
Конечно, систематические погрешности хочется взять под контроль. Поскольку это чисто инструментальный эффект, ответственность за это целиком лежит на экспериментаторах, собиравших, настраивавших и работающих на этой установке. Они прилагают все усилия для того, чтобы, во-первых, корректно определить эти погрешности, а во-вторых, их минимизировать. Собственно, они этим начинают заниматься с самых первых дней работы установки, даже когда еще собственно научная программа исследований и не началась.
Возможные источники систематических погрешностей
Современный коллайдерный эксперимент очень сложен. В нём есть место огромному количеству источников систематических погрешностей на самых разных стадиях получения экспериментального результата. Вот некоторые из них.
Погрешности могут возникать на уровне «железа», при получении сырых данных:
- дефектные или неработающие отдельные регистрирующие компоненты или считывающие элементы. В детекторе миллионы отдельных компонентов, и даже если 1% из них оказался дефектным, это может ухудшить «зоркость» детектора и четкость регистрации сигналов. Надо подчеркнуть, что, даже если при запуске детектор работает на все 100%, постоянное детектирование частиц (это же жесткая радиация!) с течением времени выводит из строя отдельные компоненты, так что следить за поведением детектора абсолютно необходимо;
- наличие «слепых зон» детектора; например, если частица вылетает близко к оси пучков, то она улетит в трубу и детектор ее просто не заметит.
Погрешности могут возникать на этапе распознавания сырых данных и их превращение в физическое событие:
- погрешность при измерении энергии частиц в калориметре;
- погрешность при измерении траектории частиц в трековых детекторах, из-за которой неточно измеряется точка вылета и импульс частицы;
- неправильная идентификация типа частицы (например, система неудачно распознала след от π-мезона и приняла его за K-мезон). Более тонкий вариант: неправильное объединение адронов в одну адронную струю и неправильная оценка ее энергии;
- неправильный подсчет числа частиц (две частицы случайно вылетели так близко друг к другу, что детектор «увидел» только один след и посчитал их за одну).
Наконец, новые систематические погрешности добавляются на этапе позднего анализа события:
- неточность в измерении светимости пучков, которая влияет на пересчет числа событий в сечение процесса;
- наличие посторонних процессов рождения частиц, которые отличаются с физической точки зрения, но, к сожалению, выглядят для детектора одинаковыми. Такие процессы порождают неустранимый фон, который часто мешает разглядеть искомый эффект;
- необходимость моделировать процессы (в особенности, адронизацию, превращение кварков в адроны), опираясь частично на теорию, частично на прошлые эксперименты. Несовершенство того и другого привносит неточности и в новый экспериментальный результат. По этой причине теоретическую погрешность тоже часто относят к систематике.
В отдельных случаях встречаются источники систематических погрешностей, которые умудряются попасть сразу во все категории, они совмещают в себе и свойства детекторного «железа», и методы обработки и интерпретации данных. Например, если вы хотите сравнить друг с другом количество рожденных частиц и античастиц какого-то сорта (например, мюонов и антимюонов), то вам не стоит забывать, что ваш детектор состоит из вещества, а не из антивещества! Этот «перекос» в сторону вещества может привести к тому, что детектор будет видеть мюонов меньше, чем антимюонов, подробности см. в заметке Немножко про CP-нарушение, или Как жаль, что у нас нет детекторов из антивещества!.
Всю эту прорву источников потенциальных проблем надо распознать и оценить их влияние на выполняемый анализ. Здесь никаких абсолютно универсальных алгоритмов нет; исследователь должен сам понять, на какие погрешности надо обращать внимание и как грамотно их оценить. Конечно, тут на помощь приходят разные калибровочные измерения, выполненные в первые год-два работы детектора, и программы моделирования, которые позволяют виртуально протестировать поведение детектора в тех или иных условиях. Но главным в этом искусстве всё же является физическое чутье экспериментатора, его квалификация и накопленный опыт.
Почему важна грамотная оценка систематики
Беспечная оценка систематических погрешностей может привести к двум крайностям, причем обе очень нежелательны.
Заниженная погрешность — то есть неоправданная уверенность экспериментатора в том, что погрешности в его детекторе маленькие, хотя они на самом деле намного больше, — исключительно опасна, поскольку она может привести к совершенно неправильным научным выводам. Например, экспериментатор может на их основании решить, что измерения отличаются от теоретических предсказаний на уровне статистической значимости 10 стандартных отклонений (сенсация!), хотя истинная причина расхождения может просто состоять в том, что он проглядел источник ошибок, в 10 раз увеличивающий неопределенность измерения, и никакого расхождения на самом деле нет.
В борьбе с этой опасностью есть соблазн впасть в другую крайность: «А вдруг там есть еще какие-то погрешности? Может, я что-то не учел? Давай-ка я на всякий случай увеличу погрешности измерения в 10 раз для пущей безопасности.» Такая крайность плоха тем, что она обессмысливает измерение. Неоправданно завышая погрешность, вы рискуете получить результат, который будет, конечно, правильным, но очень неопределенным, ничем не лучше тех результатов, которые уже были получены до вас на гораздо более скромных установках. Такой подход, фактически, перечеркивает всю работу по разработке технологий, по изготовлению компонентов, по сборке детектора, все затраты на его работу и на анализ результатов.
Грамотный и ответственный анализ систематики должен удерживать оптимальный баланс (максимальная достоверность при максимальной научной ценности), не допуская таких крайностей. Это очень тонкая и сложная работа, и первые страницы в большинстве современных экспериментальных статей по физике частиц посвящены тщательному обсуждению систематических (а также статистических) погрешностей.
Мы не будем обсуждать подробности того, как обсчитывать систематические погрешности. Подчеркнем только, что это серьезная наука с множеством тонкостей и подводных камней. В качестве примера умеренно простого обсуждения некоторых вопросов см. статью Systematic Errors: facts and fictions.
Погрешность измерений | КИПиА Портал
Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.
Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.
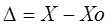 (1.2), где X — результат измерения; Х0 — истинное значение этой величины.
(1.2), где X — результат измерения; Х0 — истинное значение этой величины.
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением
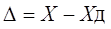 (1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
(1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
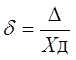 (1.4)
(1.4)
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.
Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Систематические и прогрессирующие погрешности средств измерений вызываются:
- первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
- вторые — старением элементов средства измерения.
Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Погрешности средств измерений.
Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:
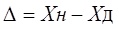 (1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
(1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:
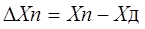 (1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
(1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному
(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).
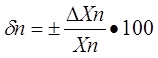 (1.7)
(1.7)
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).
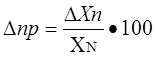 (1.8)
(1.8)
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.
Погрешности средств измерений подразделяются также на статические и динамические.
Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.
Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.
Факторы влияющие на погрешность измерений.
Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений
Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.
Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.
Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.
Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.
Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.
Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.
Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.
Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.
Шумы — любой сигнал не несущий полезной информации.
Классификация погрешностей
Погрешности измерений
Результат любого измерения отличается от истинного значения измеряемой величины на некоторое значение, зависящее от принятой модели объекта, метода измерения, характеристик технических средств, квалификации оператора, условий при которых производится измерение. Отклонение результата измерения от истинного значения измеряемой величины называется погрешностью измерения. Погрешность является достаточно сложным понятием и нуждается в развитой системе классификации.
По способу числового выражения различают абсолютную и относительную погрешности.
Абсолютная погрешность D выражается в единицах измеряемой физической величины:
D = х – хи (3.1)
где х – значение, полученное при измерении;
хи – истинное значение измеряемой величины.
Указание абсолютной погрешности во многих случаях является удобным и естественным способом охарактеризовать точность измерений. Однако при этом не удается производить сравнение точности измерений в случаях, когда размеры измеряемых величин существенно отличаются друг от друга. Ясно, что, например, измерение расстояния 1 км с абсолютной погрешностью 1 см намного точнее, чем измерение с той же абсолютной погрешностью расстояния 1 м.
Относительная погрешность gотн, равна отношению абсолютной погрешности измерения к истинному значению измеряемой величины:
gотн = 
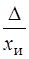 =
= 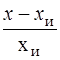 . (3.2)
. (3.2)
Поскольку обычно абсолютная погрешность D много меньше истинного значения хи, относительную погрешность gотн удобно умножать на 100, выражая ее в процентах. Например, если в результате измерения напряжения было получено значение 225 В, тогда как истинное значение составляет 220 В, то абсолютная погрешность D = 225 – 220 = 5 В, относительная погрешность gотн = 5 / 220 = 0,023 или gотн = 2,3 %.
В зависимости от характера проявленияпогрешности делят на систематические, случайные и грубые (промахи). Такое разделение целесообразно для удобства обработки результатов измерений.
Систематической погрешностью измерения называется составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Причиной появления систематических погрешностей могут быть неисправности измерительной аппаратуры, несовершенство метода измерения, неправильная установка измерительных приборов и отступление от нормальных условий их работы, особенности и неправильные действия самого оператора. Систематические погрешности в принципе могут быть выявлены и почти полностью устранены. Для этого требуется проведение тщательного анализа возможных источников погрешностей в каждом конкретном случае. К сожалению, несмотря на все усилия, всегда остаются некоторые не исключенные, остаточные систематические погрешности. Задачей экспериментатора является определение их наибольших, граничных значений.
Случайной погрешностью измерения называется составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же физической величины. Наличие случайных погрешностей выявляется при проведении ряда измерений этой величины, когда оказывается, что результаты измерений не совпадают друг с другом. Если систематические погрешности исключены, то полученные при отдельных наблюдениях результаты вследствие случайных причин будут рассеяны в окрестности истинного значения. Если же систематические погрешности присутствуют, то результаты наблюдений будут соответственно смещены в сторону от истинного значения.
Обычно случайные погрешности возникают из-за одновременного действия многих случайных причин, каждая из которых в отдельности мало влияет на результат измерения. Поэтому нет простых способов избавиться от случайных погрешностей. Нужно либо коренным образом изменять условия измерительного эксперимента, либо удовлетвориться отысканием области, в которой лежит истинное значение измеряемой величины с заданной вероятностью. Математические дисциплины, устанавливающие поведение случайных величин, такие как теория вероятностей и математическая статистика, представляют для этого необходимые средства.
В некоторых случаях оказывается, что результат того или иного отдельного измерения резко отличается от результатов других измерений, выполненных при тех же контролируемых условиях. Причиной этого может быть ошибка оператора, возникновение сильной кратковременной помехи, толчок, нарушение электрического контакта и т.д. Естественно, что такой результат, содержащий грубую погрешность (промах), следует выявить, исключить и не учитывать при дальнейшей статистической обработке результатов. Надо сказать, что выявление грубых погрешностей не всегда является простой задачей. Для этого разработаны специальные процедуры, некоторые из которых будут описаны ниже в этой главе.
Рис.3.1 иллюстрирует рассеяние результатов наблюдений в окрестности истинного значения хи для случаев, когда 1) – имеются только случайные погрешности, 2) – когда наряду со случайными погрешностями присутствует и систематическая составляющая, 3) – когда имеются все виды погрешностей, включая грубую (промах) при полученном результате одного из наблюдений хгр.
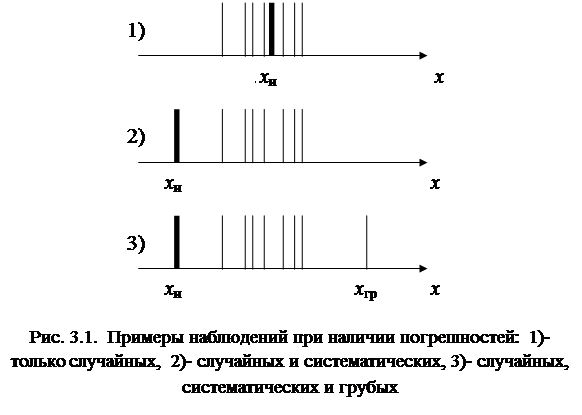
Природа ипроисхождение систематических погрешностей обусловлены несовпадением принятых моделей объекта, средства измерения и измерительного процесса с реальными условиями. Такое несовпадение имеет место всегда. Но степень и последствия его различны. Они определяются спецификой конкретного эксперимента. Задачей измерений является обнаружение и по возможности более полная коррекция возникающих из-за этого систематических погрешностей. Ее решение во многом зависит от мастерства экспериментатора, от того, насколько глубоко он изучил конкретные условия и особенности применяемых им методов и средств. Вместе с тем существуют некоторые общие причины возникновения систематических погрешностей, а, следовательно, и общие приемы их обнаружения и исключения. В соответствии с причинами возникновения погрешности подразделяют на:
– методические,
– инструментальные,
– субъективные.
Методические погрешности происходят от несовершенства метода измерения, упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения.
В любом случае информацию о значении методической погрешности нельзя почерпнуть из нормативно-технической информации об используемом средстве измерения, например, из паспорта на него. Дело в том, чти методическая погрешность либо совсем не зависит от характеристик средства измерения, либо зависит относительно, то есть проявляется в каждом конкретном случае в различной степени.
Например, измерение высоты полета самолета барометрическим методом использует известную зависимость давления воздуха от высоты. Однако эта зависимость содержит такой параметр как температура воздуха. Можно учесть сведения о температуре за бортом и произвести необходимую коррекцию результата измерений. К сожалению, распределение температуры по высоте имеет очень сложный профиль, зависящий от многих причин и изменяющийся со временем. Поэтому приходится удовлетворяться знанием некоторой эффективной температуры, обеспечивающей лишь частичную коррекцию. В данном случае погрешность определяется выбранным методом измерения и не может быть исключена посредством каких бы то ни было манипуляций с барометром – прибором, который задействован для измерения высоты.
Нередко погрешности связаны с неточным знанием значений констант, входящих в расчетные формулы. Хрестоматийным примером является ошибка, которую допустил Р.Милликен при измерении элементарного электрического заряда e. Он в своем опыте наблюдал за движением заряженных капель масла в электрическом поле и при обработке результатов эксперимента использовал значение вязкости воздуха, которое оказалось заниженным. Что и привело к результату, содержащему неисключенную систематическую погрешность около 0,5 %. Затем эта погрешность перекочевала в значения многих физических величин и констант, при определении которых использовалось значение е, полученное Милликеном. Среди них оказались такие важные как постоянная Планка и число Авагадро. На то, чтобы найти и устранить все эти ошибки потребовалось почти три десятилетия.
Важным источником методических погрешностей является воздействие средства измерения на исследуемый объект. Например, измерение температуры массивным термометром может нарушить изучаемый тепловой режим и привести к получению искаженных результатов. Точно так же попытки произвести точные измерения напряжения в высокоомных электрических цепях вольтметром, имеющим недостаточно большое входное сопротивление, едва ли будут успешными. Внесение входного сопротивления вольтметра в такую цепь самым существенным образом нарушит ее работу и не позволит получить качественные результаты измерений. При измерениях в низкоомных цепях последствия не столь драматичны, но все равно шунтирование входным сопротивлением вольтметра участка цепи, на котором измеряется напряжение, приводит к погрешности. Эту погрешность следует считать методической, поскольку она определяется не столько свойствами прибора, сколько соотношением между его характеристиками и параметрами цепи.
Инструментальные погрешности измерения зависят от погрешностей применяемых средств измерения, то есть приборов, преобразователей, мер и т.п. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и некоторые другие причины вызывают появление инструментальных погрешностей. Невозможно создать идеальное средство измерения, совсем свободное от погрешностей. Однако есть возможность оценить предельные значения погрешностей реальных измерительных устройств. можно при конструировании приборов потребовать, чтобы их погрешности (абсолютные, относительные или приведенные) не превышали определенных, заранее установленных значений. В соответствии с такими максимально допускаемыми погрешностями средствам измерений приписывается тот или иной класс точности. Поскольку, как указывалось выше, требуемая точность определяется целью измерительного эксперимента, выбранное средство измерения должно иметь соответствующий класс точности, т.е. обеспечивать получение результатов измерений с приемлемой инструментальной погрешностью. К сожалению возможны случаи, когда в процессе измерения возникают инструментальные погрешности, превышающие те, что указаны в паспорте на применяемое средство измерения или соответствующие его классу точности в качестве максимально допускаемых. Это может случиться, например, из-за того, что поверка средств измерения производится периодически, а эксплуатация – непрерывно. Есть определенная вероятность, что в какой-то момент между поверками параметры прибора окажутся отличными от предполагаемых, а погрешности выйдут за допускаемые пределы.
Погрешности измерения возникают также из-за неправильной установки средства измерения, влияния на него магнитных и электрических полей, наличия дополнительных и динамических погрешностей. Дополнительные погрешности обусловлены отклонением условий, при которых работает прибор, от нормальных. Динамические погрешности возникают из-за инерционности применяемых технических средств при достаточно быстрых изменениях измеряемой величины. Все эти погрешности отличаются от инструментальных, поскольку они не столько связаны с самими средствами измерений, сколько с условиями, при которых они работают (ГОСТ 8.009-84). Их устранение производится иными способами, нежели устранение инструментальных погрешностей.
Субъективные погрешности вызываются неправильными отсчетами показаний прибора человеком (оператором). Это может случиться, например, из-за неправильного направления взгляда при наблюдении за показаниями стрелочного прибора (погрешность от параллакса). Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности. Компьютерные измерения также свободны от них.
Заметим, что выделение в составе систематических погрешностей методической, инструментальной, субъективной и других составляющих представляется естественным, так как отражает различные способы их исключения или оценки. Но это вовсе не означает то, что указанные погрешности (методические, инструментальные и прочие) всегда проявляют себя как систематические, то есть остаются постоянными или закономерно изменяются. При других обстоятельствах они могут вести себя случайно и относиться к случайным погрешностям.
Как уже отмечалось, обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению либо исключению посредством введения поправки.
Поправкой называется значение величины, одноименной с измеряемой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности. Таким образом, поправка численно равна абсолютной погрешности измерения, взятой с противоположным знаком.
В некоторых случаях используют поправочный множитель – число, на которое надо умножить результат измерения, чтобы исключить систематическую погрешность.
Поправка или поправочный множитель определяются при помощи поверки технического средства, составления и использования соответствующих таблиц и графиков, Применяются также расчетные способы нахождения поправочных значений.
Систематические и случайные ошибки в физике
Введение в Систематические и случайные ошибки
Во второй части Руководства по практическим навыкам физики мы рассмотрели надежность, точность и достоверность, а также влияние на них различных типов ошибок. В этой части Руководства по практическим навыкам физики мы рассмотрим экспериментальные ошибки (систематические и случайные ошибки) более подробно.
В этой статье мы обсуждаем:
Экспериментальные ошибки
Что такое экспериментальные ошибки?
Существует два типа ошибок эксперимента:
- Случайная ошибка
- Систематическая ошибка
Систематические ошибки влияют на точность, тогда как случайные ошибки влияют на достоверность экспериментальных результатов.

Начните с вашей следующей практической оценки по физике
Получите глубокие знания и понимание всего модуля, прежде чем его будут преподавать в школе. Узнайте больше о нашем курсе по физике.

Систематические и случайные ошибки
Что такое систематические ошибки?
Систематические ошибки будут постоянно сдвигать измерения от их истинного значения на одну и ту же величину или дробь и в одном и том же направлении. Они не влияют на надежность (поскольку они всегда одинаковы), но влияют на точность.Они обычно возникают из-за проблемного или неправильно используемого оборудования, например, плохая калибровка.
Что такое случайные ошибки?
Случайные ошибки будут сдвигать каждое измерение от его истинного значения на случайную величину и в случайном направлении. Это повлияет на надежность (поскольку они случайные), но может не повлиять на общую точность результата.
Каковы источники систематических или случайных ошибок?
Ниже перечислены различные типы ошибок и их причины. Каждый из них может быть описан как случайная или систематическая ошибка.
| Ошибка | Описание | Систематическая или случайная ошибка |
| Ошибка масштаба | Если элемент оборудования откалиброван неправильно (например, деревянная линейка уменьшилась), все измерения будут смещены той же долей. | Систематическая ошибка |
| Нулевая ошибка | Если единица оборудования имеет смещение (например, баланс массы показывает показание, которое не равно нулю, когда на нем ничего нет), все измерения будут смещены на одно и то же количество. | Систематическая ошибка |
| Ошибка параллакса | Если вы производите измерение путем сравнения индикатора со шкалой (например, считывание шкалы на вольтметре или использование ртутного термометра), угол, под которым вы ее просматриваете, будет повлиять на чтение. | Систематическая ошибка, если вы всегда смотрите на циферблат под одним и тем же углом. Случайная ошибка, если вы каждый раз просматриваете циферблат под случайным углом. |
| Ошибки, возникающие в окружающей среде | В идеале переменные управления должны оставаться постоянными, но некоторые из них могут быть вне вашего контроля, e.грамм. давление воздуха, температура, влажность, вибрации. | Изменения в управляющих переменных могут привести к систематическим и случайным ошибкам. Одно последовательное изменение даст систематическую ошибку. Случайные изменения приведут к случайным ошибкам. |
| Время реакции | Если измерение зависит от времени вашей реакции, то вы можете отреагировать слишком рано или слишком поздно в разное время. | Случайная ошибка. |
| Ошибки измерения из-за недостаточной точности | Если вы измеряете что-то, что находится между двумя отметками на шкале (например,грамм. вы используете линейку для измерения чего-либо длиной 10,25 мм), вы не можете измерить ее точное значение, и вам нужно будет округлить ее вверх или вниз (выглядит ли она как 10 мм или 10,5 мм?). | Случайная ошибка. |
Как насчет «человеческой ошибки»?
«Человеческая ошибка» не является источником экспериментальной ошибки. Вы должны классифицировать конкретные ошибки как случайные или систематические и определить источник ошибки.
Человеческая ошибка не может быть заявлена как экспериментальная ошибка.
Процентные ошибки
Процентные ошибки выражают неопределенность или расхождение в значении в процентах от значения.
Неопределенность описывает диапазон значений, которые может принимать результат или измерение, и связана с надежностью или точностью. Если значение указано как x ± 5%, то это значение может быть больше или меньше на 5%.
Расхождение связано с разницей между окончательным результатом эксперимента и принятым значением и, следовательно, связано с точностью.
Как уменьшить систематические ошибки
Систематическая ошибка возникает из-за оборудования , поэтому самый прямой путь к – это использование калиброванного оборудования и устранение любых ошибок нуля или параллакса .
Даже если на ваши измерения влияют, некоторые систематические ошибки могут быть устранены при анализе данных. В анализе мы обычно рисуем график, который дает прямую линию, мы рисуем линию наилучшего соответствия и измеряем ее градиент. Измеряя градиент, мы смотрим только на изменения, а не на абсолютные значения.Нулевые ошибки приведут к смещению линии вверх и вниз (то есть к y-точке пересечения графика), но не повлияют на градиент. Следовательно, мы исключаем ноль ошибок, что повышает точность.
Как уменьшить случайные ошибки
Поскольку случайные ошибки являются случайными и могут сдвигать значения как выше, так и ниже, их можно устранить путем повторения и усреднения . Истинная случайная ошибка будет усредняться до нуля, если будет произведено и усреднено достаточное количество измерений (по линии наилучшего соответствия).Вот почему повторение измерений может повысить надежность конечного результата эксперимента.
При анализе построение графика и линии наилучшего соответствия служит для уменьшения случайной ошибки в конечном экспериментальном результате. Во-первых, выбросы могут быть устранены. Во-вторых, линия наилучшего соответствия рисуется так, чтобы вместить как можно больше данных путем разрезания между набором точек данных. Таким образом, данные усредняются, причем большинство взвешиваний дается наиболее сходным значениям.Это уменьшает влияние случайных ошибок и повышает надежность.

© Matrix Education и www.matrix.edu.au, 2020. Несанкционированное использование и / или копирование этого материала без явного и письменного разрешения автора и / или владельца этого сайта строго запрещено. Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au предоставлена полная и четкая ссылка с соответствующим и конкретным указанием на оригинальное содержание.
1. Введение
Роль клинической лаборатории заключается в измерении и тестировании образцов пациентов. Эти измерения являются центральной частью современного клинического управления; они используются клиницистами для диагностики болезненных состояний, определения курса лечения и определения прогноза. Современная клиническая лаборатория использует множество инструментов для количественной оценки и измерения различных аналитов и сообщает результаты, которые используются клиницистами.Наиболее важными показателями, которыми должен обладать тест для использования в клинической лаборатории, являются техническая точность и точность [1].
Тест технически точен, если он дает достоверную информацию. Точный тест даст аналогичные результаты, когда тест повторяется несколько раз. Точность (или, вернее, достоверность) является мерой близости результатов теста к истинному значению. Точность измеряет надежность и воспроизводимость. Эти показатели дополняют друг друга, и хороший клинический тест должен быть точным и точным [2].Некоторые полагают, что правильность следует использовать для обозначения соответствия измерения истинному значению и точности, чтобы охватить как достоверность, так и точность.
Точность и точность связаны с концепцией, называемой ошибкой измерения: каждое измерение связано со степенью ошибки или неопределенности. Цель лабораторной медицины – минимизировать погрешность измерения, чтобы она не оказывала неблагоприятного влияния на процесс принятия клинических решений. Ошибка измерения никогда не может быть по-настоящему аннулирована, но ее можно уменьшить до шкалы, приемлемой для клиницистов, директоров лабораторий и регулирующих органов лабораторий [2, 3].
Ошибки измерения могут быть случайными, то есть они могут быть непредсказуемыми. Все измерения имеют случайную ошибку. Случайные ошибки происходят из-за непредсказуемых изменений в образце, инструменте, процессе измерения или анализе, и можно сказать, что они следуют гауссову распределению, то есть случайная ошибка следует случайности и случайности, и, таким образом, законы вероятности применяются к случайной ошибке. По мере того как приборы становятся более точными, распределение случайной ошибки по Гауссу сужается, и случайная ошибка уменьшается.В то же время, если мы повторяем эксперимент или тестируем несколько раз, мы можем усреднить случайную ошибку из наших измерений. то есть среднее значение нескольких повторных измерений становится ближе к истинному значению по мере увеличения числа повторений. Это служит основой для представления доверительных интервалов для измерений [2, 4].
Смещение или систематическая ошибка – это форма ошибки измерения, которая искажает результаты в одну сторону. Повторение измерений не может устранить смещение. Другими словами, смещение – это ненулевая ошибка, которая будет последовательно влиять на результаты и может показывать проблему с процессом измерения, часто требующим корректирующих действий.Корректирующее действие может быть в форме калибровки путем введения поправочного коэффициента или путем изменения компонентов измерения. Систематическая ошибка может быть кратковременной или долгосрочной, при этом очень кратковременная систематическая ошибка часто проявляется как случайная ошибка.
Систематическая ошибка и случайная ошибка кумулятивно влияют на результаты измерений (рисунок 1). Таким образом, погрешность измерения часто рассматривается как полная погрешность, что обусловливает как смещение, так и случайную ошибку. Лаборатории часто имеют пределы для общей ошибки, смещения и случайной ошибки.Все тесты необходимо постоянно проверять на наличие ошибок, а выявление систематической ошибки является частью функции клинической лаборатории. Погрешность измерения можно рассматривать как шум, который может скрыть сигнал или истинное значение теста. При наличии шума получение выводов из сигнала, который может изменить истинное значение клинически значимым образом, может поставить под угрозу здоровье пациента. В результате лаборатория должна стремиться идентифицировать шум, минимизировать его или уменьшить его влияние на результаты пациента.В связи с этим систематическая ошибка особенно опасна, поскольку она искажает результаты теста таким образом, который невозможно исправить повторными измерениями. К сожалению, систематическую ошибку очень трудно идентифицировать и / или количественно определить. В этой главе мы сосредоточимся на подходах для выявления систематической ошибки с использованием внутрилабораторных сравнений [5, 6].
Рисунок 1.
На этом рисунке показан совокупный эффект систематической ошибки и случайной ошибки. Ось X представляет определенное значение, а ось Y представляет частоту появления каждого значения.
2. Систематическое обнаружение ошибок с помощью экспериментов по контролю качества
Проще говоря, целью экспериментов по контролю качества является определение результатов лабораторных испытаний с измерением известных образцов или образцов, то есть образцов, в которых истинное значение тестируемый аналит известен. Эти методы в основном настроены на обнаружение случайной ошибки и проверку точности прибора. Тем не менее, те же результаты могут быть использованы для выявления систематической ошибки и систематической ошибки [7].
Лаборатории могут использовать сертифицированные эталонные материалы для измерения и выявления систематической ошибки.Если эталонный образец измеряется при каждом аналитическом прогоне, можно ожидать, что результаты измерений эталонного образца покажут случайное распределение вокруг истинного значения, но если результаты постоянно ниже или выше эталонного значения, то вы можете предположить, что смещение существует [2, 8].
Для измерения систематической ошибки необходим метод сравнения методов для определения систематической ошибки. Любая найденная систематическая ошибка должна быть исправлена с использованием эксперимента по восстановлению и калибровки.
2.1. Участки Levey-Jennings
Первым шагом в выявлении систематической ошибки является визуальный контроль процесса контроля качества. График Леви-Дженнингса показывает флуктуацию измерений эталонного образца вокруг среднего значения во времени. Контрольные линии диаграммы включают контрольные пределы, 2 линии стандартного отклонения, 1 линию стандартного отклонения и среднюю контрольную линию.
Среднее, стандартное отклонение и контрольные пределы рассчитываются путем исследования репликации, где сертифицированный эталонный материал неоднократно измеряется.Повторные измерения позволяют рассчитать среднее и стандартное отклонение уровней контрольной выборки. Пробные пределы – это среднее ± 3 стандартных отклонения. Следующим шагом является устранение результатов исследования репликации, которые выходят за пределы 3 стандартных отклонений. Затем среднее значение и стандартное отклонение пересчитываются и снова устанавливаются пределы испытаний. Опять же, результаты за пределами испытаний исключаются. Процесс продолжается до тех пор, пока все оставшиеся результаты не окажутся в пробных пределах. Эти окончательные пределы испытаний, среднее значение и стандартное отклонение устанавливаются в качестве контрольных показателей для этого контрольного образца.
Количество исследований репликации, которые необходимо выполнить, можно рассчитать на основе числа допустимых сбоев. Расчет размера выборки основан на установленных уровнях достоверности и надежности. Достоверность (точность) – это разница между частотой ошибок 1 и I типа. Надежность – это степень точности. Для частоты отказов 0 (т. Е. Мы не допускаем каких-либо неверных результатов), уравнение можно записать в виде:
n = ln1-trustlnreliabilityE1
Уровень достоверности часто устанавливается равным 0.95 и надежность на 0,90 или 0,80. Если мы разрешаем события отказа, то расчет размера выборки основан на следующем уравнении:
1-Confidence = ∑i = 1fni1-ReliabilityiReliabilityn-iE2
, где f – частота отказов и nis размер выборки.
На графике Леви-Дженнингса ось X представляет время, а ось Y представляет измеренное значение. Опорные линии проводятся параллельно оси X, что соответствует средним, средним ± 1 стандартным отклонениям, средним ± 2 стандартным отклонениям и средним ± 3 стандартным отклонениям.Следующим шагом является построение измеренных значений контрольного материала для каждого прогона на графике (рисунок 2).
Рисунок 2.
Пример участка Леви-Дженнингса. Ось X отображает время измерения (например, день), а ось Y отображает значение измерения для этой единицы времени. Линии, обозначающие среднее значение и 1, 2 и 3 стандартных отклонения от среднего значения, поясняются на рисунке.
2.2. Правила Вестгарда
Правила Вестгарда – это набор рекомендаций, установленных доктором Джеймсом Вестгардом для выявления случайных и систематических ошибок в лабораторных экспериментах по контролю качества.Они основаны на повторных измерениях по меньшей мере двух эталонных образцов с каждым аналитическим прогоном. Некоторые из правил Вестгарда касаются идентификации случайной ошибки и обнаружения ошибок в пределах прогонов [2, 7]. Другие правила Вестгарда направлены на выявление систематической ошибки и обнаружение ошибок между прогонами. В этой главе мы сосредоточимся на последних правилах.
2 2S правило: считается, что результаты контроля качества не подтвердились, и присутствует смещение, если два последовательных контрольных значения находятся между 3 стандартными отклонениями и 2 пределами стандартного отклонения с одной и той же стороны контрольной линии средних значений.
4 1S правило: считается, что результаты контроля качества не подтвердились, и смещение присутствует, если четыре последовательных контрольных значения находятся на одной стороне от средней контрольной линии и находятся как минимум на одно стандартное отклонение от среднего.
10 x правило: считается, что результаты контроля качества не дали результатов, и присутствует смещение, если 10 последовательных контрольных значений находятся на одной стороне от средней контрольной линии.
Эти правила показаны на рисунке 3.
Рисунок 3.
Примеры систематической ошибки на графике Леви-Дженнингса: A. Пример правила 2-2S, B. Пример правила 4-1S, C. Пример правила 10x.
2.3. Сравнение методов
Сравнение методов используется для первоначальной валидации анализа, а также для изучения точности теста. Цель сравнения методов состоит в том, чтобы определить, измеряет ли анализ то, что предполагается измерить, и насколько точно он его измеряет. Результаты сравнения методов также позволяют скорректировать результаты, если обнаружена систематическая ошибка (т.е.е. калибровка). Принцип сравнения методов заключается в том, что существует золотой стандарт или стандартный эталонный материал, если количество аналита в образце точно известно (или известно с высокой степенью точности). Мы можем использовать этот эталонный стандарт в качестве компаратора по сравнению с результатами нашего анализа и определить степень смещения, существующего в наших измерениях. По сути, это означает, что мы измеряем относительную эффективность нашего анализа по отношению к эталонному стандарту.
В идеале, идентификация смещения должна привести к поиску источника смещения и систематической ошибки, и должны быть предприняты попытки устранить причину наблюдаемого смещения.Тем не менее, есть случаи, когда не выявлено ни одной неисправности или решаемой проблемы; в этих случаях, если анализ обладает достаточной точностью и стабильностью, а также клиническими достоинствами, мы можем использовать результаты сравнения методов для корректировки на наблюдаемое смещение.
Смещение может принимать две основные формы: постоянное смещение и пропорциональное смещение. Постоянное смещение – это разница между наблюдаемым измерением и ожидаемым измерением, которая является постоянной во всем диапазоне наблюдений. Постоянное смещение (β0) представлено в статистике регрессии как перехват.Пропорциональное смещение (β1), с другой стороны, пропорционально наблюдаемой величине измерения и изменяется в диапазоне измерений. Пропорциональное смещение представлено в статистике регрессии как наклон линии регрессии. Если ожидаемое значение измерения равно Yifor для каждого образца i, и наблюдаемое значение измерения для образца iis Xi, то мы можем сформировать линейную регрессию между ожидаемыми значениями и наблюдаемыми значениями:
Yi = β0 + β1Xi + εiE3
, где εi – случайная ошибка ожидаемых наблюдений в предположении Юдена, согласно которому случайная ошибка наблюдаемых значений меньше случайной ошибки для ожидаемых значений.
Формула регрессии – это представление наилучшей линии регрессии, которая показывает отношение наблюдаемого значения к ожидаемому значению. На рисунке 4 показаны линии регрессии для различных уровней постоянного и пропорционального смещения.
Рисунок 4.
A. Если систематической ошибки не существует. Б. Показывает постоянное смещение. C. Показывает пропорциональное смещение.
Если смещения не существует, то Yi = Xi.
Простая формула линейной регрессии позволяет нам вычислять постоянное и пропорциональное смещение, используя простую невзвешенную оценку наименьших квадратов.В моделях обычных наименьших квадратов (OLS) различные значения-кандидаты для вектора параметра β1 тестируются для создания линий регрессии. Затем для каждого i-го наблюдения остаток для этого наблюдения вычисляется путем измерения вертикального расстояния между точкой данных (Yi, Xi) и линией регрессии, сформированной с использованием значения кандидата. Сумма квадратов невязок (SSR) определяется как мера общего соответствия модели. Значение кандидата, которое минимизирует сумму квадратов невязок, рассматривается как оценщик OLS для наклона.Для простых сравнительных исследований метода, в которых присутствуют только два компаратора, модель можно упростить следующим образом:
β1 = ∑XiYi − 1n∑Xi∑Yi∑Xi2−1n∑Xi2 = CovarianceXYVarianceXE4
Постоянное смещение можно рассчитать путем вычитания среднего ожидаемое значение от среднего наблюдаемого значения, взвешенного по пропорциональному смещению:
β0 = Y¯ − β1X¯E5
Постоянное и пропорциональное смещение обычно имеет разные первопричины. Постоянное смещение часто происходит из-за недостаточной коррекции пустого образца, и его довольно легко устранить и исправить.Пропорциональные проблемы иногда могут быть вызваны различием в составе образцов калибратора и стандартных образцов или матриц биологических испытаний. Матрица эталонного стандарта обычно находится рядом с фактической матрицей образцов пациента и, таким образом, может содержать искажающие факторы, которые могут отрицательно повлиять на измерение. Все же калибраторы часто не имеют биологической матрицы. Если источник пропорционального смещения вызван проблемами калибровки, то повторная калибровка может исправить проблему.
Проблема с предположением Юдена состоит в том, что он считает, что в наших наблюдениях нет случайных сбоев, предположение, которое является ложным, поскольку мы знаем, что каждое измерение связано со степенью неопределенности и неточности.В качестве альтернативы, мы можем использовать регрессию Деминга, где случайная ошибка для ожидаемых и наблюдаемых значений учитывается при расчете пропорционального и постоянного смещения. В регрессии Деминга вычисляется отношение дисперсий случайных ошибок наблюдаемых и ожидаемых значений:
δ = σε2ση2E6
, где σε2 – дисперсия случайных ошибок ожидаемых значений, а ση2 – дисперсия случайных ошибок наблюдаемых значений. Используя это отношение, оценщик OLS для пропорционального смещения может быть задан как:
β1 = VarY − δVarX + VarY − δVarX2 + 4δCovarXY22CovarXYE7
Эта формула регрессии также известна как оценка максимального правдоподобия [9].
Если существует линейная зависимость между ошибками и измерениями (или предполагается), то альтернативным методом обнаружения ошибок является создание графиков Бланда-Альтмана. На этих графиках среднее значение парных значений для ожидаемых и наблюдаемых значений нанесено на ось х, а разность каждой пары – на оси у. В этом методе средняя разница значений называется смещением, и стандартное отклонение разностей также рассчитывается для определения пределов согласия, которое составляет среднее значение разности ± 1.96SD.
Подход Бланда-Альтмана позволяет визуально проверить пропорциональное смещение. Однако, разделив пределы согласия на среднее значение ожидаемых значений, мы можем получить показатель, называемый процентной ошибкой. Допустимые уровни процентной погрешности для разных аналитов были определены и стандартизированы. В случаях, когда процентная ошибка превышает допустимые уровни, для обнаруженного смещения необходимы корректирующие действия [10].
2.4. Статистика R
Одной из важных статистических данных для простой линейной регрессии является вычисление коэффициента Пирсона.Этот коэффициент показывает, насколько хорошо сравниваемые результаты изменяются вместе и может иметь значения от минус 1 до 1. Этот коэффициент можно рассчитать путем деления ковариации двух переменных на произведение их стандартных отклонений:
r = CovarXYσXσyE8
чем ближе коэффициент r к 1, тем больше линейная зависимость между двумя переменными. Некоторые интерпретируют коэффициент r как меру корреляции с коэффициентами r более 0,8, показывающими корреляцию.Однако в лабораторной медицине корреляция 0,8 фактически означает большую степень смещения. На самом деле лаборатории должны стремиться к идеальной степени линейности (r> 0,99), чтобы гарантировать, что систематическая ошибка минимизирована. Достижение коэффициента Пирсона <0,975 сигнализирует о наличии систематической ошибки и должно побудить лабораторию провести дальнейшее исследование (с использованием t-критерия и f-критерия), чтобы определить источник этой ошибки.
Степень согласия или коэффициент детерминации (R2).Этот коэффициент рассчитывается из отношения объясненной дисперсии к общей дисперсии Y:
R2 = ∑Ŷi − Y¯2∑Yi − Y¯2E9
, где Ŷi – расчетное значение Y на основе регрессии для i- th наблюдения и Yiis фактическое значение Y для i-го наблюдения.
В качестве альтернативы коэффициент детерминации может быть просто вычислен путем возведения в квадрат коэффициента Пирсона. Хотя коэффициент r Пирсона показывает наличие линейности, коэффициент детерминации помогает нам определить, насколько хорошо линия регрессии соответствует фактическим точкам данных.При оценке метода сравнения необходимо оценить этот коэффициент, так как он показывает соответствие модели: чем ближе коэффициент к 1, тем лучше линия регрессии соответствует фактическим точкам данных. Тем не менее, следует отметить, что даже при числах, очень близких к 1, может существовать существенное отклонение. Например, смещение в 5% приведет к получению значения R в квадрате 0,99, а смещение в 10% – к значению R в квадрате 0,96. Для целей лабораторной медицины мы должны стремиться к получению значения R в квадрате больше 0.99.
2.5. T-тест и F-тест
В случаях, когда есть подозрение о значительном отклонении (как определено статистикой r или R квадрата Пирсона), мы должны определить, является ли отклонение результатом разницы в средней концентрации анализа или в дисперсии анализа. Чтобы проверить среднее значение, мы запускаем парный t-тест, а для проверки дисперсии – f-тест.
Парный t-тест выполняется путем сравнения средних значений наблюдаемых и ожидаемых значений; более конкретно, средняя разница значений (мкД) используется для сравнения.T-статистика может быть рассчитана следующим образом:
t = µDσDnE10
, где n – количество точек данных, а σD – стандартное отклонение средней разности. Чтобы определить значимость результатов (значение p), t-статистику следует искать в таблице t, соответствующей степени свободы; степень свободы в парных t-тестах равна n – 1.
T-критерий со значительным p-значением указывает на наличие значительного отклонения от среднего значения методов. Следующим шагом будет определение того, представляет ли систематическая ошибка постоянное или пропорциональное смещение.Это может быть сделано путем изучения кривой регрессии или уравнения. Наличие пересечения означает постоянное смещение, в то время как наличие наклона, отличного от 1, означает пропорциональную ошибку. Корректировка для постоянного смещения проста и потребует добавления константы к результатам измерения. Однако для исправления пропорционального смещения требуется эксперимент по восстановлению, как описано в разделе 3.8 ниже.
f-критерий сравнивает ожидаемую дисперсию значений с наблюдаемой дисперсией; в то время как t-критерий сравнивает центр тяжести точек данных (среднее значение), f-критерий определяет распределение и дисперсию точек данных (дисперсию).T-критерий более чувствителен к различиям в значениях в середине диапазона данных, в то время как f-критерий более чувствителен к различиям в крайностях диапазона данных. Значительный f-критерий будет означать случайную ошибку в измерении или, другими словами, неточность. Для вычисления f-критерия используется следующее уравнение (большее из двух отклонений всегда будет числителем, а меньшее – знаменателем в этой дроби):
f = Var1Var2E11
Степень свободы f-критерия is (n-1, n-1) и порог значимости можно посмотреть в f-таблице, соответствующей степени свободы.
Важно выполнить f-тест до t-теста; Одно из основных допущений t-критерия состоит в том, что стандартные отклонения точек данных схожи между двумя группами, т. е. для достоверности результатов t-критерия не должно быть существенной неточности. При наличии значительной неточности определение наличия значительного смещения следует проводить с использованием Кокрановского варианта t-критерия.
В Кокрановском варианте t-критерия стандартное отклонение не может быть объединено между двумя группами:
t = μDVar1 + Var2nE12
Также должно быть рассчитано критическое значение для t-статистики:
Criticalt = tnVar1 + Var2Var1 + Var2nE13
где t – t-показатель, соответствующий n-1 степеням свободы [11].
2.6. Профиль точности
Профилирование точности отошло от трактовки смещения и неточности как отдельных объектов. Фактически, большинство руководств (основанных на принципах общей ошибки или принципах неопределенности измерений) сочетают смещение и неточность для критериев приемлемости. Чтобы рассчитать смещение и неточность, нам нужно провести исследование воспроизводимости. Воспроизводимость количественных исследований достигается путем повторных измерений образца в серии, а затем проведения нескольких серий исследований воспроизводимости.
Общее измерение смещения будет представлять собой разницу между средним значением аналита, полученного в результате повторного измерения, и опорным значением:
Смещение = общее среднее значение – опорным значениемE14
Смещение и неточность используются для формирования интервала допуска; это интервал, в котором с определенной степенью достоверности указывается определенная доля результатов для падения выборки. Интервал допуска может быть выражен как:
Интервал допуска = эталонное значение + смещение ± промежуточная точностьE15
Для лабораторной медицины интервал допуска аналитов должен быть меньше, чем пределы приемлемости.В Соединенных Штатах пределы приемлемости устанавливаются и регулируются поправками для улучшения клинической лаборатории 1988 года (CLIA88). Эти пределы приемлемости приведены под следующим заголовком: 42 CFR Часть 493, Подраздел I – Программы проверки квалификации для тестирования без отказа (https://www.gpo.gov/fdsys/pkg/CFR-2011-title42-vol5/pdf/CFR -2011-title42-vol5-part493.pdf).
Важным фактором из промежуточной точности, который необходим при расчете интервала допуска, является стандартное отклонение воспроизводимости (SR).Стандартное отклонение воспроизводимости может быть рассчитано по следующему уравнению:
SR2 = 1nVarbetweenseriesp − 1 + n − 1Varwithinseriesn − pE16
, где n – количество повторений измерения в серии, а p – количество серий измерений воспроизводимости.
Преимущество вычисления промежуточной точности заключается в том, что мы можем использовать ее в сочетании с повторяемостью внутри серии для определения неопределенности смещения:
Неопределенность смещения = 1,96nSR2-Sr2 + Sr2np1 / 2E17
Sr2 является внутренним рядом повторяемость и может быть рассчитана с использованием следующего уравнения:
Sr2 = Varwithinseriespn − 1E18
Неопределенность смещения по существу равна 1.96 раз стандартное отклонение смещения, что соответствует 95% доверительному интервалу для определения смещения.
Воспроизводимость между сериями рассчитывается с использованием следующего уравнения:
SL2 = 1nVarbetweenseriesp − 1-Sr2E19
Воспроизводимость между сериями используется при расчете коэффициента Ми (Ks). Ме фактор является другим компонентом промежуточной точности. Поскольку вычисление коэффициента Ми является сложным, мы разбили его на ряд уравнений.Первым шагом является вычисление отношения H:
H = SL2Sr2E20
. Следующим шагом является вычисление G2:
G2 = H + 1nH + 1E21
, который, в свою очередь, используется для вычисления C:
C = 1 + 1npG21 / 2E22
Последний шаг – умножить C на t-показатель, связанный со степенью свободы (dof):
Степень свободы = H + 12H + 1n2p − 1 + 1−1nnpE23
А:
Ks = C × tdofE24
Рассчитав коэффициент Ми и стандартное отклонение воспроизводимости, мы теперь можем получить промежуточную точность:
Промежуточная точность = Ks × SRE25
Таким образом, мы можем переписать интервал допуска как [12] :
Допустимое отклонение Интервал = опорное значение + смещение ± Кз × SRE26
2.7. Процедуры взвешивания
Проблема с простой линейной регрессией заключается в том, что она основана на ряде предположений; Одно из проблемных допущений состоит в том, что стандартное отклонение случайной ошибки является постоянным во всем диапазоне измерений. Это предположение, однако, часто неверно, поскольку стандартная ошибка измерения часто намного больше вблизи пределов диапазона измерений (около предела обнаружения и самого высокого диапазона линейности). Решением в лабораторной медицине может быть проведение экспериментов по линейности и ограничение диапазона измерений на основе результатов линейности.Несмотря на это, эффект случайного изменения на линии регрессии остается. Чтобы исправить это, решение состоит в том, чтобы использовать процедуру взвешивания.
Простейшая процедура взвешивания состоит в использовании стандартного отклонения вариации для каждой точки данных исследования сравнения методов. Для этого необходимо, чтобы исследование метода сравнения повторялось несколько раз (20-30 раз). Это позволяет рассчитать стандартное отклонение измерения для каждой точки (Si). Весовой коэффициент будет тогда обратным к этому стандартному отклонению:
wi = 1SiE27
Этот вес затем может быть включен в уравнения сравнения методов.Например, коэффициент r можно пересчитать следующим образом:
r = ∑wiXi − X¯Yi − Y¯∑wiXi − X¯2∑wiYi − Y¯212E28
Взвешивание часто может значительно снизить процент смещения, особенно в крайних случаях измерения по сравнению с невзвешенной регрессией. Взвешивание с помощью инверсии стандартного отклонения имеет тенденцию нормализовать относительное смещение в крайних точках измерения, в то время как взвешивание с помощью инверсии дисперсии способствует коррекции смещения для нижних уровней измерения (меньшее смещение при более низких концентрациях).Решение о взвешивании и / или выборе процедуры взвешивания должно основываться на характеристиках анализа и требованиях к производительности [13].
2.8. Процент восстановления
Для оценки пропорционального смещения необходим эксперимент восстановления. Эксперименты по восстановлению выполняются путем расчета степени восстановления при добавлении известного количества аналита к образцу: это делается путем деления измеряемой пробы на две равные аликвоты и выполнения измерения для обеих аликвот.К одной из аликвот добавляют известное количество целевого аналита (аликвота 1). Для другой аликвоты (аликвота 2) добавляют равное количество разбавителя и измерение повторяют. Затем можно рассчитать процент восстановления:
Recovery% = количество аналита в аликвоте1 – количество аналита в аликвоте2Количество добавленного аналита в аликвоту 1 × 100E29
Процент восстановления или смещения часто используется в лабораторной медицине для определения пропорционального смещения. Большинство регулирующих органов установили критические значения для процента извлечения для различных аналитов.Преимущество использования процента восстановления состоит в том, что он нормализуется до 100, что позволяет легче понять имеющуюся шкалу смещения [2].
3. Обнаружение смещения без компараторов
До этого момента мы обсуждали методы обнаружения смещения, использующие эталонный материал или компаратор для оценки наличия смещения. Несмотря на то, что это было общепринятым стандартом для многих лабораторных регулирующих органов, существуют аргументы против такого подхода к обнаружению систематической ошибки: во-первых, предположение о сравнительных исследованиях методов заключается в том, что значения эталонного материала (контрольных образцов) являются истинными и не страдают . неточностиНеопределенность измерения считается минимальной в этих образцах. Тем не менее, если эти образцы значительно не отличаются от матрицы биологического образца, степень неопределенности измерений будет существовать в этих образцах, что приведет к неточным оценкам смещения и неточности лабораторных инструментов и методов. С другой стороны, проведение повторных контрольных образцов с каждым прогоном и необходимость повторной проверки прибора и методов после каждого изменения параметров требует значительных затрат времени, рабочей силы и стоимости.
Альтернативно, систематическая ошибка может быть определена с использованием образцов пациента. Это может быть сделано либо путем отслеживания результатов известных нормальных пациентов (то есть тех, которые, как ожидается, будут иметь результат в пределах референтного диапазона, основанного на их клиническом и физиологическом состоянии), либо следуя тренду всех результатов аналита во времени. Использование образцов пациентов имеет преимущество, заключающееся в том, что в расчет систематической ошибки включена присущая ему биологическая неопределенность.
3.1. Среднее нормальное (AON)
При таком подходе компаратор для контроля качества будет иметь средние значения аналита у нормальных людей.Это требует, чтобы мы знали среднее значение популяции и стандартное отклонение для этого аналита. Если мы измеряем аналит у нормального человека, мы ожидаем, что результаты приблизятся к средней численности населения. Отклонения нормальных результатов от ожидаемой эталонной нормы могут сигнализировать о наличии систематической ошибки.
В AON среднее значение нормальных образцов сравнивается со средним эталонным значением. Среднее эталонное значение должно быть установлено лабораторией на основе совокупности, которую она обслуживает; Лучше всего это сделать как часть первоначальной проверки анализа, когда для определения контрольных диапазонов проводится выборка большого размера нормальных людей.Этот эксперимент позволяет нам рассчитать среднее население, стандартное отклонение и стандартную ошибку (SD / √N). Мы ожидаем, что среднее значение норм от нашего аналитического прогона попадет в 95% доверительный интервал среднего значения для населения.
95% -й доверительный интервал = среднее для населения ± 1,96 стандартная ошибкаE30
При каждом аналитическом прогоне следует использовать выборку нормальных результатов для расчета среднего значения норм для этого аналитического прогона. Если расчетное среднее значение превышает 95% ДИ населения, то мы обнаружили систематическую ошибку в аналитическом прогоне.
В методе AON, поскольку размер нормальной выборки увеличивается, вероятность обнаружения смещения также увеличивается. Расчеты размера для метода AON определяются отношением биологической дисперсии целевого анализируемого вещества (CVb) к дисперсии метода (CVa) (CVb / CVa), а также ожидаемой вероятностью обнаружения смещения. Чтобы помочь с этими вычислениями, можно использовать номограмму Чембровского [14] или, альтернативно, методы, использованные в [15]. Также возможно выполнить AON, выполнив независимый t-тест с двумя выборками.
3.2. Скользящие средние значения пациента
В отличие от метода AON, при скользящих средних значениях пациента все результаты анализа включаются в оценку смещения. Принцип скользящих средних показателей состоит в том, что образцы, проверенные в лаборатории, следуют повторяющейся схеме. Это предположение означает, что общий биологический и клинический спектр пациентов и отдельных лиц, тестируемых в лаборатории, является постоянным на протяжении аналитических прогонов. При изменении средних значений для пациентов мы ожидаем, что средние результаты анализа для двух перекрывающихся поднаборов пациентов будут постоянными.В этом методе, например, среднее значение, рассчитанное для первых 100 пациентов, должно быть аналогично среднему значению, рассчитанному на основе результатов пациентов с номерами от 2 до 101 и т. Д.
Скользящее среднее можно рассчитать с использованием экспоненциально взвешенного скользящего среднего (Xm, я). Важно учитывать, что при перемещении средних значений для пациента вес 1, равный предыдущему среднему значению (X¯M, i − 1), должен быть больше, чем вес (r), присвоенный самым последним результатам (X¯i) ( другими словами, среднее значение каждой партии взвешивается по предыдущим средним значениям).Это может быть указано как:
X¯M, i = rX¯i + 1 − rX¯M, i − 1E31
Вес, назначенный текущим значениям, обычно устанавливается в диапазоне от 0,05 до 0,25 с рекомендуемым значением 0,1.
Компаратор в скользящих средних для пациента является контрольными пределами. Мы ожидаем, что средневзвешенное значение для пациента попадет в контрольные пределы для этого теста. Любая скользящая средняя пациента за пределами этого контрольного предела означает наличие смещения. Уравнение контрольного предела приведено ниже.
Контрольные пределы экспоненциального скользящего среднего = X¯M, 0 ± Lσr2 − r1−1 − r2iE32
, где Lis – постоянный набор, основанный на уровне достоверности (для 95% CI, L равен 2), и σ – стандартное отклонение текущей партии.
Скользящие средние значения пациента также можно оценить с помощью алгоритма Булла. В этом подходе скользящее среднее (X¯b) рассчитывается для подмножеств из 20 выборок с 19 значениями пациента и одним значением, представляющим предыдущее скользящее среднее. Эти значения взвешиваются по-разному (т.е. предыдущему скользящему среднему присваивается больший вес, чем 19 новым выборкам).
Общая формула для скользящего среднего Булла может быть записана как:
X¯b, i = 2 − rX¯b, i − 1 + rDE33
, где X¯b, то есть текущая скользящая средняя, увеличивает вес для текущие значения (с возможными значениями 0 X¯b, i = X¯b, i − 1 + ∑j = 1NXj − Xb, i − 1N2E34 , где N – это количество результатов в партии. Контрольные пределы скользящего среднего Bull устанавливаются как X¯b, 0 ± 3% X¯b, 0, при этом X¯b, 0 является целевым значением для этого аналита. Преимущество скользящих средних заключается в том, что они могут отфильтровывать эффект выбросов, тем самым устраняя путаницу из-за неточности. Алгоритмы скользящих средних очень эффективны для обнаружения смещения: они могут регулярно определять процент смещения от 1% и более.Большинство автоматизированных гематологических анализаторов используют скользящие средние значения для проверки наличия систематической ошибки в своих анализах. Однако алгоритмы скользящего среднего пациента страдают от проблем с реализацией и не широко используются за пределами гематологических анализаторов [2]. Расширение скользящих средних значений для пациента представляет собой применение анализа временных рядов и прогнозирование для выявления систематической ошибки. В анализе временных рядов предыдущие тренды результатов аналита используются для прогнозирования (прогнозирования) тенденции в будущем.Если наблюдаемые результаты аналита отклоняются от прогнозируемой тенденции, тогда может существовать ошибка измерения. В условиях лабораторной медицины нам необходимо уметь обнаруживать систематическую ошибку в коротких временных рядах и отличать погрешность измерения от шума и хаоса, возникающих из-за биологической изменчивости. Здесь мы представим концепцию использования анализа временных рядов для обнаружения смещения, но мы не будем подробно объяснять методологию, поскольку она выходит за рамки этой главы. В прогнозных моделях серия точек данных используется для создания одного или нескольких шаблонов проекции для будущих трендов.Это делается с использованием моделей прогнозирования, таких как ARIMA (авторегрессионное интегрированное скользящее среднее). Эти прогнозы часто верны для очень краткосрочных прогнозов (следующие 1 или 2 точки данных), но для дальнейшего прогнозирования шум и хаос приводят к снижению точности прогноза. Однако, изучая соотношение прогнозируемых и наблюдаемых значений и документируя их изменения по мере нашего прогнозирования в будущем, мы можем определить, представляет ли наблюдаемая модель детерминистический хаотический характер биологического измерения или представляет собой ошибку измерения; для ошибки измерения мы ожидаем, что коэффициент корреляции останется постоянным во времени; однако в условиях хаоса мы ожидаем, что коэффициент корреляции со временем будет ухудшаться [16]. Существуют и другие подходы, использующие анализ временных рядов, которые могут помочь в систематической идентификации ошибок. Один из этих подходов использует тесты единичного корня, такие как тест Дики-Фуллера [17]. Эти тесты проверяют, является ли временной ряд стационарным во времени, то есть постоянны ли среднее значение и дисперсия во времени. Напротив, нестационарные временные ряды будут иметь различное среднее значение и / или различную дисперсию во времени. При использовании этого подхода любое отклонение от стационарности может сигнализировать либо о дрейфе (пропорциональное смещение) и / или смещении (постоянное смещение), либо даже об увеличении неточности во времени (разность-стационарная нестационарность) [17].Если тест Дики-Фуллера возвращает значительное значение p, то мы можем сказать, что ряд является стационарным, и значительная ошибка измерения отсутствует. Откройте вашу модель. Если ваша модель содержит ошибки, связанные с функциями обратного вызова, Diagnostic Viewer открывается и отображает следующие ошибки в Модель Нагрузка ступень. Чтобы открыть окно Просмотр диагностики, на вкладке Отладка ,
нажмите Diagnostics или нажмите ссылку просмотреть ошибки или предупреждения
отображается в нижней части окна редактора Simulink ® . В Simulink Editor на вкладке Моделирование выберите Параметры модели > Свойства модели и изучите ошибку обратного вызова. После исправления любых ошибок обратного вызова симулируйте модель для диагностики ошибок симуляции
и предупреждения. Diagnostic Viewer перечисляет ошибки и предупреждения поэтапно. каждый
Этап в Диагностическое средство просмотра представляет одно событие, такое как
загрузка модели, обновление диаграммы, моделирование или сборка. Отфильтруйте предупреждения, нажав, чтобы сначала можно было устранить ошибки. Чтобы найти источник ошибки, щелкните гиперссылку в сообщении. Модель
в источнике это выделено. Если блок имеет несколько портов, вы можете навести курсор на каждый
порт, чтобы увидеть номер порта. После исправления всех ошибок снова смоделируйте модель и просмотрите Diagnostic Viewer для выявления оставшихся проблем. Если ошибка или предупреждение имеют предопределенное исправление, панель диагностических сообщений
отображает раздел Предлагаемые действия . Вы можете использовать Исправлена кнопка , представленная в этом разделе, чтобы исправить связанные
ошибка или предупреждение. Для получения дополнительной информации см. Предлагаемые действия. Если объект в вашей модели генерирует предупреждение о том, что вы не хотите получать уведомление
иногда вы можете подавить предупреждение из указанного источника, используя Подавить кнопку .Вы можете восстановить предупреждение из этого источника
с помощью кнопки Восстановить . Например, если счетчик
Свободно работающий блок генерирует предупреждение о переполнении, которое является преднамеренным в вашем
дизайн, вы можете подавить только предупреждения о переполнении из этого конкретного блока, без
жертвуя уведомлением о других переполнениях в вашей модели. Чтобы сгенерировать код для вашей модели, на вкладке C Code щелкните Сборка . При возникновении сбоя во время генерации кода программа просмотра диагностики предоставляет
гиперссылки для удобной навигации к источнику сообщения об ошибке или предупреждения. Ошибки Неопределенность Многие единичные факторы основаны на определениях. Есть ровно 5280 футов в миле и
2,54 сантиметра на дюйм, например. Единичные факторы, основанные на определениях, известны с
полная уверенность. Там нет ошибки или неопределенности, связанные с этими числами.
Измерения, однако, всегда сопровождаются ограниченным количеством ошибок или неопределенностей,
что отражает ограничения в методах, используемых для их создания. Существует два источника ошибок в измерении: (1) ограничения в чувствительности
используемые инструменты и (2) недостатки в методах, используемых для измерения.
Эти ошибки можно разделить на два класса: систематические и случайные. Систематические ошибки Систематическая ошибка может быть вызвана несовершенством используемого оборудования или
ошибки, которые совершает индивид во время измерения.Баланс неверно
калибровка приведет к систематической ошибке. Последовательное чтение бюретки неправильно бы
привести к систематической ошибке. Случайные ошибки Случайные ошибки чаще всего возникают из-за ограничений в оборудовании или методах, используемых для
сделать измерение. Предположим, например, что вы хотели собрать 25 мл раствора.
Вы можете использовать стакан, мерный цилиндр или бюретку. Измерения объема, сделанные с
Стакан на 50 мл с точностью до 5 мл.Другими словами, вы бы с такой же вероятностью
получить 20 мл раствора (5 мл слишком мало), как 30 мл (5 мл слишком много). Вы могли бы уменьшить
количество ошибок с помощью градуированного цилиндра, который способен измерять
в течение 1 мл. Ошибка может быть уменьшена еще больше с помощью бюретки, которая
способен доставлять объем с точностью до 1 капли или 0,05 мл. Что из следующего
Процедуры могут привести к систематическим ошибкам, и что приведет к случайным ошибкам? (a) Использование 1-квартовой упаковки молока для измерения 1-литровых проб молока. (b) Использование баланса, чувствительного к 0,1 грамму, для получения 250 мг витамина
C. (c) Использование 100-миллилитрового градуированного цилиндра для измерения 2,5 миллилитров раствора. Нажмите здесь, чтобы
проверьте свой ответ на практической задаче 6 3.3. Анализ временных рядов и прогнозирование для выявления систематической ошибки
Совет
Примечание
Примечание
Ошибки
, Практическая задача 6

 Рис. 1 поясняет различие между случайными и систематическими погрешностями. В ситуации, изображенной на рис. 1, а, систематическая погрешность
Рис. 1 поясняет различие между случайными и систематическими погрешностями. В ситуации, изображенной на рис. 1, а, систематическая погрешность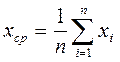 . (3)
. (3)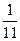 (48,0 + 47,9 + … + 48,1 + 48,2) = 48,1 мг.
(48,0 + 47,9 + … + 48,1 + 48,2) = 48,1 мг.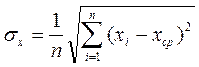 (4)
(4)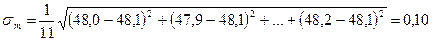 мг.
мг.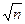 :
: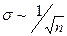 . (6)
. (6)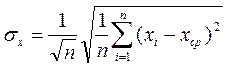 .
.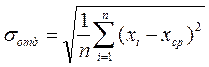 .
. Систематические погрешности
Систематические погрешности