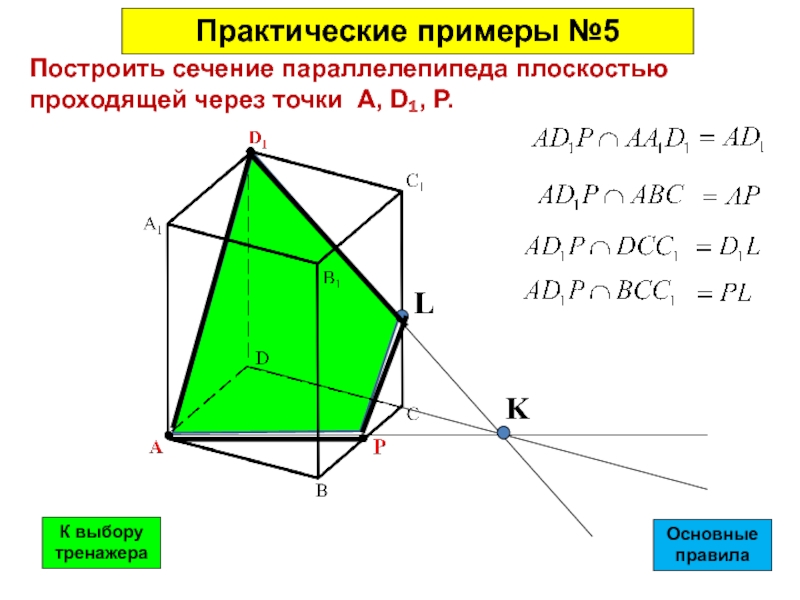
Сечения – Умскул Учебник
На этой странице вы узнаете- Как дракон с помощью сечений разрушал город?
- Чем вода похожа на сечение?
- Что общего у следа на снегу и следа в сечении?
Заглянем в кинотеатр имени Математики. Какой фильм сейчас будут показывать? Располагайтесь поудобнее, приятного просмотра…
СеченияКак дракон с помощью сечений разрушал город?
…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм.
Но внезапно с другой, темной стороны планеты, появился дракон, коренной обитатель планеты. Ему не понравилось вторжение людей, и решил он стереть в пыль все строения.
Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии.
Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника.
Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры.
Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания.
Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.
Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью.
Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно.
Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях. Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.
Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.
Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах.
При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости.
Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии. В этой статье мы не будем заострять на них внимание, прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Зачем может потребоваться сечение?
Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни.
Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.
А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”.
| Чем вода похожа на сечение? Посмотрим на бутылку с водой. Верхний уровень воды можно принять за плоскость, которая рассекает тело бутылки. Наклоняя бутылку и меняя положение воды, можно увидеть различные сечения, которые могут в ней появиться. |
Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.
Методы построения сеченийОднако сечения нужно правильно построить. Для их построения существует несколько методов:
- Метод следов;
- Метод внутреннего проектирования;
- Комбинированный метод.
Разберем их по порядку.
Зимой очень интересно гулять по лесу и разглядывать следы животных: вот пробежал заяц, а это, кажется, была маленькая лисица. Здесь просто снег упал с веток дерева.
Все эти тела оставляют след на снегу.
| Что общего у следа на снегу и следа в сечении? Сечение так же, как и любое животное на снегу, оставляет след на гранях многогранника. |
Если мы возьмем карандаш и проведем прямую на листе, он оставит след. Также и плоскость сечения как бы проводит карандашом по граням фигур, оставляя после себя следы.
След плоскости а в плоскости основания многогранника — прямая, по которой секущая плоскость пересекает плоскость основания многогранника.
Вспомним, что плоскость бесконечна, значит, и след можно продолжать в разные стороны бесконечно.
Однако для построения сечений необходимости бесконечно его продолжать нет: достаточно до пересечения с ребром многогранника или продолжением ребра.
Построим сечение куба, которое проходит через точки К, М и Т, чтобы чуть подробнее разобраться в методе следов.
При построении сечений существует очень важный лайфхак: если точки лежат в одной плоскости (то есть в одной грани), то их можно соединить.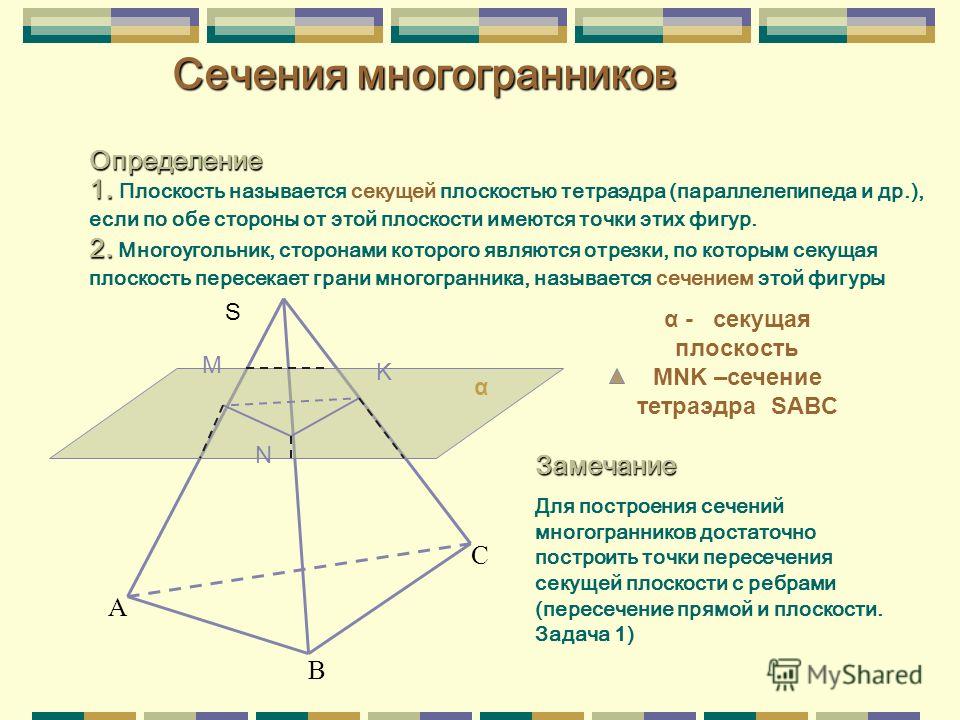
1. Заметим, что в нашем кубе это точки К и Т в плоскости (АВВ1) и точки М и Т в плоскости (ВСС1). Поэтому мы можем их соединить.
2. КТ и МТ в нашем случае — это следы плоскости сечения. Продолжим их за точку К и за точку М. Аналогично продолжим стороны АВ и ВС до тех пор, пока их продолжения не пересекутся со следами.
Пусть продолжения прямых АВ и ТК пересекутся в точке Н, а продолжения прямых ТМ и ВС пересекутся в точке F.
3. Обратим внимание, что точки Н и F лежат на продолжении ребер основания, а значит, лежат в плоскости основания куба. Пользуясь лайфхаком, их можно соединить. Таким образом, получим треугольник, который как бы разрезает наш куб.
4. Однако наше сечение не закончено. Вспомним, что все вершины многоугольника должны лежать на ребрах куба, то есть точки Н и F не подходят. Но на самом деле осталось совсем немного закончить построение.
5. Заметим, что прямая HF пересекает ребра AD, DC, назовем точки этих пересечений как N и L.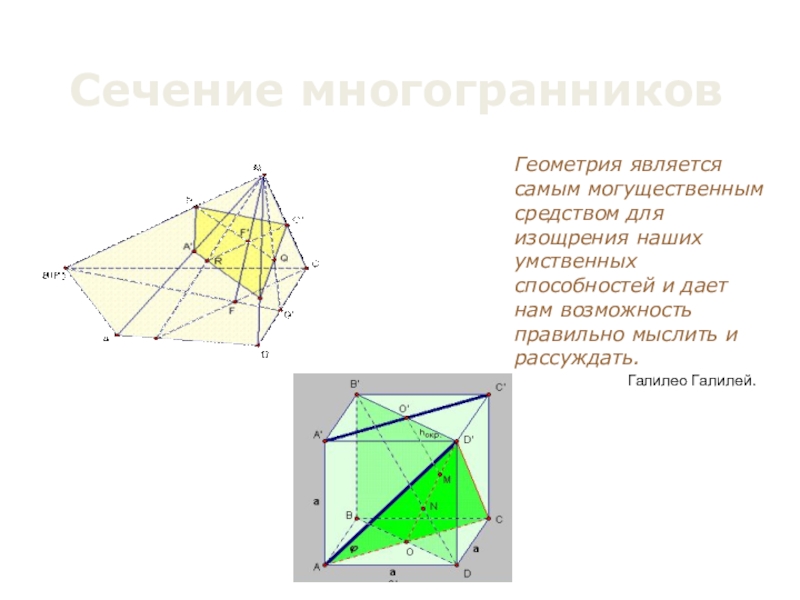
А также соединим все точки, которые окажутся в одной плоскости.
6. И вот мы получили сечение. Многоугольник TKNLM — сечение куба.
Итак, основной способ построить сечение методом следов — продолжить след сечения до его пересечения с ребрами многогранника или продолжениями его ребер.
А также пользоваться лайфхаком: точки в одной плоскости можно соединять.
Рассмотрим метод внутреннего проектирования.
Иногда метод следов может не помочь: след будет идти параллельно ребру или пересекаться с его продолжением далеко за пределами листа.
В таких случаях часто используется следующее свойство: параллельные плоскости пересекаются другой плоскостью по параллельным прямым. Подробнее про это свойство можно прочесть в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Польза этого свойства в том, что если сечение пройдет через параллельные плоскости, то оно пересечет их по параллельным линиям. А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.
А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.
Но будем разбираться на практике. Построим сечение треугольной призмы, проходящее через точки К, М, Т.
1. Первым делом соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1) и точки Т и М в плоскости (АВС).
2. КТ проходит почти параллельно ребру АА1, следовательно, использовать метод следов не рационально.
3. Теперь посмотрим на плоскости (АВС) и (А1В1С1) — они параллельные. А значит прямую сечения можно параллельно перенести в одну из них.
В плоскости (АВС) лежит прямая ТМ, а в плоскости (А1В1С1) лежит точка К, которая является вершиной сечения. Тогда из точки К в плоскости верхнего основания нам нужно провести прямую, параллельную ТМ до пересечения с ребром призмы. Назовем эту точку Е.
Назовем эту точку Е.
4. А теперь мы можем соединить Е и М, так как они лежат в одной плоскости. Четырехугольник КЕМТ — сечение призмы.
Осталось разобраться, в чем заключается комбинированный метод? Он включает в себя и метод следов, и метод внутреннего проектирования, то есть приемы из каждого метода могут применяться вместе в одной и той же задаче.
Все зависит от удобства решения и его быстроты: там, где невозможно применить метод внутреннего проектирования, можно применить метод следов. А там, где применять метод следов неудобно (или невозможно), можно применить метод внутреннего проектирования.
Примеры построения сеченийРассмотрим несколько примеров построения сечений в различных фигурах.
Пример 1. В правильном тетраэдре провели апофему АТ, на середине которой отметили точку К. АЕ:ЕС = 1:5. Р — точка на ребре CD. Постройте сечение тетраэдра, проходящее через точки К, Е и Р.
Решение.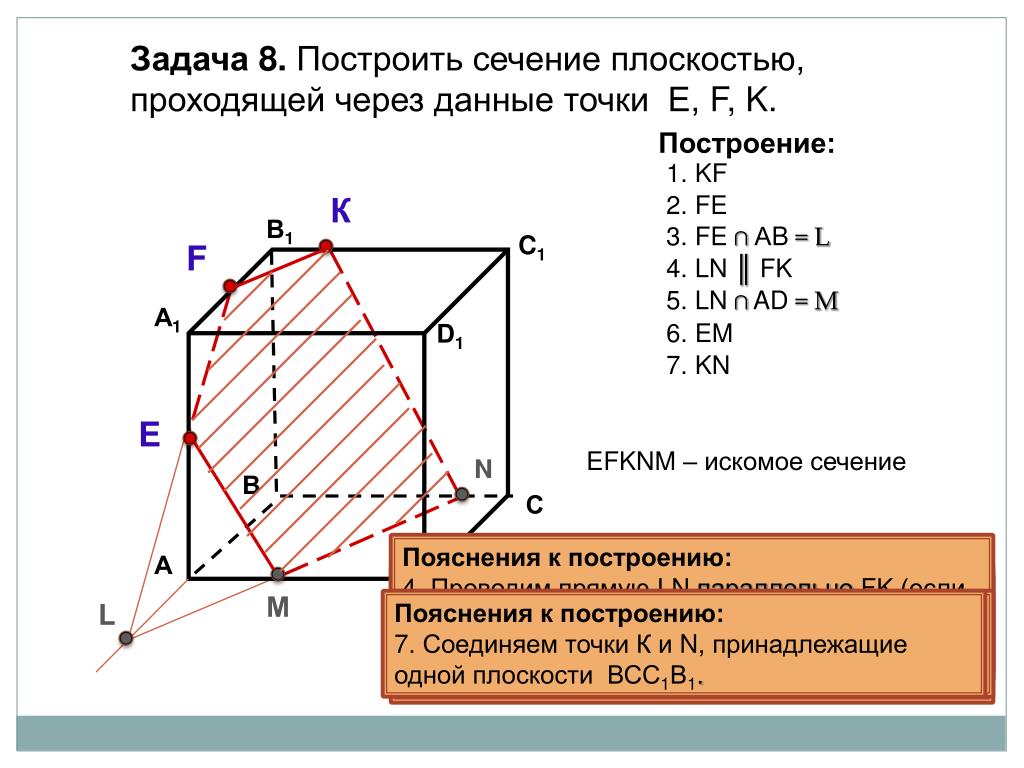 Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
1. Начнем решение с того, что соединим точки, лежащие в одной плоскости. Е и Р лежат в плоскости (ACD), значит их можно соединить.
2. Рассмотрим плоскость (АСG). Проведем прямую CG. Точки К и Е лежат в одной плоскости, то есть их также можно соединить.
3. Воспользуемся методом следов и продлим прямые ЕК и CG до их пересечения в точке Т.
4. Теперь точки Т и Р будут лежать в одной плоскости основания, следовательно, их можно соединить. Пусть прямая ТР пересекает ребро BD в точке М.
Тогда точки М и К лежат в одной плоскости (ABD) — их тоже можно соединить.
5. Продлим прямую МК до пересечения с ребром АВ в точке О. Точки О и Е лежат в одной плоскости (АВС), соединим их. Сечением тетраэдра будет четырехугольник ОЕРМ.
Пример 2. Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
Решение. 1. Соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1).
Воспользуемся методом следов и продолжим прямую ТК до пересечения с продолжением стороны АС в точке Р.
2. Точки Р и М лежат в одной плоскости (АВС), то есть их можно соединить. Пусть прямая РМ пересечет ребро ВС в точке Е.
Воспользуемся методом внутреннего проектирования и проведем из точки Т прямую, параллельную ЕМ. Пусть она пересечет ребро А1В1 в точке О.
3. Осталось соединить точки, лежащие в одной плоскости. Это точки К и Е в плоскости (ВСС1) и точки О и М в плоскости (АВВ1).
Тогда КТОМЕ — сечение призмы.
Пример 3. Дан куб ABCDA1B1C1D1. М — середина ребра АА1. Постройте сечение куба, которое будет параллельно диагонали куба А1С и будет проходить через точки М и В.
Решение. 1. Достроим прямую АС и рассмотрим плоскость (АА1С). Проведем в ней прямую, параллельную А1С из точки М. Пусть она пересечет АС в точке К.
2. Тогда МК — средняя линия треугольник АА1С, значит К — середина АС.
Подробнее про среднюю линию треугольника можно прочесть в статье «Треугольники».
3. Точка К будет принадлежать сечению. Точки В и К лежат в плоскости (АВС) — их можно соединить.
4. В основании куба находится квадрат, его диагонали равны и точкой пересечения делятся пополам.
Подробнее про квадрат и его свойства можно прочитать в статье «Параллелограмм».
Поскольку К — середина диагонали АС, эта же точка будет серединой диагонали BD.
Следовательно, прямую ВК можно продлить до точки D.
5. Осталось только соединить точки, которые лежат в одной плоскости. Это точки М и D в плоскости (ADD1) и точки М и В в плоскости (ABB1).
Тогда сечением будет треугольник DMB.
Мы рассмотрели сечения и основные способы их построения. В них нет ничего сложного и стоит помнить, что любое сечение можно представить в реальной жизни. Например, попробовать разрезать пластилиновые фигуры.
Фактчек- Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. При этом в многогранниках сечения представлены в виде многоугольников, вершины которых лежат на ребрах фигуры.
- Существует несколько методов построения сечения в многогранниках: метод следов, метод внутреннего проектирования и комбинированный метод.
- Метод следов заключается в том, что по следу сечения можно построить его полностью. След сечения — прямая, по которой секущая плоскость пересекает грань многогранника. В методе следов часто нужно продлевать линии и ребра до их пересечения.
- Метод внутреннего проектирования позволяет параллельно переносить сторону сечения в параллельных плоскостях.
 Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
Это может быть удобно в случаях, когда метод следов невозможно или трудно применить. - Комбинированный метод — метод, который сочетает в себе и метод следов, и метод внутреннего проектирования.
Задание 1.
Какая форма сечения будет, если треугольную пирамиду разрезать параллельно основанию?
- Треугольник;
- Четырехугольник;
- Шестиугольник;
- Произвольный многоугольник с любым количеством углов.
Задание 2.
Где могут лежать вершины многоугольника, который образовывает сечение?
- Только в вершинах многогранника;
- На ребрах многогранника;
- Только на гранях многогранника;
- В любой точке на многограннике.
Задание 3.
Что такое след сечения?
- Продолжения сторон сечения;
- Вершины многоугольника, который образовывает сечение;
- Прямая, по которой секущая плоскость пересекает плоскость основания многогранника;
- Все вышеперечисленные варианты.

Задание 4.
Что можно сделать с точками, которые лежат на одной грани?
- Соединить;
- Ни в коем случае нельзя их соединять;
- Построить сечение, опираясь на две разные стороны, не соединяя стороны;
- Ни один из перечисленных вариантов.
Задание 5.
Как можно воспользоваться методом внутреннего проектирования?
- Произвольно переносить линии сечения в любых гранях;
- Произвольно переносить линии сечения в параллельных гранях;
- Перпендикулярно переносить линии сечения в перпендикулярных гранях;
- Параллельно переносить линии сечения в параллельных гранях.
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 4
Презентация к уроку геометрии “Построение сечений тетраэдра”
Материал опубликовал
#10 класс #Геометрия #ФГОС #Учебно-дидактические материалы #Задача / упражнение / практикум #Учитель-предметник #Школьное образование #УМК любой
Построение сечений тетраэдра
Для решения многих геометрических задач необходимо строить их сечения многогранника различными плоскостями.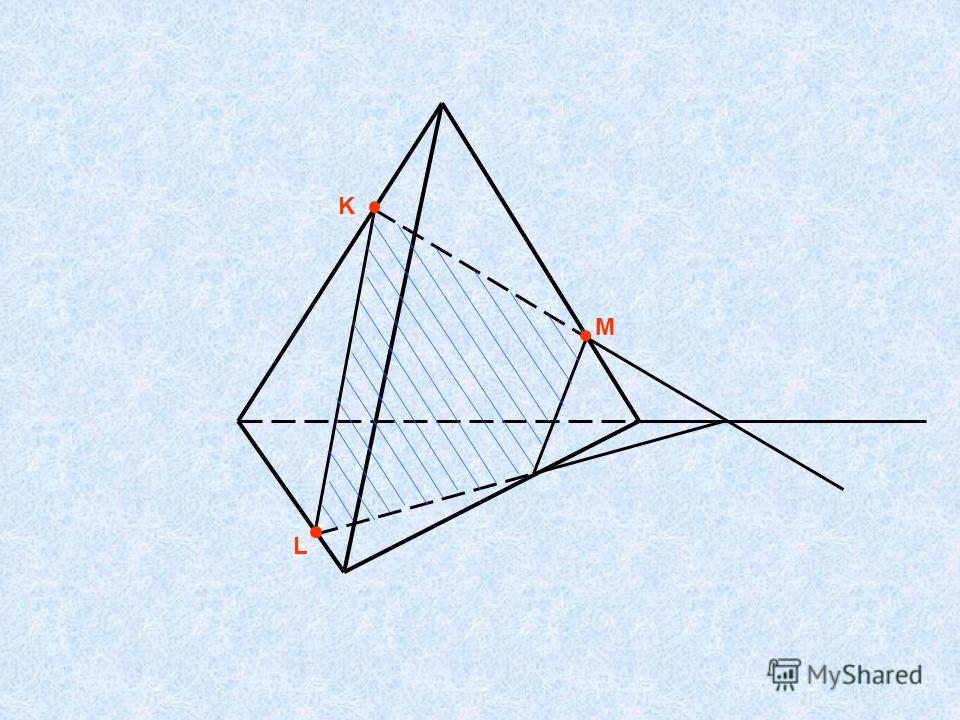
сечение Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки – сечение тетраэдра.
Какие многоугольники могут получиться в сечении ? Тетраэдр имеет 4 грани В сечениях могут получиться: Четырехугольники Треугольники
При этом необходимо учитывать следующее: 1. Соединять можно только две точки, лежащие в плоскости одной грани. Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками. 2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам. 3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
D
A
B
C
Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K
D
A
B
C
M
N
K
Проводим MK. 2. Проводим NK.
3. Проводим MN.
4. MNK –
искомое сечение.
2. Проводим NK.
3. Проводим MN.
4. MNK –
искомое сечение.
Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K. E F K L A B C D M 1. Проводим КF. 2. Проводим FE. 3. Продолжим EF, продол- жим AC. 5. Проводим MK. 7. Проводим EL EFKL – искомое сечение 6. MK AB=L 4. EF AC =М
1.Все вершины сечения лежат на рёбрах многогранника. Свойства правильно построенного сечения. 2.Все стороны сечения лежат в гранях многогранника. 3.В каждой грани лежит не более одной стороны сечения.
Построение на готовых чертежах
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.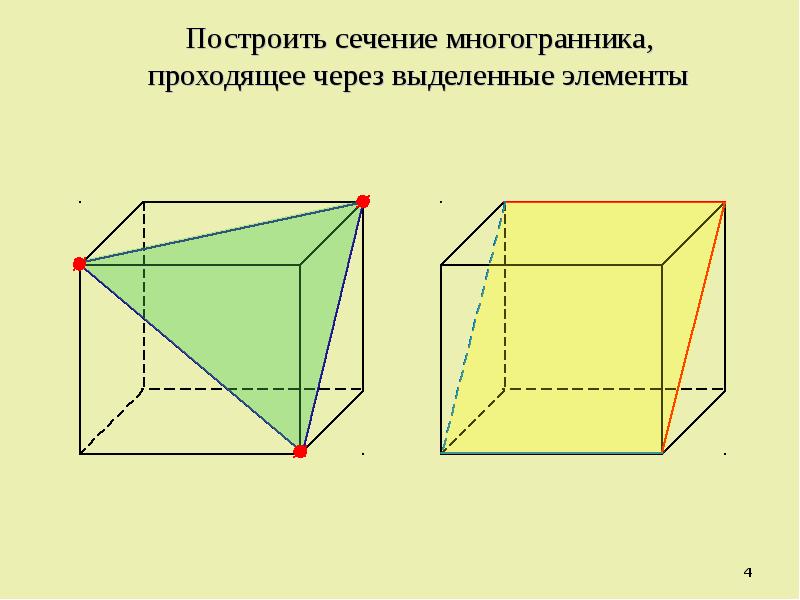
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Построить сечение тетраэдра плоскостью, проходящей через точки М, N, P.
Домашнее задание
Геометрия поперечного сечения
Скачать страницу Геометрия поперечного сечения.
Геометрия границ для анализа течения в естественных водотоках определяется в терминах профилей земной поверхности (поперечных сечений) и измеренных расстояний между ними (длины досягаемости). Поперечные сечения расположены с интервалами вдоль ручья, чтобы охарактеризовать пропускную способность ручья и прилегающей к нему поймы. Они должны проходить через всю пойму и должны быть перпендикулярны ожидаемым линиям потока. Иногда для выполнения этого требования необходимо расположить поперечные сечения по криволинейной или изогнутой линии.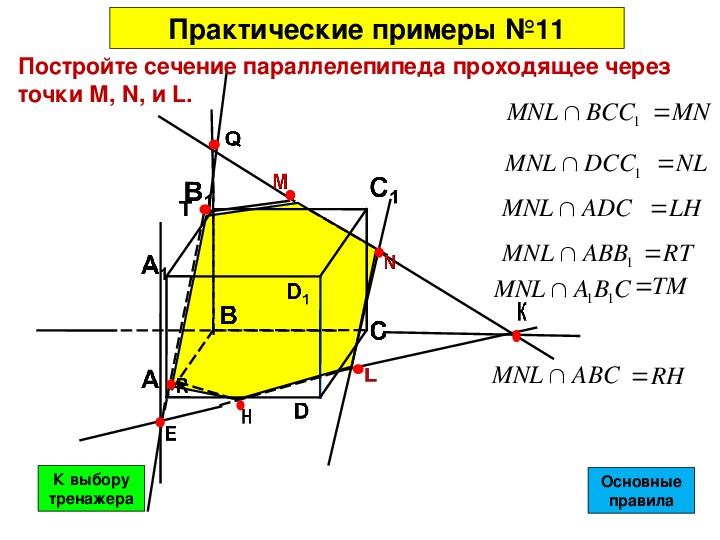
Пример размещения поперечных сечений показан ниже на рисунке ниже. Общий подход к размещению поперечных сечений заключается в обеспечении того, чтобы поперечные сечения были перпендикулярны линиям потока. Это требует оценки того, как будут выглядеть линии потока в прибрежных районах вдали от основного русла. Один из вариантов — провести осевую линию потока вниз по основному каналу вдоль того места, которое воспринимается как центр масс потока. То же самое нужно сделать для левого и правого берегов. Предполагаемые пути потока для русла и береговых зон показаны пунктирными линиями на рисунке ниже. Эти линии не только помогут в построении поперечных сечений, перпендикулярных линиям потока, но также представляют путь для измерения длин досягаемости между поперечными сечениями.
Поперечные сечения требуются в репрезентативных местах по всему участку ручья и в местах, где происходят изменения расхода, уклона, формы или шероховатости, в местах, где начинаются или заканчиваются дамбы, а также на мостах или регулирующих сооружениях, таких как плотины.
Выбор уравнения потерь на трение также может влиять на расстояние между поперечными сечениями. Например, расстояние между поперечными сечениями может быть максимальным при расчете профиля М1 (профиль подпора) с помощью уравнения среднего коэффициента трения или когда уравнение среднего гармонического коэффициента трения используется для расчета профилей М2 (профиль просадки). Программное обеспечение HEC-RAS позволяет программе выбрать уравнение усреднения.
Программное обеспечение HEC-RAS позволяет программе выбрать уравнение усреднения.
Каждый поперечный разрез в наборе данных HECRAS идентифицируется меткой реки, участка и речной станции. Поперечное сечение описывается путем ввода станции и высоты (данные X-Y) слева направо, если смотреть вниз по течению. Идентификатор речной станции может соответствовать стоянке вдоль канала, милям или любой фиктивной системе нумерации. Система нумерации должна быть согласованной, поскольку программа предполагает, что более высокие числа относятся к восходящему потоку, а меньшие — к нисходящему.
Каждой точке данных в поперечном сечении присваивается номер станции, соответствующий горизонтальному расстоянию от начальной точки слева. Для описания каждого поперечного сечения может использоваться до 500 точек данных. Данные поперечного сечения традиционно определяются в направлении вниз по течению. Программа считает, что левая сторона потока имеет наименьшие номера станций, а правая — самые высокие. Данные поперечного сечения могут иметь отрицательные значения пикетирования. Размещение необходимо вводить слева направо в порядке возрастания. Однако одно и то же значение пикетажа может иметь более одной точки. Левый и правый пикеты, отделяющие основное русло от береговых участков, должны быть указаны в редакторе данных разреза. Слишком низкие конечные точки поперечного сечения (ниже расчетной отметки поверхности воды) будут автоматически расширены по вертикали, и в выходных данных для этого сечения появится примечание, указывающее, что поперечное сечение необходимо расширить. Программа добавляет дополнительный смачиваемый периметр для любой воды, которая вступает в контакт с расширенными стенами.
Данные поперечного сечения могут иметь отрицательные значения пикетирования. Размещение необходимо вводить слева направо в порядке возрастания. Однако одно и то же значение пикетажа может иметь более одной точки. Левый и правый пикеты, отделяющие основное русло от береговых участков, должны быть указаны в редакторе данных разреза. Слишком низкие конечные точки поперечного сечения (ниже расчетной отметки поверхности воды) будут автоматически расширены по вертикали, и в выходных данных для этого сечения появится примечание, указывающее, что поперечное сечение необходимо расширить. Программа добавляет дополнительный смачиваемый периметр для любой воды, которая вступает в контакт с расширенными стенами.
Другие данные, которые требуются для каждого поперечного сечения, включают: длину участка вниз по течению; коэффициенты шероховатости; коэффициенты сжатия и расширения. Эти данные будут подробно рассмотрены далее в этой главе.
Доступны многочисленные опции программы, позволяющие пользователю легко добавлять или изменять данные поперечного сечения.
Коническое сечение | геометрия | Britannica
- Ключевые люди:
- Блез Паскаль Аполлоний Пергский Жирар Дезарг Колин Маклорен Конон Самосский
- Похожие темы:
- эллипс гипербола парабола круг директриса
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
коническое сечение , также называемое коническим
, в геометрии любая кривая, полученная пересечением плоскости и прямого кругового конуса. В зависимости от угла плоскости относительно конуса пересечение представляет собой окружность, эллипс, гиперболу или параболу. Особые (вырожденные) случаи пересечения возникают, когда плоскость проходит только через вершину (с образованием одной точки) или через вершину и другую точку на конусе (с образованием одной прямой или двух пересекающихся прямых). См. рисунок.
В зависимости от угла плоскости относительно конуса пересечение представляет собой окружность, эллипс, гиперболу или параболу. Особые (вырожденные) случаи пересечения возникают, когда плоскость проходит только через вершину (с образованием одной точки) или через вершину и другую точку на конусе (с образованием одной прямой или двух пересекающихся прямых). См. рисунок. Основные описания, но не названия, конических сечений можно проследить до Менехма (расцвет творчества около 350 г. до н. э.), ученика Платона и Евдокса Книдского. Аполлоний Пергский (ок. 262–190 до н. э.), известный как «Великий геометр», дал названия коническим сечениям и первым определил две ветви гиперболы (предполагающие наличие двойного конуса). Восьмитомный трактат Аполлония о конических сечениях
Викторина “Британника”
Числа и математика
Аналитическое определение
Коники также могут быть описаны как плоские кривые, являющиеся путями (локусами) точки, движущейся так, что отношение ее расстояния от фиксированной точки (фокуса) к расстоянию от фиксированной линии (директрисы) является постоянным, называется эксцентриситетом кривой. Если эксцентриситет равен нулю, кривая представляет собой окружность; если равен единице, парабола; если меньше единицы, эллипс; а если больше единицы, гипербола. См. рисунок.
Если эксцентриситет равен нулю, кривая представляет собой окружность; если равен единице, парабола; если меньше единицы, эллипс; а если больше единицы, гипербола. См. рисунок.
Каждая коническая секция соответствует графику полиномиального уравнения второй степени формы A x 2 + B Y 2 +2 C x +2 C x +2 +2 . D x + 2 E y + F = 0, where x and y are variables and A , B , C , D , E и F — коэффициенты, зависящие от конкретной коники. Подходящим выбором координатных осей уравнение любой коники можно привести к одной из трех простых r-форм: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 – у 2 / b 2 = 1, или y 2 = 2 p x 9,
соответствующие эллипсу, гиперболе и параболе соответственно. (Эллипс, где a = b , на самом деле является окружностью.) Широкое использование систем координат для алгебраического анализа геометрических кривых началось с Рене Декарта (1596–1650). См. История геометрии: Декартова геометрия.
(Эллипс, где a = b , на самом деле является окружностью.) Широкое использование систем координат для алгебраического анализа геометрических кривых началось с Рене Декарта (1596–1650). См. История геометрии: Декартова геометрия.
Греческое происхождение
Ранняя история конических сечений связана с проблемой «удвоения куба». Согласно Эратосфену из Кирены (ок. 276–190 до н. э.), жители Делоса обратились к оракулу Аполлона за помощью в прекращении чумы (ок. 430 до н. э.) и получили указание построить Аполлону новый алтарь, в два раза превышающий объем старого алтаря. и такой же кубической формы. Озадаченные, делосцы посоветовались с Платоном, который заявил, что «оракул имел в виду не то, что бог хотел алтарь вдвое большего размера, а то, что он хотел, ставя им задачу, пристыдить греков за их пренебрежение математикой и их презрение к математике». по геометрии». Гиппократ с Хиоса (ок. 470–410 до н. э.) впервые обнаружил, что «делийская проблема» может быть сведена к нахождению двух средних пропорций между a and 2 a (the volumes of the respective altars)—that is, determining x and y such that a : x = x : y = y : 2 и .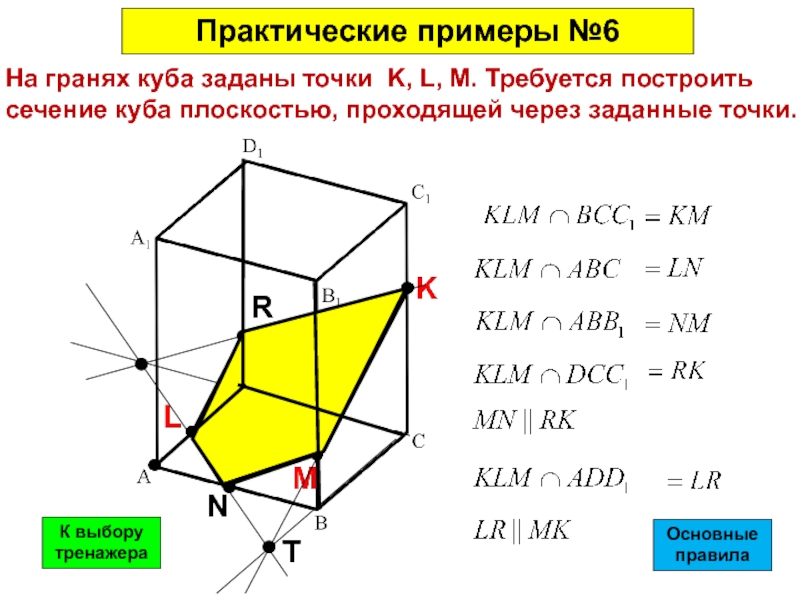 Это эквивалентно решению одновременно любых двух уравнений x 2 = A Y , Y 2 = 2 A X и X 40046 40046 40046 40046 40046 40046 40046 40046 40046 40046. а 2 , которые соответствуют двум параболам и гиперболе соответственно. Позже Архимед (ок. 290–211 до н. э.) показал, как с помощью конических сечений разделить сферу на два сегмента, имеющих заданное отношение.
Это эквивалентно решению одновременно любых двух уравнений x 2 = A Y , Y 2 = 2 A X и X 40046 40046 40046 40046 40046 40046 40046 40046 40046 40046. а 2 , которые соответствуют двум параболам и гиперболе соответственно. Позже Архимед (ок. 290–211 до н. э.) показал, как с помощью конических сечений разделить сферу на два сегмента, имеющих заданное отношение.
Диокл (ок. 200 г. до н. э.) геометрически продемонстрировал, что лучи, например, от Солнца, параллельные оси параболоида вращения (образованного вращением параболы вокруг ее оси симметрии), встречаются в фокусе. Говорят, что Архимед использовал это свойство, чтобы поджечь вражеские корабли. Анфимий Тралльский, один из архитекторов собора Святой Софии в Константинополе (завершен в 537 г. по Р.Х.), упомянул о центральных свойствах эллипса как о средстве обеспечения того, чтобы алтарь мог освещаться солнечным светом в течение всего дня.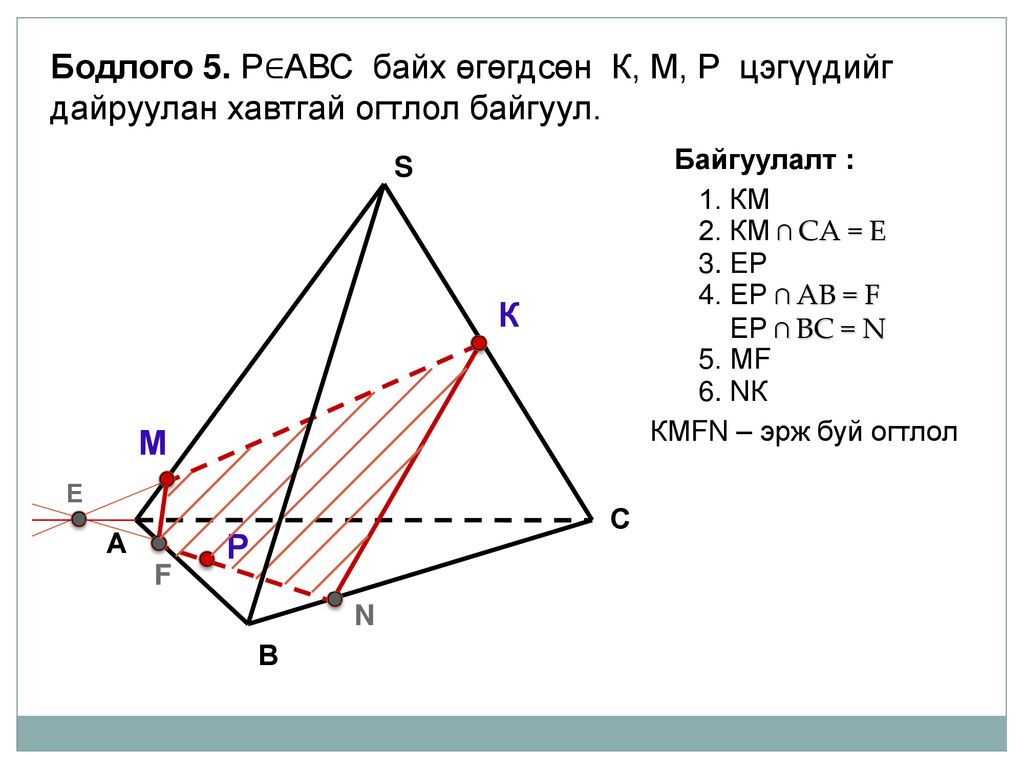
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Пост-греческие приложения
Конические сечения нашли свое первое практическое применение помимо оптики в 1609 году, когда Иоганн Кеплер вывел свой первый закон движения планет: планета движется по эллипсу с Солнцем в одном фокусе. Галилео Галилей опубликовал первое правильное описание пути снарядов — параболу — в своих «Диалогах о двух новых науках» (1638). В 1639 г.французский инженер Жирар Дезарг инициировал изучение тех свойств коник, которые инвариантны относительно проекций ( см. проективная геометрия). Архитекторы восемнадцатого века создали моду на шепчущие галереи — такие, как в столице США и в соборе Святого Павла в Лондоне, — в которых шепот в одном фокусе эллипсоида (эллипса, вращающегося вокруг одной оси) можно услышать в другом. сосредоточиться, но больше нигде. От вездесущей параболической спутниковой тарелки ( см. на рисунке) до использования ультразвука в литотрипсии продолжают находить новые применения для конических сечений.

 И этот след — это сторона многоугольника, который образовывает сечение.
И этот след — это сторона многоугольника, который образовывает сечение.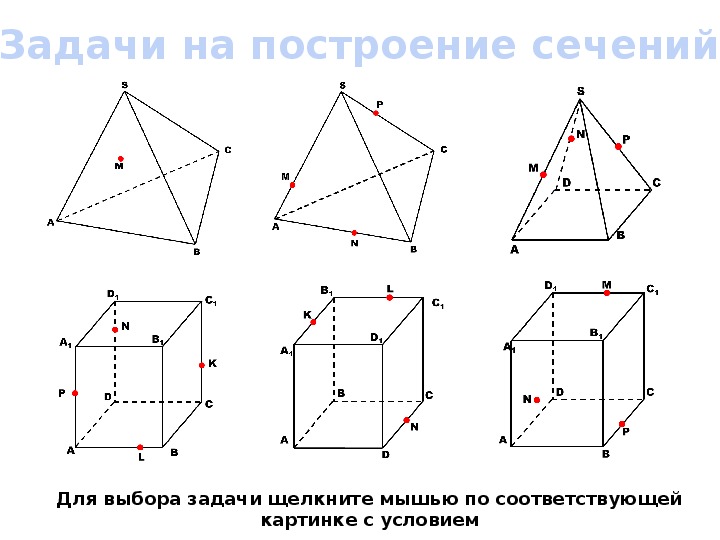 Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.