Сечение поверхности плоскостью. (Лекция 6)
Похожие презентации:
Сечение поверхности плоскостью. (Лекция 6)
Пересечение поверхности плоскостью
Позиционные задачи
Пересечение поверхности и плоскости. Сечение поверхностей 2-го порядка
Сечение поверхности плоскостью частного положения
Пересечение поверхностей. Способ вспомогательных секущих плоскостей
Метричесие задачи поверхности. (Лекция 3)
Пересечение поверхностей. (Лекция 7)
Частные случаи пересечения поверхностей второго порядка
Построение линии пересечения поверхности проецирующей плоскостью
Лекция 6
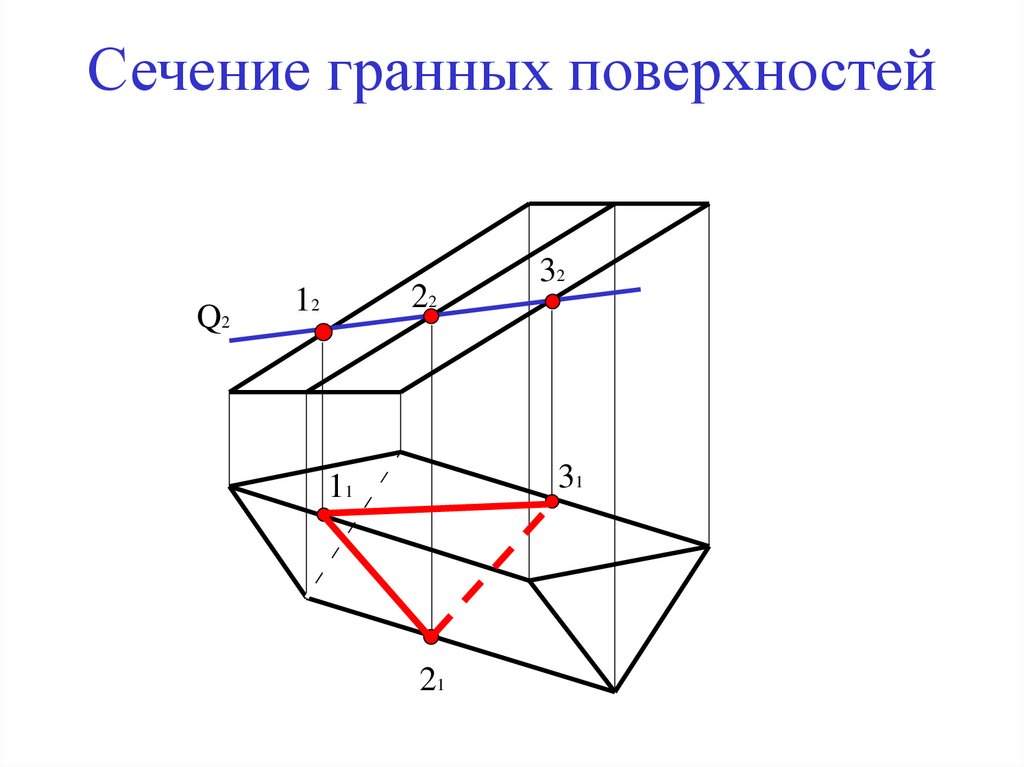
Сечение поверхности плоскостью
Алгоритм решения задачи
1. Объекты ( и ) рассекают
вспомогательной секущей
плоскостью Г
B
Г
b
2. Находят линию
пересечения
вспомогательной плоскости
с каждым из объектов
аА
Г а ; Г b
3. На полученных линиях
пересечения определяют
общие точки, принадлежащие
заданным поверхностям
4.
 Выбирают следующую секущую плоскость и повторяют
Выбирают следующую секущую плоскость и повторяюталгоритм
5. Полученные точки соединяют с учетом видимости
искомой линии пересечения
Методические указания
• Плоскость, пересекающая поверхность, может
занимать общее и частное положение
относительно плоскостей проекций
• В общем случае вид сечения – кривая линия
• Сечение поверхности вращения плоскостью
является фигурой симметричной. Ось
симметрии фигуры сечения лежит в плоскости
общей симметрии заданной поверхности и
плоскости, при условии:
проходит через ось вращения поверхности;
перпендикулярности секущей плоскости
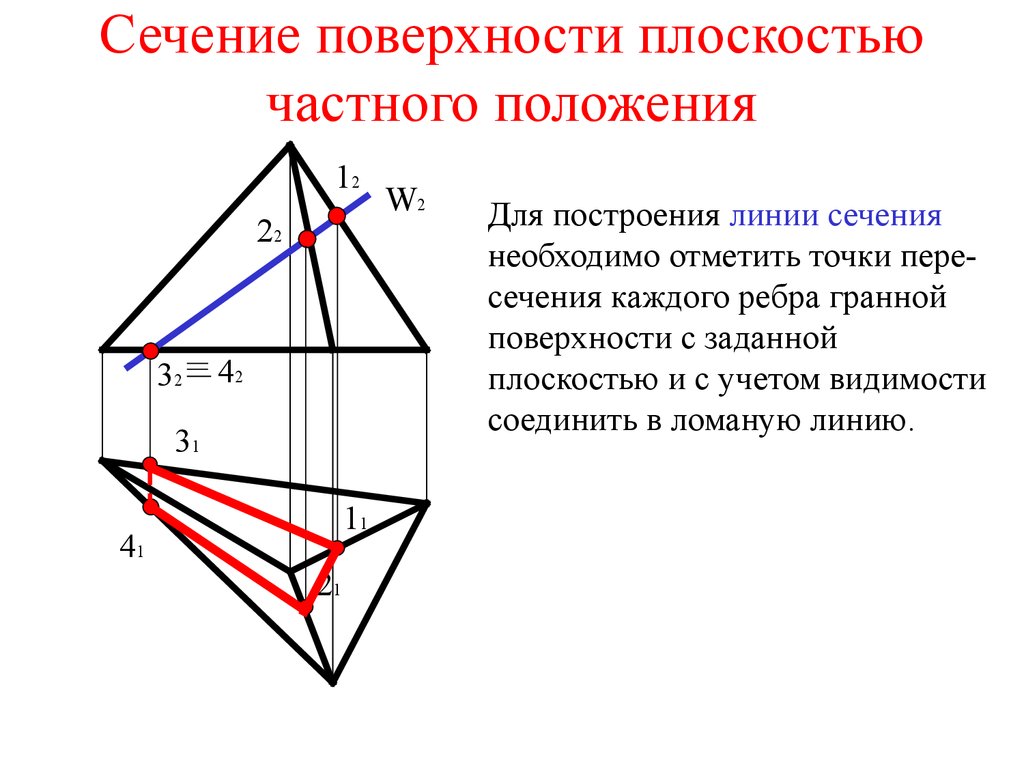
• Сечением многогранной поверхности является
ломаная линия, вершины которой лежат на
ребрах поверхности
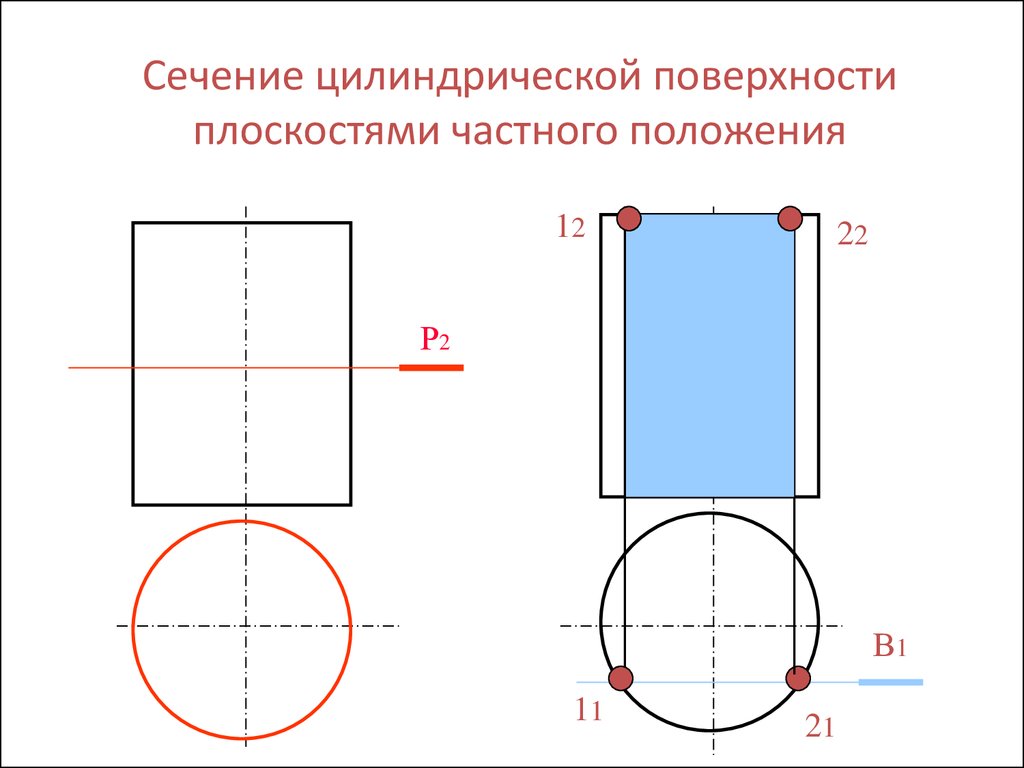
Сечения прямого кругового цилиндра
1
2
3
1
3
При рассечении прямого кругового цилиндра плоскостями можно
получить:
1- окружность, 2- эллипс, 3 – прямые линии
2
Сечение сферы
Любая плоскость пересекает сферу по окружности.
 Окружность на
Окружность наплоскость проекций может проецироваться в натуральную величину
(плоскость уровня), в виде отрезка, равного диаметру (проецирующая
плоскость) и в виде эллипса (плоскость общего положения)
Q2
22
3 ПО.
О2
12
О1
21
Ф1
(11 )
При построении линии сечения сферы плоскостью частного положения
Q(Q2) прежде всего находим на П2 проекции экстремальных точек. Это
точки пересечения следа Q2 с очерком сферы – 12 и 22. На П1 проекции
11 и 21 располагаем на следе плоскости Ф1 с учетом их видимости.
Q2
22
О2 32 (42)
Г2
12
41
О1
21
Ф1
(11 )
31
С помощью плоскости Г(Г2) зафиксируем совпадающие проекции точек
(32 и 42) на пересечении Г2 со следом заданной плоскости Q2. Проекции
будут точки изменения видимости линии сечения на П1.
Q2
22
О2 32 (42)
Г2
b2
52 (62)
12
(61 )
41
b1
О1
21
Ф1
(11 )
(51 )
31
Экстремальные точки эллипса (высшую и низшую) находим, разделив
пополам отрезок 12 22 перпендикуляром, опущенным из точки О2.
 В основании перпендикуляра фиксируем две совпадающие проекции точек (52 и
В основании перпендикуляра фиксируем две совпадающие проекции точек (52 и62). На П1 проекции 51 и 61 располагаем на параллели b1 как невидимые.
Q2
22
О2 32 (42)
Г2
b2
52 (62)
с2
12
(61 )
41
b1
О1
21
Ф1
(11 )
с1
(51 )
31
Для уточнения формы кривой – эллипса находим промежуточные точки
( на чертеже не обозначены). Совпадающие точки фиксируем
произвольно на следе Q2 и переносим их на П1с помощью параллели с.
Q2
22
О2 32 (42)
Г2
b2
52 (62)
с2
12
(61 )
41
b1
О1
21
Ф1
(11 )
с1
(51 )
31
Объединяем все построенные на П1 точки в линию (эллипс) с учетом ее
видимости относительно сферы. Видимость линии будет меняться в
точках 31 и 41, построенных заранее в соответствии с алгоритмом
решения задачи.
Q2
22
О2 32 (42)
Г2
b2
52 (62)
с2
x
П2 x1
П4
12
П2
(61 )
П1
41
b1
О1
21
(11 )
Ф1
О4
с1
(51 )
31
На П1 дополняем построенную проекцию эллипса большой осью,
проходящей через экстремальные точки 51 и 61.
 Показать натуральную
Показать натуральнуюлинию сечения можно, применив преобразование чертежа – замену
плоскости проекций
Q2
22
О2 32 (42)
Г2
b2
52 (62)
с2
12
П2
Rc
(61 )
П1
П2 x1
П4
41
b1
О1
21
(11 )
Rc
Ф1
О4
с1
(51 )
31
На дополнительной плоскости проекций П4 линия сечения – окружность
проецируется в натуральную величину.
Сечения прямого кругового конуса
1
3
5
3
4
1
2
2
4
5
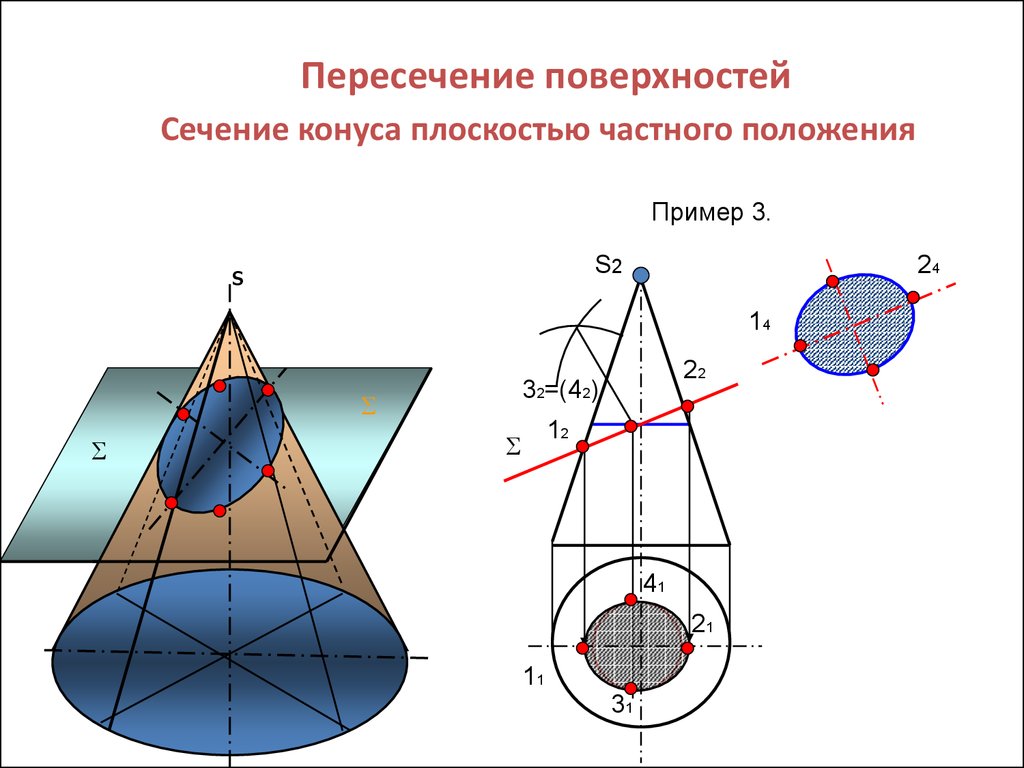
При пересечении прямого кругового конуса с плоскостью в зависимости
от ее расположения получаются:
1 – окружность; 2 – эллипс; 3 – парабола; 4 – гипербола; 5 – прямые линии
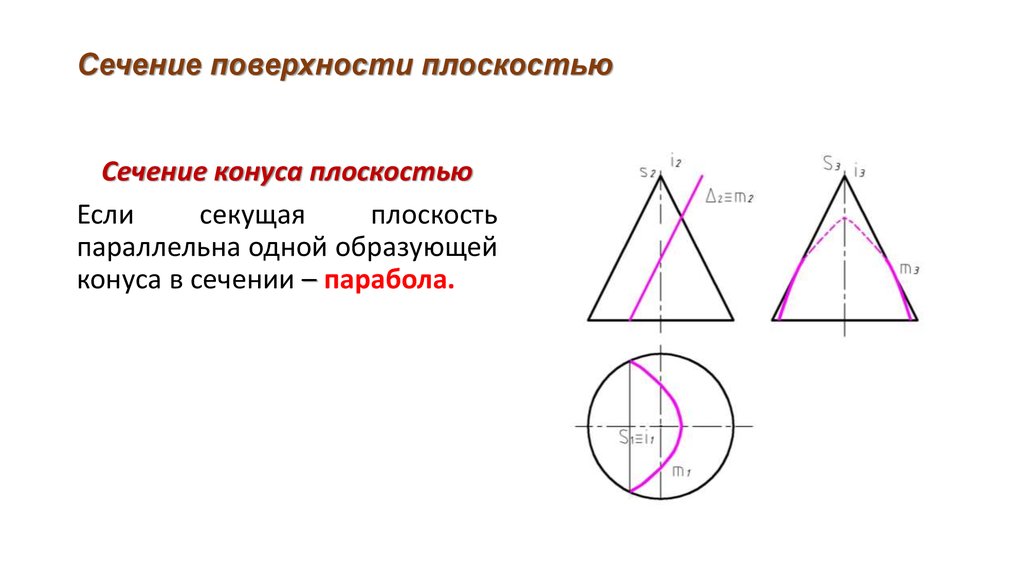
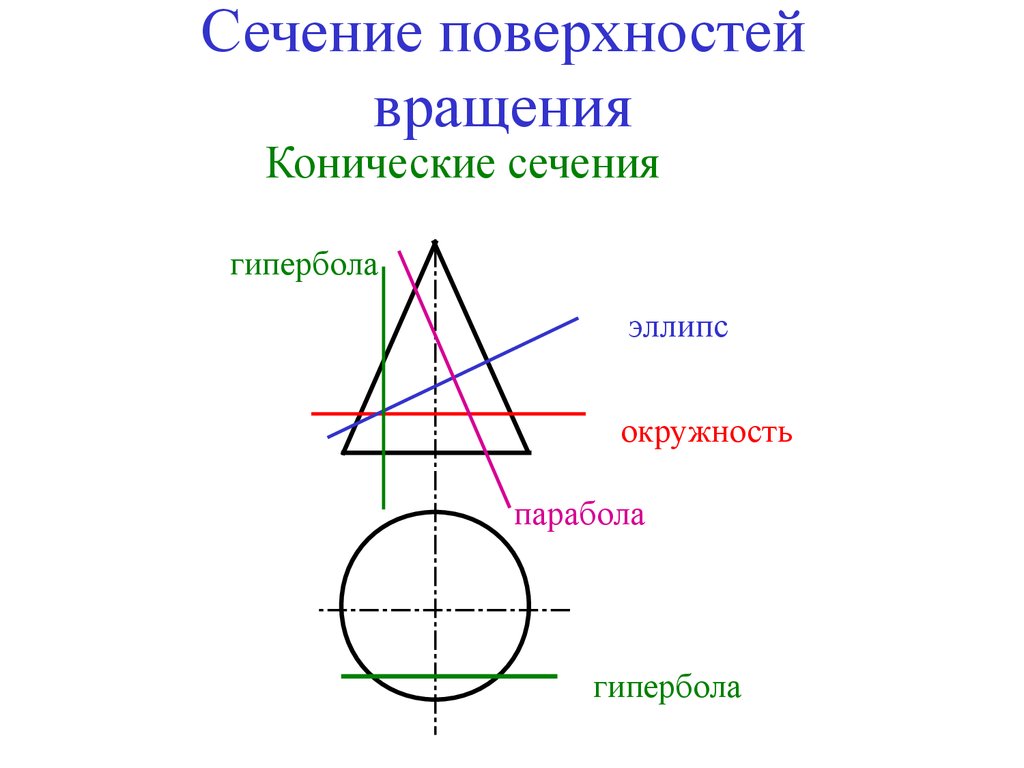
В сечении конической поверхности вращения плоскостью
могут быть получены различные геометрические образы
В плоскости Г – точка,
Δ – окружность,
Θ – эллипс,
Σ – гипербола,
Ф – парабола,
Ψ – одна прямая,
Ω – две прямые.
Сечения конической поверхности вращения плоскостями
S2
Г2
S3
Ф2
Δ2
42
12
22
2 = m2
(43)
33
32
13
Ψ2
S1
41
11
21
31
Ω1
Σ1
23
2 ПО.
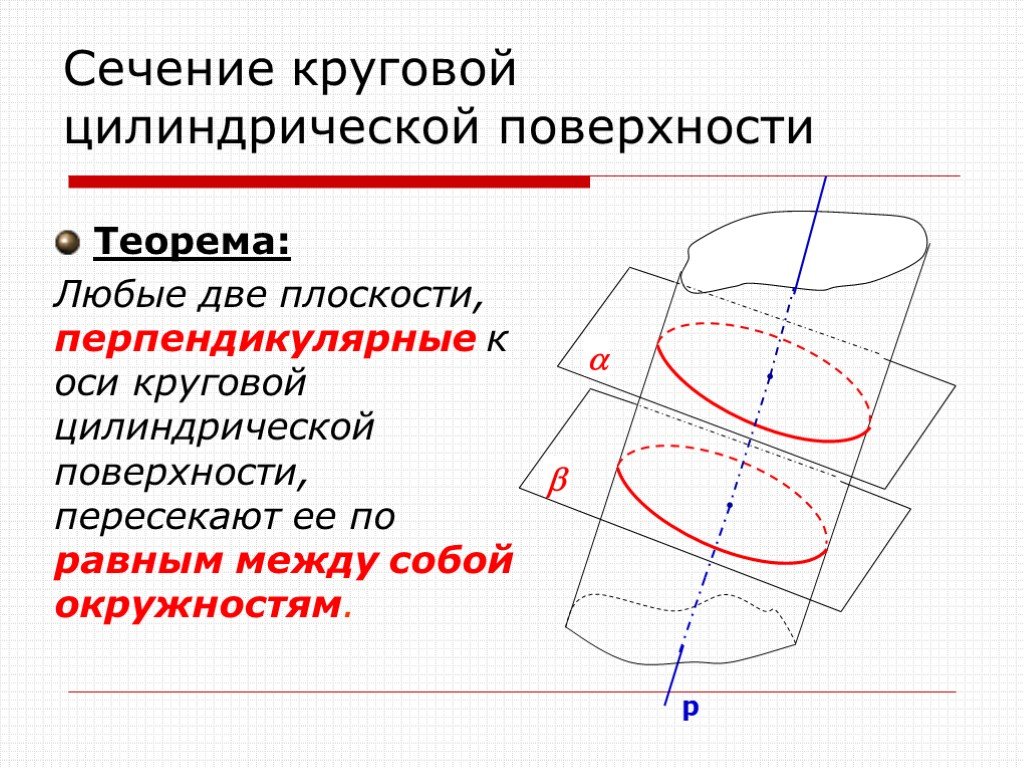
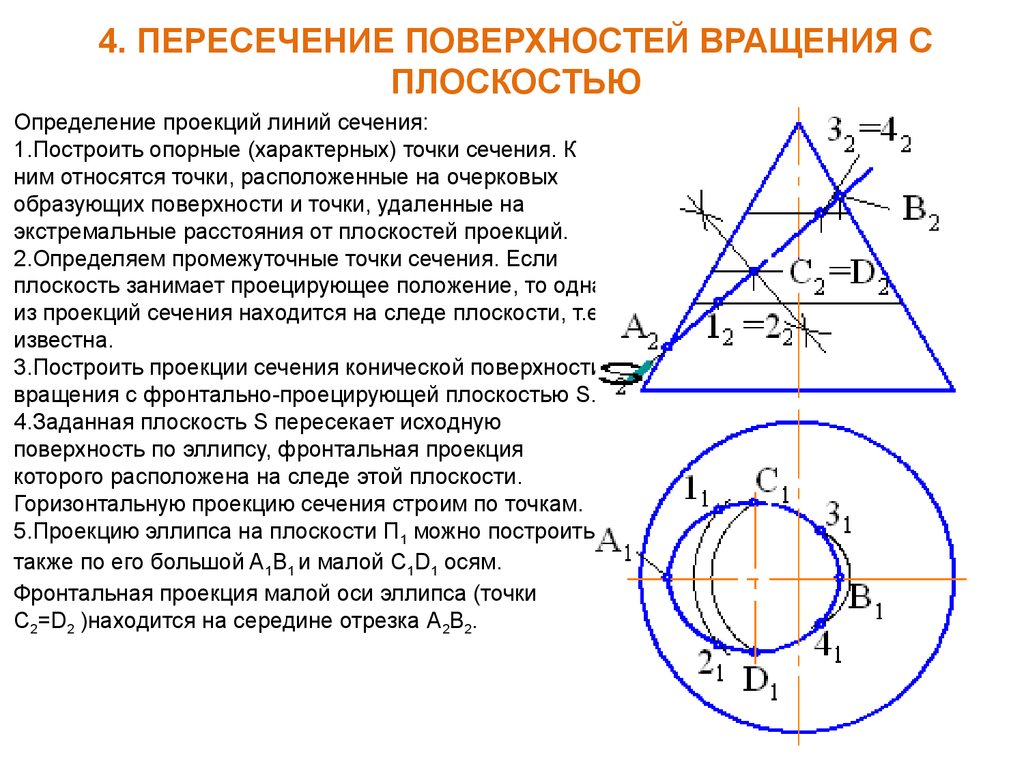
Анализ расположения следа секущей плоскости относительно
очерка конуса показывает, что линией сечения будет кривая 2-го порядка
гипербола.
S
2
12
(13 )
=
Г2
22 Щ
(32 )
33
=
2 ПО.
23
31
Ф1
=
=
11
21
Точки пересечения следа плоскости с фронтальным очерком являются
экстремальными точками линии сечения, определяемыми плоскостями Г и Ф.
Строим их на П3.
18. Точки линии сечения 4 и 5, лежащие на профильном очерке конуса, являются точками изменения видимости на П3 и промежуточными на П1.
S2
12
42 X
(52 )
Г2 ‘
(13 )
53
=
Г2
22 Щ
(32 )
31
Ф1
33
43
=
2 ПО.
23
51
=
11
=
21
41
Точки линии сечения 4 и 5, лежащие на профильном очерке конуса,
являются точками изменения видимости на П3 и промежуточными на П1.
19. Промежуточные точки (без обозначения) линии сечения строим с помощью плоскостей Г’’ и Г’’’.
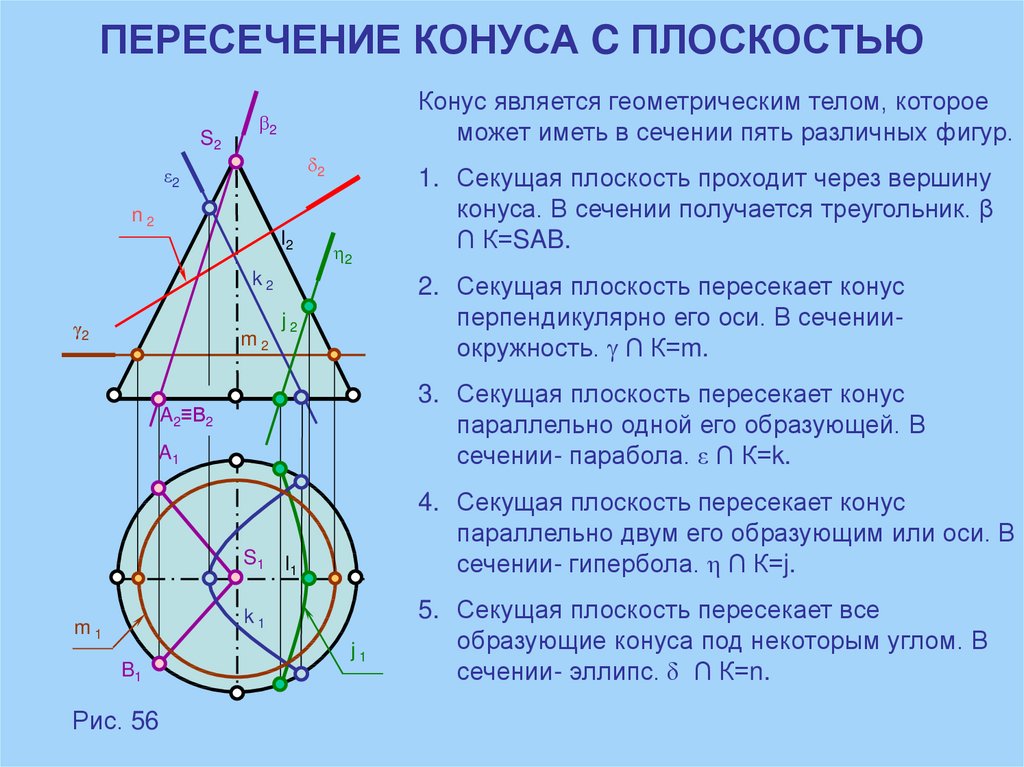 На П1 объединяем все точки в проекцию линии сS
На П1 объединяем все точки в проекцию линии сS2
2 ПО.
12
42 X
(52 )
Г2 ‘
(13 )
53
43
=
Г2 ”’
Г2
22 Щ
(32 )
31
Ф1
33
=
Г2 ”
23
51
=
11
=
21
41
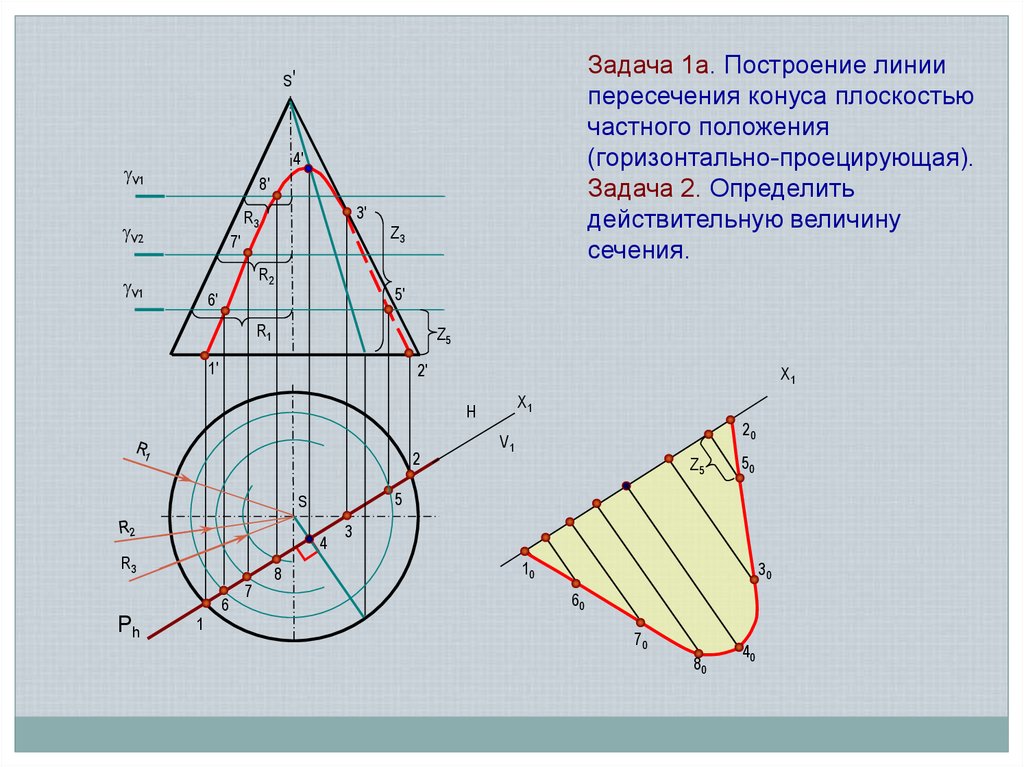
Промежуточные точки (без обозначения) линии сечения строим с
помощью плоскостей Г’’ и Г’’’. На П1 объединяем все точки в проекцию
линии сечения.
20. При объединении точек параболы на П3 следует учитывать её видимость относительно конуса. Видимость линии изменяется в точках 4 и 5, построен
S2
2 ПО.
12
42 X
(52 )
Г2 ‘
(13 )
53
43
=
Г2 ”’
Г2
22 Щ
(32 )
31
Ф1
33
=
Г2 ”
23
51
=
11
=
21
41
При объединении точек параболы на П3 следует учитывать её видимость
относительно конуса. Видимость линии изменяется в точках 4 и 5,
построенных в соответствии с алгоритмом решения.
English Русский Правила
Издания | Библиотечно-издательский комплекс СФУ
Все года изданияТекущий годПоследние 2 годаПоследние 5 летПоследние 10 лет
Все виды изданийУчебная литератураНаучная литератураЖурналыГазетыМатериалы конференций
Все темыЕстественные и точные наукиАстрономияБиологияГеографияГеодезия. КартографияГеологияГеофизикаИнформатикаКибернетикаМатематикаМеханикаОхрана окружающей среды. Экология человекаФизикаХимияТехнические и прикладные науки, отрасли производстваАвтоматика. Вычислительная техникаБиотехнологияВодное хозяйствоГорное делоЖилищно-коммунальное хозяйство. Домоводство. Бытовое обслуживаниеКосмические исследованияЛегкая промышленностьЛесная и деревообрабатывающая промышленностьМашиностроениеМедицина и здравоохранениеМеталлургияМетрологияОхрана трудаПатентное дело. Изобретательство. РационализаторствоПищевая промышленностьПолиграфия. Репрография. ФотокинотехникаПриборостроениеПрочие отрасли экономикиРыбное хозяйство. АквакультураСвязьСельское и лесное хозяйствоСтандартизацияСтатистикаСтроительство. АрхитектураТранспортХимическая технология. Химическая промышленностьЭлектроника. РадиотехникаЭлектротехникаЭнергетикаЯдерная техникаОбщественные и гуманитарные наукиВнешняя торговляВнутренняя торговля. Туристско-экскурсионное обслуживаниеВоенное делоГосударство и право. Юридические наукиДемографияИскусство.
КартографияГеологияГеофизикаИнформатикаКибернетикаМатематикаМеханикаОхрана окружающей среды. Экология человекаФизикаХимияТехнические и прикладные науки, отрасли производстваАвтоматика. Вычислительная техникаБиотехнологияВодное хозяйствоГорное делоЖилищно-коммунальное хозяйство. Домоводство. Бытовое обслуживаниеКосмические исследованияЛегкая промышленностьЛесная и деревообрабатывающая промышленностьМашиностроениеМедицина и здравоохранениеМеталлургияМетрологияОхрана трудаПатентное дело. Изобретательство. РационализаторствоПищевая промышленностьПолиграфия. Репрография. ФотокинотехникаПриборостроениеПрочие отрасли экономикиРыбное хозяйство. АквакультураСвязьСельское и лесное хозяйствоСтандартизацияСтатистикаСтроительство. АрхитектураТранспортХимическая технология. Химическая промышленностьЭлектроника. РадиотехникаЭлектротехникаЭнергетикаЯдерная техникаОбщественные и гуманитарные наукиВнешняя торговляВнутренняя торговля. Туристско-экскурсионное обслуживаниеВоенное делоГосударство и право. Юридические наукиДемографияИскусство. ИскусствоведениеИстория. Исторические наукиКомплексное изучение отдельных стран и регионовКультура. КультурологияЛитература. Литературоведение. Устное народное творчествоМассовая коммуникация. Журналистика. Средства массовой информацииНародное образование. ПедагогикаНауковедениеОрганизация и управлениеПолитика и политические наукиПсихологияРелигия. АтеизмСоциологияФизическая культура и спортФилософияЭкономика и экономические наукиЯзыкознаниеХудожественная литератураХудожественные произведения
ИскусствоведениеИстория. Исторические наукиКомплексное изучение отдельных стран и регионовКультура. КультурологияЛитература. Литературоведение. Устное народное творчествоМассовая коммуникация. Журналистика. Средства массовой информацииНародное образование. ПедагогикаНауковедениеОрганизация и управлениеПолитика и политические наукиПсихологияРелигия. АтеизмСоциологияФизическая культура и спортФилософияЭкономика и экономические наукиЯзыкознаниеХудожественная литератураХудожественные произведения
Все институтыВоенно-инженерный институтУчебно-военный центрГуманитарный институтКафедра ИТ в креативных и культурных индустрияхКафедра культурологии и искусствоведенияКафедра рекламы и социально-культурной деятельностиЖелезногорский филиал СФУИнженерно-строительный институтКафедра автомобильных дорог и городских сооруженийКафедра инженерных систем, зданий и сооруженийКафедра проектирования зданий и экспертизы недвижимостиКафедра строительных конструкций и управляемых системКафедра строительных материалов и технологий строительстваИнститут архитектуры и дизайнаКафедра архитектурного проектированияКафедра градостроительстваКафедра дизайнаКафедра дизайна архитектурной средыКафедра изобразительного искусства и компьютерной графикиИнститут гастрономииБазовая кафедра высшей школы ресторанного менеджментаИнститут горного дела, геологии и геотехнологийКафедра геологии месторождений и методики разведкиКафедра геологии, минералогии и петрографииКафедра горных машин и комплексовКафедра инженерной графикиКафедра маркшейдерского делаКафедра открытых горных работКафедра подземной разработки месторожденийКафедра технической механикиКафедра технологии и техники разведкиКафедра шахтного и подземного строительстваКафедра электрификации горно-металлургического производстваИнститут инженерной физики и радиоэлектроникиБазовая кафедра “Радиоэлектронная техника информационных систем”Базовая кафедра инфокоммуникацийБазовая кафедра физики конденсированного состояния веществаБазовая кафедра фотоники и лазерных технологийКафедра нанофазных материалов и нанотехнологийКафедра общей физикиКафедра приборостроения и наноэлектроникиКафедра радиотехникиКафедра радиоэлектронных системКафедра современного естествознанияКафедра теоретической физики и волновых явленийКафедра теплофизикиКафедра экспериментальной физики и инновационных технологийКафедры физикиИнститут космических и информационных технологийБазовая кафедра “Интеллектуальные системы управления”Базовая кафедра “Информационные технологии на радиоэлектронном производстве”Базовая кафедра геоинформационных системКафедра высокопроизводительных вычисленийКафедра вычислительной техникиКафедра информатикиКафедра информационных системКафедра прикладной математики и компьютерной безопасностиКафедра разговорного иностранного языкаКафедра систем автоматики, автоматизированного управления и проектированияКафедра систем искусственного интеллектаИнститут математики и фундаментальной информатикиБазовая кафедра вычислительных и информационных технологийБазовая кафедра математического моделирования и процессов управленияКафедра алгебры и математической логикиКафедра высшей и прикладной математикиКафедра математического анализа и дифференциальных уравненийКафедра математического обеспечения дискретных устройств и системКафедры высшей математики №2афедра теории функцийИнститут нефти и газаБазовая кафедра пожарной и промышленной безопасностиБазовая кафедра проектирования объектов нефтегазового комплексаБазовая кафедра химии и технологии природных энергоносителей и углеродных материаловКафедра авиационных горюче-смазочных материаловКафедра бурения нефтяных и газовых скважинКафедра геологии нефти и газаКафедра геофизикиКафедра машин и оборудования нефтяных и газовых промысловКафедра разработки и эксплуатации нефтяных и газовых месторожденийКафедра технологических машин и оборудования нефтегазового комплексаКафедра топливообеспеченя и горюче-смазочных материаловИнститут педагогики, психологии и социологииКафедра информационных технологий обучения и непрерывного образованияКафедра общей и социальной педагогикиКафедра психологии развития и консультированияКафедра современных образовательных технологийКафедра социологииИнститут торговли и сферы услугБазовая кафедра таможенного делаКафедра бухгалтерского учета, анализа и аудитаКафедра гостиничного делаКафедра математических методов и информационных технологий в торговле и сфере услугКафедра технологии и организации общественного питанияКафедра товароведения и экспертизы товаровКафедра торгового дела и маркетингаОтделение среднего профессионального образования (ОСПО)Институт управления бизнес-процессамиБазовая кафедра Федеральной службы по финансовому мониторингу (Росфинмониторинг)Кафедра бизнес-информатики и моделирования бизнес-процессовКафедра маркетинга и международного администрированияКафедра менеджмент производственных и социальных технологийКафедра цифровых технологий управленияКафедра экономики и управления бизнес-процессамиКафедра экономической и финансовой безопасностиИнститут физ. культуры, спорта и туризмаКафедра медико-биологических основ физической культуры и оздоровительных технологийКафедра теоретических основ и менеджмента физической культуры и туризмаКафедра теории и методики спортивных дисциплинКафедра физической культурыИнститут филологии и языковой коммуникацииКафедра восточных языковКафедра журналистики и литературоведенияКафедра иностранных языков для гуманитарных направленийКафедра иностранных языков для естественнонаучных направленийКафедра иностранных языков для инженерных направленийКафедра романских языков и прикладной лингвистикиКафедра русского языка и речевой коммуникацииКафедра русского языка как иностранногоКафедра теории германских языков и межкультурной коммуникацииИнститут фундаментальной биологии и биотехнологииБазовая кафедра “Медико-биологические системы и комплексы”Базовая кафедра биотехнологииКафедра биофизикиКафедра водных и наземных экосистемКафедра геномики и биоинформатикиКафедра медицинской биологииИнститут цветных металлов и материаловеденияБазовая кафедра “Технологии золотосодержащих руд”Кафедра автоматизации производственных процессов в металлургииКафедра аналитической и органической химииКафедра инженерного бакалавриата СDIOКафедра композиционных материалов и физико-химии металлургических процессовКафедра литейного производстваКафедра металловедения и термической обработки металловКафедра металлургии цветных металловКафедра обогащения полезных ископаемыхКафедра обработки металлов давлениемКафедра общаей металлургииКафедра техносферной безопасности горного и металлургического производстваКафедра физической и неорганической химииКафедра фундаментального естественнонаучного образованияИнститут экологии и географииКафедра географииКафедра охотничьего ресурсоведения и заповедного делаКафедра экологии и природопользованияИнститут экономики, государственного управления и финансовБазовая кафедра антимонопольного и тарифного регулирования рынков ФАСБазовая кафедра цифровых финансовых технологий Сбербанка РоссииКафедра бухгалтерского учета и статистикиКафедра международной и управленческой экономикиКафедра социально-экономического планированияКафедра теоретической экономикиКафедра управления человеческими ресурсамиКафедра финансов и управления рискамиКрасноярская государственная архитектурно-строительная академияКрасноярский государственный технический университетКрасноярский государственный университетМежинститутские базовые кафедрыМежинститутская базовая кафедра “Прикладная физика и космические технологии”Политехнический институтБазовая кафедра высшей школы автомобильного сервисаКафедра конструкторско-технологического обеспечения машиностроительных производствКафедра материаловедения и технологии обработки материаловКафедра машиностроенияКафедра прикладной механикиКафедра робототехники и технической кибернетикиКафедра стандартизации, метрологии и управления качествомКафедра тепловых электрических станцийКафедра теплотехники и гидрогазодинамикиКафедра техногенных и экологических рисков в техносфереКафедра техносферной и экологической безопасностиКафедра транспортаКафедра транспортных и технологических машинКафедра химииКафедра электротехникиКафедра электроэнергетикиСаяно-Шушенский филиал СФУХакасский технический иститутЮридический институтКафедра гражданского праваКафедра иностранного права и сравнительного правоведенияКафедра конституционного, административного и муниципального праваКафедра международного праваКафедра предпринимательского, конкурентного и финансового праваКафедра теории и истории государства и праваКафедра теории и методики социальной работыКафедра трудового и экологического праваКафедра уголовного праваКафедра уголовного процеса и криминалистики
культуры, спорта и туризмаКафедра медико-биологических основ физической культуры и оздоровительных технологийКафедра теоретических основ и менеджмента физической культуры и туризмаКафедра теории и методики спортивных дисциплинКафедра физической культурыИнститут филологии и языковой коммуникацииКафедра восточных языковКафедра журналистики и литературоведенияКафедра иностранных языков для гуманитарных направленийКафедра иностранных языков для естественнонаучных направленийКафедра иностранных языков для инженерных направленийКафедра романских языков и прикладной лингвистикиКафедра русского языка и речевой коммуникацииКафедра русского языка как иностранногоКафедра теории германских языков и межкультурной коммуникацииИнститут фундаментальной биологии и биотехнологииБазовая кафедра “Медико-биологические системы и комплексы”Базовая кафедра биотехнологииКафедра биофизикиКафедра водных и наземных экосистемКафедра геномики и биоинформатикиКафедра медицинской биологииИнститут цветных металлов и материаловеденияБазовая кафедра “Технологии золотосодержащих руд”Кафедра автоматизации производственных процессов в металлургииКафедра аналитической и органической химииКафедра инженерного бакалавриата СDIOКафедра композиционных материалов и физико-химии металлургических процессовКафедра литейного производстваКафедра металловедения и термической обработки металловКафедра металлургии цветных металловКафедра обогащения полезных ископаемыхКафедра обработки металлов давлениемКафедра общаей металлургииКафедра техносферной безопасности горного и металлургического производстваКафедра физической и неорганической химииКафедра фундаментального естественнонаучного образованияИнститут экологии и географииКафедра географииКафедра охотничьего ресурсоведения и заповедного делаКафедра экологии и природопользованияИнститут экономики, государственного управления и финансовБазовая кафедра антимонопольного и тарифного регулирования рынков ФАСБазовая кафедра цифровых финансовых технологий Сбербанка РоссииКафедра бухгалтерского учета и статистикиКафедра международной и управленческой экономикиКафедра социально-экономического планированияКафедра теоретической экономикиКафедра управления человеческими ресурсамиКафедра финансов и управления рискамиКрасноярская государственная архитектурно-строительная академияКрасноярский государственный технический университетКрасноярский государственный университетМежинститутские базовые кафедрыМежинститутская базовая кафедра “Прикладная физика и космические технологии”Политехнический институтБазовая кафедра высшей школы автомобильного сервисаКафедра конструкторско-технологического обеспечения машиностроительных производствКафедра материаловедения и технологии обработки материаловКафедра машиностроенияКафедра прикладной механикиКафедра робототехники и технической кибернетикиКафедра стандартизации, метрологии и управления качествомКафедра тепловых электрических станцийКафедра теплотехники и гидрогазодинамикиКафедра техногенных и экологических рисков в техносфереКафедра техносферной и экологической безопасностиКафедра транспортаКафедра транспортных и технологических машинКафедра химииКафедра электротехникиКафедра электроэнергетикиСаяно-Шушенский филиал СФУХакасский технический иститутЮридический институтКафедра гражданского праваКафедра иностранного права и сравнительного правоведенияКафедра конституционного, административного и муниципального праваКафедра международного праваКафедра предпринимательского, конкурентного и финансового праваКафедра теории и истории государства и праваКафедра теории и методики социальной работыКафедра трудового и экологического праваКафедра уголовного праваКафедра уголовного процеса и криминалистики
По релевантностиСначала новыеСначала старыеПо дате поступленияПо названиюПо автору
Текст в электронном виде
Интеграция науки и образования: современные проблемы, достижения и инновации в области экологии и…
Литература Испании
Проспект Свободный – 2022
Цветоведение для дизайнеров
Машины и оборудование предприятий стройиндустрии
Художественная культура Сибири
Эконометрика
Военная слава России: выдающиеся полководцы и флотоводцы XVIII века.
 Генерал-аншефы
Генерал-аншефыDOLGANICA: язык, культура, персоналии
Интернет-коммуникация и жанры русского электронного эпистолярия
Экспертиза и управление недвижимостью. Для курсового проектирования
Этноязыковые процессы у коренных народов
Поверхность сечения Пуанкаре | Dr. Kaos
Поверхность сечения Пуанкаре | Доктор КаосПоверхность сечения Пуанкаре (также называемая сечением Пуанкаре или картой Пуанкаре) — это мощный метод извлечения фундаментальных свойств из потоков в виде дискретных карт. Траектория или набор траекторий периодически отбираются путем просмотра последовательных пересечений с плоскостью в фазовом пространстве.
Многие физические, химические и биологические процессы в природе описываются набором связанных автономных дифференциальных уравнений первого порядка или автономных потоков. Широко используемым методом при изучении этих систем является метод поверхности сечения Пуанкаре (также называемый сечением Пуанкаре или картой Пуанкаре).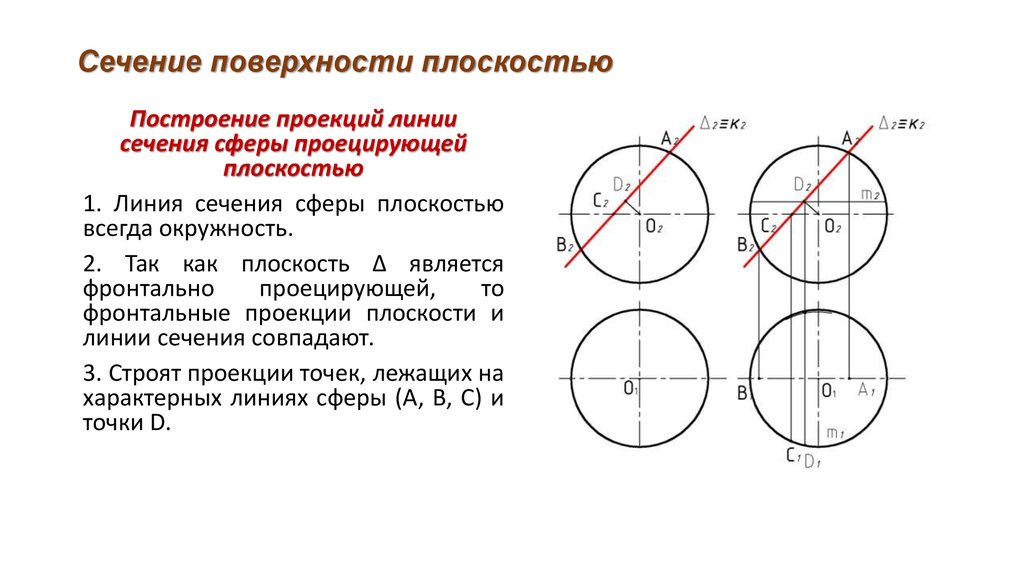 На сечении Пуанкаре динамика может быть описана дискретным отображением, размерность фазового пространства которого на единицу меньше ($n-1$) исходного непрерывного потока. Этот метод разделения обеспечивает естественную связь между непрерывными потоками и дискретными картами. В некоторых случаях эти карты облегчают анализ многих фундаментальных динамических свойств основного потока. Тщательно отобранный разрез Пуанкаре также дает визуальные подсказки о природе лежащего в основе аттрактора. Эти преимущества сделали метод поверхности сечения Пуанкаре одним из самых популярных инструментов анализа нелинейной динамики и хаоса.
На сечении Пуанкаре динамика может быть описана дискретным отображением, размерность фазового пространства которого на единицу меньше ($n-1$) исходного непрерывного потока. Этот метод разделения обеспечивает естественную связь между непрерывными потоками и дискретными картами. В некоторых случаях эти карты облегчают анализ многих фундаментальных динамических свойств основного потока. Тщательно отобранный разрез Пуанкаре также дает визуальные подсказки о природе лежащего в основе аттрактора. Эти преимущества сделали метод поверхности сечения Пуанкаре одним из самых популярных инструментов анализа нелинейной динамики и хаоса.
%matplotlib встроенный утилиты импорта utils.plot_poincare_surface()
Поверхность сечения создается путем просмотра последовательных пересечений траектории или набора траекторий с плоскостью в фазовом пространстве. Обычно плоскость натянута на ось координат и канонически сопряженную ось импульса. Мы увидим, что поверхности сечения, сделанные таким образом, обладают хорошими свойствами.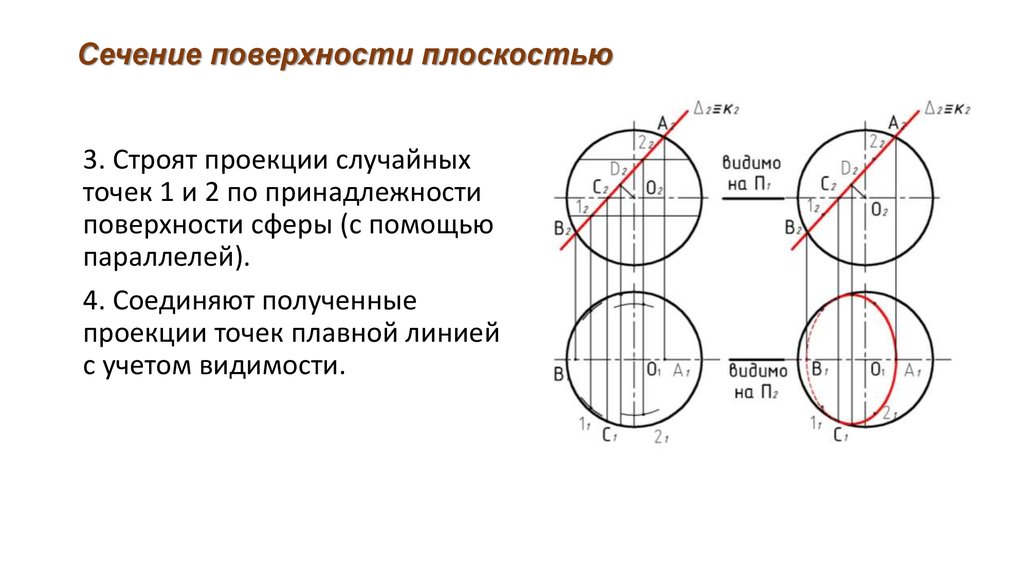
Например, в уравнениях Лоренца для большинства начальных условий кажется, что траектория оглядывается на две поверхности, которые напоминают знаменитые крылья бабочки, перетекающие одно крыло к другому нерегулярным образом. Что еще более интересно, траектории являются апериодическими, то есть при последовательном увеличении траектории остаются отдельными и демонстрируют самоподобные полосы, наблюдаемые во многих хаотических потоках и картах. Эту детальную структуру лучше всего раскрывает сечение Пуанкаре.
Мы начинаем со случайно выбранных $N=30$ точек и интегрируем уравнения Лоренца для $t_{max} = 400$.
%matplotlib встроенный импортировать matplotlib.pyplot как plt N=30 t, x_t = utils.solve_lorenz (10,0, 8,0/3, 28,0, N, 400)
Мы снова используем бмх стиль сюжета. Каждый цвет на графике представляет собой другую траекторию со случайно выбранными начальными условиями. Мы добавляем область подграфика в нижний левый угол рисунка и увеличиваем небольшой участок графика.
Каждый цвет на графике представляет собой другую траекторию со случайно выбранными начальными условиями. Мы добавляем область подграфика в нижний левый угол рисунка и увеличиваем небольшой участок графика.
plt.style.use('bmh')
рис, топор = plt.subplots(figsize=[10, 10])
хс = []
з = []
# увеличить левый нижний угол осей вставки, а также его ширину и высоту.
оси = ax.inset_axes ([0,06, 0,07, 0,3, 0,3])
# часть исходного изображения
х1, х2, у1, у2 = -3,0, -2,5, 24,8, 25,8
axins.set_xlim (x1, x2)
axins.set_ylim(y1, y2)
axins.set_xticklabels('')
axins.set_yticklabels('')
axins.set_facecolor('белый')
ax.indicate_inset_zoom (аксины)
для я в диапазоне (N):
х, у, г = х_т[я,:,:].Т
xi, zi = utils.find_zero_crossings(x,y,z)
ax.plot(xi, zi, '.')
axins.plot(xi, zi, '.')
plt.xlabel('$x$')
plt.ylabel('$z$')
plt.title('Разрез Пуанкаре в точке $y=0$')
plt.show()
На рисунке выше показано сечение Пуанкаре аттрактора Лоренца, построенное путем построения плоскости $x-z$ каждый раз, когда траектория проходит через крылья бабочки при $y=0$.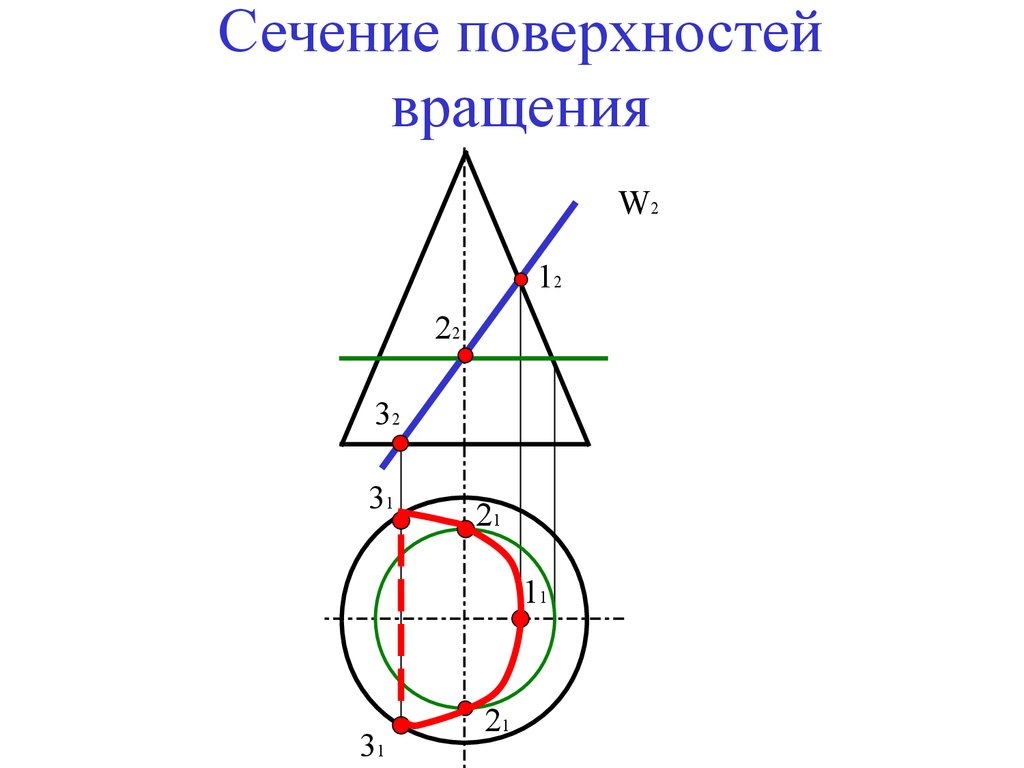 На рисунке показана ось симметрии, расположенная в точке $x=0$. Точки, кажется, не образуют единую нить вокруг оси симметрии, но последовательные увеличения показывают мелкомасштабную структуру.
На рисунке показана ось симметрии, расположенная в точке $x=0$. Точки, кажется, не образуют единую нить вокруг оси симметрии, но последовательные увеличения показывают мелкомасштабную структуру.
Хаотические траектории можно визуально отличить от других, рассматривая сечения Пуанкаре. Например, периодическое поведение проявляется в виде фиксированных точек в сечении Пуанкаре, тогда как квазипериодическое поведение демонстрирует замкнутую кривую или точки. Однако сечение Пуанкаре на рисунке выше категорически отличается от периодических или квазипериодических потоков. Отдельный набор точек выше указывает на то, что эволюция траекторий во времени хаотична и чрезвычайно чувствительна к начальным условиям. Кроме того, поперечное сечение аттрактора Лоренца, как и сам аттрактор Лоренца, имеют фрактальную структуру и нецелочисленную фрактальную размерность.
в
следующий раздел
, мы посмотрим, как мы можем вычислить фрактальная размерность .
- М. Энон, Двумерное отображение со странным аттрактором. Коммуникации в математической физике. Том 50 Номер. 1, 1976.
Поверхность сечения Пуанкаре (также называемая сечением Пуанкаре или картой Пуанкаре) — это мощный метод извлечения фундаментальных свойств из потоков в виде дискретных карт. Траектория или набор траекторий периодически отбираются путем просмотра последовательных пересечений с плоскостью в фазовом пространстве.
фазовое пространство странный аттрактор
28 апреля 2019 г.
- Лоренц Аттрактор
Мы начнем с изучения дифференциальных уравнений Лоренца (также известных как аттрактор Лоренца), используя… - Поверхность Пуанкаре сечения
Поверхность сечения Пуанкаре (также называемая сечением Пуанкаре или картой Пуанкаре) является мощной… - Фрактальное измерение
При изучении динамических систем есть много величин, которые идентифицируют как «энтропию». Уведомление…
Уведомление…
- Фазовое пространство (5)
- Странный аттрактор (2)
- Хаос (5)
- Временные ряды (4)
Создать поверхность из нескольких секцийВы можете создать поверхность из нескольких секций поверхность, проведя одну или несколько кривых секций вдоль хребта.
Определение параметров сглаживанияВы можете определить параметры сглаживания на многосекционных поверхностях. Выберите стерженьВы можете выбрать стержень для направления многосекционных поверхностей. Ограничение многосекционной поверхностиВкладка Relimitation позволяет вам указать тип relimitation.
Использовать элемент Canonical Вы можете обнаруживать плоские поверхности
для использования в качестве плоскостей для объектов, требующих одного в своем определении. Использовать площадь ЗаконВы можете определять и контролировать форму многосекционного поверхность между его частями. Чтобы создать многосекционную поверхность, позволяющую использовать закон площади, выполните следующие действия. могут использоваться входы:
Определим закон, который будет использоваться для создания мультисекций поверхность. В нашем примере создано три эскиза с замкнутыми контурами и заполнено. Корешок между этими разделами был создан:
Создание связиСуществует три вида связи при создании многосекционная поверхность. Эти связи вычисляют распределение изопараметров на поверхности. Соединение двух последовательных секцийСоединение основано на криволинейной оси абсцисс.
Муфта между направляющимиСоединение секций осуществляется хребтом. Если направляющая является конкатенацией нескольких кривых, результирующие многосекционные поверхность будет содержать столько поверхностей, сколько кривых внутри направляющей. Доступны несколько типов муфт, в зависимости от конфигурации сечения:
Ручное соединениеЕсли количество вершин отличается от одной секции к другой, вам необходимо выполнить ручную муфту.
|

 Уведомление…
Уведомление…
 Это полезно для создания трехмерных представлений формы.
которые симметричны относительно плоскости. Условия касания
можно наложить на две симметричные половины.
Это полезно для создания трехмерных представлений формы.
которые симметричны относительно плоскости. Условия касания
можно наложить на две симметричные половины.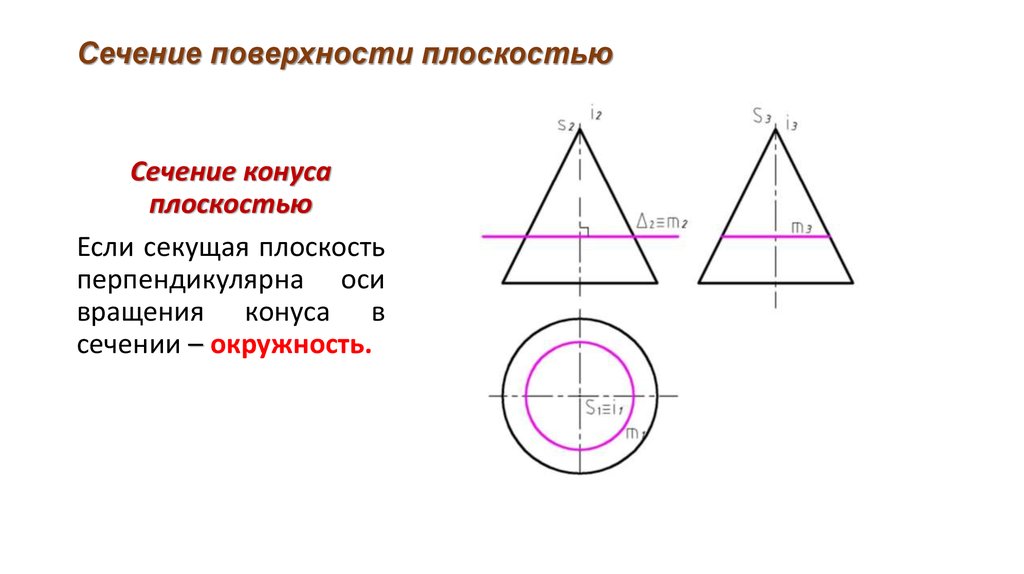

 Он определяет отклонение закона длины, которое должно быть применено
к промежуточным участкам, чтобы сгладить получившуюся форму.
Он определяет отклонение закона длины, которое должно быть применено
к промежуточным участкам, чтобы сгладить получившуюся форму.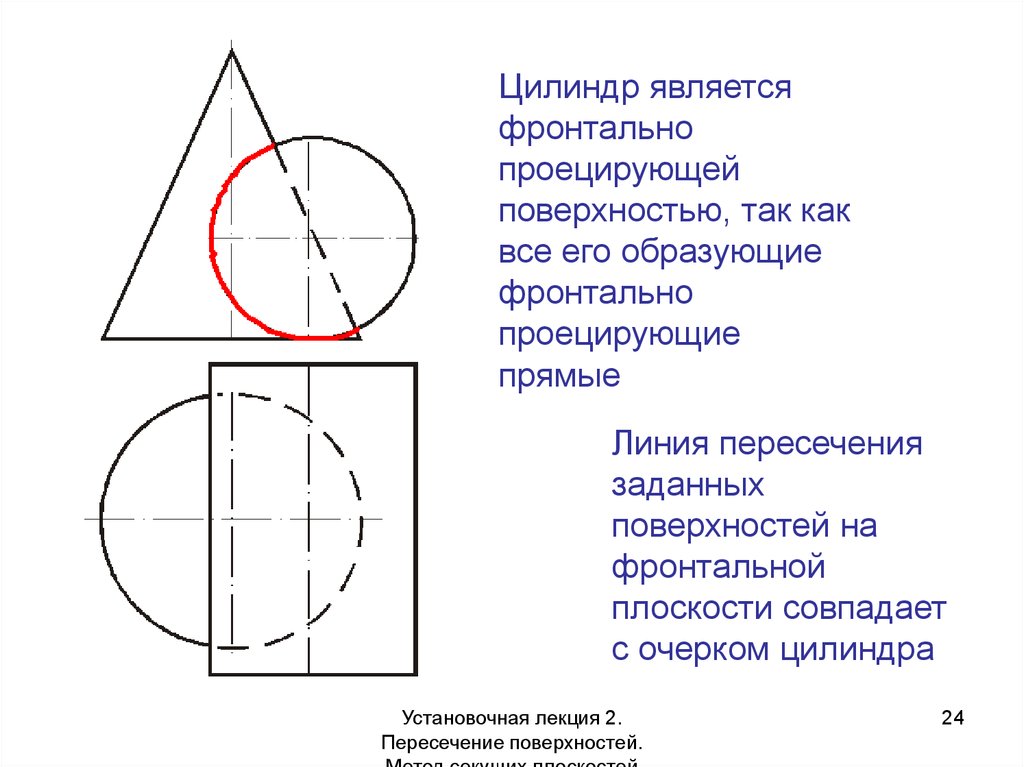
 Если они не имеют одинакового количества вершин, они не могут быть связаны
используя этот вариант.
Если они не имеют одинакового количества вершин, они не могут быть связаны
используя этот вариант.