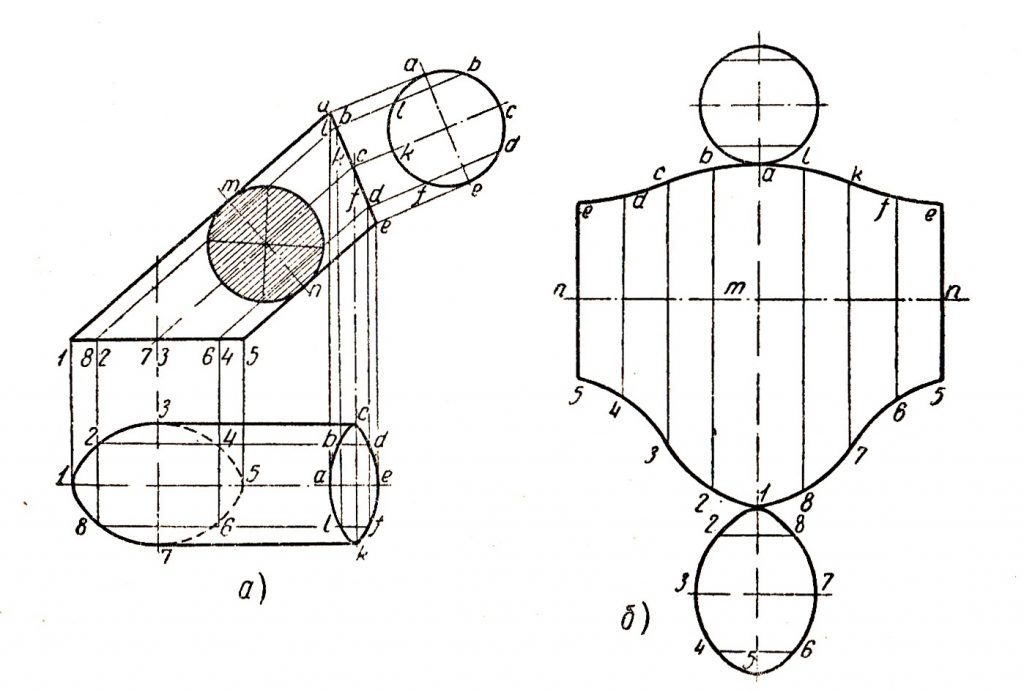
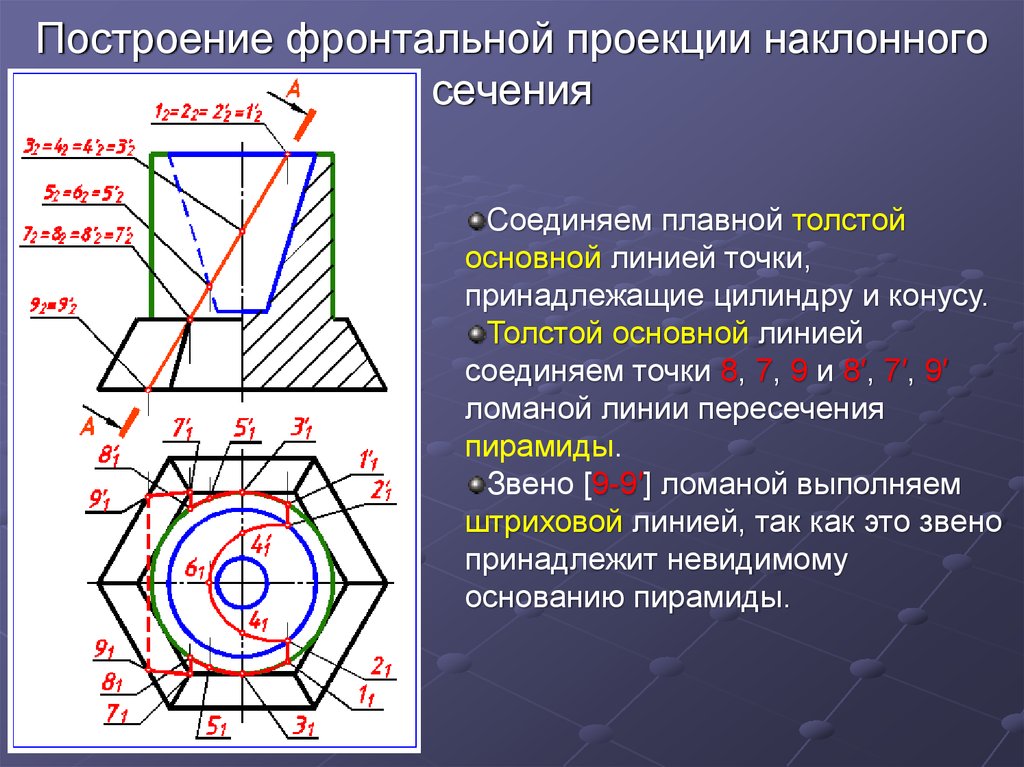
4 Построение наклонного сечения
Сечение – изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости.
Положение секущей плоскости указывают на чертеже линией сечения (рис. 9). Для линии сечения должна применяться разомкнутая линия. На начальном и конечном штрихах следует ставить стрелки указывающие направление взгляда. Стрелка должна наноситься на расстоянии 2 – 3 мм от конца штриха. Начальные и конечные штрихи не должны пересекать контур соответствующего изображения. У начала и конца линии сечения ставят одну и ту же прописную букву русского алфавита, буквы пишут около стрелок с внешней стороны угла. Сечение должно быть отмечено надписью по типу «А–А» (всегда двумя буквами через тире).
Рис. 9
Сечения делятся
на вынесенные и наложенные. Вынесенные
сечения располагаются на свободном
поле чертежа и являются предпочтительными.
Построение вынесенного сечения можно производить как рассмотренное в начертательной геометрии построение истинной величины плоской фигуры – методом перемены плоскостей проекций. Все размеры, расположенные вдоль оси вынесенного сечения, замеряются по точкам пересечения ребер и образующих детали с линией сечения, а размеры, перпендикулярные к ним, определяются на виде сверху. Вынесенное сечение строится по точкам, построение которых показано на примере точки 5 (рис. 10).
Рис. 10
На симметричных
деталях, чтобы показать внутреннее
устройство в аксонометрической проекции,
делают вырез ближней четверти (см. рис.
5). Этот вырез не связывают с разрезом
на ортогональных проекциях. Так, например,
на горизонтальной проекции оси симметрии
(вертикальная и горизонтальная) делят
изображение на четыре четверти.
Правила построения аксонометрических проекций подробно изложены в учебном пособии «Аксонометрические проекции»[5].
Пример построения аксонометрической проекции детали с вырезом одной четверти показан на рис. 11. Построенная в тонких линиях деталь мысленно разрезается фронтальной и профильной плоскостями, проходящими через осиОхиОу.Заключенную между ними четверть детали удаляют, при этом становится видна внутренняя конструкция детали.
Разрезая деталь,
плоскости оставляют на ее поверхности
след. Один такой след лежит во фронтальной,
другой в профильной плоскости разреза.
Каждый из этих следов представляет
собой замкнутую ломаную линию, состоящую
из отрезков, по которым плоскость разреза
пересекается с гранями детали и
поверхностью цилиндрического отверстия.
Фигуры, лежащие в плоскостях разреза,
аксонометрической проекции заштриховывают.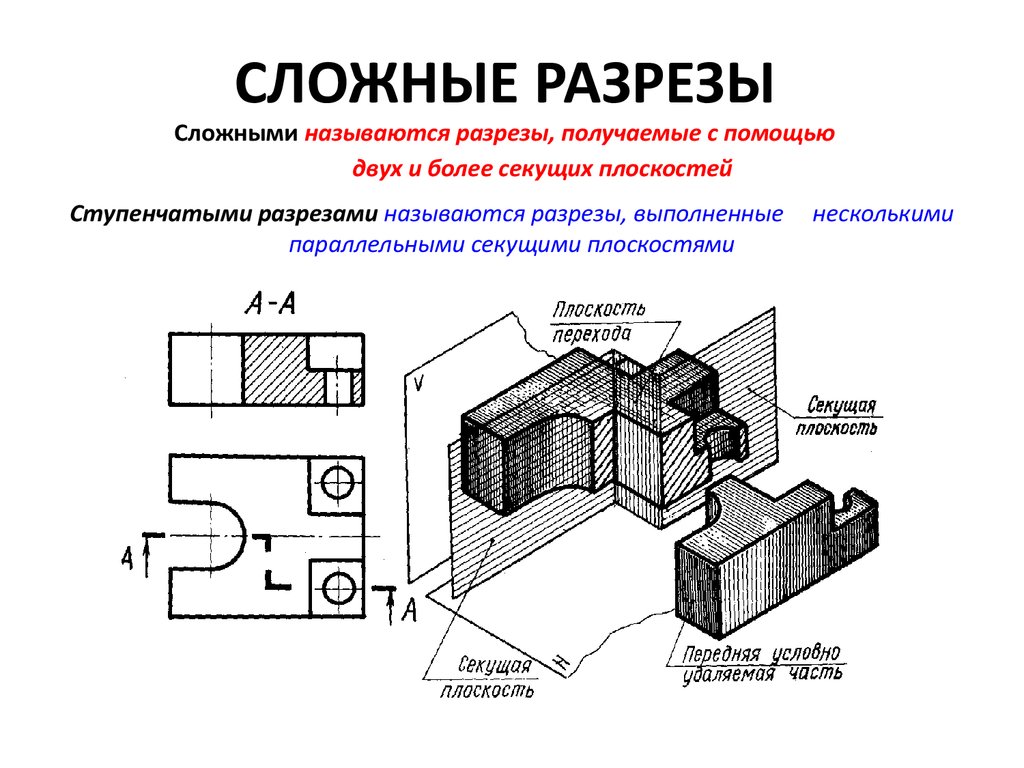
Рис. 11
Пример оформления графической работы приведён на рис. 12.
Рис. 12
Построение натуральной величины сечения наклонной плоскостью
При построении натурального вида сечения деталь пересекают фронтально проецирующей плоскостью (рис. 39). Линию сечения показывают разомкнутой линией с указанием стрелками направления взгляда и обозначают ее с двух сторон одинаковыми прописными буквами русского алфавита.
Сечение по построению и расположению должно соответствовать направлению, указанному стрелками. Допускается располагать сечение на любом месте поля чертежа, а также с поворотом, с добавлением при этом соответствующего знака.
Рис. 39. Построение натуральной величины сечения
Длина сечения в натуральную величину видна на виде спереди и равна расстоянию от т.1 до т.4.
Параллельно секущей
плоскости проводим ось симметрии,
которая будет являться ось наклонного
сечения.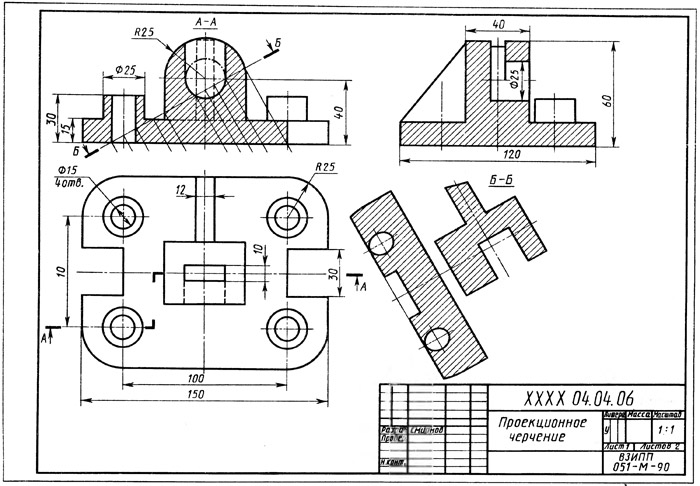
Из каждой точки пересечения
наклонной плоскостью какой-либо
поверхности (наружная цилиндрическая,
внутренние призматические – горизонтальная
и вертикальная) под углом 90о к секущей плоскости проводим лучи. Они,
в свою очередь, перпендикулярны оси
симметрии будущего наклонного сечения
и будут задавать натуральные величины
расстояний до каждой из точек от границ
сечения.
Опускаем лучи из точек 1, С, 2, D, 3, Е, F, 4 на горизонтальную проекцию. Точки 1, 2, 3 и 4 расположены на наружной поверхности цилиндра, точки С, D, Е и F на вертикальной призматической поверхности. Расстояния от оси симметрии до каждой из точек, за исключением т. С и F, взятые с горизонтальной проекции, будут задавать ширину данного сечения.
Откладываем данные
расстояния от оси симметрии наклонного
сечения в обе стороны на соответствующих
лучах. Точки С и F
расположены на самой оси. Последовательно
соединяем точки, учитывая, что секущая
плоскость пересекает граненые поверхности
горизонтального и вертикального
отверстий, а значит, в пересечении будут
линии в виде отрезков.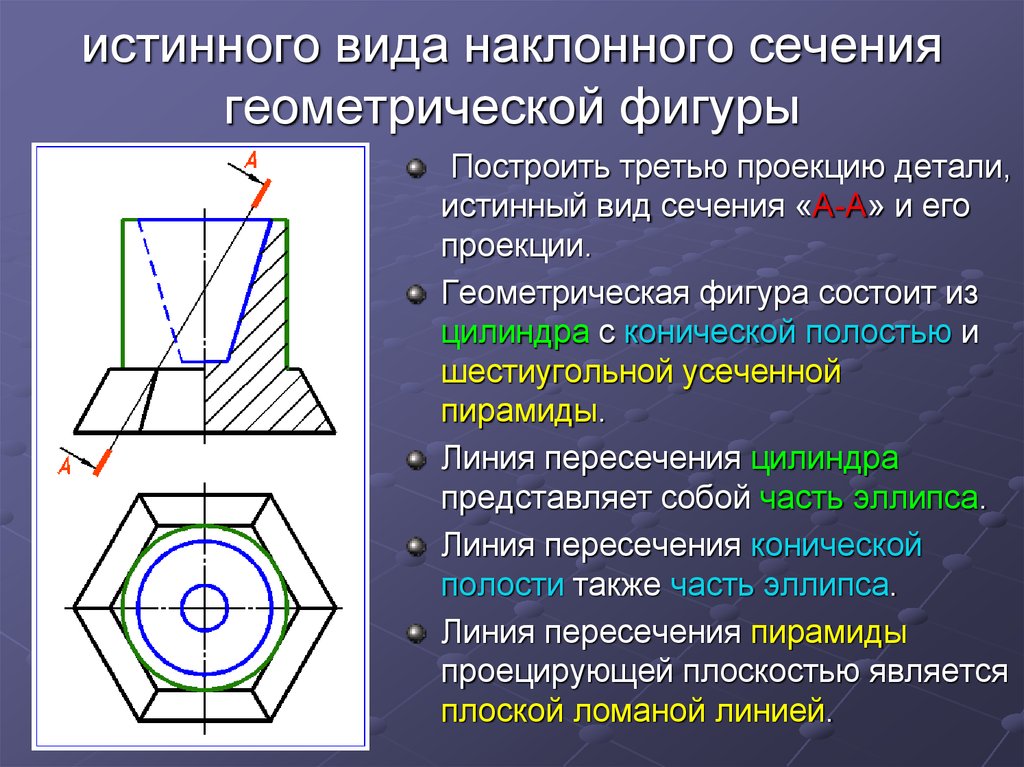
Наружная поверхность
представляет собой цилиндр, поэтому
линиями пересечения будут являться
дуги. Конфигурация сечения видна на
горизонтальной проекции (выделена
красным цветом), но в данном случае
натуральной величиной не является, так
как секущая плоскость расположена под
произвольным углом к горизонтальной
плоскости, а не параллельна ей.
Заштриховываем действительный вид сечения. Линии штриховки должны проводиться под угол 45˚ к линии чертежа. Если ось сечения или его контурная линия тоже наклонена к рамке чертежа под углом 45˚, то для штриховки следует брать угол 30˚ или 60˚.
Обводим границы сечения сплошной толстой основной линией.
Приложение 1
Приложение 2
БИБЛИОГРФИЧЕСКИЙ СПИСОК
ГОСТ 2.
301-68 – 2.319-81. Общие правила выполнения
чертежей. М.: Издательство стандартов,
1983. – 215 с.ГОСТ 2.104-68. Основные надписи. М.: Издательство стандартов, 1983.
Федоренко В.А., Шошин А.И. Справочник по машиностроитель-ному черчению. М.: Высшая школа, 1983. – 416 с.
Брилинг Н.С. Справочник по строительному черчению. М.: Стройиздат, 1987. – 446 с.
Кириллов А.Ф. Черчение и рисование. М.: Высшая школа, 1980. – 375 с.
Короев Ю.И. Строительное черчение и рисование. М.: Высшая школа, 1983. – 289 с.
301-68 – 2.319-81. Общие правила выполнения
чертежей. М.: Издательство стандартов,
1983. – 215 с.ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ ………………………………………………………………..3
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ РАБОТЫ .…………………………3
ЗАДАНИЕ 1.ОФОРМЛЕНИЕ ЧЕРТЕЖА ……………………………….4
ЗАДАНИЕ 2. . РЕЗЬБОВЫЕ СОЕДИНЕНИЯ ..…………………………6
ЗАДАНИЕ 3. ТЕХНИЧЕСКАЯ ФОРМА …………………………………16
ЗАДАНИЕ 4 ГЕОМЕТРИЧЕСКОЕ ТЕЛО ….…………………………..28
ПРИЛОЖЕНИЕ 1 …………………………………………………………33
ПРИЛОЖЕНИЕ 2 …………………………………………………………46
БИБЛИОГРАФИЧЕСКИЙ
СПИСОК…………………………………….
59
Наклонные плоскости
Объект, помещенный на наклонную поверхность , будет часто скользить по поверхности. Скорость, с которой объект скользит по поверхности, зависит от того, насколько наклонена поверхность; чем больше наклон поверхности, тем выше скорость, с которой объект будет скользить по ней. В физике наклонная поверхность называется наклонной плоскостью. Известно, что объекты ускоряются вниз по наклонным плоскостям из-за неуравновешенной силы. Чтобы понять этот тип движения, важно проанализировать силы, действующие на объект на наклонной плоскости. На диаграмме справа показаны две силы, действующие на ящик, расположенный на наклонной плоскости (предполагается, что трение отсутствует). Как показано на диаграмме, их всегда 9.0011 не менее двух сил
, действующих на любой объект, расположенный на наклонной плоскости, – сила тяжести и нормальная сила. Сила тяжести (также известная как вес) действует в направлении вниз; однако нормальная сила действует в направлении, перпендикулярном поверхности (на самом деле нормаль означает «перпендикулярно»).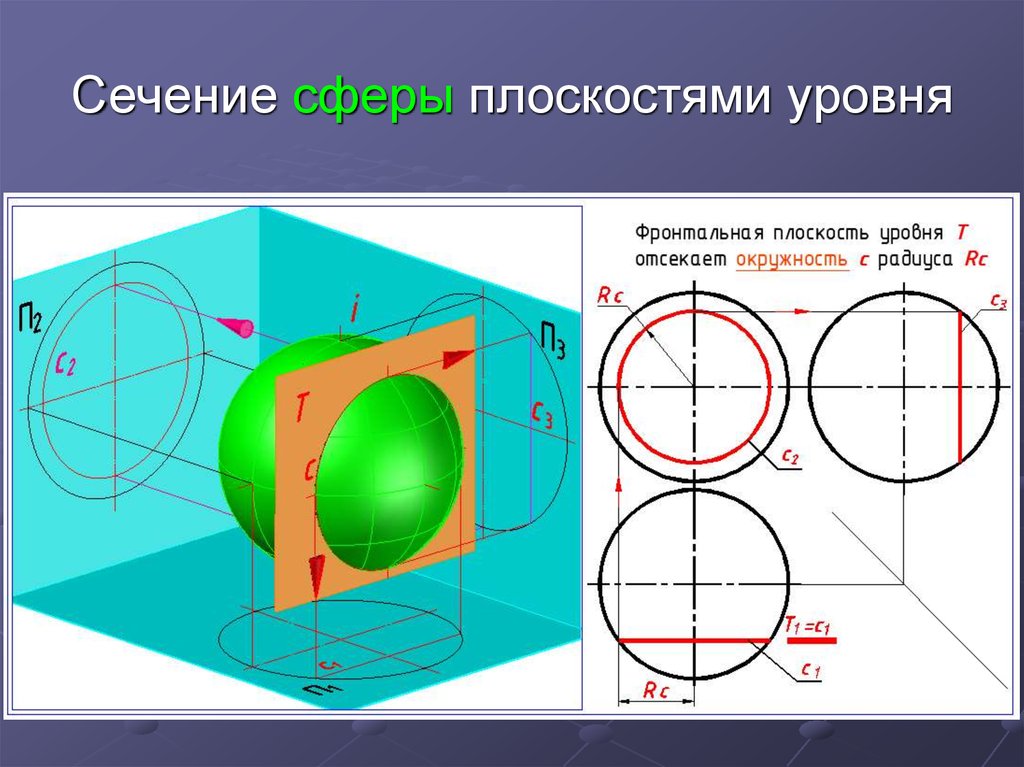
Первая особенность задач с наклонной плоскостью состоит в том, что нормальная сила равна , а не направлены в ту сторону, к которой мы привыкли. До этого момента в курсе мы всегда видели нормальные силы, действующие в восходящем направлении, противоположном направлению силы тяжести. Но это только потому, что объекты всегда находились на горизонтальных поверхностях, а не на наклонных плоскостях. Правда о нормальных силах заключается не в том, что они всегда направлены вверх, а в том, что они всегда направлены перпендикулярно поверхности, на которой находится объект.
Задача определения результирующей силы, действующей на объект на наклонной плоскости, является сложной задачей, поскольку две (или более) силы не направлены в противоположные стороны. Таким образом, одну (или несколько) сил придется разложить на перпендикулярные составляющие, чтобы их можно было легко добавить к другим силам, действующим на объект.
Обычно любую силу, направленную под углом к горизонтали, разлагают на горизонтальную и вертикальную составляющие. Однако это не тот процесс, который мы будем проводить с наклонными плоскостями. Вместо этого процесс анализа сил, действующих на объекты на наклонных плоскостях, будет включать определение весового вектора (F grav ) на две перпендикулярные составляющие. Это вторая особенность задач наклонной плоскости. Сила тяжести будет разложена на две составляющие силы — одну, направленную параллельно наклонной поверхности, и другую, направленную перпендикулярно наклонной поверхности. На приведенной ниже диаграмме показано, как сила тяжести была заменена двумя составляющими — параллельной и перпендикулярной составляющей силы.
Перпендикулярная составляющая силы тяжести направлена против нормальной силы и, таким образом, уравновешивает нормальную силу. Параллельная составляющая силы тяжести не уравновешивается никакой другой силой.
Этот объект впоследствии будет ускоряться вниз по наклонной плоскости из-за наличия неуравновешенной силы. Именно параллельная составляющая силы тяжести вызывает это ускорение. Параллельная составляющая силы тяжести является результирующей силой.
Задача определения величины двух составляющих силы тяжести — это простой способ использования уравнений. Уравнения для параллельной и перпендикулярной составляющих:
При отсутствии трения и других сил (растяжения, приложенных и т. д.) ускорение объекта на наклонной поверхности равно значению параллельной составляющей (м *g*синус угла), деленное на массу (m). Это дает уравнение
(при отсутствии сил трения и других сил)
При наличии трения или других сил (приложенной силы, силы натяжения и т.
д.) ситуация несколько усложняется. Рассмотрим схему, показанную справа. Перпендикулярная составляющая силы по-прежнему уравновешивает нормальную силу, поскольку объекты не ускоряются перпендикулярно наклону. Тем не менее, сила трения также должна учитываться при определении чистой силы. Как и во всех задачах о чистой силе, чистая сила представляет собой векторную сумму всех сил. То есть все отдельные силы складываются вместе как 9.0003 векторов . Перпендикулярная составляющая и нормальная сила в сумме дают 0 Н. Параллельная составляющая и сила трения в сумме дают 5 Н. Суммарная сила равна 5 Н и направлена вдоль наклона к полу.
Приведенную выше задачу (и все задачи с наклонной плоскостью) можно упростить с помощью полезного приема, известного как «наклон головы». Задача о наклонной плоскости во всех отношениях похожа на любую другую задачу о результирующей силе, за исключением того, что поверхность была наклонена на градусов на градусов. Таким образом, чтобы преобразовать проблему обратно в более удобную для вас форму, достаточно наклонить голову в том же направлении, в котором был наклон наклонить .
Или, что еще лучше, просто наклоните страницу бумаги (надежное средство от TNS — «синдром наклонной шеи» или «синдром тако-шейки»), чтобы поверхность больше не казалась ровной. Это показано ниже.
После того, как сила тяжести будет разделена на две составляющие и наклонена наклонная плоскость, задача должна выглядеть очень знакомо. Просто игнорируйте силу гравитации (поскольку она была заменена двумя ее компонентами) и найдите результирующую силу и ускорение.
В качестве примера рассмотрим ситуацию, изображенную на диаграмме справа. На диаграмме свободного тела показаны силы, действующие на 100-килограммовый ящик, скользящий по наклонной плоскости. Плоскость наклонена под углом 30 градусов. Коэффициент трения между обрешеткой и склоном равен 0,3. Определить результирующую силу и ускорение ящика.
Начнем с вышеуказанной задачи, найдя силу тяжести, действующую на ящик, и компоненты этой силы, параллельные и перпендикулярные наклону.
Сила тяжести равна 980 Н, а компоненты этой силы равны F параллельно = 490 Н (980 Н • sin 30 градусов) и F перпендикулярно = 849 Н (980 Н • cos30 градусов). Теперь нормальную силу можно определить равной 849 Н (она должна уравновешивать перпендикулярную составляющую вектора веса). Силу трения можно определить по величине нормальной силы и коэффициента трения; F трение составляет 255 Н (F трение = “mu”*F норма = 0,3 • 849 Н). Чистая сила представляет собой векторную сумму всех сил. Силы, направленные перпендикулярно наклону, уравновешивают; силы, направленные параллельно наклону, не уравновешиваются. Чистая сила составляет 235 Н (490 Н – 255 Н). Ускорение составляет 2,35 м/с/с (F net /м = 235 Н/100 кг).
На двух приведенных ниже диаграммах показана диаграмма свободного тела для 1000-килограммовых американских горок при первом падении двух разных аттракционов на американских горках.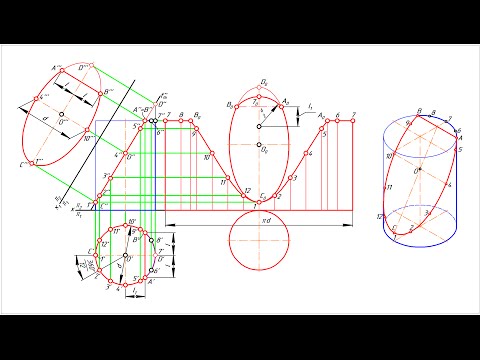
Используйте приведенные выше принципы векторного разрешения, чтобы определить результирующую силу и ускорение автомобилей американских горок. Предположим, что влияние трения и сопротивления воздуха пренебрежимо мало. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
Влияние угла наклона на ускорение американских горок (или любого объекта на склоне) можно наблюдать в двух вышеприведенных практических задачах. С увеличением угла увеличивается ускорение объекта. Объяснение этого относится к компонентам, которые мы рисовали. По мере увеличения угла составляющая силы, параллельная наклону, увеличивается, а составляющая силы, перпендикулярная наклону, уменьшается. Именно параллельная составляющая вектора веса вызывает ускорение. Таким образом, ускорения больше при больших углах наклона. На приведенной ниже диаграмме показано это соотношение для трех различных углов возрастающей величины.
Немного физики американских горок
Американские горки вызывают два острых ощущения, связанных с начальным падением по крутому склону. Острые ощущения от ускорения создаются за счет использования больших углов наклона при первом падении; такие большие углы увеличивают значение параллельной составляющей вектора веса (составляющей, вызывающей ускорение). Трепет невесомости производится за счет уменьшения величины нормальной силы до значений, меньших их обычных значений. Важно признать, что ощущение невесомости — это чувство, связанное с более низкой, чем обычно, нормальной силой. Как правило, человек весом 700 Н испытывает нормальную силу 700 Н, когда сидит на стуле. Однако, если кресло движется с ускорением вниз по наклону в 60 градусов, то человек будет испытывать нормальную силу в 350 ньютонов. Это значение меньше нормального и способствует ощущению, что вес меньше нормального, т.
е. 9.0022 невесомость .
Используйте виджет ниже, чтобы исследовать другие ситуации с наклонной плоскостью. Просто введите массу, угол наклона и коэффициент трения (используйте 0 для случаев отсутствия трения). Затем нажмите кнопку Отправить , чтобы просмотреть ускорение.
Следующие вопросы предназначены для проверки вашего понимания математики и концепций наклонных плоскостей. После того, как вы ответили на вопрос, нажмите кнопку, чтобы увидеть ответы.
1. Два мальчика играют в хоккей на соседней улице. Бродячая шайба движется по льду без трения , а затем поднимается по наклонной дороге без трения. Какая из следующих бегущих лент (A, B или C) точно изображает движение шайбы, когда она движется по ровной улице, а затем вверх по подъездной дорожке?
Объясните свой ответ.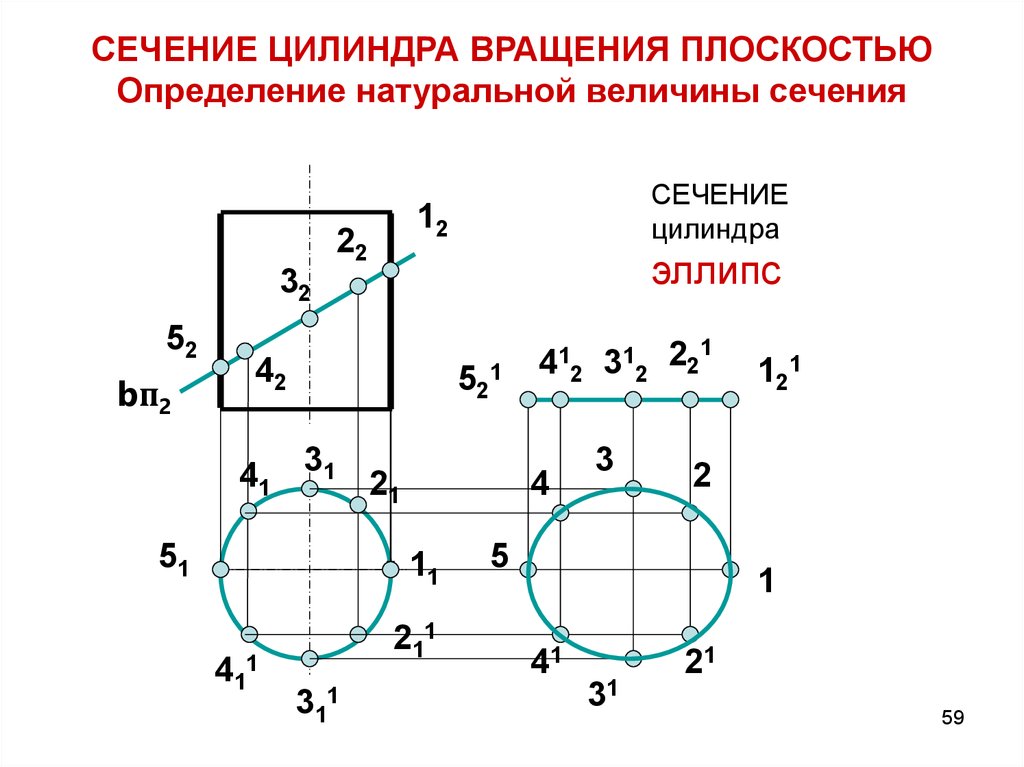
2. Маленький Джонни стоит внизу подъездной дорожки и пинает футбольный мяч. Мяч катится на север по подъездной дорожке, а затем возвращается к Джонни. Какой из следующих графиков зависимости скорости от времени (A, B, C или D) наиболее точно отображает движение мяча, когда он катится вверх по подъездной дорожке и обратно?
Объясните свой ответ.
3. Мяч для гольфа катится по горизонтальному участку грина на 18-й лунке. Затем он сталкивается с крутым нисходящим уклоном (см. Диаграмму). Участвует трение. Какой из следующих шаблонов бегущей строки (A, B или C) может быть подходящим представлением движения мяча?
Объясните, почему неуместные шаблоны неуместны.
4. Восьмой фрейм Мисси де Пенн в боулинг-лиге по средам стал катастрофой. Мяч скатился с полосы, прошел через грузовой люк в задней части здания, а затем по подъездной дорожке.
Милли Митер (товарищ по команде Мисси), которая проводила каждую свободную минуту за подготовкой к экзамену по физике, начала визуализировать график скорости движения мяча в зависимости от времени. Какой из графиков зависимости скорости от времени (A, B, C или D) будет подходящим представлением движения мяча, когда он катится по горизонтальной поверхности, а затем вниз по склону? Рассмотрим силы трения.
5. Три сотрудника лаборатории – Олив Н. Гленво, Глен Брук и Уоррен Пис – обсуждают задачу о наклоне (см. схему). Они спорят о значении нормальной силы. Олив утверждает, что нормальная сила равна 250 Н; Глен утверждает, что нормальная сила равна 433 Н; а Уоррен утверждает, что нормальная сила равна 500 Н. Хотя все три ответа кажутся разумными, правильным является только один. Укажите, какие два ответа неверны, и объясните, почему они неверны.
6.
Лон Скейпер возится с газоном, когда из его тачки вырывается 2-килограммовая шина и начинает катиться вниз по крутому холму (уклон 30°) в Сан-Франциско. Нарисуйте параллельные и перпендикулярные компоненты этого весового вектора. Определить величину компонентов с помощью тригонометрических функций. Затем определите ускорение шины. Не учитывать силу сопротивления.
Наконец, определите, какой из графиков зависимости скорости от времени будет представлять движение шины при ее скатывании по склону.
Объясните свой ответ.
7. На каждой из следующих диаграмм коробка массой 100 кг скользит по поверхности трения с постоянной скоростью 0,2 м/с. Угол наклона в каждой ситуации разный. Проанализируйте каждую диаграмму и заполните пропуски.
Следующий раздел:
5.
4 Наклонные плоскости | Техасский шлюзЦели обученияСтатическое и кинетическое трениеРабота с наклонными плоскостямиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Различие между статическим трением и кинетическим трением
- Решение задач с наклонными плоскостями
| кинетическое трение | статическое трение |
Статическое и кинетическое трение
Вспомним из предыдущей главы, что трение — это сила, противодействующая движению и постоянно присутствующая вокруг нас. Трение позволяет нам двигаться, что вы обнаружили, если когда-нибудь пробовали ходить по льду.
Существуют различные виды трения — кинетическое и статическое. Кинетическое трение действует на движущийся объект, а статическое трение действует на объект или систему в состоянии покоя. Максимальное статическое трение обычно больше, чем кинетическое трение между объектами.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу. Вы можете давить на ящик все сильнее и сильнее и не двигать его вообще. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик внезапно соскользнет и начнет двигаться. Начав движение, его легче поддерживать в движении, чем было запустить, потому что кинетическая сила трения меньше, чем статическая сила трения. Если бы вы добавили массу к ящику (например, поместив на него коробку), вам пришлось бы толкать его еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться.
Если, с другой стороны, вы смазали бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии.
На рис. 5.35 показано, как возникает трение на границе раздела двух объектов. Увеличение этих поверхностей показывает, что они являются шероховатыми на микроскопическом уровне. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения.
Рис. 5.35 Силы трения, такие как f , всегда препятствуют движению или попытке движения между соприкасающимися объектами. Трение возникает отчасти из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде.
Величина силы трения имеет две формы: одна для статического трения, другая для кинетического трения.
Когда между объектами нет движения, величина трения покоя f s равна
fs≤μsNs,fs≤μsNs,
, где μs μs — коэффициент трения покоя, а Н — величина нормальной силы. Напомним, что нормальная сила противодействует силе тяжести и действует перпендикулярно поверхности в этом примере, но не всегда.
Поскольку символ ≤ ≤ означает меньше или равно, это уравнение говорит, что трение покоя может иметь максимальное значение мксН. мксН. То есть
fs(max)=µsN.fs(max)=µsN.
Статическое трение представляет собой реактивную силу, которая увеличивается, чтобы быть равной и противоположной любой прилагаемой силе, вплоть до своего максимального предела. Когда приложенная сила превышает f с (макс.), объект будет двигаться. Когда объект движется, величина кинетического трения f k определяется выражением
fk=µkN.fk=µkN.
где μkμk — коэффициент кинетического трения.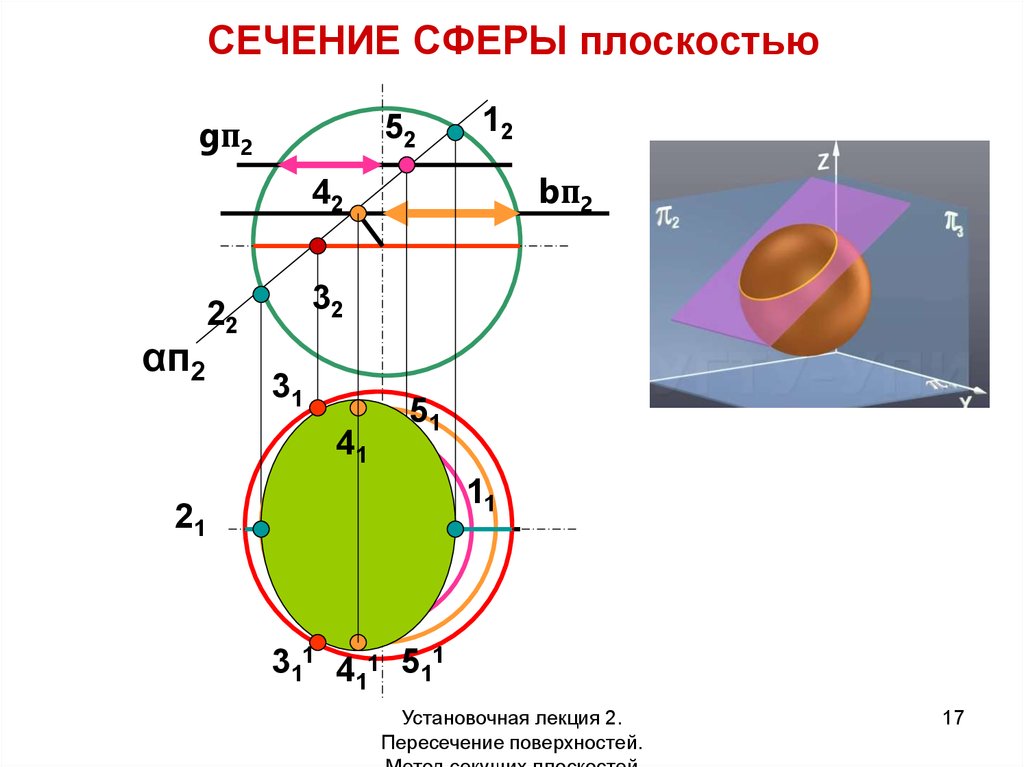
Трение варьируется от поверхности к поверхности, потому что разные вещества более шероховатые, чем другие. В таблице 5.2 сравниваются значения статического и кинетического трения для различных поверхностей. Коэффициент трения зависит от двух соприкасающихся поверхностей.
| Система | Статическое трение мкс мкс | Кинетическое трение мкк мкк |
| Резина на сухом бетоне | 1,0 | 0,7 |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Обувь на дереве | 0,9 | 0,7 |
| Обувь на льду 903:30 | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
Таблица 5.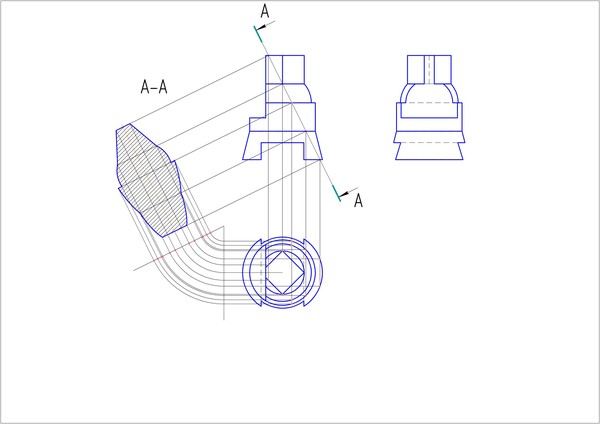
2 Коэффициенты статического и кинетического трения
Поскольку направление трения всегда противоположно направлению движения, трение происходит параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу
Вт=мг=(100 кг)(9,80 м/с2)=980 Н, Вт=мг=(100 кг)(9,80 м/с2)=980 Н,
перпендикулярно полу. Если бы коэффициент статического трения был равен 0,45, вам пришлось бы приложить параллельную полу силу, превышающую
.fs(max)=µsN=(0,45)(980 N)=440 Nfs(max)=µsN=(0,45)(980 N)=440 N
для перемещения ящика. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть равен 0,30, так что сила всего 290 Н
fk=µkN=(0,30)(980 N)=290 Nfk=µkN=(0,30)(980 N)=290 N
будет поддерживать его движение с постоянной скоростью. Если бы пол был смазан, оба коэффициента были бы намного меньше, чем без смазки.
Коэффициент трения не имеет единиц измерения и обычно представляет собой число от 0 до 1,0.
Работа с наклонными плоскостями
Ранее мы обсуждали, что когда объект лежит на горизонтальной поверхности, на него действует нормальная сила, равная по величине его весу. До сих пор мы имели дело только с нормальной силой в одном измерении, с гравитацией и нормальной силой, действующими перпендикулярно поверхности в противоположных направлениях (гравитация вниз, а нормальная сила вверх). Теперь, когда у вас есть навыки работы с силами в двух измерениях, мы можем исследовать, что происходит с весом и нормальной силой на наклонной поверхности, такой как наклонная плоскость. Для задач с наклонной плоскостью легче разбить силы на составляющие, если мы повернем систему координат, как показано на рис. 5.36. Первым шагом при постановке задачи является разложение силы веса на составляющие.
Рис. 5.36 На диаграмме показаны перпендикулярная и горизонтальная составляющие веса на наклонной плоскости.
Когда объект покоится на наклонной плоскости, составляющей угол θ θ с горизонталью, сила тяжести, действующая на объект, делится на две составляющие: сила, действующая перпендикулярно плоскости, w⊥ w⊥, и сила, действующая параллельно на плоскость, w|| ш||. Перпендикулярная сила веса, w⊥ w⊥, обычно равна по величине и противоположна по направлению нормальной силе, N. N. Сила, действующая параллельно плоскости, w|| w||, заставляет объект ускоряться вниз по склону. Сила трения f f противодействует движению объекта, поэтому она действует вверх по плоскости.
Важно соблюдать осторожность при разложении веса объекта на составляющие. Если угол наклона находится под углом θ θ к горизонтали, то величины компонентов веса равны
w||=wsin(θ)=mgsin(θ) и w||=wsin(θ)=mgsin(θ) и
w⊥=wcos(θ)=mgcos(θ).w⊥=wcos(θ) = мгкос(θ).
Вместо того, чтобы запоминать эти уравнения, полезно уметь определять их разумом. Для этого нарисуйте прямоугольный треугольник, образованный тремя весовыми векторами.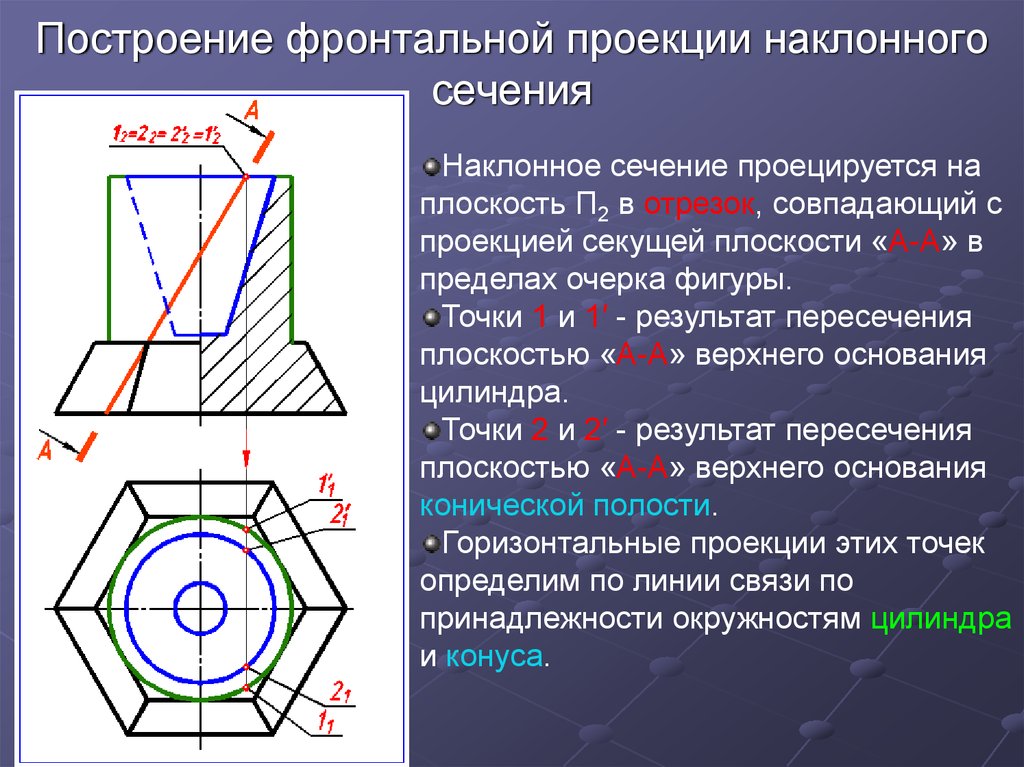
Обратите внимание, что угол наклона такой же, как угол, образованный между w w и w⊥ w⊥. Зная это свойство, можно с помощью тригонометрии определить величину весовых составляющих
cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)cos(θ)=w⊥ww⊥=wcos(θ)=mgcos(θ)
sin(θ)=w||ww ||=wsin(θ)=mgsin(θ).sin(θ)=w||ww||=wsin(θ)=mgsin(θ).
Watch Physics
Компоненты силы в наклонной плоскости
В этом видео показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.
Нажмите, чтобы просмотреть содержание
Проверка захвата
В этом видеоролике показано, как вес объекта на наклонной плоскости разбивается на составляющие, перпендикулярные и параллельные поверхности плоскости. Он объясняет геометрию для нахождения угла более подробно.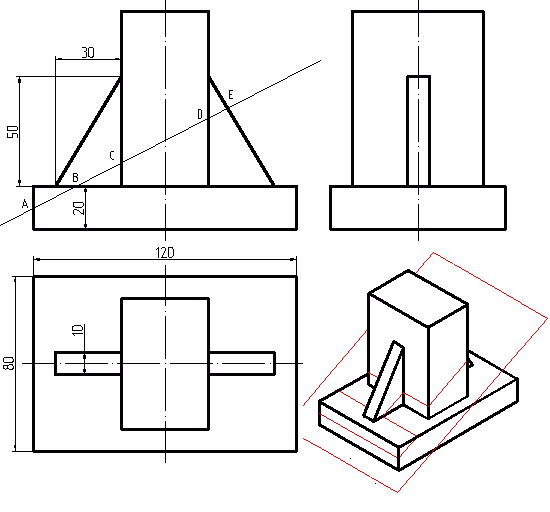
Когда поверхность плоская, можно сказать, что одна из составляющих гравитационной силы равна нулю; Который из? Что происходит с величинами перпендикулярной и параллельной составляющих гравитационной силы по мере увеличения угла наклона?
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая уменьшается, а перпендикулярная составляющая увеличивается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.
- Когда угол равен нулю, параллельная составляющая равна нулю, а перпендикулярная составляющая максимальна. По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла увеличивается, а синус угла уменьшается.
По мере увеличения угла параллельная составляющая увеличивается, а перпендикулярная составляющая уменьшается. Это связано с тем, что косинус угла уменьшается, а синус угла увеличивается.Tips For Success
Нормальная сила представлена переменной N. N. Не следует путать с символом ньютона, который также обозначается буквой N. Важно различать эти символы, тем более что единицами нормальной силы (NN) являются ньютоны (N). Например, нормальная сила, Н Н, с которой пол действует на стул, может быть Н=100 Н. Н=100 Н. Одно важное отличие состоит в том, что нормальная сила — это вектор, а ньютон — это просто единица.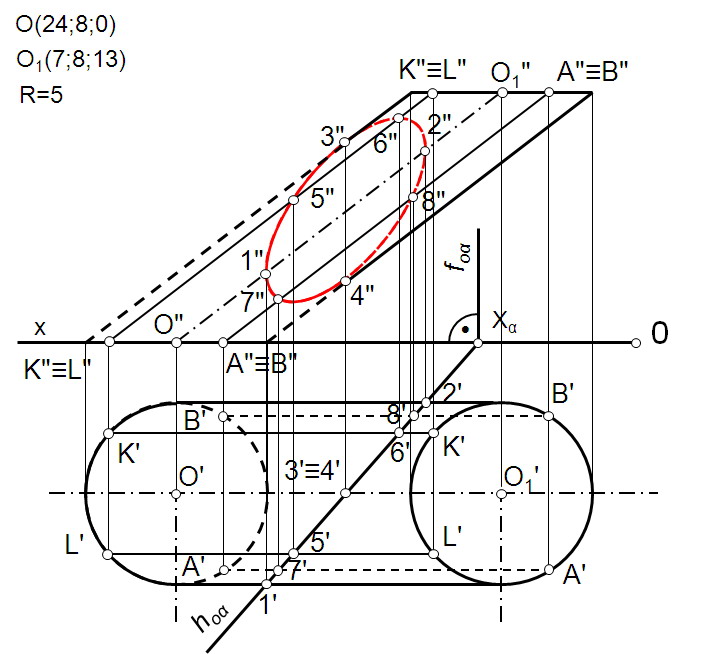
Будьте осторожны, чтобы не перепутать эти буквы в своих вычислениях!
Для обзора, процесс решения задач наклонной плоскости выглядит следующим образом:
- Нарисуйте схему задачи.
- Определите известные и неизвестные количества и определите интересующую систему.
- Нарисуйте диаграмму свободного тела (это эскиз, показывающий все силы, действующие на объект) с системой координат, повернутой под тем же углом, что и наклонная плоскость. Разделите векторы на горизонтальную и вертикальную составляющие и нарисуйте их на диаграмме свободного тела.
- Запишите второй закон Ньютона в горизонтальном и вертикальном направлениях и сложите силы, действующие на объект. Если объект не ускоряется в определенном направлении (например, в направлении x ), то F net x = 0. Если объект ускоряется в этом направлении, F net x = м и .
- Проверьте свой ответ. Разумный ли ответ? Единицы правильные?
Рабочий пример
Определение коэффициента кинетического трения на наклонной плоскости
Лыжник массой 62 кг, изображенный на рис. 5.37(а), скользит по заснеженному склону под углом 25 градусов. Найдите коэффициент кинетического трения лыжника, если известно, что трение равно 45,0 Н.
Рис. 5.37 Используйте диаграмму, чтобы найти коэффициент кинетического трения для лыжника.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой N как fk=µkN fk=µkN. Следовательно, мы можем найти коэффициент кинетического трения, сначала найдя нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону.
То есть
N=w⊥=w cos(25∘)=mg cos(25∘).N=w⊥=w cos(25∘)=mg cos(25∘).
Подставляя это в выражение для кинетического трения, получаем
fk=µkmg cos 25∘,fk=µkmg cos 25∘,
, которое теперь можно решить для коэффициента кинетического трения µ k .
Решение
Решение для µk µk дает
µk=fkw cos 25∘=fkmg cos 25∘.µk=fkw cos 25∘=fkmg cos 25∘.
Подставляя известные значения в правую часть уравнения,
мкк=45,0 Н(62 кг)(9,80 м/с2)(0,906)=0,082,мкк=45,0 Н(62 кг)(9,80 м/с2 )(0,906)=0,082.
Обсуждение
Этот результат немного меньше, чем коэффициент, указанный в таблице 5.1 для вощеной древесины на снегу, но все же разумен, так как значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой м скользит по склону, образующему угол θ с горизонтом, трение определяется формулой fk=μkmg cosθ.
fk=мкмг cosθ.
Рабочий пример
Вес на склоне, двумерная задача
Масса лыжника, включая снаряжение, составляет 60,0 кг. (См. рис. 5.38(b).) (a) Каково ее ускорение, если трением можно пренебречь? б) Чему равно ее ускорение, если сила трения равна 45,0 Н?
Рисунок 5.38 Теперь используйте диаграмму, чтобы найти ускорение лыжника, если трением можно пренебречь и если сила трения равна 45,0 Н.
Стратегия
Наиболее удобной системой координат для движения по склону является та, в которой одна координата параллельна склону, а другая перпендикулярна склону. Помните, что движения вдоль перпендикулярных осей независимы. Мы используем символ ⊥ ⊥ для обозначения перпендикуляра и || || значит параллельно.
Единственными внешними силами, действующими на систему, являются вес лыжника, трение и нормальная сила, действующая на лыжный склон, обозначенные на диаграмме свободного тела w w, f f и N N . N N всегда перпендикулярно склону, а f f параллельно ему.
Но w w не направлен ни по одной из осей, поэтому мы должны разбить его на составляющие вдоль выбранных осей. Определим w|| ш|| быть компонентом веса, параллельным наклону, и w⊥ w⊥ компонентом веса, перпендикулярным наклону. Как только это будет сделано, мы можем рассмотреть две отдельные проблемы сил, параллельных склону, и сил, перпендикулярных склону.
Решение
Величина составляющей веса, параллельной наклону, равна w||=wsin(25°)=mg sin(25°) w||=wsin(25°)=mg sin(25°) , а величина составляющей веса, перпендикулярной наклону, равна w⊥=wcos(25°)=mg cos(25°). w⊥=wcos(25°)=mg cos(25°).
(a) Пренебрегая трением: поскольку ускорение параллельно склону, нам нужно учитывать только силы, параллельные наклону. Силы, перпендикулярные склону, складываются в ноль, так как в этом направлении нет ускорения. Силы, параллельные склону, представляют собой вес лыжника, параллельный склону w|| ш|| и трение f f. При отсутствии трения по второму закону Ньютона ускорение, параллельное склону, равно
a||=Fnet ||m,a||=Fnet ||m,
Где результирующая сила, параллельная склону Fnet ||=w||=mgsin(25°) Fnet ||=w|| =mgsin(25°), так что
a||=Fnet ||m=mg sin(25°)m=g sin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2a| |=Fnet ||m=mg sin(25°)m=g sin(25°)=(9,80 м/с2)(0,423)=4,14 м/с2
— ускорение.
(b) Включая трение: Теперь у нас есть заданное значение трения, и мы знаем, что его направление параллельно склону и оно препятствует движению между контактирующими поверхностями. Таким образом, чистая внешняя сила теперь равна 9.0011
Fnet ||=w||−f,Fnet ||=w||–f,
и подставив это во второй закон Ньютона, a||=Fnet ||m a||=Fnet ||m , получим
a||=Fnet ||m=w||−fm=mg sin(25°)−fm.a||=Fnet ||m=w||−fm=mg sin(25°)−fm.
Подставляем известные значения, чтобы получить
a||=(60,0 кг)(9,80 м/с2)(0,423)−45,0 N60,0 кг,a||=(60,0 кг)(9,80 м/с2)(0,423 )−45,0 N60,0 кг,
или
a||=3,39 м/с2,a||=3,39 м/с2,
, что представляет собой ускорение, параллельное наклону, при наличии противодействующего трения 45 Н.
Обсуждение
Поскольку трение всегда препятствует движению между поверхностями, ускорение при наличии трения меньше, чем при его отсутствии.
Практические задачи
Когда объект находится на наклонной плоскости, образующей с горизонтом угол θ , как выражается составляющая силы веса объекта, параллельная наклону?
Тело массой 5 кг лежит на плоскости, наклоненной под углом 30° к горизонту.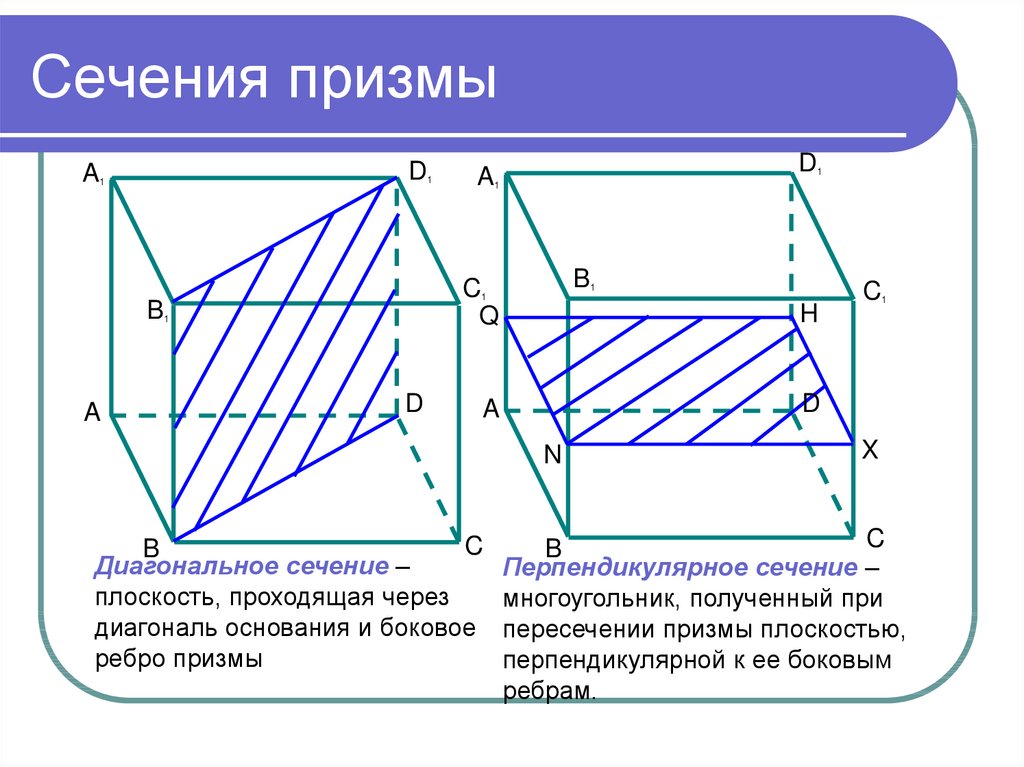
Какая составляющая силы веса параллельна наклону?
- 4.33Н
- 5.0Н
- 24,5Н
- 42.43С
Snap Lab
Трение под углом: скольжение монеты
Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в первом рабочем примере, кинетическое трение на склоне fk=µkmg cosθ fk=µkmg cosθ, а составляющая веса вниз по склону равна mg sinθ mg sinθ. Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Написание этих
fk=Fgxμkmg cosθ=mg sinθ.fk=Fgxμkmg cosθ=mg sinθ.
Решая для µk µk, поскольку tanθ=sinθ/cosθ tanθ=sinθ/cosθ мы находим, что
Материалы:
- 1 монета
- 1 книга
- 1 транспортир
- Положите монету плоской стороной на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью. Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.
- Измерьте угол наклона относительно горизонтали и найдите µk µk.
- Положите монету плоской стороной на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью.
Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться.Проверка захвата
Верно или неверно — если известны только углы двух векторов, мы можем найти угол их результирующего вектора сложения.
- Правда
- Ложь
Проверьте свое понимание
Упражнение 9
Что такое трение?
- Трение — это внутренняя сила, противодействующая относительному движению объекта.
- Трение — это внутренняя сила, которая ускоряет относительное движение объекта.
- Трение — это внешняя сила, противодействующая относительному движению объекта.
- Трение — это внешняя сила, увеличивающая скорость относительного движения объекта.
Упражнение 10
Какие существуют две разновидности трения? На что действует каждый?
- Кинетическое и статическое трение действуют на движущийся объект.
- Кинетическое трение действует на движущийся объект, а статическое трение действует на покоящийся объект.
- Кинетическое трение действует на неподвижный объект, а статическое трение действует на движущийся объект.
- Кинетическое и статическое трение действуют на покоящийся объект.
Упражнение 11
Какое значение между статическим и кинетическим трением между двумя поверхностями больше? Почему?
- Кинетическое трение имеет большее значение, потому что трение между двумя поверхностями больше, когда две поверхности находятся в относительном движении.
