Относительная и абсолютная погрешность – формула определения, как рассчитать погрешность измерения
4.2
Средняя оценка: 4.2
Всего получено оценок: 2139.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2139.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики – более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2139.
А какая ваша оценка?
Калькулятор относительной погрешности
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | – | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Точное значение величины
Приближенное значение величины
Как вычислить относительную погрешность
Относительная погрешность приближенного числа
– это отношение абсолютной погрешности к приближенному числу.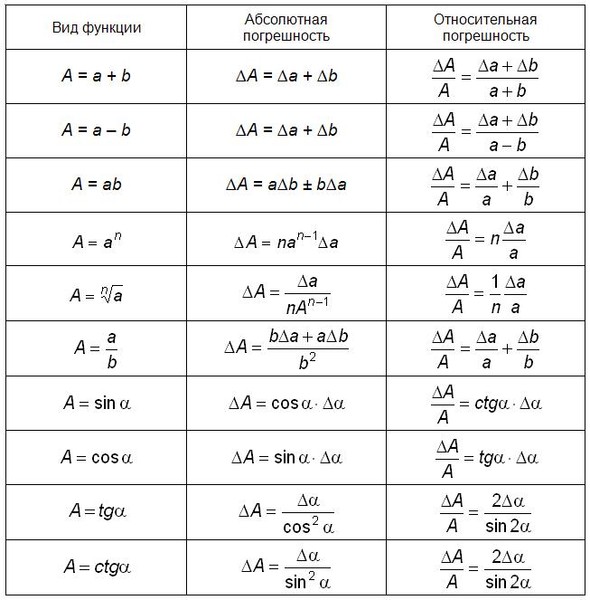
Для того чтобы вычислить относительную погрешность необходимо:
1. Вычислить абсолютную погрешность, то есть найти разность между приближенным числом и его точным значением.
2. Разделить абсолютную погрешность на точное значение величины.
3. Для получения округленного результата в процентах разделить абсолютную погрешность на приближенное значение величины и умножить получившееся частное на 100%.
Приведем пример, в помещении 23 человека, округлим это значение до 25. Тогда абсолютная погрешность = 25 – 23 = 2.
Относительная погрешность =
= 0.086956521739
Округленно =
· 100% = 8%
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Калькулятор процентной ошибки
Использование калькулятора
Калькулятор процентной ошибки вычисляет разницу между экспериментальным или наблюдаемым значением и теоретическим фактическим значением. Он создает соотношение разницы относительно фактического значения и дает его в процентах.
Ответы показывают работу по расчету процентной ошибки.
Что такое процентная ошибка?
Ошибка в процентах — это относительный размер разницы между экспериментальным или оценочным значением и истинным принятым значением.
Он сравнивает разницу в значениях с ожидаемым фактическим значением и сообщает вам, насколько далеко от вашего экспериментального или наблюдаемого значения.
Например, предположим, что вы купили пакет драже, и на этикетке указано, что он весит 10 унций. Когда вы на самом деле взвесили мармеладки, они составили 10,3 унции. Процентная ошибка вычисляет отношение 0,3 унции к 10 унциям, а затем выдает его в процентах. В этом случае процентная ошибка составляет 3%.
Может быть, вы налили себе 30 драже. Затем вы дважды проверили этикетку с пищевой ценностью и увидели, что в порции содержится 20 драже. Процентная ошибка вашего первоначального размера порции по сравнению с рекомендуемым размером порции составляет 30 – 20 = 10. Поместите это в соотношение с рекомендуемой порцией 20, и вы получите процентную ошибку 50%. Таким образом, ваш первоначальный размер порции был на 50 % больше, чем ожидалось.
Калькулятор также находит:
- Экспериментальное значение — когда известна погрешность в процентах
- Теоретическое значение — когда известна процентная ошибка
- Абсолютная ошибка — числовая разница между расчетными и фактическими значениями
- Относительная ошибка — абсолютная ошибка относительно того, каким должно быть фактическое значение
Как рассчитать процентную ошибку
Процентная ошибка также известна как ошибка аппроксимации.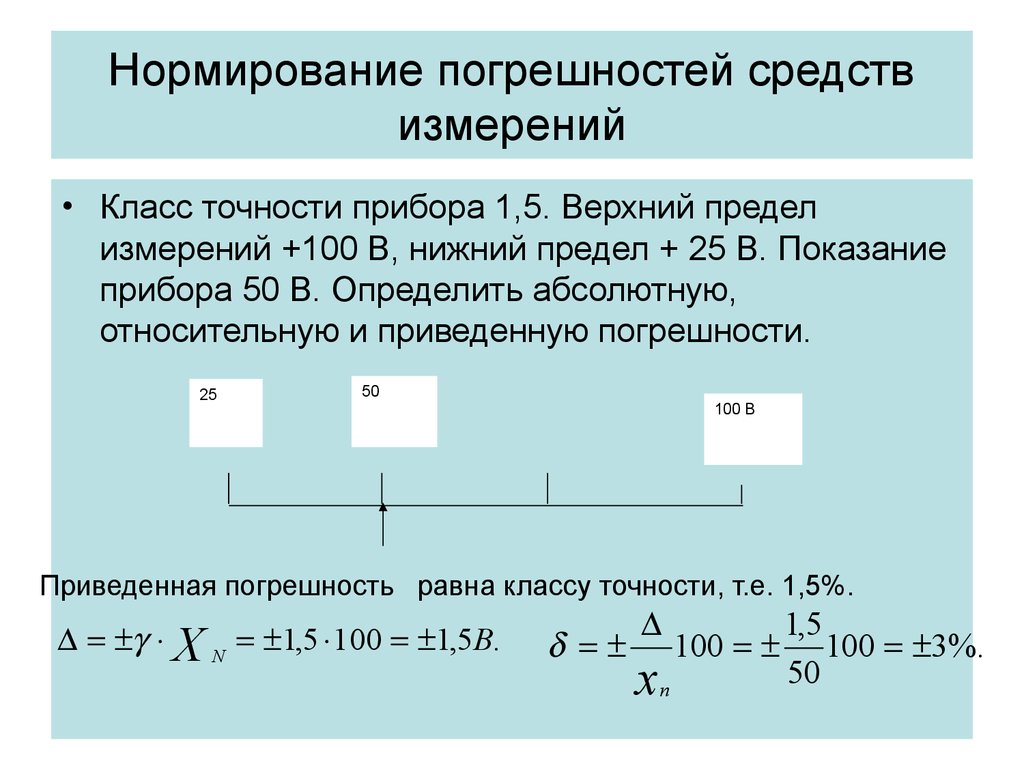
Он равен абсолютному значению экспериментального значения минус теоретическое значение, деленное на теоретическое значение, умноженное на 100.
- Вычесть теоретическое значение из экспериментального значения
- Получить абсолютное значение результата
- Разделите это на теоретическое значение
- Умножьте на 100, чтобы получить процент
В терминах экспериментальных и теоретических значений формула процентной ошибки:
\[ \% {\text{ошибка}} = \left|{\dfrac {Экспериментальный – Теоретический}{Теоретический}}\right| \умножить на 100\\]
или
\[ \% {\text{ошибка}} = \left|{\dfrac {E – T}{T}}\right| \умножить на 100\\]
Вы можете заметить, что эта формула похожа на то, как вы рассчитываете процентное изменение, как в нашем
Калькулятор процентного изменения.
Формула абсолютной погрешности
Абсолютная погрешность представляет собой абсолютное значение разницы между измеренными и истинными значениями. Если ваши весы весят что-то вроде 1,2 фунта, но фактическое значение составляет 1,5 фунта, ваши весы отклоняются на 0,3 фунта. Абсолютная ошибка составляет 0,3 фунта.
\[ {\text{абсолютная ошибка}} = | {Е – Т} | \]
Формула относительной ошибки
Относительная ошибка — это абсолютная ошибка относительно того, каким должно быть истинное значение. Если ваши весы отклоняются на 0,3 фунта, а истинное значение составляет 1,5 фунта, относительная ошибка составляет 0,3 / 1,5 = 0,2.
\[ \text{относительная ошибка} = \left| {\ dfrac {E – T} {T}} \ справа | \]
Примечания к расчету процентной погрешности
Теоретическое значение в химии, физике или научных экспериментах в целом — это установленное идеальное значение, которое можно ожидать в результате эксперимента.
Другие термины, которые вы можете увидеть для обозначения этого значения, — это принятые, фактические, ожидаемые, точные и истинные. Это значение находится в знаменателе уравнения процентной ошибки.
Экспериментальное значение — это наблюдаемый результат эксперимента. Другие термины, которые вы можете увидеть для представления этого значения, — это измеренное, наблюдаемое, оценочное и приблизительное.
В числителе формулы ошибки вы вычисляете абсолютную разницу между экспериментальным значением и теоретическим значением или абсолютное расстояние между двумя значениями на числовой прямой. Порядок значений не имеет значения, потому что вы берете абсолютное значение.
Если вы столкнетесь с формулами процентной ошибки, которые несколько отличаются от приведенных здесь, обратите внимание на приведенные выше альтернативные термины и помните, что | а – б | = | б – а |.
Экспериментальная формула значения
Используйте формулу процентной ошибки для решения E , экспериментальное или наблюдаемое значение.
В этом уравнении P означает процентную ошибку. Обратите внимание, что есть два возможных решения.
\[ \ {P} = \left|{\dfrac {E – T}{T}}\right| \умножить на 100\\] \[ \dfrac{P}{100} = \left|{\dfrac {E – T}{T}}\right| \] \[ \ pm \ dfrac {P} {100} = {\ dfrac {E – T} {T}} \] \[ \pm \dfrac{P}{100}{T} = {E – T} \] \[ {T} \pm \dfrac{P}{100}{T} = {E} \] \[ {E} = {T} \pm \dfrac{P}{100}{T} \] \[ {E} = {T} \left( 1 \pm \dfrac{P}{100} \right) \]
Формула теоретического значения
Вы можете использовать полученную выше экспериментальную формулу ошибки, чтобы найти T . Снова здесь P означает процентную ошибку. Обратите внимание, что есть два возможных решения.
\[ {T} = \dfrac{E}{\left( 1 \pm \dfrac{P}{100} \right) } \]
Пример вычисления процентной погрешности
Предположим, вы провели эксперимент по измерению точки кипения воды, и ваш средний результат равен 101,5°C.
Это ваше экспериментальное или измеренное значение. Поскольку фактическая температура кипения воды составляет 100 ° C, это будет ваше теоретическое значение.
Вы хотите найти % ошибки средней точки кипения воды в вашем эксперименте, 101,5°C относительно 100°C.
Подставьте свои числа в формулу процентной ошибки:
\[ \% {\text{ошибка}} = \left|{\dfrac {E – T}{T}}\right| \умножить на 100\\] \[ = \dfrac{(101,5 – 100)}{|100|} \умножить на 100\ \] \[ = \dfrac{1.5}{100} \times 100\ \] \[= 0,015 \умножить на 100\ \] \[=1,5\%\; \текст{ошибка} \]
Таким образом, ваша экспериментальная точка кипения имеет 1,5-процентную ошибку по сравнению с теоретической точкой кипения воды.
Процентная ошибка – формула, способы расчета и примеры решения
Как следует из названия, процентная ошибка – это разница между точным или известным значением чего-либо и его приблизительным или измеренным значением в процентном выражении.
В научных экспериментах он используется для сообщения о разнице между экспериментальным значением и его истинным или точным значением. Он рассчитывается как процент от точного значения. В качестве примера из реальной жизни, если вы посмотрите на автомат с жевательной резинкой и подсчитаете, сколько там шариков жевательной резинки, а затем подсчитаете количество шариков жевательной резинки, тогда вы сможете измерить процент ошибки, которую вы сделали. в вашем предположении.
Процентная ошибка позволяет увидеть, насколько вы далеки от точного значения в оценке ценности чего-либо. Эти ошибки могут возникать из-за неточности оборудования, измерений (человеческий фактор или ошибка инструмента) или некоторых корректировок, внесенных в методы расчета (округление и т. д.). Существует простая и понятная формула для расчета этой процентной ошибки, которая приведена ниже:
Процентная ошибка = (Приблизительное или экспериментальное значение – Точное или известное значение/Точное или известное значение)*100
Если процентная ошибка близка к 0, то ваше приближение очень близко к фактическому или истинному значению.
Эта формула очень важна для определения точности ваших вычислений. Для большинства приложений процентная ошибка представляется как положительное число, но для некоторых наук, таких как химия, принято выражать его как отрицательное число, поскольку положительное значение в химии указывало бы на потенциальную проблему с экспериментом или реакциями, которые не учитываются.
Как рассчитать процент?
Для расчета процентной ошибки в любом эксперименте или наблюдении необходимо выполнить следующие шаги:
Вы получите значение «ошибки», вычитая одно значение из другого. Если вы не сохраняете знак, то порядок не имеет значения, но если вы сохраняете отрицательный знак, вы получаете значение «ошибки», вычитая точное значение из измеренного значения.
Затем вы делите это значение «ошибки» на известное или точное значение (не измеренное или экспериментальное значение).
Это деление даст вам десятичное число.
Умножьте это десятичное значение на 100, чтобы преобразовать его в процентное значение.
Наконец, вы должны добавить обозначение % перед вычисленным значением, чтобы сообщить о своей процентной ошибке.
Решенные примеры погрешности в процентах
У нас есть несколько различных примеров по расчету погрешностей в процентах, чтобы углубиться в концепцию и получить больше ясности:
1. Организаторы подсчитали, что на концерте будет 90 человек. но на самом деле на концерт пришло 120 человек. Рассчитайте процент ошибки в догадке организаторов.
Формула для процентной ошибки =
\[\frac{\text{Расчетное или приблизительное значение – известное или точное значение}}{\text{известное или точное значение}}\ast\] 100
Подставляя вышеуказанные значения мы получаем; % ошибки = \[\frac{\mid 90-120\mid }{120}\ast 100 = \frac{30}{120}\ast100\] = 25%
2. Оле Рёмер был датским астрономом, который наблюдал что в зависимости от расстояния Юпитера от Земли периоды спутников Юпитера, казалось, колебались.
Спутникам требовалось больше времени, чтобы появиться из-за планеты, если Юпитер находился дальше от Земли, чем в противном случае. Он связал это со скоростью света и дал приблизительное значение 220 000 км/с для скорости света. Принятое значение скорости света в настоящее время равно 29.9800 км/с. Какова процентная ошибка наблюдения Ремера?
% ошибка = \[\frac{\mid2,20,000-299,800 \mid}{299,800}\ast \] 100 = 26,62%
Метод нахождения процентной ошибки
Найти процентную ошибку довольно просто. Студенты должны знать несколько важных вещей для нахождения процентной ошибки. Они должны знать оценочное значение и исходное значение, чтобы найти процентную ошибку.
Во-первых, они должны найти разницу между расчетным значением и первоначальным значением. Значение может быть отрицательным или положительным. Учащиеся могут игнорировать отрицательный знак. Они должны вычесть исходное значение из расчетного значения.
Найдя разницу, учащиеся должны разделить разницу на исходное значение и умножить на сто, чтобы получить процентное значение.
Это способ найти процент ошибки для любого эксперимента.
Весьма полезно для студентов разных специальностей. Поэтому учащиеся должны понимать формулу и метод расчета процентной ошибки. Vedantu предоставляет наилучшую информацию о процентной ошибке. Студенты могут посетить веб-сайт Vedantu, чтобы получить необходимое определение, формулу и примеры, связанные с процентной ошибкой. Это может помочь студентам хорошо подготовиться к экзаменам.
Решенные примеры для процентной ошибки
Здесь приведены несколько решенных примеров, которые могут помочь учащимся понять тип вопросов, задаваемых на экзамене, связанных с процентной ошибкой, а также понять метод нахождения процентной ошибки.
1. Мужчина установил прилавок и думал, что ежедневно прилавок будут посещать 100 человек, но каждый день приходило только 80 человек. Вычислите процент ошибки.
Решения: Учащиеся должны применить формулу:
Расчетное значение: 100
Оригинальное значение: 80
процент ошибки = оцененное значение- исходное значение
Оригинальное значение
100-80
80
¼ x 100 = 100 /4 = 25%
19
¼ x 100 = 100 /25%
1119
¼ x 100 /4 = 25%
19
.
Преимущества поиска процентных ошибок
Нахождение процентных ошибок дает множество преимуществ. Ниже приведены некоторые преимущества поиска процентных ошибок:
Процентная ошибка важна для определения точности. Точность означает степень близости измеренного значения к его исходному значению. Процентная ошибка рассчитывается путем деления разницы расчетного значения и исходного значения на исходное значение и умножения на 100.
Наиболее важным преимуществом определения процентной ошибки является определение того, насколько вы близки к истинному значению. Процентная ошибка может быть как незначительной, так и очень высокой в зависимости от ваших наблюдений. Таким образом, если процентная ошибка очень мала, ею можно пренебречь, но если процентная ошибка высока, вам придется снова вычислять или измерять вещи, чтобы получить абсолютное значение.
Несколько обработанных примеров:
1. Подсчитано, что расстояние до Луны в конкретный день составляет 235 755 миль.
Но фактическое расстояние составляет 250 655 миль. Вычислите процент ошибки.
Ответ. Процент ошибки можно рассчитать как:
235 755 – 250 655/250 655 = 0,059 x 100 = 5,9%
2. Джон планировал поход с друзьями. Он оценил высоту пешеходной тропы в 215 футов на милю. Но когда он пошел со своими друзьями, он обнаружил, что фактическая высота тропы составляет 230 футов / милю. Какова была погрешность в процентах в расчетах Джона?
Ответ. \[\frac{215-230}{230} =\frac{15}{230}\] = 0,065 x 100 = 6,5%
3. Школа организовала праздник, открытый для всех. Учителя и студенты подсчитали, что каждый день его будут посещать 1000 человек. Но фактическое количество людей, посетивших фестиваль, составило 1050 человек. Подсчитайте процент ошибки.
Ответ. \[\frac{1000-1050}{1050} =\frac{50}{1050}\] = 0,047 x 100 = 4,7%
4. Мужчина хотел подготовить квадратный газон перед своим домом. Он оценил его площадь в 450 квадратных метров.
Но когда он начал копать для сада, фактическая площадь, которую нужно было покрыть, составляла 470 квадратных метров. Вычислите процент ошибки.
Ответ. \[\frac{450-470}{470} =\frac{20}{470}\] = 0,042 x 100 = 4,2%
Заключение
Процентная ошибка – это разница между измеренным значением и точным значением любого количество под наблюдением. Он рассчитывается как процент от точного или известного значения. Его значение можно рассчитать по формуле:
\[\frac{\text{Расчетное или приблизительное значение – известное или точное значение}}{\text{известное или точное значение}}\ast\] 100
Знак процентной ошибки не учитывается в большинстве приложений за исключением химии и некоторых других наук, где принято сохранять знак минус. Процентная ошибка – это тип вычисления ошибки. Несколько других типов вычислений распространенных ошибок — это относительная ошибка и абсолютная ошибка.
Когда мы делаем анализ, мы можем делать ошибки.