Расчет ветровых нагрузок | Альпром
Итак , вы долго согласовывали, делали и наконец смонтировали свою самую лучшую наружную рекламу.
Красота! Все довольны. Но чу… после первого сильного ветра вам звонит рассерженный клиент с шокирующим известием – реклама упала!
Кошмар рекламщика стал явью…Что же случилось ?
А случилось следующее – при проектировании наружной рекламы был проигнорирован или выполнен неверно расчет ветровой нагрузки на наружную рекламу : на материал и на крепежные элементы.
Как избежать этого, как обезопасить себя от такого плачевного итога своей работы?
Ответ прост – при проектировании и монтаже наружной рекламы необходимо учитывать порывы ветра, стремящиеся сорвать ваше изделие, необходимо рассчитать и принять во внимание ветровую нагрузку на наружную рекламу.
Давайте запомним несложную формулу расчета ветровой нагрузки, которая измеряется в кг/кв.м.:
Pw = k * q
Расшифровываем хитрые буквицы
Pw – давление ветра, нормальное к воспринимающей поверхности.
k – аэродинамический коэффициент, зависящий от формы и положения подверженного ветру
объекта.
q – скоростной напор ветра (кг/кв.м), соответствующий наибольшей для данного места скорости ветра c учётом особых порывов.
Величина q в зависимости от скорости ветра определяется следующим образом:
q = 7 / g * кв.V / 2
7 – вес воздуха (1,23 кг/куб.м) при Pатм.= 760 мм рт.ст. и tатм.= 15 °С
g – ускорение силы тяжести (9,81 м/кв.сек)
V- наибольшая скорость ветра (м/сек) на данной высоте h, т.е.
Высота h над уровнем земли, м
Скорость ветра V, км/ч м/с
Скоростной напор q, кг/кв.м
| Высота h над уровнем земли, м | Скорость ветра V, км/ч м/с | Скоростной напор q, кг/кв.м |
| 0 – 8 | 103,7 28,8 | 51 |
| 8 – 20 | 128,9 35,8 | 80 |
q = кв.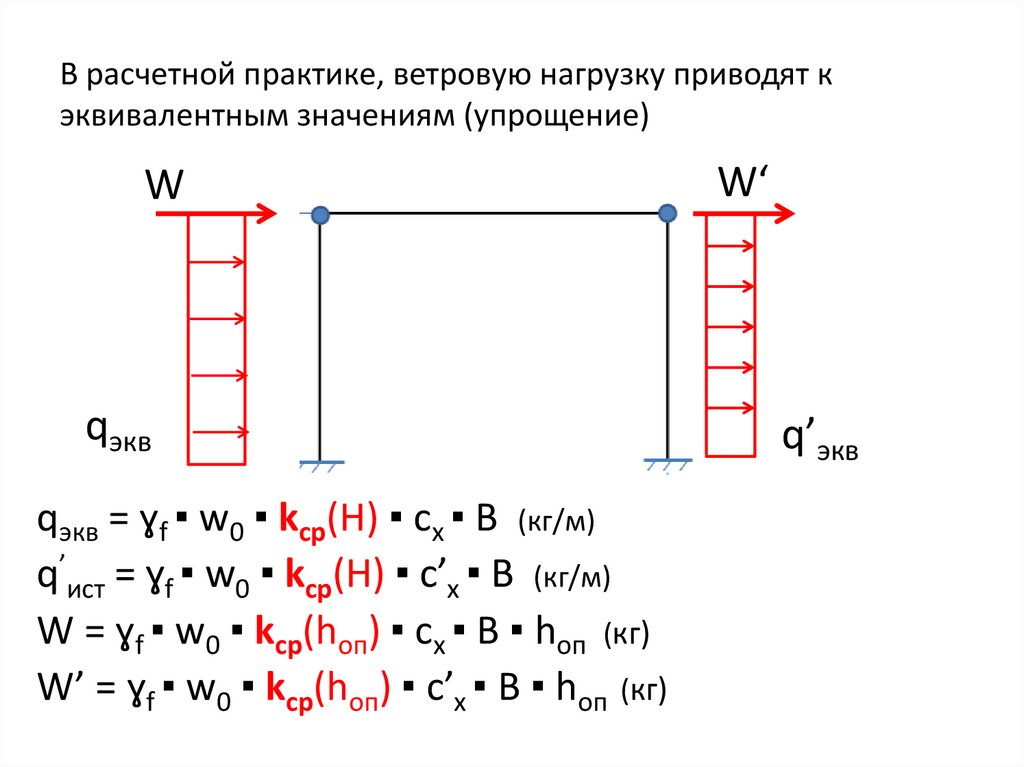 V / 16
V / 16
Вертикально установленное полотно, закреплённое в раме или натянутое на троссах
| Конструкция – b-ширина, d-высота | Соотношение размеров | Площадь, S | Аэродинамический коэффициент, k |
| Вертикально установленное полотно, закреплённое в раме или натянутое на троссах | d/b < 5 | b * d | 1,2 |
| d/b >= 5 | b * d | 1,6 |
Вот так вот оказывается все совсем просто.
Хотите узнать о расчете ветровых нагрузок больше и получить консультацию наших специалистов?
Прямо сейчас звоните +7(8482) 78-20-44 или напишите на электронную почту [email protected]
Программы и формулы для расчета ветровой нагрузки
Программы для расчета ветровой нагрузки
Формулы для расчета ветровой нагрузки
Источник: СНиП 2.01.07-85 (с изм. 1 1993)
1 1993)
Давление ветровой нагрузки определяется по формуле:
Wm = W0kc
где Wo- нормативное значение давления (см. таб.1)
k – коэффициент, учитывающий изменение ветрового давления по высоте, определяется по таб.2 в зависимости от типа местности. Принимаются следующие типы местности:
- А – открытые побережья морей, озёр и водохранилищ, пустыни, лесостепи, тундра;
- В – городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой не более 10 м;
- С – городские районы с застройкой зданниями высотой более 25 м.
с – аэродинамический коэффициент.
W0 = 0,61V02
где V0 -численно равно скорости ветра, м/с, на уровне 10 м над поверхностью земли для местности типа А, соответствующей 10-минутному интервалу осреднения и превышаемой в среднем раз в 5 лет (если техническими условиями, утверждёнными в установленном порядке, не регламентированы другие периоды повторяемости скоростей ветра).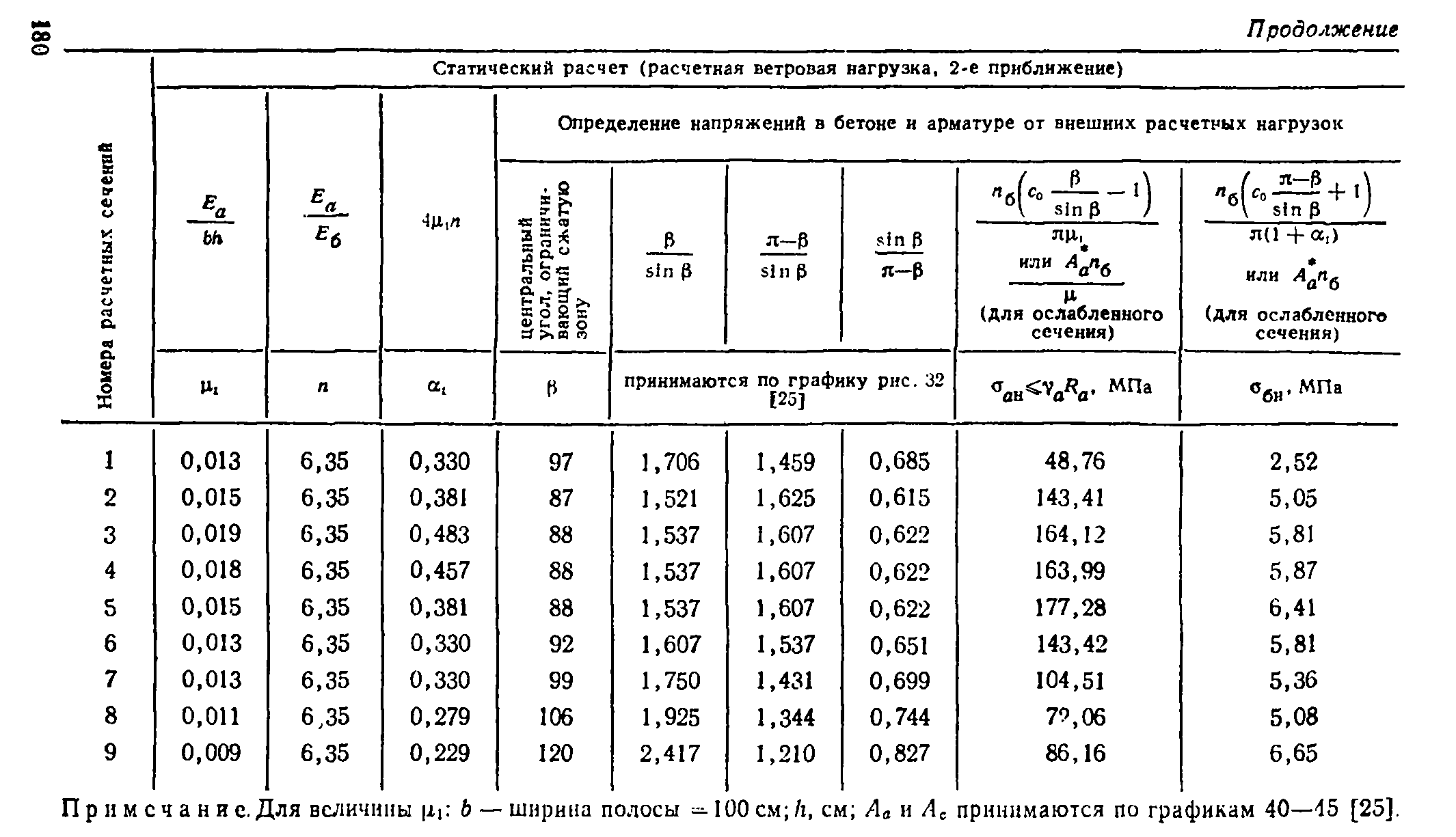
Таблица 1.
| Ветровые районы СССР | Ia | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Wo,кПа(кгс/м3) |
(23) |
0,23 (23) |
0,30 (30) |
0,38 (38) |
0,48 (48) |
0,60 (60) |
0. (73) |
0,85 (85) |
Таблица 2.
| Высота z,м | коэффициент k для типов местности | ||
| A | B | C | |
| < 5 | 0,75 | 0,5 | 0,4 |
| 10 | 1 | 0,65 | 0,4 |
| 20 | 1,25 | 0,85 | 0,55 |
| 40 | 1,5 | 1,1 | 0,8 |
| 60 | 1,7 | 1,3 | 1 |
| 80 | 1,85 | 1,45 | 1,15 |
| 10 | 2 | 1,6 | 1,25 |
| 150 | 2,25 | 1,9 | 1,55 |
| 200 | 2,45 | 2,1 | 1,8 |
| 250 | 2,652 | 2,3 | 2 |
| 300 | 2,75 | 2,5 | 2,2 |
| 350 | 2,75 | 2,75 | 2,35 |
| >480 | 2,75 | 2,75 | 2,75 |
Таблица 3.
| Высота z,м | Коэффициент пульсаций давления ветра z для типов местности | ||
| A | B | C | |
| £ 5 | 0,85 | 1,22 | 1,78 |
| 10 | 0,76 | 1,06 | 1,78 |
| 20 | 0,69 | 0,92 | 1,5 |
| 40 | 0,62 | 0,8 | 1,26 |
| 60 | 0,58 | 0,74 | 1,14 |
| 80 | 0,56 | 0,7 | 1,06 |
| 100 | 0,54 | 0,67 | 1 |
| 150 | 0,51 | 0,62 | 0,9 |
| 200 | 0,49 | 0,58 | 0,84 |
| 250 | 0,47 | 0,56 | 0,8 |
| 300 | 0,46 | 0,54 | 0,76 |
| 350 | 0,46 | 0,52 | 0,73 |
| ³ 480 | 0,46 | 0,5 | 0,68 |
Таблица 4. Определение аэродинамического коэффициента для разных типов сооружений
Определение аэродинамического коэффициента для разных типов сооружений
4.1. Сфера
| b, град | 0 | 15 | 3 | 45 | 75 | 90 | |
| с | 1 | 0,8 | 0,4 | -0,2 | -0,8 | -1,2 | -1,25 |
| b, град | 105 | 120 | 135 | 150 | 175 | 180 | |
| с | -1 | -0,6 | -0,2 | 0,2 | 0,3 | 0,4 |
4. 2. Призматические сооружения
2. Призматические сооружения
| l | 5 | 10 | 20 | 35 | 50 | 100 | беск. |
| k | 0,6 | 0,65 | 0,75 | 0,85 | 0,9 | 0,95 | 2 |
Пример расчета ветровой нагрузки:
Для трубы диаметром D=500 мм, высотой h=1000 мм, расположенной на высоте 10 м. Скорость ветра v0=8 м/с. Местность-город.
W = W0kc = (0,61*64)*0,65*0,75 = 19,032 (кПа)
Как правильно рассчитать ветровую нагрузку и закрепить кровлю, чтобы ее точно не сорвало
Из-за ошибок, допущенных при строительстве, у домов нередко срывает кровли во время непогоды.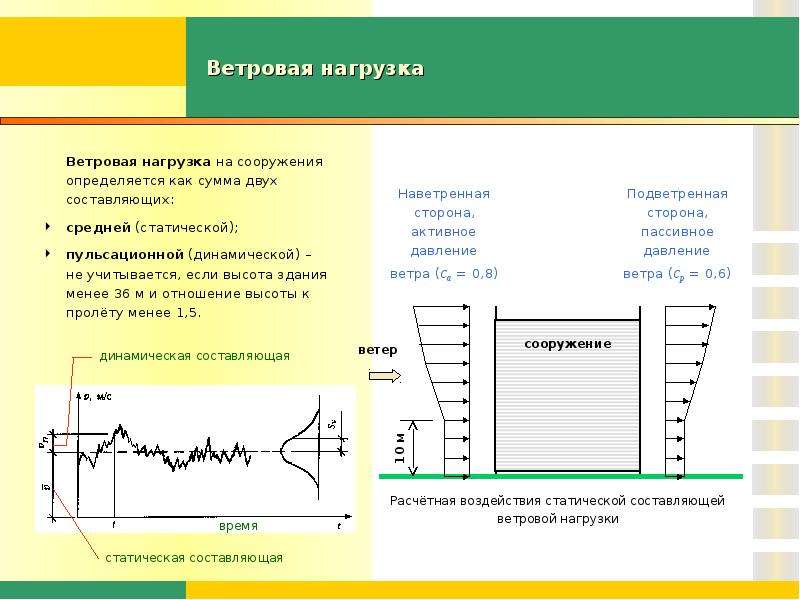 Кажется, что не так часто случаются сильные ураганы и смерчи, но даже один катаклизм в год может полностью разрушить крышу.
Кажется, что не так часто случаются сильные ураганы и смерчи, но даже один катаклизм в год может полностью разрушить крышу.
Это происходит потому, что исполнители работ не рассчитывают количество крепежа для мембраны по необходимым формулам и обычно делают все по принципу «на глазок». В итоге плохо закрепленная кровля может попросту оторваться и ее надо будет заново монтировать. Также от точного расчета зависит расход материалов, которые при неправильных подсчетах приходится докупать, либо иногда остается лишнее.
Рассказываем, как сделать правильный расчет ветровой нагрузки для крепления кровли и определить количество крепежа, чтобы конструкция устояла перед стихийным бедствием и долго служила.
Как ветровая нагрузка действует на кровлю
Представьте себе, что на постройку непрерывно с разной скоростью и силой дует ветер. Потоки воздуха создают давление, которое способно навредить покрытию кровли. При этом совершенно необязательно, чтобы ветер дул перпендикулярно или по касательной к поверхности крыши – даже если он направлен вдоль плоской кровли, он создает значительную отрывающую нагрузку.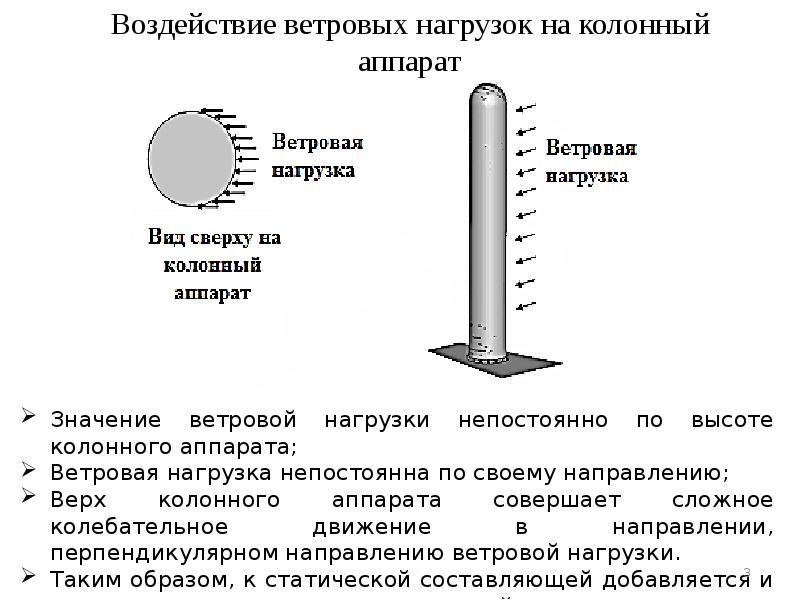
Суммируя все ветреные дни и добавив катаклизмы, которые хоть и редко, но случаются, мы получаем постепенное непрерывное разрушение материала. Именно поэтому возникает необходимость рассчитывать ветровую нагрузку и количество креплений кровельного материала.
Как рассчитывают ветровую нагрузку для крепления кровли
От ветровой нагрузки зависит, сколько нужно использовать крепежных элементов и какую выбрать ширину рулона мембраны. Чем выше нагрузка, тем больше нужно крепежа на квадратный метр. Ширину мембраны также приходится уменьшать, чтобы крепеж уместился в шов.
Чтобы самостоятельно рассчитать ветровое воздействие на кровлю, можно воспользоваться методикой в 7 пункте документа, разработанного специалистами ТЕХНОНИКОЛЬ вместе с ЦНИИПромзданий.
Существует и более простой способ расчета ветровой нагрузки
Если вы хотите быстро получить точный результат и не связываться со сложными формулами, таблицами и картами, воспользуйтесь нашим онлайн-калькулятором для кровли из материалов ТЕХНОНИКОЛЬ.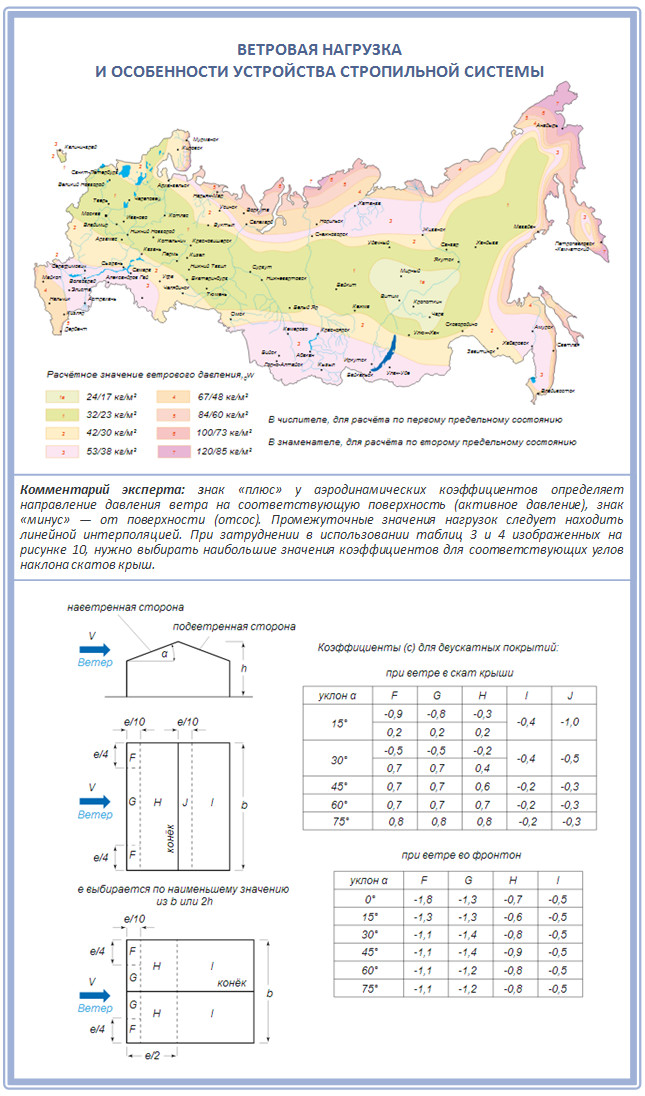
Калькулятор помогает рассчитать не только ветровую нагрузку для плоских крыш, но и количество необходимого крепежа на каждом участке, а также требуемую ширину рулонов гидроизоляции.
Расчеты основаны на действующих российских нормах СП 20.13330.2016 и СП 17.13330.2017.
В калькулятор встроена карта России с районированием по давлению ветра, так что вам не нужно самостоятельно искать на картах и в таблицах нужные значения. Достаточно выбрать место и кликнуть или указать точное название населенного пункта.
Вы выбираете тип местности – открытую, равномерно покрытую препятствиями или высотную городскую застройку. По этим двум параметрам калькулятор выдает первое значение – пиковую ветровую нагрузку согласно СП 20.133330.2016 п.11.
Далее переходим к основанию кровли и выбираем – тяжелый бетон, ОСП и металлическое основание профлист (0,7 мм или 0,75–2,5 мм). При выборе профлиста калькулятор предложит еще пять вариантов в зависимости от шага между гофрами.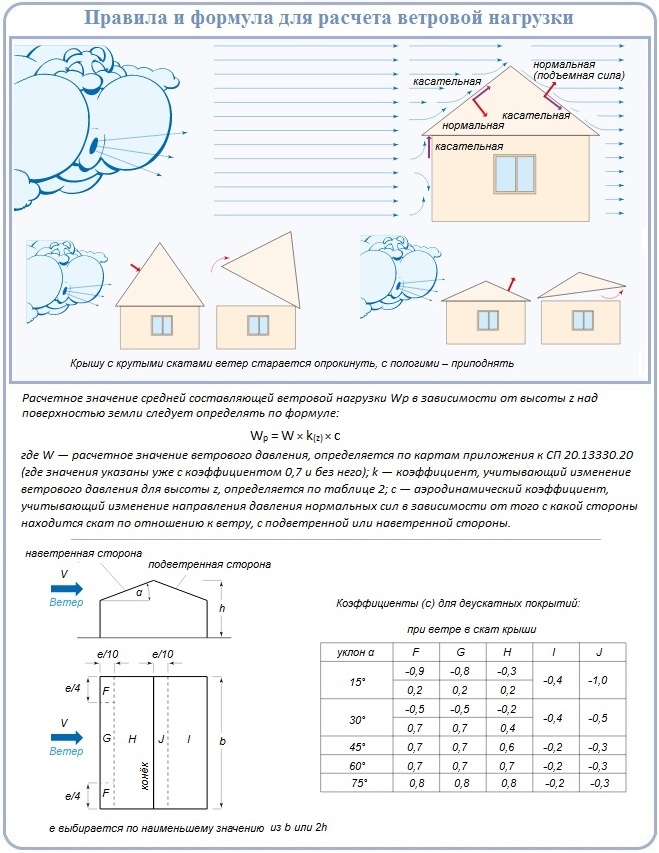 Вы также можете указать свой вариант.
Вы также можете указать свой вариант.
На третьем этапе нужно указать толщину утеплителя, который вы будете использовать, и способ его укрепления. Также возможен вариант без утеплителя.
На этапе гидроизоляции нужно указать способ ее фиксации. В калькуляторе предусмотрено два варианта крепления: механический и балластный. Если у вас балластный, также нужно указать его тип – армированная стяжка или гранитный щебень. Далее выбирайте тип мембраны: битумная или полимерная. Кстати, у каждого материала можно посмотреть характеристики и всю необходимую информацию, нажав на кнопку с вопросом.
Пятый этап включает работу с геометрией объекта, где нужно вводить параметры участка кровли. Калькулятор рассчитывает значение только для плоских крыш прямоугольной формы, поскольку методика расчета использует пиковые значения аэродинамических коэффициентов ветровой нагрузки. Вам нужно указать высоту здания и его габариты. Высоту принимаем по самой высокой точке здания – парапетной зоне.
После вы получаете промежуточный расчет, где видите основные результаты, например, ширину рулона и шаг крепежа, и проверяете введенные значения, которые можно подкорректировать, если ошиблись.
После этого получаете готовый отчет, где рассчитано:
- деление кровли на участки (центральная, парапетная, угловая) и ветровое давление на каждый из них;
- какую ширину рулонов гидро- и теплоизоляции использовать;
- сколько потребуется крепежа на один квадратный метр и его шаг.
На любой стадии расчета можно «откатить» назад на любой этап и изменить исходные данные. А также сохранить и отправить себе на почту в виде ссылки, чтобы потом вернуться к нему, если вы что-то не доделали. Благодаря формату PDF расчет можно вносить в проект или просто удобно хранить и использовать эти данные.
Расчёт ветровой нагрузки на здания ЖК “Пётр и Екатерина”
Данные расчеты проведены на основе численного решения трехмерных уравнений газовой динамики с учетом турбулентности внешнего ветрового потока.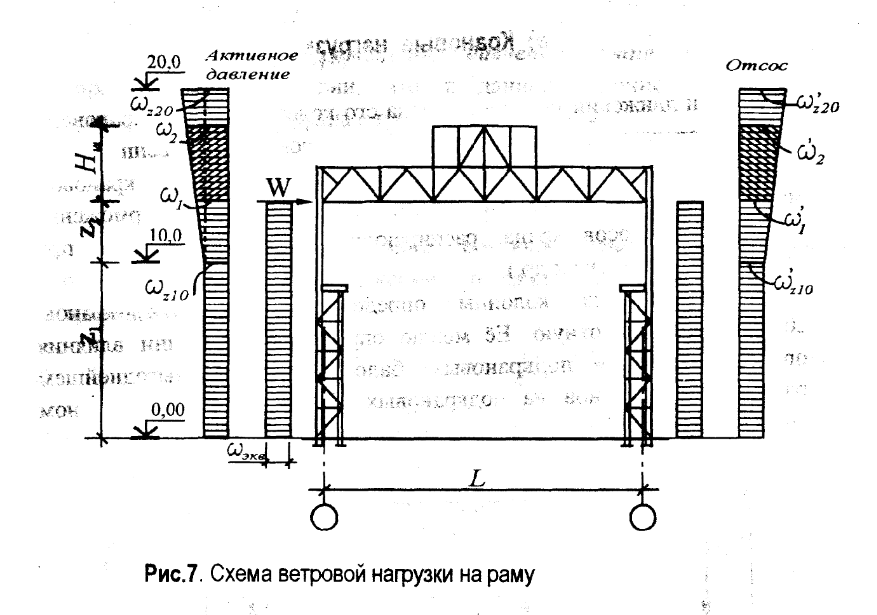 В расчеты закладывался логарифмический профиль скорости ветра в приземном слое атмосферы, определяемый в соответствии с ветровой нагрузкой, рассчитанной по нормативной документации для 2-го ветрового района (город Санкт-Петербург) и типа местности «А». Выбор типа местности как «А» несмотря на то, что здание расположено в черте города, связан с наличием вблизи строящихся зданий обширного водного пространства и многокилометрового лесопаркового массива.
В расчеты закладывался логарифмический профиль скорости ветра в приземном слое атмосферы, определяемый в соответствии с ветровой нагрузкой, рассчитанной по нормативной документации для 2-го ветрового района (город Санкт-Петербург) и типа местности «А». Выбор типа местности как «А» несмотря на то, что здание расположено в черте города, связан с наличием вблизи строящихся зданий обширного водного пространства и многокилометрового лесопаркового массива.
В результате математического моделирования были получены поля давления и скорости, формирующиеся при обтекании высотного жилого здания. Полученные при расчете ветровой нагрузки на здание данные в дальнейшем использовались для расчета на прочность в специализированном программном комплексе.
Ветровая нагрузка на мачты.
Отличительной особенностью подобных высотных строений является размещение на их кровле свободно и на мачтах различного радио- и телекоммуникационного оборудования, а также шпили и молниеприёмные устройства. При этом, иногда недостаточно определить только расчётное давление на мачты. Как в этом случае рассчитать ветровую нагрузку?
При этом, иногда недостаточно определить только расчётное давление на мачты. Как в этом случае рассчитать ветровую нагрузку?
Для подобных объектов, высота которых более чем в 10 раз превышает их толщину, современные строительные нормы требуют также учитывать резонанс и такие аэродинамические неустойчивые колебания, как галопирование, флаттер, дивергенцию и т.д. В некоторых случаях производители прямо указывают на какую ветровую нагрузку рассчитаны их мачты. В данном случае она должна сравниваться с расчётной нагрузкой на высоте установки. Для данного расчёта аналитическое приближение не выявило условий возникновения аэродинамических неустойчивых колебаний, поэтому для данной мачту такой расчёт не требовался и остался за гранью исследования. Была определена лишь расчётная ветровая нагрузка на мачту.
Механическая прочность баннерных тканей и расчет ветровых нагрузок На улице вывески, щиты, короба и перетяжки подвергаются не только температурным колебаниям, но и высоким механическим нагрузкам. Ветровая нагрузка, измеряемая в кг(кН)/м², определяется по формуле: Pw = k ⋅ q,
Pw – давление ветра, нормальное к воспринимающей поверхности. Это давление считается положительным.
q – скоростной напор ветра (кг/м²), соответствующий наибольшей для данного места скорости ветра c учетом особых порывов. 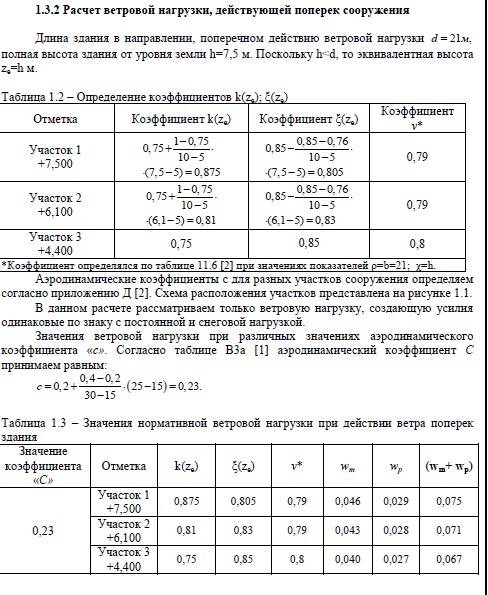 Величина q в зависимости от скорости ветра определяется следующим образом:
q = γ : g ⋅ V² : 2
γ – вес воздуха (1,23 кг/м³) при P атм. = 760 мм рт. ст. и t атм. = 15 °С
q = 1,23 : 9,81 ⋅ V² : 2
q = V² : 16
Примечание: В таблице указаны максимальные значения скорости ветра, характерные европейской территории для конструкций, расположенных на открытом месте. При необходимости точного расчета с учетом географических районов (прибрежных зон), застройки места расположения баннера, наличия редких/обширных зеленых насаждений следует обратиться к нормативным документам СниП 2.01.07-85* («Нагрузки и воздействия») и воспользоваться расчетными данными.
Пример расчета максимальной ветровой нагрузки для конструкции, верхняя точка которой расположена на высоте 5 м над уровнем земли. Размер знака 3 х 1,5 м. При использовании приведенных ранее таблиц, производится простой расчет:
| |||
Расчет ветровой нагрузки на осветительную конструкцию
Осветительная опора в процессе эксплуатации испытывает ветровые нагрузки. При заказе инженерной конструкции необходимо учитывать этот параметр во избежание обрушения корпуса при сильном ветре. Инженерные расчеты учитывают максимальную силу ветра в районе эксплуатации с учетом того, что вес ствола может быть увеличен из-за налипшего на поверхность снега и льда. А когда расчет проводится для силовых опор, учитывается также нагрузка от самонесущего изолированного провода.
При заказе инженерной конструкции необходимо учитывать этот параметр во избежание обрушения корпуса при сильном ветре. Инженерные расчеты учитывают максимальную силу ветра в районе эксплуатации с учетом того, что вес ствола может быть увеличен из-за налипшего на поверхность снега и льда. А когда расчет проводится для силовых опор, учитывается также нагрузка от самонесущего изолированного провода.
Порядок расчета нагрузок
Для определения нагрузок, оказываемых на ствол воздушными массами, ранее применялись СНиП 2.01.07-85. В настоящее время действует актуализированная версия этих строительных правил под номером 20.13330.2016.
Согласно информации, изложенной в этом документе, в понятие ветровых нагрузок входят:
- Ветровое воздействие, которое оказывают перемещающиеся воздушные массы на стальную конструкцию.
- Пиковые нагрузки, которые оказывает ветер на светильники, кронштейны, провода и другие элементы опоры.

- Вихревое воздействие, которое возникает при огибании воздухом корпуса опоры.
- Неустойчивые колебания.
При составлении проекта опоры прочность конструкции делается избыточной. То есть опора может выдержать ветровую нагрузку в 140% относительно прогнозируемой в конкретном регионе.
Общий показатель нагрузки w рассчитывается как сумма средней и пульсационной нагрузки. Второй параметр вводится в связи с тем, что ветер не может дуть постоянно с одной скоростью. Изменение его силы приводит к тому, что корпус конструкции испытывает динамическое воздействие.
При вычислении средней ветровой нагрузки учитываются следующие параметры:
- Нормативная сила ветра, которая указана в приложении к строительным правилам 20.13330.2016. Она рассчитана заранее для различных регионов нашей страны. Вся территория РФ разделена на 7 ветровых регионов с нормативной нагрузкой от 0,17 до 0,85 кПа.

- Поправочный коэффициент, который вводится для учета изменения ветровой нагрузки по высоте. В зависимости от окружающей местности сила ветра может увеличиваться, поэтому опору нужно делать более прочной.
Различают несколько типов местности для определения поправочных коэффициентов:
- Берег моря, степь, населенные пункты с одноэтажной застройкой.
- Леса и населенные пункты со зданиями высотой от 10 метров.
- Населенные пункты с близко расположенными высотными зданиями высотой от 25 метров.
Кроме того, учитывается аэродинамический коэффициент. Он зависит от формы корпуса высотной опоры. Необходимые значения коэффициентов берутся из свода правил.
Стандартные осветительные опоры из стали изготавливаются по типовой проектной документации.
Услуги по изготовлению опор
Стандартные осветительные опоры из стали изготавливаются по типовой проектной документации. Прочность конструкций рассчитывается так, чтобы выдерживать силу ветра в большинстве регионов России. Если необходимо установить конструкцию в особых климатических зонах, стволы делаются на основании индивидуально разработанных проектах. В этом случае производится отдельный расчет ветровых нагрузок.
Прочность конструкций рассчитывается так, чтобы выдерживать силу ветра в большинстве регионов России. Если необходимо установить конструкцию в особых климатических зонах, стволы делаются на основании индивидуально разработанных проектах. В этом случае производится отдельный расчет ветровых нагрузок.
Индивидуальный проект составляется опытными инженерами, которые используют для расчетов специализированное программное обеспечение. Благодаря этому изготовленные опоры соответствуют требованиям действующих ГОСТ и могут использоваться при сильном ветре.
Куда обратиться?
Вам нужны опоры наружного освещения? Заказать их можно в нашей производственной компании. Типовые модели представлены на складе и доставляются в минимальные сроки. Если нужно сделать корпус для эксплуатации при сильном ветре, срок производства составит до 8 недель. При необходимости мы делаем также закладные детали фундамента нужной длины.
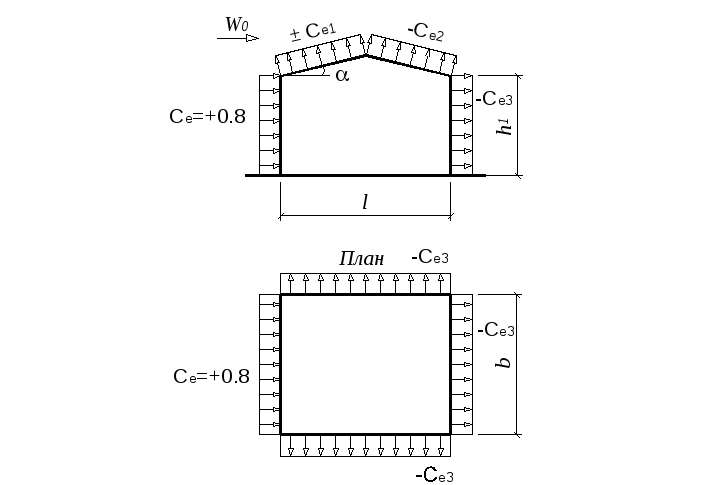
Определение ветровых нагрузок на конструкции навесов по норме EN 1991-1-4
При расчете навесов, например, кровли топливозаправочной станции, необходимо определить также нагрузки, соответствующие требованиям раздела 7. 3 нормы EN 1991-1-4. В следующей статье так будет показан пример расчета V-образной кровли с небольшим наклоном.
3 нормы EN 1991-1-4. В следующей статье так будет показан пример расчета V-образной кровли с небольшим наклоном.
Определение коэффициентов
При определении нагрузки всегда необходимо применить коэффициент силы c f и общий коэффициент давления cp,net согласно таблицам 7.6 и 7.8. В случае заполнения конструкции, например складскими материалами, находящимися под или непосредственно рядом с навесом, необходимо определить с помощью интерполяции в таблицах также степень заполнения и ее значение в интервале от ϕ = 0 (открытый навес) до ϕ = 1 (заполненный навес).
Для определения результирующего общего коэффициента давления выполняется также, как и у закрытых зданий, классификация поверхностей. Однако это применимо только для расчета покрытия кровли и его крепежных элементов.
Положение и форма результирующей силы ветра
Для расчета несущей конструкции необходимо на расстоянии d/4 от наветренного края приложить результирующую силу ветра. d – размер поверхности кровли в направлении ветра На рисунке 7.17 затем показано шесть возможных положений нагрузки в зависимости от знака коэффициента силы.
d – размер поверхности кровли в направлении ветра На рисунке 7.17 затем показано шесть возможных положений нагрузки в зависимости от знака коэффициента силы.
Поскольку ветровая нагрузка является поверхностной, а не узловой, и действует на покрытие кровли, а ее центр тяжести располагается в 1/4 длины кровли, требуется подобрать такой случай нагружения, который будет все это учитывать. Однако это внецентренное расположение нагрузки обусловливает более сложный расчет устойчивости у возможных центральных опор. Потому, одним из возможных решений является расположение поверхностной нагрузки в форме квадратичной параболы, так как ее центр тяжести будет находиться в 1/4 длины кровли.
Пример V-образной кровли
Длина = 15 м
Ширина = 12 м
Высота разжелобка = 6 м
Наклон кровли = -5 °
Ветровая нагрузка = 0,5 кН/м²
Открытый навес → ϕ = 0
cf = +0,3 максимум всех ϕ
cf = -0,5 минимум, ϕ = 0
Результирующая сила ветра
Программы RFEM и RSTAB содержат в себе генераторы нагрузок для закрытых зданий, прямоугольных в плане. К тому же, в них можно задать нагружение, которое действуюет, только на стены или на кровлю, а также на все здание.
К тому же, в них можно задать нагружение, которое действуюет, только на стены или на кровлю, а также на все здание.
Однако с помощью генераторов нельзя автоматически рассчитать несущие конструкции навесов. Тем не менее, после расчета коэффициентов можно генератор нагрузки применить к отдельным уровням навеса.
Fw,max = cf · qp(ze) · Aref = 0,3 · 0,5 · 15 · 12cos 5° = 27,10 kN
Fw,min = cf · qp(ze) · Aref = -0,5 · 0,5 · 15 · 12cos 5° = -45,17 kN
Согласно пункту 7.5., силы трения в нашем примере не учитываются.
Наибольшие ординаты параболической нагрузки
Во внимание принимается только положение нагрузок 2 и 5, так как благодаря симметрии нет необходимости учитывать положение нагрузок 3 и 6.
q(Pressure) = 27,1123 = 6,775 кН/м = 0.45 кН/м²q(Suction) = -45.17123 = -11,293 кН/м = -0,75 кН/м²
На основе данных ординат нагрузок потом можно с помощью квадратичного уравнения вычислить, например в программе Excel, переменные значения нагрузки в положении x, а затем экспортировать их в программу RFEM или RSTAB.
ASCE 7-10 Пример расчета ветровой нагрузки
Полностью рабочий пример расчета ветровой нагрузки ASCE 7-10SkyCiv выпустила бесплатный калькулятор ветровой нагрузки, в котором есть несколько кодовых ссылок, включая процедуру ветровой нагрузки ASCE 7-10. В этом разделе мы собираемся продемонстрировать, как рассчитать ветровые нагрузки, используя модель склада S3D ниже:
Рисунок 1. Модель склада в SkyCiv S3D в качестве примера.
Рисунок 2.Расположение сайта (из Google Maps).
Таблица 1. Строительные данные, необходимые для нашего расчета ветра.
| Расположение | Кордова, Мемфис, Теннесси |
| Вместимость | Разное – Структура завода |
| Рельеф | Плоский приусадебный участок |
| Габаритные размеры | 64 фута × 104 фута в плане Высота карниза 30 футов Высота апекса на отметке.  36 футов Уклон крыши 3:16 (10,62 °) 36 футов Уклон крыши 3:16 (10,62 °) С отверстием |
| Облицовка | Прогоны на расстоянии 2 фута Стеновые стойки на расстоянии 2 футов |
В нашем примере ветровой нагрузки ASCE 7-10 будет определено расчетное давление ветра для большой трехэтажной конструкции завода.На рис. 1 показаны размеры и каркас здания. Данные по зданию приведены в Таблице 1.
Хотя существует ряд программ, в которых расчет ветровой нагрузки уже интегрирован в их разработку и анализ, лишь некоторые из них обеспечивают подробный расчет этого конкретного типа нагрузки. Пользователям потребуется выполнить ручные вычисления этой процедуры, чтобы проверить, совпадают ли результаты с результатами, полученными с помощью программного обеспечения.
Формула для определения расчетного ветрового давления:
Для закрытых и частично закрытых домов:
\ (p = qG {C} _ {p} – {q} _ {i} ({GC} _ {pi}) \) (1)
Для открытых построек:
\ (p = q {G} _ {f} {C} _ {p} – {q} ({GC} _ {pi}) \) (2)
Где:
\ (G \) = коэффициент воздействия порыва
\ ({C} _ {p} \) = коэффициент внешнего давления
\ (({GC} _ {pi}) \) = коэффициент внутреннего давления
\ (q \) = скоростное давление в фунтах на квадратный дюйм, определяемое по формуле:
\ (д = 0. 2 \) (3)
2 \) (3)
\ (q \) = \ ({q} _ {h} \) для стен с подветренной стороны, боковых стен и крыш, оценивается по средней высоте крыши, \ (h \)
\ (q \) = \ ({q } _ {z} \) для наветренных стен, оценка по высоте, \ (z \)
\ ({q} _ {i} \) = \ ({q} _ {h} \) для отрицательного внутреннего давления, \ ((- {GC} _ {pi}) \) оценка и \ ({q} _ {z} \) для оценки положительного внутреннего давления \ ((+ {GC} _ {pi}) \) частично закрытого зданий, но можно принять консервативное значение как \ ({q} _ {h} \).
\ ({K} _ {z} \) = коэффициент скоростного давления
\ ({K} _ {zt} \) = топографический фактор
\ ({K} _ {d} \) = коэффициент направленности ветра
\ ( V \) = основная скорость ветра
Ниже мы подробно рассмотрим каждый параметр.Кроме того, мы будем использовать процедуру направленного действия (глава 30 ASCE 7-10) для решения расчетных значений давления ветра.
Категория риска Первое, что нужно сделать при определении расчетного давления ветра, – это классифицировать категорию риска конструкции, основанную на использовании или занятости конструкции. В этом примере, поскольку это заводская структура, она классифицируется как Категория риска IV . См. Таблицу 1.5-1 ASCE 7-10 для получения дополнительной информации о классификации категорий риска.
В этом примере, поскольку это заводская структура, она классифицируется как Категория риска IV . См. Таблицу 1.5-1 ASCE 7-10 для получения дополнительной информации о классификации категорий риска.
ASCE 7-10 предоставляет карту ветров, на которой соответствующая базовая скорость ветра в месте может быть получена из рисунков 26.5-1A – 1C. Категория размещения определяется и классифицируется в Международном строительном кодексе.
При просмотре карт ветров возьмите номер наивысшей категории определенной категории риска или занятости. В большинстве случаев, включая этот пример, они одинаковы. Как видно из рисунка 26.5-1B, Кордова, Мемфис, Теннесси каким-то образом находится рядом с красной точкой на Рисунке 3 ниже, и отсюда базовая скорость ветра \ (V \) составляет 120 миль в час.Обратите внимание, что для других мест вам потребуется интерполировать базовое значение скорости ветра между контурами ветра.
Рис. 3. Базовая карта скорости ветра из ASCE 7-10.
SkyCiv теперь автоматизирует расчет скорости ветра с помощью нескольких параметров. Попробуйте наш SkyCiv Free Wind Tool
Калькулятор ветровой нагрузки SkyCiv
Категория воздействияСм. Раздел 26.7 ASCE 7-10, в котором подробно описана процедура определения категории воздействия.
В зависимости от выбранного направления ветра экспозиция конструкции должна определяться с наветренного сектора 45 °. Принимаемая экспозиция должна быть такой, которая вызовет наибольшую ветровую нагрузку в указанном направлении.
Описание каждой классификации воздействия подробно описано в разделах 26.7.2 и 26.7.3 стандарта ASCE 7-10. Чтобы лучше проиллюстрировать каждый случай, в таблице ниже приведены примеры каждой категории.
Таблица 2. Примеры зон, классифицированных в соответствии с категорией воздействия (глава C26 ASCE 7-10).
| Экспозиция | Пример |
|---|---|
| Экспозиция B |
|
| Экспозиция C |
|
| Экспозиция D |
|
Для нашего примера, поскольку расположение конструкции находится на сельскохозяйственных угодьях в Кордове, Мемфис, Теннесси, без каких-либо построек высотой более 30 футов, поэтому территория классифицируется как Exposure C . Полезным инструментом для определения категории воздействия является просмотр вашего потенциального сайта через спутниковое изображение (например, Google Maps).
Полезным инструментом для определения категории воздействия является просмотр вашего потенциального сайта через спутниковое изображение (например, Google Maps).
Коэффициенты направленности ветра \ ({K} _ {d} \) для нашей конструкции равны 0,85, поскольку здание является основной системой сопротивления ветровой нагрузке, а также имеет компоненты и облицовку, прикрепленные к конструкции. Это показано в таблице 26.6-1 ASCE 7-10, как показано ниже на рисунке 4.
Рисунок 4. Коэффициент направленности ветра в зависимости от типа конструкции (Таблица 26.6-1 ASCE 7-10).
Топографический фактор, \ ({K} _ {zt} \) Поскольку конструкция расположена на плоской сельскохозяйственной земле, мы можем предположить, что топографический фактор, \ ({K} _ {zt} \), равен 1,0. В противном случае коэффициент можно определить с помощью рисунка 26.8-1 ASCE 7-10. Чтобы определить, требуются ли дальнейшие расчеты топографического фактора, см. Раздел 26.8.1. Если ваш участок не соответствует всем перечисленным условиям, то топографический фактор можно принять равным 1.0.
Чтобы определить, требуются ли дальнейшие расчеты топографического фактора, см. Раздел 26.8.1. Если ваш участок не соответствует всем перечисленным условиям, то топографический фактор можно принять равным 1.0.
Рис. 5. Параметры, необходимые для расчета топографического фактора, \ ({K} _ {zt} \) (Таблица 26.8-1 ASCE 7-10).
Примечание. Факторы топографии могут быть автоматически рассчитаны с помощью программного обеспечения SkyCiv Wind Design
. Коэффициент скорости давления, \ ({K} _ {z} \)Коэффициент скоростного давления, \ ({K} _ {z} \), можно рассчитать с помощью таблицы 27.3-1 стандарта ASCE 7-10. Этот параметр зависит от высоты над уровнем земли точки, в которой учитывается давление ветра, и категории воздействия.{2 / α} \) (5)
Где:
Таблица 3. Значения и \ ({z} _ {g} \) из таблицы 26.9-1 стандарта ASCE 7-10.
| Экспозиция | α | \ ({z} _ {g} \) (футы) |
| B | 7 | 1200 |
| С | 9,5 | 900 |
| D | 11,5 | 700 |
Обычно коэффициенты скоростного давления на средней высоте крыши, \ ({K} _ {h} \), и на каждом уровне этажа, \ ({K} _ {zi} \), являются значениями, которые мы потребуется для расчета расчетного давления ветра. В этом примере, поскольку давление ветра с наветренной стороны носит параболический характер, мы можем упростить эту нагрузку, предположив, что равномерное давление применяется к стенам между уровнями пола.
В этом примере, поскольку давление ветра с наветренной стороны носит параболический характер, мы можем упростить эту нагрузку, предположив, что равномерное давление применяется к стенам между уровнями пола.
Структура завода состоит из трех (3) этажей, поэтому мы разделим наветренное давление на эти уровни. Кроме того, поскольку крыша является двускатной, среднюю высоту крыши можно принять как среднее значение высоты карниза и вершины крыши, что составляет 33 фута
.Таблица 4. Расчетные значения коэффициента скоростного давления для каждой высоты возвышения.
| Высота (фут) | \ ({K} _ {z} \) |
| 10 | 0,85 |
| 20 | 0,90 |
| 30 | 0,98 |
| 33 | 1,00 \ ({K} _ {zh} \) |
Из уравнения (3) мы можем найти скоростное давление \ (q \) в PSF на каждой рассматриваемой высоте.
Таблица 5.Расчетные значения скоростного напора на каждой высоте возвышения.
| Высота (фут) | \ ({K} _ {z} \) | \ (q \) (psf) | Замечания |
| 10 | 0,85 | 26,63 | 1 этаж |
| 20 | 0,90 | 28,20 | 2 этаж |
| 30 | 0,98 | 30,71 | Карниз крыши |
| 33 | 1.00 | 31,33 | Средняя высота крыши, \ ({q} _ {h} \) |
Коэффициент воздействия порыва, \ (G \), установлен на 0,85, поскольку конструкция считается жесткой (раздел 26.9.1 ASCE 7-10).
Предполагается, что в конструкции завода есть проемы, которые удовлетворяют определению частично закрытого здания в Разделе 26. 2 из ASCE 7-10. Таким образом, коэффициент внутреннего давления \ (({GC} _ {pi}) \) должен составлять +0,55 и -0,55 на основе таблицы 26.11-1 стандарта ASCE 7-10.
2 из ASCE 7-10. Таким образом, коэффициент внутреннего давления \ (({GC} _ {pi}) \) должен составлять +0,55 и -0,55 на основе таблицы 26.11-1 стандарта ASCE 7-10.
Рис. 6. Коэффициент внутреннего давления, \ (({GC} _ {pi}) \), из таблицы 26.11-1 ASCE 7-10.
Коэффициент внешнего давления, \ ({C} _ {p} \)Для закрытых и частично закрытых зданий коэффициент внешнего давления \ ({C} _ {p} \) рассчитывается с использованием информации, представленной на рисунках с 27.4-1 по 27.4-3. Для частично закрытого здания с двускатной крышей используйте Рисунок 27.4-1.
Коэффициенты внешнего давления для стен и крыши рассчитываются отдельно с использованием параметров здания L, B и h, которые определены в примечании 7 к рисунку 27.4-1.
Таким образом, нам нужно рассчитать L / B и h / L:
Средняя высота кровли, h = 33 ′
Длина здания, L = 64 ′
Ширина здания, B = 104 ′
L / B = 0,615
h / L = 0,516
h / B = 0,317
Из этих значений мы можем получить коэффициенты внешнего давления \ ({C} _ {p} \) для каждой поверхности с помощью таблицы 27.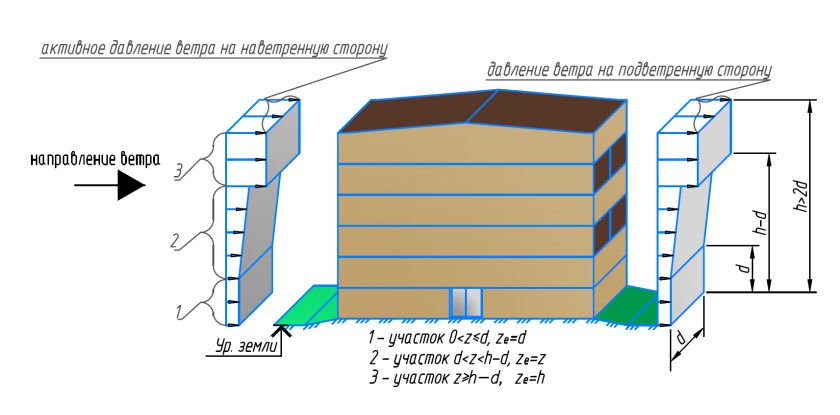 4-1 ASCE 7-10. Обратите внимание, что мы можем использовать линейную интерполяцию, когда значения угла крыши, θ, L / B и h / L находятся между значениями, указанными в таблице. В нашем примере коэффициенты внешнего давления для каждой поверхности показаны в таблицах с 6 по 8.
4-1 ASCE 7-10. Обратите внимание, что мы можем использовать линейную интерполяцию, когда значения угла крыши, θ, L / B и h / L находятся между значениями, указанными в таблице. В нашем примере коэффициенты внешнего давления для каждой поверхности показаны в таблицах с 6 по 8.
Таблица 6. Расчетные коэффициенты внешнего давления для поверхностей стен.
| Поверхность | \ ({C} _ {p} \) |
| Наветренная стена | 0,8 |
| Подветренная стена | -0.5 |
| Боковая стенка | -0,7 |
Таблица 7. Расчетные коэффициенты внешнего давления для поверхностей кровли (ветровая нагрузка по L).
| Коэффициенты внешнего давления для крыши \ ({C} _ {p} \) (вдоль L) | ||||||
| ч / л | Наветренная | Подветренная | ||||
| 10 ° | 10,62 ° | 15 ° | 10 ° | 10,62 ° | 15 ° | |
0. 5 5 | -0,9 -0,18 | -0,88 -0,18 | -0,7 -0,18 | -0,50 | -0,50 | -0,50 |
| 0,516 | -0,91 -0,18 | -0,89 -0,18 | -0,71 -0,18 | -0,51 | -0,51 | -0,50 |
| 1,0 | -1,3 -0,18 | -1,26 -0,18 | -1,0 -0.18 | -0,70 | -0,69 | -0,60 |
Таблица 8. Расчетные коэффициенты внешнего давления для поверхностей кровли (ветровая нагрузка по B).
| Коэффициенты внешнего давления для крыши \ ({C} _ {p} \) (вдоль B) | ||
| h / B | Расположение | \ ({C} _ {p} \) |
| 0,317 | 0 до h | -0,9 -0,18 |
| ч / 2 до ч | -0.9 -0,18 | |
| ч до 2 ч | -0,5 -0,18 | |
| > 2 часа | -0,3 -0,18 | |
Коэффициент внешнего давления с двумя значениями, показанными в таблицах 7 и 8, должен быть проверен для обоих случаев.
Используя уравнение (1), можно рассчитать расчетное давление ветра. Результаты наших расчетов представлены в таблицах 8 и 9 ниже.Обратите внимание, что на структуру будут действовать четыре случая, поскольку мы будем рассматривать давления, решаемые с помощью \ ((+ {GC} _ {pi}) \) и \ ((- {GC} _ {pi}) \), и \ (+ {C} _ {p} \) и \ (- {C} _ {p} \) для крыши.
Таблица 9. Расчетное ветровое давление для поверхностей стен.
| Расчетное давление, \ (p \), для стен | |||||||
| Этаж | \ ({q} _ {z} \), psf | Наветренная | Подветренная сторона | Боковая стенка | |||
| \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | ||
| 10 | 26.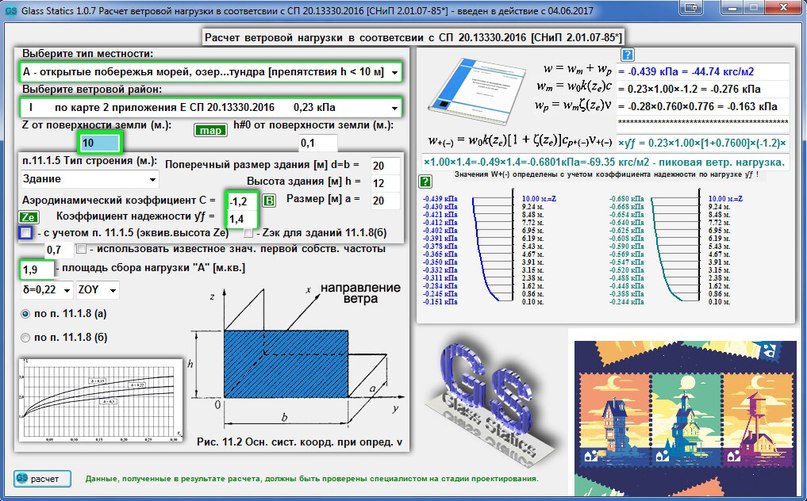 63 63 | 0,88 (0,88) | 35,35 (35,35) | -30,55 (-30,55) | 3,92 (3,92) | -35,88 (-35,88) | -1,41 (-1,41) |
| 20 | 28,20 | 1,94 (1,94) | 36,41 (36,41) | ||||
| 30 | 30,71 | 3,65 (3,65) | 38,12 (38,12) | ||||
| 33 | 31,33 | 4,07 (4,07) | 38,54 (38.54) | ||||
(результаты ветровой нагрузки SkyCiv)
Таблица 10. Расчетное ветровое давление для поверхностей кровли.
| Расчетное давление на крышу, фунт-сила фут (по длине) | Расчетное давление на крышу, фунт-футы (вдоль В) | ||||
| Поверхность | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | Расположение (от наветренной кромки) | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) |
| Наветренный | -40. 87 (-40,87) 87 (-40,87) | -6,41 (-6,40) | 0 до h / 2 | -41,20 (-41,20) | 12,44 (12,44) |
| -22,03 (-22,03) | 12,44 (12,44) | ч / 2 до | ч-41,20 (-41,20) | ||
| подветренная сторона | -30,71 (-30,71) | 3,76 (3,83) | ч. До 2 ч. | -30,55 (-30,55) | |
| > 2 часа | -25,22 (-25,22) | ||||
(результаты ветровой нагрузки SkyCiv)
Чтобы применить эти давления к конструкции, мы рассмотрим одну раму на конструкции.Пример применения случая 1 и 2 (для обоих \ (({GC} _ {pi}) \)) показан на рисунках 7 и 8. Направление ветра, показанное на вышеупомянутых рисунках, соответствует длине L здания. .
Обратите внимание, что положительный знак означает, что давление действует по направлению к поверхности, а отрицательный знак – от поверхности. Длина бухты 26 футов.
Рис. 7. Расчетное давление ветра, приложенное к одной раме – \ ((+ {GC} _ {pi}) \) и случай абсолютного максимального давления на крышу.
Рис. 8. Расчетное давление ветра, приложенное к одной раме – \ ((- {GC} _ {pi}) \) и случай абсолютного максимального давления на крышу.
SkyCiv упрощает эту процедуру, просто определяя параметры. Попробуйте наш SkyCiv Free Wind Tool
Калькулятор ветровой нагрузки SkyCiv
Расчетное давление ветра для компонентов и оболочки (C&C) Компоненты и оболочки определены в главе C26 стандарта ASCE 7-10 следующим образом: «Компоненты принимают ветровые нагрузки напрямую или от облицовки и передают нагрузку на MWFRS», в то время как «облицовка принимает ветровые нагрузки напрямую.Примеры компонентов включают «крепеж, прогоны, стойки, настил крыши и фермы крыши», а для облицовки – «настенные покрытия, навесные стены, кровельные покрытия, наружные окна и т. Д.»
Д.»
Из главы 30 ASCE 7-10 расчетное давление для компонентов и оболочки должно быть рассчитано с использованием уравнения (30.4-1), показанного ниже:
\ (p = {q} _ {h} [({GC} _ {p}) – ({GC} _ {pi})] \) (6)
Где:
\ ({q} _ {h} \): скоростное давление, рассчитанное на средней высоте крыши, h (31.33 psf)
\ (({GC} _ {pi} \)): коэффициент внутреннего давления
\ (({GC} _ {p} \)): коэффициент внешнего давления
Для этого примера \ (({GC} _ {p} \)) будет найден, используя Рисунок 30.4-1 для Зоны 4 и 5 (стены) и Рисунок 30.4-2B для Зоны 1-3 (крыша). . В нашем случае правильное значение зависит от уклона крыши θ, который составляет 7 ° <θ ≤ 27 °. \ (({GC} _ {p} \)) можно определить для множества типов крыш, изображенных на рисунках 30.4-1 - 30.4-7 и 27.4-3 в главах 30 и 27 ASCE 7-10, соответственно.
Мы будем рассчитывать только расчетное давление ветра для прогонов и стоек. Зоны для компонентов и давления оболочки показаны на рисунке 9.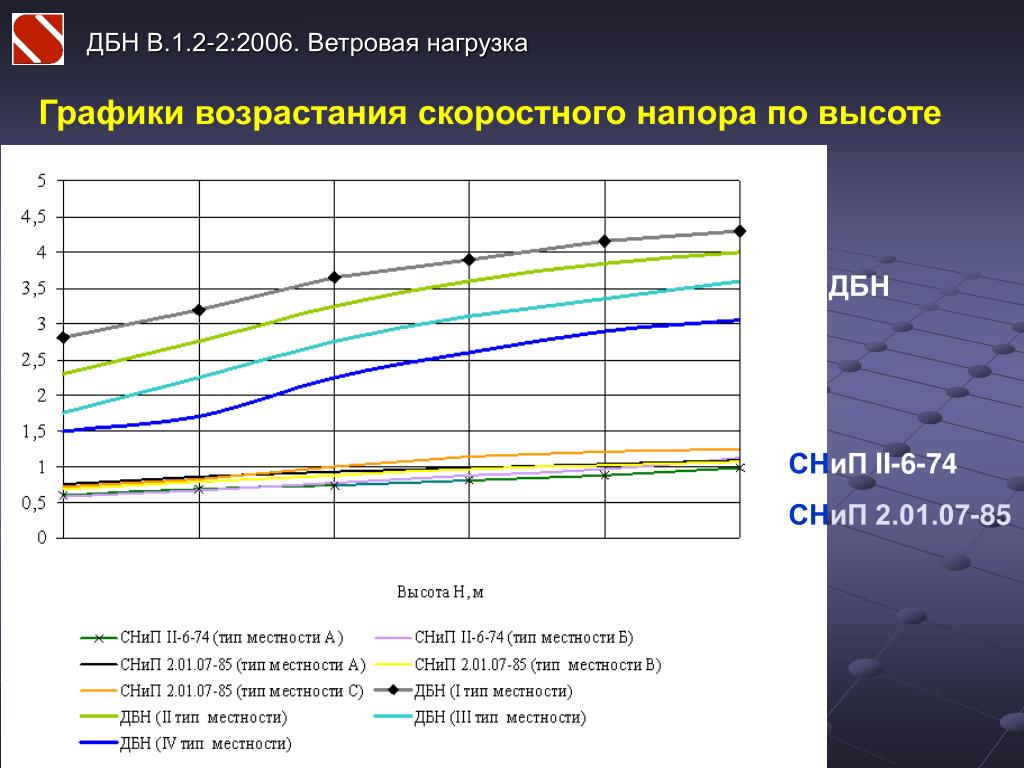
Рисунок 9. Расположение расчетных давлений C&C.
Расстояние a от краев может быть рассчитано как минимум 10% от наименьшего горизонтального размера или 0,4h, но не менее либо 4% от наименьшего горизонтального размера, либо 3 фута.
a: 10% от 64 футов = 6,4 фута> 3 фута
0,4 (33 фута) = 13.2 фута 4% от 64 футов = 2,56 фута
a = 6,4 фута
На основе рисунка 30.4-1, \ (({GC} _ {p} \)) можно рассчитать для зон 4 и 5 на основе эффективной площади ветра. Обратите внимание, что определение эффективной ветровой площади в главе C26 ASCE 7-10 гласит: «Для лучшего приближения к фактическому распределению нагрузки в таких случаях ширина эффективной ветровой площади, используемая для оценки \ (({GC} _ { p} \)) не должно быть меньше одной трети длины области.”Следовательно, эффективная ветровая площадь должна быть максимальной:
Эффективная ветровая зона = 10 футов * (2 фута) или 10 футов * (10/3 фута) = 20 кв. Футов. или 33,3 кв. фута
Футов. или 33,3 кв. фута
Эффективная ветровая площадь = 33,3 кв. фута
Положительные и отрицательные значения \ (({GC} _ {p} \)) для стен можно аппроксимировать, используя график, показанный ниже, как часть рисунка 30.4-1:
Рисунок 10. Приблизительные значения \ (({GC} _ {p} \)) из рисунка 30.4-1 ASCE 7-10.
Таблица 11.Расчетное давление C&C для каркаса стены.
| Зона | \ (+ ({GC} _ {p} \)) | \ (- ({GC} _ {p} \)) | C&C Давление, фунт / кв. Дюйм | |
| \ (+ ({GC} _ {p} \)) | \ (- ({GC} _ {p} \)) | |||
| 4 | 0,90 | -1,0 | 10,97 45,43 | -48,56 -14,10 |
| 5 | 0,90 | -1,2 | 10.97 45,43 | -54,83 -20,36 |
Из 30. 4–2B можно определить эффективное давление ветра для Зон 1, 2 и 3. Поскольку фермы расположены на расстоянии 26 футов, следовательно, это будет длина прогонов. Эффективная ветровая площадь должна быть максимум:
4–2B можно определить эффективное давление ветра для Зон 1, 2 и 3. Поскольку фермы расположены на расстоянии 26 футов, следовательно, это будет длина прогонов. Эффективная ветровая площадь должна быть максимум:
Эффективная ветровая площадь = 26 футов * (2 фута) или 26 футов * (26/3 фута) = 52 кв. Фута или 225,33 кв. Фута.
Эффективная ветровая площадь = 225.33 кв. Фута
Положительные и отрицательные значения \ (({GC} _ {p} \)) для крыши можно аппроксимировать, используя график, показанный ниже, как часть рисунка 30.4-2B:
Рисунок 11. Значения \ (({GC} _ {p} \)) из рисунка 30.4-2B ASCE 7-10.
Таблица 12. Расчетное давление C&C для прогонов.
| Зона | + (GCp) | – (GCp) | C&C Давление, фунт / кв. Дюйм | |
| + (GCpi) | – (GCpi) | |||
| 1 | 0.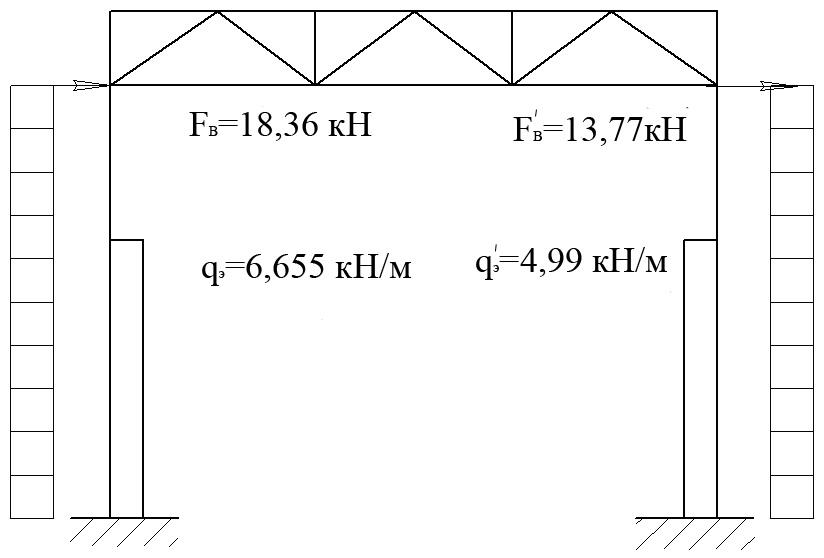 30 30 | -0,80 | -7,83 26,63 | -42,30 -7,83 |
| 2 | 0,30 | -1,2 | -7,83 26,63 | -54,83 -20,36 |
| 3 | 0,30 | -2,0 | -7,83 26,63 | -79,89 -45,43 |
Все эти расчеты могут быть выполнены с использованием программного обеспечения SkyCiv для ветровой нагрузки для ASCE 7-10, 7-16, EN 1991, NBBC 2015 и AS 1170.Пользователи могут войти в местоположение площадки, чтобы получить данные о скорости ветра и факторах топографии, ввести параметры здания и сгенерировать давление ветра. С профессиональной учетной записью пользователи могут автоматически применять это к модели конструкций и выполнять структурный анализ в одном программном обеспечении.
В противном случае, попробуйте наш SkyCiv Free Wind Tool для расчета скорости ветра и давления ветра на простых конструкциях.
Калькулятор ветровой нагрузки SkyCiv
Патрик ГарсияИнженер-конструктор, разработка продуктов
BEng (Гражданский)
Каталожные номера:
- Мехта, К.К., и Коулбурн, У. Л. (2013, июнь). Ветровые нагрузки: Руководство по положениям о ветровой нагрузке ASCE 7-10. Американское общество инженеров-строителей.
- Минимальные расчетные нагрузки для зданий и других конструкций. (2013). ASCE / SEI 7-10. Американское общество инженеров-строителей.
Как рассчитать ветровую нагрузку на основе скорости ветра
Обновлено 30 марта 2020 г.
Ли Джонсон
Проверено: Lana Bandoim, B.S.
Все наружные конструкции должны выдерживать силу ветра, поэтому возможность расчета ветровой нагрузки имеет решающее значение при проектировании зданий.Однако расчеты усложняются, если учесть большее количество факторов. Это означает, что для наиболее точного расчета ветровой нагрузки часто лучше использовать онлайн-калькулятор (см. Ресурсы), который учитывает все соответствующие факторы при наличии достаточных исходных данных.
Ресурсы), который учитывает все соответствующие факторы при наличии достаточных исходных данных.
Если вы просто ищете базовое представление о том, как рассчитать ветровую нагрузку на основе скорости ветра, вы можете выполнить быстрый расчет для приблизительной оценки.
Что такое ветровая нагрузка?
Ветровая нагрузка – это мера силы, действующей на поверхность ветром, которая может быть выражена как сила, действующая на всю поверхность, или давление (которое является просто силой на единицу площади).Следовательно, единицей измерения ветровой нагрузки в системе СИ являются Ньютоны или Паскали. Фактически, существует три типа сил, которые ветер оказывает на среднюю конструкцию: подъемная нагрузка, поперечная нагрузка и поперечная нагрузка.
Подъемная нагрузка – это подъемный эффект, оказываемый на крышу за счет прохождения воздуха вокруг нее (аналогично подъемной силе на крыльях самолета). Сдвигающая нагрузка – это горизонтальное давление, которое может наклонить здание. Наконец, боковая нагрузка больше похожа на широкое «толкание», которое может сдвинуть конструкцию с фундамента.
Сдвигающая нагрузка – это горизонтальное давление, которое может наклонить здание. Наконец, боковая нагрузка больше похожа на широкое «толкание», которое может сдвинуть конструкцию с фундамента.
В данной статье основное внимание будет уделено поперечной нагрузке, поскольку расчеты для остальных более сложны и необходимо учитывать множество различных переменных.
Калькулятор скорости ветра для расчета силы
Простейшая формула для определения ветровой нагрузки использует скорость ветра для определения величины силы, которую он оказывает. Необходимая вам формула:
Здесь ρ – плотность воздуха (которая зависит от высоты и температуры, но может быть принята равной 1.2 кг / м 3 на уровне моря и температуре 15 градусов Цельсия), v – скорость ветра, а A – это область, где дует ветер. Таким образом, это уравнение представляет собой преобразователь скорости ветра в силу, но вы можете разделить его на площадь, чтобы получить ветровую нагрузку как давление, основанное на скорости ветра.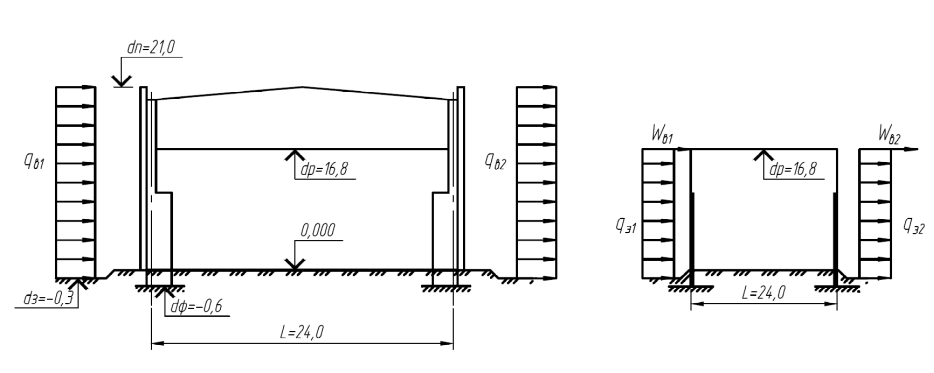
Задача использования этого уравнения заключается в нахождении значений плотности воздуха в вашем районе и точном измерении скорости ветра, которую вам необходимо вычислить (поскольку наивысшая скорость ветра определяет, сколько ветровой нагрузки требуется конструкции. чтобы выдержать).Область A достаточно легко найти для правильных форм. Например, для плоской прямоугольной поверхности вы просто умножаете ширину на высоту, чтобы найти площадь.
Добавление коэффициентов сопротивления
Если вам нужно рассчитать силу (или давление) ветра на неровной поверхности, учет эффекта сопротивления более важен. В то время как для плоской пластины вы можете использовать коэффициент лобового сопротивления, равный 1 (поэтому он не имеет значения для приведенной выше формулы), для цилиндра (например) коэффициент 0.67 учитывает уменьшенное воздействие ветра на поверхность.
Вы просто добавляете этот коэффициент в правую часть приведенного выше уравнения. Вы можете найти стандартные значения коэффициентов для наиболее распространенных форм и структур в таблицах.
Вы можете найти стандартные значения коэффициентов для наиболее распространенных форм и структур в таблицах.
Другие факторы
К сожалению, существует многих других факторов, которые влияют на ветровую нагрузку на данную поверхность, включая изменение скорости ветра с высотой, точные свойства поверхности (например, гладкое стекло по сравнению с текстурированной поверхностью) и возможное влияние окружающих конструкций на скорость ветра.
Таким образом, выполнение точных расчетов для вашей конструкции будет более сложным процессом, чем кажется в этой статье, и вам понадобится гораздо больше, чем просто скорость ветра и плотность воздуха, чтобы найти надежный ответ.
Калькулятор ветровой нагрузки | Какую силу производит ветер?
Калькулятор ветровой нагрузки позволяет вычислить силу ветра на любой конструкции . Будь то крыша, знак или стальная конструкция, с помощью этого калькулятора силы ветра вы можете определить создаваемое на ней давление ветра в зависимости от скорости ветра, помогая вам убедиться, что она достаточно прочная, чтобы выдержать даже самый сильный шторм.
Ветер: друг и враг
Каждый раз, когда люди возводят сооружение, против природы разгорается вечная битва за то, чтобы оно сохранилось. Эрозия постепенно разрушает наши конструкции, крыши рушатся под тяжестью снега, а наводнения и пожары могут свести на нет дело вашей жизни за секунды.
Но один из самых разрушительных элементов – это тот, на который мы упорно полагаемся для нашего выживания: воздух. Только в 2019 году ураганы нанесли ущерб на сумму более 40 миллиардов долларов и многочисленные отключения электроэнергии. Чрезмерная ветровая нагрузка на крыши разрушает здания и угрожает жизни.Но не волнуйтесь, этот калькулятор силы ветра поможет вам оценить ветровую нагрузку, оказываемую на любую конструкцию, в зависимости от скорости ветра и площади поверхности конструкции. Таким образом, вы можете убедиться, что нестабильная крыша, окно или вывеска угрожают вашим близким и вашей собственности.
И, возможно, будучи уверенным в том, что ветер не причинит вам вреда, вы можете использовать его и создавать экологически чистую, экологически чистую и дешевую энергию с помощью собственной ветряной турбины. Или используйте его для забавных упражнений, таких как виндсерфинг или даже более сложный кайтсерфинг.
Или используйте его для забавных упражнений, таких как виндсерфинг или даже более сложный кайтсерфинг.
Какая ветровая нагрузка действует на конструкцию?
Сила, с которой частицы воздуха сталкиваются с поверхностью, называется ветровой нагрузкой на определенную конструкцию. Чтобы рассчитать точную силу, нам нужно больше информации о ветре и конструкции:
Молекулы воздуха, сталкивающиеся с объектом, создают динамическое давление, зависящее от скорости ветра и плотности воздуха . Плотность воздуха зависит от влажности, температуры и давления.В этом калькуляторе мы принимаем значение по умолчанию 1,225 кг / м3 / 0,0765 фунт / кв. Дюйм, что эквивалентно температуре 15 ° C / 59 ° F на уровне моря. Эти условия известны как стандартные температура и давление (STP). Если вы живете в месте со значительно отличающимися условиями, мы рекомендуем использовать калькулятор плотности воздуха, чтобы определить вашу плотность воздуха и соответствующим образом скорректировать значение в этом калькуляторе.

Ветровая нагрузка также зависит от эффективной площади вашей конструкции .Эффективная поверхность – это поверхность, перпендикулярная направлению ветра. В предположении, что ветер всегда параллелен горизонту, мы можем вычислить эффективную поверхность из общей поверхности и угла . Например, поверхность под углом 90 ° к земле испытывает гораздо большую ветровую нагрузку, чем крыша с уклоном 45 °, даже если скорость ветра и площадь поверхности одинаковы.
С учетом всех этих факторов калькулятор давления ветра определяет динамическое давление и ветровую нагрузку:
Динамическое давление = 0.5 * Плотность воздуха * Скорость ветра²
Ветровая нагрузка = Динамическое давление * Эффективная поверхность = Динамическое давление * Общая площадь * sin (угол)
Как пользоваться калькулятором ветровой нагрузки?
Здесь мы покажем вам, как использовать калькулятор ветровой нагрузки.
Установите характеристики ветра, а именно скорость ветра и плотность воздуха. Плотность воздуха по умолчанию должна быть адекватной, если вы не живете в очень жарком, холодном или возвышенном месте. В этом случае вы можете определить плотность воздуха с помощью инструмента, связанного с полем плотности воздуха в калькуляторе, и соответствующим образом изменить значение.
Введите важные значения вашей конструкции: общую площадь поверхности и угол. Если у вас есть проблемы с определением площади вашей конструкции, вам может помочь калькулятор площади. Угол между горизонтом и вашей структурой, так что это уклон для крыши.
После этого калькулятор силы ветра предоставит вам ожидаемое давление ветра. Таким образом, вы можете оценить ветровую нагрузку на вашу крышу и безопасно спланировать постройку без риска обрушения из-за шторма.
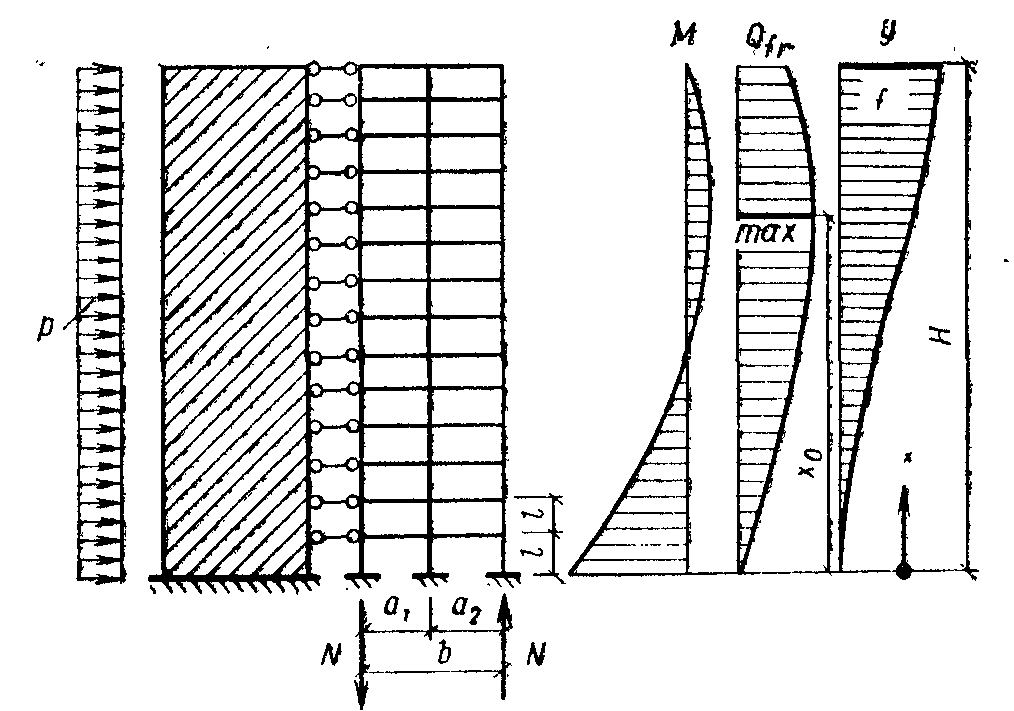
Расчеты ветровых нагрузок – Руководство по конструкции
Расчеты ветровых нагрузок в соответствии с CP 3: Глава V-2: 1972 Для анализа стриктур на воздействие ветра во всем мире используются различные коды. CP 3: Глава V – это старый код, используемый для расчета ветровых нагрузок на конструкцию. Если мы сослались на новые коды и сравнили их с этим кодом, это не показывает большой разницы. Однако этот код нельзя использовать для анализа структуры на предмет динамических действий.С помощью этого кода нельзя найти ускорения, вызываемые ветром, и его ограничения. Этот код можно использовать для общего назначения.
CP 3: Глава V – это старый код, используемый для расчета ветровых нагрузок на конструкцию. Если мы сослались на новые коды и сравнили их с этим кодом, это не показывает большой разницы. Однако этот код нельзя использовать для анализа структуры на предмет динамических действий.С помощью этого кода нельзя найти ускорения, вызываемые ветром, и его ограничения. Этот код можно использовать для общего назначения.
Давление ветра можно рассчитать по следующему уравнению.
P = CqA
Где C = Cpi -Cpe
q = Давление ветра
A = Площадь притока
Давление ветра рассчитывается с учетом скорости ветра на площадке.
q = kVz 2
K зависит от страны. Значение указывается в коде или может использоваться другое подходящее значение.
Нам нужно объединить коэффициенты ветрового давления при расчете нагрузок. Однако не всегда удается совместить коэффициент ветрового давления, полученный для наветренной и рычажной сторон. Например, когда вы рассчитываете давление ветра в здании, мы должны учитывать внутреннее давление.
Если мы планируем безнадежно применять нагрузку отдельно для наветренной и левой сторон, мы рассчитываем ветровую нагрузку отдельно, комбинируя каждый коэффициент давления с коэффициентом внутреннего давления.
Коэффициент внутреннего давления может изменяться. Как правило, у него есть фиксированные значения. Это могло быть положительно или отрицательно. Рассмотрим расчет ветровой нагрузки с наветренной стороны. Скажем, коэффициент внешнего давления равен +0,7, а коэффициент внутреннего давления -0,3 и +0,2 (для здания с незначительной вероятностью возникновения доминирующих отверстий во время сильного шторма).
Тогда коэффициент ветрового давления будет следующим.
0,7 – (-0,3) = 1,0 или
0,7 – 0,2 = 0,7
Давление ветра можно рассчитать с учетом обоих.Аналогичным образом можно рассчитать коэффициент давления на другой стороне.
Скажем, коэффициент давления с рычагом равен -0,5
-0,5 – (-0,3 = -0,2
-0,5 – 0,2 = -0,7
Теперь мы можем применить нагрузку после расчета давления.
Случай 01
Коэффициент давления наветренный 1,0
Коэффициент давления Leaved -0,2
Случай 02
Коэффициент давления Наветренный 0,7
Коэффициент давления Наружный -0,7
Таким образом, мы можем рассчитать давление ветра на каждой стороне конструкции.{3}} \) – и \ (v \) – скорость ветра (обычно максимальное значение, зарегистрированное в месте расположения здания), а \ (C_D \) – коэффициент лобового сопротивления, который зависит от формы здания. и обычно дается строительными нормами.
Хотя этот расчет всегда требуется по закону в сочетании с указанным коэффициентом безопасности, он включает несколько упрощений:
- Коэффициент сопротивления \ (C_D \) только предполагаемый, а не рассчитанный на самом деле , он может существенно варьироваться в зависимости от формы здания, и это трудно узнать из таблиц, поскольку каждая форма здания индивидуальна.
- Предполагается, что давление на здание является постоянным , на самом деле оно меняется по высоте здания и в большинстве случаев поднимается к вершине конструкции, поэтому в действительности плечо рычага ветровой нагрузки выше, чем предполагалось в предыдущем уравнении.

- Он не принимает во внимание форму местности и наличие других зданий вокруг расчетной конструкции, которые потенциально могут повлиять на поток и, в конечном итоге, на уровень нагрузки на основную конструкцию.
- Предполагается постоянное направление ветра без учета экстремальной угловатости потока, возникающей в результате шторма, и их взаимодействия с формой здания.
Хотя стоит подчеркнуть, что вышеупомянутый расчет должен быть выполнен для соответствия соответствующим строительным нормам, важно дополнить его специальным анализом вычислительной гидродинамики (CFD), который позволяет оценить ветровая нагрузка с точки зрения сил и моментов без перечисленных выше ограничений.Можно выполнить как расчет ветровой нагрузки на основе формулы, требуемой строительными нормами, так и использовать модель CFD для проверки результатов, что дает повышенную уверенность в оценке структурной целостности здания.
Оценка ветровой нагрузки и параметров конструкции на основе неполных измерений
Подход несмещенной оценки с расширенной минимальной дисперсией может использоваться для совместной оценки состояния / параметра / входных данных на основе измеренных откликов конструкции. Однако необходимо измерить реакцию конструкции на смещение и ускорение на каждом этаже для одновременной идентификации параметров конструкции и неизвестной ветровой нагрузки. Предлагается новый метод определения структурного состояния, параметров и неизвестной ветровой нагрузки по неполным измерениям. Оценка выполняется в модальном режиме с расширенной минимальной дисперсией без смещения, основанном на неполных измерениях реакции на смещение конструкции и ускорение, вызванное ветром. Выполнимость и точность предложенного метода подтверждены численно путем определения ветровой нагрузки и параметров конструкции на десятиэтажной конструкции сдвигового здания с неполными измерениями.Обсуждается влияние решающих факторов, включая продолжительность выборки и количество измерений. Кроме того, практическое применение разработанного обратного метода оценивается по результатам испытаний в аэродинамической трубе конструкции здания высотой 234 м. Результаты показывают, что с помощью предложенного подхода можно точно идентифицировать структурное состояние, параметры и неизвестную ветровую нагрузку.
Однако необходимо измерить реакцию конструкции на смещение и ускорение на каждом этаже для одновременной идентификации параметров конструкции и неизвестной ветровой нагрузки. Предлагается новый метод определения структурного состояния, параметров и неизвестной ветровой нагрузки по неполным измерениям. Оценка выполняется в модальном режиме с расширенной минимальной дисперсией без смещения, основанном на неполных измерениях реакции на смещение конструкции и ускорение, вызванное ветром. Выполнимость и точность предложенного метода подтверждены численно путем определения ветровой нагрузки и параметров конструкции на десятиэтажной конструкции сдвигового здания с неполными измерениями.Обсуждается влияние решающих факторов, включая продолжительность выборки и количество измерений. Кроме того, практическое применение разработанного обратного метода оценивается по результатам испытаний в аэродинамической трубе конструкции здания высотой 234 м. Результаты показывают, что с помощью предложенного подхода можно точно идентифицировать структурное состояние, параметры и неизвестную ветровую нагрузку.
1. Введение
Ветровая нагрузка является одной из основных нагрузок на этапе проектирования высотных зданий [1, 2].Исследования показывают, что ветровая нагрузка на высокое здание варьируется в зависимости от состояния местности, формы здания и окружающих зданий [3]. В большинстве процессов проектирования ветровая нагрузка рассчитывается согласно нормам проектирования [4, 5]. Однако трудно рассчитать временные характеристики ветровой нагрузки на основе проектных кодов, поскольку расчетные нормы ветровой нагрузки определяются на основе статистической информации. Испытания в аэродинамической трубе и компьютерное гидродинамическое моделирование в настоящее время используются для определения изменяющейся во времени ветровой нагрузки на данную конструкцию [6, 7].Однако ни один из методов не может точно воспроизвести наблюдающуюся турбулентность и характеристики окружающих зданий. Полевые измерения считаются наиболее точным способом получения изменяющейся во времени ветровой нагрузки на высокие здания. Однако из-за ограничений метода измерения ветровой нагрузки измерение ветровой нагрузки в реальном времени затруднено полевыми измерениями. По сравнению с измерением ветровой нагрузки измерение смещения и ускорения, вызванного ветром, проще и точнее.
Однако из-за ограничений метода измерения ветровой нагрузки измерение ветровой нагрузки в реальном времени затруднено полевыми измерениями. По сравнению с измерением ветровой нагрузки измерение смещения и ускорения, вызванного ветром, проще и точнее.
В последние годы было разработано множество методов оценки силы [8–10]. Law et al. идентифицировала ветровую нагрузку на 50-метровую мачту с оттяжками на основе откликов конструкции путем регуляризации уравнения идентификации [11]. Лу и Лоу предложили метод определения неизвестной нагрузки с использованием мер чувствительности динамического отклика по отношению к входной нагрузке [12]. Лю и Шепард разработали метод динамической идентификации сил, основанный на подходе расширенных наименьших квадратов в частотной области [13].Ma et al. представили метод фильтра Калмана с рекурсивной оценкой для определения неизвестного возбуждения [14, 15]. Вышеупомянутые подходы требуют, чтобы неизвестная нагрузка была, как правило, точечной нагрузкой, действующей при определенной степени свободы. Однако ветровые нагрузки, действующие на строительную конструкцию, меняются в зависимости от пространства и времени, и методы, описанные в предыдущих работах, нельзя напрямую использовать для определения ветровой нагрузки на строительные конструкции.
Однако ветровые нагрузки, действующие на строительную конструкцию, меняются в зависимости от пространства и времени, и методы, описанные в предыдущих работах, нельзя напрямую использовать для определения ветровой нагрузки на строительные конструкции.
Для решения вышеупомянутой проблемы Hwang et al. предложил подход фильтрации Калмана в модальной области для оценки модальных нагрузок на конструкцию с использованием ограниченного измеренного отклика [16, 17].Zhi et al. разработали метод фильтрации Калмана и подходящую технику ортогональной декомпозиции для оценки модальной ветровой нагрузки на высокие здания [18, 19]. В 2007 году Гиллинс и Мур предложили подход для совместной оценки входного состояния в динамической системе с дискретным временем, основанный на несмещенном решении с минимальной дисперсией [20]. Lourens et al. применил этот метод для оценки структурных откликов и неизвестных входов как в численных, так и в экспериментальных исследованиях [21]. Этот метод не требует никаких предположений или предварительных знаний о неизвестных входных данных, и его можно использовать для идентификации ветровой нагрузки в физической области [22]. К сожалению, вышеупомянутые подходы к оценке ветровой нагрузки предполагали, что параметры конструкции известны априори. Однако для реальных строительных конструкций структурные параметры обычно определяются на основе модели конечных элементов, и трудно точно рассчитать структурные параметры из-за старения материала и повреждения конструкций.
К сожалению, вышеупомянутые подходы к оценке ветровой нагрузки предполагали, что параметры конструкции известны априори. Однако для реальных строительных конструкций структурные параметры обычно определяются на основе модели конечных элементов, и трудно точно рассчитать структурные параметры из-за старения материала и повреждения конструкций.
Для решения этой проблемы Wan et al. предложил метод под названием EGDF, который является расширением несмещенной оценки минимальной дисперсии для связанной идентификации состояния / входа / параметра для нелинейных систем в пространстве состояний [23].Сонг разработал метод совместной оценки входного состояния для совместной оценки входного параметра состояния, основанный на методе оценки несмещенной минимальной дисперсии без оценки (UMVU) [24]. Однако методы EGDF и UMVU требуют, чтобы необходимо измерять реакции ускорения в местах, где применяются неизвестные входные данные, то есть требуются полные измерения ускорения на всех степенях свободы для одновременной оценки ветровой нагрузки и неизвестных параметров конструкции.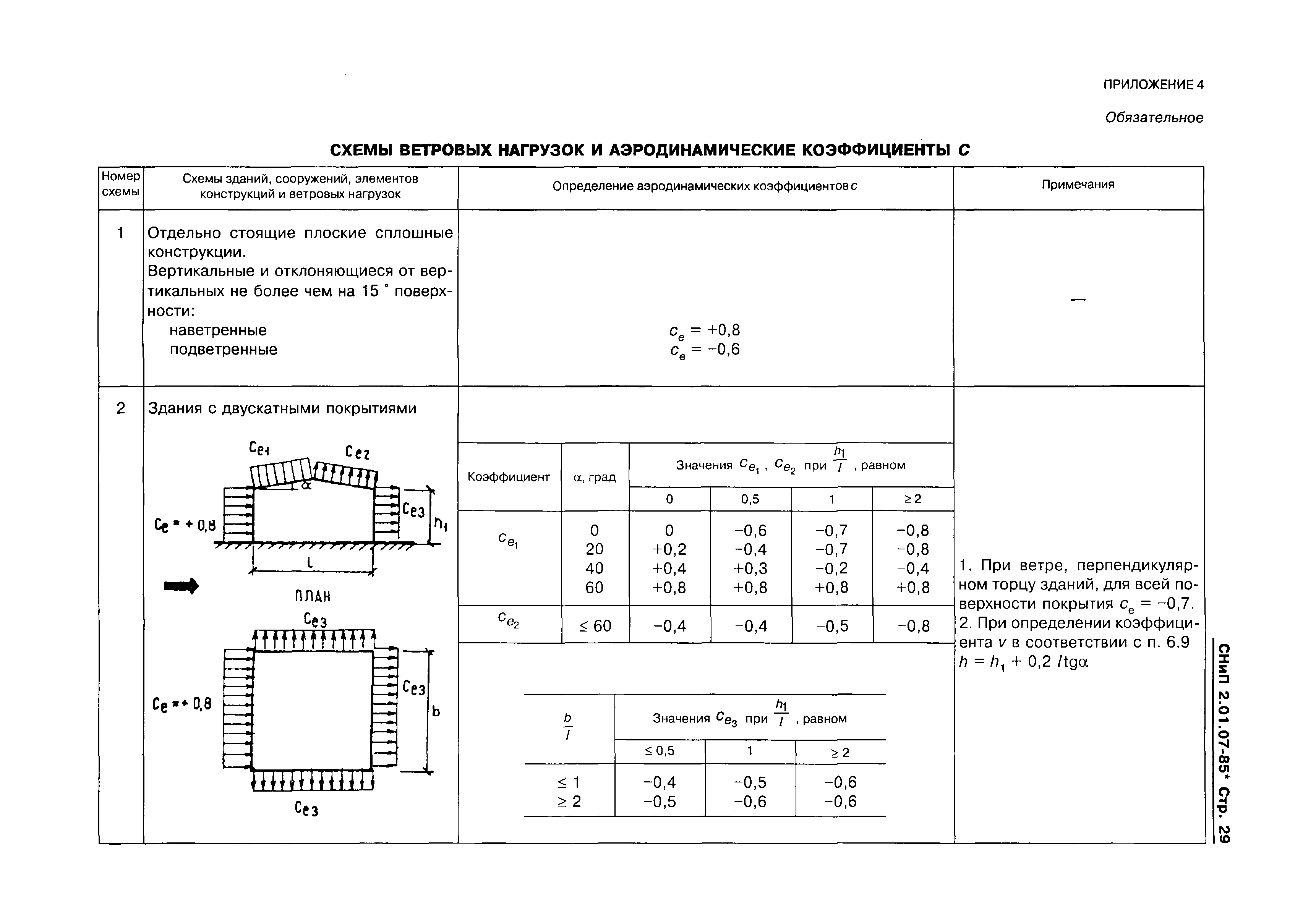
В этом исследовании предлагается новый метод модальной расширенной несмещенной оценки минимальной дисперсии для совместной оценки состояния / параметра / ветровой нагрузки по неполным измерениям.Предлагаемый метод позволяет одновременно оценивать ветровые нагрузки и параметры конструкции без использования полных измерений ускорения. Более того, слияние данных реакций ускорения и откликов на межэтажные смещения используется для предотвращения дрейфов выявленных откликов смещений и ветровых нагрузок. Содержание статьи организовано следующим образом. В разделе 2 выводится предлагаемый метод модальной расширенной несмещенной оценки минимальной дисперсии и даются необходимые математические доказательства.В Разделе 3 рассматривается численная проверка путем определения ветровых нагрузок и параметров конструкции из неполных измерений на десятиэтажной конструкции здания, работающей на сдвиг. Кроме того, обсуждается влияние ключевых факторов, включая продолжительность выборки и количество измерений. В разделе 4 проводится испытание в аэродинамической трубе синхронной системы сканирования с несколькими давлениями на строительной конструкции высотой 234 м для проверки предложенного метода. Чтобы упростить расчет, для подтверждения эксперимента выполняется эквивалентная модель.Наконец, в разделе 5 подведены итоги обсуждения и заключения.
В разделе 4 проводится испытание в аэродинамической трубе синхронной системы сканирования с несколькими давлениями на строительной конструкции высотой 234 м для проверки предложенного метода. Чтобы упростить расчет, для подтверждения эксперимента выполняется эквивалентная модель.Наконец, в разделе 5 подведены итоги обсуждения и заключения.
2. Несмещенная оценка расширенной модальной минимальной дисперсии
2.1. Модель системы
Уравнение движения конструкции здания со степенью свободы n может быть записано следующим образом: где, и – матрицы массы, демпфирования и жесткости конструкции, соответственно; – вектор ветровой нагрузки; “ – ветровые ускорение, скорость и вектор смещения соответственно.
На основе теории преобразования модальных координат [25] вектор структурного смещения может быть получен следующим образом: где – нормализованная по массе матрица модальной формы, а – вектор модального смещения.Путем предварительного умножения и использования уравнения (2) уравнение (1) может быть записано следующим образом: где – модальная матрица масс, – модальная матрица демпфирования, – модальная матрица жесткости и – модальный вектор ветровой нагрузки.
Для системы с пропорциональным демпфированием можно получить следующее: где – собственная частота демпфирования и , а – модальный коэффициент демпфирования i .
Уравнение (3) можно переписать следующим образом:
В общем, из-за ограничения количества и расположения датчиков дается сокращенное представление уравнения (6): где, и – первые m Модальное ускорение порядка , модальная скорость и вектор модального смещения соответственно.а также .
Расширенный вектор состояния состоит из модального смещения, модальной скорости и неизвестных структурных параметров: где обозначает неизвестный вектор структурных параметров. – это и -й коэффициент жесткости конструкции. α и β – коэффициенты затухания Рэлея. Предполагая, что неизвестные структурные параметры не зависят от времени, дифференциальное уравнение первого порядка уравнения (8) может быть получено следующим образом: где – нелинейная функция, состоящая из вектора состояния, вектора модальной ветровой нагрузки и времени t .
Обозначьте это с как интервал выборки и определите и как оценочные значения и в момент времени, соответственно. Учитывая технологический шум, линеаризованное выражение уравнения (9) может быть выражено следующим образом: где – вектор технологического шума с нулевым средним и ковариационной матрицей.
Кроме того, получается следующее [26]:
Подставляя в левую часть уравнения (9), можно получить уравнение пространства состояний:
Измеряются только частичные реакции смещения и ускорения, вызванные ветром.Вектор измерения выражается следующим образом: где обозначает реакции смещения, вызванные ветром, и обозначает реакции ускорения, вызванные ветром.
Используя теорию модального преобразования координат, уравнение измерения на временном шаге k может быть выражено следующим образом: где обозначает межэтажные смещения, является матрицей отображения, связанной с степенями свободы измеренного смещения, и является матрицей отображения связанные с степенями свободы измеренного ускорения.
Кроме того, получается следующее:
С учетом шума измерения линеаризованное уравнение измерения может быть выражено следующим образом: где – вектор шума измерения на временном шаге k- с нулевым средним и ковариацией.
Далее получается: где
2.2. Собственное значение и чувствительность собственного вектора
Изменения собственных значений и собственных векторов системы из-за изменений в параметрах системы используются для вычисления матрицы и.Для этого случая в качестве неизвестных параметров выбраны коэффициент жесткости конструкции и коэффициент демпфирования. Проблема собственных значений систем с пропорциональным демпфированием может быть решена согласно [27] следующим образом: где – собственное значение l , – собственный вектор l , а – неизвестный параметр j . Предполагая, что режимы m используются для совместной оценки входных параметров состояния для n -степеней свободы, производная собственного вектора может быть вычислена на основе метода Ванга [28], как показано в следующем уравнении: где
Таким образом, производная матрицы собственных значений с учетом структурного параметра может быть получена на основе уравнения (19):
Чувствительность матрицы собственных векторов к параметру может быть задана в соответствии с уравнением (20):
Производная демпфирования Затем матрица, зависящая от структурного параметра, может быть рассчитана следующим образом:
Для данного случая собственная частота и коэффициент демпфирования выбираются в качестве неизвестных параметров. Собственное значение и чувствительность собственного вектора могут быть вычислены на основе [29] следующим образом:
Собственное значение и чувствительность собственного вектора могут быть вычислены на основе [29] следующим образом:
В соответствии с уравнением (4) может быть получено следующее уравнение: в котором находится диагональный элемент l в матрице.
Затем производная матрицы демпфирования, зависящая от модального параметра, может быть вычислена следующим образом:
Затем производная матрицы собственных значений с учетом модального параметра может быть получена на основе уравнения (25):
Чувствительность матрицы собственных векторов модальному параметру можно указать:
2.3. Несмещенная оценка модальной расширенной минимальной дисперсии
2.3.1. Обновление времени
Обновление времени для прогнозируемой оценки состояния во время может быть вычислено согласно уравнению (12) следующим образом:
Согласно уравнениям (10) и (31) ошибка прогнозируемой оценки состояния может быть вычислена как следует: где матрицы коэффициентов и. и – ошибки оценки состояния и модальной ветровой нагрузки во времени, соответственно.
и – ошибки оценки состояния и модальной ветровой нагрузки во времени, соответственно.
Ковариационная матрица, относящаяся к прогнозируемой оценке состояния, затем может быть выражена следующим образом: где,, и.
2.3.2. Оценка модальной ветровой нагрузки
Определяя нововведение в соответствии с уравнением (16), можно получить следующее уравнение: где ошибка определяется следующим уравнением:
В несмещенном виде из уравнения (35) следует, что, и следовательно, согласно уравнению (34), может быть получено. Предположим, что форма расчетной модальной ветровой нагрузки имеет следующий вид:
Следовательно, можно получить. Это указывает на то, что расчетная модальная ветровая нагрузка несмещена тогда и только тогда, когда удовлетворяет.
Согласно уравнению (35) ковариация ошибки может быть получена следующим образом:
Обычно, где c – положительное действительное число. Это указывает на то, что уравнение (34) не удовлетворяет гомоскедастичности. Следовательно, оценка, приведенная в уравнении (36), не является оценкой минимальной дисперсии модальной ветровой нагрузки в соответствии с теоремой Гаусса – Маркова [30].
Следовательно, оценка, приведенная в уравнении (36), не является оценкой минимальной дисперсии модальной ветровой нагрузки в соответствии с теоремой Гаусса – Маркова [30].
Для получения несмещенной оценки минимальной дисперсии модальной ветровой нагрузки необходимо определить оптимальное значение матрицы в уравнении (36).Предположим, что ковариационная матрица в уравнении (37) положительно определена (т.е.), обратимая матрица может быть найдена. Путем умножения на уравнение (34) можно получить следующее уравнение:
Теперь ковариация, которая удовлетворяет гомоскедастичности. В предположении, что столбец имеет полный ранг, тогда несмещенная оценка минимальной дисперсии может быть получена на основе теоремы Гаусса – Маркова [30] следующим образом:
Следовательно, получается оптимальное значение:
Ошибка оценки модального ветра нагрузка может быть задана на основе уравнений (36) и (39):
Согласно уравнению (41) ковариационная матрица, относящаяся к расчетной модальной ветровой нагрузке, рассчитывается следующим образом:
2.
 3.3. Обновление измерений
3.3. Обновление измеренийОпределите окончательную форму обновленной оценки состояния следующим образом: где – матрица усиления. Ошибка обновленной оценки состояния может быть вычислена в соответствии с уравнениями (12) и (43):
Следовательно, что указывает на несмещенность для всех возможных, если и только если
На основе уравнений (44) и (45) , ковариационная матрица, относящаяся к обновленной оценке состояния, может быть получена следующим образом:
Для получения несмещенной оценки минимальной дисперсии состояния необходимо определить оптимальное значение матрицы усиления.На основе метода множителей Лагранжа [31] оптимальная матрица усиления может быть вычислена путем минимизации следа при несмещенном условии, показанном в уравнении (45): где
Подставляя уравнение (47) в (43), несмещенный минимум Оценка дисперсии состояния может быть рассчитана следующим образом:
Аналогичным образом, подставив уравнение (47) в (46), ковариационная матрица, связанная с, может быть выражена следующим образом:
На основе уравнений (41) и (44) ковариация матрицы и могут быть получены следующим образом:
Теперь предполагаемый отклик на смещение, отклик на скорость, параметры конструкции и ветровую нагрузку во времени можно рассчитать следующим образом: где, и – оценка отклика на модальное смещение, отклика на модальную скорость и конструктивные параметры, соответственно, полученные из государственной оценки.
3. Численное моделирование
Для проверки осуществимости и точности предложенного метода рассматривается десятиэтажная конструкция здания, работающая на сдвиг и подверженная ветровой нагрузке. Массовый коэффициент каждого этажа равен, а коэффициент жесткости каждого этажа равен. Предполагается, что демпфирование является демпфированием Рэлея, которое рассчитывается как с пропорциональными коэффициентами и. Соответствующий коэффициент демпфирования для первых двух режимов вибрации составляет приблизительно 5%.
Колебание скорости ветра численно моделируется на основе метода авторегрессионной модели.Спектральная плотность мощности является спектральной по Давенпорту. Вертикальный профиль ветра принимается в качестве профиля мощности с показателем степени и базовой высотой в соответствии с Национальным кодексом нагрузки Китая [32]. Средняя скорость ветра на опорной высоте составляет. На рис. 1 показаны смоделированные колебания скорости ветра на пятом и десятом этажах. На рисунке 2 показано сравнение спектральной плотности мощности между смоделированными колебаниями скорости ветра и спектральным спектром Давенпорта на пятом и десятом этажах. На рис. 2 показано, что смоделированная спектральная плотность мощности очень хорошо согласуется со спектральной характеристикой Давенпорта.Ветровая нагрузка, действующая на конструкцию здания, рассчитывается согласно [22]. Плотность воздуха принята равной. Коэффициент лобового сопротивления установлен равным 1,3, а площадь ортогонального открытого ветра каждого этажа – равной.
На рисунке 2 показано сравнение спектральной плотности мощности между смоделированными колебаниями скорости ветра и спектральным спектром Давенпорта на пятом и десятом этажах. На рис. 2 показано, что смоделированная спектральная плотность мощности очень хорошо согласуется со спектральной характеристикой Давенпорта.Ветровая нагрузка, действующая на конструкцию здания, рассчитывается согласно [22]. Плотность воздуха принята равной. Коэффициент лобового сопротивления установлен равным 1,3, а площадь ортогонального открытого ветра каждого этажа – равной.
3.1. Совместное состояние / Параметр / Оценка ветровой нагрузки на основе неполных измерений
В этом разделе межэтажное смещение и ускорение, взятые в качестве «измерений», рассчитываются на основе метода Newmark- β и накладываются на 2% среднеквадратичное значение (RMS). ) белый шум.Для оценки используются только семь наборов измерений, включая семь ускорений и семь межэтажных смещений. Места проведения измерений указаны в таблице 1.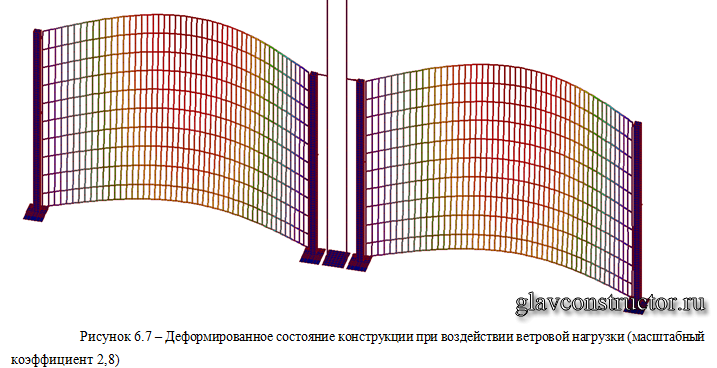 Неизвестными структурными параметрами являются коэффициенты жесткости конструкции на каждом этаже и два коэффициента демпфирования Рэлея. Начальное значение расширенного вектора состояния, где. Матрица начальной ковариации ошибок расширенного вектора состояния равна. Ковариационная матрица шума технологического процесса равна, а ковариационная матрица шума измерения равна.На рисунке 3 показано сравнение расчетных откликов на смещение конструкции с точными значениями на пятом и десятом этажах для временной и частотной областей. На рисунке 4 показано сравнение расчетных скоростных характеристик конструкции с точными значениями на пятом и десятом этажах для временной и частотной областей. Расчетные кривые совпадают с точными. Это указывает на то, что предлагаемый метод способен идентифицировать структурные реакции. Кроме того, два очевидных пика на 1,185 Гц и 3.527 Гц можно получить на рисунках 3 и 4. Два пика соответствуют первым двум поступательным собственным частотам здания.
Неизвестными структурными параметрами являются коэффициенты жесткости конструкции на каждом этаже и два коэффициента демпфирования Рэлея. Начальное значение расширенного вектора состояния, где. Матрица начальной ковариации ошибок расширенного вектора состояния равна. Ковариационная матрица шума технологического процесса равна, а ковариационная матрица шума измерения равна.На рисунке 3 показано сравнение расчетных откликов на смещение конструкции с точными значениями на пятом и десятом этажах для временной и частотной областей. На рисунке 4 показано сравнение расчетных скоростных характеристик конструкции с точными значениями на пятом и десятом этажах для временной и частотной областей. Расчетные кривые совпадают с точными. Это указывает на то, что предлагаемый метод способен идентифицировать структурные реакции. Кроме того, два очевидных пика на 1,185 Гц и 3.527 Гц можно получить на рисунках 3 и 4. Два пика соответствуют первым двум поступательным собственным частотам здания.
| ||||||||||
Кроме того, согласно предложенному методу, неизвестная ветровая нагрузка идентифицируется по неполным измерениям. Выявленная ветровая нагрузка и относительные ошибки между выявленной ветровой нагрузкой и точной в процентах на пятом и десятом этажах численной модели показаны на рисунке 5. Рисунок 5 показывает, что итерационный процесс не может сходиться сразу, но примерно через 8 s, относительные ошибки хорошо сходятся до менее 5%. В таблице 2 показаны средние ошибки и среднеквадратичные ошибки между идентифицированными ветровыми нагрузками и точными на каждом этаже. Из таблицы 2 максимальные средние ошибки и среднеквадратичные ошибки выявленных ветровых нагрузок равны 4.12% и 4,56% соответственно. Это означает, что идентифицированные ветровые нагрузки очень хорошо совпадают с точными после итерационной сходимости.
Выявленная ветровая нагрузка и относительные ошибки между выявленной ветровой нагрузкой и точной в процентах на пятом и десятом этажах численной модели показаны на рисунке 5. Рисунок 5 показывает, что итерационный процесс не может сходиться сразу, но примерно через 8 s, относительные ошибки хорошо сходятся до менее 5%. В таблице 2 показаны средние ошибки и среднеквадратичные ошибки между идентифицированными ветровыми нагрузками и точными на каждом этаже. Из таблицы 2 максимальные средние ошибки и среднеквадратичные ошибки выявленных ветровых нагрузок равны 4.12% и 4,56% соответственно. Это означает, что идентифицированные ветровые нагрузки очень хорошо совпадают с точными после итерационной сходимости.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
На рис. пятый и десятый коэффициенты жесткости конструкции.Это указывает на то, что коэффициенты жесткости могут сходиться к реальному значению в течение 2 с. Результаты оценки коэффициентов демпфирования Рэлея α и β показаны на рисунке 7. По сравнению с коэффициентом жесткости коэффициент демпфирования сходится немного медленнее и может сходиться к реальному значению примерно за 5 с. В таблице 3 приведены расчетные значения и погрешности структурных параметров. Максимальная погрешность коэффициента жесткости составляет 4,30%. Оценочные ошибки для коэффициентов демпфирования α и β равны 4.25% и 4,24% соответственно. Это свидетельствует о том, что предлагаемый метод позволяет идентифицировать структурные параметры при неполных измерениях.
Оценочные ошибки для коэффициентов демпфирования α и β равны 4.25% и 4,24% соответственно. Это свидетельствует о том, что предлагаемый метод позволяет идентифицировать структурные параметры при неполных измерениях.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.1.1. Влияние продолжительности отбора проб
Для исследования устойчивости предложенного метода обсуждается влияние продолжительности отбора проб на ветровую нагрузку и оценку параметров конструкции. Количество и расположение измерений такие же, как в таблице 1. Общая продолжительность измерений установлена на 1 с, 10 с, 30 с и 60 с.В таблице 4 показаны среднеквадратичные ошибки расчетной ветровой нагрузки на каждом этаже при различной продолжительности выборки. Расчетные результаты структурных параметров приведены в Таблице 5. Из Таблицы 4 максимальные среднеквадратичные ошибки ветровой нагрузки в течение 1 с, 10 с, 30 с и 60 с составляют 14,23%, 7,68%, 4,58% и 4,55%. , соответственно. Из таблицы 5 максимальные ошибки структурных параметров за 1 с, 10 с, 30 с и 60 с составляют 32,78%, 6,99%, 4,66% и 4,25% соответственно. Это указывает на то, что ошибки оценки уменьшаются с увеличением продолжительности времени.Таблица 5 показывает, что ошибки оценки ветровой нагрузки и параметров конструкции составляют менее 5%, когда продолжительность отбора проб достигает 30 с. Кроме того, сравнение оценочных результатов между 30 и 60 секундами показывает, что точность оценки немного увеличивается. Следовательно, учитывая вычислительные затраты, длительность выборки 30 с является достаточной для этого численного моделирования.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.1.2. Влияние количества измерений
В этом разделе обсуждается влияние количества измерений на совместную оценку состояния / параметра / ветровой нагрузки.Рассматриваемый набор измерений составляет от четырех до девяти, и каждый набор измерений включает в себя межэтажные смещения и реакции ускорения. В таблице 6 показано количество измерений и соответствующие местоположения.
| ||||||||||||||||||||
Временные характеристики расчетных ветровых нагрузок на пятом и десятом этажах при разном количестве измерений представлены на Рисунке 8.Рисунок 8 показывает, что тренды изменения выявленных ветровых нагрузок идентичны точным. Однако существует очевидная ошибка между расчетным значением и точным, когда количество измерений меньше шести. Среднеквадратичные ошибки идентифицированной ветровой нагрузки на каждом этаже при разном количестве измерений перечислены в таблице 7. Таблица 7 показывает, что по мере увеличения числа измерений среднеквадратичная ошибка расчетной ветровой нагрузки уменьшается. Максимальная погрешность при шести, пяти и четырех наборах измерений составляет 5.33%, 7,08% и 10,78% соответственно. Это указывает на то, что ошибка оценки значительно увеличивается, когда количество измерений меньше шести.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Временные характеристики оцененных ошибок пятого и десятого коэффициентов жесткости конструкции для различного количества измерений показаны на рисунке 9. Рисунок 9 показывает, что в начале итерации есть некоторые колебания.Однако примерно через 2 с итерация сходится к истинному значению. На рисунке 10 показаны расчетные ошибки коэффициентов демпфирования α и β . На рисунке 10 показано, что и α , и β имеют большие колебания в начале итерации и сходятся к истинному значению примерно через 10 с при более чем семи измерениях. Однако результаты оценки колеблются вокруг истинного значения, когда количество измерений меньше семи.Это указывает на то, что коэффициенты демпфирования чувствительны к количеству измерений и колеблются около истинного значения, если количество измерений недостаточно. В таблице 8 приведены результаты оценки структурных параметров с указанием количества измерений (т.е. от 4 до 9). Максимальные ошибки оцениваемых параметров при четырех-девяти измерениях составляют 13,01%, 11,76%, 9,83%, 4,30%, 3,71% и 3,63% соответственно. Это указывает на то, что с увеличением количества измерений точность оценки структурных параметров увеличивается.Максимальные ошибки коэффициента жесткости конструкции и коэффициентов демпфирования α и β при шести наборах измерений составляют 5,98%, 9,83% и 5,33% соответственно. Однако погрешности оценки каждого структурного параметра менее 5% при семи сериях измерений. Результаты показывают, что для этого конкретного примера следует использовать не менее семи наборов измерений.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.Проверка с помощью тестов в аэродинамической трубе
Чтобы проверить эффективность предложенного метода в практическом инженерном применении, в данном исследовании в качестве примера рассматривается высотное здание с 58 этажами. Размеры здания 234 м (высота) × 39 м (ширина) × 39 м (длина). Испытание в аэродинамической трубе синхронной системы сканирования с несколькими давлениями для одновременной оценки состояния, неизвестных структурных параметров и ветровой нагрузки было проведено в лаборатории аэродинамической трубы в Харбинском технологическом институте (Шэньчжэнь), Китай.Согласно китайскому национальному кодексу нагрузки (GB 50009-2012) [32], площадка вокруг испытательного здания принимается за местность C. Профиль ветра рассматривается как степенной закон с показателем 0,22. Масштаб длины этого испытания в аэродинамической трубе составляет 1: 300. На рисунке 11 показаны смоделированные профили средней скорости ветра и интенсивности турбулентности.
Модель имеет тот же масштаб длины, что и при моделировании поля ветра, то есть 1: 300. Размер модели составляет 780 мм (высота) × 130 мм (ширина) × 130 мм (длина), как показано на рисунке. 12.В этом испытании в аэродинамической трубе направление ветра было определено как угол θ d от 0 ° до 360 ° с шагом 15 °, как показано на рисунке 13. Общее количество кранов давления, установленных на здании, составляло 441. по 98 на каждой боковой поверхности и 49 на верхней поверхности. Данные по давлению были собраны с помощью системы микроэлектронного сканера давления производства PSI. Частота дискретизации данных составляла 330 Гц, длительность выборки – 120 с. Скорость ветра в верхней части модели с 10-летним периодом повторяемости составляет 39.6 м / с на основе китайского национального кода нагрузки [32].
4.1. Эквивалентная модель высотного здания
Для строительных конструкций с большими степенями свободы сложно или даже невозможно оценить ветровую нагрузку и параметры конструкции в строгом соответствии с конструкцией прототипа. Как правило, для практического анализа требуется упрощенная эквивалентная модель с меньшими степенями свободы. Эквивалентная модель требует, чтобы отклики на вибрацию двух систем были одинаковыми.Это означает, что рабочая энергия между прототипной структурой и эквивалентной структурой равна. На основе метода, предложенного в [33], эквивалентная масса и эквивалентная жесткость могут быть получены следующим образом: где – распределение массы конструкции-прототипа, – распределение жесткости конструкции-прототипа, – смещение конструкции-прототипа, – эквивалентная масса и – эквивалентная жесткость.
На основе метода разложения по модам смещение может быть представлено следующим образом: где – модальное смещение j -ое, а – вектор формы моды j -й.Для высотных строительных конструкций первая мода принимается за основную. Затем эквивалентную массу и эквивалентную жесткость можно рассчитать следующим образом:
В таблице 9 приведен вклад энергии первых пяти модальных реакций ускорения, модальных скоростных откликов и модальных откликов смещения, которые рассчитываются в соответствии со следующим уравнением: где – среднеквадратичное значение ответов, рассчитанное на основе правильного ортогонального разложения [34]. Видно, что вклад в энергию первых пяти мод превышает 99%.Таким образом, упрощенная эквивалентная модель выбрана как сдвиговая строительная конструкция с пятью степенями свободы. Предположим, что качество упрощенной модели сосредоточено на 12-м, 24-м, 36-м, 48-м и 58-м этажах, соответствующих высоте 50 м, 98 м, 146 м, 194 м и 234 м соответственно. Эквивалентные массовые коэффициенты и коэффициенты жесткости рассчитываются на основе уравнений (55) и (56), соответственно, которые показаны в таблице 10. В таблице 11 приведены первые пять собственных частот прототипа конструкции и эквивалентной модели.Было обнаружено, что относительные погрешности первых трех собственных частот не превышают 5%. На рисунке 14 показано сравнение первых двух форм колебаний прототипной структуры и эквивалентной структуры. Можно обнаружить, что формы колебаний эквивалентной структуры согласуются с формой колебаний прототипа. Демпфирование этой конструкции рассматривается как демпфирование Рэлея с коэффициентом демпфирования, соответствующим первым двум модам колебаний, равным 5%.
| ||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
4.2. Оценка ветровой нагрузки и конструктивных параметров
Отклик высотного здания, вызванный ветром, не может быть измерен непосредственно путем измерения давления на жесткой модели при испытании в аэродинамической трубе.Следовательно, индуцированные ветром реакции, включая реакции смещения, скорости и ускорения, рассчитываются на основе результатов испытаний в аэродинамической трубе и структурных динамических свойств конструкции прототипа здания с использованием метода Newmark- β . Чтобы подтвердить осуществимость предложенного метода, только три набора измерений, включая реакции структурного межэтажного смещения и реакции ускорения на 12-м, 36-м и 58-м этажах, взяты в качестве «измерений.Неизвестными параметрами являются пять коэффициентов жесткости и два коэффициента демпфирования Рэлея эквивалентной модели. Неизвестные возбуждения представляют собой эквивалентную ветровую нагрузку на эквивалентной модели. Начальное значение вектора состояния. Матрица начальной ковариации ошибок равна. Ковариационные матрицы технологического шума и шума измерения равны и соответственно.
На рисунках 15 и 16 показаны результаты оценки откликов конструкции на смещение и скоростных характеристик на 24-м и 58-м этажах соответственно.Можно обнаружить, что временные характеристики предполагаемых ответов очень хорошо совпадают с точными ответами. Между тем, было обнаружено, что спектр мощности оцененных ответов хорошо согласуется со спектрами точных ответов, за исключением небольших различий в высокочастотных компонентах (> 0,8 Гц) ответов на 24-м этаже. Это происходит главным образом потому, что (1) на 24-м этаже нет информации об измерениях, а результаты оценки на 24-м этаже получены в результате модального преобразования и (2) ошибки модальной информации между эквивалентной моделью и моделью-прототипом велики в высшие режимы (т.е., четвертый и пятый режимы).
На Рисунке 17 показано сравнение временных характеристик эквивалентной ветровой нагрузки между точными и расчетными значениями на 24-м и 58-м этажах. Можно заметить, что расчетные кривые очень хорошо согласуются с точными. Ошибки оценки эквивалентной ветровой нагрузки перечислены в таблице 12. Из таблицы 12 максимальная средняя ошибка и среднеквадратичная ошибка идентифицированной ветровой нагрузки составляют 4,95% и 5,89%. На рисунке 18 показаны результаты оценки эквивалентных коэффициентов жесткости.Это указывает на то, что коэффициенты жесткости могут сходиться к реальному значению в течение 5 с. Результаты оценки коэффициентов демпфирования показаны на рисунке 19, и можно обнаружить, что коэффициенты демпфирования могут сходиться к реальному значению в течение примерно 10 с. Расчетные значения и погрешности конструктивных параметров приведены в таблице 13. Погрешности коэффициента жесткости менее 5%, кроме 12-го этажа. Ошибки коэффициента демпфирования α и β равны 3.8% и 2,11% соответственно. Результаты сравнения показывают, что обратный метод, представленный в этом исследовании, применим к практической инженерии.
| ||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||
5. Заключение
В этой статье предлагается метод оценки совместного состояния / параметра / ветровой нагрузки во временной области по неполным измерениям на основе модальной расширенной несмещенной оценки минимальной дисперсии.Рекурсивная процедура включает четыре части: обновление времени, оценка модальной ветровой нагрузки, обновление измерений и преобразование координат. Отклики измерения включают отклики межэтажного смещения и ускорения на частичных этажах. Качество оценки предложенного метода подтверждается численно путем одновременного определения структурного состояния, параметров и ветровой нагрузки десятиэтажной конструкции здания, работающей на сдвиг, по неполным измерениям. Обсуждается влияние решающих факторов, включая продолжительность выборки и количество измерений, на сходимость и точность предлагаемого метода.Кроме того, испытание в аэродинамической трубе синхронной системы сканирования с несколькими давлениями на строительной конструкции высотой 234 м используется для демонстрации предлагаемого подхода для реальной конструкции. Для экспериментальной проверки выведена упрощенная эквивалентная модель с пятью степенями свободы. Результаты показывают, что предлагаемый метод показывает большой потенциал в качестве альтернативного способа одновременного определения неизвестных структурных параметров, ветровой нагрузки и реакции, вызванной ветром, в результате неполных измерений.
Доступность данных
Данные, использованные для подтверждения выводов этого исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации этой статьи.
Благодарности
Эта работа была поддержана Национальным фондом естественных наук Китая (грант № 51608153) и Шэньчжэньской программой инноваций в области знаний (гранты № JCYJ20170413105418298, JCYJ20180306171737796 и JCYJ201708111538).
Расчет и моделирование ветровой нагрузки – Glew Engineering
Рисунок 1: Коэффициенты ветровой нагрузки (давление и площадь)
Факторы, влияющие на ветровую нагрузку
Итак, насколько точно уравнение 1? Поскольку при расчете ветровой нагрузки он использует только самые основные значения, он может дать оценку величины силы ветра.Однако для более точного представления ветровой нагрузки можно умножить силу на ряд других коэффициентов, которые более точно учитывают условия, в которых будет находиться конструкция. Первый шаг к повышению точности достигается за счет включения «коэффициента экспозиции» и «коэффициента реакции на порывы», показанных в уравнении 2.
| F = P × A × C d × K z × G | (2) |
Где:
K z = коэффициент воздействия
G = коэффициент реакции на порыв
(K z ) представляет увеличение скорости воздуха по мере увеличения высоты над землей. уровень увеличивается.Низкий объект, большая часть площади которого находится внутри пограничного слоя, будет испытывать небольшую силу (K z ≈ 0). Объект высотой 100 футов будет иметь K z около 1, в то время как One World Trade Center на высоте 1776 дюймов будет иметь K z более 2,5.
Коэффициент реакции на порывы (G) отражает постоянство скорости воздуха по высоте объекта. Чем выше от земли, тем выше скорость ветра, и G ≈ 1. Ближе к земле, с граничными эффектами и турбулентностью от окружающих деревьев и зданий, скорость ветра может быть более неравномерной.G увеличивается до 2, когда высота объекта приближается к 0.
Международный строительный кодекс (ранее Единый строительный кодекс) использует вышеуказанные факторы, а также заменяет простой коэффициент сопротивления табличным «коэффициентом полезного давления». . Этот коэффициент более точно учитывает уклоны, карнизы и другие дополнения, влияющие на воздушный поток вокруг здания. Однако это уравнение IBC предназначено только для использования в зданиях высотой менее 75 футов. Ассоциация телекоммуникационной индустрии предлагает свою собственную версию в стандарте TIA-222-G, изменяющую уравнение с топографическими факторами и факторами воздействия в зависимости от среды установки башни.Опять же, у этой версии есть свои ограничения, так как она разработана специально для работы с мачтами и антеннами. Прародитель всех этих версий уравнения ветровой нагрузки приведен в ASCE-7 Американского общества инженеров-строителей. Эта версия имеет наиболее сложный и подробный набор коэффициентов для изменения давления ветра, площади проекции и коэффициентов сопротивления. Тем не менее, независимо от того, насколько сложным может быть выбранное уравнение ветровой нагрузки, оно все равно выводит только одно значение силы.
Ограничения для ручного расчета ветровой нагрузки
Вышеупомянутые расчеты могут предложить очень точное моделирование предельной ветровой нагрузки на конструкцию, но они не дают полной картины.Они не могут указать, где может быть сосредоточена ветровая нагрузка на сложную конструкцию, или смоделировать возникающие в результате напряжения и прогиб конструкции. Для более полного понимания того, как конструкция будет реагировать на высокие ветровые нагрузки, инженер может использовать программы вычислительной гидродинамики (CFD) и анализа методом конечных элементов (FEA) для моделирования взаимодействия ветра и конструкции в целом. Однако точность результатов зависит от точности компьютерной модели, поэтому существует компромисс между точностью, необходимой для анализа, и временем, доступным для моделирования конструкции и проведения симуляций.
Совместное использование расчетов ветровой нагрузки и CFD
Как обычно, самый безопасный и тщательный метод анализа реакции конструкции на ветер – использовать как ручные вычисления, так и CFD. Результаты этих различных методов должны в конечном итоге согласоваться. Если есть существенные различия в двух результатах, то один из методов требует исправления или улучшения. В следующих нескольких блогах мы сравним ручные расчеты и результаты CFD для простых структур, чтобы выяснить, насколько хорошо они соотносятся.
Ресурсы
- Международный совет кодов. (2014). Международный Строительный кодекс 2015 г. . Загородный клуб Хиллз, Иллинойс: ICC.
- Ассоциация индустрии телекоммуникаций. (2011). 2012 TIA-222-G Строительный стандарт для антенных опорных конструкций и антенн . Арлингтон, Вирджиния.
- Американское общество инженеров-строителей. (2010). ASCE 7 Минимальные расчетные нагрузки для зданий и других конструкций .

 73
73 Для того чтобы изготовленное изделие отвечало необходимым прочностным требованиям, необходимо выяснить: выдержит ли используемый материал те нагрузки, которые могут на него воздействовать в период краткосрочной или длительной эксплуатации. После произведенных расчетов ветровых нагрузок необходимо сравнить их с прочностными характеристиками баннера (винилового, полиэтиленового, тканого синтетического или натурального) с учетом специфики материала (например, влагопоглощения с последующим разрушением), возможной потери пластичности при низких температурах и скорости его старения.
Для того чтобы изготовленное изделие отвечало необходимым прочностным требованиям, необходимо выяснить: выдержит ли используемый материал те нагрузки, которые могут на него воздействовать в период краткосрочной или длительной эксплуатации. После произведенных расчетов ветровых нагрузок необходимо сравнить их с прочностными характеристиками баннера (винилового, полиэтиленового, тканого синтетического или натурального) с учетом специфики материала (например, влагопоглощения с последующим разрушением), возможной потери пластичности при низких температурах и скорости его старения.

 9
9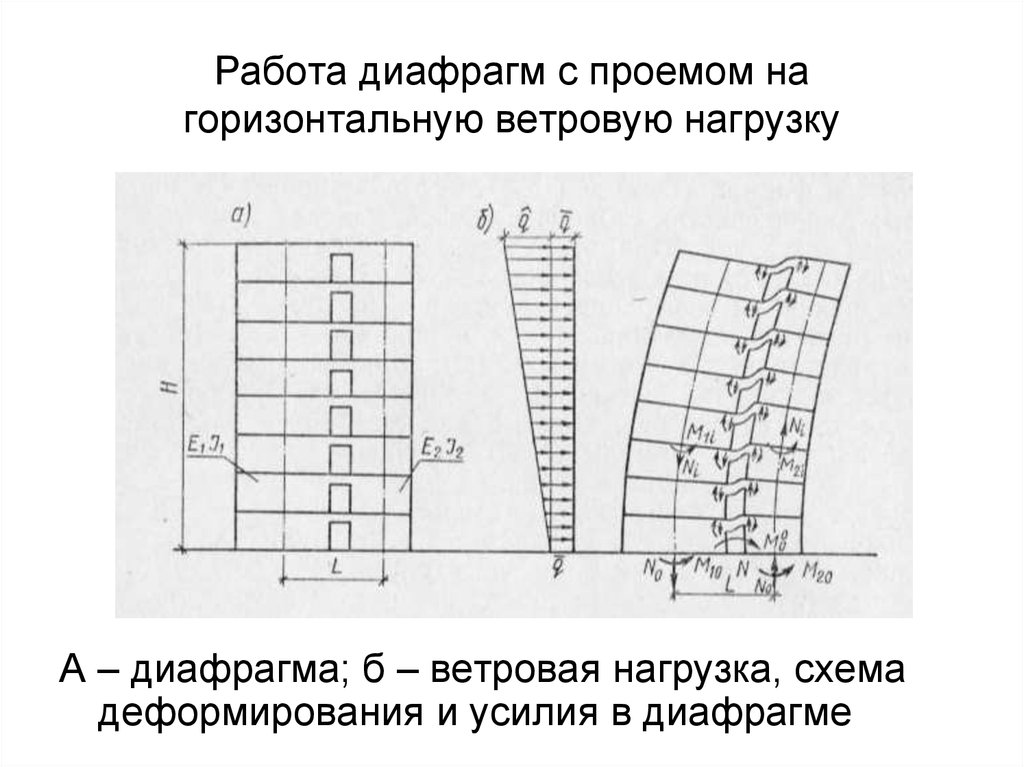
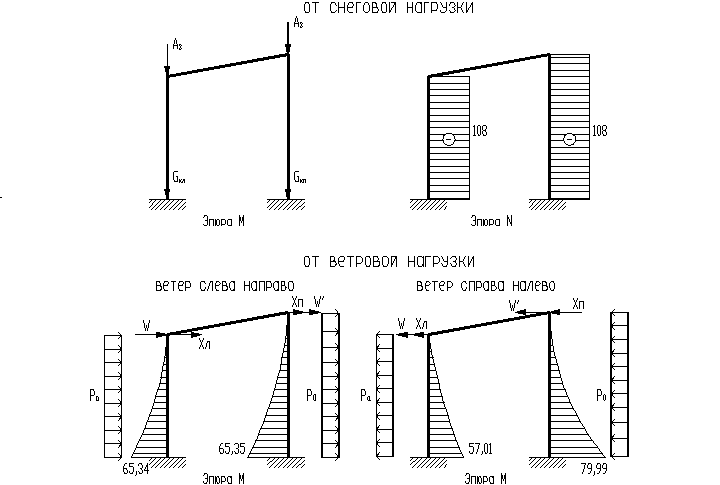
 расчистка.
расчистка.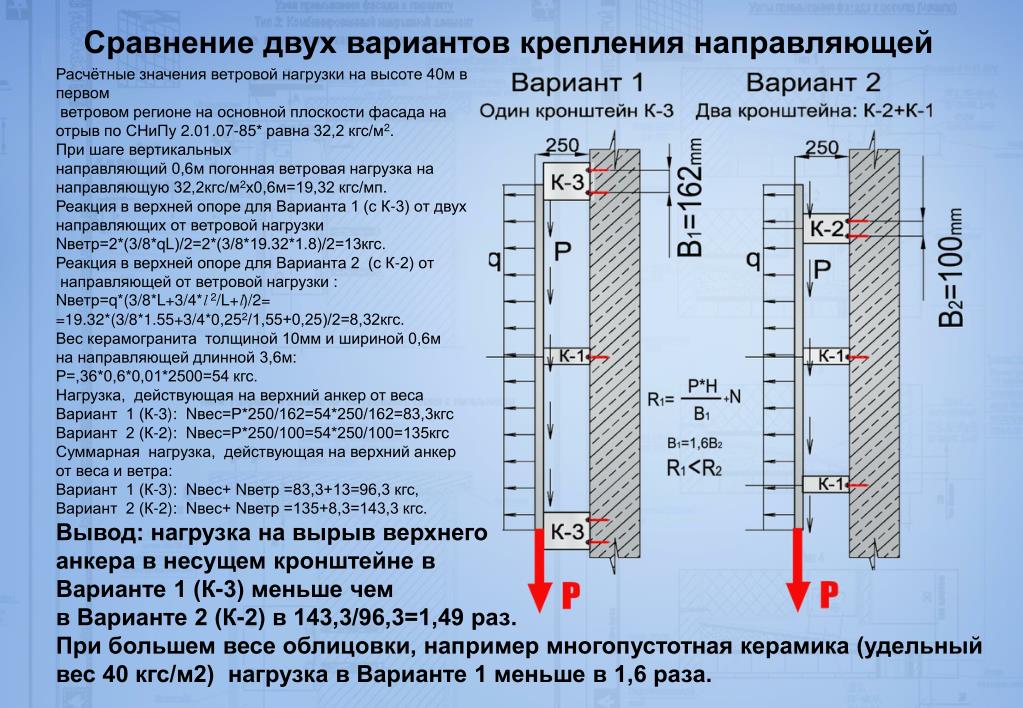
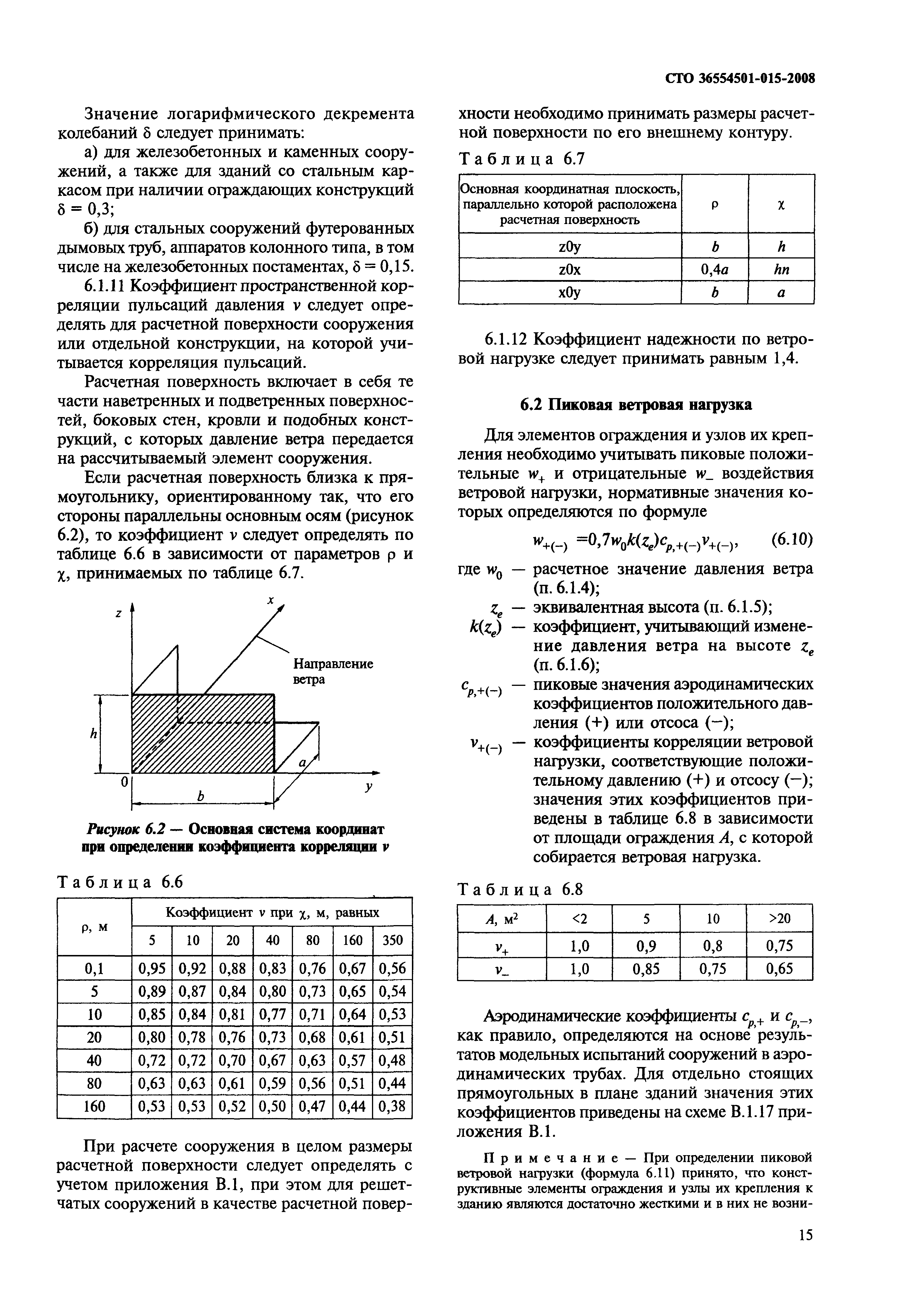
 56
56