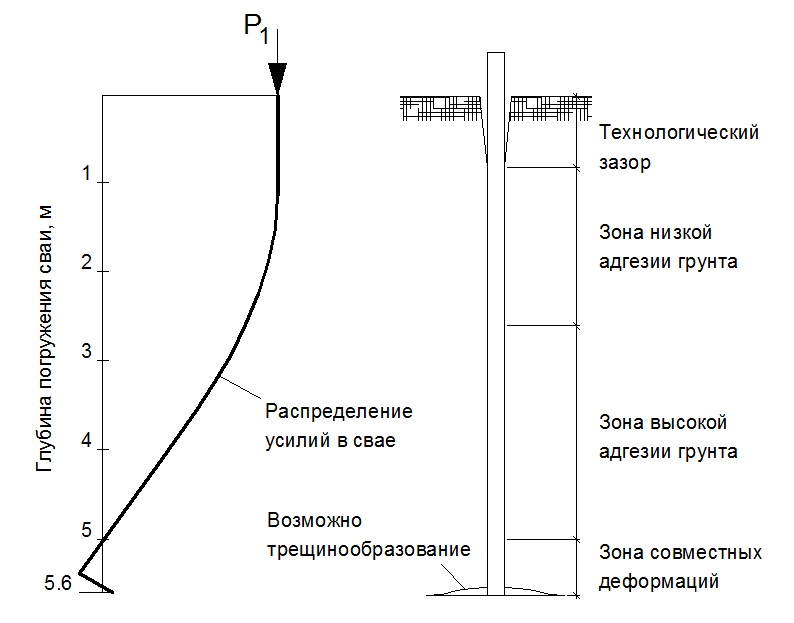
Расчет свай на горизонтальное воздействие
Расчет и анализ сопротивления свай воздействию нагрузок до сих пор является актуальной задачей современной геотехнической науки. Сегодня существует большое множество всевозможных аналитических, эмпирических и численных методик по расчету свайных фундаментов. Однако уровень их достоверности является предметом повышенного интереса в научной и проектной среде. Целью исследования данной работы является сравнение различных расчетных методик по оценке несущей способности сваи на горизонтальное воздействие и сопоставление этих расчетов с данными полевых испытаний.
Неизбежно на протяжении всей истории практики строительства возникала необходимость возведения или усиления фундаментов зданий. В этом аспекте широкое применение находили фундаменты глубокого заложения, в том числе свайные фундаменты. Одним из частных случаев устройства такого фундамента является проектирование свайной системы, воспринимающей горизонтальные воздействия.
Ранние методы расчета свай на горизонтальное воздействие на рубеже XIX-XX вв. и позднее, выполнялись как для шпунтового ограждения в предположении абсолютно жесткого стержня, который поворачивался под воздействием горизонтальной нагрузки, при этом происходил сдвиг грунта в верхней зоне. Сопротивление грунта рассчитывалось по классической теории предельного напряженного состояния грунта. Сегодня такие методы как правило не применяются, так как многочисленными экспериментами была доказана их несостоятельность.
и позднее, выполнялись как для шпунтового ограждения в предположении абсолютно жесткого стержня, который поворачивался под воздействием горизонтальной нагрузки, при этом происходил сдвиг грунта в верхней зоне. Сопротивление грунта рассчитывалось по классической теории предельного напряженного состояния грунта. Сегодня такие методы как правило не применяются, так как многочисленными экспериментами была доказана их несостоятельность.
В дальнейшем работу сваи в грунте предложили рассчитывать как балку на упругом основании в соответствии с гипотезой Фусса-Винклера. В основе метода лежит дифференциальное уравнение изогнутой оси стержня.
В силу упрощения аналитических расчетов (даже по сравнению с методами базирующиеся на теории общих упругих деформаций), и приемлемого уровня достоверности результатов (при удачном подборе коэффициента постели) данная методика получила широкое распространение. На ее основе были предложены различные модификации, в основном сводящиеся к различному учету изменения коэффициента постели по глубине. Этот метод до сих пор является основным в российской практике проектирования и регламентируется действующим Сводом Правил 22.13330.
Этот метод до сих пор является основным в российской практике проектирования и регламентируется действующим Сводом Правил 22.13330.
Однако, методика расчета свай на горизонтальную нагрузку на основе теории местных упругих деформаций имеет целый ряд существенных недостатков, в основном вытекающих из ее предпосылок, к некоторым из них относятся:
- данная методика не учитывает деформации точек грунтовой среды, расположенных в непосредственной близости от области воздействия нагрузки, не лежащих в одной плоскости;
- значения коэффициентов постели не удается получить экспериментальными способами для каждой площадки строительства[9], поэтому эти значения принимаются по обобщенным табличным данным, что мягко говоря, ошибочно, так как табличные значения не могут отражать широкого спектра физико-механических характеристик грунтов и различных механизмов взаимодействия сваи с грунтовой средой при широком диапазоне технологических, геометрических, силовых и прочих факторов;
- различные эмпирические доработки, моделирующие квазинелинейное изменение коэффициента постели по глубине, имеют искусственный характер и не находят экспериментальных подтверждений;
- методика не учитывает целый спектр краевых условий, влияющих на истинный нелинейный характер изменения деформаций и напряжений грунтовой анизотропной среды.

Такой, достаточно скудный, математический аппарат данной методики предопределяет тщетность многочисленных попыток доработать эту методику, посредством введения различных корректирующих эмпирических коэффициентов, до приемлемого и широкого уровня ее использования.
Изложенные обстоятельства обуславливают необходимость дальнейшей разработки достоверных аналитических выражений, основанных на математической модели взаимодействия свайной системы с окружающим грунтовым массивом. Очевидно, что для этого, прежде всего, необходимо уточнить расчетную свойств массива. Для этого в качестве таких моделей поведения грунта могут применяться модели получившие достаточно широкое применение разработанные при использовании модель грунтовой среды которая бы отражала истинный характер зависимости механических от физических характеристик грунта при различных воздействиях, с учетом пластических и реологических аппарата континуальной механики и реализованные в программных комплексах базирующиеся в том числе, на методах конечных элементов. При этом перспективным направлением (хотя, возможно и не ближайшего будущего) представляются методики аппарата механики дискретных сред при микроструктурном подходе.
При этом перспективным направлением (хотя, возможно и не ближайшего будущего) представляются методики аппарата механики дискретных сред при микроструктурном подходе.
О факторах влияния на механизм взаимодействия сваи c грунтом
Механизм взаимодействия сваи и окружающего грунта, является комплексным и сложным процессом который зависит от многих факторов:
- природные факторы – истории образования грунтовых массивов (которая, в частности, определяет степень недоуплотненности или переуплотненности, слагающих их грунтов), их текущего и прогнозного состояния (в том числе напряженно-деформированного). Сложности напластования инженерно-геологических элементов территории. Строения и состава окружающих грунтов их физических и механических свойств;
- типа свай, их физических и геометрических параметров;
- глубины погружения сваи;
- технологии погружения;
- конфигурации нагрузок и воздействий, действующих на сваю;
- процессов, изменяющихся во времени и др.

Не малую роль в механизме взаимодействия свай с грунтом выполняет тип свай и технология их устройства. В 1969 году, в Великобритании проводились научно-экспериментальные работы, направленные на изучение взаимодействия свайных фундаментов с грунтами. Для эксперимента использовались забивные сваи из стальных труб Ø168 мм, длиной 5.6м, погруженные в глинистые грунты твердых консистенций. Серию испытаний проводили в течение года после забивки. Результаты исследований показали, что при погружении свай вдавливанием и забивкой, в устье скважины – в области верхней части сваи, формировался технологический зазор глубиной до 8 диаметров сваи. При этом, в процессе наблюдения за грунтом в области технологического зазора в течение одного года было установлено, что зазор не был закрыт в процессе реологического восстановления грунта. По данным измерений сила сцепления (адгезии) грунта со сваей была незначительной на глубине от 8 до 14 диаметров сваи, а при больших глубинах (>16d) была зафиксирована максимальная адгезия грунта, превышавшая сдвиговую прочность недренированного грунта до 20%. Поэтому очевидно, что при подобных обстоятельствах, при приложении горизонтальной нагрузки на поверхности грунта, сопротивление нагрузке будет определяться преимущественно материалом самой сваи.
Поэтому очевидно, что при подобных обстоятельствах, при приложении горизонтальной нагрузки на поверхности грунта, сопротивление нагрузке будет определяться преимущественно материалом самой сваи.
По результатам анализа экспериментов было установлено, что несущая способность свай на горизонтальную нагрузку при прочих равных, также зависит от: уровня переуплотнения грунта (OCR) и жесткости (гибкости) ствола сваи.
Уровень переуплотнения грунта (OCR) в данном случае выступает как количественная характеристика, отражающая генетические условия образования и возраст дисперсных грунтов. Данная характеристика непосредственно влияет на эффективное горизонтальное напряжение в массиве грунта, а значит и на уровень горизонтальных напряжений, действующих на ствол сваи, выраженных через коэффициент бокового давления покоя Ko.
О влиянии природных (инженерно-геологических) факторов говорит и то обстоятельство, что, например, деформации грунта для случаев испытания свай в песчаных и глинистых грунтах неодинаковы. Так, в песках при перемещении сваи грунт оседает со стороны ее задней грани и смещается вперед и в разные направления со стороны передней грани. В связных грунтах грунт уплотняется под нагрузкой, а в предельном состоянии сваей прорезается полость при одновременном сохранении вертикальной стенки со стороны задней грани.
Так, в песках при перемещении сваи грунт оседает со стороны ее задней грани и смещается вперед и в разные направления со стороны передней грани. В связных грунтах грунт уплотняется под нагрузкой, а в предельном состоянии сваей прорезается полость при одновременном сохранении вертикальной стенки со стороны задней грани.
Не малую роль имеет конфигурация нагрузок и воздействий, действующих на сваю. Понятно, что на перемещение сваи под нагрузкой будет влиять и направление действия нагрузки по отношению к главным осям свайного элемента, и повторяемость этой нагрузки, и соотношение различных по форме воздействий, и интенсивность воздействия, и другие факторы. Так интенсивность нагрузки действует на характер сопротивления сваи, когда при разных значениях нагрузки изменяется доля сил трения на поверхности сваи, которая по данным некоторых опытов составляла до 36% от общего сопротивления сваи в грунте.
Сравнительная оценка методов расчета несущей способности свай на горизонтальную нагрузку
Высокая трудоемкость ручных расчетов при использовании нелинейных математических моделей поведения грунтовой среды в прошлом предопределило развитие эмпирических упрощенных методик расчета свайных фундаментов. Сегодня при высоком уровне развития цифровой индустрии и повсеместном использовании численных расчетов в решении инженерных задач имеется возможность использовать и развивать сложные математические модели механики сплошной и дискретной среды. Современный уровень вычислительных мощностей позволяет полностью отказаться от использования упрощенных и малодостоверных эмпирических методик, базирующихся на гипотезе Фусса-Винклера или применять их сугубо для оценочных расчетов в первом приближении.
Сегодня при высоком уровне развития цифровой индустрии и повсеместном использовании численных расчетов в решении инженерных задач имеется возможность использовать и развивать сложные математические модели механики сплошной и дискретной среды. Современный уровень вычислительных мощностей позволяет полностью отказаться от использования упрощенных и малодостоверных эмпирических методик, базирующихся на гипотезе Фусса-Винклера или применять их сугубо для оценочных расчетов в первом приближении.
Компьютерный анализ геотехнических задач позволяет учитывать различные факторы, влияющие на конечный результат в автоматическом режиме, при малых временных затратах. Эти расчеты не требует учета огромного количества эмпирических коэффициентов, регламентируемых действующей нормативной документацией в строительстве. Достоверность результатов численных расчетов ни в какой мере не зависит от классификации свай по критерию жесткости или длины погружения и прочего. Численные расчеты позволяет учитывать различные комбинации факторов влияния: конфигурации системы воздействия на сваю, физическую и геометрическую нелинейность надземных конструкций, фундаментов и оснований, в том числе с учетом реологических процессов и пр.
Современные конечно-элементные комплексы (Plaxis, Midas, RS3 и пр.), позволяют использовать параметрические модели свай которые имеют определенные пользовательские преимущества: снижение времени и трудоемкости моделирования на препроцессоре, упрощенное геометрическое моделирование, более высокая вероятность успешной сходимости задачи, широкий спектр возможностей на постпроцессорном этапе, включая получение данных не только о напряженно-деформированном состоянии элементов, а также данных о значениях и распределениях внутренних усилий и пр. Здесь существенным видится и то, что в качестве исходных данных можно задавать параметры несущей способности свай по боковой поверхности (fi), или по основанию (Ri), определенные по действующей методике Свод Правил 24.13330.2011. Перечисленные преимущества дают широкие возможности при решении инженерных задач, однако у медали есть и обратная сторона. Параметрическое моделирование свайных фундаментов строится на упрощенной математической функции поведения элемента, при этом происходит замещение объемного твердотельного элемента на одномерный элемент. Т.е. распределение усилий, расчет напряжений и деформаций происходит в приближенном виде. При этом, вначале, происходит расчет, по заданным параметрам по функции поведения параметрического элемента, заданной (скрытой) разработчиком ПО (как правило линейной), и только потом, отдельно, решается его взаимодействие с конечными элементами окружающей сетки моделирующей грунтовый массив. Такая двойная схема – расчетная схема сваи в расчетной модели грунтов – приводит к последовательному формированию и расчету двух матриц жесткости, (при этом, как правило, используются разные показатели жесткости: жесткость, определенная по СП или в эксперименте и жесткость прилегающего грунта). Многочисленными расчетами доказано, что такая расчетная схема существенно искажает результат.
Т.е. распределение усилий, расчет напряжений и деформаций происходит в приближенном виде. При этом, вначале, происходит расчет, по заданным параметрам по функции поведения параметрического элемента, заданной (скрытой) разработчиком ПО (как правило линейной), и только потом, отдельно, решается его взаимодействие с конечными элементами окружающей сетки моделирующей грунтовый массив. Такая двойная схема – расчетная схема сваи в расчетной модели грунтов – приводит к последовательному формированию и расчету двух матриц жесткости, (при этом, как правило, используются разные показатели жесткости: жесткость, определенная по СП или в эксперименте и жесткость прилегающего грунта). Многочисленными расчетами доказано, что такая расчетная схема существенно искажает результат.
Таким образом, при использовании численных методик хороший уровень достоверности расчетов свай может быть достигнут только при использовании объемных твердотельных конечных элементов (solids) высокого уровня (16, 32 и более узлов) при формулировании задачи в пространственной постановке с учетом математических моделей поведения грунтов. При этом дополнительное моделирование взаимодействия ствола сваи с прилегающем грунтом «эффект трения», например посредством введения интерфейсных элементов, повышает достоверность результата.
При этом дополнительное моделирование взаимодействия ствола сваи с прилегающем грунтом «эффект трения», например посредством введения интерфейсных элементов, повышает достоверность результата.
Результат анализа свай на горизонтальное воздействие
По результатам данного исследования можно сделать следующие выводы:
- Действительный механизм взаимодействия сваи с грунтом зависит от множества факторов. Существующие методики расчета свайных фундаментов учитывают только те или другие краевые условия, что приводит к различным оценкам сопротивления свай под нагрузкой. Достоверность расчетных методик зависит как от типов используемых свай, так и от инженерно-геологических условий. Сегодня до сих пор не существует универсальной методики расчета свайных фундаментов которая бы учитывала сложный механизм взаимодействия свай с различными грунтовыми средами при широком спектре нагрузок или воздействий;
- При использовании численных методов в оценке несущей способности свайных фундаментов и перемещений возможно получение результатов с высокой степенью приближения к данным полевых экспериментов.
 Однако, уровень достоверности численных расчетов существенно зависит от применяемой модели грунта;
Однако, уровень достоверности численных расчетов существенно зависит от применяемой модели грунта; - Возможность получения высокого уровня достоверности численных расчетов для данного типа задач, говорит о целесообразности применения данного подхода. При этом, выбор расчетной модели должен производится с учетом ее математической формулировки механизма взаимодействия сваи с окружающим грунтом, принимая во внимание инженерно-геологические условия площадки, информационную обеспеченность в виде исходных данных, конструктивные условия, требования к решаемой задаче и пр.
Результаты исследования показали, что достоверность численных расчетов, для анализа сопротивления свай горизонтальному воздействию, говорит о целесообразности применения данной методики для решения практических задач геотехники. При использовании данных методик приоритетным является использование продвинутых, более совершенных, нелинейных моделей поведения грунтов (HS, CamClay и других).
Положения нормативных документов и рекомендаций по расчету свайных оснований
- Подробности
- Категория: Генерация
- ГЭС
- сооружения
- расчеты
Содержание материала
- Расчет свайных оснований ГTC
- Конструкция ГTC
- Нагрузки на свайные ГTC
- Документы и рекомендации
- Взаимодействия с грунтом
- Расчет на вертикальную
- Расчет на горизонтальные
- Расчет свайных групп
- Методика исследований
- Параметры в несвязных грунт.

- Параметры связных грунтах
- Расчет водонасыщ. песчаных
- Влияние действия нагрузок
- Учет взаимовлияния свай
Страница 4 из 14
- Основные положения нормативных документов и рекомендации по расчету свайных оснований
Нормативные документы по расчету свайных оснований [28, 31] разработаны на основе богатого опыта применения их в промышленном и гражданском строительстве. Несущая способность свай при действии осевых нагрузок определяется по двучленной формуле, учитывающей лобовое сопротивление грунта под нижним концом и трение по боковой поверхности сваи. При этом приведенные расчетные сопротивления грунтов определены в результате статистической обработки большого экспериментального материала, полученного при испытаниях в основном забивных железобетонных свай сравнительно небольшой длины. Поэтому расчеты по СНиП II-17-77 железобетонных свай для гражданских и промышленных зданий обычно дают хорошие результаты, особенно при возможности их оценки и корректировки на основе полевых испытаний грунтов и инвентарных свай.
При проектировании оснований гидротехнических сооружений с длинными трубчатыми стальными сваями расчет несущей способности их по СНиП II-17-77 либо не может быть выполнен, либо нуждается в существенной корректировке. Ряд проведенных исследований [24] позволяет утверждать, что использование методики СНиП в этих случаях дает заниженные значения несущей способности, кроме того, отсутствие оборудования для проведения полевых исследований грунтов и испытания свай на больших глубинах морских акваторий усложняет проектирование оснований гидротехнических сооружений.
В еще меньшей степени пригоден для гидротехнических свайных сооружений расчет на горизонтальные нагрузки, приведенный в приложении к этому СНиП и в Руководстве по проектированию свайных фундаментов. Свая рассматривается как балка на линейно-деформируемом основании, характеризуемом коэффициентом постели, линейно изменяющимся по глубине. Приведенные значения коэффициента пропорциональности отвечают условиям очень малых горизонтальных перемещений голов свай, в пределах которых работу грунтовой среды можно считать линейной.
 Расчет может быть выполнен только для свай постоянного поперечного сечения в однородном грунте при шарнирном или абсолютно жестком закреплении головы. Сваи рассчитываются на постоянную горизонтальную нагрузку без учета возможного циклического, многократного характера ее приложения.
Расчет может быть выполнен только для свай постоянного поперечного сечения в однородном грунте при шарнирном или абсолютно жестком закреплении головы. Сваи рассчитываются на постоянную горизонтальную нагрузку без учета возможного циклического, многократного характера ее приложения.При действии вертикальных нагрузок несущая способность сваи по грунту определяется по формуле
где N – расчетная нагрузка (вертикальная), передаваемая на сваю; Ф – расчетная несущая способность одиночной сваи по грунту основания; кн – коэффициент надежности, зависящий от числа свай в фундаменте; Nр – нагрузка, допускаемая на сваю.
При действии на свайный фундамент в виде куста центральной вертикальной силы Νф расчетная нагрузка между отдельными сваями распределяется равномерно:
где п – число свай в фундаменте.
При приложении к группе свай вертикальной нагрузки и момента усилия в опорах определяются по формуле
Расчетная несущая способность свайного куста по грунту основания Фф определяется как сумма несущих способностей независимых одиночных свай: Фф = ΣΦ.
Фундаменты в виде свайных групп рассчитываются по деформациям как массивные сооружения на естественном основании с подошвой на уровне низа свай. Горизонтальная нагрузка распределяется между всеми сваями равномерно, без учета их взаимовлияния.
Особенности работы свай в конструкциях мостовых опор и морских портовых сооружениях, однако, без специфики расчета длинных свай, применяемых, например, для анкеровки сооружений континентального шельфа, учитываются МСН 171-71 [4].
Необходимо отметить, что, в связи с развитием добычи нефти и газа в открытом море, в последние годы за рубежом большое внимание уделяется вопросам исследования и расчета свай и свайных фундаментов применительно к условиям строительства и эксплуатации морских платформ.
В настоящее время разработано несколько нормативных документов по расчету свай для морских нефтегазопромысловых сооружений. Наиболее известны нормы Американского нефтяного института (API) [42] для проектирования забивных свайных фундаментов глубоководных стационарных платформ.

Широкое распространение получил при строительстве платформ в Северном морс голландский метод расчета сваи [24], в котором несущая способность свай определяется по результатам статического зондирования с помощью стандартного конуса. Полевые испытания грунтов дают сразу расчетное значение удельного сопротивления под нижним концом и по боковой поверхности сваи.
В Норвегии действуют нормы DNV [58], в которых составляющая несущей способности по боковому трению определяется по одному из трех методов: а, β или λ, в зависимости от способа получения расчетных характеристик грунтового основания.
Сопоставительные расчеты показывают, что американские нормы дают достаточно осторожные результаты при оценке несущей способности свай на осевые нагрузки, как и рекомендации СНиП.
 При этом способе внимание обращается на методы исследования грунтов в их естественном состоянии и на возможности получения расчетных характеристик грунта различными способами.
При этом способе внимание обращается на методы исследования грунтов в их естественном состоянии и на возможности получения расчетных характеристик грунта различными способами.В отмеченных выше зарубежных нормативных документах наряду с расчетом на осевые нагрузки регламентируется расчет свай на горизонтальные нагрузки; при этом, как правило, учитывается изменение сопротивления грунта по глубине и в зависимости от перемещения свай. Однако параметры кривых нелинейного деформирования грунта определяются в каждом случае по различным рекомендациям. При расчете свай нормы учитывают их взаимодействие через грунтовую среду в предположении упругой работы грунта в межсвайном массиве.
 Не останавливаясь подробно на обзоре этих рекомендаций [15, 24, 46], приведем лишь основные положения, относящиеся к вопросам расчета свай на действие комбинированных нагрузок.
Не останавливаясь подробно на обзоре этих рекомендаций [15, 24, 46], приведем лишь основные положения, относящиеся к вопросам расчета свай на действие комбинированных нагрузок.- Большинство существующих методов расчета свайных оснований гражданских, промышленных и гидротехнических сооружений на комбинированные нагрузки, в том числе включенные в отечественные нормативные документы [28, 31], основаны на предположении, что грунт представляет собой упругое основание Фусса-Винклера, характеризуемое коэффициентом постели, изменяющимся по глубине пропорционально или по другим законам. Их применимость, как правило, ограничена перемещениями в уровне поверхности грунта порядка 10 мм.
- Имеются работы, в которых в прямой или косвенной форме даются нелинейные зависимости “нагрузка – перемещение головы сваи” [3, 7, 46]. В них перемещение головы сваи обычно выражается через переменную глубину условной заделки или переменную глубину пластической зоны – при использовании упруго-пластической модели грунтового основания.
 Основными недостатками этих зависимостей является большое количество используемых эмпирических параметров и весьма приближенное отражение реальной деформируемости основания. Есть предположения [21, 50], с помощью которых можно рассчитать сваю с переменным коэффициентом постели, характеризующим способность основания к нелинейной местной деформации. Однако авторами не приводятся рекомендации по определению коэффициентов, учитывающих напряженное состояние грунта, или они строго ограничены условиями проведенных опытов.
Основными недостатками этих зависимостей является большое количество используемых эмпирических параметров и весьма приближенное отражение реальной деформируемости основания. Есть предположения [21, 50], с помощью которых можно рассчитать сваю с переменным коэффициентом постели, характеризующим способность основания к нелинейной местной деформации. Однако авторами не приводятся рекомендации по определению коэффициентов, учитывающих напряженное состояние грунта, или они строго ограничены условиями проведенных опытов. - В расчетных методиках приближенно отражена как разнообразность слоев грунта с различными механическими свойствами, так и переменность изгибной жесткости по длине свай гидротехнических сооружений, что не позволяет надежно определять напряженно-деформированное состояние системы “свая-грунт”
- В нормативных документах по проектированию свайных фундаментов [28, 31] при вычислении расчетной нагрузки на каждую сваю куста, так же как и при определении несущей способности, не учитывается возможное перераспределение усилий в сваях за счет “кустового эффекта”.
 Но, как показали исследования, при определении несущей способности свайной группы следует учитывать совместную работу опор в фундаменте [46, 50].
Но, как показали исследования, при определении несущей способности свайной группы следует учитывать совместную работу опор в фундаменте [46, 50]. - Для расчета взаимодействия свай, как правило, используются методы, основанные на решениях теории упругости, поскольку они наиболее просто позволяют оценить взаимодействие нагруженных свай через основание [55]. Однако эти теоретические методы и .результаты расчетов не имеют пока надежного экспериментально го подтверждения в связи с отсутствием необходимого материала по испытаниям реальных сооружений с тщательным измерением напряжений и деформаций конструкций и прилегающего массива грунта.
- При расчете свайных групп на действие горизонтальной нагрузки наряду с “упругими” решениями значительное развитие и распространение находят в последнее время методы, основанные на контактных расчетных моделях [49, 52], имеющие ряд преимуществ в практических расчетах, но которым свойствен один из основных недостатков — невозможность теоретического учета перераспределительной способности грунта.

- Анализ результатов многочисленных исследований взаимовлияния свай в группе [3, 7, 46] позволяет отметить следующее:
взаимодействие свай через грунтовую среду приводит к увеличению деформативности группы, снижению ее горизонтальной сопротивляемости и неравномерности в распределении усилий между отдельными опорами;
интенсивность взаимовлияния в группе зависит главным образом от числа свай и расстояния между ними;
влияние таких факторов, как глубина погружения свай, их диаметр, высота приложения нагрузки и ее интенсивность и других, в большинстве исследований не зарегистрировано.
- Назад
- Вперёд
- Назад
- Вперёд
- Вы здесь:
- Главная
- Архив
- Генерация
- Здания и сооружения тепловых электростанций
Еще по теме:
- Гидротехнические сооружения учебник
- Гидравлика зданий ГЭС
- Расчетная обеспеченность работы гидроэлектростанции
- Гидро расчеты сельских ГЭС
- Гидравлические потери на трение ЭС
Выдергивающая нагрузка на сваю: методика расчета своими руками
При планировании строительства различных малоэтажных конструкций на винтовых сваях обязательно проведение расчётов предполагаемых нагрузок с учётом влияющих на них факторов. К одной из них относится выдёргивающая сила, которая, в зависимости от важности объекта и его массивности, может дополнительно потребовать проведения полевых испытаний. В результате проводится анализ и сравнивается расчётная нагрузка на сваю с полученными данными, а затем выбирается подходящая свайная конструкция.
К одной из них относится выдёргивающая сила, которая, в зависимости от важности объекта и его массивности, может дополнительно потребовать проведения полевых испытаний. В результате проводится анализ и сравнивается расчётная нагрузка на сваю с полученными данными, а затем выбирается подходящая свайная конструкция.
Содержание
- 1 Требуется ли учитывать выдёргивающие нагрузки
- 2 Критерий необходимости учёта выдёргивающей нагрузки
- 3 Как определить коэффициент условий работы сваи
- 4 Как определить сопротивление грунта обратной засыпки
- 5 Расчёт выдёргивающих нагрузок на основание
- 5.1 Основное условие для проведения расчётов
- 6 Расчёт выдёргивающей нагрузки
- 7 Испытания свай на выдёргивающие нагрузки
- 7.1 Испытания на вдавливание
- 7.2 Испытания на выдёргивание
- 8 Особенности проведения испытаний винтовых свай
- 9 Заключение
Требуется ли учитывать выдёргивающие нагрузки
Свайное основание подвержено множеству нагрузокПри проектировании свайных фундаментов под дом одним из ключевых моментов расчёта несущей способности опор является учёт деформаций. Они влияют не только на устойчивость конструкции основания, а и на возможность образования проседаний.
Они влияют не только на устойчивость конструкции основания, а и на возможность образования проседаний.
Особенно это актуально при выполнении строительных работ на рыхлых, скалистых, сейсмически-активных и промерзающих грунтах. То есть такой расчёт требуется проводить в тех случаях, когда расчётная схема устойчивости свай существенно отличается от стандартной.
При строительстве достаточно часто применяют сваи диаметром 108 мм, которых хватает для строительства одноэтажных объектов из древесины или пеноблоков. Опоры обладают высокой прочностью и при этом имеют оптимальную стоимость. Согласно действующим стандартам они способны выдерживать нагрузки в пределах 4-5 т и эффективно справляться с поперечными и продольными сдвигающими силами.
Использование лопастей в конструкции позволяет эффективно справляться с выдёргивающими напряжениями в результате пучения грунта. Однако же сваи 108 мм, несмотря на это, требуют обязательного просчёта на выдёргивание, особенно если требуется возвести двухэтажный дом.
Критерий необходимости учёта выдёргивающей нагрузки
Согласно СП 22.13330.2011, критерием для учёта выдёргивающей нагрузки является выполнение следующего условия:
где Fn – нормативная выдергивающая сила;
Gn – нормативный вес свайного основания;
β – угол действия выдёргивающей силы относительно вертикали;
γс – коэффициент, определяющий условия работы сваи;
R“0 – расчётная величина сопротивления грунта обратной засыпки;
A0 – величина площади проекции верхней части свайного основания на плоскость, которая перпендикулярна направлению действия выдёргивающей силы.
Выдергивающая нагрузка может быть не учтена только в том случае, когда она по направлению действия совпадает с осевой линией винтовой сваи.
Как определить коэффициент условий работы сваи
Чтобы определить γс, необходимо воспользоваться следующей формулой:
где γ1 может принимать значения 0,8, 1,0 или 1,2 при расстояниях между осями опор под дом равными 1,5, 2,5 и 5 м соответственно;
γ2 принимается равным 1,0 при нормальных режимах монтажа свай, либо 1,2 — при аварийном и монтажном режиме работы;
γ3 может принимать следующие значения:
- 1,0 – при промежуточном прямом распределении устройств;
- 0,8 – для промежуточных угловых, свайных, свайно-угловых, концевых распределениях порталов устройств;
- 0,7 – для специальных порталов устройств.

γ4 может быть равным 1,0 при использовании грибовидных оснований и анкерных плит с защемлёнными стойками в грунте, либо 1,15 для анкерных плит с шарнирными опорами на основание.
Как определить сопротивление грунта обратной засыпки
Сопротивление грунта под подошвой стоек вычисляется по следующей формуле:
где γс1 и γс2 – коэффициенты условий работы. Первый коэффициент определяется на основе Таблицы 1, а второй принимается равным 1.
Таблица 1. Значения коэффициента γс1 для различных типов грунтаКоэффициенты М с различными индексами, которые присутствуют в формуле (3), берутся из Таблицы 2.
Таблица 2. Значения коэффициентов М в зависимости от угла внутреннего тренияОстальные переменные, присутствующие в формуле (3), определаются в соответствии с СП 22.13330.2011.
Максимальное давление на грунтовые слои подошвы фундамента под воздействием вертикальных и горизонтальных нагрузок в одном или обоих направлениях не должно превышать расчётную величину, равную 1,2 R.
Расчёт выдёргивающих нагрузок на основание
Расчёт винтовых свай под дом необходимо определять с учётом основных и особых нагрузок отдельно или при их одновременном воздействии. Кроме того, нужно выполнять расчёты по основным типам деформаций. При этом обязательно учитывается тип грунта и материала свай.
Определение основных параметров для расчётов может быть выполнено также при помощи полевых испытаний. При наличии неточной информации о несущих способностях нестабильного грунта может потребоваться дополнительное тестовое бурение в нескольких местах участка.
Основное условие для проведения расчётов
Выдёргивающая нагрузка на винтовую или буронабивную сваю под дом с воздействием сжимающих и/или растягивающих сил в вертикальном либо горизонтальном направлениях сводится к выполнению следующего условия:
Набивная сваягде F – приведённая действующая нагрузка на основание в верхней точке опор;
FR – допустимая горизонтальная нагрузка в верхней точке фундамента.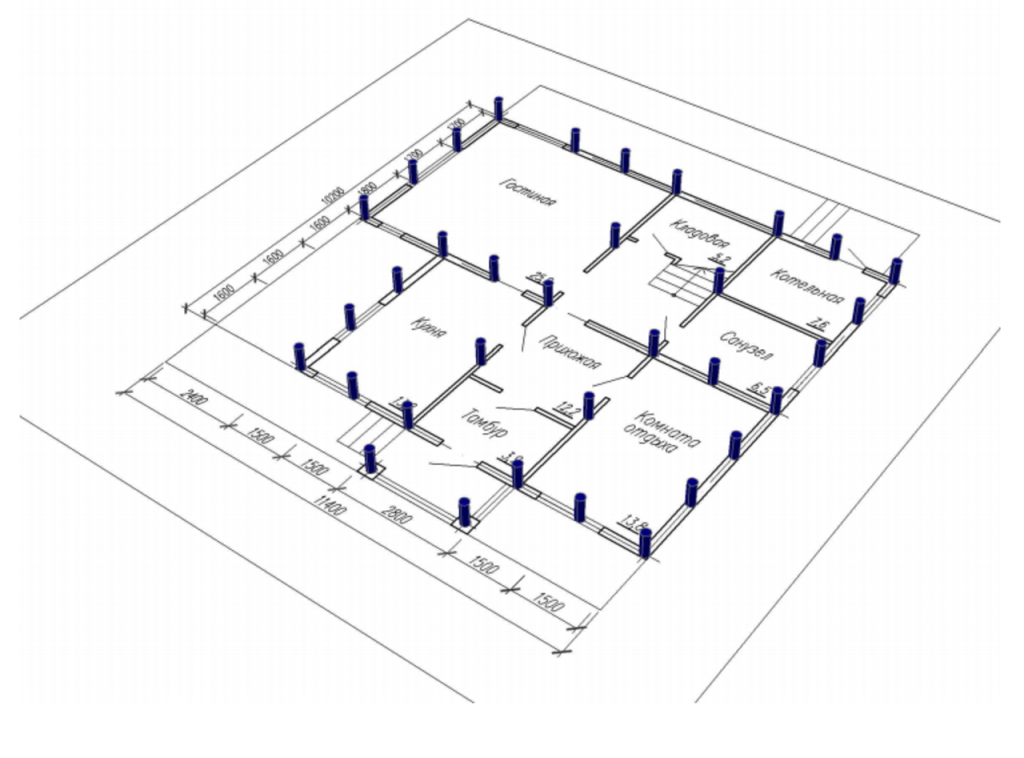
Параметр FR определяется на основе проведения расчётов на опрокидывание со сжатием или выдёргиванием. Среди двух рассчитанных величин выбирается та, которая имеет наименьшее значение.
Расчёт выдёргивающей нагрузки
Формула для вычисления выдёргивающей нагрузки F на фундамент имеет следующий вид:
где γf – коэффициент, характеризующий надёжность несущей конструкции, который в данном случае берётся равным 0,9;
Gn – значение веса конструкции фундамента;
γс – коэффициент условий работы, который принимается равным 1;
Fu,a – предельное сопротивление винтовых свай на выдёргивание;
γn – коэффициент надёжности сваи.
Винтовые опоры диаметром 108 ммВыдёргивающее сопротивление зависит только от величины бокового трения.
На основе расчётов выдёргивающей нагрузки определают диаметр винтовых свай, которые потребуются для создания надёжного основания.
Если нагрузки на выдёргивание имеют значительную величину, то применяют буронабивные сваи с выполнением уширения пятки либо винтовые с диаметром более 108 мм. Наиболее устойчивыми к выдёргивающим силам являются буронабивные конструкции.
Наиболее устойчивыми к выдёргивающим силам являются буронабивные конструкции.
Однако их применение невозможно на грунтах с непробиваемыми пластами. Поэтому проектировщику приходится принимать достаточно сложное решение по возникшим технических проблемам.
Основным преимуществом применения винтовых свай диаметром 108 мм является возможность передачи выдёргивающих нагрузок в грунт. Дом построенный на их основе будет иметь более выгодную конструкцию, чем при использовании буронабивных опор, по параметру веса, надёжности и распределения нагрузки.
Испытания свай на выдёргивающие нагрузки
Для определения выдёргивающих нагрузок проводят статические испытания винтовых свай. При наличии песчаных слоёв грунта измерения проводят через 3 суток, а для глинистых — только после 6 суток. Для буронабивных свай испытательные работы следует выполнять только после набора бетоном прочности, определяемой по данным взятых образцов, созданных во время закладки опоры.
Испытания на вдавливание
Испытание винтовых свай статическим методомВ перечень основных испытаний на вдавливание опор под дом входят следующие этапы:
- Равномерная нагрузка.
- Дифференцированная нагрузка.
- Дифференцированная нагрузка, выполняемая по гистерезисной зависимости.
Величина нагрузки определяется необходимостью определения заданного уровня точности измерений. Обычно для равномерной нагрузки она составляет 0,07-0,1 от общей расчётной, а для дифференцированной – 0,2-0,4 для начальной ступени и 0,07-0,1 для последующих.
Переход между степенями нагружения осуществляется только после определения выхода на полную остановку усадки. Критерием является отсутствие изменений в течение 2-х последних часов наблюдения. Исключением из данного правила становятся песчаные и глинистые грунты, где создаётся необходимость проведения ускоренных испытаний. В таком случае вывод о стабилизации сваи принимается в течение часа при отсутствии смещений менее 0,1 мм.
На каждой ступени нагружения регистрируют показания измерительных приборов о вертикальном смещении сваи. Интервалы замеров длятся от 15 до 30 минут. Общее количество интервалов должно быть не менее трёх. Если выбрано нечётное число ступеней, то нагрузку на первой принимают равной величине всех последующих. После этого строят временную зависимость от вертикального смещения, а затем сравнивают с нормативным значением СП 22.13330.2011. Предельным считается такое значение, которое соответствует 0,1 от нормативной нагрузки.
Посмотрите видео, как проводится испытание опор с помощью вдавливания.
Испытания на выдёргивание
Испытания на выдёргивание винтовых свай под дом диаметром 108 мм определаются параметрами грунта, а также величиной предполагаемых нагрузок. Включают в себя следующие виды нагружения:
- Увеличивающаяся ступенчатая нагрузка с выжиданием достижения стационарного состояния в положении сваи.

- Пульсирующее ступенчатое воздействие с повышением нагрузки в несколько этапов: 1,25, 2,5 либо 5 мс. Суть заключается в проведении нагружения на каждой ступени от нуля до максимума, а затем полностью убирается без выжидания выхода в стационарное состояние. Изменение ступеней осуществляется только после стабилизации смещения опоры по вертикали по сравнению с предыдущей.
- Знакопеременная нагрузка. На опору действует многократное нагружение одинаковой величины на выдёргивание и вдавливание, которые изменяют свой знак при переходе через ненагруженную точку.
- Непрерывно возрастающая нагрузка – на сваю действует постоянная выдёргивающая сила. При изменении величины нагружения не выжидают полной стабилизации, так как вполне достаточно достижения некоторого условного значения. Предельным значением нагрузки считается такое, когда перемещение опоры вверх не превышает 0,1 от величины её диаметра. Для переменных нагрузок и пульсирующих изменение положения не должно быть больше, чем 0,05 от диаметра сваи.

Выполнение испытаний для винтовых свай рекомендуется для уточнения расчётных значений сопротивления фундамента на выдёргивание и вдавливание.
Особенности проведения испытаний винтовых свай
Испытания винтовых опорВинтовые сваи 108 мм под дом испытывают статическими нагрузками с применением следующих методов:
- Ступенчатой нагрузкой с выжиданием стационарного состояния по вертикальным смещениям на каждой из величин нагружения.
- Непрерывно увеличивающейся нагрузкой.
- Знакопеременным или пульсирующим нагружением.
При ввинчивании винтовой сваи в грунт регистрируются следующие параметры: число оборотов, длительность заглубления, осевая пригрузка и крутящий момент. Периодичность записи данных в журнал определяется величиной погружения сваи на каждые полметра.
Пригрузка вдоль оси определяется плотностью грунта и его структурой. Численно она определяется путём деления теоретического числа оборотов сваи к реальному. Если соотношение имеет значение менее 1, то пригрузка повышается, а при большем — снижается. Оптимальным вариантом, который говорит о правильности настройки испытательной установки, считается равенство полученного значения единице.
Если соотношение имеет значение менее 1, то пригрузка повышается, а при большем — снижается. Оптимальным вариантом, который говорит о правильности настройки испытательной установки, считается равенство полученного значения единице.
Посмотрите видео, как проводятся испытания винтовых опор.
Заключение
После проведения расчётов и полевых испытаний на выдёргивающие нагрузки для свай диаметром 108 мм под дом проектировщиком решается вопрос о том, какую конструкцию фундамента выбрать и как разместить опоры. Было показано, как провести все необходимые расчёты по определению нагружения на выдёргивание, позволяющие избежать множества проблем при эксплуатации объекта.
Описаны процедуры проведения полевых испытаний на вдавливание и выдёргивание свай, которые являются дополнительным контролем правильности расчётов, а также источником сведений о несущей способности грунта.
Несущая способность свай в поперечном направлении: сравнительное исследование индийских стандартов и теоретического подхода
Несущая способность сваи в поперечном направлении: сравнительное исследование индийских стандартов и теоретического подхода
Скачать PDF
- Статья о профессиональных интересах
- Опубликовано:
- П. К. Джаясри Orcid: orcid.org/0000-0002-2229-4076 1 ,
- К. В. Арун 2 ,
- Р. Ормила 1 &
- …
- H.
 SREELAKSHMI 1 9008
SREELAKSHMI 1 9008- …
- H. SREELAKSHMI 1 9008
- …
- H. SREELAKSHMI 1 9008
- …
- H. SREELAKSHMI 17 9008
7.- …
- H. SREELAKSHMI 9008
7- …
- H.
Журнал Института инженеров (Индия): Серия A том 99 , страницы 587–593 (2018)Процитировать эту статью
19 тыс.
 обращений
обращений4 Цитаты
Сведения о показателях
Abstract
Согласно индийским стандартам сваи с поперечной нагрузкой обычно анализируются с использованием метода, принятого в стандарте IS 2911-2010 (Часть 1/Раздел 2). Но практикующие инженеры придерживаются мнения, что метод ИС очень консервативен по своей конструкции. Эта работа направлена на определение степени консервативности традиционного подхода к проектированию ИС. Это делается посредством сравнительного исследования между подходом IS и теоретической моделью, основанной на уравнении Весича. Данные журнала бурения шести различных мостов были получены в Департаменте общественных работ штата Керала.
 Залитые на месте сваи с неподвижной головкой, заделанные в три грунта, рассматривались и анализировались по отдельности. Сваи также были смоделированы в программном обеспечении STAAD.Pro на основе IS-подхода, и результаты были проверены с использованием Matlock и Reese (в материалах пятой международной конференции по механике грунтов и проектированию фундаментов, 1961) уравнение. Результаты были представлены в виде процентного изменения значений изгибающего момента и прогиба, полученных разными методами. Результаты, полученные с помощью математической модели, основанной на уравнении Весича, и результаты, полученные в соответствии с подходом IS, были сопоставлены, и метод IS был признан неэкономичным и консервативным.
Залитые на месте сваи с неподвижной головкой, заделанные в три грунта, рассматривались и анализировались по отдельности. Сваи также были смоделированы в программном обеспечении STAAD.Pro на основе IS-подхода, и результаты были проверены с использованием Matlock и Reese (в материалах пятой международной конференции по механике грунтов и проектированию фундаментов, 1961) уравнение. Результаты были представлены в виде процентного изменения значений изгибающего момента и прогиба, полученных разными методами. Результаты, полученные с помощью математической модели, основанной на уравнении Весича, и результаты, полученные в соответствии с подходом IS, были сопоставлены, и метод IS был признан неэкономичным и консервативным.Введение
Всегда требуется, чтобы сваи выдерживали боковые нагрузки в дополнение к нагрузкам сжатия и растяжения. Боковая нагрузка этих свай зависит от свойств грунта. Свая ведет себя как поперечно нагруженная балка при боковых нагрузках и передает боковую нагрузку на окружающий грунт за счет бокового сопротивления грунта.
 Свая смещается по горизонтали в ответ на приложенную нагрузку, что приводит к изгибу, вращению или перемещению сваи.
Свая смещается по горизонтали в ответ на приложенную нагрузку, что приводит к изгибу, вращению или перемещению сваи.В зависимости от фиксации оголовка сваи с поперечной нагрузкой подразделяются на сваи с фиксированным оголовком и сваи со свободным оголовком в зависимости от того, закреплена верхняя часть сваи или нет. А по принципу функционирования они классифицируются как висячие сваи и концевые опорные сваи. Висячие сваи передают нагрузку за счет поверхностного трения между заглубленной поверхностью сваи и окружающим грунтом. А концевые опорные сваи передают нагрузки через свои нижние концы, опирающиеся на твердый пласт.
Анализ поперечно нагруженных свай в различных программах показал, что, кроме STAAD.Pro, все остальные методы завышали прогиб головы сваи [1]. Поскольку сваи, подвергающиеся боковым нагрузкам, рассчитываются на основе максимально допустимого прогиба, анализ STAAD.Pro может быть эффективно использован для оценки прогибов головы сваи с некоторым коэффициентом умножения из-за постоянно более низких значений прогиба.
 Точность результатов в STAAD.Pro будет зависеть от жесткости пружины, которая, в свою очередь, связана с модулем реакции грунтового основания ( k s ) почвы. Разработано несколько уравнений для оценки k s для упругих грунтов на основе испытаний и теоретических анализов, из которых методы определения значения k s на основе соотношения Весича [2] дали приемлемую точность [3]. IS 2911-2010 (Часть 1/Раздел 2) использует эквивалентный консольный подход для расчета поперечно нагруженных свай. Исследования, проведенные с использованием балочного подхода на упругом основании, оказались более эффективными, чем метод IS [4].
Точность результатов в STAAD.Pro будет зависеть от жесткости пружины, которая, в свою очередь, связана с модулем реакции грунтового основания ( k s ) почвы. Разработано несколько уравнений для оценки k s для упругих грунтов на основе испытаний и теоретических анализов, из которых методы определения значения k s на основе соотношения Весича [2] дали приемлемую точность [3]. IS 2911-2010 (Часть 1/Раздел 2) использует эквивалентный консольный подход для расчета поперечно нагруженных свай. Исследования, проведенные с использованием балочного подхода на упругом основании, оказались более эффективными, чем метод IS [4].Подход традиционно используемого стандарта IS 2911 [5] при расчете несущей способности свай в поперечном направлении является консервативным, как утверждают инженеры-практики Департамента общественных работ, Govt. Кералы. В связи с этим предпринята попытка изучить поведение свай разных типов, опирающихся на разные грунтовые среды, с использованием метода НК и математического моделирования на основе уравнения Весича с использованием стандартного пакета программ STAAD.
 Pro. Этим предполагается установить, насколько консервативен метод ИС по сравнению с математическим подходом.
Pro. Этим предполагается установить, насколько консервативен метод ИС по сравнению с математическим подходом.Методология
Данные, включая структурные чертежи и детали бурения шести мостов из штампованных балочных плит, были получены в Департаменте общественных работ штата Керала. Тируванантапурам, Керала. В качестве мест для строительства моста были выбраны Куричиккал, Пуллутский мост-1, Ваккаил, Пуллутский мост-2, Эжавапалам и Ченгалаи. Случайным образом были выбраны три состояния почвы, а именно средний песок, мягкая глина и жесткая глина. Различные нагрузки, действующие на каждый мост, были рассчитаны на основе геометрических деталей, а также с использованием IRC-6 (2014) [6]. Учитывались следующие нагрузки: статическая нагрузка (палубная плита, поручни, износостойкое покрытие, подшипник, опора, опора, грунтовая стена, стенка крыла, земляная насыпь и оголовок сваи), временная нагрузка, временная нагрузка пешеходной дорожки, нагрузка от разрушения, давление грунта, температурное напряжение и усадочное напряжение.
Таблица 1 Сводка расчетов нагрузки для шести мест расположения моста Из полученных таким образом суммарных горизонтальных и вертикальных нагрузок, действующих на группу свай, были определены горизонтальные и вертикальные нагрузки, действующие на одну сваю на каждой площадке моста, которые приведены в таблице 1.
Из полученных таким образом суммарных горизонтальных и вертикальных нагрузок, действующих на группу свай, были определены горизонтальные и вертикальные нагрузки, действующие на одну сваю на каждой площадке моста, которые приведены в таблице 1.Полноразмерная таблица
IS 2911 (Часть 1/Разд. 2)-2010 Подход
Поведение поперечно нагруженных свай было проанализировано на основе IS 2911 [5] . Подход ИС всегда дает приближенное решение из-за сложности многих задач. Первым шагом было определить, ведет ли себя свая как короткая жесткая единица или как бесконечно длинный гибкий элемент. Это было сделано путем расчета коэффициента жесткости Т для конкретной комбинации сваи и грунта. После расчета коэффициента жесткости критерии поведения короткой жесткой сваи или длинной упругой сваи связаны с заглубленной длиной L сваи. Затем была рассчитана глубина от поверхности земли до точки виртуальной фиксации, которая использовалась в обычном упругом анализе для оценки бокового отклонения и изгибающего момента.

Боковое сопротивление грунта для зернистых грунтов и нормально сцементированной глины с переменным модулем грунта было проанализировано в соответствии с модулем реакции земляного полотна, для которого рекомендуемые значения приведены в IS 2911 [5], как показано в таблицах 2 и 3.
Таблица 2 Модуль реакции основания для сыпучих грунтов, η h , кН/м 3Полная таблица
Таблица 3 Модуль реакции основания в связных грунтах, k 1 , кН/м 3 .Полноразмерная таблица
Используя модуль реакции земляного полотна, коэффициент жесткости T для зернистых грунтов и коэффициент жесткости R для связных грунтов был найден из уравнений. (1) и (2).
$${\text{Коэффициент жесткости в м}},\quad T = \sqrt[5]{{\frac{EI}{{\eta_{h} }}}}$$
(1)
$${\text{Коэффициент жесткости в м}},\quad R = \sqrt[4]{{\frac{EI}{KB}}}$$
(2)
где E – модуль Юнга материал сваи, МН/м 2 , I – момент инерции поперечного сечения сваи, м 4 , η h – модуль реакции земляного полотна зернистого грунта в МН/м 3 и B – ширина ствола сваи (диаметр в случае круглых свай) в м
$$K = \frac {{0.
 3k_{1} }}{1.5B}$$
3k_{1} }}{1.5B}$$(3)
где k 1 – модуль реакции земляного полотна в связных грунтах в кН/м 3 .
Изгибающий момент и прогиб для свай с неподвижным оголовком рассчитываются по уравнениям. (4) и (5) соответственно.
$${\text{Фиксированный конечный момент}},\quad M_{F} = \frac{{H(e + z_{f})}}{2}$$ 9{3}$$
(5)
где H – поперечная нагрузка в кН, y – прогиб головы сваи в мм, E – модуль Юнга материала сваи в кН/м 2 , I – Момент инерции поперечного сечения сваи в м 4 , z f — глубина до точки закрепления в м, а e — длина консоли над землей/основанием до точки приложения нагрузки в м.
Глубина до точки крепления и длина консоли над землей/основанием до точки приложения нагрузки были получены из соответствующих в IS 2911 [5]. Значения реакции грунтового основания, полученные для каждого участка моста, показаны в таблице 4.
Таблица 4 Значения модуля реакции грунтового основанияПолноразмерная таблица
Математическая модель, основанная на уравнении Весича
Было проанализировано поведение поперечно нагруженных свай с использованием математической модели, основанной на уравнении Весича.
 Весич [2] проанализировал бесконечную горизонтальную балку на упругом основании и сравнил результаты с результатами, полученными с использованием теории реакции грунтового основания, связав модуль реакции грунтового основания с параметрами упругости. Модуль реакции грунтового основания различных слоев грунта на каждом участке моста был рассчитан с использованием уравнения Весича, приведенного в уравнении. (6). 9{2} } \right)$$
Весич [2] проанализировал бесконечную горизонтальную балку на упругом основании и сравнил результаты с результатами, полученными с использованием теории реакции грунтового основания, связав модуль реакции грунтового основания с параметрами упругости. Модуль реакции грунтового основания различных слоев грунта на каждом участке моста был рассчитан с использованием уравнения Весича, приведенного в уравнении. (6). 9{2} } \right)$$(8)
где c u = 6 Н [8], N — значение SPT грунта, а c u — прочность грунта на сдвиг в недренированном состоянии, кН/ м 2 .
Численное моделирование
Свая моделировалась как элемент балки в программе STAAD.Pro. Грунтовые пружины использовались для идеализации опоры грунта для сваи в горизонтальном направлении при числе узлов по длине сваи. Постоянные пружины оценивались по модулю реакции грунтового основания k s дано в уравнении. (6).
Предварительная обработка была выполнена для того, чтобы задать свойства материала для пружины на основе данных каротажа.
Таблица 5 Свойства материалов, присвоенные сваям в STAAD.Pro Изначально геометрия сваи создавалась по чертежу. Затем этим сваям были присвоены свойства материала из бетона М40. Следующим шагом было создание условий поддержки на обоих конечных узлах. Вся длина сваи была разделена путем добавления узлов через равные промежутки времени. Пружинные опоры были созданы в соответствии с различными типами грунта по длине сваи с использованием уравнения. (5), а затем он был назначен в узлах для их соответствующей глубины. Свойства материалов, присвоенные сваям, приведены в таблице 5.
Изначально геометрия сваи создавалась по чертежу. Затем этим сваям были присвоены свойства материала из бетона М40. Следующим шагом было создание условий поддержки на обоих конечных узлах. Вся длина сваи была разделена путем добавления узлов через равные промежутки времени. Пружинные опоры были созданы в соответствии с различными типами грунта по длине сваи с использованием уравнения. (5), а затем он был назначен в узлах для их соответствующей глубины. Свойства материалов, присвоенные сваям, приведены в таблице 5.Полноразмерная таблица
Сваи были нагружены на закрепленный конец путем приложения горизонтальной нагрузки и вертикальной нагрузки, как показано в Таблице 1. Анализ модели был потом проводили. Значения изгибающего момента и смещения были получены в результате анализа. Максимальный изгибающий момент был получен на закрепленном конце по диаграмме изгибающего момента.
Рис. 1 На рисунке 1 показана модель грунтового источника для моста Куричиккал, основанная на подходе IS. Максимальное значение изгибающего момента в узлах вместе с диаграммой изгибающего момента показано на рис. 2.
На рисунке 1 показана модель грунтового источника для моста Куричиккал, основанная на подходе IS. Максимальное значение изгибающего момента в узлах вместе с диаграммой изгибающего момента показано на рис. 2.Источник : IS 2911 (Часть 1/Разд. 2)-2010
График, показывающий глубину закрепления, где L 1 = 3-кратный диаметр сваи.
Изображение в полный размер
Рис. 2Источник : Matlock and Reese [9]
График, показывающий значения коэффициента изгибающего момента.
Полноразмерное изображение
Валидация численной модели
K s , выбранный из IS 2911-2010 для основного состояния почвы, использовался для моделирования почвенных пружин в STAAD.Pro. В этом подходе K s , полученное из Таблицы 4, было присвоено всем опорным пружинам как жесткость пружины и проанализировано для получения изгибающего момента и прогиба свай.

Результаты, полученные таким образом с помощью STAAD.Pro, были проверены путем сравнения с результатом, полученным с помощью уравнения Мэтлока и Риза [9]. Уравнение Мэтлока и Риза [9] для изгибающего момента и прогиба поперечно нагруженных свай приведены в уравнениях. (9) и (10) (рис. 3).
Рис. 3Источник : Мэтлок и Риз [9{3} }}{{E_{P} I_{P} }}$$
(10)
где C м — коэффициент момента, C Y — коэффициент прогиба, H — поперечная нагрузка в кН, T – коэффициент жесткости в м, E P – модуль Юнга материала сваи в кН/м 2 , I P – момент инерции поперечного сечения сваи, м 4 η ч – модуль реакции грунтового основания в МН/м 3 . Значение коэффициента изгибающего момента и коэффициента прогиба были получены из IS 29.11 [5].
Результаты, полученные с помощью уравнения Матлока и Риза [9], и результаты, полученные с помощью STAAD.
 Pro, были сопоставлены и сведены в таблицу 6. и STAAD.Pro с Ks на основе IS 2911-2010
Pro, были сопоставлены и сведены в таблицу 6. и STAAD.Pro с Ks на основе IS 2911-2010 Полноразмерная таблица
На основе сравнения значений, полученных для изгибающего момента и прогиба с использованием решения Reese и Matlock [9] и STAAD.Pro дал приемлемый процент вариации . Для изгибающего момента, а также для прогиба, полученное процентное отклонение было ниже, что является вполне приемлемым, и, следовательно, значения, полученные с помощью STAAD.Pro, были подтверждены.
Результаты и обсуждение
Прогибы и изгибающие моменты, рассчитанные по IS 2911, приведены в таблице 7.
Таблица 7 Прогибы и изгибающие моменты по IS 2911 по IS 2911(часть 1/сек 2)-2010 и с использованием Стандартного программного комплекса STAAD.Pro со значением модуля реакции грунтового основания K s , рассчитанным по IS 2911(часть 1/сек 2)-2010 сравнили и свели в таблицу 8. Таблица 8 Результаты изгибающего момента и прогиба по IS 2911-2010 и STAAD. Pro с Ks на основе IS 2911-2010
Pro с Ks на основе IS 2911-2010 Полноразмерная таблица
При анализе полученных результатов было видно, что момент и прогиб двумя методами показывали широкий диапазон в зависимости от условий грунта и независимо от того, была ли висячая свая или опорная свая. Для несвязного грунта в случае как висячей сваи, так и опорной сваи процентное изменение изгибающего момента составляло около 38 %, а прогиба — около 39 %.%. Полученная вариация была немного выше в случае условий связного грунта. Для связного грунта в случае как висячей, так и концевой несущей сваи процентное изменение изгибающего момента составляло около 60%, а прогиба – около 84%.
Значения изгибающего момента и прогиба, полученные по ГОСТ 2911(ч.1/с2)-2010 и с использованием Стандартного программного комплекса STAAD.Pro со значением модуля реакции грунтового основания К с , рассчитанным по уравнению Весича сравнивается и приводится в таблице 9..
Таблица 9 Результаты изгибающего момента и прогиба по IS 2911-2010 и STAAD. Pro с Ks на основе уравнения Весича
Pro с Ks на основе уравнения Весича Таблица в натуральную величину с K s на основе уравнения Весича можно сделать вывод, что для несвязного грунта процентное изменение изгибающего момента составляет около 66%, а прогиба составляет около 90%. Это не имеет значения для висячей или опорной сваи. Но дело обстоит иначе для связного грунта. Висячие сваи в связном грунте демонстрируют изменение изгибающего момента примерно на 75 %, а прогиб составляет примерно 95%. В то время как опорные сваи в одном и том же состоянии грунта показывают лишь около 50 % изменения изгибающего момента, а прогиб составляет около 75 %.
В обоих анализах, то есть при анализе сравнения между значениями, полученными для изгибающего момента и прогиба, как указано в IS 2911 [5] и с использованием стандартного программного пакета STAAD. Pro со значением модуля реакции грунтового основания К с , рассчитанным по самому ГОСТ 2911(ч. 1/с 2)-2010 и со значением модуля реакции грунтового основания К s , рассчитанные по уравнению Весича [2], значения изгибающего момента и прогиба оказались намного выше, когда они рассчитывались в соответствии с общепринятым стандартом IS 2911 [5].

Заключение
Была сделана попытка количественно оценить степень консервативности метода IS при расчете поперечно нагруженных свай. Изгибающий момент и прогиб, полученные с использованием стандартного метода IS 2911 [5], оказались на 80 % выше, чем полученные по математической модели пружины в STAAD.Pro на основе уравнения Весича. Поскольку Департамент общественных работ Кералы в настоящее время принимает обычную IS 2911 [5] для расчета поперечно нагруженных свай в мостах, они учитывают более высокое значение изгибающего момента, а также прогиба, чем полученное из математической модели, основанной на уравнении Весича. Таким образом, конструкции, выполненные с использованием этого стандарта IS 2911 [5], оказались неэкономичными и консервативными.
Ссылки
К.С. Бирид, Анализ прогиба головки сваи на основе теории, программного обеспечения и полевых испытаний, в Proceedings of Indian Geotechnical Conference , Пуна (2015), стр.
 17–19
17–19А.С. Весич, Изгиб балки, опирающейся на изотропные упругие тела. Дж. Инж. мех. Отд. ASCE 87 (2), 35–53 (1961)
Google ученый
Дж. Садрекарими, М. Акбарзад, Сравнительное исследование методов определения коэффициента реакции грунтового основания. Электрон. Дж. Геотех. англ. 14 (Пакет E), 1–14 (2009)
Google ученый
Дж. К. Шукла, П. Дж. Шукла, Д. Л. Шах, Сравнение поперечной несущей способности сваи с использованием упрощенного метода линейной пружины и IS 2911 (2010), в Proceedings of Indian Geotechnical Conference , Roorkee (2013), стр. 22–24
IS 2911 (Часть I/ Раздел II): 2010 г., Проектирование и строительство свайных фундаментов (Бюро индийских стандартов, Нью-Дели)
IRC 6:2014, Стандартные спецификации и свод правил для автомобильных мостов, Раздел II — Нагрузки и напряжения (Индийский дорожный конгресс , Нью-Дели)
“>
Дж. Э. Боулз, Анализ и проектирование фундамента, 5-е изд. (The McGraw-Hill Companies, Inc., Нью-Йорк, 1997), стр. 123, 308, 502–503
Дж. Э. Боулз, Анализ фундамента и дизайн , 4-е изд. (The McGraw-Hill Companies, Inc., Нью-Йорк, 1988 г.), с. 308
Google ученый
Х. Мэтлок, Л.К. Риз, Анализ фундамента морских свайных конструкций, Труды пятой международной конференции по механике грунтов и проектированию фундаментов , Франция, том. 2 (1961), стр. 91–97
Ссылки на скачивание
Благодарности
Авторы благодарят инженеров Департамента общественных работ штата Керала за их помощь и поддержку в сборе данных.
Информация об авторе
Авторы и организации
Инженерный колледж Тривандрам, Тируванантапурам, Керала, Индия
П. К. Джаясри, Р. Урмила и Х. Шрилакшми
- 9000
Департамент общественных работ Кералы, Тируванантапурам, Керала, Индия
К.
 В. Арун
В. Арун
Авторы
- П. К. Джаясри
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- К. В. Арун
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- R. Oormila
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- H. Sreelakshmi
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Автор, ответственный за корреспонденцию
П. К. Джаясри.
Права и разрешения
Перепечатка и разрешения
Об этой статье
Горизонтальная реакция грунтового основания в свайных фундаментах
Введение
Горизонтальную реакцию грунтового основания в свайных фундаментах часто определяют по методу Брома (Broms, 1964).
 Этот метод широко используется, поскольку он учитывает длину свай (короткие или длинные), тип грунта (связный или несвязный) и граничные условия на оголовке сваи (свободный или фиксированный).
Этот метод широко используется, поскольку он учитывает длину свай (короткие или длинные), тип грунта (связный или несвязный) и граничные условия на оголовке сваи (свободный или фиксированный).Метод вводит некоторые упрощения, такие как жестко-идеально пластическое поведение при взаимодействии сваи с грунтом и зависимость реакции грунтового основания от типа грунта. Его главный недостаток заключается в том, что его нельзя наносить на слоистый субстрат.
Классификация отклика сваи
Согласно Broms (1964), первым этапом анализа является определение длины сваи (короткая, средняя или длинная). Характеристика зависит от механических и формообразующих характеристик сваи, а также от механических свойств грунта.
Соответственно реакция сваи классифицируется как показано Таблица 1 . Ориентировочные значения k 0 и n h 9Коэффициенты 0038 для переуплотненных глин и нормально уплотненных глин s и песков представлены в таблицах 2 и 3 (Kavvadas, 2008) соответственно.

Таблица 1 : Классификация отклика сваи на основе Broms (1964).
Таблица 2 : Предлагаемые значения модуля Винкера реакции земляного полотна для переуплотненных глин, полученные в результате испытаний стандартной квадратной плиты шириной B=0,305 м (Kavvadas, 2008).
Таблица 3 : Предлагаемые значения коэффициента n h для песков и нормально сцементированных глин (Kavvadas, 2008).
На основании полученной реакции сваи (короткая, промежуточная или длинная), типа грунта и того, определяется ли свая как со свободной или с фиксированной головкой, Бромс (1964) классифицировал определенные случаи, касающиеся земляного полотна. реакции и развиваемого изгибающего момента. Эти случаи анализируются ниже.
Короткие сваи
Согласно Broms (1964), короткая свая разрушается, когда приложенная горизонтальная нагрузка превышает предельное боковое сопротивление грунта.

Связные грунты — свая со свободной головкой
разработан, как показано на Рисунок 1 .
Рисунок 1 : Деформация (преувеличенная) короткой , свободнонапорной сваи под действием максимальной горизонтальной нагрузки N u в несвязных грунтах. Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю.K — коэффициент бокового давления грунта, который рассчитывается как отношение горизонтального эффективного напряжения к вертикальному эффективному напряжению как:
Когда свая подвергается горизонтальной нагрузке, грунт вынужден развивать свое максимальное боковое сопротивление, известное как боковое давление в пассивном состоянии. Максимальное значение коэффициента K обозначается как K P . Этот коэффициент является функцией угла трения грунта ( φ , в градусах) и рассчитывается как:
Максимальное развиваемое давление грунта на подошву сваи равно:
Broms (1964) вывел предельную горизонтальную нагрузку N u , которую свая может выдержать до разрушения грунта, как:
свая, соответственно, γ относится к массе грунта (кН/м 3 ), а e представляет собой расстояние между свободным концом сваи и поверхностью земли (м), как показано на рис.
 Рисунок 1 .
Рисунок 1 .Максимальный изгибающий момент развивается на определенной глубине z и его значение равно:
где:
Затем полученный изгибающий момент можно сравнить с несущей способностью сваи.
Бессвязные грунты – свая с фиксированной головкой
В случае коротких коротких , неподвижных свай , основанных на несвязном грунте , реакция земляного полотна не меняется по сравнению со сваей со свободной головкой. Однако как характер деформации, так и распределение изгибающего момента различаются, как показано на рис. 9.0341 Рисунок 2 .
Рисунок 2 : Деформация (преувеличенная) короткой , фиксированной головки под действием максимальной горизонтальной нагрузки N u в несвязных грунтах. Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю.
Максимальное полученное давление грунта такое же, как и в случае сваи со свободным концом; поэтому его можно рассчитать с помощью уравнения [3] .
Тем не менее, сваи с закрепленными концами могут нести более высокую предельную горизонтальную нагрузку, которая рассчитывается как: с фиксированным концом ( рис. 2 ).Связные грунты – свая со свободной головкой
Деформация короткой сваи , со свободной головкой в связной похож на случай несвязных грунтов, но реакция основания и развиваемый изгибающий момент отличаются ( Рисунок 3 ).
Рисунок 3 : Деформация (преувеличенная) сваи короткой , свободной сваи под действием максимальной горизонтальной нагрузки N u в связных грунтах . Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю.В связных грунтах прочность на сдвиг в недренированном состоянии c u используется для получения максимальной боковой реакции земляного полотна.
 c u практически представляет собой прочность грунта на сдвиг при постоянном объеме. Обычно он используется на глинистых почвах, когда скорость нагрузки намного выше, чем скорость дренажа, поэтому можно разумно предположить недренированное состояние. Следует отметить, что в описанных ниже случаях c u считается постоянным в пределах почвенного слоя.
c u практически представляет собой прочность грунта на сдвиг при постоянном объеме. Обычно он используется на глинистых почвах, когда скорость нагрузки намного выше, чем скорость дренажа, поэтому можно разумно предположить недренированное состояние. Следует отметить, что в описанных ниже случаях c u считается постоянным в пределах почвенного слоя.Соответственно, максимальное боковое давление грунта рассчитывается как:
Для получения максимальной горизонтальной нагрузки Н u требуется интегрирование поперечных сил, действующих на сваю. Интеграл поперечных сил в верхней части сваи до максимизации изгибающего момента дает:
Соответственно, соответствующий интеграл поперечных сил в нижней части сваи дает:
, где M макс, верхний = M макс, нижний . Кроме того, исходя из геометрии задачи, также можно рассмотреть следующее соотношение:
Наконец, максимальная горизонтальная нагрузка Н u связана с f , B и c 8 u как:
На основе уравнений [10], [11] , [12] и [13] максимальная горизонтальная нагрузка N u и максимальный изгибающий момент M max можно определить.

Связные грунты – свая с фиксированной головкой
В этом случае характер деформации аналогичен случаю короткой сваи со свободной головкой. Тем не менее, существуют различия в распределении бокового давления грунта и изгибающего момента ( Рисунок 4 ).
Рисунок 4 : Деформация (преувеличенная) короткой , с фиксированной головкой 9Свая 0527 подвергается максимальной горизонтальной нагрузке N u в связных грунтах . Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю.Максимальное давление грунтового основания такое же, как и в случае сваи со свободным концом, и рассчитывается по уравнению [9] . Соответствующая предельная горизонтальная нагрузка и максимальный изгибающий момент, которому подвергается свая, определяются с помощью уравнения [14] и [15] .
Длинные сваи
В отличие от коротких свай, когда длинные сваи подвергаются горизонтальной нагрузке, они разрушаются при превышении их максимального предела прочности на изгиб.
 Деформация сваи имеет тенденцию концентрироваться в пределах определенной длины L’ ( L’ ). Свая разрушается, когда на конце секции длиной L’ образуется пластический шарнир.
Деформация сваи имеет тенденцию концентрироваться в пределах определенной длины L’ ( L’ ). Свая разрушается, когда на конце секции длиной L’ образуется пластический шарнир.
Рисунок 5 : Деформация (преувеличенная) длинной , безголовой сваи под действием максимальной горизонтальной нагрузки N u в несвязные грунты. Также показано распределение реакции грунтового основания и изгибающего момента, действующих на сваю.Несвязные грунты – свая со свободной головкой
Поведение длинная , безголовая свая, основанная на несвязном грунте , при воздействии горизонтальной нагрузки отличается от короткой сваи. Характер деформации, поперечное давление грунта и распределение изгибающего момента показаны на рис. 5 .Как упоминалось выше, изгибающая способность сваи M u связана с максимальной горизонтальной нагрузкой N u .
Соответственно, N u получается как функция M u с использованием следующего уравнения: Значение M u зависит от характеристик сваи.
Значение M u зависит от характеристик сваи.The depth, f , where the plastic hinge forms is estimated as:
Cohesionless Soils – Fixed-head Pile
When a long , fixed-head pile Основанная на несвязном грунте , подвергается горизонтальной нагрузке, картина деформации аналогична модели длинной сваи со свободной головкой. Тем не менее, результирующая горизонтальная реакция грунтового основания и распределение изгибающего момента различаются, как показано на рис. 9.0341 Рисунок 6 .
Рисунок 6 : Деформация (преувеличенная) длинной , неподвижной оголовки под действием максимальной горизонтальной нагрузки N u в несвязных грунтах. Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю. Максимальное боковое давление грунта рассчитывается как:
Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю. Максимальное боковое давление грунта рассчитывается как: Как обсуждалось ранее, максимальная горизонтальная нагрузка N u получается через изгибающую способность сваи M u . Следовательно, N u вычисляется с использованием уравнения [16] , умноженного на два.
Связные грунты – свая со свободной головкой
В связных грунтах поведение длинной , свободной сваи аналогично. Разрушение обычно происходит, когда способность сваи к изгибу превышена. Как обсуждалось в случае с короткими сваями, боковое давление грунта рассчитывается с использованием недренированной прочности на сдвиг 9.0341 c u почвы.
Деформация длинной сваи со свободной головкой в связных грунтах такая же, как и в несвязных грунтах, но реакция грунтового основания и развиваемый изгибающий момент изменяются, как показано на рис.
Рисунок 7 : Деформация (преувеличенная) длинной , свободной головки под действием максимальной горизонтальной нагрузки N u в связном грунте . Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю. Максимальная горизонтальная реакция земляного полотна рассчитывается как: 7 .
7 .N u is derived as a function of M u as:
f refers to the point where the plastic hinge forms and is calculated as:
Связные грунты – свая с неподвижной головкой
В связных грунтах длинная , свая с неподвижной головкой деформируется так же, как и в несвязных грунтах. Однако боковое давление грунта и изгибающий момент изменяются, и распределение изгибающего момента будет немного изменено, как показано на рис. 9.0341 Рисунок 8 .
Рисунок 8 : Деформация (преувеличенная) длинной , неподвижной оголовки под действием максимальной горизонтальной нагрузки N u в связном грунте . Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю.
Максимальное боковое давление грунта рассчитывается по уравнению [19] . Предельная горизонтальная нагрузка, которая может быть приложена к свае до того, как она превысит допустимый изгибающий момент, определяется по следующему уравнению:0003
Пластичный шарнир формируется в точке f и аналогичным образом выводится из уравнения [21] .
Сваи средней длины
Для свай средней длины не существует единого подхода для расчета реакции земляного полотна и усилий сечения. Поэтому обычно рассматриваются методологии, используемые как для коротких, так и для длинных свай. Затем выбирается случай, дающий наибольший запас прочности.
 и, следовательно, соответственно получают минимальную горизонтальную нагрузку или грузоподъемность.
и, следовательно, соответственно получают минимальную горизонтальную нагрузку или грузоподъемность.Пример расчета
Свая с неподвижной головкой устанавливается на переуплотненном слое глины. Характеристики сваи и свойства глинистого слоя представлены в таблицах 4 и 5 соответственно. Сначала определяется реакция сваи (короткая, промежуточная или длинная), а затем рассчитываются реакция грунтового основания и изгибающий момент, действующий на сваю, с помощью одного из методов, проанализированных выше.
Таблица 4 . Конструктивные характеристики сваи, используемые в расчетном примере.
Таблица 5 . Свойства глинистого слоя.
Исходя из значения прочности недренированного грунта на сдвиг, предлагаемое значение k 0 ( Таблица 2 ) составляет k 0 4
= 35 8
. Следовательно, реакция сваи классифицируется по уравнениям Таблица 1 :Следовательно:
Соответственно, исходя из характеристик сваи и свойств грунта, свая может быть охарактеризована как короткая

Методика, которая будет использоваться, описана для короткой , фиксированной головки в связных грунтах .
Максимальное боковое давление грунта определяется по уравнению [9] :
Соответствующая предельная горизонтальная нагрузка и максимальный изгибающий момент рассчитываются с помощью уравнений [14] и [15] .
В результате максимальная горизонтальная нагрузка, которую может выдержать грунт без разрушения, составляет 22 950 кН . При такой горизонтальной нагрузке допустимый момент сваи должен быть больше M u =131 962,5 кН·м .
Схема деформации сваи, бокового давления грунта и моментной нагрузки, которой подвергается свая, изображены на Рисунок 9 .
Рисунок 9 : Деформация (преувеличенная) короткой сваи , с неподвижной головкой в связном грунте , используемом в примере. Максимальная горизонтальная нагрузка Н и . Приведены распределения реакции грунтового основания и изгибающего момента, действующих на сваю.
Максимальная горизонтальная нагрузка Н и . Приведены распределения реакции грунтового основания и изгибающего момента, действующих на сваю.Ссылки
Бромс, Б. (1964a). Боковое сопротивление сваи в связном грунте с. Журнал отделов механики грунтов и фундаментов. АССЕ, Том. 90, выпуск 2, стр. 27-63.
Бромс, Б. (1964а). Боковое сопротивление свай в несвязных грунтах . Журнал отделов механики грунтов и фундаментов. АССЕ, Том. 90, выпуск 3, стр. 123-156.
Каввадас (2008 г.). Фундаменты инженерной инфраструктуры . Национальный технический университет Афин, Греция.Сваи с боковой нагрузкой | Групповые сваи
Поведение одиночных свай по сравнению с групповыми сваями
Способность группы свай выдерживать боковые нагрузки является серьезной проблемой проектирования. Прогиб группы свай под действием боковой нагрузки обычно в 2-3 раза больше, чем прогиб одиночной сваи, нагруженной с такой же интенсивностью.
 Многие исследователи, начиная с раннего периода (например, Holloway et al. (1981) и Браун и др. (1988)) сообщили, что сваи в задних рядах групп свай имеют значительно меньшее сопротивление поперечной нагрузке, чем сваи в переднем ряду, и, следовательно, демонстрируют больший прогиб.
Многие исследователи, начиная с раннего периода (например, Holloway et al. (1981) и Браун и др. (1988)) сообщили, что сваи в задних рядах групп свай имеют значительно меньшее сопротивление поперечной нагрузке, чем сваи в переднем ряду, и, следовательно, демонстрируют больший прогиб.
Рисунок из FHWA (2010 г.)Способность группы свай выдерживать боковые нагрузки является серьезной проблемой проектирования. Прогиб группы свай под действием боковой нагрузки обычно в 2-3 раза больше, чем прогиб одиночной сваи, нагруженной с такой же интенсивностью. Многие исследователи, начиная с раннего периода (например, Holloway et al. (1981) и Браун и др. (1988)) сообщили, что сваи в задних рядах групп свай имеют значительно меньшее сопротивление поперечной нагрузке, чем сваи в переднем ряду, и, следовательно, демонстрируют больший прогиб.
Сваи в близко расположенных группах ведут себя иначе, чем одиночные изолированные сваи из-за взаимодействия сваи-грунта-сваи, которое происходит в группе.
 Общепризнанно, что из-за этих эффектов взаимодействия прогибы свай в близко расположенной группе больше, чем прогибы отдельной сваи при одинаковой нагрузке. Максимальный изгибающий момент в группе также будет больше, чем у одиночной сваи, потому что грунт ведет себя так, как будто он имеет меньшее сопротивление, позволяя группе прогибаться больше при той же нагрузке на сваю.
Общепризнанно, что из-за этих эффектов взаимодействия прогибы свай в близко расположенной группе больше, чем прогибы отдельной сваи при одинаковой нагрузке. Максимальный изгибающий момент в группе также будет больше, чем у одиночной сваи, потому что грунт ведет себя так, как будто он имеет меньшее сопротивление, позволяя группе прогибаться больше при той же нагрузке на сваю.Это неравномерное распределение нагрузки между сваями вызвано «затенением» — термином, используемым для описания перекрытия зон сдвига и последующего снижения сопротивления грунта.
Популярные методы учета эффектов взаимодействия:
- Эффективность группы свай
- P-множители
Эффективность группы свай
Стандартом для количественной оценки эффектов группового взаимодействия является коэффициент групповой эффективности Ge, определяемый как средняя поперечная грузоподъемность на сваю в группе, деленная на поперечную грузоподъемность одиночной сваи (Prakash 1990).

где (Qu)g — предельная поперечная грузоподъемность группы, n — количество свай в группе, а (Qu)s — предельная поперечная грузоподъемность одной сваи.
Факторы
Модельные и полномасштабные испытания показывают, что сваи не подвержены групповому воздействию, если они расположены далеко друг от друга. В литературе существует общее мнение, что групповые эффекты малы, когда расстояние между центрами свай превышает 6 диаметров сваи (6D) в направлении, параллельном нагрузке, и когда они превышают 3D, измеренное в направлении, перпендикулярном нагрузке.
Факторы, влияющие на эффективность группы, перечислены в порядке важности:
- Расстояние между сваями и расположение групп
- Размер группы
- Фиксатор головки сваи
- Тип и плотность почвы
- Смещение сваи
P-множители
Стандартом для количественной оценки эффектов группового взаимодействия является «p-множитель», эмпирический понижающий коэффициент для кривых p-y, предложенный Brown et al.
 (1988). Этот метод учитывает потерю сопротивления грунта как за счет эффекта затенения, так и за счет неравномерного распределения сопротивления внутри группы. Каждой строке группы присваиваются разные значения p-множителей.
(1988). Этот метод учитывает потерю сопротивления грунта как за счет эффекта затенения, так и за счет неравномерного распределения сопротивления внутри группы. Каждой строке группы присваиваются разные значения p-множителей.Браун и др. (1988) предложили использовать p-множитель для модификации кривой p-y отдельной сваи в зависимости от положения ряда свай. Для свай в данном ряду одно и то же значение fm применяется ко всем кривым p-y по длине сваи. Боковая нагрузка отдельной сваи в группе свай зависит от ее положения в группе и расстояния между центрами свай.
Процедура
В процедуре используется тот же подход, что и при p-y анализе, за исключением того, что к значениям сопротивления грунта одиночной сваи применяется множитель (fm) со значением меньше единицы. Это снижает предельное сопротивление грунта и смягчает форму кривой p-y.
Рисунок, представляющий концепцию p-множителя для латерального группового анализа (по Mokwa, 1999).1 – Соберите данные испытаний под нагрузкой для построения кривых зависимости нагрузки от прогиба для каждой сваи в группе и отдельной сваи.

2 – Разработайте и скорректируйте кривые p-y одиночной сваи для моделирования условий грунта на испытательном полигоне до тех пор, пока не будет получено хорошее соответствие между рассчитанным и измеренным откликом одиночной сваи.
3 – Определение значений множителей fm путем проб и ошибок с использованием кривых p-y, разработанных для одиночной сваи, и измеренной реакции нагрузки на прогиб для свай в группе.Факторы
Факторы, влияющие на р-множители, перечислены в порядке важности:
- Расстояние
- Тип почвы
- Размеры сваи
- Процесс установки
- Отклонения
- Фиксация головы
Резюме
В следующей таблице представлены как коэффициент эффективности группы, так и p-множители, как два метода количественной оценки снижения емкости сваи, расположенной в группе, по сравнению с одиночной сваей. В качестве индикатора используется отношение прогиба головы сваи.

Стол. Обзор факторов групповой эффективности и р-множителей в литературе
Меймон и др. (1986) Clay 2 3d 0.5 – 0.71 0.9 0.5 – – – Morrison and Reese (1986) Sand 3 3d 0,58 – 0,9 0,8 0,4 0,3 – – Браун и др. (1987) Clay 3 3d 0.68 – 0.8 0.7 0.5 0.4 – – Brown et al. (1988) Sand 3 3d 0.63 – 0.7 0.8 0.4 0.3 – – Ruesta & Townsend (1997) Sand 4 3д 0,6 – 0,91 0,8 0,7 0,3 0,3 – Rollins et al.  (1998)
(1998)Clay 3 3d 0.59 – 0.8 0.6 0.38 0.43 – – Mokwa (1999) Sand 2 4d – 0,85 0,75 – – – Rollins and Sparks (2000) Silts & Clays 3 3d – 0.6 0.38 0.43 – – Cho et al. (2001) Rock – – 0.59-0.80 0.6 0.38 0.43 – – Huang et al. (2001) Песок 3 3d 0,92 – 1,02 0,93 0,7 0,74 – – Huang et al. (2001) Sand 4 3d 0.72 – 0.  89
890.89 0.61 0.61 0.66 – Rollins & Sparks (2002) Silts & Clays 3 3d – 0,6 0,38 0,43 – – Снайдер и др. (2004) Clay 5 3.92d 0.85-0.90 1 0.81 0.59 0.71 0.59 Rollins et al. (2005) Sand 3 3.3 d 0.72 – 0.935 0.8 0.4 0.4 – – Rollins et al. (2006) Clay 3 5.65d 0.87 – 1.08 0.95 0.88 0.77 – – Clay 4 4.4d 0.75 – 1.0 0.9 0.8 0. 


 Однако, уровень достоверности численных расчетов существенно зависит от применяемой модели грунта;
Однако, уровень достоверности численных расчетов существенно зависит от применяемой модели грунта;
 Основными недостатками этих зависимостей является большое количество используемых эмпирических параметров и весьма приближенное отражение реальной деформируемости основания. Есть предположения [21, 50], с помощью которых можно рассчитать сваю с переменным коэффициентом постели, характеризующим способность основания к нелинейной местной деформации. Однако авторами не приводятся рекомендации по определению коэффициентов, учитывающих напряженное состояние грунта, или они строго ограничены условиями проведенных опытов.
Основными недостатками этих зависимостей является большое количество используемых эмпирических параметров и весьма приближенное отражение реальной деформируемости основания. Есть предположения [21, 50], с помощью которых можно рассчитать сваю с переменным коэффициентом постели, характеризующим способность основания к нелинейной местной деформации. Однако авторами не приводятся рекомендации по определению коэффициентов, учитывающих напряженное состояние грунта, или они строго ограничены условиями проведенных опытов. Но, как показали исследования, при определении несущей способности свайной группы следует учитывать совместную работу опор в фундаменте [46, 50].
Но, как показали исследования, при определении несущей способности свайной группы следует учитывать совместную работу опор в фундаменте [46, 50].
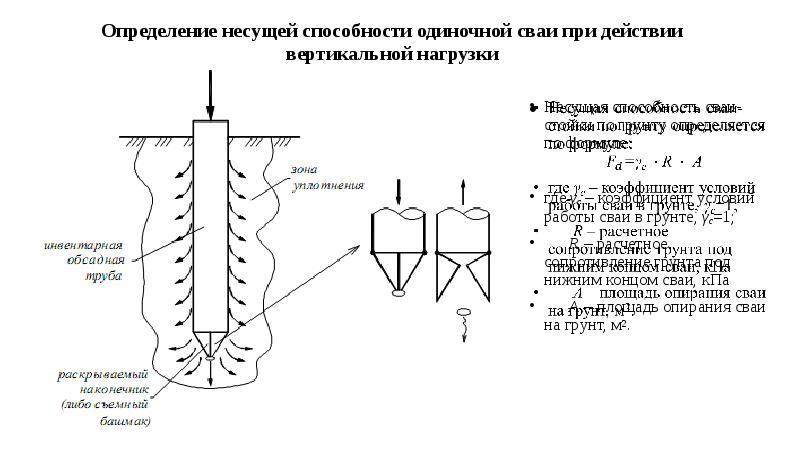
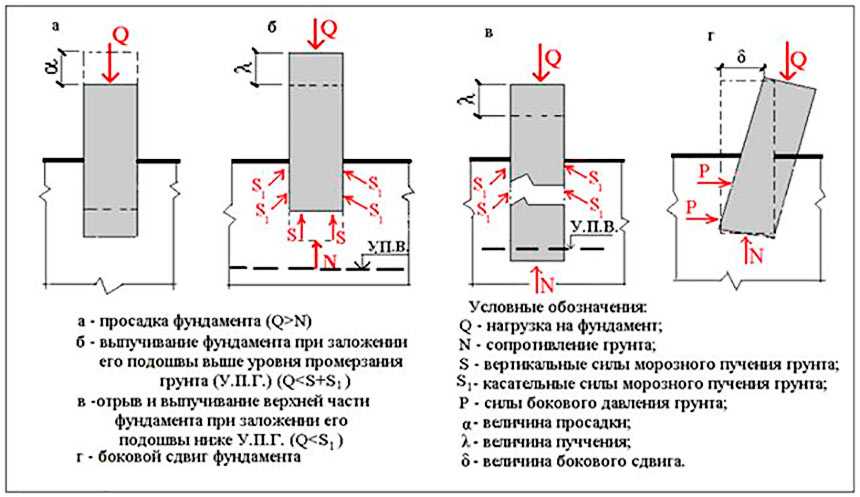

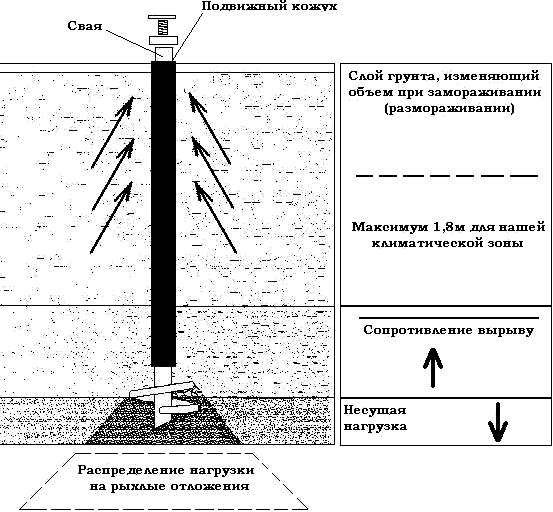 SREELAKSHMI 1 9008
SREELAKSHMI 1 9008 обращений
обращений Залитые на месте сваи с неподвижной головкой, заделанные в три грунта, рассматривались и анализировались по отдельности. Сваи также были смоделированы в программном обеспечении STAAD.Pro на основе IS-подхода, и результаты были проверены с использованием Matlock и Reese (в материалах пятой международной конференции по механике грунтов и проектированию фундаментов, 1961) уравнение. Результаты были представлены в виде процентного изменения значений изгибающего момента и прогиба, полученных разными методами. Результаты, полученные с помощью математической модели, основанной на уравнении Весича, и результаты, полученные в соответствии с подходом IS, были сопоставлены, и метод IS был признан неэкономичным и консервативным.
Залитые на месте сваи с неподвижной головкой, заделанные в три грунта, рассматривались и анализировались по отдельности. Сваи также были смоделированы в программном обеспечении STAAD.Pro на основе IS-подхода, и результаты были проверены с использованием Matlock и Reese (в материалах пятой международной конференции по механике грунтов и проектированию фундаментов, 1961) уравнение. Результаты были представлены в виде процентного изменения значений изгибающего момента и прогиба, полученных разными методами. Результаты, полученные с помощью математической модели, основанной на уравнении Весича, и результаты, полученные в соответствии с подходом IS, были сопоставлены, и метод IS был признан неэкономичным и консервативным. Свая смещается по горизонтали в ответ на приложенную нагрузку, что приводит к изгибу, вращению или перемещению сваи.
Свая смещается по горизонтали в ответ на приложенную нагрузку, что приводит к изгибу, вращению или перемещению сваи. Точность результатов в STAAD.Pro будет зависеть от жесткости пружины, которая, в свою очередь, связана с модулем реакции грунтового основания ( k s ) почвы. Разработано несколько уравнений для оценки k s для упругих грунтов на основе испытаний и теоретических анализов, из которых методы определения значения k s на основе соотношения Весича [2] дали приемлемую точность [3]. IS 2911-2010 (Часть 1/Раздел 2) использует эквивалентный консольный подход для расчета поперечно нагруженных свай. Исследования, проведенные с использованием балочного подхода на упругом основании, оказались более эффективными, чем метод IS [4].
Точность результатов в STAAD.Pro будет зависеть от жесткости пружины, которая, в свою очередь, связана с модулем реакции грунтового основания ( k s ) почвы. Разработано несколько уравнений для оценки k s для упругих грунтов на основе испытаний и теоретических анализов, из которых методы определения значения k s на основе соотношения Весича [2] дали приемлемую точность [3]. IS 2911-2010 (Часть 1/Раздел 2) использует эквивалентный консольный подход для расчета поперечно нагруженных свай. Исследования, проведенные с использованием балочного подхода на упругом основании, оказались более эффективными, чем метод IS [4].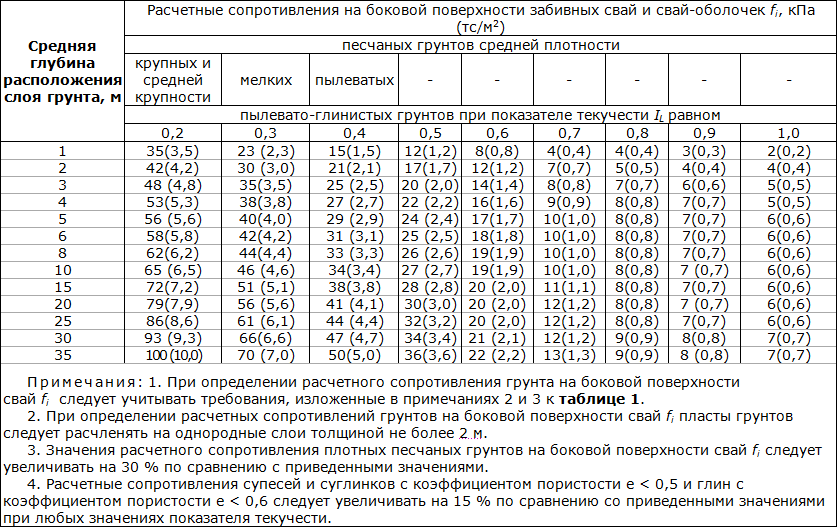 Pro. Этим предполагается установить, насколько консервативен метод ИС по сравнению с математическим подходом.
Pro. Этим предполагается установить, насколько консервативен метод ИС по сравнению с математическим подходом. Из полученных таким образом суммарных горизонтальных и вертикальных нагрузок, действующих на группу свай, были определены горизонтальные и вертикальные нагрузки, действующие на одну сваю на каждой площадке моста, которые приведены в таблице 1.
Из полученных таким образом суммарных горизонтальных и вертикальных нагрузок, действующих на группу свай, были определены горизонтальные и вертикальные нагрузки, действующие на одну сваю на каждой площадке моста, которые приведены в таблице 1.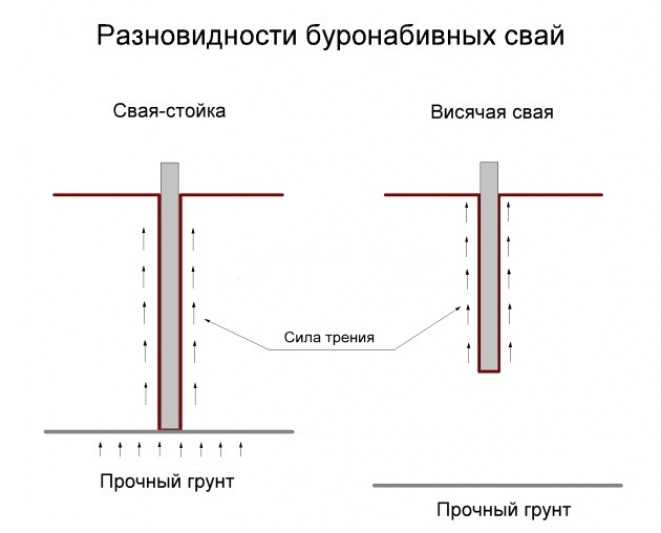
 3k_{1} }}{1.5B}$$
3k_{1} }}{1.5B}$$ Весич [2] проанализировал бесконечную горизонтальную балку на упругом основании и сравнил результаты с результатами, полученными с использованием теории реакции грунтового основания, связав модуль реакции грунтового основания с параметрами упругости. Модуль реакции грунтового основания различных слоев грунта на каждом участке моста был рассчитан с использованием уравнения Весича, приведенного в уравнении. (6). 9{2} } \right)$$
Весич [2] проанализировал бесконечную горизонтальную балку на упругом основании и сравнил результаты с результатами, полученными с использованием теории реакции грунтового основания, связав модуль реакции грунтового основания с параметрами упругости. Модуль реакции грунтового основания различных слоев грунта на каждом участке моста был рассчитан с использованием уравнения Весича, приведенного в уравнении. (6). 9{2} } \right)$$ Изначально геометрия сваи создавалась по чертежу. Затем этим сваям были присвоены свойства материала из бетона М40. Следующим шагом было создание условий поддержки на обоих конечных узлах. Вся длина сваи была разделена путем добавления узлов через равные промежутки времени. Пружинные опоры были созданы в соответствии с различными типами грунта по длине сваи с использованием уравнения. (5), а затем он был назначен в узлах для их соответствующей глубины. Свойства материалов, присвоенные сваям, приведены в таблице 5.
Изначально геометрия сваи создавалась по чертежу. Затем этим сваям были присвоены свойства материала из бетона М40. Следующим шагом было создание условий поддержки на обоих конечных узлах. Вся длина сваи была разделена путем добавления узлов через равные промежутки времени. Пружинные опоры были созданы в соответствии с различными типами грунта по длине сваи с использованием уравнения. (5), а затем он был назначен в узлах для их соответствующей глубины. Свойства материалов, присвоенные сваям, приведены в таблице 5. На рисунке 1 показана модель грунтового источника для моста Куричиккал, основанная на подходе IS. Максимальное значение изгибающего момента в узлах вместе с диаграммой изгибающего момента показано на рис. 2.
На рисунке 1 показана модель грунтового источника для моста Куричиккал, основанная на подходе IS. Максимальное значение изгибающего момента в узлах вместе с диаграммой изгибающего момента показано на рис. 2.
 Pro, были сопоставлены и сведены в таблицу 6. и STAAD.Pro с Ks на основе IS 2911-2010
Pro, были сопоставлены и сведены в таблицу 6. и STAAD.Pro с Ks на основе IS 2911-2010  Pro с Ks на основе IS 2911-2010
Pro с Ks на основе IS 2911-2010  Pro с Ks на основе уравнения Весича
Pro с Ks на основе уравнения Весича 
 17–19
17–19 В. Арун
В. Арун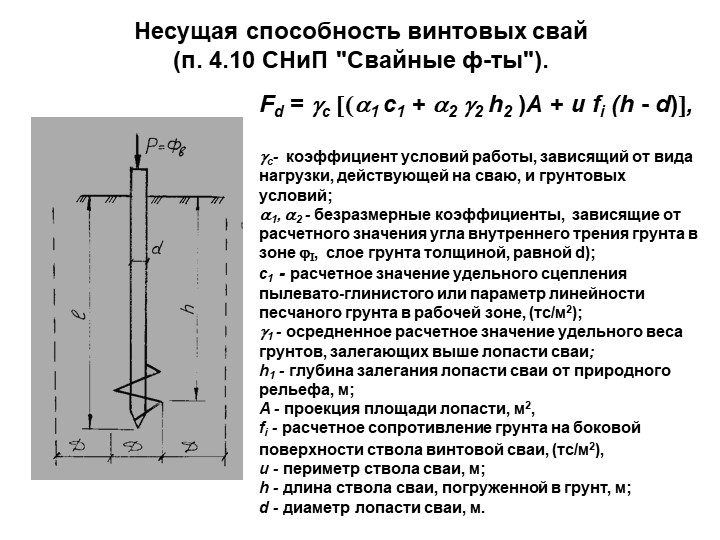 Этот метод широко используется, поскольку он учитывает длину свай (короткие или длинные), тип грунта (связный или несвязный) и граничные условия на оголовке сваи (свободный или фиксированный).
Этот метод широко используется, поскольку он учитывает длину свай (короткие или длинные), тип грунта (связный или несвязный) и граничные условия на оголовке сваи (свободный или фиксированный).
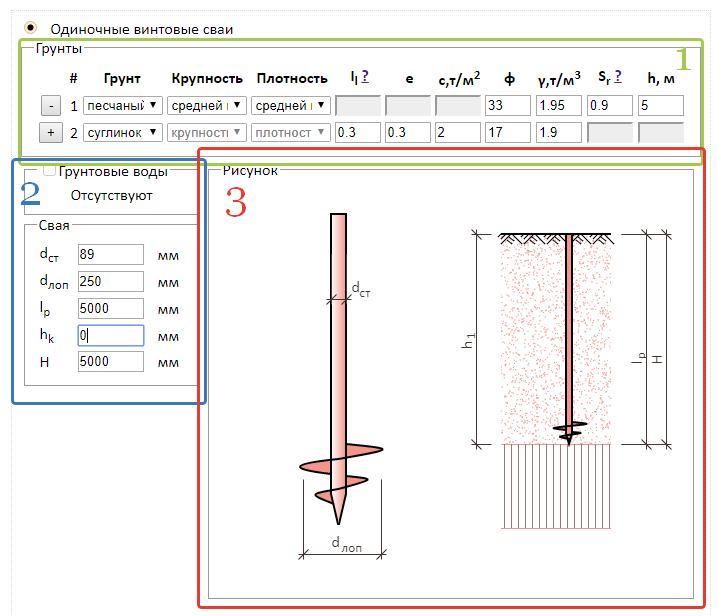
 Рисунок 1 .
Рисунок 1 .
 c u практически представляет собой прочность грунта на сдвиг при постоянном объеме. Обычно он используется на глинистых почвах, когда скорость нагрузки намного выше, чем скорость дренажа, поэтому можно разумно предположить недренированное состояние. Следует отметить, что в описанных ниже случаях c u считается постоянным в пределах почвенного слоя.
c u практически представляет собой прочность грунта на сдвиг при постоянном объеме. Обычно он используется на глинистых почвах, когда скорость нагрузки намного выше, чем скорость дренажа, поэтому можно разумно предположить недренированное состояние. Следует отметить, что в описанных ниже случаях c u считается постоянным в пределах почвенного слоя.
 Деформация сваи имеет тенденцию концентрироваться в пределах определенной длины L’ ( L’ ). Свая разрушается, когда на конце секции длиной L’ образуется пластический шарнир.
Деформация сваи имеет тенденцию концентрироваться в пределах определенной длины L’ ( L’ ). Свая разрушается, когда на конце секции длиной L’ образуется пластический шарнир. Значение M u зависит от характеристик сваи.
Значение M u зависит от характеристик сваи.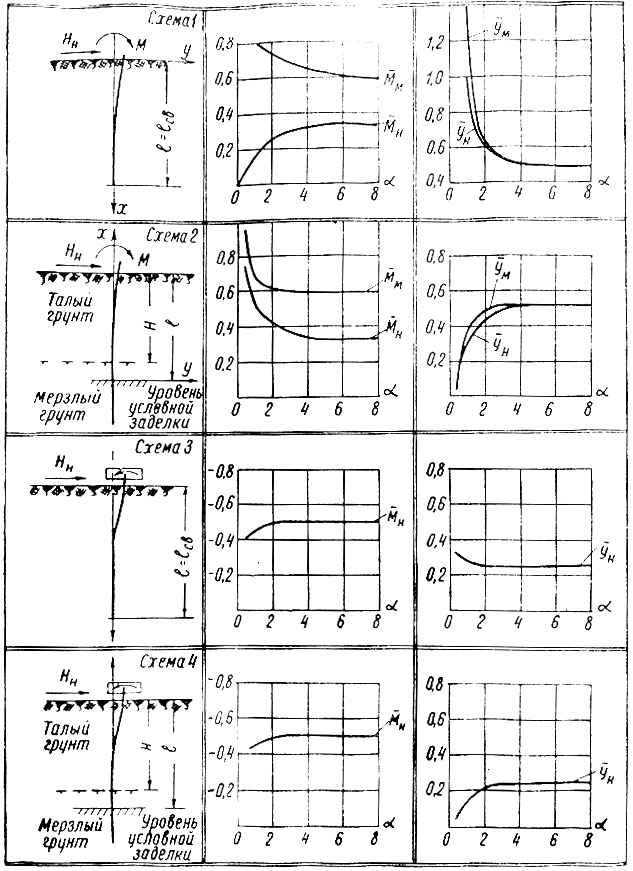 Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю. Максимальное боковое давление грунта рассчитывается как:
Также показано распределение реакции грунтового основания и изгибающего момента, действующего на сваю. Максимальное боковое давление грунта рассчитывается как: 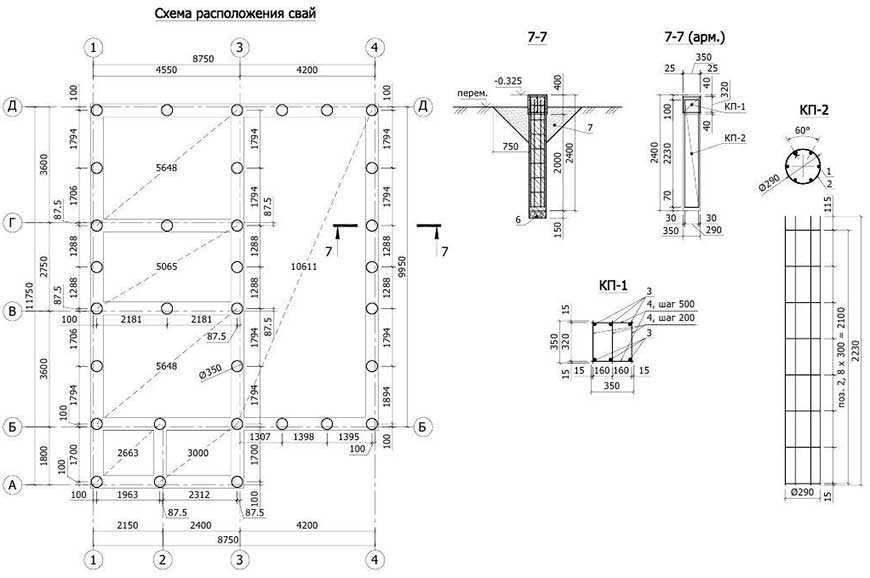 7 .
7 .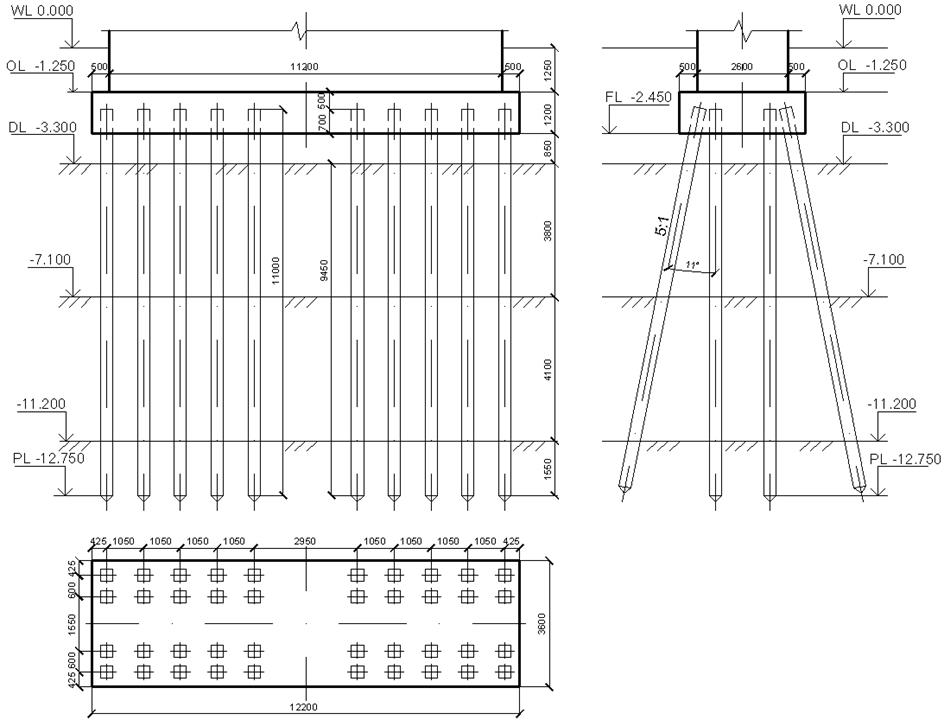
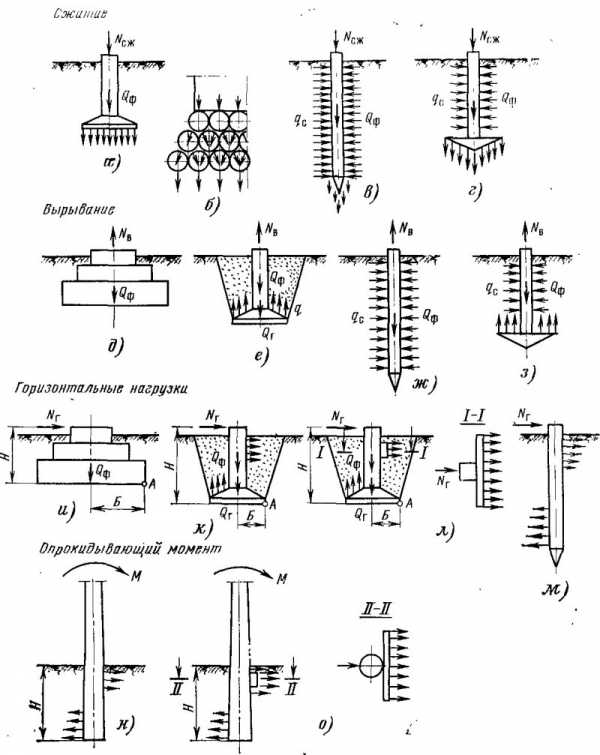 и, следовательно, соответственно получают минимальную горизонтальную нагрузку или грузоподъемность.
и, следовательно, соответственно получают минимальную горизонтальную нагрузку или грузоподъемность.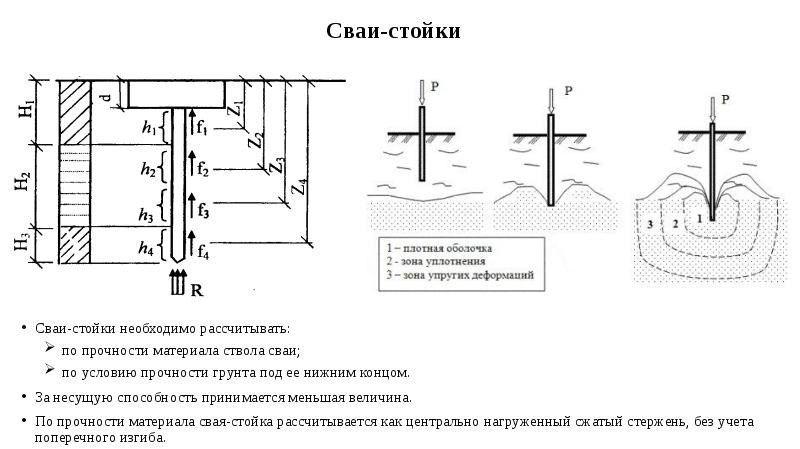
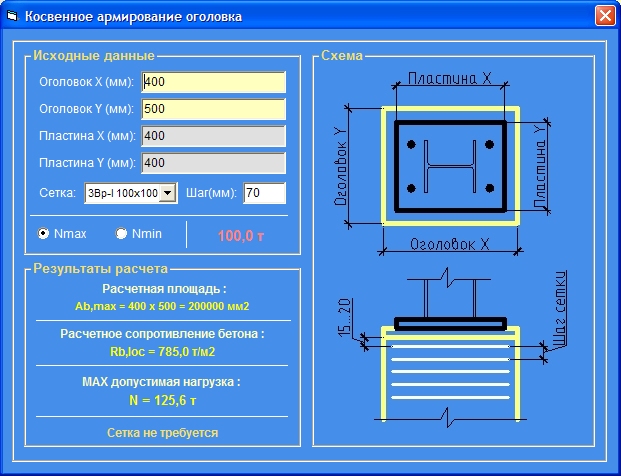 Максимальная горизонтальная нагрузка Н и . Приведены распределения реакции грунтового основания и изгибающего момента, действующих на сваю.
Максимальная горизонтальная нагрузка Н и . Приведены распределения реакции грунтового основания и изгибающего момента, действующих на сваю. Многие исследователи, начиная с раннего периода (например, Holloway et al. (1981) и Браун и др. (1988)) сообщили, что сваи в задних рядах групп свай имеют значительно меньшее сопротивление поперечной нагрузке, чем сваи в переднем ряду, и, следовательно, демонстрируют больший прогиб.
Многие исследователи, начиная с раннего периода (например, Holloway et al. (1981) и Браун и др. (1988)) сообщили, что сваи в задних рядах групп свай имеют значительно меньшее сопротивление поперечной нагрузке, чем сваи в переднем ряду, и, следовательно, демонстрируют больший прогиб. Общепризнанно, что из-за этих эффектов взаимодействия прогибы свай в близко расположенной группе больше, чем прогибы отдельной сваи при одинаковой нагрузке. Максимальный изгибающий момент в группе также будет больше, чем у одиночной сваи, потому что грунт ведет себя так, как будто он имеет меньшее сопротивление, позволяя группе прогибаться больше при той же нагрузке на сваю.
Общепризнанно, что из-за этих эффектов взаимодействия прогибы свай в близко расположенной группе больше, чем прогибы отдельной сваи при одинаковой нагрузке. Максимальный изгибающий момент в группе также будет больше, чем у одиночной сваи, потому что грунт ведет себя так, как будто он имеет меньшее сопротивление, позволяя группе прогибаться больше при той же нагрузке на сваю.
 (1988). Этот метод учитывает потерю сопротивления грунта как за счет эффекта затенения, так и за счет неравномерного распределения сопротивления внутри группы. Каждой строке группы присваиваются разные значения p-множителей.
(1988). Этот метод учитывает потерю сопротивления грунта как за счет эффекта затенения, так и за счет неравномерного распределения сопротивления внутри группы. Каждой строке группы присваиваются разные значения p-множителей.

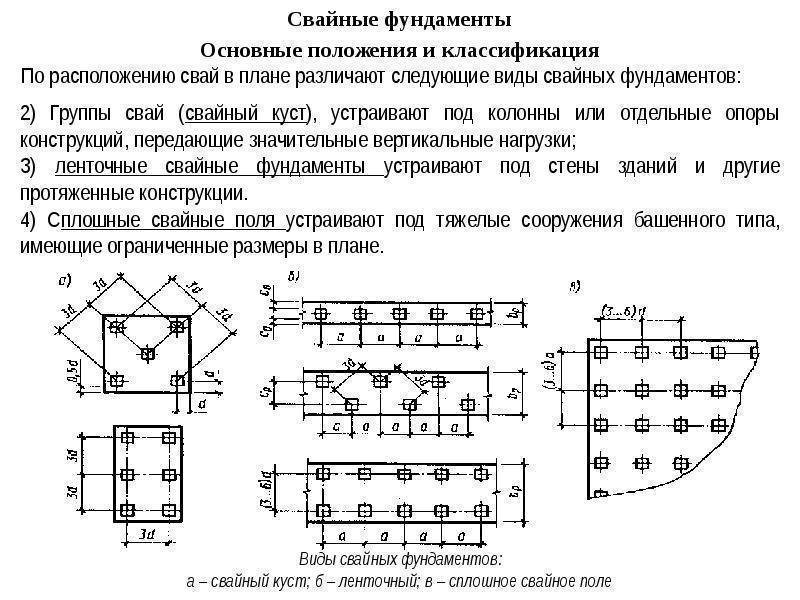 (1998)
(1998) 89
89