Правильность измерений это: Что Такое Правильность Измерений? – Метрологический надзор

Метрология и стандартизация

Поможем написать любую работу на аналогичную тему

• Реферат

  Метрология и стандартизация

  От 250 руб

• Контрольная работа

  Метрология и стандартизация

  От 250 руб

• Курсовая работа

  Метрология и стандартизация

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Метроло́гия — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Предметом метрологии является извлечение количественной информации о свойствах объектов с заданной точностью и достоверностью; нормативная база для этого — метрологические стандарты.

Метрология состоит из трёх основных разделов:

• Теоретическая или фундаментальная — рассматривает общие теоретические проблемы (разработка теории и проблем измерений физических величин, их единиц, методов измерений).
• Прикладная — изучает вопросы практического применения разработок теоретической метрологии. В её ведении находятся все вопросы метрологического обеспечения.
• Законодательная — устанавливает обязательные технические и юридические требования по применению единиц физической величины, методов и средств измерений.

Стандартиза́ция — деятельность по разработке, опубликованию и применению стандартов, по установлению норм, правил и характеристик в целях обеспечения безопасности продукции, работ и услуг для окружающей среды, жизни, здоровья и имущества, технической и информационной совместимости, взаимозаменяемости и качества продукции, работ и услуг в соответствии с уровнем развития науки, техники и технологии, единства измерений, экономии всех видов ресурсов, безопасности хозяйственных объектов с учётом риска возникновения природных и техногенных катастроф и других чрезвычайных ситуаций, обороноспособности и мобилизационной готовности страны.

Стандартизация направлена на достижение оптимальной степени упорядочения в определенной области посредством установления положений для всеобщего и многократного применения в отношении реально существующих или потенциальных задач.

За реализацию норм стандартизации отвечают органы стандартизации, наделенные законным правом руководить разработкой и утверждать нормативные документы и другие правила, придавая им статус стандартов.

В области промышленности стандартизация ведет к снижению себестоимости продукции, поскольку:

• позволяет экономить время и средства за счет применения уже разработанных типовых ситуаций и объектов;
• повышает надежность изделия или результатов расчетов, поскольку применяемые технические решения уже неоднократно проверены на практике;
• упрощает ремонт и обслуживание изделий, так как стандартные узлы и детали — взаимозаменяемые (при условии, что сборка осуществлялась без пригоночных операций).

На нашем сайте предоставлены учебные материалы для студентов, по метрологии и стандартизации. Суммарно около

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет стоимостиГарантииОтзывы

Качество измерений

В соответствии с положениями теоретической метрологии измерение может выполняться с использованием шкалы порядка (уровней), шкалы интервалов и шкалы отношений.

Во втором и третьем случаях результат измерения является случайной величиной и может записываться выражением:

где X – показание средства измерения;
– поправка.

Величина Х характеризует правильность показаний, а поправка – точность измерений. По этим параметрам измерительная техника разделяется на классы точности в соответствии с допускаемой погрешностью измерений.

Приведенная погрешность измеряется в процентах от верхнего предела измерений, относительная погрешность – то результата самого показания.

Используется ряд классов точности, в том числе: 0.1, 0.2, 0.5, 1.0, 1.5, 2.5, 4.0. Характеристикой класса является относительная погрешность, указываемая в процентах: 0.1, 0.5, 4.0.

Правильность результата измерения обеспечивается совпадением среднего значения измерений со значением измеряемой величины.

Значение Х – величина случайная, поправка не является случайной, она характеризует относительную погрешность измерения.

На рис. 1 показано распределение плотности вероятности при точных измерениях (1) и менее точных (2).

Рис.1 Распределение плотности вероятности при двух классах точности измерений

Если значение поправки с течением времени не меняется, то при многократном измерении постоянного размера одним и тем же средством измерений (в одинаковых условиях) получим:

где – средний арифметический результат измерений;
n – количество измерений; 

– среднее значение показания при измерении;
– значение поправки;
= const.

Это выражение показывает, что точность многократного измерения выше, но правильность такая же, как и при однократном измерении.

Пример 1. При метрологической аттестации вольтметра в нормальных условиях выполнено 100 измерений образцового напряжения в различных точках шкалы. Установлено, что распределение вероятности с дисперсией напряжение равно 1,5В. Смещение среднеарифметического значения в сторону меньших значений с вероятностью 0,95 достигает 0,3В. Необходимо сравнить качество однократных и многократных измерений.

Решение. Из результатов аттестации следует, что в показания вольтметра нужно вносить поправку +0,3В.

Стандартная ошибка (среднеквадратическое отклонение) составляет:

Если показания вольтметра U = 20В, то результат измерения можно записать в виде:

Результат измерения: U = 17,74 . .. 22,86 В

Точность многократного измерения выше, и соответствующие показатели качества измерения при девяти отсчетах составят:

Допустим, вольтметр дал девять показаний: 20; 21; 20,5; 21; 20,5; 21,5; 20,5; 20,5; 21,2. Тогда

Результат измерения можно записать следующим образом:

U = 20,188 … 21,892.

Погрешность составляет

При одновременном измерении одного и того же размера (параметра) разными средствами нужно верно квалифицировать исходную информацию.

Допустим, что точность и правильность однократных измерений отдельными средствами измерений известны, но в паспортных данных приборов приводится значение поправки, которую нужно ввести в показание. Результат измерения можно рассматривать как сумму двух случайных величин:

где m – число измерений.

Если X и подчиняется нормальному закону распределения, то точность и правильность определяют с использованием формул:

В рассматриваемом случае поправка рассматривается как случайная величина. Такая процедура называется

рандомизацией. Приведенные формулы показывают, что рандомизация результата измерения одного и того же параметра улучшается и по точности и по правильности.

Пример 2. В табл. 1 приведены числовые значения одиннадцати измерений одного и того же параметра разными средствами измерений. Даны поправки , заимствованные из паспортных данных. Вычислим средние значения измеренного параметра и поправок приборов:

После этого определим, в каких пределах находится измеряемое значение и каковы показатели качества результата измерения.

Номер прибора	Xi	Qi
1	48,3	0,3
2	48,5	-0,1
3	48,2
4	48,5	-0,5
5	48,4	0,2
6	48,6	-0,3
7	48,5	0,1
8	48,4
9	48,6	-0,4
10	48,0	0,5
11	48,4	-0,1

Таблица 1. Результаты измерений одного и того же параметра

Решение

1. Среднее значение показания и поправки:

2. Определим дисперсию

3. Результат измерения:

4. Дисперсия результата измерения:

5. С вероятностью, равной 0,95, можно утверждать, что значение (результат) не отличается от результата измерения больше, чем на поэтому измеряемое значение:

Погрешность

В начало

Содержание портала

1.4 Точность и прецизионность измерений – Биомеханика движений человека

Наука основана на наблюдении и эксперименте, то есть на измерениях. Точность показывает, насколько близко измерение к правильному значению для этого измерения. Например, предположим, что вы измеряете длину прыжка в длину.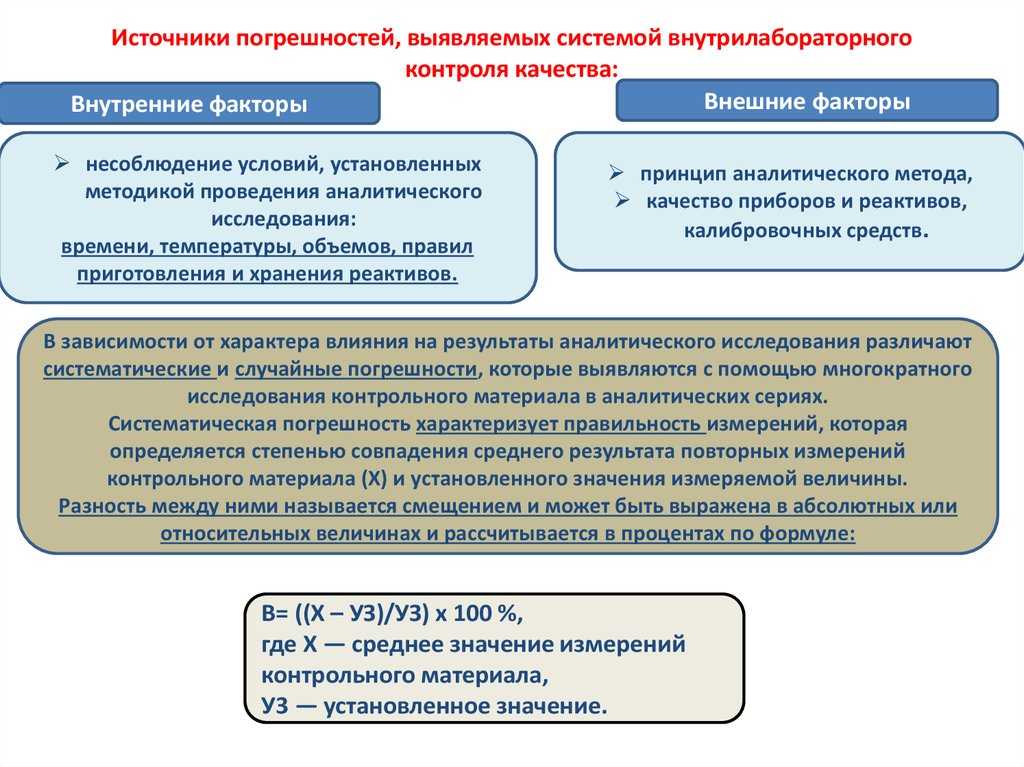 Прыжок составил 7,2 м. Вы измеряете длину прыжка три раза и получаете следующие размеры: 7,1 м, 7,3 м и 7,2 м. Эти измерения достаточно точны, поскольку они очень близки к правильному значению 7,2 м. Напротив, если бы вы получили измерение 8 м, ваше измерение не было бы очень точным.

Точность системы измерения относится к тому, насколько близко согласование между повторными измерениями (которые повторяются в тех же условиях). Рассмотрим пример измерения прыжков в длину. Точность измерений относится к разбросу измеренных значений. Одним из способов анализа точности измерений может быть определение диапазона или разницы между самым низким и самым высоким измеренными значениями. В этом случае наименьшее значение составило 7,1 м. а максимальное значение составило 7,3 м. Таким образом, измеренные значения отклонялись друг от друга не более чем на 0,2 м. Эти измерения были относительно точными, потому что их значения не слишком сильно различались. Однако, если бы измеренные значения были 7,1, 7,3 и 7,9, то измерения не будут очень точными, поскольку будут значительные отклонения от одного измерения к другому.

Измерения в примере с прыжком в длину точны и точны, но в некоторых случаях измерения точны, но неточны, или точны, но неточны. Давайте рассмотрим пример системы GPS, которая пытается определить положение бегуна в городе. Думайте о местоположении бегунов как о существующем в центре мишени «бычий глаз», а о каждой попытке GPS определить местонахождение ресторана — как о черной точке. На Рисунке 1 видно, что измерения GPS разбросаны далеко друг от друга, но все они относительно близки к фактическому положению бегуна в центре мишени. Это указывает на низкую точность, высокую точность измерительной системы. Однако на рисунке 2 измерения GPS сосредоточены довольно близко друг к другу, но далеко от целевого местоположения. Это указывает на высокую точность, низкую точность измерительной системы.

Рисунок 1. Система GPS пытается определить местонахождение бегуна в центре мишени. Черные точки обозначают каждую попытку точно определить местонахождение бегуна. Точки разбросаны довольно далеко друг от друга, что указывает на низкую точность, но каждая из них довольно близко к фактическому местоположению бегунка, что указывает на высокую точность. (кредит: Темное зло). Рисунок 2. На этом рисунке точки сосредоточены довольно близко друг к другу, что указывает на высокую точность, но они довольно далеко от фактического местоположения бегунка, что указывает на низкую точность. (кредит: Темное зло).

Степень точности и точность измерительной системы связаны с неопределенностью в измерениях. Неопределенность — это количественная мера того, насколько ваши измеренные значения отклоняются от стандартного или ожидаемого значения. Если ваши измерения не очень точны или прецизионны, то неопределенность ваших значений будет очень высокой. В более общем смысле неопределенность можно рассматривать как отказ от ответственности за ваши измеренные значения. Например, если кто-то попросил вас указать примерное время, которое вам потребуется, чтобы пройти 50-километровую гонку по пересеченной местности, вы можете сказать, что это займет у вас 8 часов плюс-минус 30 минут. Сумма плюс или минус — это неопределенность вашей ценности. То есть вы указываете, что фактическое время, которое может потребоваться вам для завершения гонки, может составлять от 7 с половиной часов до 8 с половиной часов или где-то посередине. Все измерения содержат некоторую долю неопределенности. В нашем примере измерения длины прыжка в длину мы могли бы сказать, что длина прыжка составляет 7,2 м плюс-минус 0,1 м. Неопределенность измерения, A часто обозначается как δ A («дельта A »), поэтому результат измерения будет записан как A ± δ A . В нашем бумажном примере длина прыжка может быть выражена как 7,2 м. ± 0,1.

Факторы, влияющие на неопределенность измерения, включают:

1. Ограничения измерительного устройства,
2. Мастерство человека, производящего измерение,
3. Неровности измеряемого объекта/тела,
4. Любые другие факторы, влияющие на результат (сильно зависят от ситуации).

В нашем примере такими факторами, вносящими вклад в неопределенность, могут быть следующие: наименьшее деление на линейке 0,1 м. или у человека, использующего линейку, плохое зрение. В любом случае погрешность измерения должна основываться на тщательном рассмотрении всех факторов, которые могут внести свой вклад, и их возможных последствий.

Одним из способов выражения неопределенности является процент от измеренного значения. Если измерение A выражается с неопределенностью, δ A , -процентная неопределенность (%unc) определяется как:

[латекс]\boldsymbol{\%\textbf{unc} =}[/latex][латекс]\frac{\boldsymbol{\delta}\textbf{A}}{\textbf{A}}[/latex][ латекс]\boldsymbol{\times 100\%}[/латекс]

Пример 1: Расчет процента неопределенности: угол отталкивания

Вам сказали, что для достижения максимального расстояния в прыжке в длину вы должны отталкиваться под углом 45 градусов. Вы прыгаете четыре раза, пытаясь взлететь под оптимальным углом, и измеряете угол взлета каждый раз вручную транспортиром. Вы получаете следующие измерения:

• Угол прыжка 1: 50 градусов
• Угол прыжка 2: 65 градусов
• Угол прыжка 3: 40 градусов
• Угол прыжка 4: 25 градусов

Вы определяете, что средний угол взлета, который вам удается выполнить, составляет 45 градусов ±20. Какова процентная неопределенность вашего угла взлета при использовании транспортира?

Стратегия

Во-первых, обратите внимание, что ожидаемое значение угла взлета, A , это 45 градусов. Неопределенность этого значения, δ A , составляет 20 градусов. Мы можем использовать следующее уравнение для определения процентной неопределенности веса: {A}}{\textbf{A}}[/latex][latex]\boldsymbol{\times 100\%}[/latex]

Решение

Подставьте известные значения в уравнение:

[латекс ]\boldsymbol{\%\textbf{unc} =}[/latex][latex]\boldsymbol{ \frac{20\textbf{lb}}{45\textbf{lb}}}[/latex][latex]\ жирныйсимвол{ \times 100\% = 44,4\%}[/latex]

Обсуждение

Можно сделать вывод, что угол разбега составляет 45 градусов ±44,4%. Подсказка для будущих расчетов: при расчете процентной неопределенности всегда помните, что вы должны умножить дробь на 100%. Если вы этого не сделаете, у вас будет десятичная величина, а не процентное значение.

• Точность измеренного значения показывает, насколько близко измерение к правильному значению. Неопределенность в измерении представляет собой оценку величины, на которую результат измерения может отличаться от этого значения.
• Точность измеренных значений относится к тому, насколько близко согласование между повторными измерениями.

Глоссарий

точность

степень, в которой значение меры согласуется с правильным значением для этого измерения

процент неопределенности

отношение неопределенности измерения к значению измерения, выраженное в процентах

точность

степень, в которой повторяющиеся измерения согласуются друг с другом

Как рассчитать точность измерений

Обновлено 2 ноября 2020 г.

Кевин Бек

Наука в значительной степени основана на количественных данных. Сбор полезных данных, в свою очередь, зависит от некоторых измерений, при этом масса, площадь, объем, скорость и время являются одними из этих критически важных показателей.

Ясно, что точность, которая описывает, насколько точно измеренное значение приближается к его истинному значению, жизненно важна во всех научных начинаниях. Это верно не только по наиболее очевидным сиюминутным причинам, таким как необходимость знать температуру снаружи, чтобы правильно одеться, но и потому, что неточные измерения сегодня приводят к накоплению неверных данных в долгосрочной перспективе. Если данные о погоде, которые вы собираете прямо сейчас, неверны, климатические данные о 2018 году, которые вы просматриваете в будущем, также будут неверными.

Чтобы определить точность измерения, обычно необходимо знать истинное значение этого измерения. Например, «честная» монета, подброшенная очень большое количество раз, должна выпадать орлом в 50% случаев и решкой в ​​50% случаев на основе теории вероятности. В качестве альтернативы, чем более воспроизводимым является измерение (то есть, чем выше его точность ), тем более вероятно, что значение будет близко к реальному значению в природе.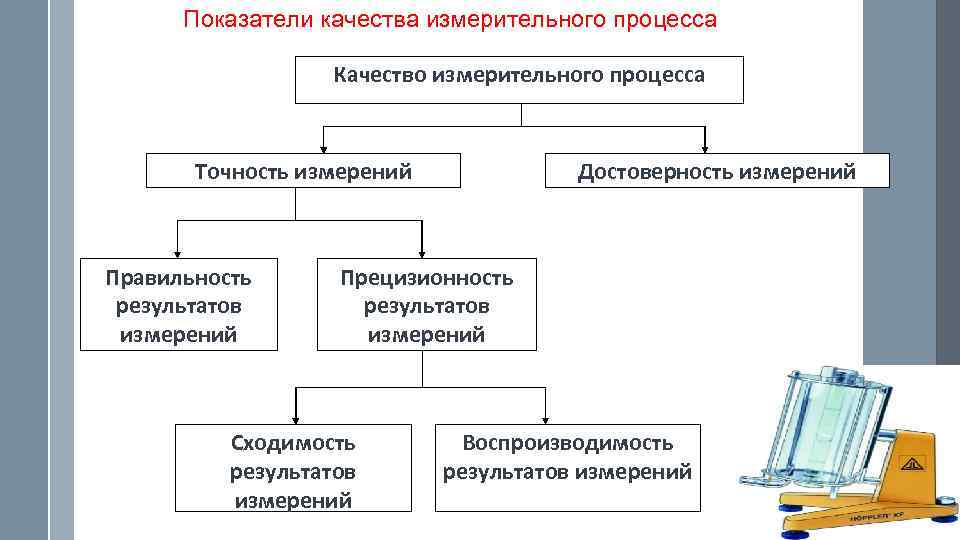 Если оценки чьего-либо роста, основанные на показаниях 50 очевидцев, находятся в диапазоне от 5 футов 8 дюймов до 6 футов 0 дюймов, вы можете с большей уверенностью заключить, что рост человека близок к 5 футам 10 дюймов, чем если бы оценки находились в диапазоне от 5 футов 8 дюймов до 6 футов 0 дюймов. от 5 футов 2 дюймов до 6 футов 6 дюймов, несмотря на то, что последний дает то же среднее значение 5 футов 10 дюймов.

Чтобы экспериментально определить точность измерений, необходимо определить их отклонение ​.

Соберите как можно больше измерений того, что вы измеряете

Позвоните по этому номеру ​ N ​. Если вы оцениваете температуру с помощью разных термометров неизвестной точности, используйте как можно больше разных термометров.

Найдите среднее значение ваших измерений

Сложите измерения и разделите на Н ​. Если у вас есть пять термометров и измерения в градусах Фаренгейта составляют 60°, 66°, 61°, 68° и 65°, среднее значение равно

\frac{60 + 66 + 61 + 68 + 65}{5} = \frac {320}{5} = 64°

Найдите абсолютное значение разницы каждого отдельного измерения от среднего

Это дает отклонение каждого измерения. Причина, по которой необходимо абсолютное значение, заключается в том, что некоторые измерения будут меньше истинного значения, а некоторые будут больше; простое сложение необработанных значений даст в сумме ноль и ничего не скажет о процессе измерения.

Найдите среднее значение всех отклонений, сложив их и разделив на N

Полученная статистика предлагает косвенную меру точности вашего измерения. Чем меньшую долю самого измерения представляет собой отклонение, тем больше вероятность того, что ваше измерение будет точным, хотя необходимо знать истинное значение, чтобы быть абсолютно уверенным в этом.