Построение уклона и конусности – –

ПОСТРОЕНИЕ УКЛОНОВ И КОНУСНОСТИ — КиберПедия

Уклоны .Величина наклона одной прямой по отношению к другой прямой называется уклоном. Уклон выражается тангенсом угла α между этими прямыми.

Рис. 1

Уклоны обычно выражают отношением двух чисел, например 1:3, из которых числитель можно графически изобразить как один из катетов АС прямоугольного треугольника, а знаменатель — как другой катет АВ этого же треугольника .Уклон может быть выражен в процентах, например 25% .

На чертежах обозначение уклона наносят на полке линии-выноски, упирающейся в линию уклона. Полка линии-выноски параллельна линии направления, по отношению к которой задан уклон. Перед числовым значением уклона наносят знак. Вершина угла знака направлена в сторону уклона, а нижняя линия знака параллельна полке линии-выноски. (Рис.1)

Построение уклона. Дан отрезок АВ и на нем точка С. Надо провести прямую с уклоном 1:5 к линии АВ через заданную на ней точку С. От точки С откладывают пять равных отрезков произвольного размера. На перпендикуляре, проведенном из точки 5 к прямой АВ, откладывают один отрезок того же размера, получают точку D. Прямая проведенная через точки С и D будет иметь уклон 1:5 к прямой АВ.(рис.2)

 

Рис.2

 

Конусность (рис.3)

Конусностью называется отношение диаметра D основания прямого кругового конуса к его высоте Н.

Для усеченного конуса конусность выражается отношением разности диаметров D и d нормальных сечений кругового конуса к расстоянию между ними . Обозначение конусности наносится на линии-выноске со стрелкой. Перед размерным числом, характеризующим конусность, наносят знак, острый угол которого должен быть направлен в сторону вершины конуса. (рис.3 )

Рис.3

ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ

 

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАБОТЫ.

Начертите 8 окружностей радиусом 20 мм.

1.2..I Деление на 4 равные части. (рис.4а.). Проведите в окружности 2 взаимно перпендикулярные оси. Эти оси делят окружность на 4 равные части. Соедините точки А,В,С,D) сплошной основной линией, получите вписанный квадрат.
1.2.2.Деление на 8 равных частей(рис.4б).

Разделите полученные 4 дуги пополам, проведя циркулем засечки радиусом 20-30 мм из концов этих дуг. Соединяя точки пересечения засечек с центром окружности,, вы разделите окружность на 8 равных частей. Соедините полученные 8 точек, получите вписанный восьмиугольник.
1.2.З.Деление на 3 равные части (рис.4 в).

Радиусом 20мм проведите дугу с центром в точке D. Засеките на окружности точки 1 и 2 и соедините их с точкой С.

1.2.4.Деление на 6 равных частей

(рис.4 г).

Приняв за центры концы диаметра, сделайте циркулем радиусом 20мм засечки на окружности (точки 1,2,3,4). Соедините их и точки А и В , получите правильный шестиугольник.

1.2.5.Деление на 12 равных частей (рис.4 д.)

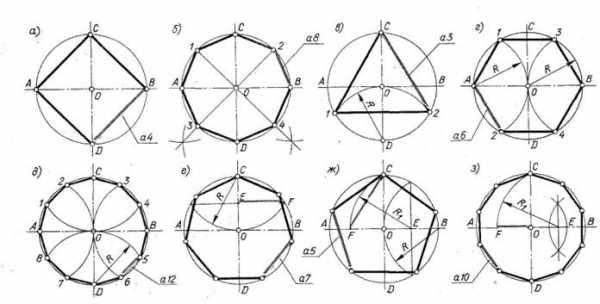Приняв за центры концы двух взаимно перпендикулярных диаметров (точки А,В,С,Д)), сделайте радиусом 20мм 8 засечек на окружности. Полученные 12 точек соедините.

Рис.4

1.2.6. Деление на 7 равных частей (рис.4 е).

Приняв за центр один из концов диаметра (точку С), проведите дугу радиусом 20 мм до пересечения с окружностью. Точки пересечения соедините отрезком прямой . Половина этого отрезка (EF) примерно равна стороне вписанного семиугольника. Радиусом FE сделайте поочередно 7 засечек на окружности, начав с точки С. Полученные 7 точек соедините.

1.2.7.Деление на 5 равных частей (рис.4 ж).

Приняв за центр один из концов диаметра (точку В), проведите дугу радиусом 20мм до пересечения с окружностью и точки пересечения соедините прямой. Приняв за центр точку пересечения прямой с :горизонтальным диаметром (точку Е), проведите дугу через точку С до пересечения с этим диаметром. Точку пересечения F соедините с точкой С. Отрезок СF будет примерно равен стороне вписанного пятиугольника ; ОF – стороне вписанного десятиугольника. Радиусом СF поочередно сделайте 5 засечек на окружности, начиная с точки С. Полученные 5 точек соедините.

1.2.8.Деление на 10 равных частей (рис.4з).

Радиусом ОF сделайте поочередно 10 засечек на окружности, полученные точки соедините.

 

 

СОПРЯЖЕНИЯ

1.3.1.Сопряжение двух прямых (рис.5.)

Даны две параллельные прямые АВ и СD (рис 5 в) , задан размер EF .Разделите отрезок EF пополам, и из точки О проведите дугу радиусом R=EF/2, соединяя точки Е и F

Рис5

1.3.2.Сопряжения углов (рис.5 а, б).

Даны две прямые , пересекающиеся под углом ( прямым, острым или тупым), и радиус сопряжения Е..

Проведите по два перпендикуляра к двум сторонам углаи отложите на них отрезки ,равные R.. Через полученные точки проведите прямые параллельно сторонам угла.. О – точка пересечения этих двух прямых -есть центр сопряжения. Из точки О опустите перпендикуляры на стороны угла. Точки пересечения перпендикуляров и сторон угла соедините дугой радиусом R с центром в точке О.

1.3.3.Сопряжение прямой сокружностью (рис.6а.) Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите прямую, параллельную заданной , на расстоянии R1. Из центра окружности О радиусом R2= R + R1 сделайте на прямой засечку О1 . Через О и О1 проведите прямую, получите на окружности точку К. Из точки О1 проведите О1К1 перпендикулярно заданной прямой. Из центра сопряжения О1 проведите дугу радиусом R1, соединяя точки К1 и К. Это

внешнее сопряжение

 

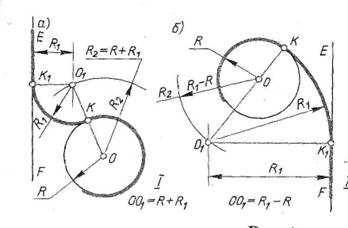Рис.6

Внутреннее сопряжение. (рис.6 б).

Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите построение аналогично предыдущему, учитывая , что в данном случае

R2 = R-R1

 

 

1.3.4.Сопряжение двух окружностей.

Внешнее сопряжение (рис.7а).

Даны две окружности радиусом R1, и R2 и радиус сопряжения R.

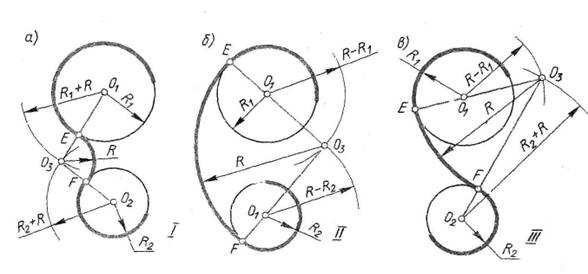Рис.7

Проведите дуги из центра О1 радиусом R.+ R 1 , из О

2 – радиусом R.+ R 2. Точка их пересечения О3 -центр сопряжения.

Внутреннее сопряжение(рис.7б)

Даны две окружности радиусом R1и R2 и радиус сопряжения R. Проведите дуги : из точки О1 радиусом R- R1, из точки О2 радиусом R-R2. Точка их пересечения О3 -центр сопряжения.

Смешанное сопряжение (рис.7 в).

Даны две окружности радиусом R1 и R2,ирадиус сопряжения R.

Проведите дуги : из центра О1 радиусом R.-R1, из центра О2 радиусом R+R2. Точка пересечения дуг О3- центр сопряжения.

 

 

cyberpedia.su

Обозначение уклона и конусности

1. Уклоны

Уклон, величина, характеризующая наклон одной прямой линии к другой. Выражают дробью или в %.

– угол направлен в сторону уклона

Рисунок 6.1

6.2 Конусность

Конусность ( С ) – это отношение диаметра основания конуса к его высоте. Для усеченного конуса

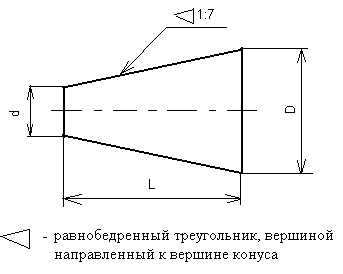
Рисунок 6.2

Вопросы для самоконтроля.

1. Что такое уклон?

2. Что такое конусность?

7. Сопряжение линий и лекальные кривые

Сопряжения применяются во многих деталях машин для плавного перехода линий.

Для построения сопряжений необходимо уметь строить касательную в данной точке окружности (рисунок 7.1 а) проводить из внешней точки прямую, касательную к окружности (рисунок 7.1 б). Помнить, что центры окружностей, соприкасающихся внешним образом, находятся на расстоянии суммы их радиусов (рисунок 7.1 в), а внутренним – на расстоянии их радиусов (рисунок 7.1 г), причем точка касания (сопряжения) всегда лежит на прямой, проходящей через их центры.

Рисунок 7.1

в г

Рисунок 7.1

Изложенное позволяет легко уяснить последовательность решений задач на сопряжения, приведенных ни рисунке 7.2. ∂, е, ж, и, к.

∂ е ж

и к

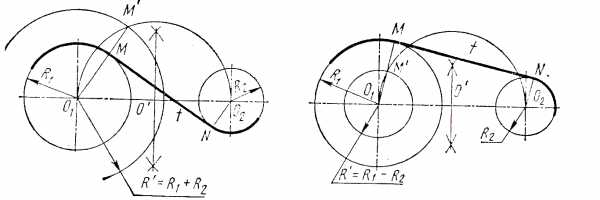
Рисунок 7.2

Лекальные кривые обводят при помощи лекал. Наиболее часто применяют в технике следующее:

7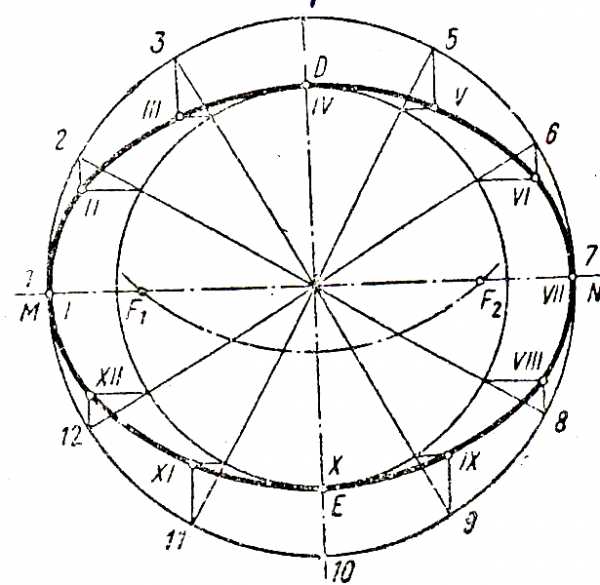.1 Эллипс. Эллипсом называется замкнутая кривая, для которой сумма расстояний от любой точки до двух точек – фокусов эллипса – есть величина постоянная. Для построения эллипса проводят две концентрические окружности, диаметры которых равны осям эллипса (рисунок 7.3). Эти окружности делят на несколько равных частей (12-16). Через точки деления на большей окружности проводят вертикальные линии, через соответствующие точки деления на малой окружности – горизонтальные линии. Пересечение этих линий даст точки эллипса I, II, III

Рисунок 7.3

7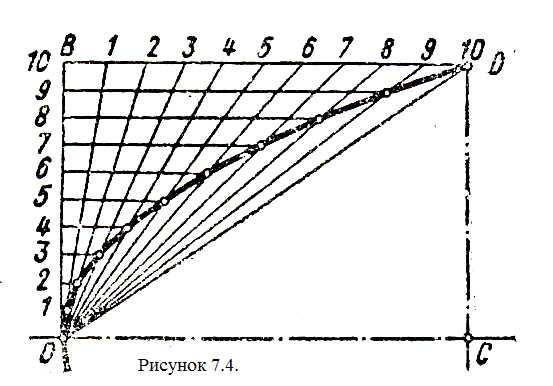.2Парабола.

Параболой называется кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки, называемой фокусом параболы.

Даны вершина параболы О, одна из точек параболы D и направление оси ОС (рисунок 7.4). На отрезках ОС и СD строят прямоугольник, стороны этого прямоугольника ОВ и ВD делят на произвольное одинаковое число равных частей и нумеруют точки деления согласно рис. Вершину О соединяют с точками деления стороны ВD, а из точек деления отрезка ОВ проводят прямые, параллельные оси. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы (другие способы построения параболы см. в рекомендуемой литературе).

7.3 Циклоида. Траектория точки А, принадлежащей окружности, перекатываемой без скольжения по прямой, называется циклоидой (рисунок 7.5). Для ее построения от исходного положения точки А на направляющей прямой отк5ладывают отрезок АА₁, равный длине данной окружности – 2πR. Окружность и отрезок АА₁ делят на одинаковое число равных частей.

Восставляя перпендикуляры из точек деления прямой АА₁ до пересечения с прямой, проходящей через центр данной окружности параллельно АА₁, намечают ряд последовательных положений центра перекатываемой окружности О₁, О₂, О₃,…, О₈. Описывая из этих центров окружности радиуса R, отмечают точки пересечения с ними прямых, проходящих параллельно АА₁ через точки деления окружности 1, 2, 3, 4 и т.д.

Рисунок 7.5

В пересечении горизонтальной прямой, проходящей через точку 1, с окружностью, описанной из центра О₁, находится одна из точек циклоиды; в пересечении прямой, проходящей через точку 2, с окружностью, проведенной из центра О₂, находится другая точка циклоиды и т.д. Соединяя полученные точки плавной кривой, получаем циклоиду.

4. Синусоида. Для построения синусоиды делят окружность заданного радиуса на равные части (6, 8, 12, и т.д.) и на продолжении осевой линии от условного начала – точки А – проводят отрезок прямой АВ, равный 2πR. Затем прямую делят на такое же число равных частей, как и окружность (6, 8, 12 и т. Д.). Из точек окружности 1,2, 3, …, 12 проводят прямые линии параллельно выбранной прямой до пересечения с соответствующими перпендикулярами, восстановленными или опущенными из точек деления прямой.Полученные точки пересечения (1^/, 2^/ , 3^/, …, 12^/) и будут точками синусоиды с периодом колебания, равным 2πR.

π

Рисунок 7.6

7.5 Эвольвента (развертка круга). Эвольвентой называется траектория, описываемая каждой точкой прямой линии, перекатываемой по окружности без скольжения.

В машиностроении по эвольвенте очерчивают профиль головок зубьев зубчатых колес.

Для построения эвольвенты окружность предварительно делят на произвольное число n равных частей; в точках деления проводят касательные к окружности, направленные в одну сторону. На касательной, проведенной через последнюю точку деления, откладывают отрезок, равный длине окружности 2πR, и делят его на то же число n равных частей. Откладывая на первой касательной одно деление, равное , на второй – два, на третьей – три и т.д., получают ряд точек I, II, III,IV и т.д., которые соединяют по лекалу

Вопросы для самоконтроля.

1. На каких двух положениях геометрии основано построение сопряжений?

2. Перечислите элементы сопряжений.

3. Как построить эллипс?

studfiles.net

Задание на графическую работу “Уклон.Конусность”

Графическая работа

Уклон. Конусность

Задание: на листе формата А3 выполнить по заданным размерам контур детали с построением уклона, конусности в масштабе 1:1. Нанести размеры

Примечание. Линии построения уклона и конусности сохранить.

В основной надписи указать название деталей в соответствии с вариантом.

Цель задания:

– изучить правила оформления чертежей по ГОСТ 2.301-68, ГОСТ 2.302-68; ГОСТ 2.303-68

– изучить правила построения уклона и конусности в соответствии с п.2.40, 2.41 ГОСТ 2.307-68.

– изучить основные правила нанесения размеров на чертежах ГОСТ 2307-68

– приобрести навыки геометрических построений

Методические указания: прежде чем выполнить задание необходимо ознакомиться с п.2.40, 2.41 ГОСТ 2.307-68.

Для получения уклона через заданную точку нужно построить прямоугольный треугольник с одной из вершин в заданной точке К так, как это показано на рис.3.1. Отношение катетов должно соответствовать отношению, указанному в обозначении уклона.

Построение конусности при заданной высоте L и диаметре D одного из оснований можно выполнить графически следующим образом: построить на заданной оси вспомогательный конус, у которого произвольно взятое основание а укладывается в высоте столько раз, сколько задано в обозначении конусности. Затем провести образующие искомого конуса параллельно образующим вспомогательного конуса через концы заданного диаметра, как показано на рис.3.2.

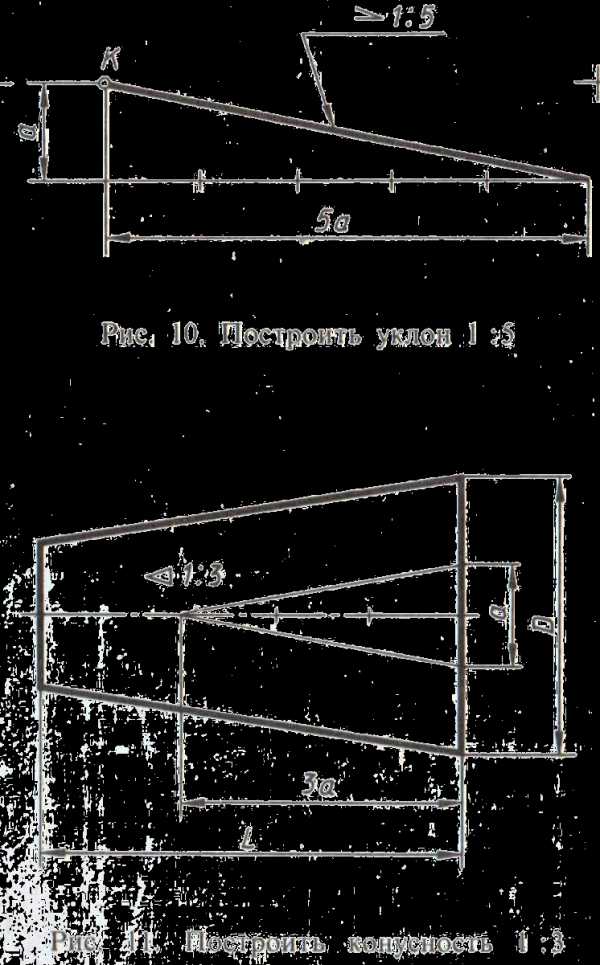
Рис. 3.1- построение уклона

Рис. 3.2- построение конусности

Конусность можно рассчитать по формуле

К=D/l,

где D – диаметр основания конуса,l – высота.

Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид:

К = (D-d)/ l

Обозначение конусности на чертеже

рис. 3.3- обозначение конусности

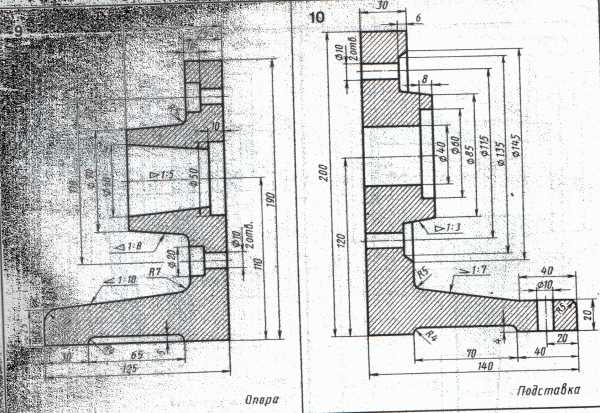
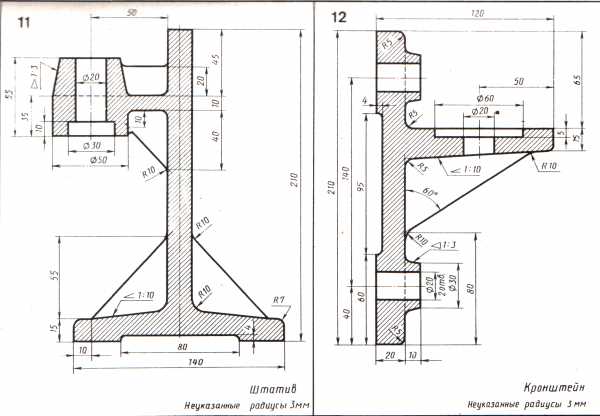
Варианты заданий к выполнению графической работы

Таблица 3.1

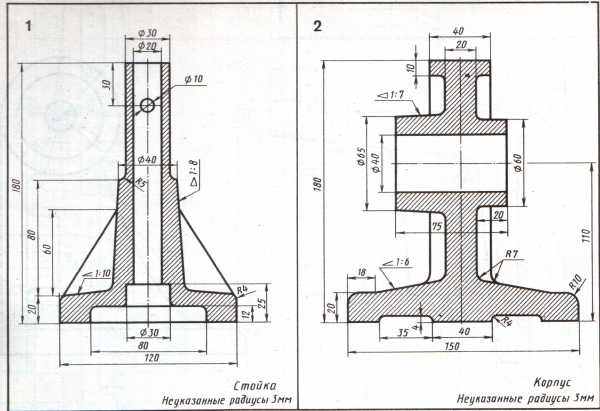
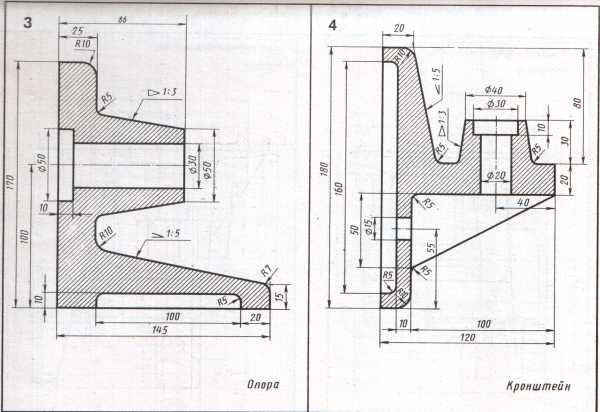
продолжение табл. 3.1

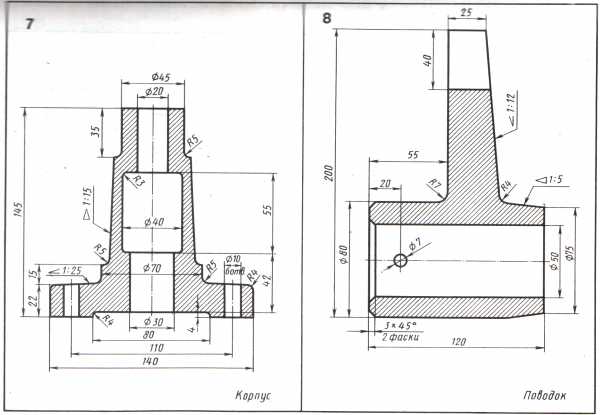
продолжение табл. 3.1

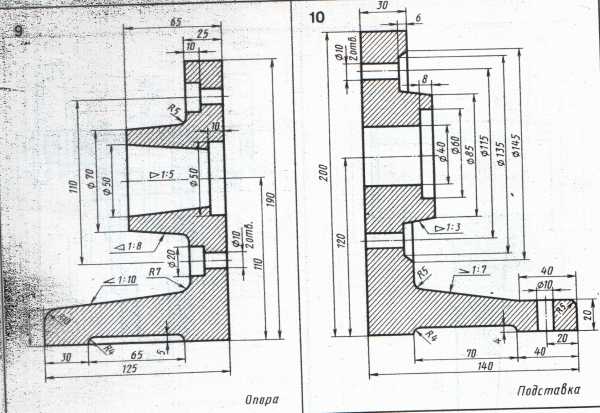
infourok.ru

Уклон и конусность – прочее, уроки

Уклон и конусность. Урок позволяет более наглядно ознакомится с понятием уклона и конусности. 

– Ознакомиться с правилами построения и условными обозначениями уклона и конусности.
– Вырабатывать умение в применении изученных условностей при выполнении чертежей.
– Формировать навыки работы чертежными инструментами.
– Привить познавательный интерес к предмету, формировать самостоятельность и аккуратность.

Просмотр содержимого документа
«Уклон и конусность»

УКЛОН И КОНУСНОСТЬ

Цель урока

• Ознакомиться с правилами построения и условными обозначениями уклона и конусности. – Вырабатывать умение в применении изученных условностей при выполнении чертежей. – Формировать навыки работы чертежными инструментами. – Привить познавательный интерес к предмету, формировать самостоятельность и аккуратность.

• Во многих деталях машин используются уклон и конусность.
• Уклон встречается в профилях прокатной стали, в крановых рельсах, в косых шайбах и прочих деталях.
• Конусность встречается в каждом токарном, фрезерном или сверлильном станке, в режущем инструменте, которые имеют конусные хвостовики и в ряде других деталей.

УКЛОН – это величина, которая характеризует наклон одной прямой относительно другой.

Где встречается уклон?

В технологии машиностроения!

Где встречается уклон?

В строительстве зданий и сооружений!

Где встречается уклон?

В автомобильном транспорте!

Обозначается уклон знаком  . На чертеже уклон выражается отношением двух чисел или в процентах.

Знак ставится перед числовым значением уклона над полкой линии-выноски. Острый угол знака должен быть направлен в ту же сторону, что и острый угол уклона.

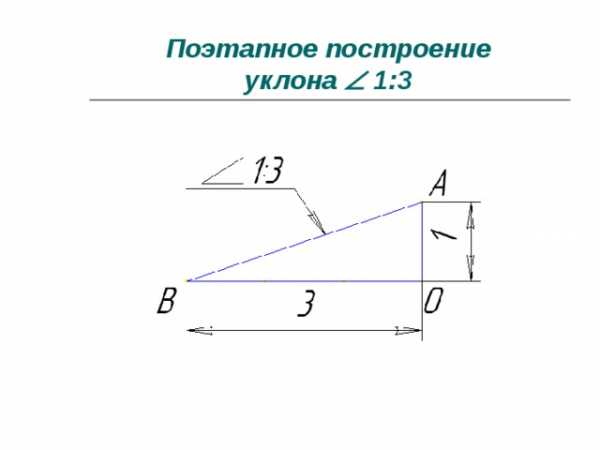
Поэтапное построение уклона  1:3

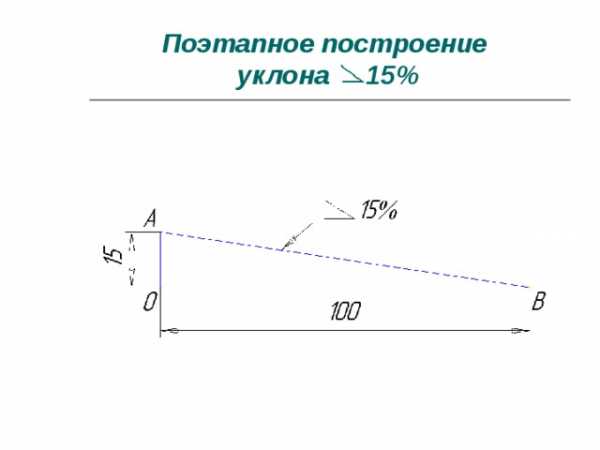
Поэтапное построение уклона 15%

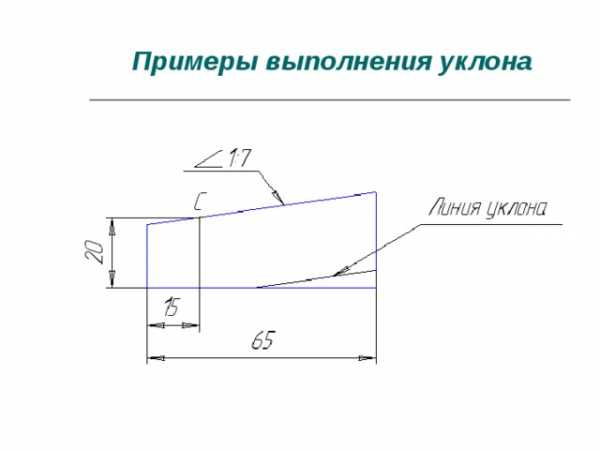
Примеры выполнения уклона

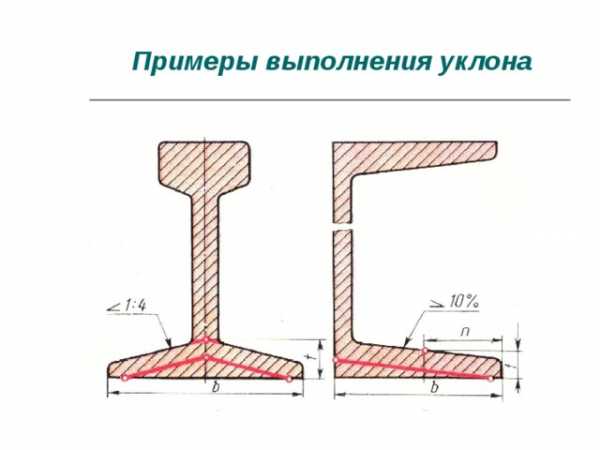
Примеры выполнения уклона

КОНУСНОСТЬ – это отношение диаметра основания конуса к его высоте.

Где встречается конусность?

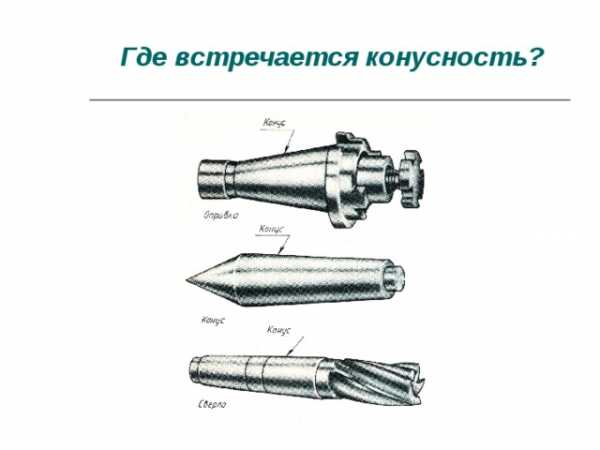
Где встречается конусность?

Конусность обозначается знаком  , вершина знака должна быть направлена в сторону вершины конуса. Конусность может быть задана отношением двух чисел или в процентах.

Конусность C определяется по формуле где D – диаметр конуса, мм; L – высота конуса, мм.

C = D : L ,

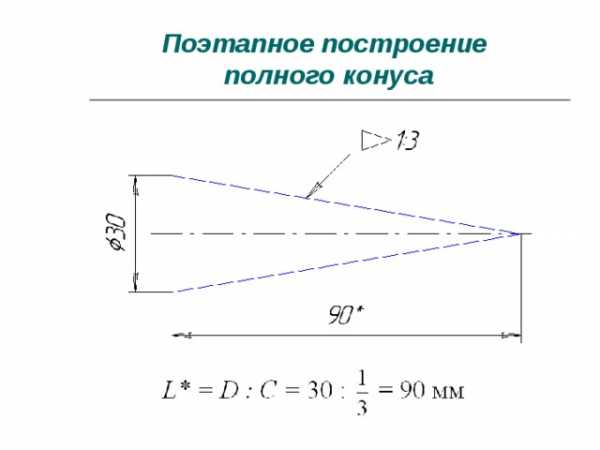
Поэтапное построение полного конуса

Конусность усеченного конуса C определяется по формуле где D – диаметр большего основания конуса, мм; d – диаметр меньшего основания конуса, мм; L – высота конуса, мм.

C = ( D – d ): L ,

Поэтапное построение усеченного конуса

Формулы для определения D, d и L

Диаметр большего основания конуса определяется по формуле

D = d + C  L

Диаметр меньшего основания конуса определяется по формуле

d = D – C  L

Высота конуса определяется по формуле

L = ( D – d ): C

Контрольные вопросы

1. Что называется уклоном? 2. В чем выражается уклон? 3. Какой знак ставится перед числовым значением уклона? 4. Что называется конусностью? 5. Какой знак ставится перед числовым значением конусности?

kopilkaurokov.ru

2.Построение уклонов и конусностей.

Уклон– наклон одной прямой линии к другой. Уклоном i прямой BC относительно AB называют отношение разности выот двух точек А и В к горизонтальному расстоянию l между ними или отношение катета AD к катету BC. i = h/l= AC/BC=tg(альфа)

Уклон обозначается знаком угла в обратную сторону и острый угол которого всегда расположен в сторону уклона.

КонусностьК – отношение разности диаметров D-d двух поперечных сечений конуса к расстоянию между ними l.

ПОстроение конусности 1:n относительно данной оси сводится к построению уклона 1:2n с каждой стороны оси. Конусность обозначается равнобедренным треугольником, лежащим на боку, острый угол которого направляют в сторону вершины конуса.

Изображение предметов на черчежах.

1. Виды.

Лагерь:173-180

Новичихина:66-80

2. Разрезы.

Разрезы разделяются, в зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций, на:

горизонтальные – секущая плоскость параллельна горизонтальной плоскости проекций.

вертикальные – секущая плоскость перпендикулярна горизонтальной плоскости проекций ;

наклонные –секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого .

В зависимости от числа секущих плоскостей разрезы разделяются на:

простые – при одной секущей плоскости ;

сложные – при нескольких секущих плоскостях.

Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций , и профильным, если секущая плоскость параллельна профильной плоскости проекций.

Разрезы называются продольными, если секущие плоскости направлены вдоль длины или высоты предмета и поперечными, если секущие плоскости направлены перпендикулярно длине или высоте предмета.

У начала и конца линии сечения, а при необходимости и у мест пересечения секущих плоскостей ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда, и в местах пересечения со стороны внешнего угла.

Разрез должен быть отмечен надписью по типу «А-А» (всегда двумя буквами через тире).

Фронтальным и профильным разрезам, как правило, придают положение, соответствующее принятому для данного предмета на главном изображении чертежа. Горизонтальные, фронтальные и профильные разрезы могут быть расположены на месте соответствующих основных видов.

При ломаных разрезах секущие плоскости условно повертывают до совмещения в одну плоскость, при этом направление поворота может не совпадать с направлением взгляда

Разрез, служащий для выяснения устройства предмета лишь в отдельном, ограниченном месте, называется местным

Местный разрез выделяется на виде сплошной волнистой линией или сплошной тонкой линией с изломом. Эти линии не должны совпадать с какими-либо другими линиями изображения

Часть вида и часть соответствующего разреза допускается соединять, разделяя их сплошной волнистой линией или сплошной тонкой линией с изломом. Если при этом соединяются половина вида и половина разреза, каждый из которых является симметричной фигурой, то разделяющей линией служит ось симметрии

сложные – при нескольких секущих плоскостях

Сложные разрезы бывают ступенчатые, если секущие плоскости параллельны (например, ступенчатый горизонтальный разрез Б-Б, рис. 6), и ломанным, если секущие плоскости пересекаются (например, разрезы А-А).

Положение секущей плоскости указывают на чертеже линией сечения. Для линии сечения должна применяться разомкнутая линия. При сложном разрезе штрихи проводят также у мест пересечения секущих плоскостей между собой. На начальном и конечном штрихах следует ставить стрелки, указывающие направление взгляда

У начала и конца линии сечения, а при необходимости и у мест пересечения секущих плоскостей ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда, и в местах пересечения со стороны внешнего угла.

Разрез должен быть отмечен надписью по типу «А-А»

При ломаных разрезах секущие плоскости условно повертывают до совмещения в одну плоскость, при этом направление поворота может не совпадать с направлением взгляда.

Если совмещенные плоскости окажутся параллельными одной из основных плоскостей проекций, то ломаный разрез допускается помещать на месте соответствующего вида . При повороте секущей плоскости элементы предмета, расположенные за ней, вычерчивают так, как они проецируются на соответствующую плоскость, с которой производится совмещение.

studfiles.net

10. Геометрические построения

10.1. Построение уклона и конусности

    Уклон – это величина, которая характеризует наклон одной линии по отношению к другой.

    Уклон i прямой АС относительно прямой АВ (рис. 10.1) определяется как отношение разности высот двух точек А и С к горизонтальному расстоянию между ними.  

                                                  .                                                      (1)

Уклон может быть выражен простой дробью, десятичной или в процентах.

Рис. 10.1. Уклон прямой

Рис. 10.2. Построение прямой с уклоном 1:5

    Задача. Через точку А провести прямую АС с уклоном 1:5 к горизонтальной прямой (рис. 10.2). Из точки А проводят горизонтальный луч и откладывают на нем пять произвольных равных отрезков. На перпендикуляре, восстановленном из конечной точки В, откладывают одну такую часть. Уклон гипотенузы АС треугольника АСВ будет равен 1:5.

    Конусность К определяется как отношение разности диаметров D и d двух поперечных сечений конуса к расстоянию между ними (рис. 10.3).

                                         (2)

Рис. 10.3. Конусность

Рис. 10.4. Построение конусности 1:5

    Конусность, как и уклон, выражается простой дробью, десятичной или в процентах.

   На рис. 10.4 показано построение конусности 1:5. ВС=FЕ.

 

 

10.2. Сопряжения

    Касание есть плавный переход одной линии в другую. Сопряжение есть плавный переход одной линии в другую, выполненный при помощи промежуточной линии. Чаще всего промежуточной линией служит дуга окружности.

    Построение сопряжений основано на следующих геометрических положениях:

    а) переход окружности на прямую только тогда будет плавным, когда данная прямая является касательной к окружности (рис. 10.5, а). Радиус окружности, проведенный в точку касания А, перпендикулярен к касательной прямой;

    б) переход в данной точке А с одной окружности на другую только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 10.5, б).

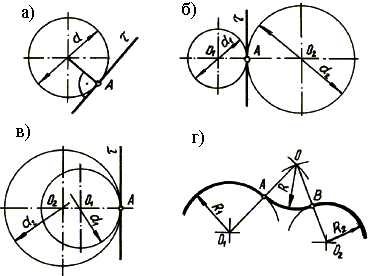
Рис. 10.5. Основные понятия сопряжения

    Точка касания А и центры окружностей О₁ и О₂ лежат на одной прямой. Касание называется внешним, если центры О₁ и О₂ располагаются по разные стороны от касательной (рис. 10.5,б), и внутренним, если центр находится по одну сторону от общей касательной (рис. 10.5, в).

    В теории сопряжений применяются специфические термины, а именно (рис. 10.5, г): точка О – центр сопряжения; R – радиус сопряжения: точки А и В – точки сопряжения; дуга АВ – дуга сопряжения.

    Решение задач на построение сопряжений основано на методе геометрических мест.

    Геометрическим местом (ГМ) центров окружности сопряжения касательной к прямой является прямая, параллельная данной и отстоящей от нее на расстоянии радиуса окружности сопряжения (рис. 10.6, а).

Рис. 10.6. Геометрические места

    Геометрическим местом центров окружности сопряжения, касательной к сопрягаемой окружности, является окружность, радиус которой равен сумме радиусов окружности сопряжения и окружности сопрягаемой для внешнего сопряжения (рис. 10.5, б) и разности радиусов этих окружностей (рис. 10.5, в) для внутреннего сопряжения.

Алгоритм решения задач на построение сопряжений двух линий при заданном радиусе сопряжения может быть сформулирован следующим образом:

1. Построить геометрическое место центров окружности сопряжения для одной из сопрягаемых линий.

2. Построить аналогичное геометрическое место центров для второй сопрягаемой линии.

3. Точка пересечения построенных геометрических мест является центром сопряжения.

4. Определить точку сопряжения на первой из сопрягаемых линий.

5. Определить точку сопряжения на второй из сопрягаемых линий.

6. В границах между точками сопряжений провести дугу сопряжения.

 

studfiles.net

“Выполнение контура детали с построением уклона и конусности”

государственное автономное профессиональное образовательное учреждение

Челябинской области «Политехнический колледж»

Методическая разработка учебного занятия по ОП.06 «Инженерная графика»

Специальность 22.02.06«Сварочное производство»

тема: «Выполнение контура детали с построением уклона и конусности»

Автор: Гайдулина Н.М.

Вид учебного занятия: практическое занятие

Комплексные цели

Обучающая: формирование опорных знаний об уклонах и конусах и правилах их построения.

Развивающая: развитие пространственного и технологического мышления

Воспитательная: воспитание устойчивого интереса к профессии, создание условий для положительной мотивацию к изучению дисциплины.

Материально-техническая база:

• персональный компьютер, проектор, мультимедийная презентация;

• дидактический материал «Способы получения литых заготовок»

• рабочие чертежи деталей машин

Ход занятия:

1. Организационный момент – Приветствие, учет посещаемости, проверка готовности к работе

2. Мотивация / определение целей и задач урока, формирование интереса к материалу.

В профессиональной деятельности вам придется производить сварку металлоконструкций. И как правило в качестве заготовок вам придется использовать разновидности сортового проката, такого как швеллер, двутавр, уголок и т.д. Если посмотреть на контур данных изделий помимо прямых участков, с сопряжениями у них имеются поверхности с уклоном или с конусностью. Эти поверхности обеспечивают прочность металлоконструкции, и легкость в изготовлении проката. Поэтому, для того чтобы грамотно читать чертежи таких металлоконструкций необходимо сначала научится строить чертежи на которых имеются конусы и уклоны.

1. Актуализация опорных знаний

На предыдущих занятиях мы с вами говорили о сопряжениях (они тоже имеется на сортовом пркате), а также о делениях окружностей на равное количество частей, которое нам сегодня пригодится для построения лекальных кривых. Давайте вспомним о них.

Тест

Блок А – Выберите правильный вариант ответа:

1. Плавный переход одной линии в другую называется:
   а) соединением; б) сопряжением; в) скруглением

2. К основным элементам сопряжения относятся:

А) центры сопрягаемых окружностей

Б) радиус сопряжения и точка сопряжения;

В) центр и точки сопряжения

3. При внешнем сопряжении дуг, заданных радиусами R1 и R2, при помощи дуги, радиус которой R, центр сопряжения находиться по формулам:
а) R-R1 и R-R2; б) R+R1 и R+R2; в) R+R1 и R-R2

4. При внутреннем сопряжении дуг, заданных радиусами R1 и R2, при помощи дуги, радиус которой R, центр сопряжения находиться по формулам:
а) R-R1 и R-R2 ; б) R+R1 и R+R2; в) R+R1 и R-R2

Блок Б – Укажите виды сопряжений соответствующие чертежам

1. Сопряжение двух окружностей

2. Сопряжение прямой и окружности

3. Сопряжения параллельных прямых

Блок В – Перечислите все радиусы сопряжений, которые использовались при построении чертежа

Ответ: R10, R15, R20, R120

Блок Г – Поделить окружность на шесть и восемь равных частей

Самороверка результатов работы.

Критерии оценок:

11баллов + 4 (по два за верное изображение)

10-8б – удовлетворительно; 11-13б– хорошо; 14-15б – отлично.

IV Изучение нового материала

1. ПОСТРОЕНИЕ И ОБОЗНАЧЕНИЕ УКЛОНА

▲ Уклоном i называют величину, характеризующую наклон одной прямой линии к другой прямой. Находится как соотношение катетов прямоугольного треугольника

Перед размерным числом ставится знак уклона , вершина которого должна быть направлена в сторону уклона (ската). Выражается уклон отношением (дробью) двух чисел 1:2 или в процентах 25%.

Построение уклона.

а) Задача. Через точку А провести прямую АС с уклоном 1:5 к горизонтальной прямой.

Построение:

Из точки А проводят горизонтальный луч и откладывают на нем пять произвольных равных отрезков. На перпендикуляре, восстановленном из конечной точки В, откладывают одну такую часть. Уклон гипотенузы АС треугольника АСВ будет равен 1:5.

Б) Если уклон задается в процентах, например, 20%, то линия уклона строится так же, как гипо­тенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100%, а другого — 20%. Очевидно, что уклон 20% есть иначе уклон 1:5. – Построить уклон с процентным соотношением (рисунок3.110б) стр 146.

Вопрос: Где указывают уклон на чертеже? (стр146) – Указывают на полке-выноске, либо непосредственно у изображения.

Значения уклонов стандартизированы.

1. Обозначение и построение конусности

▲ Конусность К называют отношение разности диаметров D и d двух поперечных сечений конуса к расстоянию между ними.

Перед размерным числом ставится знак, острый угол которого должен быть направлен в сторону вершины конуса.

Выражается конусность отношением (дробью) с единицей в числителе двух чисел 1:2 (числитель равен единице) .

V. Самостоятельная работа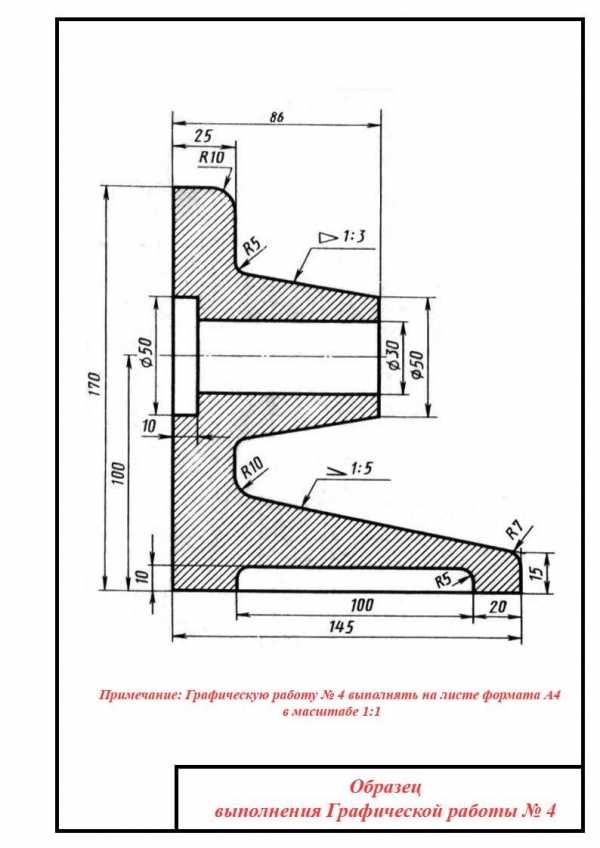

Задание:

1. Выполнить чертеж детали с уклонами.

2. Проставить все необходимые размеры

VI. Закрепление материала

Задача: а) Найти конусность если , известны размеры D=30 мм, d=20 мм и L=70 мм, то

Б) Если известны конусность С, диаметр одного из оснований конуса d  и длина конуса L, можно опреде­лить второй диаметр конуса. Например, C=l:7, d=20 мм и L=70 mm; D находят по формуле D=CL+d= 1/7x70+20=30 мм .

multiurok.ru