Построение сечений: “Построение сечений многогранников” ( геометрия 10 класс)

Простая физика – EASY-PHYSIC

Построение сечения методом следов – это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.

Задача 1.

Построить сечение параллелепипеда плоскостью, проходящей через точки  .

Задача 1. Дано

Шаг 1. Чезез точки и , которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой , которая также принадлежала бы основанию. Для этого проводим прямую , и находим точку ее пересечения с прямой – .

Задача 1. Шаг 1.

Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра – .

Задача 1. Шаг 2.

Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой , которая принадлежала бы плоскости задней грани. Для этого проведем прямую , которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой – . Через две точки задней грани проводим прямую , и находим место пересечения этой прямой с ребром – .

Задача 1. Шаг 3.

Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.

Задача 1. Шаг 4.

 

Задача 2.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Задача 2. Дано.

Шаг 1. Точки и лежат в одной плоскости, можно соединить их прямой. Прямая пересечет ребро в точке .

Задача 2. Шаг 1.

Шаг 2. Точки и также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра – .

Задача 2. Шаг 2

Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч и найдем его пересечение с прямой – ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения – точка . Точки и можно соединить отрезком.

Задача 2. Шаг 3.

Шаг 4. Находим точку пересечения отрезком ребра – точку .

Задача 2. Шаг 4

Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.

Задача 2. Шаг 5

Задача 3.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Задача 3. Дано.

Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка принадлежит грани основания, поэтому нужна точка в этой плоскости.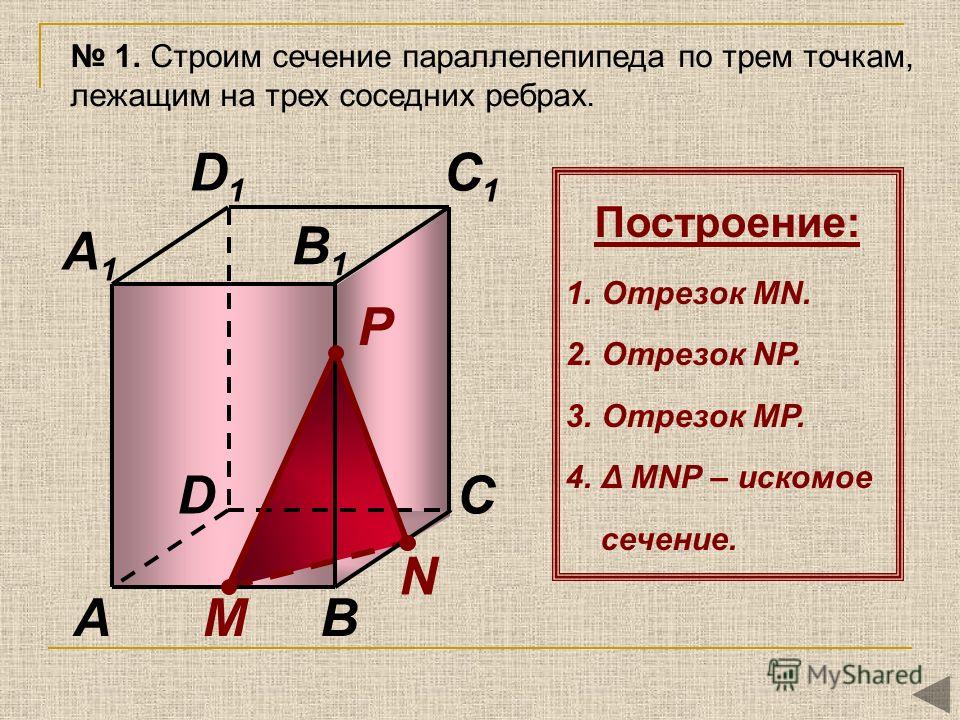

Задача 3. Шаг 1

Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой – .

Задача 3. Шаг 2.

Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром – точка .

Задача 3. Шаг 3.

Шаг 4. Теперь надо найти точку в плоскости передней  грани, потому что в этой плоскости у нас уже есть точка – точка . Для того, чтобы найти такую точку, продлим прямую  и найдем пересечение этой прямой с прямой – точка .

Задача 3. Шаг 4

Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер – точку , и ребра – точку .

Задача 3. Шаг 5.

Шаг 6. Соединяем точки и получаем многоугольник сечения.

Задача 3. Шаг 6

Окончательный вид сечения с другого ракурса:

Окончательный вид

Задача 4.

Построить сечение параллелепипеда плоскостью, проходящей через точки  . Точка в задней грани.

Задача 4. Дано

Шаг 1.  Проводим прямую через две точки одной плоскости – и .  Определяем точку пересечения данной прямой ребра – .

Задача 4. Шаг 1.

Шаг 2. Продолжение прямой пересечется с продолжением прямой – так как обе прямые принадлежат плоскости задней грани. Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .

Задача 4. Шаг 2.

Шаг 3. Точка – точка пересечения прямой ребра . Продлим также ребро и найдем пересечение прямой и прямой – точку , которая принадлежит плоскости основания.

Задача 4. Шаг 3

Шаг 4. Соединяем Точки и плоскости основания, определяем точку пересечения данной прямой с ребром – точку . Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.

Задача 4. Шаг 4.

Окончательный вид сечения с другого ракурса:

Окончание построения

Методическая разработка по теме «Построение сечений многогранников»

Муниципальное бюджетное общеобразовательное учреждение

 «Средняя общеобразовательная школа  № 53 с углубленным изучением  отдельных предметов»  города Чебоксары Чувашской Республики

 

 

 

 

 

Методическая разработка  

по теме

«Построение сечений многогранников»

 

учителя математики МБОУ  «СОШ № 53» г. Чебоксары

Емельяновой Татьяны Васильевны

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пояснительная записка

 

Методическая разработка  по теме «Построение сечений многогранников» разработана Емельяновой Татьяной Васильевной,  учителем математики МБОУ  «СОШ № 53» г. Чебоксары (категория- высшая).

Данная разработка предполагает ознакомление с основными методами решения задач на построение сечений многогранников с использованием ИКТ, применение которых способствует осознанию понятия движения и тем самым дает возможность визуализировать  обучения учащихся поэтапному построению на проекционном чертеже.

Основные цели:

–   формирование основ научного мировоззрения, базирующегося на инвариантных и  фундаментальных знаниях стереометрии;

–   формирование основ грамотного построения моделей многогранников;

–   развитие пространственных представлений и воображения учащихся при помощи специального компьютерного программного обеспечения;

–   выявление и развитие математических способностей учащихся.

Задачи:

–   ознакомление учащихся с методами построения сечений многогранников и формирование у них устойчивого интереса к математике, посредством решения задач с использованием ИКТ;

–   политехническая направленность обучения учащихся путём решения задач прикладного характера;

–   подготовка к обучению в вузе.

Данная разработка может быть предназначена для учащихся X—XI классов различных типов общеобразовательных учреждений.

 

Данная разработка рассчитана на 10 часов.

Разработка апробирована на школьном уровне. Урок по теме «Построение сечений тетраэдра» показан на республиканском семинаре в 2008 году.

 

 

Содержание разработки:

1.      Теоретические основы темы

2.      Пропедевтика.

3.      Построение сечений тетраэдра.

4.      Построение сечений параллелепипеда

5.      Пересечение двух плоскостей

6.      Призма

7.      Задания  для контроля

8.      Литература

 

 

 

 

 

 

 

 

Теоретические основы темы.

 

1. Построение точек пересечения прямой и плоскости

Следом прямой L на плоскости α называют точку пересечения прямой L c   плоскостью α.
Следом плоскости α на плоскость β называют прямую, по которой плоскость α пересекает плоскость β.

2. Построение плоских сечений многогранников.

Итальянский ученый Леонид Батист Альберти (1404-1472) подчеркивал значение геометрии в живописи и утверждал, что своими художественными представлениями человек обязан именно геометрии. Геометрия была и остается законодательницей моды в вопросах гармонии и красоты.

            При решении задач по стереометрии часто необходимо умение строить на рисунке сечения  многогранников (например, пирамиды, параллелепипеда, куба и т.д.) некоторой плоскостью. Поясним, что понимается под сечением.

Сечение многогранника плоскостью – многоугольник, представляющий собой множество всех точек пространства, принадлежащих одновременно данному многограннику и плоскости. Данную плоскость называют секущей.

         Например, на рисунке изображен параллелепипед и секущая плоскость α, пересекающая параллелепипед по четырехугольнику АВСD. Плоскость β, в которой лежит одна из граней параллелепипеда, секущей плоскостью для него не является.

Для построения сечения многогранника, а точнее его изображения, можно построить точки пересечения секущей плоскости с ребрами многогранника и соединить каждые две из них, лежащие в одной грани.

Последовательность вершин и сторон сечения не существенна, но выполнять построения необходимо с учетом аксиом и теорем стереометрии, а также правил изображения фигур.

А) Для построения прямой, по которой пересекаются некоторые две  плоскости  и β, нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей  и β;

В) Для построения  точки пересечения прямой   и плоскости  нужно построить точку пересечения прямой  и прямой m, по которой пересекаются плоскость  и любая плоскость, содержащая прямую.

3. Метод внутреннего проектирования

Сущность этого способа заключается в следующем. Имея три точки, определяющие плоскость сечения, находят их проекции на основную плоскость, а также проекцию еще не построенной точки. По трем данным точкам и четырем проекциям отыскивают четвертую точку, принадлежащую плоскости сечения. Таким же образом,  получают пятую, шестую и т.д. точки, принадлежащие поверхности геометрического тела и плоскости сечения, т.е. сечению.

 

Способы задания секущей плоскости:

•         тремя точками, которые не лежат на одной прямой;

•         прямой и точкой, не лежащей на ней;

•         двумя пересекающимися прямыми  и т.д.

Методы построения сечений

•         метод следов;

•         метод внутреннего проектирования;

•         метод переноса секущей плоскости.

 

 

Тема «Построение сечений тетраэдра».

Цель – помочь изучить раздел геометрии «Построение сечений в стереометрии». Помочь учащимся в развитии     пространственного представления, умения мысленно моделировать геометрические тела и строить их графические изображения. Постигая теорию построения учащиеся знакомятся с новыми геометрическими закономерностями, многие из которых на продолжении столетий применяются в производственной практик, используются в архитектуре и живописи.

Рассмотрим метод следов.

Построить сечение многогранника плоскостью – это значит построить прямые, являющиеся следами пересечения граней многогранника данной плоскостью.

Следом прямой L на плоскости α называют точку пересечения прямой L c   плоскостью α.
Следом плоскости α на плоскость β называют прямую, по которой плоскость α пересекает плоскость β.

Практический материал. Предложенные задания взяты из  “Живой геометрии”, которую можно использовать  при наличии интерактивной доски или проектора с функцией интерактивной доски.

	мультипликация
Постройте сечение тетраэдра SABC   плоскостью MNK.	Постройте сечение тетраэдра SABC   плоскостью MNK.
В тетраэдре SABC    точка  К лежит в плоскости ABC. Постройте сечение тетраэдра плоскостью MNK.	В тетраэдре SABC    точка М лежит в плоскости ASВ. Постройте сечение тетраэдра плоскостью MNK.
В тетраэдре SABC    точка О лежит в плоскости ABC, а точка К – на отрезке SO. Постройте сечение тетраэдра плоскостью ACK.	В тетраэдре SABC    точка О лежит в плоскости ABC, а точка M – на отрезке SO. Постройте сечение тетраэдра плоскостью BMC.

 

 

 

 

 

 

 

 

 

 

 

 Тема « Построение сечений параллелепипеда».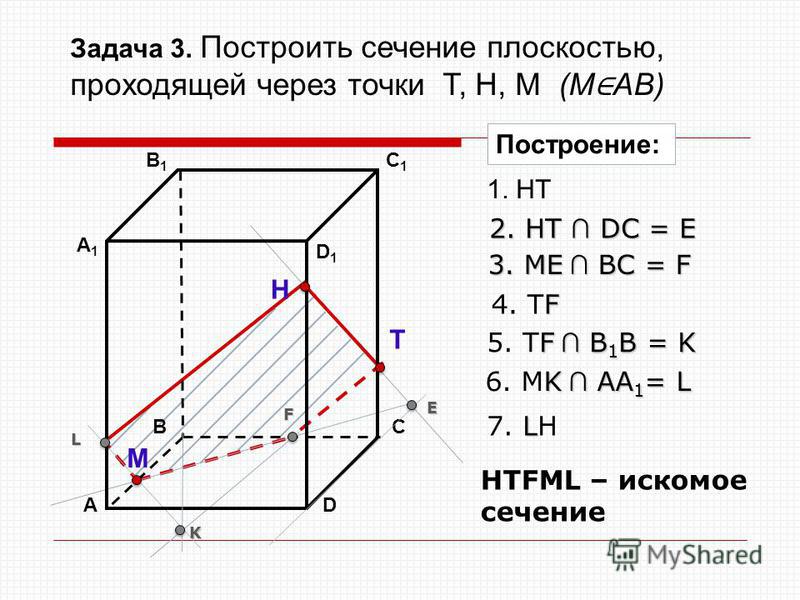

Цель урока: показать два способа построения сечений параллелепипеда

·          способ следов,

·          способ внутреннего проектирования.

 Для освоения начертательной геометрии, машиностроительного, архитектурно-строительного черчения необходимо овладеть некоторыми приемами решения стереометрических задач.

Теоретический материал.

Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырехугольники. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.

Особенность для построения сечения параллелепипеда.

Если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны (свойство 1°, п. 11).

Задача 1. Построить сечение параллелепипеда  плоскостью заданной тремя точками P, K и  M на ее боковых ребрах.

План построения иллюстрируется мультипликацией.

• Проведем через  точки Т и Р прямую а
• Проведем  прямую b через точки  А и В
• Обозначим точку их пересечения R             
• Проведем прямую d через точки T и  M
• Проведем прямую с через точки В и С
• Обозначим точку пересечения R ₁
• Соединим прямой х точки R и  R₁

Точки пересечения прямой x с ребрами AD и DC обозначим X  и Y

Многоугольник XPTMY –искомое  сечение.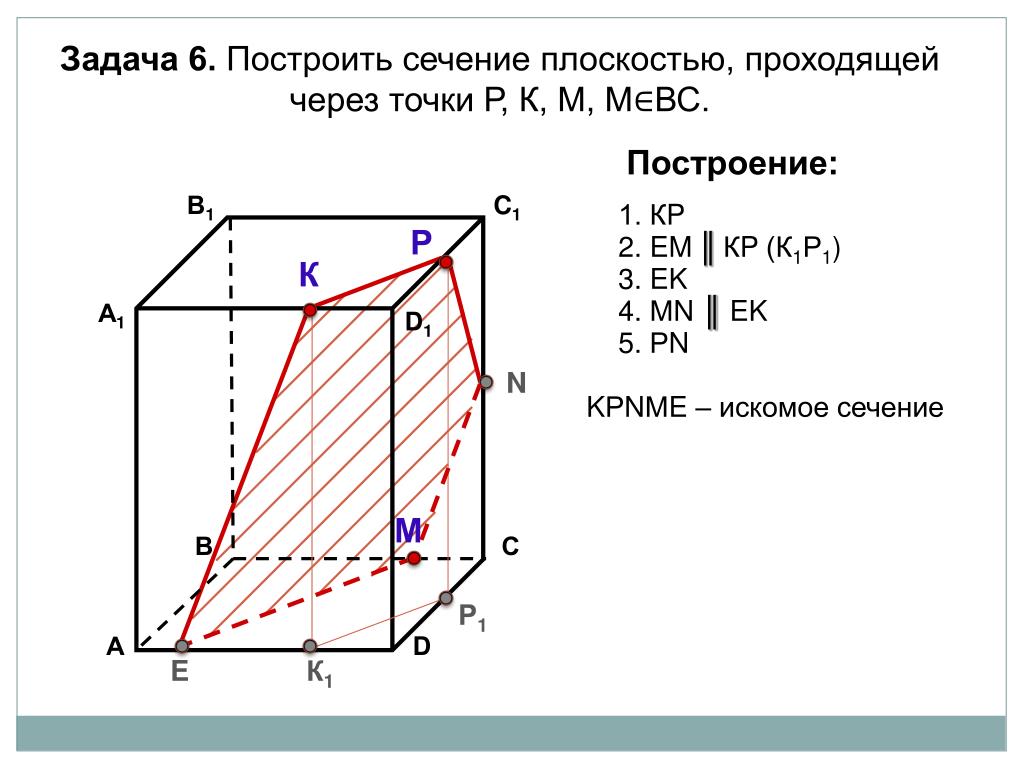

 

Примером построения сечения этим же способом могут  сечения этим же способом мо служить следующие иллюстрации:

Задача 2. Дан куб АВСDА₁В₁С₁D₁. Точки О, Е и Т принадлежат ребрам АВ, АD и СС соответственно. Постройте сечение куба плоскостью, проходящей через точки О, Е и Т.

Решение (см. рис.)

 

Задача 3. Постройте сечение куба плоскостью, проходящей   через точки Т, К и О.

Метод внутреннего проектирования

Сущность этого способа заключается в следующем. Имея три точки, определяющие плоскость сечения, находят их проекции на основную плоскость, а также проекцию еще не построенной точки. По трем данным точкам и четырем проекциям отыскивают четвертую точку, принадлежащую плоскости сечения. Таким же образом,  получают пятую, шестую и т.д. точки, принадлежащие поверхности геометрического тела и плоскости сечения, т.е. сечению.

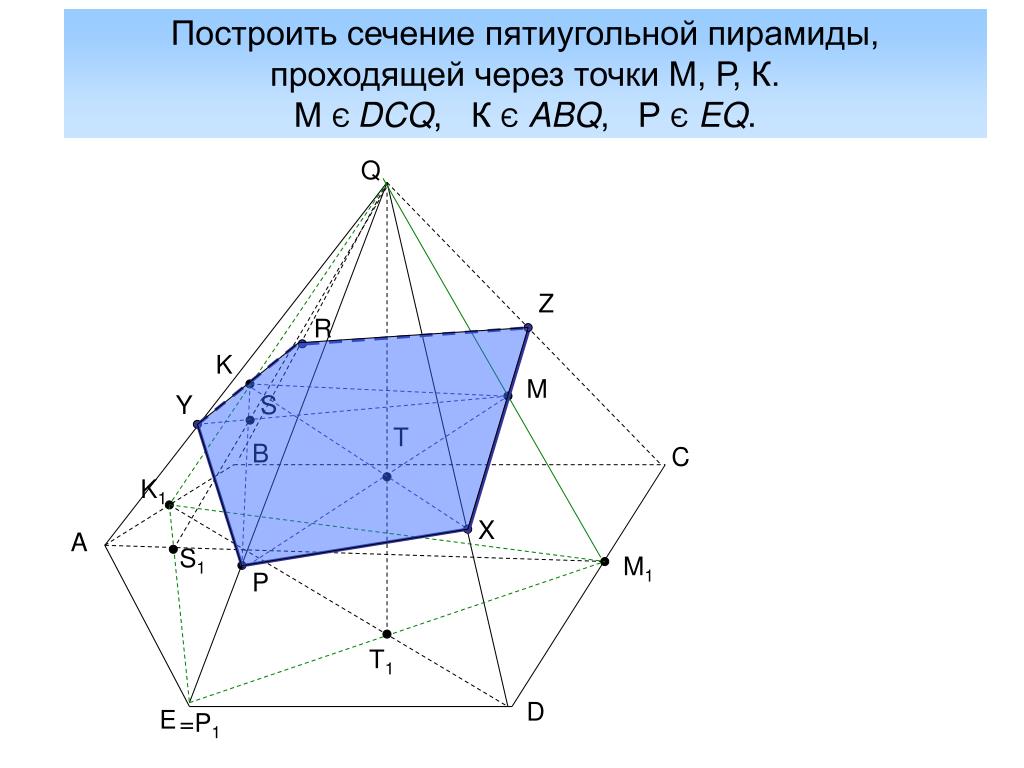
Задача 3(задача 1, 2способ) 

Анализ

Выберем направление внутреннего проектирования параллельно боковым ребрам призмы.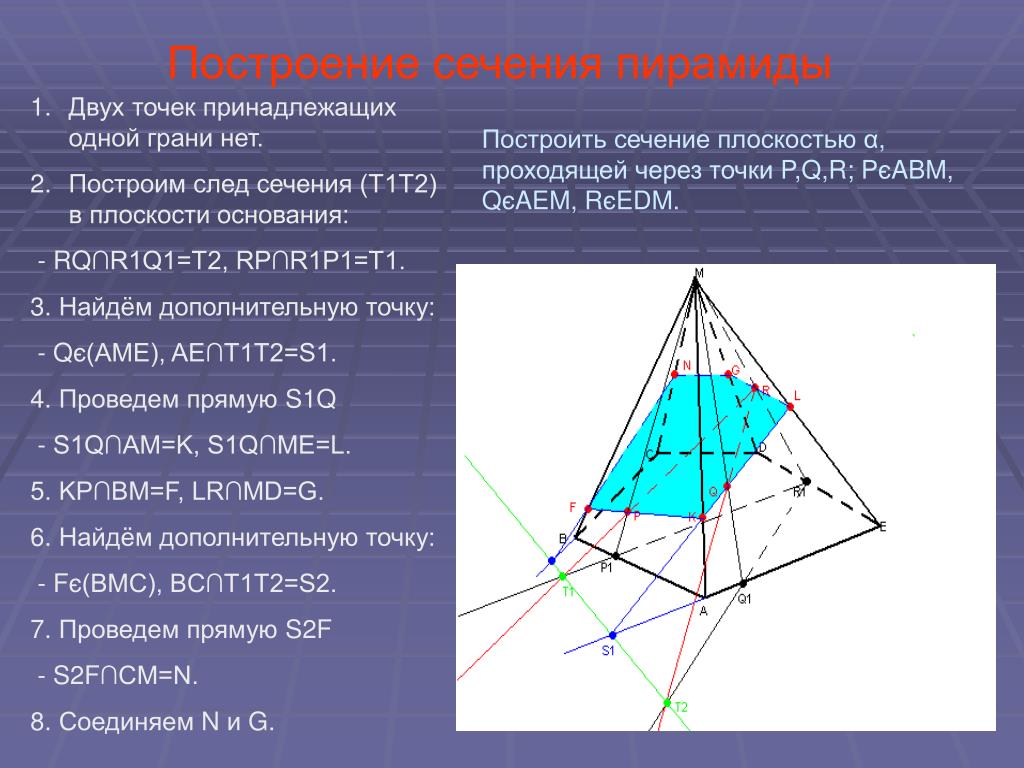 За основную плоскость примем плоскость основания ABCD, Тогда проекциями точек P,K,M  на основную плоскость будут точки A,D,C.Три точки P,K,M не лежат на одной прямой и поэтому определяют единственную плоскость. Чтобы построить сечение, достаточно определить точку  встречи этой плоскости с четвертым ребром. Эту точку можно указать, если построить прямую, принадлежащую секущей плоскости и пересекающую ребро DD₁.Очевидно, эта прямая должна принадлежать какой-то плоскости, в которой расположена прямая DD₁. Две такие плоскости уже есть ADD₁A₁ и   DCC₁D₁.В каждой из них имеется  по одной точке, принадлежащей  секущей плоскости. Но для проведения прямой  нужны две точки. Построим  диагональные плоскости. Получим линию пересечения  ОО ₁ .

Прямая РМ пересечет ОО₁ в точке S.Точки К и S принадлежат плоскости сечения и плоскости BDD₁B₁.Эти две точки определяют прямую, которая, пересекаясь с DD₁ даст искомую точку.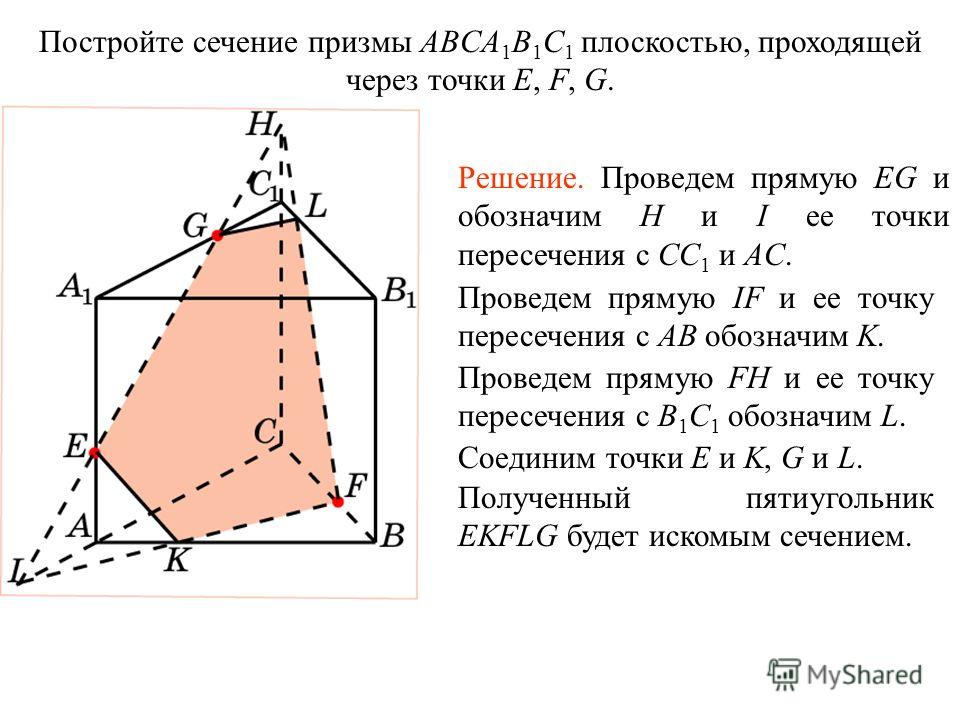

Построение.

• Строим РМ и ее проекцию А₁С₁.
• Строим плоскость BDD₁B₁. B₁D₁ – проекция искомой прямой.
• Точка О₁-проекция точки пересечения РМ с искомой прямой.
• Проводим прямую через О ₁ параллельно ВВ₁.Получаем точку S.
• Строим прямую КЕ.
• Точка Т – искомая.                                                     

Доказательство

1. Точки Р и М принадлежат плоскости сечения, отрезок РМ принадлежит плоскости сечения .Следовательно и  точкаS принадлежит этой же плоскости.
2. Точки К иS принадлежат искомой плоскости. Поэтому всякая точка прямой KS ,в том числе и точка Т ,принадлежит плоскости сечения.

Исследование

Решение всегда возможно и единственно. Поскольку точки Р, К, М не лежат на одной прямой, они определяют единственную плоскость.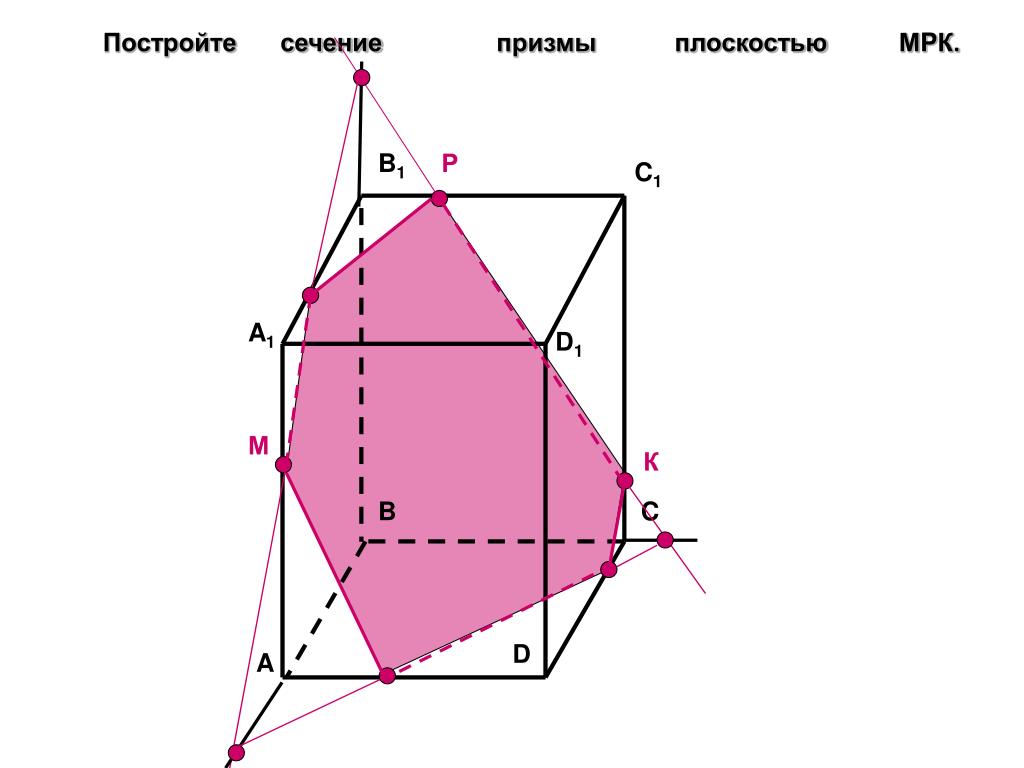

Практические задания.

Предложенные задания взяты из  “Живой геометрии”, которую можно использовать  при наличии интерактивной доски или проектора с функцией интерактивной доски.

Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9

 

Задания на построение линий пересечения двух плоскостей

	1 способ 2 способ

 

Задания для построения сечений по темам.

Призма.

 

Список использованной литературы:

1.Александров  И. Геометрические задачи на построения и методы их решения. —М., 1995.

2.Бескин Н.М. Изображение пространственных фигур — М., 1971.

3.Василевский А.Б. Методы параллельных проекций. — Мн., 1985.

4.Вотрогов  В. Методы построения изображений.— Хабаровск, 1978.

5.Гольдерберг Я.Е. С чего начинается решение стереометрической задачи.— Киев: «Радянська школа», 1990.

6.Добровольская Н.А. «Творческие задачи на создание дополнительных построений» Изд. Рост.унив. 1984 .

7.Изоак Д.Ф. О задачах на построение в стереометрии — М., 1977.

8.Математика в школе. —  1990. —№3

9.Математика: Приложение к газете «Первое сентября». —  2001—№29, 30, 31

10.  Орехов П.С. Изображения в стереометрии: Пособие для учителей. —Ижевск,1981.

11.  Раневский К. Систематический курс геометрии и методы решения задач на построение — М.: Госиздат.1987.

12.   Саранцев Г.И. Решаем задачи на геометрические преобразования —М.,1997.

13.  Шарыгин В.Н. Решение задач по стереометрии.— М.,1989.

 

Электронные ресурсы.

1.      fio.novgorod.ru/projects/project2599/index.htm  

2.      Электронный учебник «Математика 5-11. Практикум»

3.Виртуальная школа Кирилла и Мефодия. Уроки геометрии в 10 – 11-ых классах.

 

                                     

Секционирование | ЗАГС ФАС

ГЛАВНАЯ / ОБУЧЕНИЕ /

Что на этой странице?

• Требования к секционированию
• Когда раздел
  • Важные даты раздела
• Начиная
  • Методические рекомендации
  • Использование моделей
  • Распространенные сообщения об ошибках
  • Советы и приемы
• Поддержка секционирования

Это кому?

Профессорско-преподавательский состав, координаторы учебных программ – за создание курсов для секционирования

Когда раздел

Инструмент разделения на разделы нельзя использовать для перемещения учащихся между разделами после крайнего срока добавления/удаления (крайний срок пятого понедельника).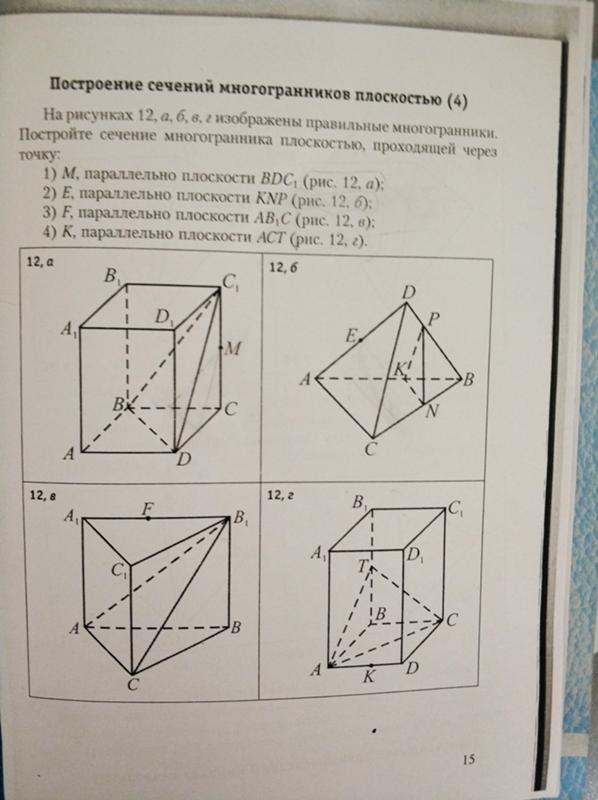 Пожалуйста, внесите необходимые изменения в разделы до этой даты.

Предварительной регистрации нет; студенты не могут быть разделены на секции до зачисления на курс. При разделении используются реальные зачисления, поэтому учащиеся должны быть полностью зачислены, чтобы вы могли разделить курс.

Важные даты разделения

Осень 2022 г.

• Инструмент секционирования открывается в my.harvard 15 августа 2022 г.
• Инструмент секционирования закрывается 4 октября 2022 г.

Начиная

Используйте инструмент разделения на разделы my.harvard, чтобы создавать или редактировать разделы для курсов с обсуждениями или лабораторными работами. Вы также можете использовать этот инструмент, чтобы переводить учащихся в классы с несколькими разделами регистрации, например языковые курсы.

Приступая к работе с разделами, вам следует ознакомиться со следующими документами:

• ИТ-справка — Инструкции по секционированию: изучите основы секционирования.
• Документация – рабочие процессы секционирования: найдите инструкции, соответствующие потребностям вашего курса.

Мы также предлагаем обучающие видеоролики, в которых освещаются основные функции инструмента создания разделов:

• Как создать новый раздел
• Как включить студенческие настройки

Методические рекомендации

• Учащиеся должны быть полностью зачислены , чтобы вы могли добавлять их в разделы.
• Все разделы должны начинаться в назначенное время начала.
• Несколько разделов курсов одновременно, что может повлиять на доступность времени студентов . Если учащийся был свободен в определенное время, но позже у него возник конфликт времени, это, вероятно, связано с тем, что он предоставил доступное время для нескольких курсов, и теперь он был зачислен в секцию для другого курса в это время.
• Никогда не редактируйте раздел обсуждения-заполнитель (обычно называемый DIS  или LAB ). Это вызывает серьезные проблемы с зачислением и не позволяет учащимся зачисляться на ваш курс. Не удаляйте и не добавляйте шаблон встречи в раздел обсуждения-заполнителя даже после истечения крайнего срока регистрации на курс.
• Нажмите кнопку “Отправить” только один раз. Каждый раз добавляет новое задание в очередь на обработку.

Использование моделей

Мы рекомендуем отдавать предпочтение учащимся, которые первыми отправили свои предпочтения. После того, как вы закончите разделение на секции, вы сможете переместить учащихся, которые не отправили свои предпочтения.

Модели, учитывающие предпочтения

Учитывать предпочтения учащихся: Перемещаются только учащиеся, предоставившие предпочтения. Вы можете переместить учащихся, которые не отправили предпочтения вручную, или запустить другую модель, не учитывающую предпочтения.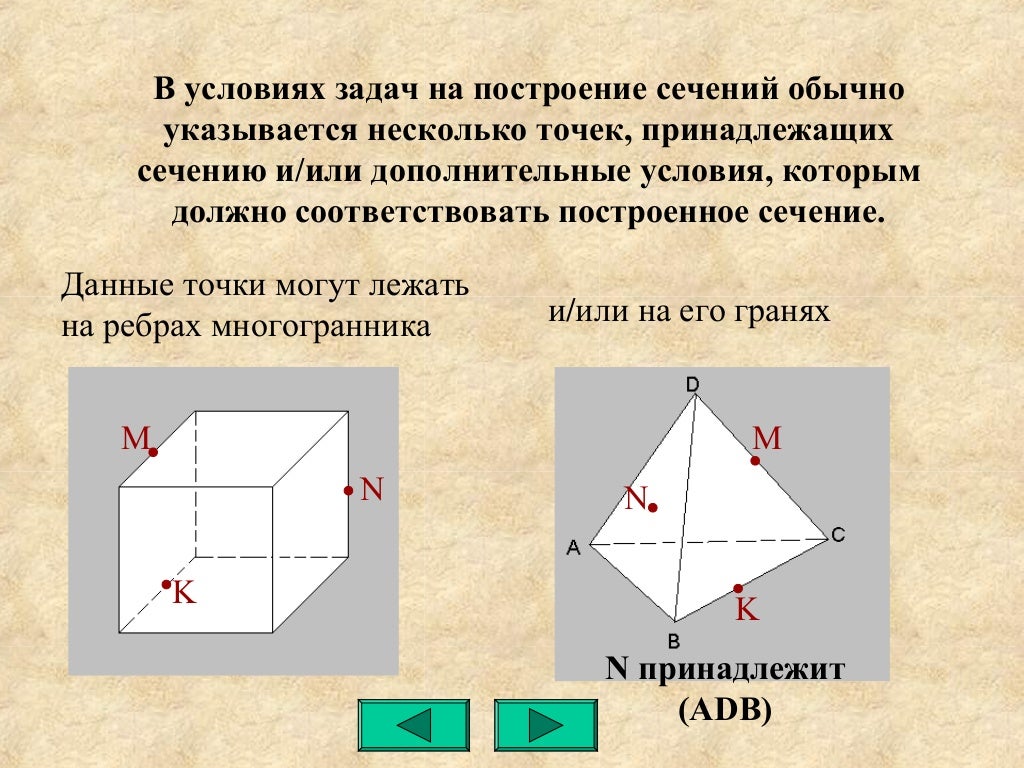

Модели, не учитывающие предпочтения

Последовательно:  Создает группы по одному разделу/учащемуся за раз в зависимости от предпочтений.

Пример: последовательная модель поместит учащегося в секцию 1, другого учащегося в секцию 2 и еще одного учащегося в секцию 3, повторяя эту схему до тех пор, пока все учащиеся не будут разделены на секции (1, 2, 3, 1, 2, 3, 1, 2). , 3).

Равномерное распределение классов: Полностью заполняет разделы перед переходом к следующему разделу.

Пример: заполните раздел 1, заполните раздел 2, заполните раздел 3.

Как устранить неполадки с сообщениями об ошибках

Распространенные сообщения об ошибках

Сообщение об ошибке	Проблема	Решение
Пользователь не имеет доступа к транзакции удаления. Транзакция не была обработана.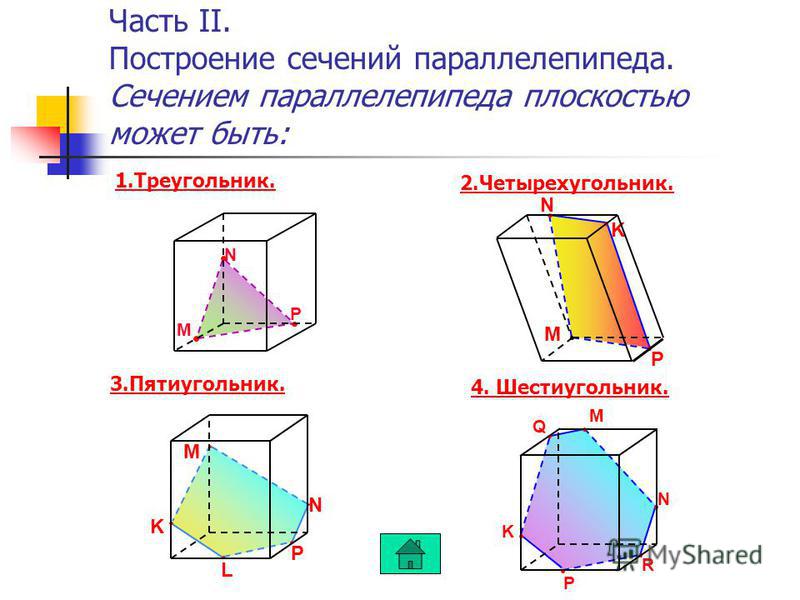	Инструмент секционирования нельзя использовать для обмена после истечения крайнего срока добавления/удаления.	Отправьте заявку на адрес sectioning@fas.harvard.edu, и отдел регистрации внесет изменения от вашего имени.
Конфликт расписания с текущим зачисленным курсом. Выберите другой класс или отмените конфликт времени.	У учащегося возник конфликт времени с разделом перехода, и его нельзя переместить. Они могут решить проблему, выбрав альтернативное время раздела.	Попросите учащегося выбрать другое время секции.
Вы не можете переключаться с одного и того же курса, если на обменный курс будет наложен штраф.	У учащегося может быть перекрестная регистрация, и его карьера может иметь другие крайние сроки добавления/удаления или базы оценок, чем FAS.	Отправьте заявку на адрес sectioning@fas.harvard.edu, и офис регистратора внесет изменения от вашего имени.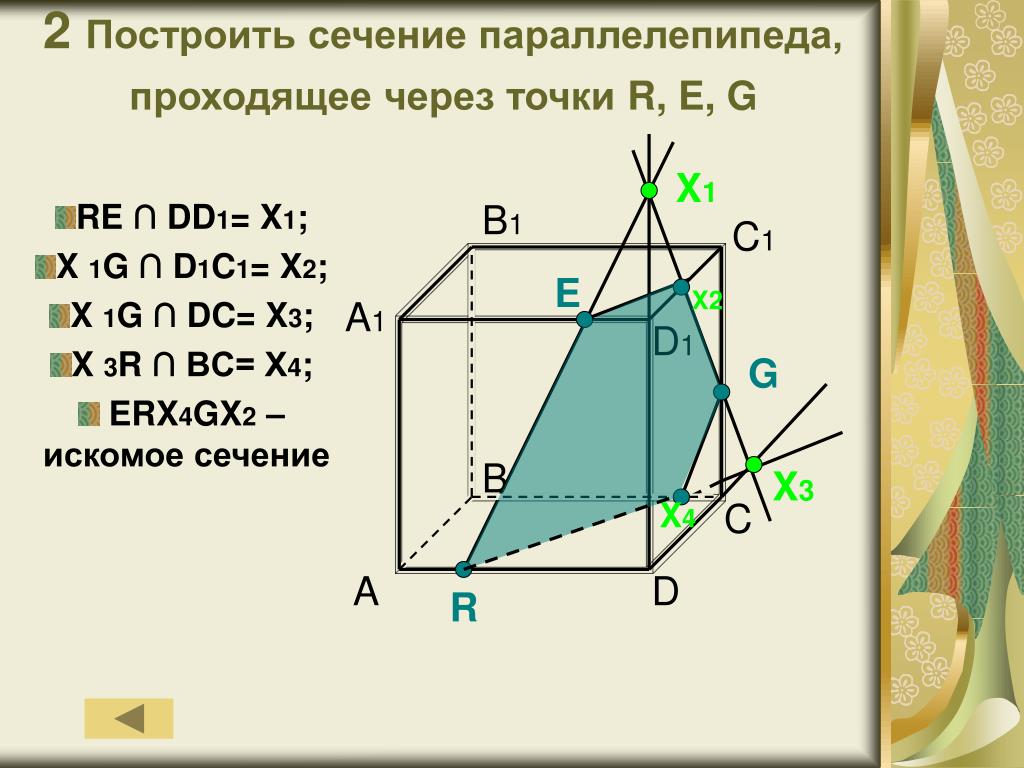
Не зачислен в класс “От”. Своп не обрабатывается.	Первичная составляющая в классе ассоциации и расписание занятий не совпадают.	Отправьте заявку на адрес sectioning@fas.harvard.edu, и отдел регистрации исправит проблему.
Своп не обработан. Держи запись.	У учащегося может быть удержание с советом или другой индикатор обслуживания.	Поговорите со студентом и попросите его разрешить удержание его записи.
Введенное в поле значение не соответствует одному из допустимых значений.	TF не был назначен преподавателям курса, или их права доступа необходимо изменить.	Отправьте заявку на адрес sectioning@fas.harvard.edu, и отдел регистрации исправит проблему.

Советы и приемы

Рассмотрите различные подходы к блокировке учащихся

Функция блокировки модели работает аналогично статусу, поэтому будет только одна заблокированная модель. Каждый раз, когда вы блокируете учеников, они появляются на одной заблокированной модели. Рассмотрите два разных подхода к блокировке учащихся: Блокировка или Отправка по ходу дела.

• Блокировка: Запустите модель и заблокируйте успешно разделенных учащихся. Блокировка студентов не подтверждает их зачисление; он просто удерживает их на месте, пока модель не будет отправлена. Запустите другую модель и снова заблокируйте новых учащихся, которые были успешно разделены. Повторяйте до тех пор, пока у вас не останется управляемое количество учеников, которые не были разделены на секции. Затем отправьте заблокированную модель и разделите оставшихся студентов вручную. ИЛИ ЖЕ,
• Отправить по ходу дела: Запустить модель и отправить для учащихся, которые были успешно разделены на секции. Затем запустите другую модель и отправьте ее для учащихся, которые на этот раз были успешно разделены на секции. Повторяйте до тех пор, пока у вас не останется управляемое количество учащихся, которые не были разделены на секции, и разместите этих учащихся вручную. Этот подход отправляет изменения регистрации по мере их выполнения, а не блокирует их.

Определите, сколько разделов вам нужно для каждого времени встречи

• Вместо того, чтобы создавать несколько одинаковых разделов для оценки студентов, создайте один большой раздел на это время, чтобы увидеть, сколько людей заинтересовано.
• Как только вы узнаете, сколько людей заинтересовано в этом разделе, создайте дополнительные разделы для этого шаблона встречи (например, M09A, M09B, M09C).

Узнайте, как ваши ученики оценивают разные разделы

• На вкладке «Отчетность » загрузите отчет о предпочтениях учащихся 9.0038 . Это позволит вам загружать все настройки, не переключаясь между вкладками.
• На вкладке Разделение вы также можете выбрать Показать все предпочтения учащихся , чтобы вы могли легко сравнивать предпочтения нескольких учащихся.

Информация для курсов с несколькими основными компонентами

Языковой курс с несколькими разделами лекций является примером курса с несколькими основными компонентами.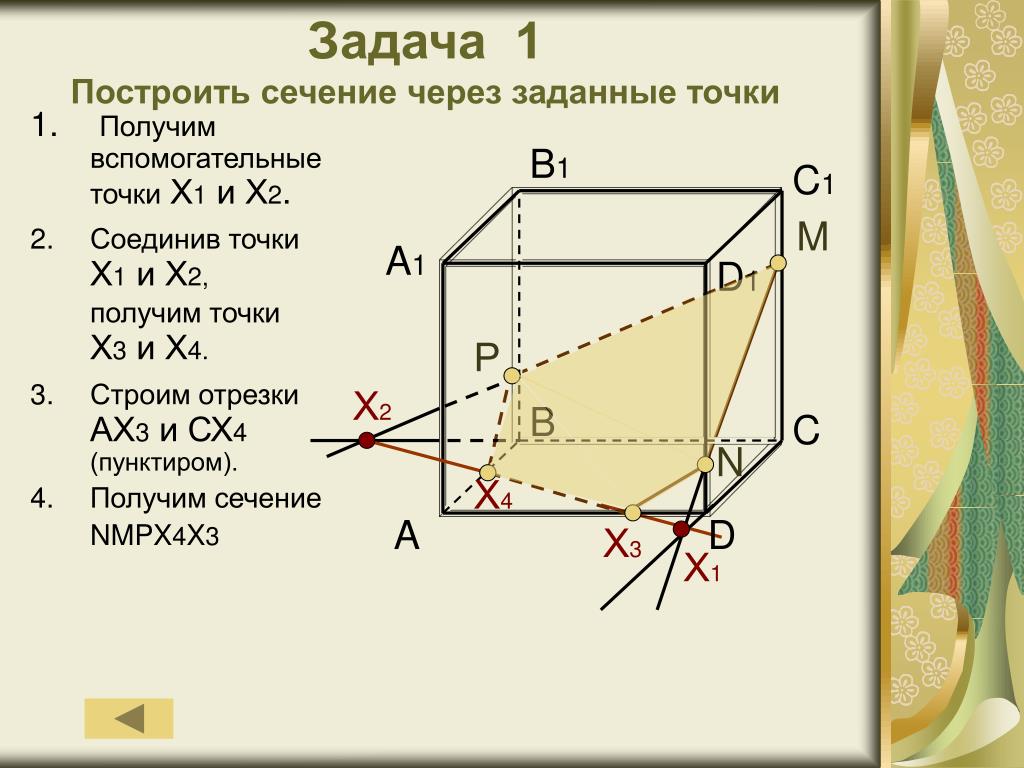

• Используйте вкладки для перехода к другим основным компонентам: На вкладке «Секционирование» будет отображаться одна вкладка для каждого основного компонента. На каждой вкладке будут отображаться только учащиеся, зарегистрированные в этом разделе основного компонента.
• Разделы обсуждения могут не отображаться в списке разделов, но вы все равно можете выбирать учащихся и переключать их между разделами обсуждения.

Перемещение студентов, чтобы сбалансировать зачисление

1. Отфильтруйте по разделу, из которого нужно вывести людей
2. Либо используйте Отчет о предпочтениях учащихся , либо  Показать все предпочтения учащихся  , чтобы узнать, кто занял место в разделе с недостаточным количеством учащихся.

Связаться со студентами, покупающими курс, или текущими зачисленными

• Свяжитесь с покупателями: Загрузить отчет о текущих покупателях
• Контактные лица:  Загрузить список (значок сетки) с вкладки “Разделение”

Нужна помощь?

Разделительная опора

Электронная почта : команда отдела регистрации ФАС по разделам для помощи в разделении
Zoom : 15 минут с командой по разделам

• Габи Браун, координатор курсов
• Олимпия Земняк, академический координатор
• Кэти Шеберле, академический специалист

Электронная почта : Академические технологии

• за помощь с Canvas

Электронная почта : Группа аудиторов ЗАГС ФАС

• за помощь в классах

Ресурсы


ИТ-помощь — раздел «Студенты» в my. harvard


Рекомендации — Запрос места в разделе

Контрольный список
— настройка курса
для секционирования


Документация – рабочие процессы секционирования

SECTIONING Синонимы: 222 Синонимов и антонимов для SECTIONING

См. определение sectioning на Dictionary.com

• as in part
• as in partition
• as in portion
• as in dissever
• as in dissect
• as in разделить

синонимы к слову рассечь0007 disjoin

• dismantle
• dissever
• disunite
• divide
• factor
• itemize
• particularize
• partition
• portion
• rend
• section
• segment
• sever
• slice
• split
• strip
• разделить
• разделить
• разорвать
• разбить
• разделить

• разделить
• apportion
• cut
• deal
• disburse
• dispense
• disperse
• distribute
• portion
• screen
• section
• segment
• separate
• share
• slice
• split
• cut in
• разрезать на
• разрезать
• разделить
• раздать
• отгородить
• отмерить
• разобрать
• size into
• split up
• wall off

• administer
• allocate
• allot
• apportion
• assign
• deal
• dispense
• distribute
• parcel
• part
• partition
• piece
• пропорция
• квота
• паек
• секция
• доля
• смена
• делим
• dole out
• mete out

• cut
• detach
• divide
• partition
• section
• segment
• sever
• split
• break up
• cut off
• split up

• anatomize
• разрезать
• разделить
• разъединить
• разъединить
• расчленить
• разделить
• разделить
• оперировать
• part
• quarter
• section
• sever
• slice
• sunder
• break up
• dislimb
• exscind
• exsect
• lay open
• prosect

• break
• break down
• carve
• разрезать
• изолировать
• разделить
• разделить
• разделить
• разделить
• разорвать
• пополам
• branch
• chop
• cleave
• cross
• demarcate
• detach
• dichotomize
• disengage
• disentangle
• disjoin
• dislocate
• dismember
• dissect
• dissever
• dissociate
• dissolve
• разъединить
• развести
• разделить пополам
• пересечь
• разойтись
• часть
• четверть
• Транс
• Rupture
• Секция
• Сегмент
• SEAV
• SHEAR
• Sunder
• UBIND
• UNDO

.

• присоединить
• собрать
• объединить
• соединить
• пару
• собрать
• соединить
• связь
• unite
• arrive
• come
• collect
• combine
• gather
• hoard
• hold
• join
• keep
• unite
• attach
• collect
• deny
• gather
• удерживать
• объединять
• сохранять
• отбрасывать
• удерживать
• объединять
• присоединять
• объединять
• connect
• couple
• join
• link
• unite
• combine
• connect
• join
• unite
• mend
• sew
• attach
• combine
• fix
• join
• починить
• остаться
• объединить
• подождать
• соединить
• закрыть
• соединить
• закрепить
• жениться
• Согласен
• Приложение
• Соберите
• Consince
• Пара
• Disarrange
• Disorganize
• Собрание
• Hold
• . Третье издание Copyright © 2013, Philip Lief Group.

  ВИКТОРИНА

  Чувствуете себя Wabbit из-за неудачного выбора слова? Пройдите этот тест на смешные прилагательные.

  НАЧНИТЕ ВИКТОРИНУ

  Как использовать разделение в предложении

  Посмотрим, что говорит нам каждый раздел, и как все они начинают сочетаться с откровениями последнего раздела.

  ПОТРЯСАЮЩИЙ КОНЕЦ УПРАЖНЕНИЯ С ДОВЕРИЕМ СЬЮЗАН ЧОЙ, ОБЪЯСНЕНИЕ КОНСТАНС ГРАДИНА 20 ноября 2020 г. VOX

  Мы пометили этот раздел для спойлеров, но на самом деле, если вы думали, что Дин с его вечным желанием смерти собирался пройти через финал сериала , вы смотрели другое шоу.

  ФИНАЛ СЕРИИ SUPERNATURAL’S BONKERS Ознаменовал конец эры FANDOMAJA ROMANONON 20 ноября 2020 г. VOX

  Раздел с интервью и выдержками из речи более интересен, в основном потому, что он содержит подробности о человеке из плоти и крови, а не только об Амазонке.

  МЫСЛИ ДЖЕФФА БЕЗОСА О БОЛЬШОМ БИЗНЕСЕ, КОСМОСЕ И WASHINGTON POSTJAMES LEDBETTER20 ноября 2020 г.WASHINGTON POST

  В разделе «Мои конкуренты» вы найдете сайты-конкуренты, которые ранжируются по ключевым словам, которые вы добавили в свой проект.

  АНАЛИЗ КОНКУРЕНЦИИ С ПОМОЩЬЮ ИНСТРУМЕНТОВ SE RANKING.

  АПТЕКА AMAZON РАБОТАЕТ: ПОКУПАТЕЛИ ТЕПЕРЬ МОГУТ ЗАКАЗЫВАТЬ РЕЦЕПТЫ НАПРЯМУЮ ЧЕРЕЗ TECH GIANTRACHEL SCHALLOM17 НОЯБРЯ 2020 г. FORTUNE

  сделать доступным.

  ИИ БОРЕТСЯ С КРИЗИСОМ РЕПЛИКАЦИИ 12 НОЯБРЯ 2020 г. MIT TECHNOLOGY REVIEW

  Многочисленные перезагрузки «Гордости и предубеждения» в наши дни практически требуют отдельного раздела в книжном магазине, поэтому, когда вы берете в руки ромком с главными героями по имени Дарси и Элль, вы можете подумать, что знаете, что вам предстоит.

  «НАПИСАННОЕ ЗВЕЗДАМИ» ЭТО ПЕРЕЗАГРУЗКА «Гордости и предубеждения», очаровательная, искрометная и совершенно сама по себе МОРТОН10 ноября 2020 г.