Построение сечение: Построение сечений простейших многогранников.

Задача 1. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: B, D и середину M ребра AC.

Задача 2. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: B и середины рёбер AD и CD.

Задача 3. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: середину K ребра AD и точки L и M, лежащие на продолжениях рёбер AB и AC за точки B и C.

Задача 4. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: середины рёбер BC, AD и точку L, лежащую на продолжении ребра AC за точку C.

Задача 5. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: середины K, L и M рёбер AD, AB и BC.

Задача 6. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: A, C и точку пересечения медиан грани ABD.

Задача 7. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: середины рёбер AD, CD и точку L, лежащую на ребре BC, если BL : LC = 1 : 2.

Задача 8.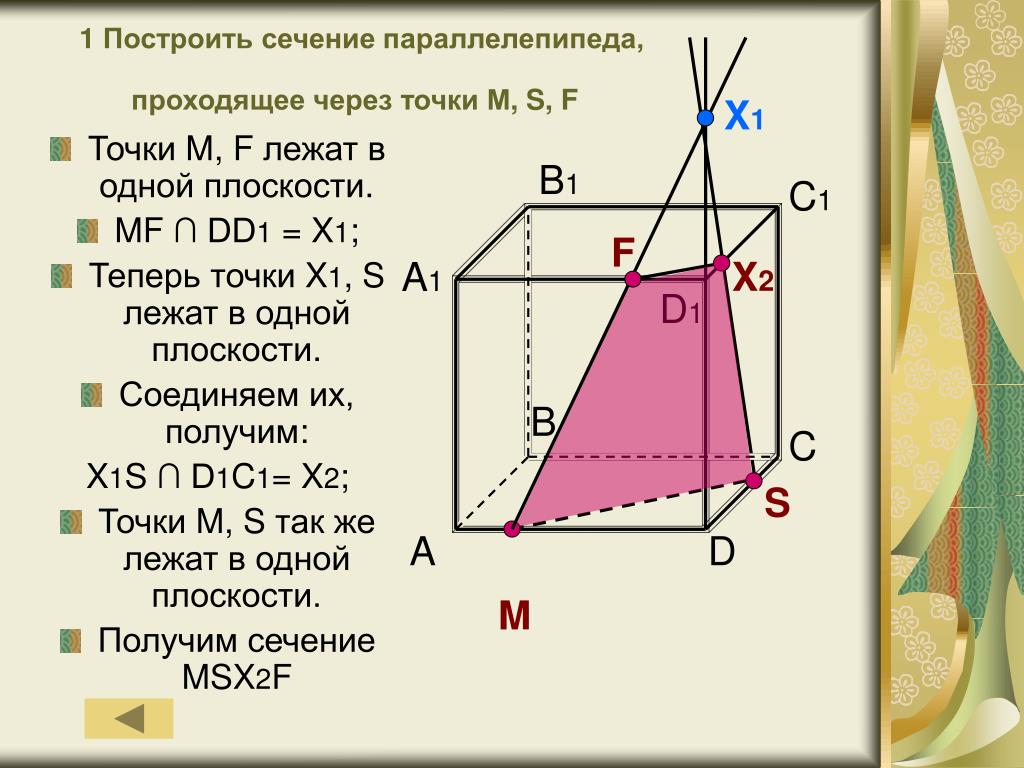 Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: K, L и M, лежащие на рёбрах AD, AB и BC соответственно, если AK : KD = BL : LA = BM : MC = 1 : 2.

Задача 9. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: точки пересечения медиан граней ABD, BCD и ABC.

Задача 10. Постройте сечение треугольной пирамиды DABC плоскостью, проходящей через следующие точки: середины рёбер BC, CD и точку, лежащую на медиане DM грани ABD.

Задача 11. Постройте сечение параллелепипеда ABCDA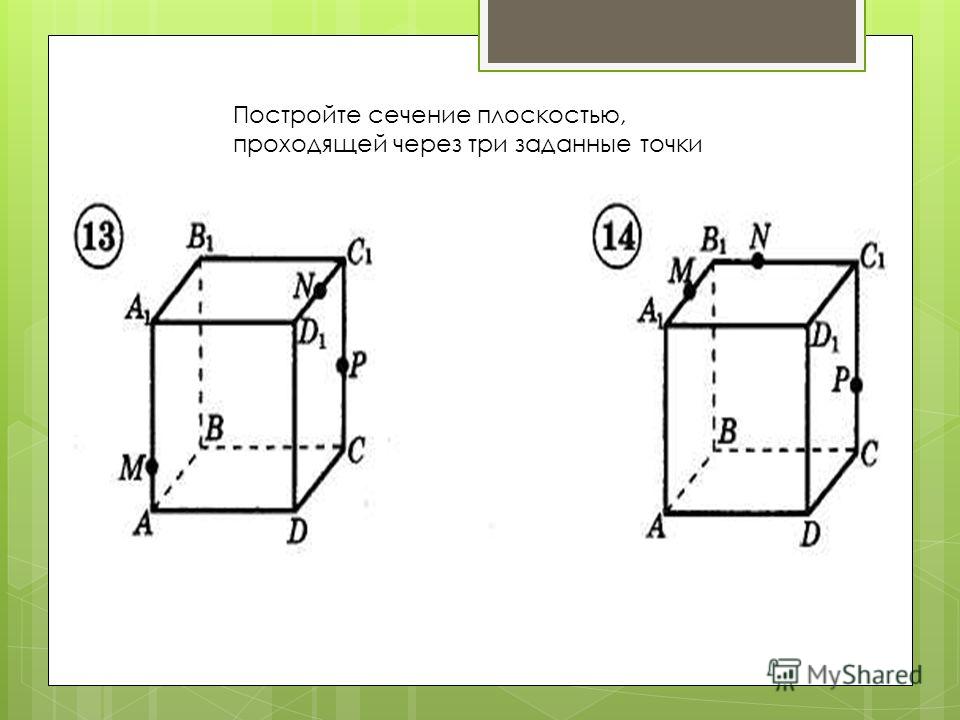 1B1C1D1 плоскостью, проходящей через следующие точки: середины рёбер AB, AD и AA1.

Задача 12. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: B, C и середину ребра A1B1.

Задача 13. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: A, C и середину ребра A1B1.

Задача 14. Постройте сечение параллелепипеда ABCDA1B 1C1D1 плоскостью, проходящей через следующие точки: середины рёбер AA1, AD и центр грани BB1C1C.

Задача 15. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: центры граней ABCD, AA1B1B и BB1C1C.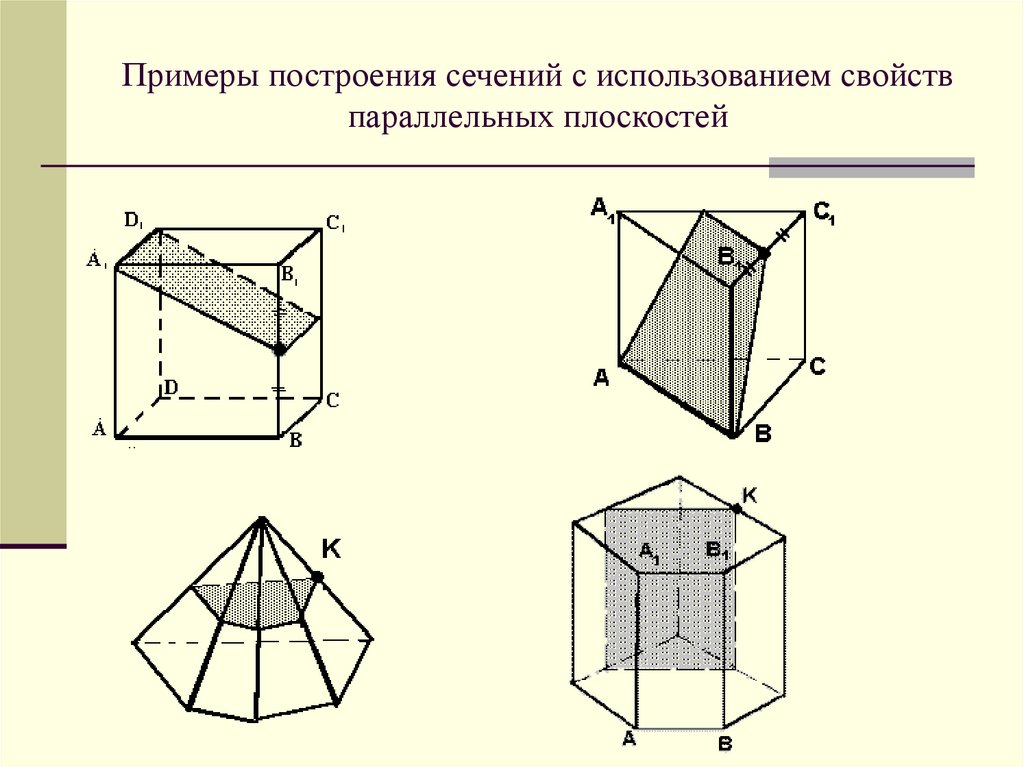

Задача 16. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: середины рёбер AB, BC и DD 1.

Задача 17. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: середины рёбер A1B1, CC1 и вершину A.

Задача 18. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: середину ребра CC1 и точки K, L, лежащие на рёбрах AB и A1B1, если BK : KA = A1L : LB1 = 1 : 2.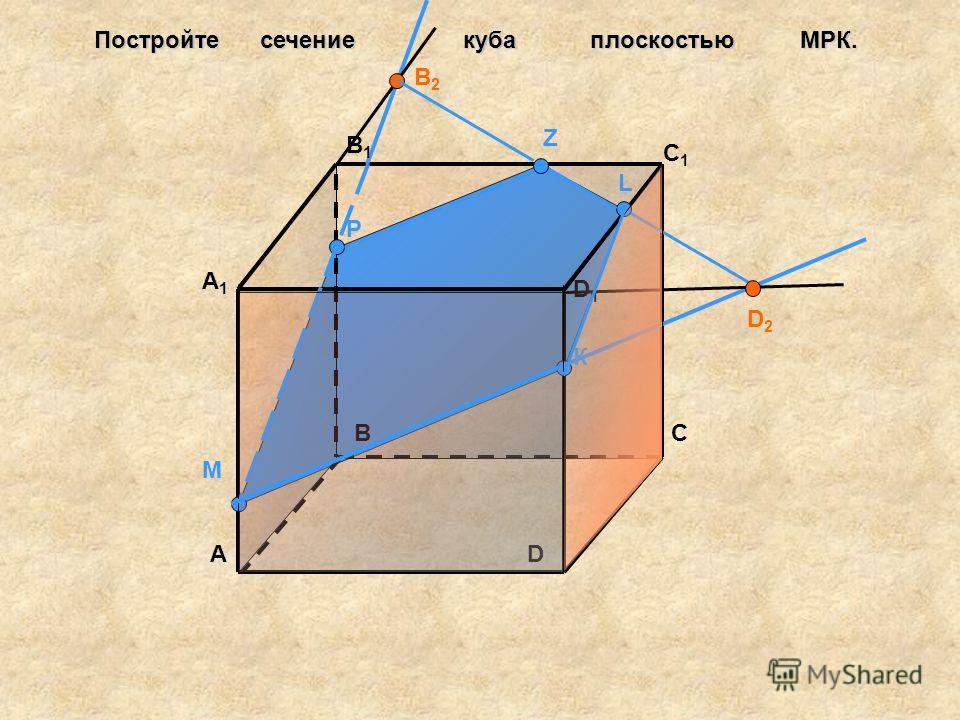

Задача 19. Постройте сечение параллелепипеда ABCDA 1B1C1D1 плоскостью, проходящей через следующие точки: середину ребра A1B1, вершину A и точку M на ребре B1C1, если B1M : MC1 = 1 : 3.

Задача 20. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: середины рёбер AD, CD и A1B1.

Задача 21. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: середины рёбер AB, BC и CC1.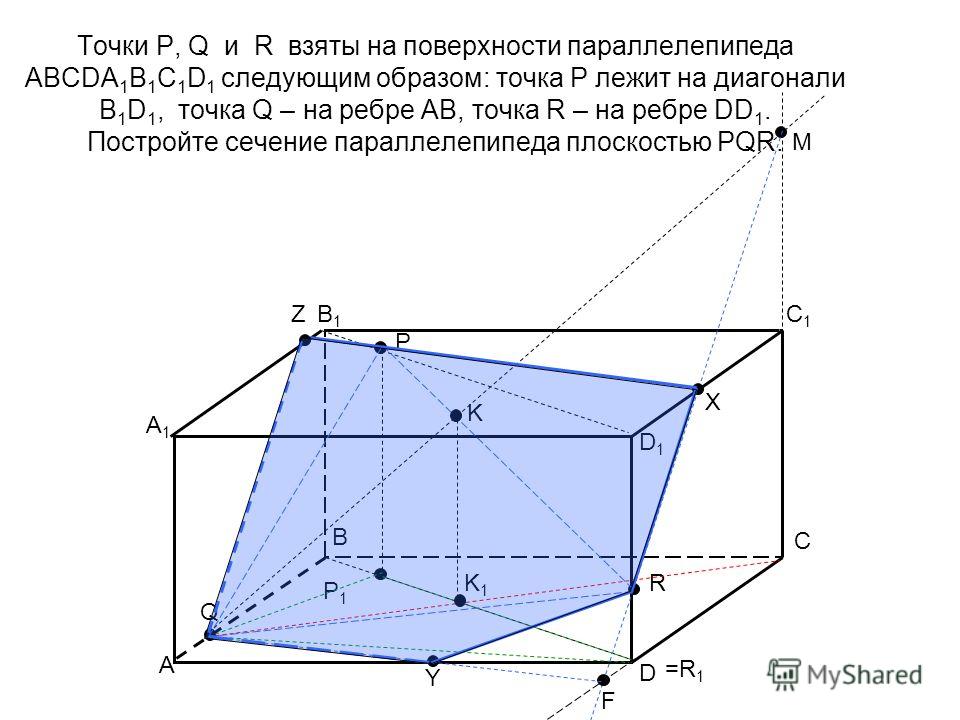

Задача 22. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через следующие точки: вершину B1, центр грани ABCD и середину ребра AA1.

Задача 23. Постройте сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через следующие точки: середину ребра AA1 и вершины B и C1.

Задача 24. Постройте сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через следующие точки: середины рёбер AA1, B1C1 и вершину B.

Задача 25. Постройте сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через следующие точки: центры граней AA1B1B, BB1C1C и точку M ребра BC, если CM : MB = 1 : 2.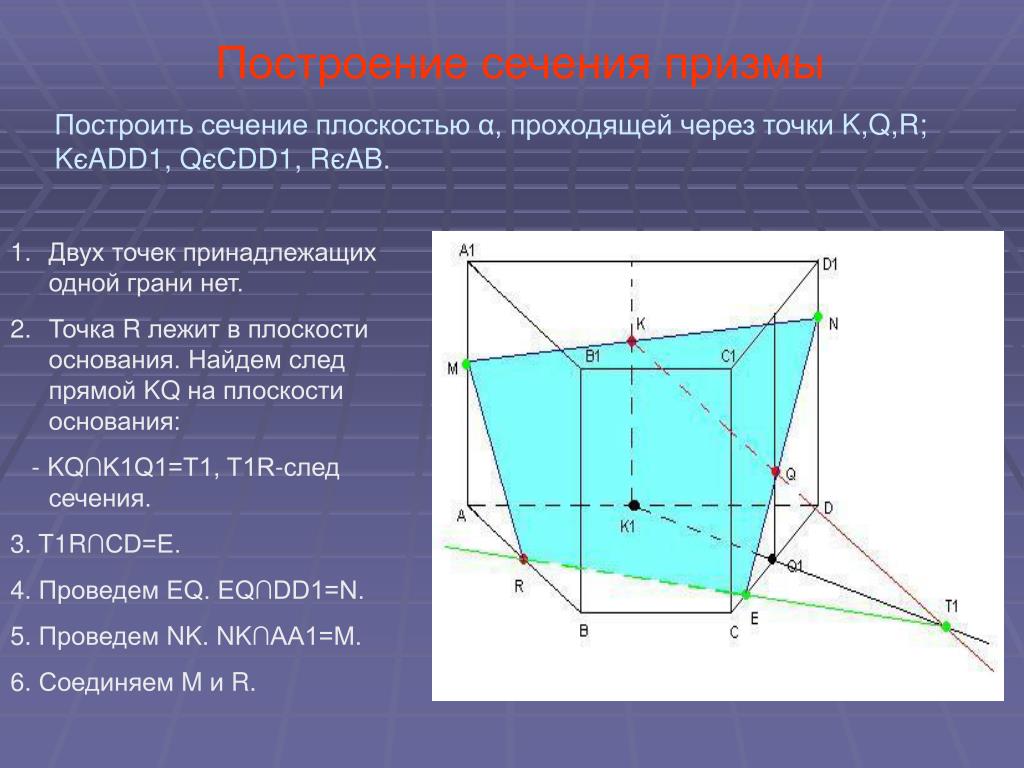

Задача 26. Постройте сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через следующие точки: середины рёбер AB, A1C1 и CC1. Решение K — середина АВ;  Р — середина А1С1;  М — середина СС1. Точки Р и М ∈ грани АСС1А1 . Проводим РМ. Проводим АС;  РМ∩АС=D. Проводим АА1;  РМ∩АА1=Е. Точки К и D ∈ плоскости АВС. Проводим КD;  КD∩ВС=F. Точки К и E ∈ плоскости ABB1. Проводим КE;  KE∩A1B1=G. Сечение KGPMF.

Задача 27. Постройте сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через следующие точки: середины рёбер AA1, A1C1 и центр основания ABC.

Задача 28. Постройте сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через следующие точки: центр грани AA1B1B, середину ребра B1C1 и точку M ребра A1C1, если A1M : MC1 = 1 : 2.

Задача 29. Постройте сечение треугольной призмы ABCA1B1C1 плоскостью, проходящей через следующие точки: центр основания ABC и центры боковых граней AA1B1B и BB1C1C.

Задача 30. Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: A, B и середина ребра SD.

Задача 31. Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: середины рёбер AB, BC и SC.

Задача 32. Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: середины рёбер AB, BC и SD.

Задача 33. Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: середины рёбер AB, AD параллельно ребру SC.

Задача 34.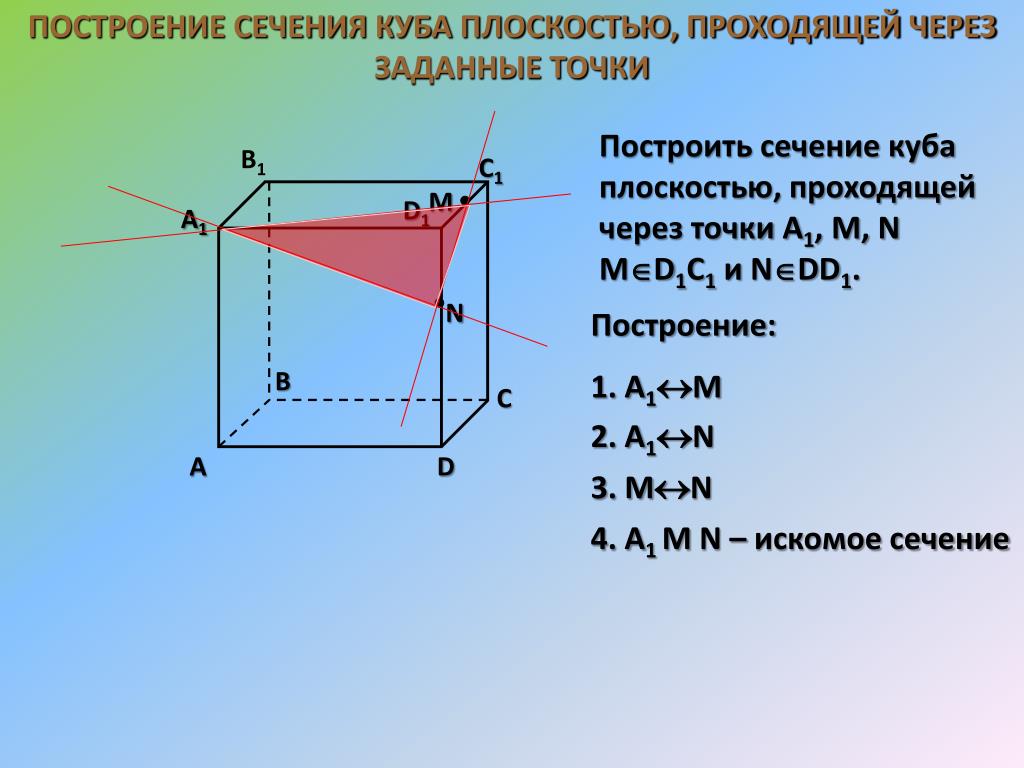 Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: середины рёбер AD, SC и точку B.

Задача 35. Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: середины рёбер AB, AD и SC.

Задача 36. Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: центр основания, середину ребра SD и точку M ребра SA, если AM : MS = 1 : 3.

Задача 37. Основание пирамиды SABCD — параллелограмм ABCD. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: середину ребра SA и точки M и N рёбер SB и SC, если BM : MS = SN : NC = 1 : 2.

Задача 38. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 —правильный шестиугольник ABCDEF. Постройте сечение призмы плоскостью, проходящей через следующие точки: A, B и F1.

Задача 39. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 —правильный шестиугольник ABCDEF. Постройте сечение призмы плоскостью, проходящей через следующие точки: A, C и D1.

Задача 40. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 —правильный шестиугольник ABCDEF.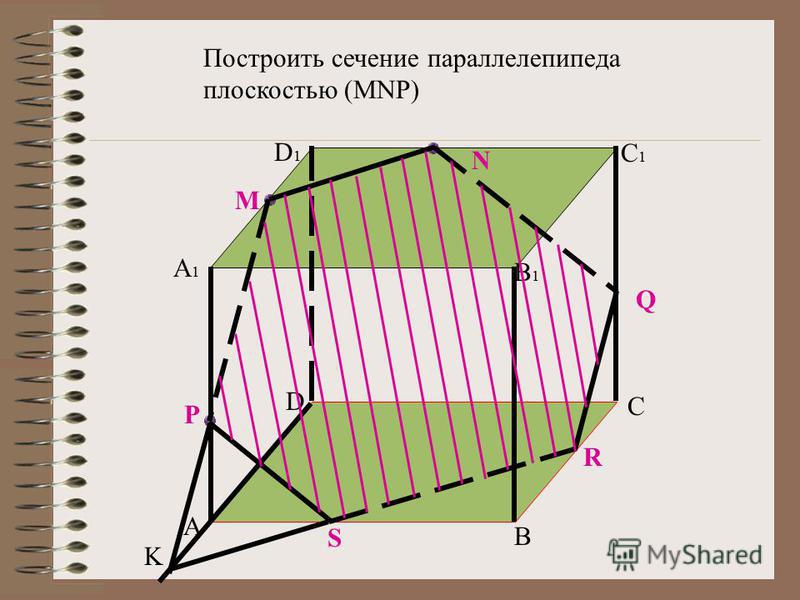 Постройте сечение призмы плоскостью, проходящей через следующие точки: B, E и середину ребра FF1.

Задача 41. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 —правильный шестиугольник ABCDEF. Постройте сечение призмы плоскостью, проходящей через следующие точки: B, D и середину ребра AA1.

Задача 42. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 — правильный шестиугольник ABCDEF. Постройте сечение призмы плоскостью, проходящей через следующие точки: B, C и E1.

Задача 43. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 — правильный шестиугольник ABCDEF.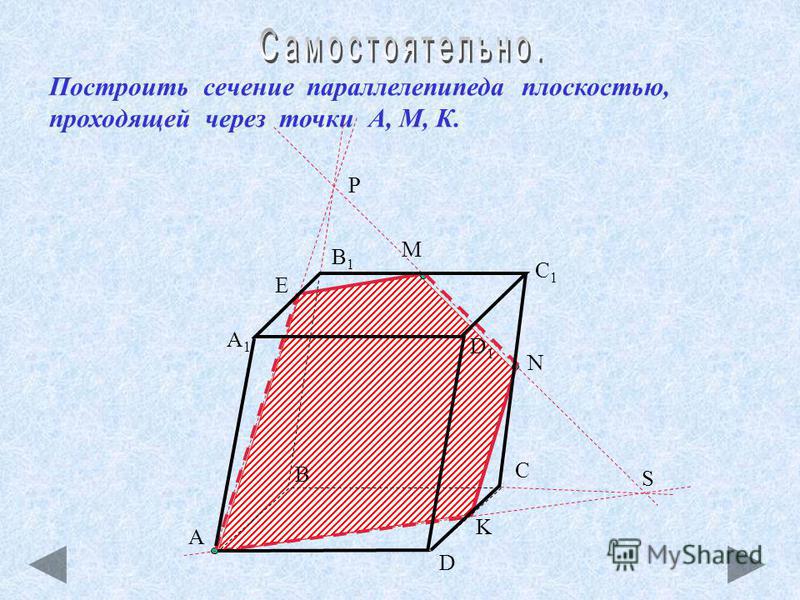 Постройте сечение призмы плоскостью, проходящей через следующие точки: B, C и середину ребра DD1.

Задача 44. Основание шестиугольной призмы ABCDEFA1B1C1D1E1F1 — правильный шестиугольник ABCDEF. Постройте сечение призмы плоскостью, проходящей через следующие точки: B, D и середину ребра FF1.

Задача 45. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: C, F и середину ребра SD.

Задача 46. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: A, B и середину ребра SD.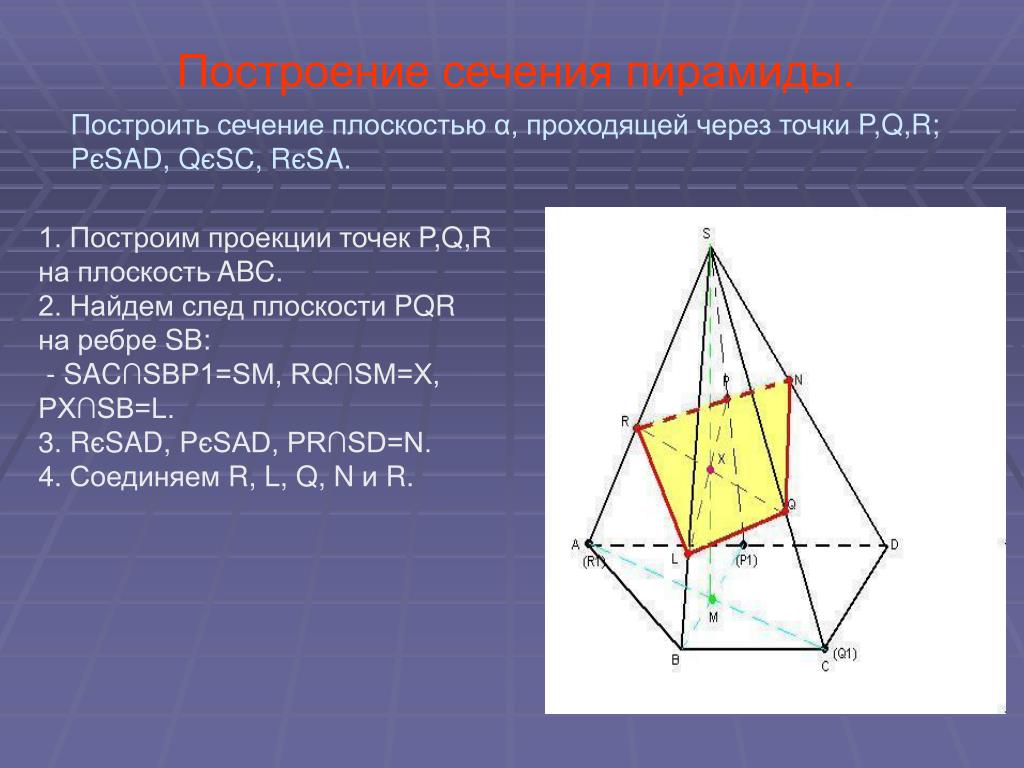

Задача 47. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: центр основания параллельно плоскости ASB.

Задача 48. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: A, C и середину ребра SD.

Задача 49. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: B и середины рёбер AS и CS.

Задача 50. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Постройте сечение пирамиды плоскостью, проходящей через следующие точки: B, C и середину отрезка, соединяющего вершину пирамиды с центром основания.

Реклама

Поддержать нас

Построение сечений призмы

Сечение призмы плоскостями

Цели урока:

Образовательные:

рассмотреть основные простейшие виды сечений призмы, рассмотреть теорию метода следов и применить ее для построения более сложных сечений.

Воспитательные: воспитание самостоятельности, умения слушать, анализировать и делать выводы

Развивающие: развитие пространственного воображения, навыков самоорганизации, работы в парах при выполнении домашнего задания, умения анализировать, обобщать и делать выводы.

Оборудование: компьютер, мультимедийный проектор, доска и мел.

Ход урока:

Организационный момент (сообщение темы урока, актуальности темы и целей урока)

Учитель: Прежде чем говорить об актуальности темы, давайте ответим себе на несколько вопросов:

1. Что такое многогранник?

Ответ: Многогранник это тело, поверхность которого состоит из нескольких многоугольников.

1. Что такое призма?

Ответ: призма это многогранник, состоящий из двух многоугольников, лежащих в параллельных плоскостях и совмещаемых параллельным переносом и всех отрезков соединяющих соответствующие точки этих многоугольников.

1. Что такое сечение?

Ответ: Сечением поверхности геометрических тел называется плоская фигура, полученная в результате пересечения тела плоскостью и состоящая из точек принадлежащих как секущей плоскости так и из точек самой поверхности данного тела.

Вот теперь поговорим, для чего нужны сечения и где они встречаются?

В математике нет ни одной темы, которая бы не находила своего широкого применения на практике. Так вот, построение сечений не является исключением. Очень часто с сечение различных геометрических тел встречаются в инженерии, в строительстве итд. Более того, порой недостаточно уметь просто строить эти сечения, а также необходимо уметь вычислять например площадь или периметр этого сечения.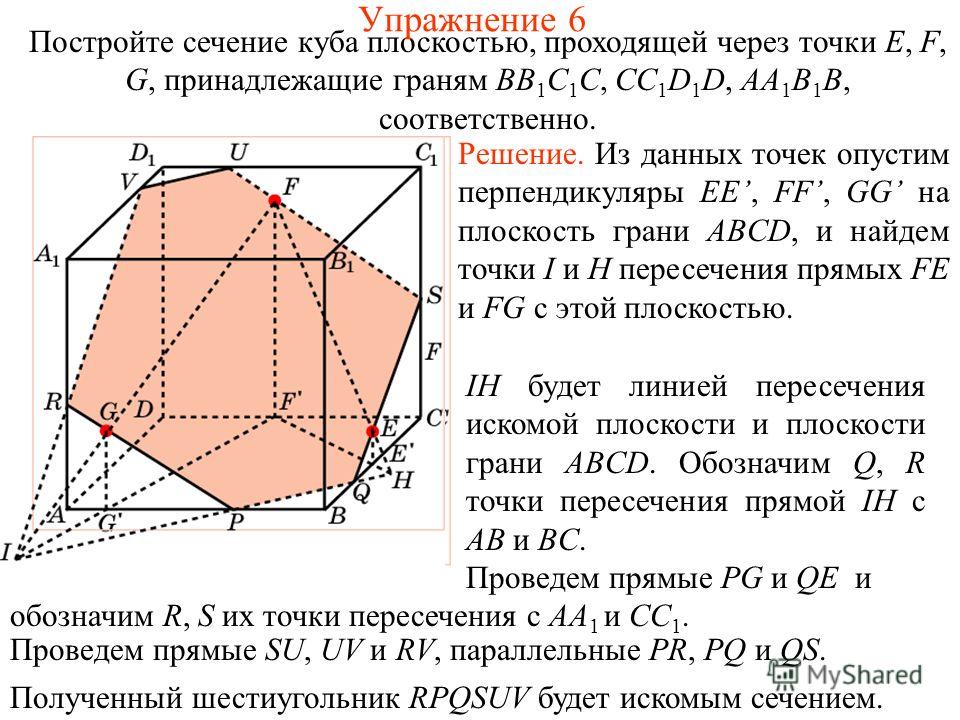 Так же задания на построение сечений и вычисление его элементов встречаются в программе профильного уровня ЕГЭ в рамках задачи №16, и как показывает практика, эти задания вызывают большие трудности у выпускников. Именно поэтому, изучение данной темы необходимо на достаточно углубленном уровне.

Итак, перейдем к рассмотрению темы и следующий вопрос будет такой:

1. Каким способом можно задать секущую плоскость?

Ответ:

• Через три точки можно провести плоскость и притом только одну

• Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну

• Через две пересекающиеся прямые можно провести плоскость и притом только одну

• Через две параллельные прямые можно провести единственную плоскость.

А сейчас рассмотрим самые простейшие виды сечений призмы:

.

Это сечение параллельное основаниям. В сечении получается многоугольник, равный основаниям.

На этом чертеже построено сечение призмы плоскостью, параллельной боковой грани.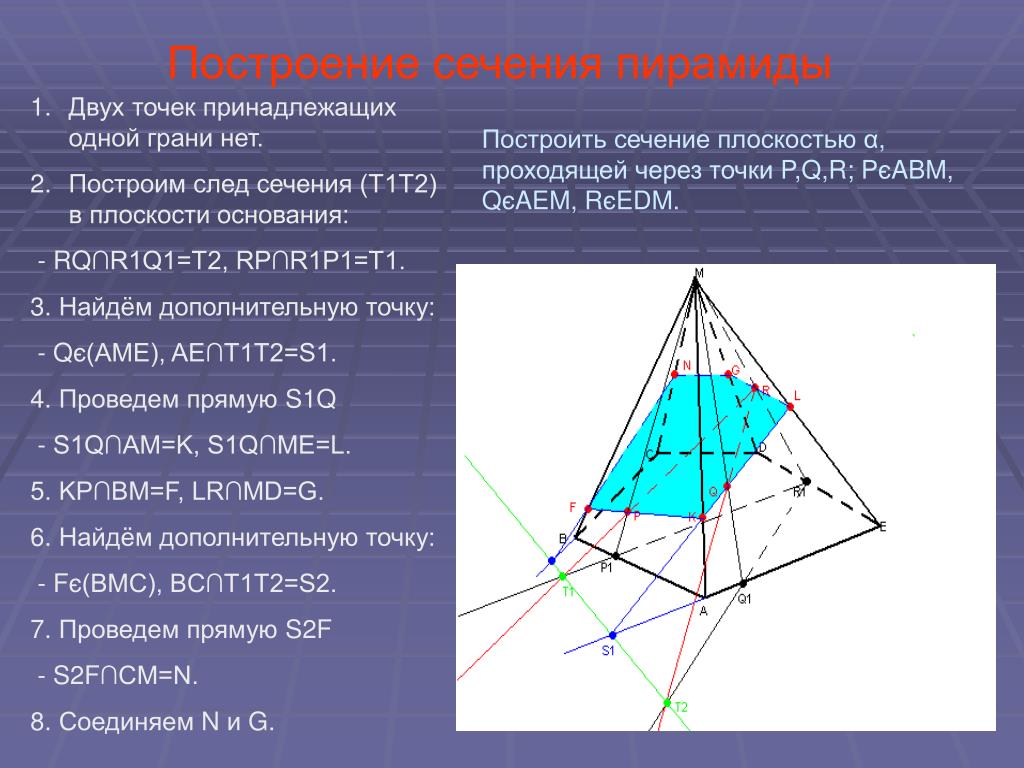 Оно представляет собой параллелограмм.

А на этом чертеже построено так называемое диагональное сечение. Это сечение, проходящее через два боковых ребра, не принадлежащие одной грани. Оно представляет собой параллелограмм.

Для построения более сложных сечений призмы может и пользоваться метод следов, где основа всего метода в следе секущей плоскости.

Определение:

Следом секущей плоскости называется прямая пересечения секущей плоскости и плоскости основания призмы.

Суть метода следов состоит в применении ряда правил построения сечений:

1. Пусть дана пятиугольная призма, точка А, принадлежащая верхнему основанию призмы и секущей плоскости и след а секущей плоскости, принадлежащий плоскости нижнего основания.

Тогда пересечение секущей плоскости верхнего основания будет представлять собой отрезок СД, проходящий через точку А, параллельный следу а.

1. Пусть снова дана пятиугольная призма. Если точка А принадлежит боковой грани, то пересечение этой грани с секущей плоскостью, проходящей через точку А строится так:

• Строим точку В, в которой плоскость грани, пересекает след а

• Затем проводим прямую АВ. Она пересекает грань по отрезку СД.

• Отрезок СД и есть пересечение этой грани с секущей плоскостью, проходящей через точку А

1. Если грань, содержащая точку А параллельна следу а, то секущая плоскость, пересекающая эту грань и проходящая через точку А,пересекает эту грань по отрезку СД, параллельному следу а.

Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. Таким образом можно получить многоугольник, который и окажется сечением призмы. В использовании этих трех правил и состоит суть метода следов для построения сечения призмы.

Рассмотрим задачу.

Построить сечение четырехугольной призмы плоскостью, проходящей через прямую а, лежащей в плоскости нижнего основания и точку Н, принадлежащей боковому ребру.

Очевидно, что прямая а это и есть след секущей плоскости.

Точка Н принадлежит грани (АВВ₁), поэтому строим точку Р, в которой плоскость этой грань пересекает след а. а именно след пересекает прямая АВ. затем строим прямую РН, которая пересечет данную грань по отрезку НМ.

Далее, так как точка М принадлежит грани (ВСС₁),то проводим ВС, которая пересечет след в точке Q. Проводим QM, пересекающую грань по отрезку MN.

Точка N принадлежит грани (СДД₁), поэтому проводим СД пересекающую след а в точке Z, затем проводим ZN, пересекающую грань призмы по отрезку NV.

Точки Nи V лежат в одной грани, поэтому проводим прямую NV.

Четырехугольник HVNV – искомое сечение.

Теперь попробуйте выполнить аналогичное задание.

Постройте сечение шестиугольной призмы плоскостью, проходящей через точку на одном из боковых ребер и прямую, лежащую в плоскости нижнего основания.( ученик выходит к доске для решения задачи)

Теперь рассмотрим еще одну задачу.

Построить сечение четырехугольной призмы плоскостью, проходящей через точку А, лежащую в плоскости верхнего основания и прямую, лежащую в плоскости нижнего основания.

По данному чертежу попробуйте сделать описания хода решения, используя правило №1. (для описания ученик выходит к доске и по чертежу расписывает пошагово ход решения)

Понятно ли вам как строить сечения призмы методом следов?

В чем состоит сложность этого метода именно для вас?

Как вы считаете, всегда ли след плоскости дается в условии?

Так вот, оказывается, что след плоскости в условии дается далеко не всегда. В этом случае этот след необходимо построить, что естественно значительно осложняет решение задачи. Но когда след будет построен, то дальнейшее построение сечения выполняется по общей методике,т.е именно так как мы сегодня строили. Такие задачи мы с вами будем решать на следующем уроке. Не останутся без нашего внимания также и простейшие сечения. например, диагональные. Мы научимся находить площади и периметры таких сечений, а также разберем основные типы задач №16 из бланков профильного уровня ЕГЭ. Но это все на последующих уроках. А сегодня нам было необходимо рассмотреть метод следов. Запишите домашнее задание:

1. Изучить теоретический материал, котрый мы сегодня рассмотрели.

2. Построить сечение пятиугольной призмы плоскостью, проходящей через точку М на боковом ребре и прямую лежащую в плоскости нижнего основания.

3. Построить сечение четырехугольной призмы плоскостью, проходящей через точку в плоскости верхнего основания и прямую, лежащую в плоскости нижнего основания.( используйте правило №1)

Спасибо. Урок окончен. До свидания.

Что такое чертежи в разрезе?

Чертежи в разрезе являются важной частью любого комплекта строительных чертежей. Они разрезают здание в нескольких масштабах, чтобы показать используемые материалы и сборки, пространственные отношения и информацию, которая не может быть четко указана на планах или фасадах. Ниже я разберу несколько типов чертежей сечений.

Содержание

1. Что такое разрез?
   • Как читать чертеж сечения?
2. Types of architectural section drawings
   • Building Sections
     • Cross Section (AKA transverse section)
     • Longitudinal Section
   • Wall Sections
     • Interior Wall Sections
     • Stair and Elevator Sections
   • Detail Sections
   • Детали плана
   • Вид сечения

Что такое чертеж сечения?

Разрез — это орфографический 2D-чертеж, в котором используется воображаемая вертикальная плоскость для «разрезания» здания. С одной стороны плоскости здание удалено, чтобы можно было увидеть конструкцию того, что нарезано. Срез обычно делается перпендикулярно стене, через которую он прорезается. Он может отображать или не отображать элементы здания на высоте за его пределами.

Архитекторы используют секции разного масштаба, чтобы изучить, как все компоненты сочетаются друг с другом, но обычно состоят из трех частей: секции здания, секции стены и детали секции (подробнее о каждой ниже). Их можно использовать для иллюстрации большого объема внутри здания или для описания того, как стропила встречаются с верхней пластиной стены. Как только эти условия выяснены, окончательные чертежи сообщают об этих условиях подрядчику.

Секции, как правило, проходят через все здание, через типичные условия (объяснение здесь), уникальные пространства, сложные объемы и нетипичные условия, которые требуют дополнительных пояснений. Чертежнику нужно будет нарисовать столько разрезов, сколько требуется для объяснения конструкции здания, но не более того. Небольшие вариации часто можно вывести из типичных деталей или других рисунков.

Разрезы необходимы, потому что, если смотреть на здание только сверху, многие из видимых элементов не могут быть полностью поняты. Такие элементы, как профили карнизов и молдингов, глубина выступа или конструкция, удерживающая фасад на месте, не видны на высоте.

Аналогичным образом, для внутренних помещений размещение акустических панелей в зрительном зале или строительство открытых лестниц в вестибюле не может быть легко сообщено только в планах и RCP.

Как читать чертеж сечения?

Вы сможете читать чертеж сечения, как только поймете, что любой элемент, который был прорезан, представлен более толстой линией, что помогает сделать эту часть рисунка «выделяющейся». Вырезанные элементы затем заштриховываются, либо обычно показывая, что это сплошной элемент, либо со специальной штриховкой, указывающей тип материала. Пустоты покажут все, что находится за их пределами, с более легким весом линии.

Разрезы показаны на планах и фасадах следующими символами ниже. В некоторых случаях секции здания могут иметь излом, так что один чертеж может пересекать несколько важных пространств, которые не была бы прорезана одной плоскостью.

Типы чертежей архитектурных разрезов

Существует несколько различных типов чертежей разрезов, которые используются в наборе строительных чертежей. Каждый выполняет определенную роль и предназначен для указания конкретной информации.

Существует своего рода иерархия чертежей разделов – каждый раздел служит ключом для раздела следующего уровня детализации. Ниже описаны типы разрезов от наименьшего масштаба (показывающего самую большую часть здания) до самого большого масштаба (показывающего наиболее подробную информацию).

Секции здания

Секции здания создаются путем разрезания всего здания от внешней стены до внешней стены. Как правило, они представляют собой масштаб внешних высот (но иногда меньше) и не предназначены для того, чтобы содержать много конкретной информации или примечаний. В некоторых случаях стены, полы, крыша и другие прорезанные элементы будут заштрихованы как один шаблон для упрощения рисования.

Секции здания могут обозначать общие узлы здания (например, типичная конструкция наружной каменной кладки). Что еще более важно, они призваны дать общее ощущение пространства, отношения между уровнями пола, крышей, атриумами и пространствами с разной высотой.

Разрезы зданий также служат ключом, показывающим места разрезов стен в здании.

Существует два основных типа строительных секций, которые описаны ниже.

Поперечные сечения представляют собой сечения здания, которые разрезают здание в более коротком направлении.

Продольные разрезы — это разрезы здания, которые разрезают здание в самом длинном направлении.

Секции стены

Секции стены представляют собой вертикальные срезы, ориентированные на конструкцию конкретной стены, обычно снаружи. Они больше по масштабу, чем секции здания, поэтому можно увидеть больше деталей (обычно 3/4 ″ = 1 ′-0 ″).

На этих чертежах показано, как крыша соприкасается со стеной, конструкция стены от крыши до уклона и конструкция фундаментной стены земляного полотна. Он также может отображать любые вертикальные изменения типов стен, смещения в стене, навесы, навесы и выступы. Они используют датум высоты, чтобы указать ключевые высоты элементов здания. Например, верхняя пластина стены с деревянным каркасом или высота подоконника окна. Они содержат вертикальные размеры и, в некоторых случаях, количество рядов кладки.

Секции стен полезны проектировщику для обеспечения непрерывности от крыши к стене и ниже уровня земли с точки зрения защиты от атмосферных воздействий, пароизоляции и теплоизоляции (изоляция).

Подобно тому, как секции здания являются ключом к секциям стен, секции стен являются ключом к деталям (описанным ниже).

В некоторых случаях может потребоваться начертить секции внутренних стен. Если есть важная информация, которую невозможно подробно описать, внутренние секции стен могут заполнить пробел. Они также позволяют строителю увидеть, как внутренняя стена может быть непрерывной (или нет) от фундамента до крыши, как в случае со стеной шахты.

Другим примером может быть вечеринка или стена смерти. Это критически важные элементы для отделения арендаторов или жилых единиц друг от друга. Их конструкция часто пожаробезопасна, и необходимо поддерживать звукоизоляцию между этими помещениями. Секция стены может помочь подрядчику увидеть, как стена приземляется на основание и продолжается до нижней стороны или над настилом крыши. Кроме того, выноски могут быть сделаны, если необходимы дополнительные детали.

Лестничные и лифтовые секции аналогичны секциям внутренних стен, но имеют больше контекста. Секция лифта обычно проходит через всю шахту лифта и, возможно, часть вестибюля лифта. Это позволит чертежнику назвать необходимые детали для построения шахты, показать шахту лифта, перекат, траверсу и т. д.

Аналогично, секции лестницы будут показывать всю лестницу от самого нижнего этажа до самого высокого. Они указывают высоту от этажа до этажа, количество и размер подступенков на лестнице, иллюстрируют ограждение и балясины, а также показывают выноски, указывающие на конструкцию лестницы.

Детальные секции

Детальные секции (обычно называемые просто «детали») представляют собой чертеж еще большего масштаба, который оттачивает одно конкретное условие. Обычно они рисуются в масштабе от 1″=1′-0″ до 3″-1′-0″.

Детали — это чертежи, которые доходят до гаек и болтов того, как строится определенное состояние. Конкретные материалы, продукты и размеры указаны в деталях, а также размеры, ключевые пометки, отметки высот, уклоны крыши или что-либо еще, чтобы помочь сообщить о намерении строительства.

Важно, чтобы эти чертежи были составлены на основе реальных размеров и форм показанных продуктов. Секция здания может отображать окно только в виде двух прямоугольников для рамы и одной линии, обозначающей плоскость стекла. Здесь детали, созданные производителем окон, должны быть интегрированы и согласованы с деталями здания. Это важнейшая роль архитектора: соединить вместе все продукты и сборки.

Детали вызываются в секциях стены, но могут быть вызваны в любом другом месте, если это условие не прорезается в секции стены.

Детали плана

Детали плана похожи на детали разреза, но нарисованы в плане, что означает, что разрез разреза выполняется горизонтально, а не вертикально. Подробнее о планах здесь.

Перспектива сечения

Перспектива сечения обычно не используется в конструкторской документации. Тем не менее, это отличные презентационные рисунки, которые не только показывают здание в разрезе, но и характер внутренних и внешних пространств в 3D.

5 отличных советов для виньетки раздела здания — CDS — подготовка к экзамену на архитектора

Предыдущий Следующий

Для Строительной документации и услуг, одного из семи разделов регистрационного экзамена на архитектора, проводимого NCARB, вам необходимо заполнить только одну виньетку – виньетку раздела здания.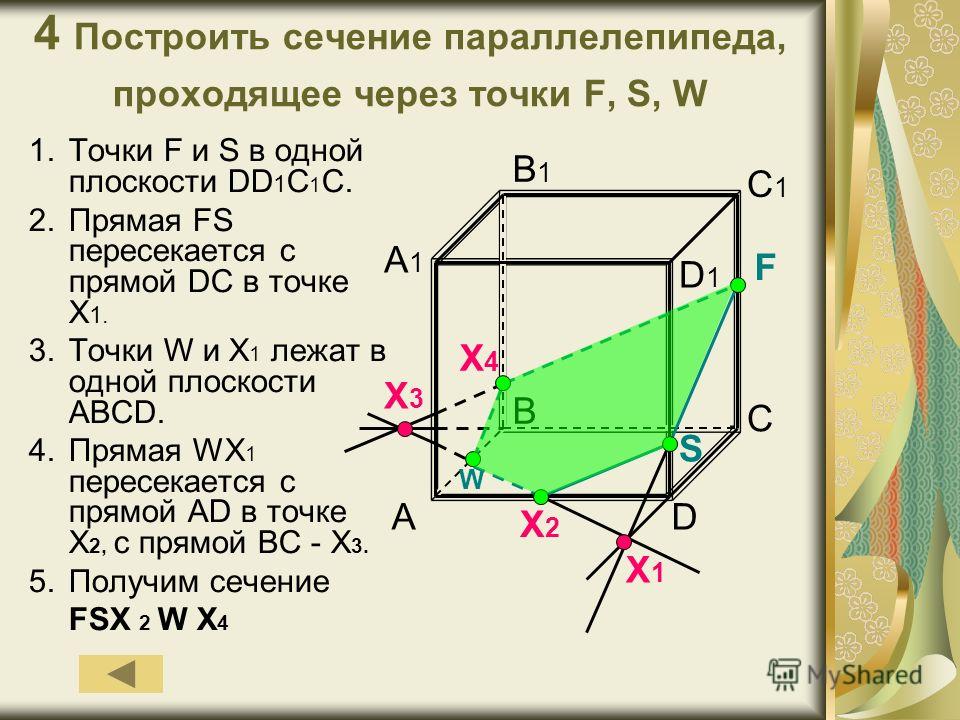 Однако, как и в виньетке “Зонирование площадки” в книге “Программирование, планирование и практика”, в этой виньетке есть только ОДНО правильное решение, так что будьте внимательны!

В виньетке «Секция здания» вам потребуется точно нарисовать разрез здания, показав те же элементы, что и на плане — стены, воздуховоды и потолочные балки, и это лишь некоторые из них.

Этот список из 5 лучших для виньетки Building Section поможет вам сосредоточиться при подготовке к отделу строительной документации и услуг. Убедитесь, что вам комфортно NCARB  программное обеспечение , отработав несколько примеров программ перед экзаменом. Вы должны полностью ознакомиться с программными инструментами до сдачи экзамена.

5 отличных советов для виньетки раздела «Строительство»

  1. Следуйте программе.  Вероятно, вы будете встречать этот совет в каждой виньетке из серии ARE, потому что он действительно самый важный.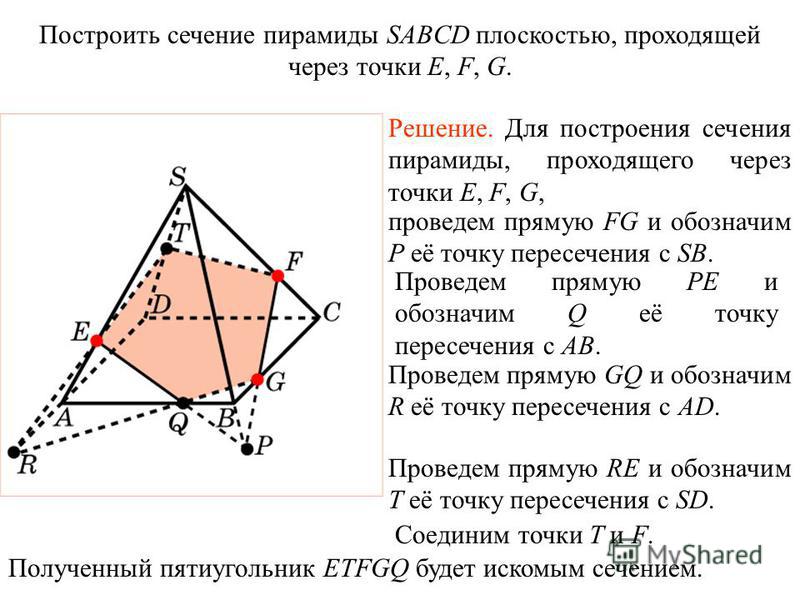 Помните, что NCARB не проверяет ваши навыки проектирования… они хотят знать, можете ли вы следовать указаниям, интерпретировать простой код и правильно читать план здания/площадки. Опять же, в этой виньетке есть только один правильный ответ, поэтому внимательно следуйте инструкциям, чтобы добиться успеха.

2. Начертите от среза линию разреза.   Убедитесь, что то, что вы показываете в разрезе, совпадает с тем, что показано на плане по линии разреза сечения. К простым ошибкам относятся показ потолочных балок, расположенных в неправильном направлении, забывание выровнять потолочные балки с планом или указание неправильного размера/номера/расположения воздуховодов в секции. Небольшие ошибки, подобные этим, могут привести к большому разочарованию, поэтому следите за тем, где проходит линия разреза.

3. Точно определите размер потолочного пространства.   Программа и план дадут вам информацию для определения глубины пространства над потолками в каждой комнате (обычно называемого «промежуточным пространством»).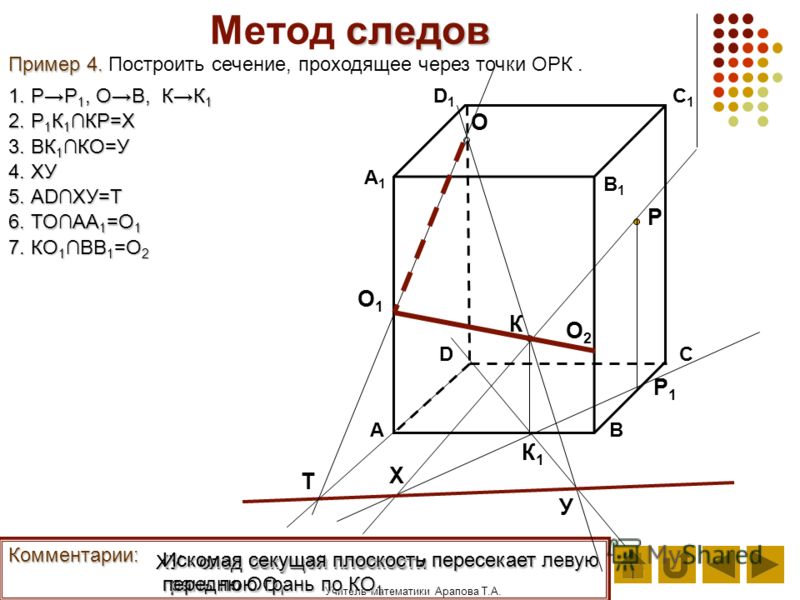 Вам нужно будет найти балки, воздуховоды и освещение в этом пространстве. Если он не соответствует размеру, оборудование не будет заполняться, что будет означать, что ваше решение неверно. Внимательно отметьте размеры воздуховодов и балок в плане в каждом пространстве, а также на линии разреза сечения и обратите внимание на место, необходимое для освещения из программы..

4. Минимизируйте общую высоту здания.  Эффективность является важной частью всех виньеток ARE, и в этом случае вы хотите минимизировать общую высоту здания, чтобы быть эффективным с точки зрения затрат. Убедитесь, что высота потолков в каждом помещении соответствует требованиям программы, а свободное пространство над потолками позволяет точно разместить все оборудование. Также убедитесь, что высота вашего парапета соответствует программе, но не выходите за рамки. Помните, вы хотите, чтобы общая высота вашего здания соответствовала программе, но не превышала ее намного, если вообще превышала ее.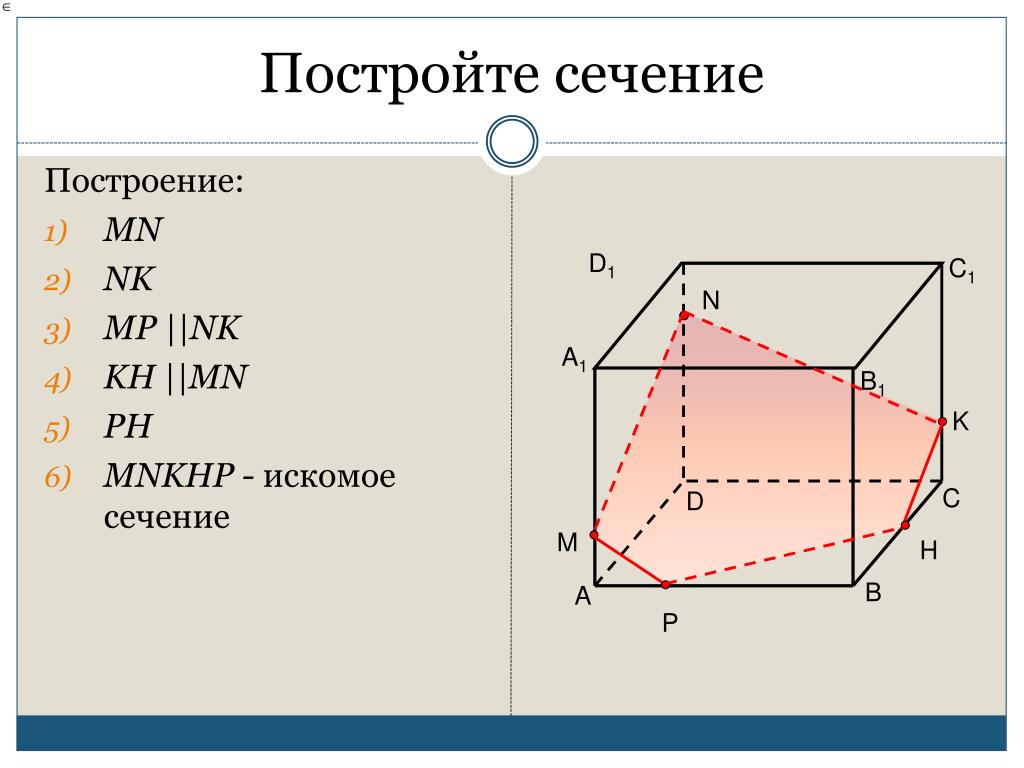

5. Расширьте все противопожарные перегородки с этажа на этаж.  Программа укажет, какие стены на плане должны быть огнестойкими. Обязательно найдите эти стены в разрезе и нарисуйте их с помощью правильного инструмента (инструмента «Огнестойкая стена»). Кроме того, противопожарные перегородки должны простираться от пола до этажа, в отличие от обычных перегородок, которые могут заканчиваться в помещении чуть выше потолка. Вы должны начать противопожарную перегородку от пола и продлить ее до нижней стороны этажа выше, чтобы сделать сборку непрерывной.

Помните, что повторение является ключом к пониманию этой программы и программного обеспечения, и, поскольку есть только один правильный ответ, вы должны убедиться, что правильно ответили с первого раза. Точно следуйте требованиям программы и перепроверьте всю свою работу, чтобы убедиться, что ваше решение правильное.

Продолжайте двигаться вперед… шаг за шагом…

Считаете ли вы эти 5 советов полезными для подготовки к CDS? Пожалуйста, дайте мне знать в комментариях ниже!

Последние сообщения

• Эпизод 56: С какой стороны дома находится комната для завтрака?
• Эпизод 55: Какого волка ты кормишь?
• Эпизод 54: Учеба не похожа на упражнения
• Эпизод 53: Зов недели: провал 5 лет назад
• Эпизод 52: Наберите как можно больше очков
• Эпизод 51: 5 причин, по которым вы проваливаете тест ARE®

Категории

• 5,0
• Объявления
• Стереотипы архитекторов
• Проектирование зданий и строительные системы
• Строительные системы
• Звонок недели
• Карьерная стратегия
• Строительная документация и услуги
• Общие
• Отклеивание
• Зеленое здание
• ВПЛ
• Только начинается
• НКАРБ
• Подкаст
• Производительность
• Профессия
• Программирование, планирование и практика
• Схематический дизайн
• Планирование и дизайн участка
• Структурные системы
• Учебный совет
• видео советы

Область скользящего переключателя

О компании Architect Exam Prep LLC

Мы — два лицензированных архитектора, которые любят обучать людей и помогать им в получении лицензии.