Построение фотограмметрической модели местности: Построение фотограмметрической модели.

Построение фотограмметрической модели.

Построение фотограмметрической модели на технокарте сводится к установке вычисленных значений базисных компо­нентов на суппортах планового и высотного механизмов засечки. Они вычисляются по формулам

₍₆₂₎

где В — горизонтальная составляющая базиса фотографирова­ния; М_m — знаменатель масштаба модели; h — превышение цен­тра проекции правого снимка над левым; угол скоса, отсчи­танный от направления базиса; — угол скоса, отсчитываемый от нормали к базису. Величина зависит от знака угла скоса,который отмечен на шкале индикатора этого суппорта индек­сами L — в случае отклонения влево и R — в случае отклонения вправо. Значение тоже может иметь разные знаки. Они устанавливаются направлениями движения этого суппорта с по­мощью стрелок, отмеченных на индикаторе этой шкалы.

По таблице выбирают шестерни и устанавливают на счетчике высот Z

М-б модели	Комплекты шестерен				М-б модели	Комплекты шестерен
	z1	z2	z3	z4		z1	z2	z 3	z4
1:800	84	42	65	104	1:2500	88	88	34	85
1:1000	84	42	40	80	1:3200	42	84	69	104
1:1250	84	42	34	85	1:4000	42	84	40	80
1:1650	88	88	65	104	1:5000	42	84	34	85
1:2000	88	88	40	80

На координатографе устанавливают шестерни согласно соотношению .

где М_m – знаменатель масштаба модели, M_k – знаменатель создаваемой карты.

Внешнее ориентирование фотограмметрической модели счи­тают законченным, если острие карандашного устройства (или марка микроскопа) не сойдет с установочной точки оптической оси па величину более чем 0,1 мм. При наличии большего сме­щения его доводят до нормы вращением взаимно перпендику­лярных исправительных винтов чертежного устройства коорди­натографа.

Корректура фотограмметрической модели.

После построения фотограмметрической модели можно было бы приступить к процессу составления топоплана. Однако вслед­ствие влияния систематических ошибок, возникающих в резуль­тате нарушений элементов внешнего ориентирования стереопары при съемке, а также аналогичных ошибок при юстировках при­бора модель окажется искаженной как в плане, так и по высоте. Это потребует ее корректировки, которая осуществляется по контрольным точкам.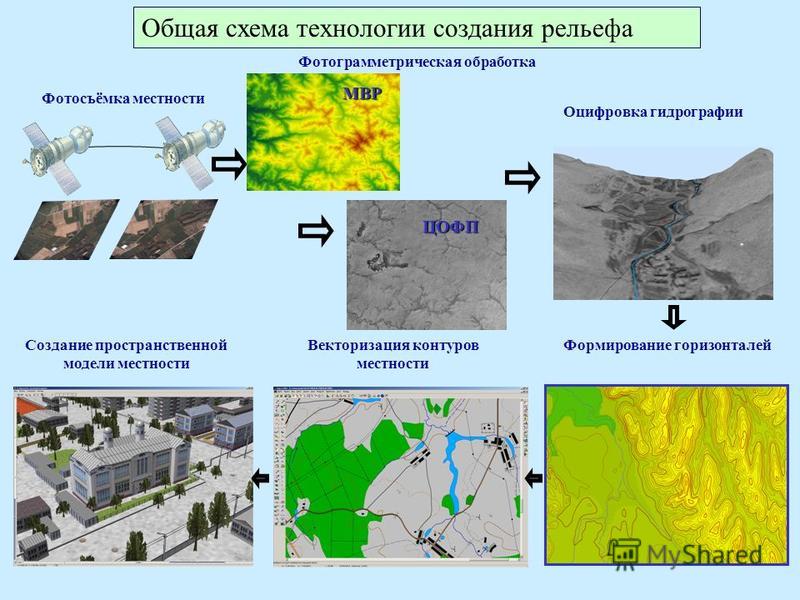

Основа такой коррекции заключается в ре­шении системы уравнений

(63)

В него входят три неизвестных ,,. Следовательно,для решения необходимо знать значение для трех контроль­ных точек: две из которых лежат на разных отстояниях от центра проектирования S₁ по направлению оси Y фотограмметрической системы координат, а третья — на краю стереоскопического пе­рекрытия пары на максимальном удалении от точки стояния.

В практике фототеодолитной съемки величина смещений по направлениям, проведенным из левой точки стояния на кон­трольные точки, редко превышает значения = ±5 мм в мас­штабе плана.

Рисунок 35 – Схема корректирования модели по контрольным точкам

Таким образом, поправки в установочные величины b_x, b_у, γ определяют непосредственно на приборе методом последовательных приближений. Движениями штурвалов Y и X игла чертежного устройства или марка цангового микроскопа совмещается на планшете с точкой 1, а стереоскопическое несовмещение марки с точкою модели устраняется движением b_x и ножным штурвалом Z.

После этого штурвалом Z па счетчике высот устанавлива­ется геодезическая отметка точки 2 и вращениями штурвалов Y и X игла чертежного устройства или марка цангового микрос­копа совмещается по положению с точкой 2 на планшете. На­блюдаемое стереоскопическое несовмещение марки с точкою 2 на модели устраняется винтом конвергенции и движением нож­ного штурвала Z. После этого все указанные действия повто­ряются.

Обычно после двух-трех приближений будут наблюдаться совмещение стереоскопической марки с точками 1 и 2 модели и совмещение иглы чертежного устройства с этими точками по положению на планшете.

Геометрическая модель считается полностью откорректиро­ванной, если при стереоскопическом наведении марки на кон­трольные точки смещения в плане не будут превышать 0,2 мм, а по высоте сечения рельефа. По окончании корректуры производят сгущение недостаю­щего планового и высотного обоснования, необходимого для об­работки смежных стереопар. Для этого в зонах их перекрытий в дальнем и ближнем плане выбирают хорошо опознаваемые точки, которые заново опознают на контактных отпечатках этих пар. Эти точки накалывают на снимках, обводят кружками и присваивают им соответствующие номера. После многократного визирования эти точки накалывают на планшет и оформляют соответствующим образом. Около них подписывают среднюю отметку с учетом поправки за кривизну Земли и рефракцию.

Осн.:1[75-86], 3[71-80]

Контрольные вопросы:

1.С какой целью производится обработка снимков на технокарте?

2. По каким формулам вычисляются значения базисных компо­нентов?

3. Где устанавливаются вычисленные значения базисных компо­нентов?

4. Допустимое смещение в плане после корректировки модели.

5. Допустимое смещение в плане после корректировки модели.

Лекция 15. Использование цифровых тахеометров в фототеодолитной съемке.

Безотражательный тахеометр GPT-7000i.

Уникальная серия безотражательных инженерных тахеометров GPT-7000i. Компания ПРИН с гордостью представ­ляет первые в мире фототахеометры. Тахеометры серии GPT-7000i оснащены двумя цифровыми фотокамерами, первая из которых встроена в зрительную трубу, а вторая – расположена над объективом и позволяет оператору получить широкоугольный снимок участка работы.

Использование фотокамер значительно расширяет возможности проведения съемочных работ. Это и сопровождение съемки цифровым изображением с контролем отснятых точек непосредственно в поле; легкое наведение на точки, близкие к зениту; удобный и наглядный вынос точек в натуру при разбивочных работах (проектные точки отображаются на дисплее характерными маркерами) и многое другое.

2.8 Построение фотограмметрической модели

Построение фотограмметрической модели заключается в определении координат точек объекта по измеренным на стереопаре снимков координатам их изображений в системе координат модели О_МХ_МY_MZ_M.

Определение координат точек модели производится по формулам прямой фотограмметрической засечки (см. раздел 2.5).

При этом координаты центра проекции S принимаются произвольными (обычно равными 0). Также произвольно выбирается величина В_Х. В большинстве случаев практики величину В_Х принимают равной

В_Х= b m,

где b – базис фотографирования в масштабе снимка,

m – знаменатель масштаба снимка.

Остальные значения элементов внешнего ориентирования определяют по 8 параметрам b_y, b_z, ₁’, ₁’, ₁’, ₂’, ₂’, ₂’, 5 из которых являются элементами взаимного ориентирования, а 3 определяют ориентацию системы координат модели.

При этом

Например, если были определены элементы взаимного ориентирования ₁’, ₁’, ₂’, ₂’, ₂’ и при этом величины параметров b_y, b_z, ₁’ были приняты равными нулю (b_y = b_z= ₁’=0), то B_Y=B_Z=0, ₁=0, ₁=₁’, ₁=₁’, ₂=₂’, ₂=₂’, ₂=₂’.

Если были определены элементы взаимного ориентирования b_y, b_z, ₂’, ₂’, ₂’, а величины параметров ₁’, ₁’, ₁’ были приняты равными нулю (₁’= ₁’= ₁’=0), то

Семь параметров , которые определят положение, ориентацию фотограмметрической модели в системе координат объекта, а также ее масштаб – называют элементами внешнего ориентирования модели. По значениям координат точек местности в системе координат фотограмметрической модели и значениям элементов внешнего ориентирования модели по формулам (2.24) определяют координаты точек в системе координат объекта.

. (2.24)

В развернутом виде формулы (2.24) имеют вид:

. (2.25)

Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения (2.25), которые представим в виде:

(2.26)

Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения (2.26), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения (2.26), а каждая высотная опорная точка (Z) – третье уравнение из выражения (2.26). Необходимо отметить, что в качестве опорных точек можно использовать центры проекции снимков стереопары, координаты которых были определены в полете.

Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.

Так как уравнения (2.26) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.

(2.27)

В уравнении поправок:

a_i, b_i, c_i – частные производные от уравнений (2.26) по соответствующим переменным ;

ℓ_X, ℓ_Y, ℓ_Z – свободные члены.

Значения коэффициентов уравнений поправок a_i, b_i, c_i вычисляют по известным значениям координат Х_М,Y_M,Z_M и X, Y, Z и приближенным значениям неизвестных.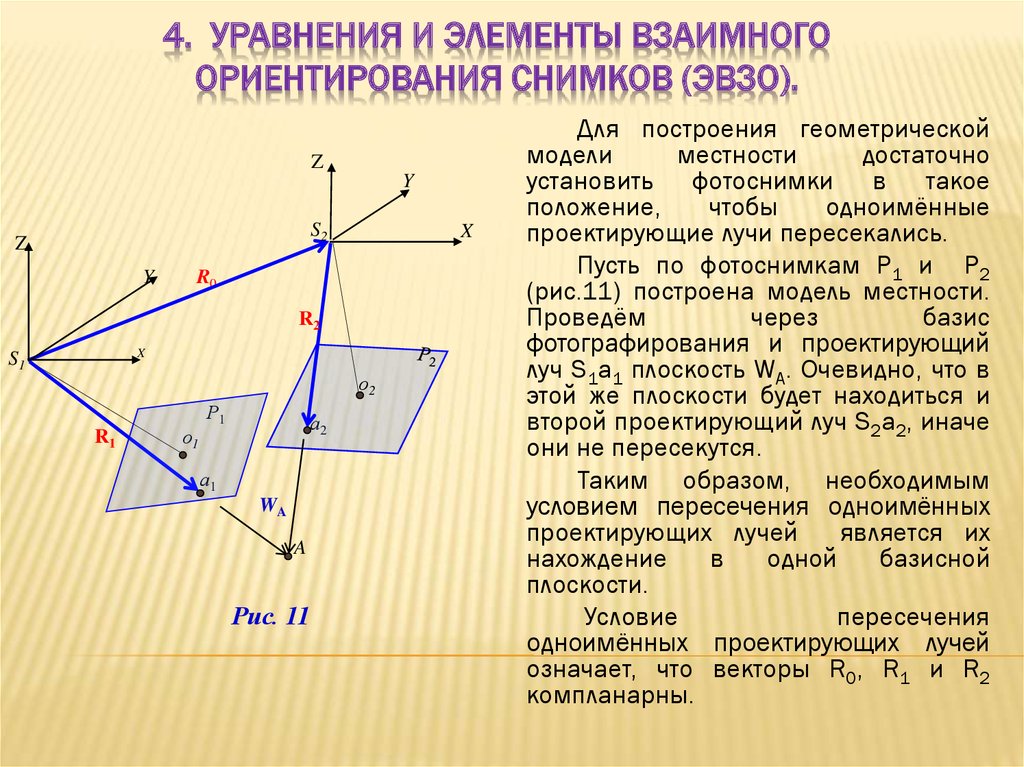 Значения свободных членов ℓ_X, ℓ_Y, ℓ_Z вычисляют таким же образом по формулам (2.26).

Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, то ее решают по методу наименьших квадратов (под условием V^TPV=min).

По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего ориентирования снимков стереопары.

Линейные элементы внешнего ориентирования снимков определяют по формулам:

, (2.28)

в которых – координаты центра проекции i-го снимка стереопары в системе координат модели.

Угловые элементы внешнего ориентирования снимков _i, _i, _i определяют в следующей последовательности:

1. Сначала получают матрицу преобразования координат i-го снимка

(2. 29)

А_М – матрица, в которой элементы a_ij вычисляют по угловым элементам внешнего ориентирования модели _М, _М, _М ;

A_i’ – матрица, в которой элементы a_ij вычисляют по угловым элементам взаимного ориентирования i-го снимка _i’, _i’, _i’.

2. Затем по элементам a_ij матрицы A_i вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:

Как использовать дрон-фотограмметрию для создания трехмерных моделей объектов

Быстрый ответ: что такое фотограмметрия?

Фотограмметрия — это наука о сборе физической информации из 2D-фотографий, часто аэрофотоснимков, снятых дронами.

Комбинируя достаточное количество перекрывающихся изображений одних и тех же объектов, программное обеспечение для фотограмметрии можно использовать для создания фотореалистичных трехмерных изображений топографических поверхностей.

Профессионалы в области геодезии и ГИС используют фотограмметрию с дронов вместе с точными данными GPS для создания 3D-карт и моделей для использования в строительстве, управлении отходами, горнодобывающей промышленности и рабочих процессах заполнителя.

Процесс, используемый для преобразования двумерных изображений дронов в трехмерные модели для анализа на платформе Propeller, может показаться загадочным. Даже давние клиенты, которые летают годами, иногда плохо разбираются в тонкостях фотограмметрии. Хотя картографирование с помощью дронов может показаться совершенно современной наукой, концепция создания карт из фотографий на самом деле восходит к 19 веку.

В этом посте мы демистифицируем науку, которая помогает нам успешно предоставлять данные с дронов для земляных работ по всему миру. Для создания точных 3D-съемок с дронов требуется всего три компонента: снимки с дронов, хороший наземный контроль и наука о фотограмметрии.

В этом посте мы сосредоточимся на фотограмметрии. Ознакомьтесь с нашими блогами : основы наземного управления и секреты получения качественных данных , чтобы узнать больше об искусстве и науке 3D-моделирования.

Что такое фотограмметрия с дронов?

По сути, «фотограмметрия» — это наука об измерении реальных расстояний по фотографиям. И не просто фото — МНОГО фото. Больше фотографий, чем вы, вероятно, думаете, необходимо. Подумайте о том, как ваши родители фотографируют вас и вашу девушку перед выпускным балом. Чем больше фотографий, тем выше точность, и вам нужны все возможные углы.

В частности, для создания точных 3D-моделей необходимы четыре компонента:

1. Оптимальная высота: Дроны должны летать на оптимальной высоте, чтобы достичь наилучшего расстояния от образца земли.
2. Перекрытие изображения на 80%: Компьютеру требуется достаточно информации, чтобы объединить изображения в ортофото — двухмерное аэрофотоснимок с поправкой на искажения.
3. Углы: Для создания цифровой модели местности или трехмерного представления формы поверхности местности требуется широкий выбор углов.
4. Стабильный полет: Для получения высококачественных фотографий для фотограмметрии с дрона требуется устойчивый и последовательный полет дрона для получения четких изображений. (Ознакомьтесь с серией блогов Surveyor’s Guide to Drones, чтобы узнать, как лучше всего это сделать.)

Комбинированные ортофотопланы и цифровые модели местности (также называемые ЦМР) создают 3D-модели вашего участка.

Как работает фотограмметрия с дрона?

Фотограмметрия использует несколько видов одного и того же объекта или визуально отличающейся точки на изображении для триангуляции ее координат x, y и z в пространстве. Чем больше признаков вы сопоставите между изображениями, тем лучше вы сможете связать изображения друг с другом и реконструировать объекты внутри них.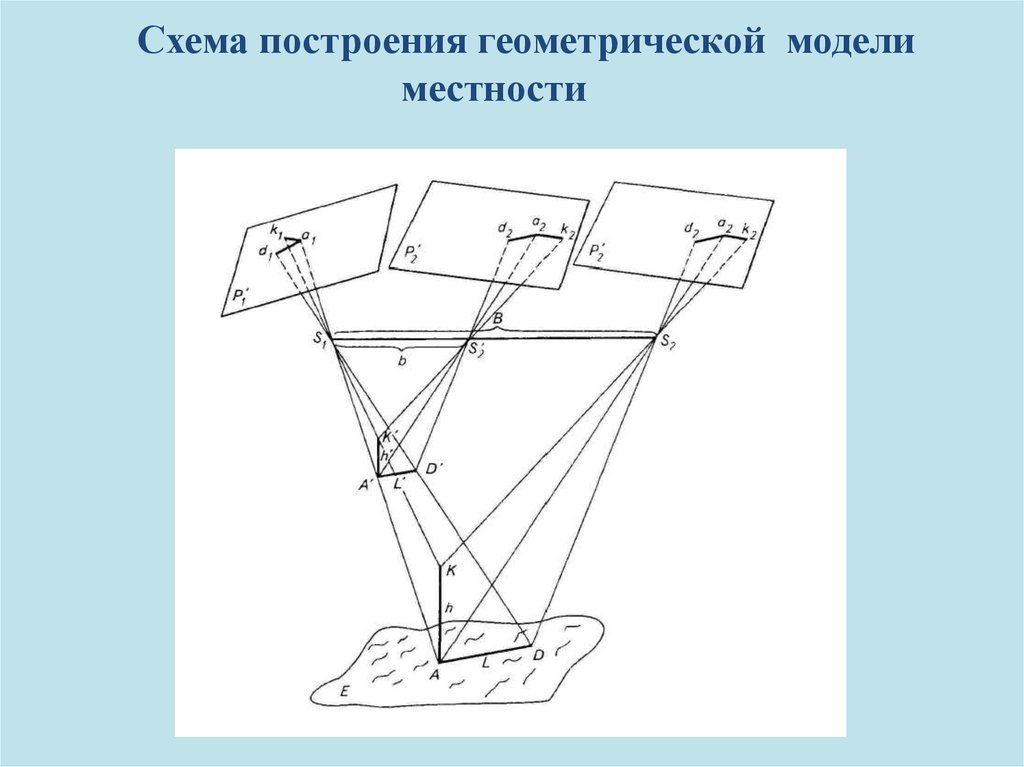

Как фотограмметрия позволяет создавать трехмерные карты с помощью дронов

Дрон делает сотни или даже тысячи перекрывающихся аэрофотоснимков, пролетая над рабочей площадкой. Затем эти изображения обрабатываются и анализируются с помощью фотограмметрии для измерения географических и ландшафтных особенностей участка. Когда вы комбинируете достаточное количество перекрывающихся изображений одних и тех же объектов, программное обеспечение для фотограмметрии может создавать фотореалистичные 3D-представления топографических поверхностей и объектов.

Проще говоря, камера высокого разрешения, установленная на дроне, снимает изображения, а программное обеспечение для фотограмметрии объединяет эти изображения для создания высокоточной трехмерной карты.

Если вы возьмете среднее изображение из опроса, вы легко сможете выделить множество «особенностей» между разными фотографиями. Чем больше функций вы сопоставите в 3D-картографировании дронов, тем лучше вы сможете связать изображения друг с другом и реконструировать захваченные в них объекты.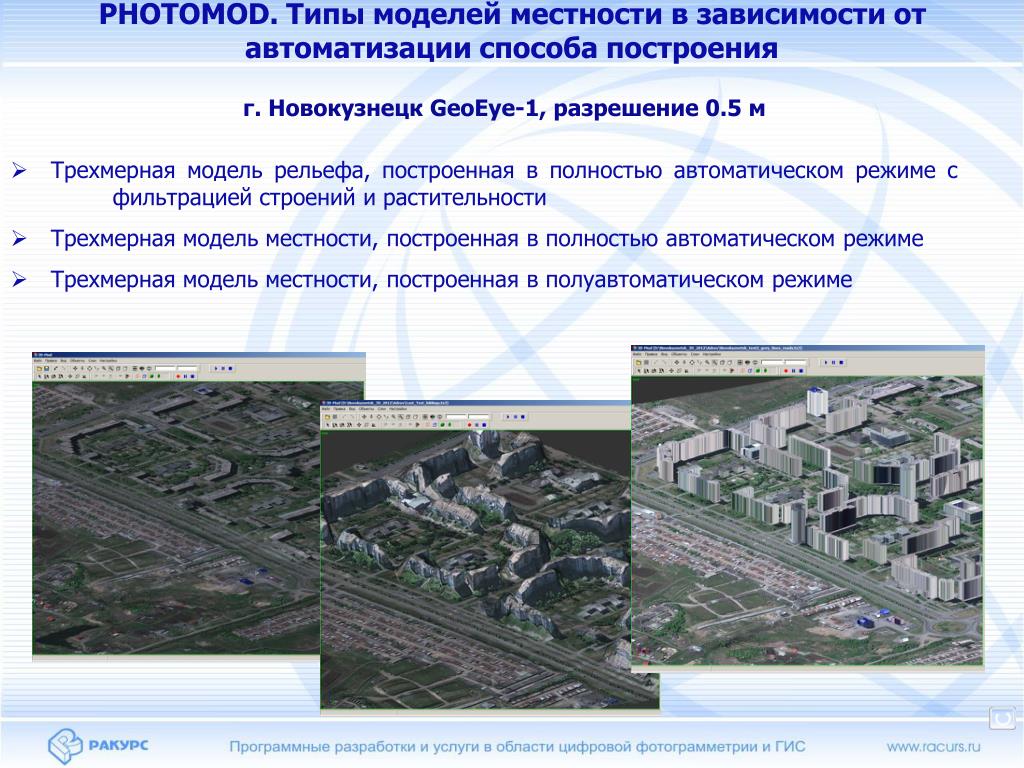

Буквально с миллионами этих объектов вы можете создать то, что известно как облако точек , или трехмерный набор точек, каждая из которых представляет совпадающую функцию для описания вашей обследованной области для компьютера. Затем вы можете превратить облако точек в любой обычный выходной файл, используемый в программном обеспечении для работы с геопространственными данными, например в трехмерную сетку или цифровую модель рельефа.

Фотограмметрия в реальной жизни

Если вам трудно представить себе, как все это работает, вы можете буквально использовать свои глаза. Ваши глазные яблоки постоянно используют фотограмметрию для создания изображений, которые вы видите.

Ваши глаза подобны двум камерам, которые постоянно обрабатывают происходящее в реальном времени. Ваши глаза расположены так, чтобы обеспечить два входа под немного разными углами. Вы можете проверить это сами, поднеся палец к лицу. Посмотрите на него с закрытым одним глазом, затем другим. Вы заметите, что ваш палец «прыгает» в пространстве относительно фоновых объектов.

Поскольку ваш мозг знает, как далеко друг от друга находятся ваши глаза, он может обрабатывать полученную информацию в точные геопространственные данные, объединяя оба потока в единую перспективу. Это часто называют восприятием глубины. Вы также можете проверить этот процесс — попробуйте поймать мяч одним закрытым глазом. Вы заметите, что это намного сложнее.

Ваш мозг создает живую карту трехмерного мира на основе двухмерных входных данных так же, как Платформа Propeller визуализирует 3D-обзор из 2D-фотографий.

Какие данные дронов используются в фотограмметрии?

Подрядчики в строительной отрасли получают много преимуществ от данных, собранных с помощью дронов. С помощью 3D-изображений, высокоточных карт и данных о высоте, которые они получают, компании могут отслеживать ход выполнения проекта и легко проверять все или часть своих рабочих площадок. Точность 3D-моделей также означает, что их можно использовать для расчета расстояний, площадей и измерений объема.

Данные аэрофотоснимков дронов идеально подходят для фотограмметрии, поскольку каждая фотография дрона имеет геотеги, то есть широта, долгота и высота, полученные с помощью GPS дрона и бортовых датчиков, встроены в метаданные изображения. Каждое изображение помечено геокоординатами, которые фиксируются датчиком GNSS на дроне, указывая, где именно это изображение находится в космосе. Метаданные изображения также включают информацию о датчике и оптике камеры дрона.

Эти изображения с геотегами сверяются с известными точками на земле, а затем могут обрабатываться такими программами, как Propeller Platform, для создания 3D-моделей с высокой детализацией и точностью. Чтобы получить наилучшую модель из данных 3D-картографирования дронов, между каждым аэрофотоснимком должно существовать 60-70-процентное перекрытие. Это делает процесс триангуляции более точным и позволяет лучше отслеживать одни и те же точки между изображениями.

Как работает программное обеспечение для фотограмметрии?

Облака точек обрисовывают формы объектов на рабочей площадке, но для получения фотореалистичной цифровой модели поверхности необходимо сопоставить эти формы с визуальными элементами. Здесь на помощь приходит сшивание изображений или ортотрансформация . Компьютер ищет общие черты, общие для нескольких изображений, снятых в одном месте, чтобы совместить изображения и объединить их с облаком точек. Это похоже на очень сложную головоломку.

Этот процесс хорошо работает на большинстве поверхностей, но возможности компьютера распознавать узоры ограничены. Если поверхность слишком невыразительна или турбулентна, как полированные окна здания или бурлящие волны океана, сшивание не очень хорошо. Вы не можете сопоставить функцию между изображениями, если она есть на одной фотографии и отсутствует на следующей, или если каждая функция выглядит так же, как и все остальные.

Интересно, чем фотограмметрия отличается от лидара? Прочтите этот пост для параллельного сравнения.

Видение общей картины

Итак, теперь у вас есть облако точек — источник «рельефных» выходных данных, таких как сетка DXF, файлы geoTIFF и т. д., — и ортомозаика, придающая этим точкам визуальное значение. Затем эта ортомозаика накладывается на модель рельефа, чтобы создать окончательную измеримую 3D-модель вашей рабочей площадки.

Оттуда вы можете использовать отраслевые инструменты измерения в платформе Propeller для расчета объемов складских запасов, определения объемов выемки/засыпки, контроля уклонов дорог, отслеживания прогресса в сравнении с проектом и многого другого. Вы также можете экспортировать свои данные для использования в другом программном обеспечении ГИС или САПР, если хотите.

Где бы вы ни собирались использовать данные с дрона, фотограмметрия даст вам более быструю и точную информацию, чем традиционные методы съемки.

Хотите использовать возможности фотограмметрии с дронов на своем рабочем месте? Давай поговорим .

Создание 3D-моделей с помощью фотограмметрии

Марк Алтавил | ГИС-данные | 19 декабря 2016 г. 2 ноября 2016 г.

Фотограмметрия — это наука о геодезических и картографических измерениях, часто по фотографиям, и между объектами. Фотограмметрия часто применяется для создания реалистичных масштабов объектов с использованием серии перекрывающихся или наложенных друг на друга фотографий. Применение пространственного анализа очевидно в таких областях, где фотограмметрия используется для реалистичного воссоздания архитектурных масштабов. Одним из преимуществ фотограмметрии является то, что обычные фотографии можно использовать для воссоздания 3D или 3D-видов. Это сделало фотограмметрию экономически эффективным способом создания 3D-объектов без использования лазерных сканеров или другого оборудования. Было показано, что для архитектуры это экономически эффективный способ создания многомасштабных моделей зданий, которые являются достаточно реалистичными.

С распространением смартфонов и дронов фотограмметрия стала широко применяться как эффективный и экономичный метод простого воссоздания 3D-моделей больших площадей и конкретных объектов или зданий. На самом деле, некоторые дроны используют смартфоны в своих системах для сбора данных фотограмметрии.[2] Смартфоны и устройства пришли на смену обычным загрузочным камерам и старому фотограмметрическому оборудованию в дронах из-за их экономической эффективности и повышенного разрешения и точности смартфонов.

Фотограмметрия в настоящее время заменяет данные цифровой модели рельефа (DEM) во многих местах, поскольку точность камер улучшается, а цифровая фотограмметрия способна генерировать гораздо более высокое разрешение и точность для цифровых моделей поверхности (DSM) для представления сложных ландшафтов.[4] Одной из проблем была скорость обработки изображений, так как часто требуется много фотографий, и их нужно сшивать вместе, что происходит намного медленнее, чем типичные исследования высот на основе GPS.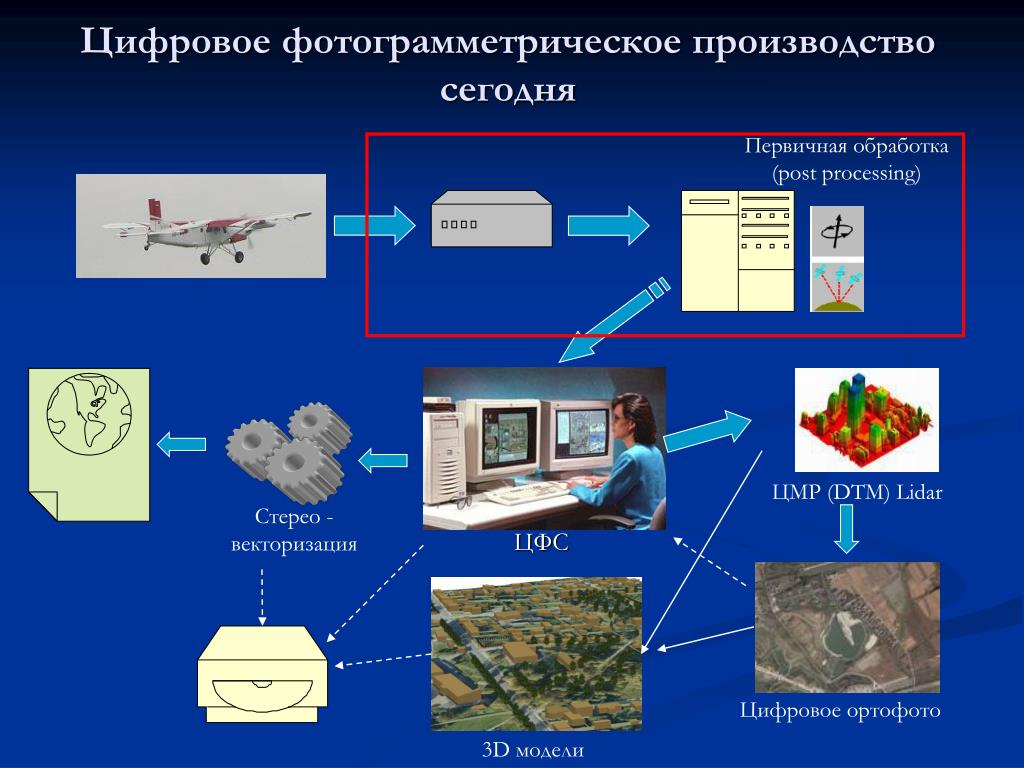 [5] Тем не менее, преимущество расширения традиционного разрешения и точности ЦМР сделало фотограмметрию теперь важным компонентом ландшафтных и объектных исследований, заинтересованных в точных трехмерных реконструкциях и анализе.

Структура из движения (SfM). Вместо одной стереопары метод SfM требует нескольких перекрывающихся фотографий в качестве входных данных для алгоритмов выделения признаков и трехмерной реконструкции. Из: Westoby et al., 2012.

Ссылки

[1] Подробнее об использовании фотограмметрии для воссоздания трехмерной архитектуры см.: Rau, J.-Y., & Cheng, C.-K. (2013). Экономически эффективная стратегия для многомасштабного фотореалистичного моделирования зданий и веб-приложений трехмерной ГИС в сфере недвижимости. Компьютеры, окружающая среда и городские системы , 38 , 35–44. https://doi.org/10.1016/j.compenvurbsys.2012.10.006

[2] Подробнее о фотограмметрии и смартфонах в дронах см.: Kim, J., Lee, S., Ahn, H., Seo, Д., Парк С. и Чой К. (2013). Возможность использования смартфона в качестве полезной нагрузки в фотограмметрической системе БПЛА. ISPRS Journal of Photogrammetry and Remote Sensing , 79 , 1–18.

[3] Дополнительную информацию об экономической эффективности интеллектуальных устройств при замене фотограмметрических систем на дронах (БПЛА) см.: Jeong, H.H., Park, J.W., Kim, J.S., & Choi, C.U. (2016). Оценка точности орто-изображения с помощью фотограмметрического беспилотного авиационного комплекса. ISPRS – Международный архив фотограмметрии, дистанционного зондирования и пространственных информационных наук , XLI-B1 , 867–872. https://doi.org/10.5194/isprsarchives-XLI-B1-867-2016

[4] Для получения дополнительной информации о фотограмметрии, используемой для ЦММ, см.: Miyasaka, T., Okuro, T., Zhao, X., & Такеучи, К. (2016). Классификация землепользования на топографии песчаных дюн с помощью объектно-ориентированного анализа, цифровой фотограмметрии и анализа ГИС на песчаной земле Хорцинь, Китай.