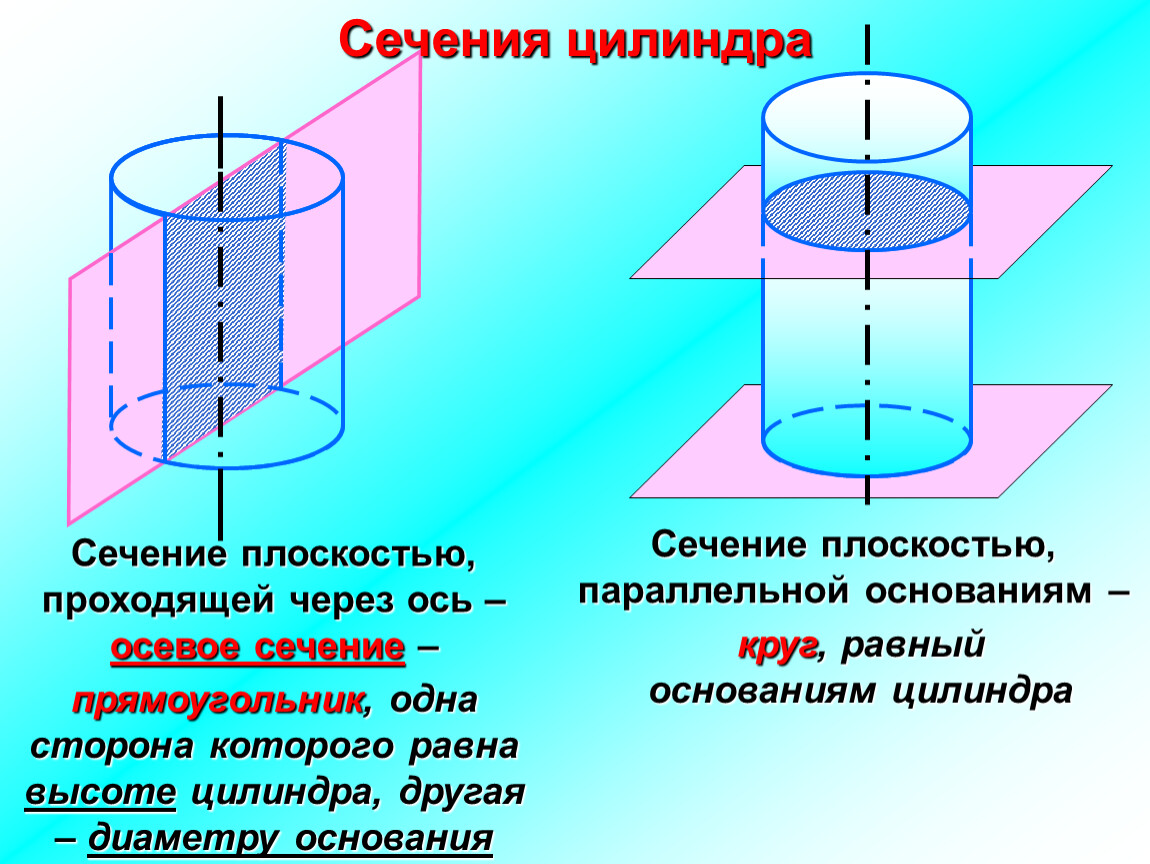
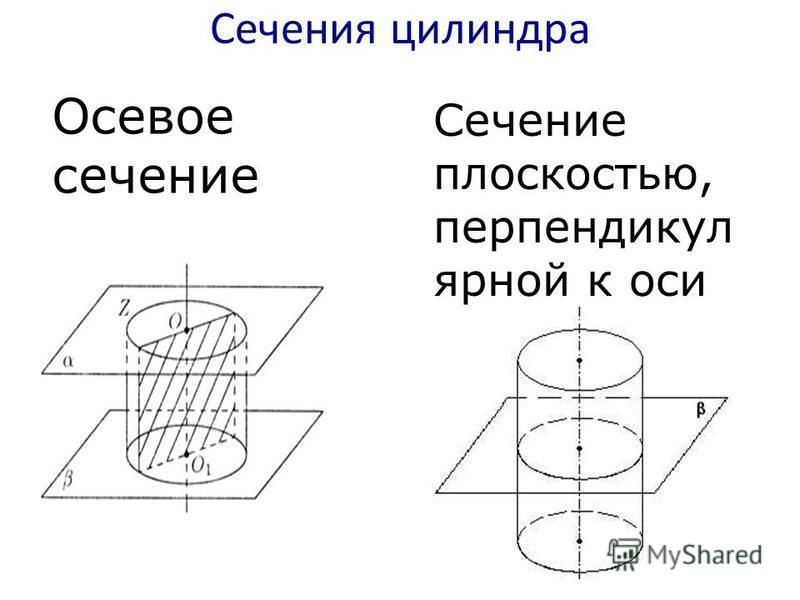
Теорема о прямой и параллельной ей плоскости
Анна Малкова
Ей не повезло.
В школьных учебниках ее и теоремой-то редко называют. Говорят, что это «лемма». Или «следствие». Или «задача». Как будто это что-то необязательное и незначительное. А на самом деле это важнейшая теорема о прямой и параллельной ей плоскости.
Даже если в школе ее доказывают — не говорят, зачем она нужна. Доказали — и забыли.
Но при этом в стереометрии — и особенно в задачах ЕГЭ по математике — есть множество ситуаций, когда без этой важнейшей теоремы не обойтись.
Встречайте:
Теорема о прямой и параллельной ей плоскости:
Пусть прямая m параллельна плоскости . Если плоскость проходит через прямую m и пересекает плоскость по прямой c, то c параллельна m.
Для чего нам эта теорема? Например, для того, чтобы построить сечение пирамиды плоскостью, параллельной плоскости основания.
1. Постройте сечение тетраэдра плоскостью, проходящей через точки M, N, K.
Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной MK.
Прямая MK параллельна AB, лежащей в плоскости основания ABC. Значит,
Плоскость сечения проходит прямую MK, параллельную плоскости ABC. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости AВC параллельна прямой MK. Трапеция MKNT — искомое сечение.
Таких задач, где в сечении пирамиды получается трапеция (или параллелограмм), в вариантах Профильного ЕГЭ очень много.
2. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 8, точка K — середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
Пусть точка M — середина AB. Тогда как средняя линия
Пусть точка N — середина PD. Поскольку KN — средняя линия и тогда
Построим сечение пирамиды плоскостью KMN. Пусть плоскости KMN и ABC пересекаются по прямой МE. Покажем, что
Пусть плоскости KMN и ABC пересекаются по прямой МE. Покажем, что
По теореме о прямой и параллельной ей плоскости,
Это значит, что Прямая ME содержит точку О, являющуюся проекцией вершины P на плоскость ABC. Трапеция KNEM – искомое сечение.
б) Найдём площадь сечения.
где — высота трапеции KNEM.
Пусть H — середина KN,
тогда
Есть еще одна теорема — такая же полезная, как и теорема о прямой и параллельной ей плоскости. Вот она:
Теорема. Пусть плоскости и пересекаются по прямой р. Плоскость параллельна прямой р. Тогда она пересекает плоскости и по прямым, параллельным .
Как ее назвать? Согласитесь, сложно придумать короткое название. Для себя (не для оформления на экзамене!) можно запомнить эту картинку как «домик» или «книжечку». Главное — запомнить формулировку и увидеть, как теорема применяется в решении задач.
Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Теорема о прямой и параллельной ей плоскости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Информация на странице «Теорема о прямой и параллельной ей плоскости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 07.07.2023
Сечение куба плоскостью
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
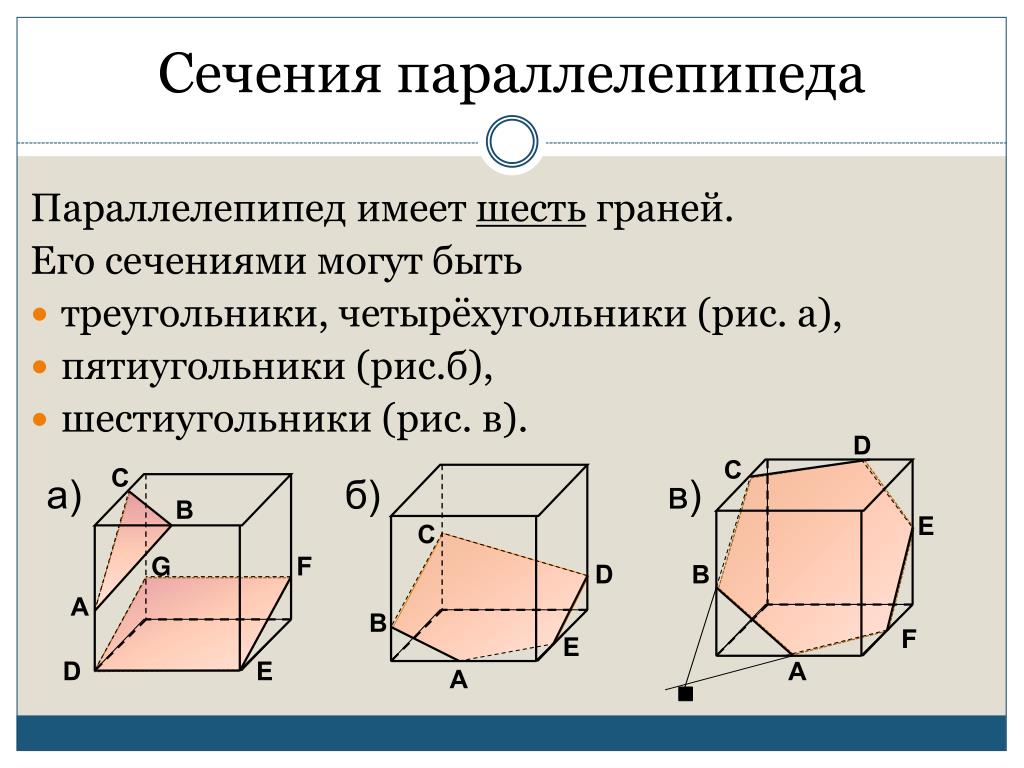
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях.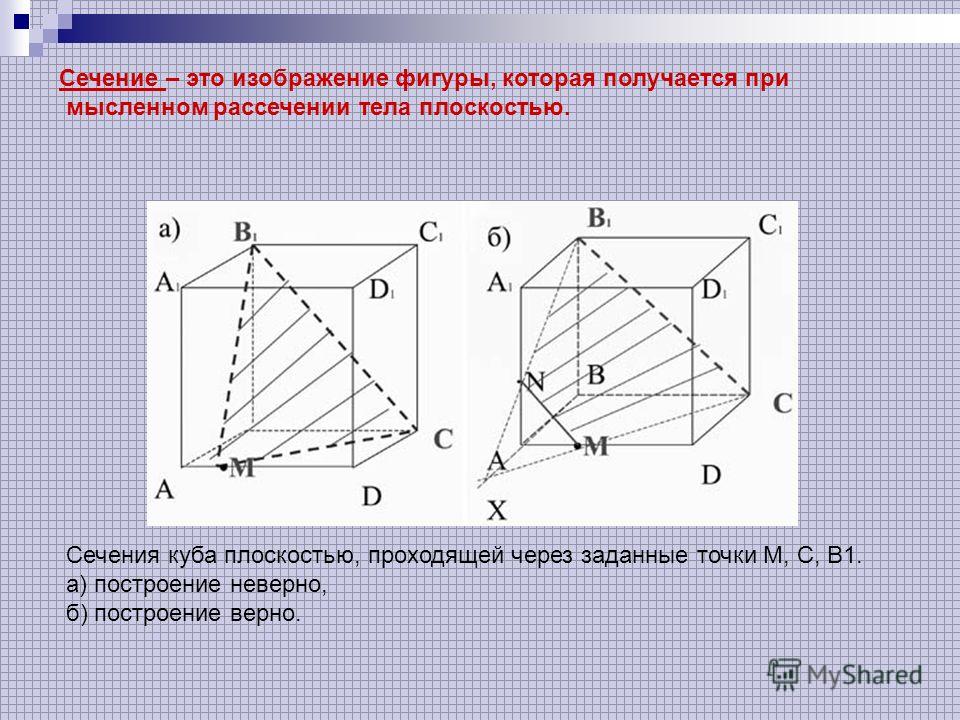 Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1).
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый).
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Работа с поперечными сечениями
Просмотр…
Включение/отключение поперечного сечения
Щелкните значок Включить сечение на панели инструментов 3D-документа, чтобы отобразить поперечное сечение(я).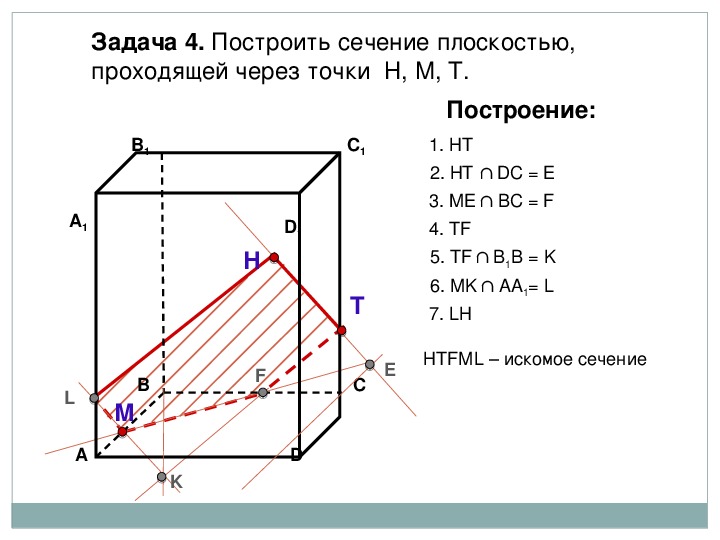 Нажмите ее еще раз, чтобы скрыть поперечное сечение(я).
Нажмите ее еще раз, чтобы скрыть поперечное сечение(я).
Значение по умолчанию — одна плоскость ( ). SpinFire «запомнит» последнюю использованную настройку.
Показать или скрыть секущие плоскости
Когда секущая плоскость включена, по умолчанию она отображается в виде прозрачного серого прямоугольника. Вы можете сделать плоскость прозрачной, чтобы разрез был более четким.
- Щелкните правой кнопкой мыши в любом месте секущей плоскости, чтобы открыть контекстное меню.
- Нажмите Показать плоскости сечения .
Чтобы восстановить плоскость, щелкните правой кнопкой мыши в любом месте фона сцены, затем выберите Показать плоскости сечения в нижней части контекстного меню рабочей области.
Обратите внимание, что когда команда включена, соответствующий значок в контекстном меню выделяется.
Показать или скрыть края и грани профиля
Когда разрешено сечение плоскости, по умолчанию подсвечиваются грани и ребра.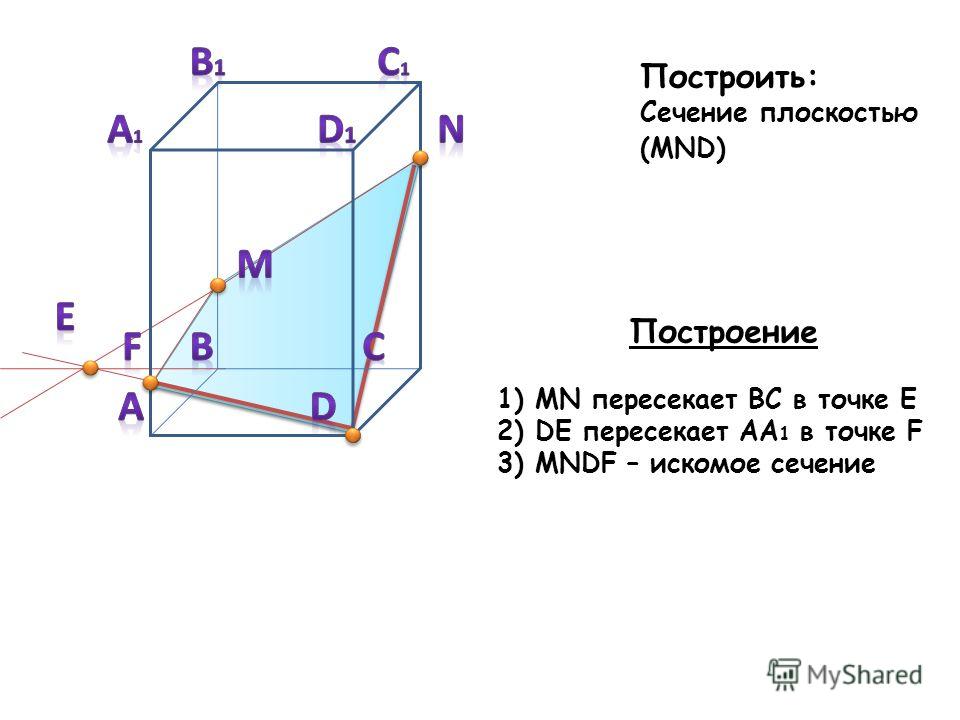 (Информацию о настройке цветов по умолчанию см. в разделе «Параметры».)
(Информацию о настройке цветов по умолчанию см. в разделе «Параметры».)
Чтобы скрыть выделение:
- Щелкните правой кнопкой мыши в любом месте секущей плоскости, чтобы открыть контекстное меню.
- Нажмите Показать края профиля или Показать грани профиля .
Чтобы восстановить выделение, повторите шаги, описанные выше.
Обратите внимание, что при включении команды соответствующий значок в контекстном меню подсвечивается.
Показать или скрыть поперечное сечение деталей и узлов.
По умолчанию поперечное сечение влияет на каждую часть сборки. Однако вы можете показать или скрыть поперечное сечение для каждой детали и узла в вашей модели.
У вас должна быть включена плоскость поперечного сечения, прежде чем вы сможете включить или отключить поперечное сечение для объектов в сборке.
- На панели Сборка щелкните правой кнопкой мыши имя детали, подсборки или сборки, для которой вы хотите отключить или включить поперечное сечение.
 Откроется контекстное меню сборки.
Откроется контекстное меню сборки. - Наведите курсор на Раздел , чтобы увидеть всплывающее меню.
- Нажмите Вырезать материал . По умолчанию команда Cut Material проверяется, когда для объекта включено поперечное сечение.
Изменить цвета по умолчанию, используемые для граней и краев профиля
Чтобы изменить цвет краев или граней профиля:
- Откройте меню «Сечение» на панели инструментов 3D-документа. (Щелкните стрелку вниз справа от значка раздела на панели инструментов 3D-документа.)
- Щелкните Определить… , чтобы открыть диалоговое окно Определить сечение (вкладка Параметры).
- Нажмите кнопку ЦВЕТ КРОМОК ПРОФИЛЯ или ЦВЕТ ПОВЕРХНОСТИ ПРОФИЛЯ и выберите цвет.
- Щелкните Применить для предварительного просмотра. Нажмите OK , чтобы сохранить изменения.
Создать. ..
..
Подменю Выровнять и Разместить по предлагают несколько вариантов создания и определения плоскости поперечного сечения.
Создать стандартную плоскость поперечного сечения
- Откройте меню Сечение. (Щелкните стрелку вниз справа от значка раздела на панели инструментов 3D-документа.)
- Нажмите Выровнять .
- Щелкните Плоскость XY , Плоскость XZ или Плоскость YZ . Красные точки на модели обозначают доступные вершины модели. Штриховка появляется, когда указатель правильно расположен над точкой вершины.
- Щелкните точку на модели, чтобы расположить плоскость.
Создание сечения по трем точкам
- Откройте меню Сечение. (Щелкните стрелку вниз справа от значка раздела на панели инструментов 3D-документа.)
- Укажите на Поместите по .

- Нажмите 3 точки . Красные точки на модели обозначают доступные точки на модели. Штриховка появляется, когда указатель правильно расположен над точкой.
- Щелкните три точки на модели, чтобы расположить плоскость.
Точки не могут лежать на одной прямой.
Создание поперечного сечения по двум точкам
- Откройте меню Сечение. (Щелкните стрелку вниз справа от значка раздела на панели инструментов 3D-документа.)
- Укажите на Поместите по .
- Нажмите 2 точки . Красные точки на модели обозначают доступные точки на модели.
- Щелкните две точки на модели, чтобы расположить плоскость.
Создание поперечного сечения с использованием двух точек экрана
- Откройте меню Раздел. (Щелкните стрелку вниз справа от значка раздела на панели инструментов 3D-документа.)
- Укажите на Поместите по .

- Нажмите 2 точки экрана .
- Щелкните две точки в окне просмотра, чтобы расположить плоскость.
Позиция…
Использование ручек для перемещения плоскости
Чтобы сдвинуть плоскость вдоль оси плоскости, щелкните и перетащите один из белых захватов, слегка смещенных от центра каждого края. Появляются желтые стрелки направления, указывающие, в каком направлении вы можете перемещать самолет.
Чтобы повернуть плоскость вокруг горизонтальной или вертикальной оси, щелкните и перетащите один из красных захватов, расположенных в центре каждого края. Появляются желтые стрелки направления, указывающие, в каком направлении вы можете перемещать самолет.
Чтобы сдвинуть плоскость вдоль оси нормали, щелкните и перетащите один из белых захватов, расположенных в центре плоскости и в каждом углу. Появляются желтые стрелки направления, указывающие, в каком направлении вы можете перемещать самолет.
Перемещение секущей плоскости с шагом
Перемещение секущей плоскости
- Откройте меню Сечение. (Нажмите стрелку вниз справа от значка сечения на панели инструментов 3D-документа.)
- Щелкните Определить…
- Выберите вкладку Перемещение в диалоговом окне Определить сечение.
- В поле Step введите количество единиц, на которое самолет должен перемещаться при каждом нажатии кнопки направления ( << и >> ).
- Используйте кнопки << и >> для перемещения плоскости.
- Нажмите Применить , чтобы увидеть эффект движения.
- Щелкните OK , чтобы сохранить результаты и закрыть диалоговое окно.
Повернуть секущую плоскость
- Откройте меню Сечение. (Нажмите стрелку вниз справа от значка раздела на панели инструментов 3D-документа.
 )
) - Нажмите Определить…
- Выберите вкладку Перемещение в диалоговом окне Определить сечение.
- В поле Угол введите количество градусов, на которое должна поворачиваться плоскость при каждом нажатии кнопки направления ( << и >> ).
- Используйте кнопки << и >> , чтобы повернуть плоскость вокруг оси Y и/или оси Z.
- Нажмите Применить , чтобы увидеть эффект движения.
- Нажмите OK , чтобы сохранить результаты и закрыть диалоговое окно.
Размещение плоскости сечения
В диалоговом окне “Определить сечение” можно указать точку, в которой плоскость будет пересекаться.
- Откройте меню Раздел. (Нажмите стрелку вниз справа от значка сечения на панели инструментов 3D-документа.)
- Щелкните Определить…
- Выберите вкладку Положение в диалоговом окне Определить сечение.

- Выберите один из следующих методов позиционирования плоскости:
Выберите точку или систему координат:
- В раскрывающемся меню выберите метод выбора элемента. Доступны следующие методы:
Выбрать точку — выбрать точку на модели.
Выберите систему координат – Выберите систему координат в сцене. Точка пересечения будет исходной точкой кадра системы координат.
- Нажмите кнопку Выбрать .
- Выберите точку на модели или выберите систему координат.
- Щелкните OK , чтобы сохранить положение и закрыть диалоговое окно.
или
Введите координаты :
- 903 04
- Введите координаты точки в поля X , Y и Z . Эта точка определяется относительно выбранной системы координат — в данном случае глобальной системы координат.

- Щелкните Применить , чтобы увидеть результат изменения положения.
- Щелкните OK , чтобы сохранить положение и закрыть диалоговое окно.
Ориентация секущей плоскости
- Откройте меню Сечение. (Щелкните стрелку вниз справа от значка сечения на панели инструментов 3D-документа.)
- Щелкните Определить…
- Выберите вкладку Ориентация в диалоговом окне Определить сечение.
- Выберите один из следующих способов выравнивания плоскости:
Выберите элемент:
- В раскрывающемся меню выберите способ выбора элемента. Доступны следующие методы:
Выбрать 2 точки — выберите две точки на модели.
Выберите 3 точки (нормальная плоскость) — выберите три точки на модели.
Выбрать ребро – Выберите ребро на модели.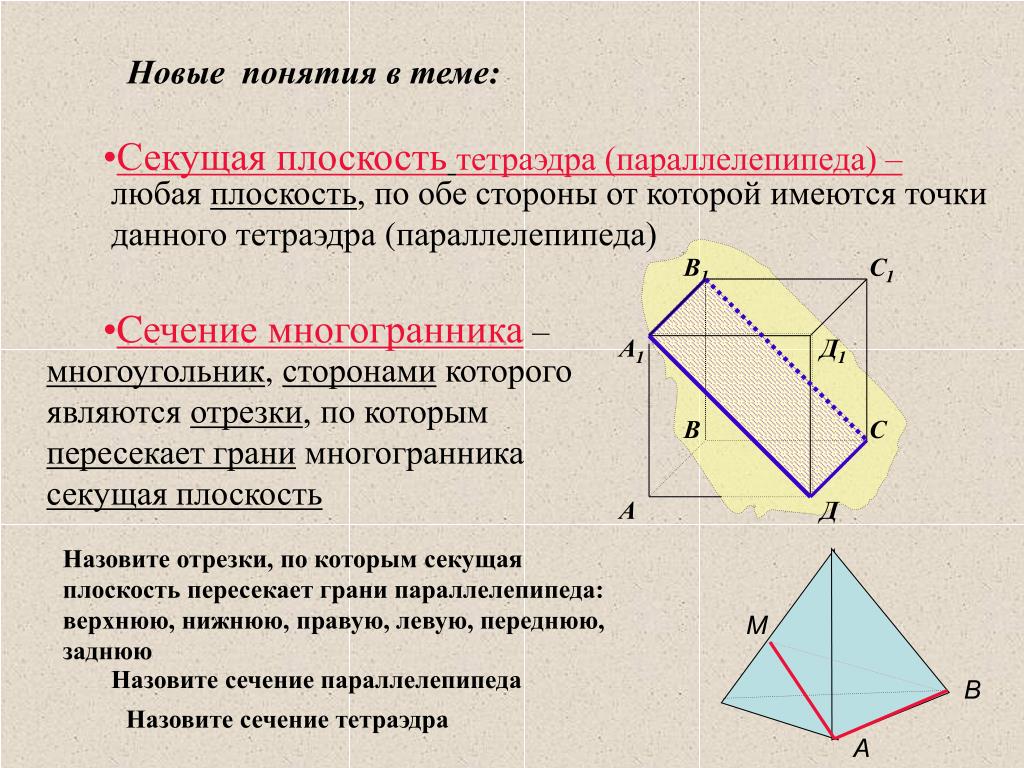
Выберите ось системы координат – Выберите ось системы координат в сцене. Плоскость будет выровнена вдоль выбранной оси.
- Нажмите кнопку Выбрать .
- Выберите точки или ребро на модели или выберите ось системы координат.
- Щелкните OK , чтобы сохранить положение и закрыть диалоговое окно.
или
Введите координаты Переключатель оси X, Y или Z. Проекция и расчеты… Режим проекции Включение/отключение параллельной плоскости проекции: Расчеты Выполните следующие шаги, чтобы определить площадь, длину периметра или центральную точку разреза или площадь проекции ( Панель быстрого доступа: Лента: Средство 3D-просмотра — Инструменты — 3D-разрез Панель 3D-сечения имеет элементы управления для настройка визуального отображения 3D моделей и секущих плоскостей. Элементы управления частями модели и секциями Сверху находятся настройки, позволяющие изменить отображение частей модели и визуальных элементов управления секциями. Опция Описание Включено Включает вид сечения 3D-модели. При активации этой опции отображается деталь 3D-модели, созданная в результате пересечения модели с плоскостью. Шоу Гизмо Gizmo позволяет перемещать и вращать секущую плоскость в рабочей области с помощью мыши. Gizmo соответствует выбранной плоскости в списке. При активации этой опции отображаются детали модели, вырезанные одной или несколькими плоскостями. Управление плоскостями сечения На панели инструментов есть параметры для настройки положения плоскости сечения. Значок Имя Описание Самолеты ID Список номеров добавленных плоскостей сечения. Чтобы изменить или удалить плоскость, сначала выберите ее в списке. Добавляет новый самолет Добавляет новый самолет. Новая плоскость добавляется под углом 90 градусов к ранее добавленной. Можно тремя щелчками мыши добавить три взаимно перпендикулярные плоскости. Добавленная плоскость проходит через геометрический центр модели. Удаляет выбранную плоскость Удаляет выбранную плоскость. Определяет плоскость Определяет плоскость по выбранным точкам на модели одним из предложенных способов. При активации любой из опций гизмо скрывается. Если список плоскостей пуст, добавляется новая плоскость, в противном случае изменяется выбранная плоскость в списке. способов определения плоскости: •На три очка. • По выбранному объекту. •Изменить базовую точку. По трем точкам Определяет плоскость, проходящую через три плоскости. По выбранному объекту Поверхность – определяется плоскость, касательная к выбранной точке на поверхности модели. Прямая кромка – определяется плоскость, перпендикулярная кромке. Ребро по дуге окружности — определяется плоскость, содержащая выбранную окружность. Базовая точка устанавливается в центре круга. Изменение базовой точки Плоскость сечения смещается таким образом, чтобы пройти через выбранную точку. Нормальное направление плоскости не меняется. Выравнивает выбранную плоскость с плоскостью YZ Изменяет нормальное направление выбранной плоскости. Размещает плоскость параллельно плоскости YZ. Добавляет плоскость сечения, если список сечений пуст. При добавлении плоскость проходит через геометрический центр модели. Выравнивает выбранную плоскость с плоскостью XZ Изменяет нормальное направление выбранной плоскости. Размещает плоскость параллельно плоскости XZ. Добавляет плоскость сечения, если список сечений пуст. Выравнивает выбранную плоскость с плоскостью XY Изменяет нормальное направление выбранной плоскости. Размещает плоскость параллельно плоскости XY. Добавляет плоскость сечения, если список сечений пуст. При добавлении плоскость проходит через геометрический центр модели. Изменяет направление выбранной плоскости Изменяет направление выбранной плоскости на противоположное. Параметры положения секущей плоскости Опция Описание Позиция В группе есть поля для ввода координат X, Y, Z базовой точки выбранной секущей плоскости. Расстояние Задает расстояние между выбранной плоскостью и центром объекта в процентах от радиуса ограничивающей окружности.
(Обратите внимание, что вам, возможно, придется повернуть плоскость сечения, чтобы увидеть проекцию.
Средство просмотра > Панель 3D-раздела
1_images/pril_(4)1_22.jpg) Панель доступна в режиме 3D Viewer. Команды и параметры панели 3D-сечения позволяют настроить просмотр 3D-модели. Для отображения частей модели, разреза и гизмо используйте настройки, расположенные вверху формы. Возможно создание нескольких плоскостей одновременно.
Панель доступна в режиме 3D Viewer. Команды и параметры панели 3D-сечения позволяют настроить просмотр 3D-модели. Для отображения частей модели, разреза и гизмо используйте настройки, расположенные вверху формы. Возможно создание нескольких плоскостей одновременно.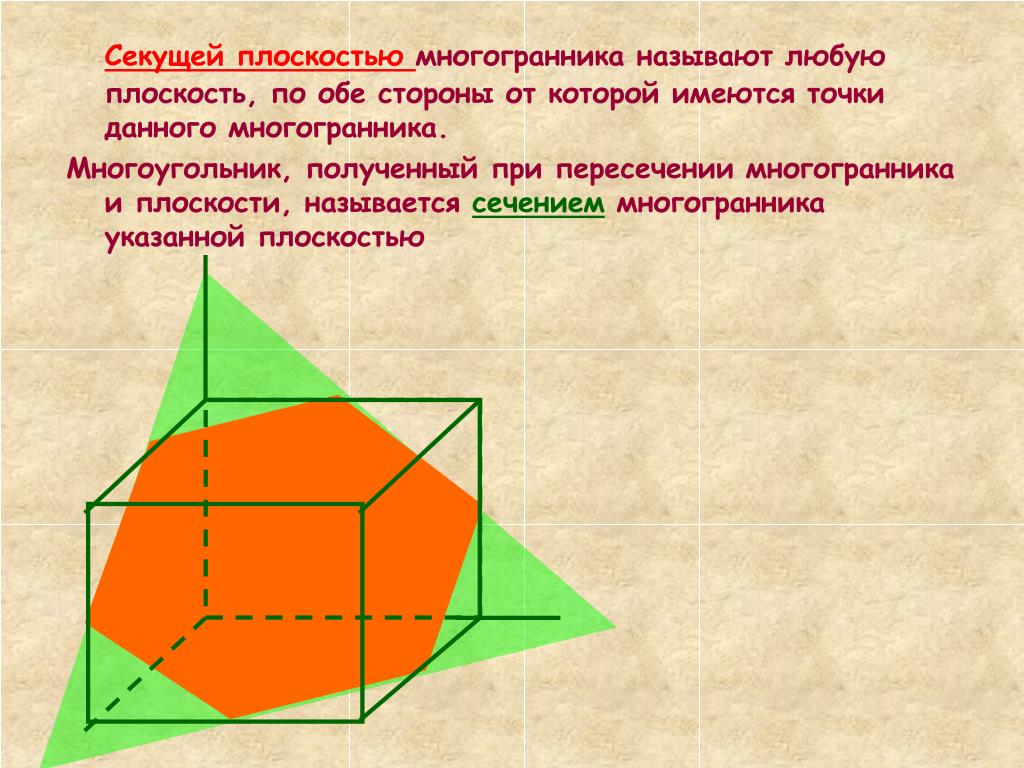 Когда эта опция отключена, отображаются неразрезанные части модели. Вы можете использовать эту опцию, когда у вас есть более одной плоскости, и вы хотите вырезать сектор под острым углом.
Когда эта опция отключена, отображаются неразрезанные части модели. Вы можете использовать эту опцию, когда у вас есть более одной плоскости, и вы хотите вырезать сектор под острым углом.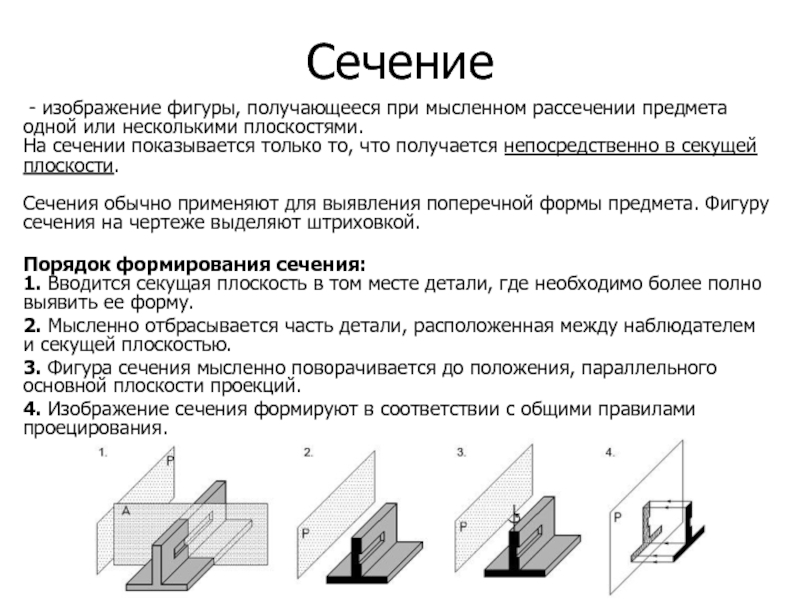
 При добавлении плоскость проходит через геометрический центр модели.
При добавлении плоскость проходит через геометрический центр модели.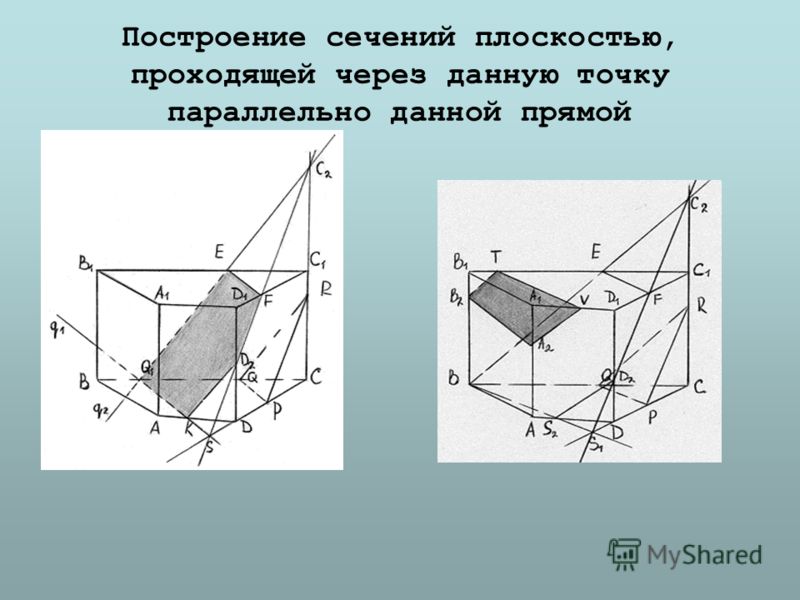

 Откроется контекстное меню сборки.
Откроется контекстное меню сборки.

 )
)