Расстояние и отклонение точки от плоскости
Пусть – плоскость, заданная уравнениеми– произвольная точка пространства. Тогдарасстояние от точкидо плоскостивыражается формулой
(10)
В знаменателе этой дроби стоит длина вектора – нормального вектора плоскостиТаким образом,чтобы найти расстояние от точки до плоскости, надо подставить координаты точки в уравнение плоскости и разделить полученное число на длину нормального вектора; при этом мы получим число, которое может быть отрицательным – в этом случае берём его по абсолютной величине.
Если в формуле (10) убрать знак модуля, то мы получим величину
(11)
называемую отклонением точки от плоскости
Очевидно, и
Замечание. Определённое по формуле (11)
отклонение отличается от того отклонения,
которое принято в ряде учебников (а
именно,еслииесли).
Геометрический смысл отклоненияточки от плоскости точно такой же, как у отклонения точки от прямой на плоскости (см. раздел “Прямая на плоскости”). А именно,отклонение по абсолютной величине равно расстоянию, причём если точканаходится от плоскостипо ту сторону, в которую направлен нормальный векториесли она находится по другую сторону(см. рис. 11).
Рис.11.
Разберём задачи на расстояния и отклонения.
Задача 16. Найти расстояние между плоскостямии
Решение.Плоскости параллельны, так как их нормальные векторыиколлинеарны:Поэтому расстояние между этими плоскостями равно расстоянию от какой-нибудь точки первой плоскости до второй плоскости. Возьмём точку первой плоскости:Тогда
Задача 17.В прямоугольном параллелепипедеНайти расстояние от вершиныдо плоскости
Решение.
Введём
систему координат с началомкак показано на рисунке 12.
Рис.12.
Используя формулу (4), мы можем записать уравнение плоскости “в отрезках”:
(12)
Нам требуется найти расстояние от точки до плоскости, заданной уравнением (12). Перенесём единицу в левую часть равенства:Применим формулу (10):
Задача 19. Определить, лежит ли точка между плоскостямии
Решение.Обозначим эти плоскости черезиТак как плоскости имеют один и тот же нормальный вектор и не совпадают (это видно из уравнений плоскостей), то плоскости параллельны. Вычислим по формуле (11) отклонения:
Рис.13.
Задача 20.
Даны
плоскостии точкиОпределить, точкиилежат внутри одного, смежных или
вертикальных углов, образованных
плоскостямии
Решение.Вычисляем отклонения:
–
значит, илежат по одну сторону от плоскости
–
значит, илежат по разные стороны от плоскостиОтсюда следует, чтоилежат внутрисмежныхдвугранных углов.
Пусть – прямая с направляющим вектороми– точка прямой(см. рис. 14).Расстояние от точки до прямойвыражается формулой
(13)
Рис.14.
Пусть – скрещивающиеся прямые,– их направляющие векторы и– какие-либо точки, лежащие на прямыхсоответственно (см. рис. 15).Расстояние между скрещивающимися прямыми можно вычислить по формуле
(14)
Рис.15.
Замечание.
Если
прямыепересекаются (но не совпадают), то формула
(14) к ним также применима и она показывает,
что расстояние между прямыми равно 0.По формуле(14)нельзя вычислять
расстояния между параллельными прямыми.
Задача 21. Найти расстояние от точкидо прямой
Решение.Из уравнения прямой найдём её направляющий вектор и точку:иОтсюдаПо формуле (13) получим:
Задача 22.Найти расстояние между прямымии
Решение.
Задача 23. Найти расстояние между прямымии
Решение.Обозначим данные прямыеиНаправляющий вектор прямойравенПрямаяпараллельна осипоэтому за направляющий вектор этой
прямой можно взять векторТак както можно применять формулу (14).
В качестве
точекэтих прямых возьмёмиПо формуле (14) получаем:
Задача 24.Ребро куба равноНайти расстояние между скрещивающимися диагоналями двух смежных граней куба.
Решение(см. рис. 16).
Рис.16.Будем временно считать, что ребро куба равно 1, затем полученную величину умножим на Вычислим расстояние между прямымии(другие диагонали дадут такой же результат). Введём систему координат, как показано на рисунке. Имеем:Направляющие векторыпрямых равны:По формуле (14) получаем:
Следовательно,
Задача 25.Выяснить взаимное расположение плоскостейи
Решение. Нормальные
векторы этих плоскостей равны:Вычислим их смешанное произведение:Таким образом, векторыкомпланарны. Так как никакие два из этих
векторов не коллинеарны, то возможны
следующие варианты взаимного расположения
плоскостей (см.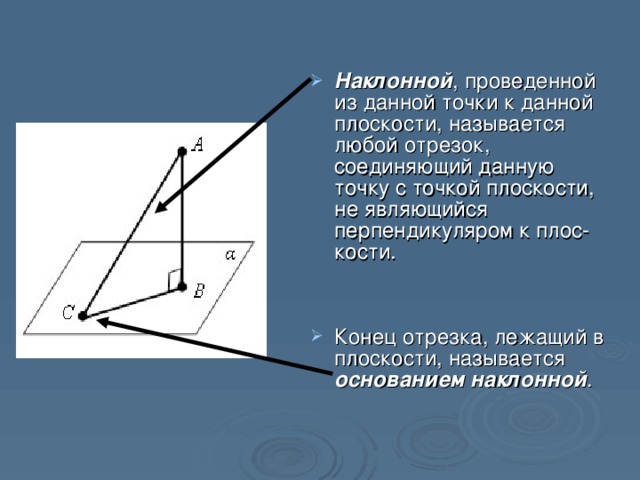
рис. 17): (а) плоскости
попарно пересекаются по трём параллельным
прямым, (б) плоскости проходят через
одну прямую.
Чтобы различить эти две ситуации, решим систему уравнений
Из первого уравнения Подставим во второе:откудаа значит,Подставим в третье уравнение:т.е.что невозможно. Таким образом, система решений не имеет, т.е. плоскости не имеют общей точки, а значит, имеет место случай (а).
Задача 26.Составить уравнение геометрического места точек, равноудалённых от прямыхи
Решение.Обозначим данные прямые черезиПрямые имеют один и тот же направляющий
векторзначит, они параллельны или совпадают.
Возьмём по одной точке этих прямых:Так кактои– различные параллельные прямые.
Проведём плоскостьчерез прямыеив этой плоскости проведём прямуюпосередине междуиа затем через прямуюпроведём плоскостьперпендикулярную плоскости(см.
рис. 18).
Очевидно, плоскость – это и есть искомое геометрическое место точек, равноудалённых от прямыхиНормальным вектором плоскостиможет служить вектор
Нормальный вектор плоскостиперпендикулярен векторамипоэтому можно взять
В качестве точки плоскости можно взять точку– середину отрезкаИмеем:Подставив в формулу (4), получим:или
28
Отклонение точки от прямой
В данной статье мы рассмотрим понятие отклонения точки от прямой на плоскости. Приведем примеры нахождения отклонения точки от прямой.
Отклонение точки от прямой на плоскости − это расстояние от точки до прямой, взятой со знаком “+”, если эта точка и начало координат лежат по разные стороны прямой, и со знаком “−”, если точка и начало координат лежат по одну сторону от прямой.
Если прямая проходит через начало координат, то отклонение точки от прямой предполагается равным расстоянию от точки до прямой, взятой со знаком “+”, если точка лежит по ту сторону от прямой, куда направлен пормальный вектор прямой, и равным расстоянию от точки до прямой, взятой со знаком “−”, в противном случае.
Обозначим отклонение точки от прямой символом δ, а расстояние от точки до прямой символом d. На рисунке Рис.1 отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 и начало координат O лежат по разные стороны прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 и начало координат O лежат по одну сторону от прямой L.
На рисунке Рис.2 прямая L проходит через начало координат. Поэтому, отклонение точки M1 от прямой L равно δ=+d1, так как точка M1 лежит по ту сторону прямой L, куда направлен нормальный вектор n прямой L, а отклонение точки M2 от прямой L равно δ=−d2, так как точка M2 лежит по противоположную сторону прямой, куда направлен нормальный вектор n прямой L
Рассмотрим нормальное уравнение прямой L (Рис.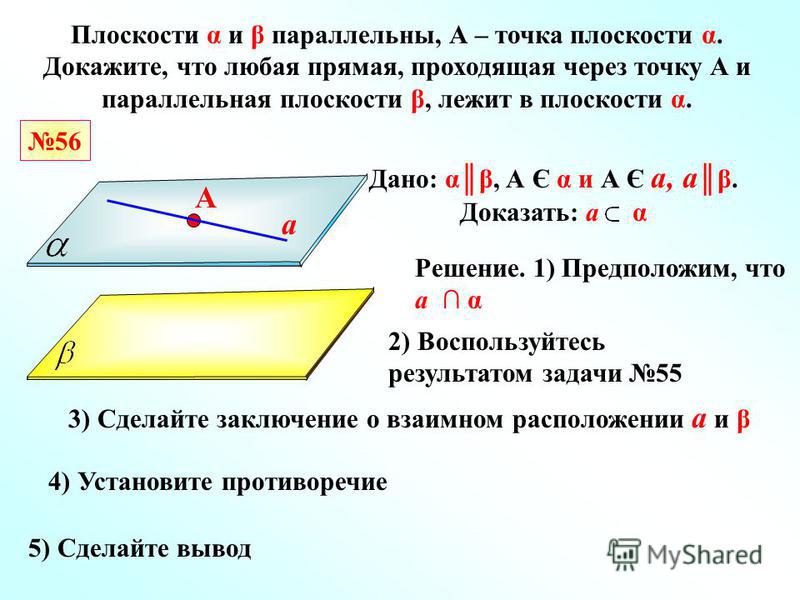
3):
| xcosφ+ysinφ−r=0. | (1) |
где r− расстояние начала координат до прямой L, а φ− угол между нормальным вектором прямой L и осью Ox.
Покажем, что левая часть нормального уравнения прямой дает отклонение точки M(x,y) от прямой, заданной уравнением (1). Для этого докажем следующую теорему:
Теорема 1. Пусть прямая L определяется нормальным уравнением прямой (1). Тогда отклонением точки M с координатами x, y от прямой L равно δ=xcosφ+ysinφ−r.
Доказательство. Проведем через нормальный вектор прямой L линию OQ (Рис.3). Проекция точки М на прямую OQ будет точка S. Отклонение δ точки M от прямой L будет равно SR.
Тогда
| δ=SR=OS−OR=OS−r. | (2) |
Но
где n− единичный нормальный вектор прямой L, α−угол между векторами n и .
Из (3) и (4) следует:
С другой стороны
так как нормальный вектор прямой имеет координаты n={cosφ, sinφ}, а точка M − M(x, y).
Сопоставляя (2), (5) и (6), получим:
| δ=xcosφ+ysinφ−r. |
Теорема доказана.
Таким образом, как следует из теоремы 1, для вычисления отклонения некоторой точки M0(x0, y0) от прямой, нужно в левую часть нормированного уравнения прямой (1) подставить координаты точки M0:
| δ=x0 cosφ+y0 sinφ−r. |
Заметим, расстояние от точки M0 до прямой L будет равно модулю отклонения данной точки от прямой.
Пример 1. Задано нормальное уравнение прямой:
Найти отклонение точки M(5,-3) от прямой (7).
Решение.
Подставим координаты точки M(5,−3) в левую часть уравнения (7):
Ответ. Отклонение точки M(5,−3) от прямой (7) равно:
Пример 2. Задано общее уравнение прямой:
| 4x−3y+1=0. | (8) |
Найти отклонение точки M(1,1) от прямой (8).
Решение. Один из простых методов решения − это приведение общего уравнения прямой к нормальному виду (подробнее об этом читайте в статье “нормальное уравнение прямой”). Для приведения уравнения (8) к нормальному виду, нужно умножить данное уравнение на нормирующий множитель:
Так как в уравнении (8) третий коэффициент равен +1, то знак нормирующего множителя должен быть противоположным:
Умножив уравнение (8) на нормирующий множитель, получим:
Теперь найдем отклонение точки M(1,1) от прямой (8). Для этого вставим координаты точки M в левую часть уравнения(8):
Ответ. Отклонение точки M(1,1) от прямой (8) равно:
линейная алгебра – Создание средней плоскости из набора точек
спросил
Изменено 5 лет, 7 месяцев назад
Просмотрено 1к раз
$\begingroup$
Мне нужно создать плоскость в трехмерном пространстве из набора точек, где начало координат усреднено между этими точками в соответствии с известной нормалью этой плоскости.
Хорошо, я не знаю, смогу ли я выразить себя достаточно хорошо, поэтому я сначала попытаюсь объяснить это в двухмерном пространстве.
Предположим, у нас есть набор точек и мы хотим усреднить их положение по одной из осей (скажем, по оси Y):
5| x x <-- Точки для усреднения 4| Икс 3| 2| Икс 1| х х ------------------------------
А вот как это будет выглядеть после усреднения
5| <-- Точки для усреднения 4| 3| хх х хх х 2| 1| ------------------------------
Тогда "плоскость" может быть описана любой точкой с координатой y=3 и нормалью к оси x, верно? Хорошо, теперь я не хочу делать то же самое в трехмерном пространстве. Нормаль результирующей плоскости всегда задана, как и точки. Но как мне рассчитать этот средний самолет? Я попытался найти решение в Интернете (возможно, я искал не то), однако я не смог найти никакого решения для этого.
- линейная алгебра
$\endgroup$
7 9N \mathbf{r}_i$, то плоскость определяется математически как $$ \mathbf{n} \cdot \left( \mathbf{r}-\mathbf{r}_A \right) =0 $$
, где $ \mathbf{r}=(x,y,z)$ описывает любых местоположений в точке, а $\cdot$ является внутренним векторным произведением.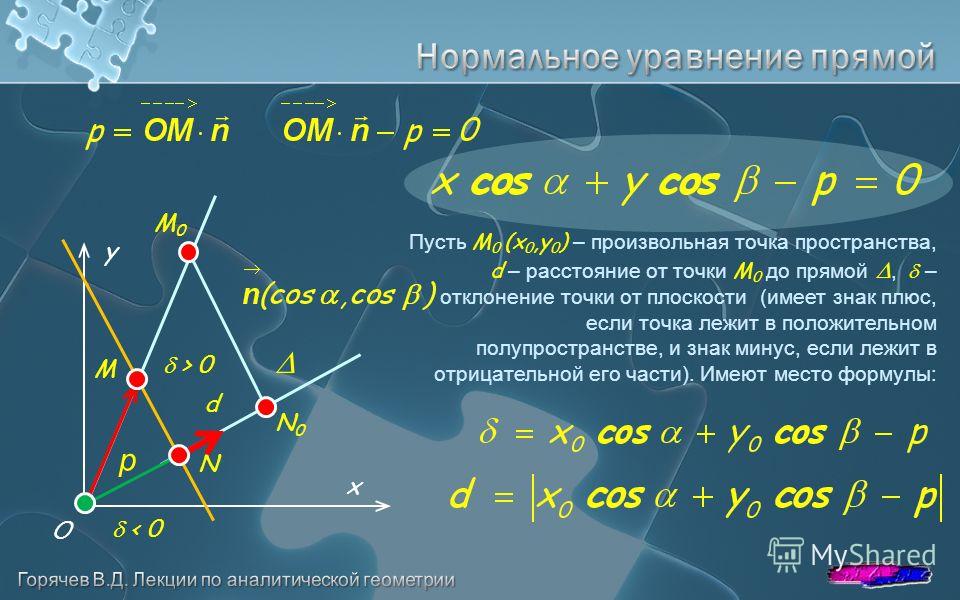
Теперь, чтобы спроецировать ваши существующие точки $\mathbf{r}_i$ на плоскость, вычтите их расстояние до плоскости по нормали $\mathbf{n}$. Расстояние равно $$d_i =\mathbf{n} \cdot \left( \mathbf{r}_i - \mathbf{r}_A \right)$$ 9{\rm плоскость} & = \mathbf{r}_i - d_i\, \mathbf{n} \\ & = \mathbf{r}_i - \left(\mathbf{n} \cdot \left( \mathbf{r}_i - \mathbf{r}_A \right) \right) \mathbf{n} \end{align}$$
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 92$, пусть $d = d(p, q)$ (где это гиперболическое расстояние) и обозначим через $c$ геодезическую с единичной скоростью от $p$ до $q$.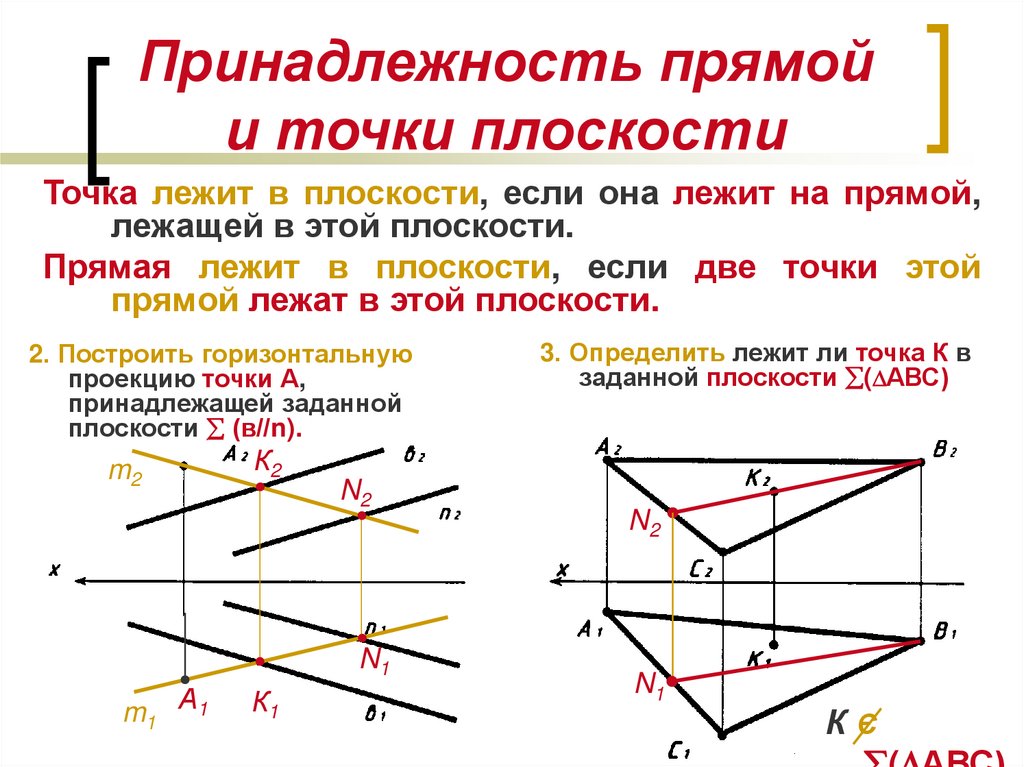
Пусть $\gamma_1$ — геодезическая с единичной скоростью, начинающаяся в $p$, и пусть $\gamma_2$ — геодезическая с единичной скоростью, начинающаяся в $q$, и предположим, что:
- $\gamma_1$ перпендикулярно $c $ в $p$.
- $\gamma_2$ перпендикулярно $c$ в точке $q$.
- $\gamma_1(t)$ и $\gamma_2(t)$ находятся на "одной стороне" геодезической $c$ при $t > 0$.
Как при $t > 0$ вычислить $$d(\gamma_1(t), \gamma_2(t))$$ через $d$? Мне сказали, что $$d(\gamma_1(t), \gamma_2(t)) = d \cosh(t),$$ и что это можно доказать с помощью полей Якоби, но я понятия не имею, как начать доказывая этот вопрос. Я знаю, что длина поля Якоби может измерять это «геодезическое отклонение» для двух геодезических, начинающихся в одной и той же точке, но здесь геодезические начинаются в разных точках. 93$ с угловой метрикой (исходя из ограниченной евклидовой метрики)? Под «похожими» я подразумеваю $$d(\gamma_1(t), \gamma_2(t)) = d \cos(t), $$ для небольших положительных $t$?
- риманова геометрия
- гиперболическая геометрия
- сферическая геометрия
$\endgroup$
0
$\begingroup$
Точки $p, q, \gamma_1(t), \gamma_2(t)$ охватывают четырехугольник Саккери 92(т)
$$
или
$$
\sinh(s/2)= \cosh(t) \sinh(d/2).