Отклонение точки от плоскости: 4.2.7. Отклонение и расстояние от точки до плоскости

Расстояние и отклонение точки от плоскости

Пусть – плоскость, заданная уравнениеми– произвольная точка пространства. Тогдарасстояние от точкидо плоскостивыражается формулой

(10)

В знаменателе этой дроби стоит длина вектора – нормального вектора плоскостиТаким образом,чтобы найти расстояние от точки до плоскости, надо подставить координаты точки в уравнение плоскости и разделить полученное число на длину нормального вектора; при этом мы получим число, которое может быть отрицательным – в этом случае берём его по абсолютной величине.

Если в формуле (10) убрать знак модуля, то мы получим величину

(11)

называемую отклонением точки от плоскости

Очевидно, и

Замечание. Определённое по формуле (11) отклонение отличается от того отклонения, которое принято в ряде учебников (а именно,еслииесли).

Мы будем пользоваться формулой (11).

Геометрический смысл отклоненияточки от плоскости точно такой же, как у отклонения точки от прямой на плоскости (см. раздел “Прямая на плоскости”). А именно,отклонение по абсолютной величине равно расстоянию, причём если точканаходится от плоскостипо ту сторону, в которую направлен нормальный векториесли она находится по другую сторону(см. рис. 11).

Рис.11.

Разберём задачи на расстояния и отклонения.

Задача 16. Найти расстояние между плоскостямии

Решение.Плоскости параллельны, так как их нормальные векторыиколлинеарны:Поэтому расстояние между этими плоскостями равно расстоянию от какой-нибудь точки первой плоскости до второй плоскости. Возьмём точку первой плоскости:Тогда

Задача 17.В прямоугольном параллелепипедеНайти расстояние от вершиныдо плоскости

Решение. Введём систему координат с началомкак показано на рисунке 12.

Рис.12.

Используя формулу (4), мы можем записать уравнение плоскости “в отрезках”:

(12)

Нам требуется найти расстояние от точки до плоскости, заданной уравнением (12). Перенесём единицу в левую часть равенства:Применим формулу (10):

Задача 19. Определить, лежит ли точка между плоскостямии

Решение.Обозначим эти плоскости черезиТак как плоскости имеют один и тот же нормальный вектор и не совпадают (это видно из уравнений плоскостей), то плоскости параллельны. Вычислим по формуле (11) отклонения:

Так как отклонения одного знака, то точка не лежитмежду плоскостями (см. рис. 13).

Рис.13.

Задача 20. Даны плоскостии точкиОпределить, точкиилежат внутри одного, смежных или вертикальных углов, образованных плоскостямии

Решение.Вычисляем отклонения:

–

значит, илежат по одну сторону от плоскости

–

значит, илежат по разные стороны от плоскостиОтсюда следует, чтоилежат внутрисмежныхдвугранных углов.

Пусть – прямая с направляющим вектороми– точка прямой(см. рис. 14).Расстояние от точки до прямойвыражается формулой

(13)

Рис.14.

Пусть – скрещивающиеся прямые,– их направляющие векторы и– какие-либо точки, лежащие на прямыхсоответственно (см. рис. 15).Расстояние между скрещивающимися прямыми можно вычислить по формуле

(14)

Рис.15.

Замечание.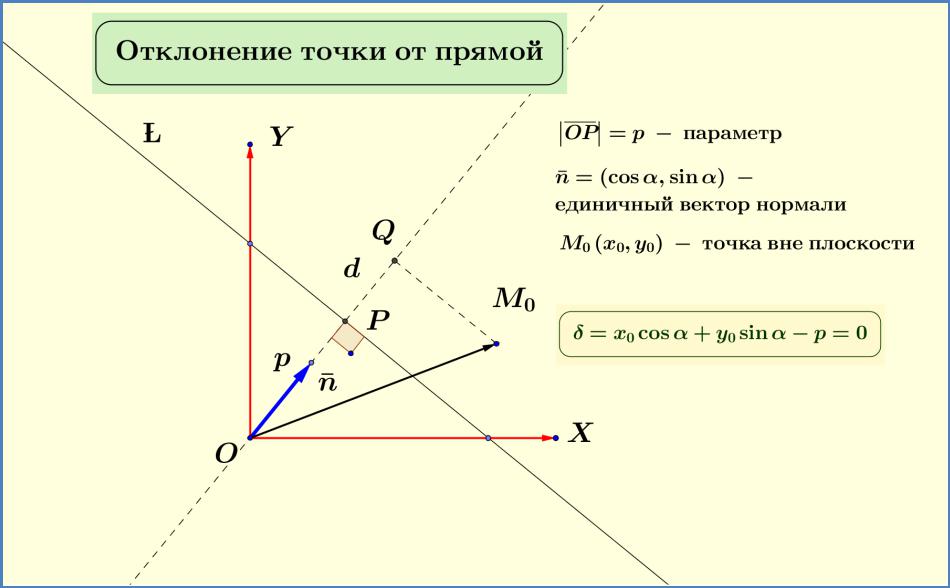 Если прямыепересекаются (но не совпадают), то формула (14) к ним также применима и она показывает, что расстояние между прямыми равно 0.По формуле(14)нельзя вычислять расстояния между параллельными прямыми.

Задача 21. Найти расстояние от точкидо прямой

Решение.Из уравнения прямой найдём её направляющий вектор и точку:иОтсюдаПо формуле (13) получим:

Задача 22.Найти расстояние между прямымии

Решение. Обозначим данные прямыеиПрямые параллельны, они имеют один и тот же направляющий векторпоэтому формулу (14) применять нельзя. Применим формулу (13), т.е. найдём расстояние от точки одной прямой до другой прямой. Имеем:Отсюдапо формуле (13) получаем:

Задача 23. Найти расстояние между прямымии

Решение.Обозначим данные прямыеиНаправляющий вектор прямойравенПрямаяпараллельна осипоэтому за направляющий вектор этой прямой можно взять векторТак както можно применять формулу (14).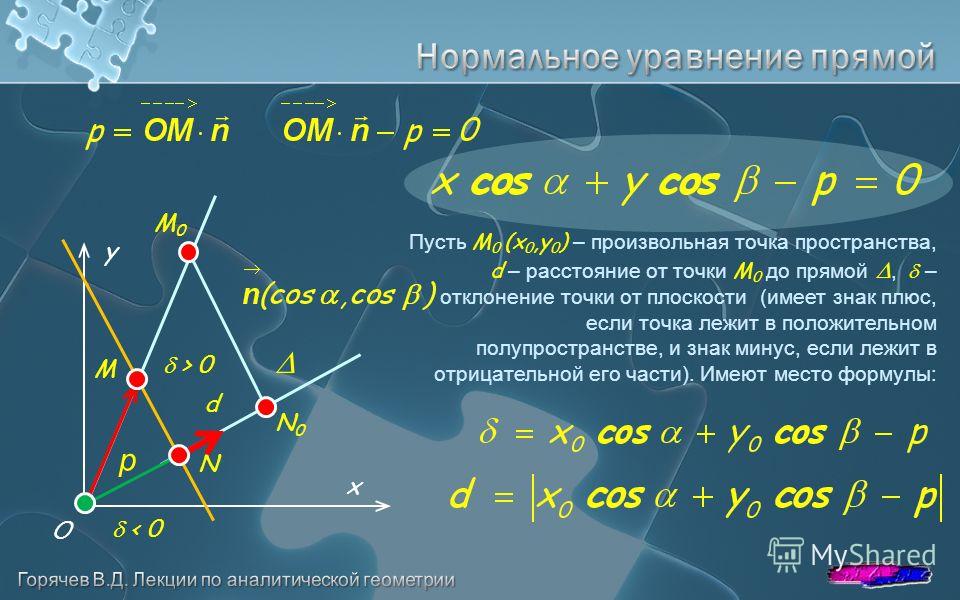 В качестве точекэтих прямых возьмёмиПо формуле (14) получаем:

Задача 24.Ребро куба равноНайти расстояние между скрещивающимися диагоналями двух смежных граней куба.

Решение(см. рис. 16).

Рис.16.

Будем временно считать, что ребро куба равно 1, затем полученную величину умножим на Вычислим расстояние между прямымии(другие диагонали дадут такой же результат). Введём систему координат, как показано на рисунке. Имеем:Направляющие векторыпрямых равны:По формуле (14) получаем:

Следовательно,

Задача 25.Выяснить взаимное расположение плоскостейи

Решение. Нормальные векторы этих плоскостей равны:Вычислим их смешанное произведение:Таким образом, векторыкомпланарны. Так как никакие два из этих векторов не коллинеарны, то возможны следующие варианты взаимного расположения плоскостей (см. рис. 17): (а) плоскости попарно пересекаются по трём параллельным прямым, (б) плоскости проходят через одну прямую.

Рис. 17

Чтобы различить эти две ситуации, решим систему уравнений

Из первого уравнения Подставим во второе:откудаа значит,Подставим в третье уравнение:т.е.что невозможно. Таким образом, система решений не имеет, т.е. плоскости не имеют общей точки, а значит, имеет место случай (а).

Задача 26.Составить уравнение геометрического места точек, равноудалённых от прямыхи

Решение.Обозначим данные прямые черезиПрямые имеют один и тот же направляющий векторзначит, они параллельны или совпадают. Возьмём по одной точке этих прямых:Так кактои– различные параллельные прямые. Проведём плоскостьчерез прямыеив этой плоскости проведём прямуюпосередине междуиа затем через прямуюпроведём плоскостьперпендикулярную плоскости(см.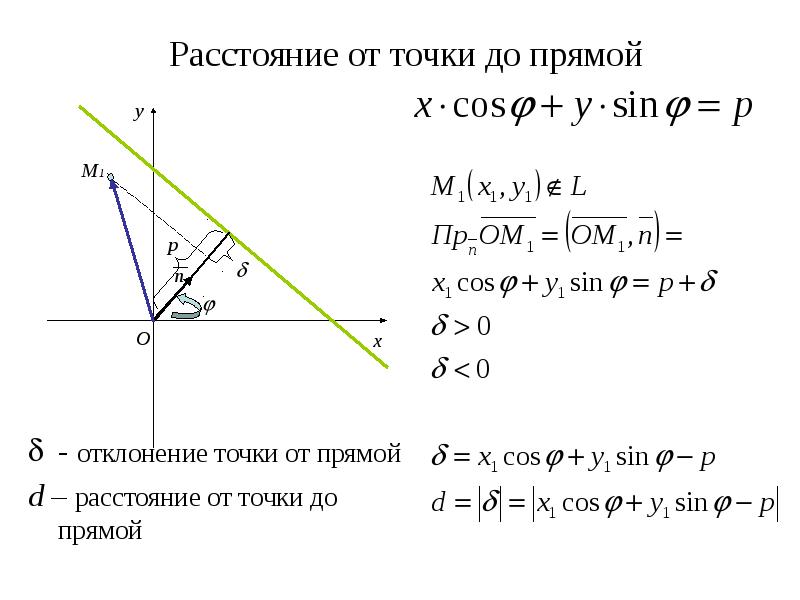 рис. 18).

Рис. 18

Очевидно, плоскость – это и есть искомое геометрическое место точек, равноудалённых от прямыхиНормальным вектором плоскостиможет служить вектор

Нормальный вектор плоскостиперпендикулярен векторамипоэтому можно взять

В качестве точки плоскости можно взять точку– середину отрезкаИмеем:Подставив в формулу (4), получим:или

28

9.8. Отклонение точки от плоскости

Введем понятие отклонения точки от плоскости .

Пусть – расстояние от точки до плоскости (длина перпендикуляра, опущенного из точки на плоскость ).

Определение 9.2. Отклонением точки от плоскости назовем число + , когда точка и начало координат лежат по разные стороны от плоскости , и число − в случае, когда точка и начало координат лежат по одну сторону плоскости .

Теорема 9.1. Отклонение точки 0( 0, 0, 0) от плоскости, задаваемой нормированным уравнением (9.

11) определяется выражением

	= 0 + 0 + 0 − .		(9.12)

25 из 30

Рис. 9.5. Отклонение точки от плоскости

26 из 30

Доказательство. Спроектируем точку на направление нормали OP. Выполняется

= PQ = OQ − OP = OQ − p.

Заметим, что OQ = пр ̅ 0 = 0 + 0 + 0 .

Сопоставляю полученные выражения получаем искомое утверждение теоремы.

Замечание. Для нахождение отклонения точки от плоскости достаточно в левую часть нормированного уравнения плоскости подставить координаты точки.

27 из 30

Определение 9.3. Совокупность всех плоскостей, проходящих через одну и ту же прямую , называют пучком плоскостей (с центром на ).

Если 1 + 1 + 1 + 1 = 0 и 2 + 2 + 2 + 2 = 0

суть уравнения двух различных и непараллельных плоскостей, пересечением которых служит некоторая прямая L, и произвольные числа, не обращающиеся одновременно в ноль, то

( 1 + 1 + 1	+ 1) + ( 2 + 2 + 2	+ 2)	(9. 13)
= 0

есть уравнение плоскости, проходящей через прямую L.

28 из 30

Справедливо и противоположное утверждение. Произвольная плоскость, проходящая через прямую L определяется уравнением (9.13) при некоторых и .

Определение 9.4. Совокупность всех плоскостей, проходящих через дону и ту же точку 0( 0, 0, 0), называют связкой плоскостей (с центром в 0).

Нетрудно убедится, что уравнение

	( − 0) + ( − 0) + ( − 0) = 0.		(9.14)

Определяет некоторую плоскость, проходящую через точку M0,

в направлении, задаваемом нормальным вектором = (A, B, C). Поэтому, с одной стороны, уравнение (9.14) при заданном

векторе нормали – уравнение плоскости, проходящей через заданную точку M0 в заданном направлении.

29 из 30

А, с другой стороны, – уравнение (9.14) – связка плоскостей с центром в точке M0, при произвольных векторах нормали.

30 из 30

Расстояние от точки до плоскости

Вот краткий набросок того, как рассчитать расстояние от точки $P=(x_1,y_1,z_1)$ в плоскость, определяемую вектором нормали $\vc{N}=(A,B,C)$ и точка $Q=(x_0,y_0,z_0)$. Уравнение для плоскость, определяемая $\vc{N}$, и $Q$ есть $A(x-x_0)+B(y-y_0) +C(z-z_0) = 0$, что можно записать как $Ax+By+Cz+D=0$, где $D=-Ax_0-By_0-Cz_0$.

Этот апплет демонстрирует настройку задачи и метод, который мы будем использовать для вывода формулы расстояния от плоскости до точка $P$.

Загрузка апплета

Расстояние от точки до плоскости. Эскиз способа расчета расстояния от точки $\color{red}{P}$ (выделена красным) до плоскости.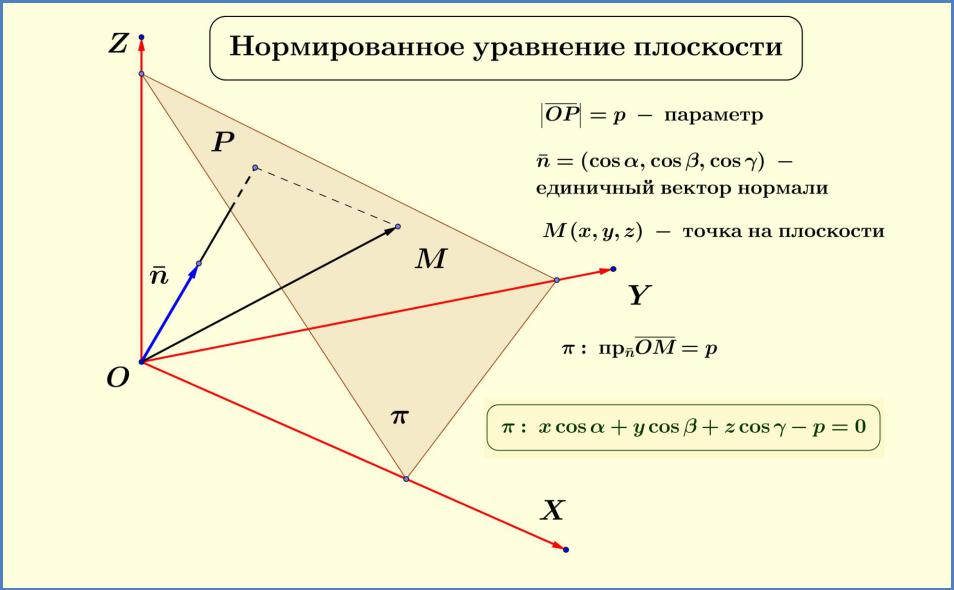 Вектор $\color{green}{\vc{n}}$ (выделен зеленым цветом) является единичным вектором нормали к плоскости. Вы можете перетаскивать точку $\color{red}{P}$, а также вторую точку $\vc{Q}$ (желтого цвета), которая ограничена плоскостью. Хотя вектор $\color{green}{\vc{n}}$ не меняется (поскольку плоскость фиксирована), он перемещается вместе с $\color{red}{P}$, чтобы всегда находиться в конце серого цвета. отрезок прямой из $\color{red}{P}$, перпендикулярный плоскости. Это расстояние от $\color{red}{P}$ до плоскости равно длине этого сегмента серой линии. Это расстояние является длиной проекции вектора из $Q$ в $P$ (фиолетового цвета) на вектор нормали $\color{green}{\vc{n}}$.

Дополнительная информация об апплете.

Кратчайшее расстояние от точки до плоскости проходит по прямой перпендикулярно плоскости. Следовательно, расстояние от точки $P$ до плоскости лежит по прямой параллельно вектору нормали, который показан серым отрезком. Если мы обозначим через $R$ точку, в которой отрезок серой линии касается плоскости, то $R$ — ближайшая к $P$ точка плоскости. 2}}. \конец{выравнивание*} Это расстояние отображается на голубом ползунке, помеченном справа $d$. фигуры. 92}}. \конец{выравнивание*} Из этой окончательной формулы видно, что расстояние не зависит в точке $Q=(x_0,y_0,z_0)$. Пока $Q$ в самолете $Ax+By+Cz+D=0$, то мы знаем, что $D=-Ax_0-By_0-Cz_0$. Две приведенные выше формулы для $d$ эквивалентны независимо от того, где находится $Q$ в плоскости. Из рисунка видно, что расстояние $d$ не должно меняться при перемещайте $Q$ по плоскости. Вектор $\vc{v}$ меняется, но его проекция на $\vc{n}$ постоянна.

Вы можете увидеть пример использования этой формулы для расчета расстояния от точки до плоскости.

линейная алгебра – Плоскость наилучшего соответствия заданному набору точек

Все остальные ответы потрясающие. Я предоставляю другой способ сделать это. Вы можете использовать РАНСАК. Этот метод может быть не более эффективным, чем другие методы.

Простая теория, лежащая в основе этого метода, состоит в том, чтобы выбрать случайные образцы из входного образца и создать математическую модель, которая лучше описывает вашу проблему.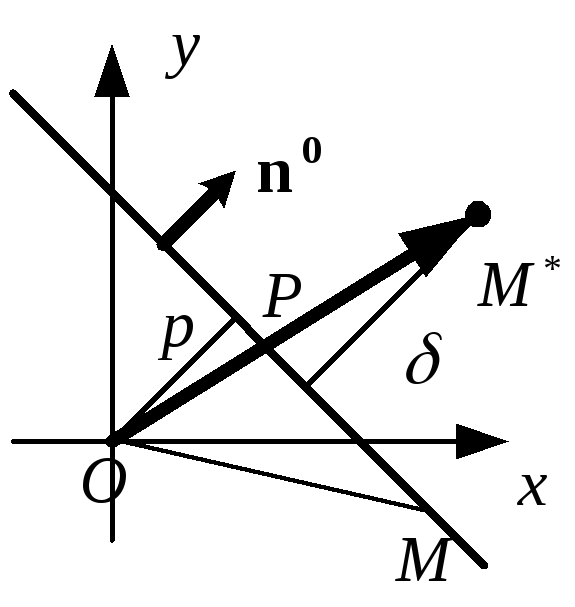 После этого найдите ошибку этой математической модели по отношению ко всем выборкам и подсчитайте количество выборок, ошибка которых находится в пределах заданного порога (эти выборки называются инлиерами). Выполните эту процедуру для нескольких итераций и верните модель с большим количеством вставок. 92}}$$ Эти уравнения взяты из ответа Клода.

Если это значение меньше заданного порога, вы можете засчитать эту точку как дополнительную. Повторите этот процесс для определенного количества итераций. Следующая программа на Python реализует этот метод.

 импортировать numpy как np
импортировать matplotlib.pyplot как plt
деф ЭОП(p1,p2,p3):
 """для заданных трех точек, находит уравнение плоскости"""
 v1 = p3 - p1
 v2 = р2 - р1
 ср = нп.кросс(v1, v2)
 А, В, С = ср
 D = np.dot (cp, p3)
 возврат А, В, С, D
def RANSAC (X, itr = 5000, порог = 500):
 """
 Входы:
 X- координаты выборки 
 itr - количество итераций
 порог - порог ошибки 
 выход:
 Три координаты самолета, если RANSAC нашел наилучшее соответствие
 """
 N = X. shape[0] #размер smaple
 п=0
 для i в диапазоне (itr):
 idx = np.random.randint(N,size=(1,3))[0] # создание трех случайных индексов
 Xsample = X[idx] #собираем координаты с этими индексами
 p1,p2,p3 = Xsample# распаковка трех точек
 A,B,C,D = EoP(p1,p2,p3) #Уравнение плоскости
 # распечатать(А,Б,С,Г)
 вкладыши = 0
 #Теперь для каждой точки во входной выборке определите, является ли она вкраплением
 для р в X:
 xi, yi, zi = p
 d = np.abs((A*xi+B*yi+C*zi+D)/np.sqrt(xi**2+yi**2+zi**2))
 если d<порог:
 inliers+=1 # нахождение вставок, удовлетворяющих условию расстояния
 если вкладыши > n:
 Абест = А
 Bлучший = B
 Cлучший = C
 Dлучший = D
 если вкладыши > 0:
 возврат (Abest, Bbest, Cbest, Dbest)
 возврат Нет
если __name__ == "__main__":
 rdm = np.random.RandomState(10) # для повторения случайного состояния
 X = rdm.