Оси в Автокаде. Как создается осевая линия в Автокаде/AutoCAD
В Автокаде осевые линии строятся следующим образом:
1) Сначала с помощью команды «Отрезок» или «Полилиния» чертятся оси AutoCAD нужного размера.
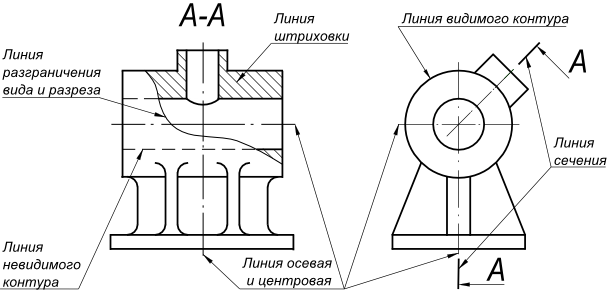
2) Далее нужно загрузить подходящий тип линии в чертеж. В соответствии с ГОСТ 2.303 – 68 «Основные линии чертежа», осевые и центровые линии, а также линии сечения, которые являются осями симметрии, изображаются штрихпунктирной тонкой линией (см. рис. 1).
Рис. 1. Осевая линии в Автокаде соответствует типу линии штрихпунктирная.
Чтобы загрузить данный тип линии, нужно воспользоваться «Диспетчером типов линий», который вызывается на вкладке «Главная» – панель «Свойства» (читать подробнее – как загрузить линии в Автокад).
3) Присвоить подходящий тип линии и при необходимости настроить его. Давайте более подробно рассмотрим данный шаг.
Выносим и настраиваем оси в Автокаде
Если вопрос, как начертить оси в Автокаде, не вызывает никаких трудностей, то с настройкой типа линий следует немного повозиться. Поэтому приступаем к практическому примеру (см. рис. 2).
Поэтому приступаем к практическому примеру (см. рис. 2).
Рис. 2. Осевые линии AutoCAD.
Для эффективной работы в Автокаде используются слои. Поэтому создадим слой «Осевые линии», назначим ему красный цвет и установим тип линии «ACAD_ISO10W100», как показано на рис. 3 (читать подробнее про работу со слоями в AutoCAD).
Рис. 3. Создание и настройка слоя для осевых линий AutoCAD.
Далее рассмотрим последовательность простановки осевых линий в AutoCAD. В соответствии с представленным примером, целесообразно сделать заготовку для кругового массива. Это нужно, чтобы правильно проставить осевые линии для каждого отверстия. Для этого сделаем один сегмент. Выполним команду построения дуги (Начало, Центр, Конец). Точки следует проставлять в последовательности, указанной на рис. 4.
Рис. 4. Создание сегмента для правильной простановки осевых линий.
Далее следует раскопировать этот элемент по кругу. Для этого нужно воспользоваться командой «Круговой массив» (читать подробнее про команду «Массив»). Результат представлен на рис. 5.
Результат представлен на рис. 5.
Рис. 5. Создание осевых линий с помощью команды «Круговой массив».
ПРИМЕЧАНИЕ: Если ваш результат некорректный и осевая линия выглядит сплошной, то всё дело в масштабе типа линии. Его нужно дополнительно настроить (см. видеоурок «Масштаб типов линий AutoCAD и СПДС»).
Как начертить линию в Автокаде (центровую)?
Для создания центровых линий окружностей служит команда «Маркер центра». Она расположена на вкладке «Аннотации» – панель «Размеры».
Выполняется команда просто:
- Достаточно указать окружность, центр которой необходимо отобразить на чертеже.
- Для настройки центровых линий нужно вызвать «Диспетчер размерных линий».
- На вкладке «Символы и стрелки» в группе «Маркеры центра» внести нужные изменения (см. рис. 6).
Более подробно про работу с размерными стилями читайте в статье «Как изменить размер в Автокаде».
Рис. 6. Команда AutoCAD «Маркер центра».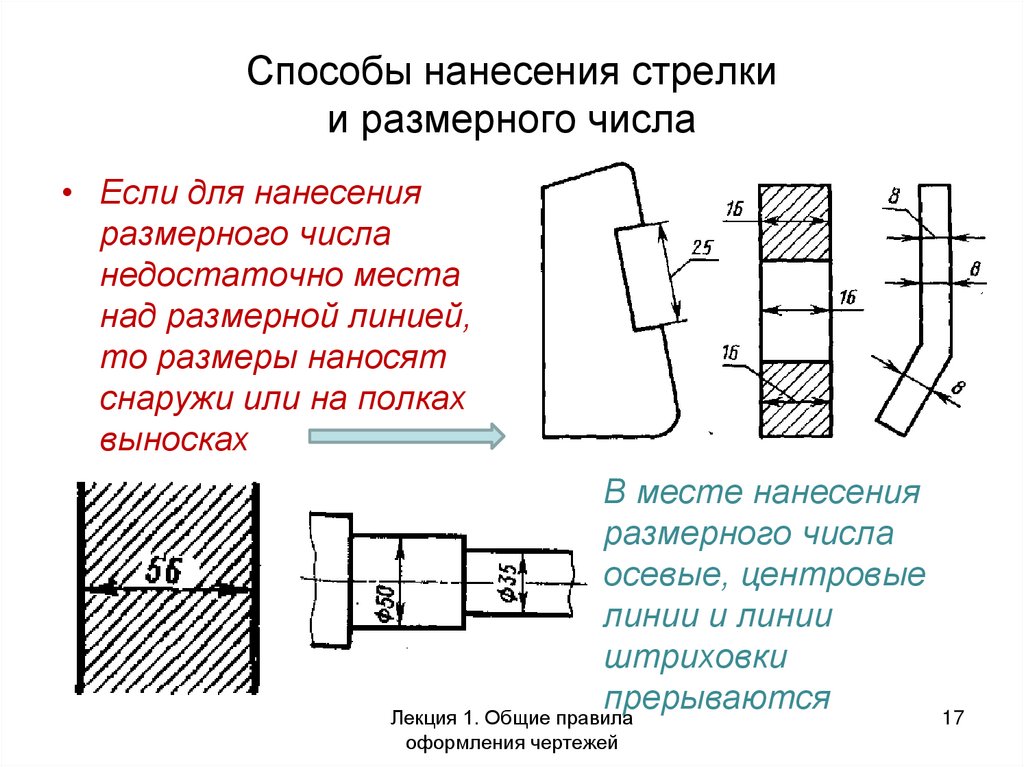
Мы разобрались, как в Автокаде создать линию, чтобы она соответствовала общепринятым правилам оформления чертежей. Научились их грамотно чертить и настраивать. Обязательно попробуйте сделать описанный пример на практике!
- Редактирование
мир инженерной графики : тест” Оформления чертежа”
Тема «Оформление чертежа»
Вариант 1
Задание: прочитай вопрос и выбери один вариант правильного ответа.
1. Какое обозначение по ГОСТу имеет формат размером 210×297 ?
А) А1;
Б)А2;
2. На каком месте чертежа располагается основная надпись?
А) в левом нижнем углу;
Б) в правом нижнем углу;
В) в левом верхнем углу.
3. На какую величину должны выступать за контур изображения осевые и центровые линии?
А) 3…5 мм;
Б)5…10 мм;
В)10…15 мм.
4. Какой знак или букву следует нанести перед размерным числом при указании диаметра окружности?
А) D;
Б) R;
5. Что обозначает знак R перед размерным числом?
А) длину окружности;
Б) диаметр полуокружности;
В) радиус окружности.
6. Каким типом линий на чертеже обводят видимый контур детали?
А) сплошной тонкой линией;
Б) сплошной основной толстой линией;
В)
разомкнутой линией.
7. Какой из вариантов соответствует масштабу увеличения?
А) М 1:2;
Б) М 1:1;
В) 2:1;
8. Где наносят размерные числа?
А) над размерной линией;
Б) под размерной линией;
В) в любом месте.
9. Каким типом линий выполняют на чертеже невидимый контур
детали?
А) сплошной тонкой линией;
Б) сплошной основной толстой линией;
В) штриховой линией.
10. В каких единицах указывают линейные размеры на чертежах?
А) в метрах;
Б) в дециметрах;
В) в миллиметрах;
Тема «Оформление чертежа»
Вариант 2
Задание: прочитай вопрос и выбери один вариант правильного ответа
1. На каком расстоянии от краев листа
проводят рамку чертежа?
На каком расстоянии от краев листа
проводят рамку чертежа?
А) слева, сверху, снизу, справа-
5 мм;
Б) слева, сверху, снизу – по
10 мм, справа-
25 мм;
В) слева-
20 мм, сверху, справа и снизу – по
5 мм.
2. Каким типом линий выполняются осевые и центровые линии на чертежах?
А) сплошной тонкой линией;
Б) штрихпунктирной линией;
В) штриховой линией.
3. Какой из вариантов соответствует масштабу уменьшения?
А) М 1: 2;
Б) М 1: 1;
В) М 2:1.
4. Какие размеры по ГОСТу имеет формат А4?
А) 297×210 мм ;
Б) 297×420мм;
В)594×841мм.
5. В зависимости от толщины какой линии выбираются толщины линий чертежа?
А) штрихпунктирной линии;
Б) сплошной тонкой линии;
В) сплошной основной толстой линии.
6. Каким типом линий выполняются размерные и выносные линии?
А) сплошной основной толстой линией;
Б) штриховой линией;
7. Какой из этих форматов имеет большие размеры?
А) А0;
Б) А3;
В)
А4.
8. Какой из вариантов соответствует натуральному масштабу?
А) М 1:2;
Б) М 1:1;
В) М 2:1.
9. Какой из этих форматов имеет меньшие размеры?
А) А1;
Б) А2;
В) А4.
10. Каким типом линий выполняют рамку чертежа?
А) штрихпунктирной линией;
Б) сплошной основной толстой линией;
В) штриховой линией.
Новый метод определения кажущегося осевого центра вращения поясничного и грудного отделов позвоночника
. 2011;48(5):587-96.
doi: 10. 1682/jrrd.2010.09.0168.
1682/jrrd.2010.09.0168.
Санджум П. Самаг 1 , Чарльз Д. Розен, Каримдад Отародифард, Мэтью Корнсвит, Гейб Палмер, Тай К. Ли
принадлежность
- 1 Лаборатория ортопедической биомеханики, Департамент по делам ветеранов Система здравоохранения Лонг-Бич, Лонг-Бич, Калифорния 90822, США.
- PMID: 21674408
- DOI: 10.1682/jrrd.2010.09.0168
Бесплатная статья
Санджум П. Самаг и соавт.
J Rehabil Res Dev.
2011.
Бесплатная статья
. 2011;48(5):587-96.
doi: 10.1682/jrrd.2010.09.0168.
Авторы
Санджум П. Самаг 1 , Чарльз Д. Розен, Каримдад Отародифард, Мэтью Корнсвит, Гейб Палмер, Тэй К. Ли
принадлежность
- 1 Лаборатория ортопедической биомеханики, Департамент по делам ветеранов Система здравоохранения Лонг-Бич, Лонг-Бич, Калифорния 90822, США.
- PMID: 21674408
- DOI: 10.1682/jrrd.2010.09.0168
Абстрактный
Одним из основных вопросов кинематики позвоночника является определение кажущегося осевого центра вращения позвоночника. Предыдущие исследования по этой теме дали противоречивые результаты. Целью данного исследования было определение кажущегося осевого центра вращения для семи поясничных и шести грудных сегментов позвоночника путем разработки и проверки нового метода. Специальное устройство с шестью степенями свободы, обеспечивающее полный диапазон движения, использовалось с программным обеспечением для записи и анализа движения. Эта система отслеживала сетку маркеров на образце при приложении крутящего момента как по часовой стрелке, так и против часовой стрелки при 3,53 Нм, 7,05 Нм, 10,58 Нм и 14,10 Нм. Область, охватывающая кажущийся осевой центр вращения, определялась путем определения пяти маркеров с наименьшим количеством движения. Угловое смещение маркера рассчитывалось как угол между виртуальной линией, проведенной между двумя точками в условиях начального и конечного крутящего момента. Вращение в обе стороны усреднялось. Поясничный и грудной отделы позвоночника имели в среднем кажущийся осевой центр вращения на заднем крае концевых пластинок позвонков и переднем крае позвоночного канала со средними коэффициентами углового смещения по часовой стрелке и против часовой стрелки 0,87 и 0,9.
Предыдущие исследования по этой теме дали противоречивые результаты. Целью данного исследования было определение кажущегося осевого центра вращения для семи поясничных и шести грудных сегментов позвоночника путем разработки и проверки нового метода. Специальное устройство с шестью степенями свободы, обеспечивающее полный диапазон движения, использовалось с программным обеспечением для записи и анализа движения. Эта система отслеживала сетку маркеров на образце при приложении крутящего момента как по часовой стрелке, так и против часовой стрелки при 3,53 Нм, 7,05 Нм, 10,58 Нм и 14,10 Нм. Область, охватывающая кажущийся осевой центр вращения, определялась путем определения пяти маркеров с наименьшим количеством движения. Угловое смещение маркера рассчитывалось как угол между виртуальной линией, проведенной между двумя точками в условиях начального и конечного крутящего момента. Вращение в обе стороны усреднялось. Поясничный и грудной отделы позвоночника имели в среднем кажущийся осевой центр вращения на заднем крае концевых пластинок позвонков и переднем крае позвоночного канала со средними коэффициентами углового смещения по часовой стрелке и против часовой стрелки 0,87 и 0,9.
Похожие статьи
Влияние ползучести и восстановления на биомеханические характеристики in vitro многоуровневых грудопоясничных сегментов позвоночника человека.
Бушер И., ван Дин Дж. Х., ван дер Вин А. Дж., Кингма И., Мейер Г. Дж., Веркерке Г. Дж., Вельдхуизен АГ. Бушер I и др. Clin Biomech (Бристоль, Эйвон). 2011 июнь; 26 (5): 438-44. doi: 10.1016/j.clinbiomech.2010.12.012. Epub 2011 19 января. Clin Biomech (Бристоль, Эйвон). 2011. PMID: 21251737
Миграция мгновенной оси движения при аксиальной ротации в поясничных сегментах и роль дугоотростчатых суставов.
Вачовски М.М., Хавеллек Т., Хуберт Дж., Леманн А., Мансур М., Дюмон С., Дорнер Дж., Рааб Б.В., Кубейн-Мейзенбург Д., Нэгерл Х.
 Вачовски М.М. и соавт.
Акта Биоэнг Биомех. 2010;12(4):39-47.
Акта Биоэнг Биомех. 2010.
PMID: 21361255
Вачовски М.М. и соавт.
Акта Биоэнг Биомех. 2010;12(4):39-47.
Акта Биоэнг Биомех. 2010.
PMID: 21361255Парные движения в грудном и поясничном отделах позвоночника человека и свиньи.
Кингма И., Бушер И., ван дер Вин А.Дж., Веркерке Г.Дж., Вельдхуизен А.Г., Хомминга Дж., ван Дин Дж.Х. Кингма I и др. Дж. Биомех. 2018 21 марта; 70:51-58. doi: 10.1016/j.jbiomech.2017.11.034. Epub 2017 6 декабря. Дж. Биомех. 2018. PMID: 29246473
Биомеханический анализ ротационных движений после эндопротезирования диска: последствия для пациентов с деформациями у взрослых.
McAfee PC, Cunningham BW, Hayes V, Sidiqi F, Dabbah M, Sefter JC, Hu N, Beatson H. McAfee PC и др. Позвоночник (Фила Па, 1976). 1 сентября 2006 г .
 ; 31 (19 Дополнение): S152-60. doi: 10.1097/01.brs.0000234782.89031.03.
Позвоночник (Фила Па, 1976). 2006.
PMID: 16946633
; 31 (19 Дополнение): S152-60. doi: 10.1097/01.brs.0000234782.89031.03.
Позвоночник (Фила Па, 1976). 2006.
PMID: 16946633Кинематическая оценка одно- и двухуровневой тотальной замены диска поясничного отдела Maverick каудальнее длинного грудопоясничного спондилодеза.
Zhu Q, Itshayek E, Jones CF, Schwab T, Larson CR, Lenke LG, Cripton PA. Чжу Кью и др. Eur Spine J. 2012 Jun;21 Suppl 5(Suppl 5):S599-611. doi: 10.1007/s00586-012-2301-4. Epub 2012, 25 апреля. Европейский позвоночник Дж. 2012. PMID: 22531900 Бесплатная статья ЧВК.
Посмотреть все похожие статьи
Цитируется
AutoBend: автоматизированный подход к оценке функции межпозвонкового сустава на основе цифровых моделей, состоящих только из костей.

Джонс К.Е., Броклхерст Р.Дж., Пирс С.Е. Джонс К.Е. и др. Интегр Орг Биол. 2021 13 окт;3(1):obab026. doi: 10.1093/iob/obab026. Электронная коллекция 2021. Интегр Орг Биол. 2021. PMID: 34661062 Бесплатная статья ЧВК.
Морфофункциональные изменения в позвоночнике при повышении водной адаптации у крокодиломорфов.
Молнар Дж.Л., Пирс С.Е., Бхуллар Б.А., Тернер А.Х., Хатчинсон Дж.Р. Молнар Дж.Л. и соавт. R Soc Open Sci. 2015 ноябрь 4;2(11):150439. doi: 10.1098/rsos.150439. Электронная коллекция 2015 ноябрь. R Soc Open Sci. 2015. PMID: 26716001 Бесплатная статья ЧВК.
Типы публикаций
термины MeSH
Осевая и центральная симметрия
Осевая симметрия является преобразованием, поэтому каждая точка $$P$$ на плоскости отображает другую точку $$P’$$ также на плоскости, так что ось $$e$$ будет серединным перпендикуляром к отрезку $$PP’$$. Осевые симметрии являются обратными изометриями, потому что они сохраняют расстояния между его точками и его гомологичными точками, но его ориентация обратна. Осевая симметрия возникает не только между предметом и его отражением, поскольку многие фигуры, которые могут разбиваться на две части посредством линии, симметричны относительно линии. Эти объекты имеют одну (или несколько) осей симметрии.
Осевые симметрии являются обратными изометриями, потому что они сохраняют расстояния между его точками и его гомологичными точками, но его ориентация обратна. Осевая симметрия возникает не только между предметом и его отражением, поскольку многие фигуры, которые могут разбиваться на две части посредством линии, симметричны относительно линии. Эти объекты имеют одну (или несколько) осей симметрии.
Осевая симметрия возникает, когда точки одной фигуры совпадают с точками другой фигуры, принимая за точку отсчета линию, известную под названием оси симметрии. В осевой симметрии мы находим то же явление, что и в изображении, отраженном в зеркале.
Мы называем точки, принадлежащие симметричной фигуре, гомологичными точками, то есть $$A’$$ гомологична $$A$$, $$B’$$ гомологична $$B$$, и $$C’$$ гомологичен $$C$$. Кроме того, существующие расстояния между точками исходной фигуры равны расстояниям между точками симметричной фигуры. В этом случае: Осевая симметрия также может иметь место в объекте относительно одной или нескольких осей симметрии.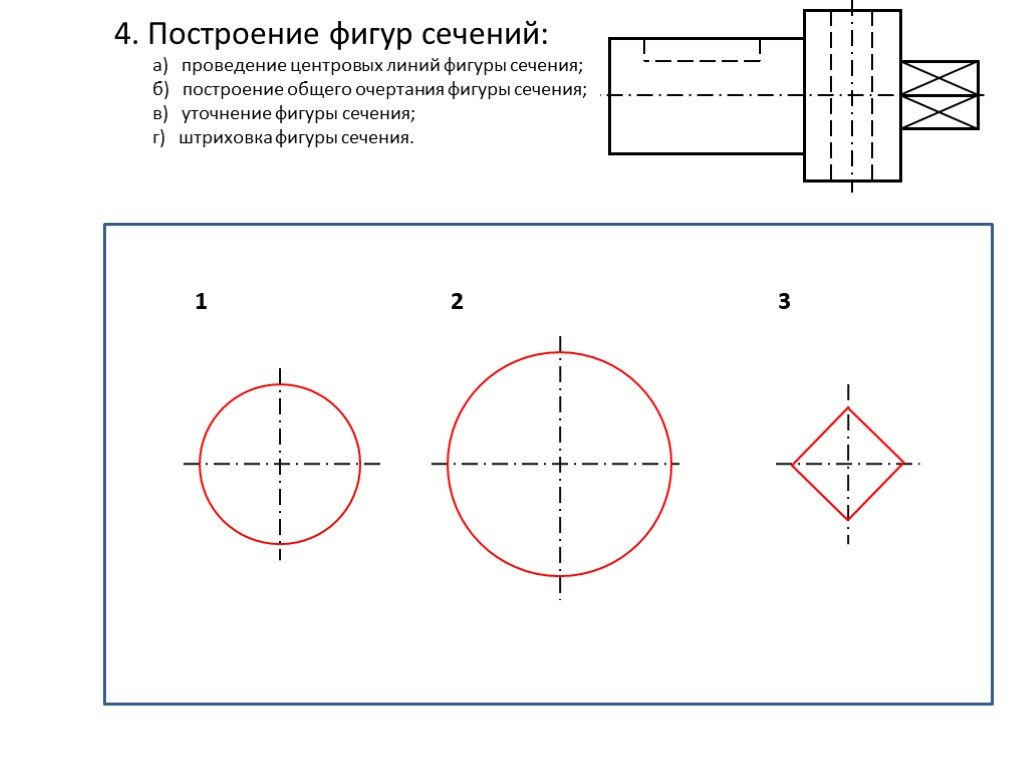
Если мы изогнем фигуру по оси симметрии, мы можем ясно заметить, что точки противоположных частей совпадают, то есть обе части соответствуют.
Далее мы изучим выражение осевых симметрий в координатах.
Пусть $$P ‘= (x, y)$$ и $$P ‘= (x’, y ‘)$$ – две точки плоскости, выразим ее в координатах в соответствии с положением ее оси:
Ось симметрии является осью координат Y:
В этом случае алгебраическое представление преобразования можно выполнить с помощью следующей системы:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 и 1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} $$$
Далее мы собираемся вычислить симметрию точки $$P$$ с помощью симметрии, осью которой является их координатная ось. Пусть $$P = (2,2)$$ — точка плоскости, тогда ее симметрия вычисляется с помощью следующей системы уравнений:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} =
\begin{pmatrix} -1 и 0 \\ 0 и 1 \end{pmatrix} \cdot
\begin{pmatrix} 2 \\ 2 \end{pmatrix}
\Стрелка вправо \влево\{ \begin{array}{l} x’=-2 \\ y’=2 \end{массив}
\правильно. $$$
$$$
Следовательно, симметричной точкой относительно оси координат y является точка $$P’=(-2,2)$$.
Ось симметрии является осью координат x:
В этом случае алгебраическое представление преобразования может быть выполнено с помощью следующей системы: $$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} 1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} $$$
Продолжаем предыдущий пример, вспомним, что у нас была точка P с координатами $$(2,2)$$ и в предыдущем примере мы вычислили ее симметричную относительно оси координат $$y$$. Теперь мы вычислим ее симметричную относительно оси координат $$x$$ и назовем эту новую точку $$P”$$. Вычислим ее координаты с помощью следующей системы уравнений:
$ $$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} =
\begin{pmatrix} 1 и 0 \\ 0 & -1 \end{pmatrix} \cdot
\begin{pmatrix} 2 \\ 2 \end{pmatrix}
\Rightarrow \left\{ \begin{array}{l} x’=2 \\ y’=-2 \end{array}
\правильно. $$$
$$$
Следовательно, симметричной точкой относительно оси координат x является точка $$P”=(2,-2)$$.
Чтобы закончить осевые симметрии, мы собираемся изучить, что происходит с композицией осевых симметрий:
Композицией двух симметрий с параллельными осями $$e$$ и $$e’$$ является трансляция, вектор которой имеет длину, удвоенную расстояние между осями, направление перпендикулярно осям и его смысл тот это идет от $$e$$ до $$e’$$.
- Композиция двух симметрий с перпендикулярными осями $$e$$ и $$e’$$ является центральной симметрией относительно точки пересечения двух осей симметрии.
Возьмем снова точку $$P = (2,2)$$ и применим к ней симметрию относительно оси координат y, а затем симметрию относительно оси координат $$x$$. В последнем примере симметричной точкой для оси координат $$y$$ была точка $$P’ = (-2,2)$$. Тогда для вычисления симметрии относительно оси координат $$x$$ решаем следующую систему уравнений:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} =
\begin{pmatrix} 1 и 0 \\ 0 & -1 \end{pmatrix} \cdot
\begin{pmatrix} -2 \\ 2 \end{pmatrix}
\Rightarrow \left\{ \begin{array}{l} x’=-2 \\ y’=-2 \end{array}
\правильно. \circ$$.
\circ$$.
Точка является центром симметрии фигуры, если она определяет центральную симметрию.
Далее мы увидим выражение в координатах центральной симметрии, изменяющей центр симметрии.
Координаты с помощью центральной симметрии $$O=(0,0)$$:
На следующем изображении мы видим, как ведет себя центральная симметрия, являющаяся центром начала координат точки:
Далее треугольник и его гомолог видны с помощью симметрии:
В обоих случаях преобразование связано со следующей системой: $$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} $$$
Зная отрезок $$AB$$, образованный точками $$A = (1,0)$$ и $$B = (2,3)$$, вычислим его симметрию относительно центра координат . Для этого вычислим симметрию точек $$A$$ и $$B$$. Точно, симметрия $$A$$ равна $$A’$$:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} =
\begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot
\begin{pmatrix} 1 \\ 0 \end{pmatrix}
\стрелка вправо \влево\{ \begin{array}{l} x’=-1 \\ y’=0 \end{массив}
\правильно. $$$
$$$
Следовательно, $$A ‘= (-1,0)$$ . Симметрия точки $$B$$ равна $$B’$$:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} \стрелка вправо \влево\{ \begin{array}{l} x’=-2 \\ y’=-3 \end{массив} \правильно. $$$
Следовательно, симметрией отрезка $$AB$$ является отрезок $$A’B’$$, проходящий через точки $$A’ = (-1,0)$$ и $$B ‘= ( -2, -3)$$.
Координаты с помощью центральной симметрии $$O=(a, b)$$:
Точка $$P’$$, гомологичная точке $$P=(x, y)$$ посредством центральной симметрии центра $$O=(a, b)$$:
А фигура, гомологичная треугольнику, имеет такой вид:
Следовательно, связанная с ним система: $$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} + \begin{pmatrix} 2a \\ 2b \end{pmatrix} $$$
, где мы помним, что значения $$(a, b)$$ являются координатами центра симметрии.


 Вачовски М.М. и соавт.
Акта Биоэнг Биомех. 2010;12(4):39-47.
Акта Биоэнг Биомех. 2010.
PMID: 21361255
Вачовски М.М. и соавт.
Акта Биоэнг Биомех. 2010;12(4):39-47.
Акта Биоэнг Биомех. 2010.
PMID: 21361255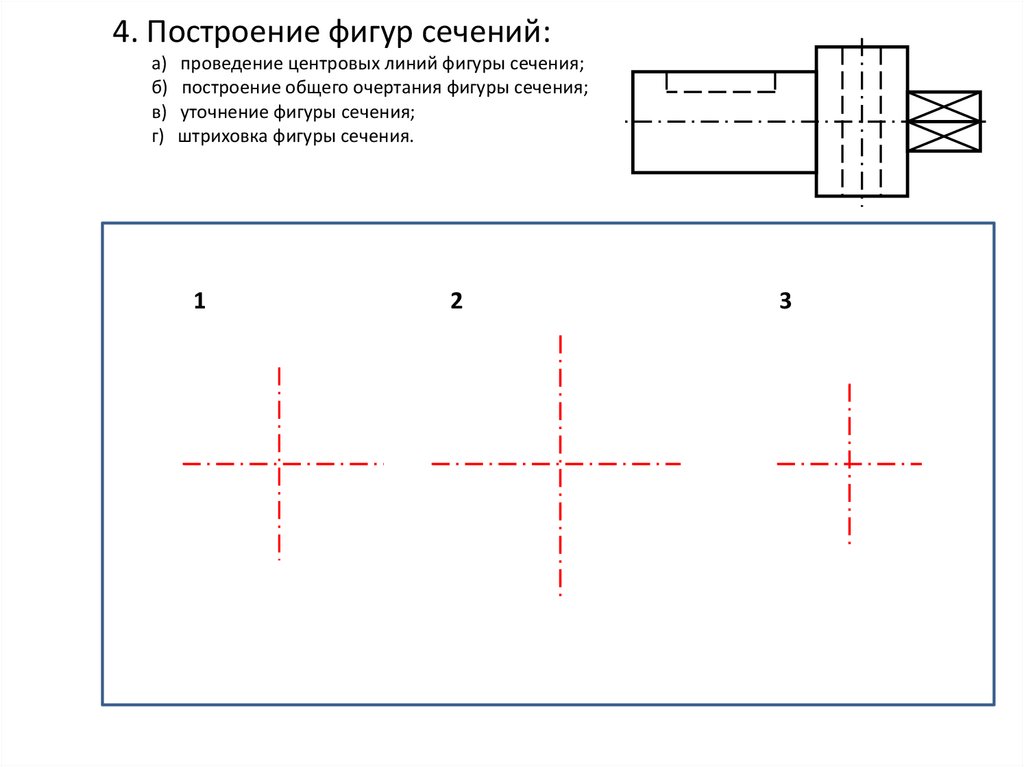 ; 31 (19 Дополнение): S152-60. doi: 10.1097/01.brs.0000234782.89031.03.
Позвоночник (Фила Па, 1976). 2006.
PMID: 16946633
; 31 (19 Дополнение): S152-60. doi: 10.1097/01.brs.0000234782.89031.03.
Позвоночник (Фила Па, 1976). 2006.
PMID: 16946633