Разное

Ось в черчении: тема Проекционное черчение) – Стр 3

alexxlab 02.01.2023 Нет комментариев

ЧЕРЧЕНИЕ. Школьный интернет-учебник – Проецирование 2-4

 

Обычный рисунок изображает предмет, как он представляется глазу наблюдателя. Способ перспективного изображения используют при создании архитектурных проектов. Применение рисунка в производстве неудобно, так как он искажает форму и размеры предмета.

Чертёж, выполненный в прямоугольных (ортогональных) проекциях, является основным видом изображения, которым пользуются в технике. Он дает представление о форме и размерах предмета, но часто уступает в наглядности,  когда очень сложно представить деталь или изделие по чертежу, например рис 1а и б.  По ортогональным проекциям предмета довольно трудно представить его форму.

Рис. 1. Чертёж в прямоугольных проекциях

 В этих случаях выполняют дополнительно изображение этого предмета в аксонометрической проекции, которые значительно нагляднее (можно посмотреть здесь и здесь).

Аксонометрические проекции отличаются наглядностью.

Поэтому аксонометрические проекции применяют в тех случаях, когда трудно представить деталь.

Аксонометрический чертеж (аксонометрия) – это изображение, полученное параллельным проецированием фигуры вместе с осями на некоторую плоскость так, чтобы ни одна из осей не совпадала с направлением проецирования.

   
Построение аксонометрических проекций

 В зависимости от наклона изображаемого предмета к плоскости проекций и угла, образуемого проецирующими лучами с плоскостью, получают аксонометрические проекции различного типа.

ГОСТ 2.317-69 (СТ СЭВ 1979-79) устанавливает пять видов аксонометрических проекций. Рассмотрим два наиболее употребительных вида.

Если передняя и задняя грани куба параллельны плоскости V, а проецирование осуществляется параллельными лучами, направленными под острым углом к плоскости, то получается косоугольная фронтальная диметрическая проекция.

Если расположить куб так, чтобы его грани были наклонены к плоскости V под одинаковыми углами, и проецирование производить перпендикулярными к плоскости лучами, то получится изометрическая проекция (сокращенно изометрия).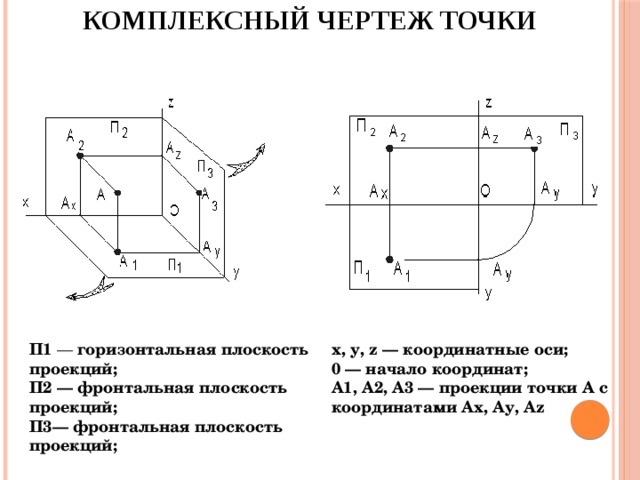

 

Положение осей

Построение аксонометрических проекций начинают с проведения аксонометрических осей.

Оси фронтальной диметрической проекции располагают, как показано на рис. 2, а: ось Х – горизонтально, ось Z – вертикально, ось Y – под углом 45° к горизонтальной линии. Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 2, б.

 Положение осей изометрической проекции показано на рис. 2, в. Оси Х  и Y располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 2, г).

Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.

 

Рис. 2. Способы построения осей аксонометрических проекций

 На рис. 3, а и б показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 3, а). Наклон оси в 30° (рис. 3, б) получается при соотношении длин отрезков 3 : 5   (3 и 5 клеток).

Рис. 3. Построение аксонометрических осей на бумаге в клетку

 При построении фронтальной диметрической проекции по осям Х и Z (и параллельно им) откладывают действительные размеры; по оси У (и параллельно ей) размеры сокращают в 2 раза, отсюда и название “диметрия”, что по-гречески означает “двойное измерение”.

При построении изометрической проекции по осям Х, У, Z (и параллельно им) откладывают действительные размеры предмета, отсюда и название “изометрия”, что по-гречески означает “равные измерения”.

 

Построение фронтальной диметрической и изометрической проекций

 Построим фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 4.


 Рис. 4. Комплексный чертеж детали

 Порядок построения проекций показан на рисунке 5:

1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты – вдоль оси

Z, длины – вдоль оси Х (рис. 5, а).

2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной диметрической проекции – сокращенную в 2 раза; для изометрии – действительную (рис. 5, б).

3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 5, в).

4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 5, г).


 Рис. 5. Способ построения аксонометрических проекций

 Сравните левую и правую колонки на рис. 5. Что общего и в чём различие данных на них построений?

Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод, что порядок построения фронтальной диметрической и изометрической проекций, в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.

 

    Инженерная графика | Лекции | Аксонометрические проекции

    По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

    Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.

    Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4. 1).


    Рисунок 4.1<>p/

    Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
    В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.


    Рисунок 4.2

    Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два  коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической

    .
    Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
    ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

    • прямоугольные изометрические и диметрические;
    • косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

    Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
    Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

    4.1.  Прямоугольные проекции

    4.
    1.1. Изометрическая проекция

    Направление аксонометрических осей приведено на Рисунке 4.3.

    Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

    Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

    Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ  и OX, соответственно.

    Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4. 4.


    Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

    4.1.2. Диметрическая проекция

    Положение аксонометрических осей проводится на Рисунке 4.5.

    Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

    Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5  большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и  OX, соответственно.

    Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4. 6.



    Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

    Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

    4.2 Косоугольные проекции

    4.2.1 Фронтальная диметрическая проекция

    Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 300 и 600.

    Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

    Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

    Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол  7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.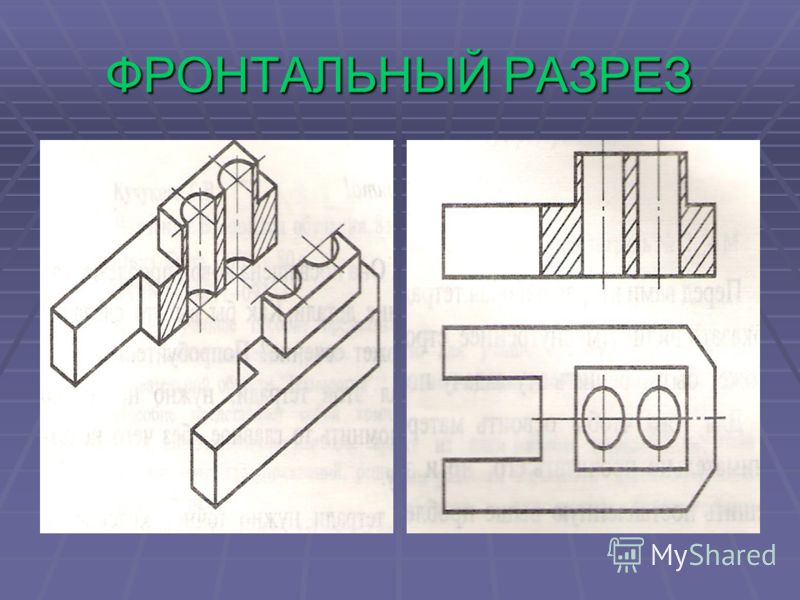

    Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

    Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.


    Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

    4.3 Построение эллипса

    4.3.1 Построения эллипса по двум осям

    На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

    Одна из этих окружностей делится на несколько равных (или неравных) частей.

    Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

    Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.


                          а                                б                                              в
    Рисунок 4.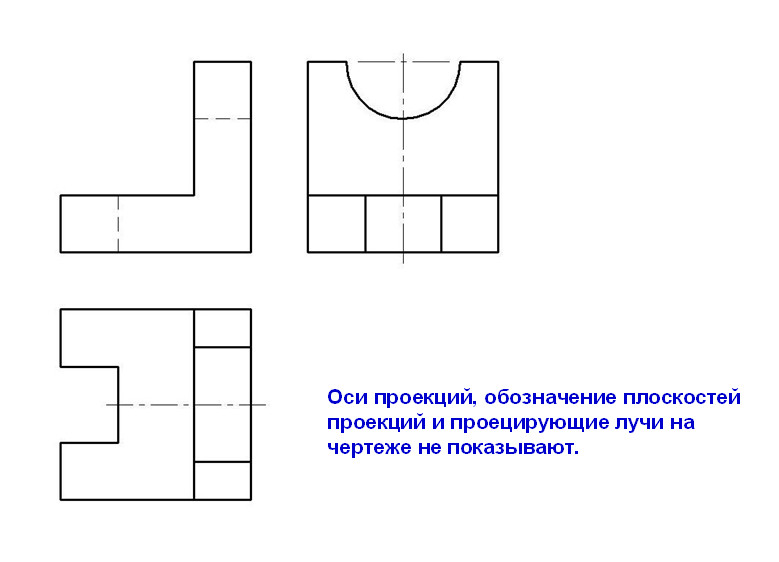 9 – Построение эллипса по двум осям (а), по хордам (б)

    4.3.2 Построение эллипса по хордам

    Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

    4.4 Штриховка сечений

    Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.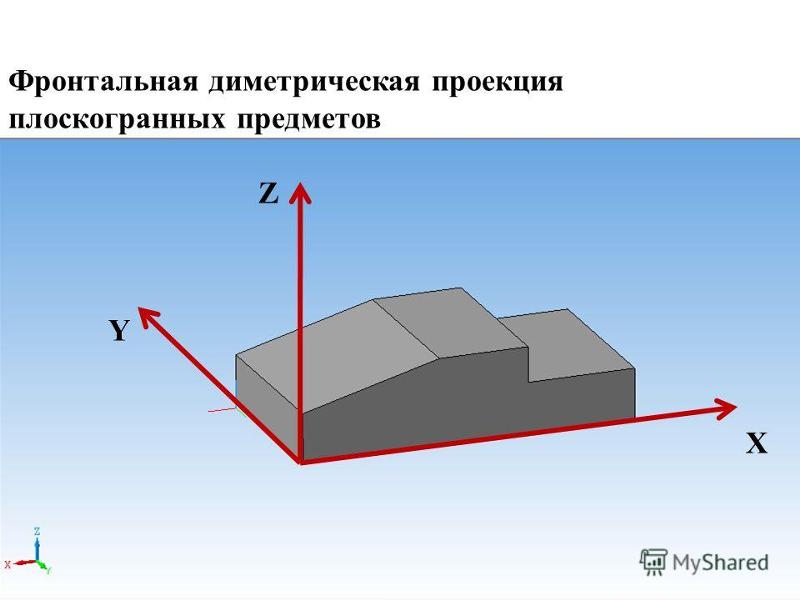 10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).


                                         а                                                                                б
    Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

    По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

    Drawabox.com | Часть первая: Основы | Урок 1: Линии, эллипсы и прямоугольники | Эллипсы

    Вот куда идет сообщение!

      Ненавидите читать? Без проблем. Мы можем прочитать вам текст .

      Эта функция доступна совершенно бесплатно . Хотя мы будем следить за тем, насколько возможно покрыть связанные с этим расходы, мы надеемся, что так и останется.

      Просто нажмите «Слушайте с помощью Drawabox»!

      Что такое эллипс?

      Эллипсы чрезвычайно важны и, как известно, раздражают при рисовании. Вы найдете их повсюду в механических чертежах. Автомобили, космические корабли, танки, машины — все, что создано человеком, вероятно, широко использует эллипсы.

      Они также занимают видное место в органических рисунках, особенно когда мы смотрим на сечения колбасоподобных форм.

      Давайте уделим немного времени изучению того, что они собой представляют, как ведут себя и как их можно использовать.

      2D против 3D

      Итак, прежде чем мы перейдем к сложным вещам, помните: рисование — это (по крайней мере, в рамках этого курса) о том, чтобы взять трехмерные вещи (например, мир, в котором мы живем) и запечатлеть их на двумерная поверхность , будь то лист бумаги, холст или спина моего друга, который был настолько глуп, что 16-летний мальчик сделал для него татуировку, которая, по сути, навсегда приклеилась к его телу.

      Это означает, что рисование на самом деле связано с выяснением того, как представлять трехмерные объекты, и с пониманием того, как линии и формы, которые мы используем для их захвата, меняются в зависимости от того, как эти трехмерные формы перемещаются и вращаются в пространстве.

      На протяжении всего курса я буду обозначать вещи как

      в 3D-пространстве или в 2D-пространстве . Обратите внимание на то, что я использую в той или иной ситуации, потому что это имеет значение.

      Круги в трехмерном пространстве

      Для наших целей в этом курсе мы будем использовать эллипсы в двухмерном пространстве (нарисованные на странице) для представления кругов, существующих в трехмерном пространстве.

      В зависимости от того, смотрите ли вы на нее как на двухмерную или трехмерную, эта анимированная диаграмма изображает одну из двух вещей:

      • В двухмерном пространстве это ряд эллипсов, от самого широкого до самого узкого.

      • В 3D-пространстве это круг, который вращается от лица, обращенного к зрителю, к обращению от него.

      Градус

      От того, как наш круг (в трехмерном пространстве) повернут относительно зрителя, будет зависеть, насколько широким будет нарисован наш эллипс. Эта ширина (всегда измеряемая по самому узкому промежутку , проходящему через центр эллипса) называется «градусом», потому что она привязана к углу поворота (в градусах) самого круга относительно зритель.

      Когда круг (в 3D-пространстве) обращен к зрителю, он будет самым широким – 90 градусов. Это то же самое, что рисовать круг на странице. По мере того, как трехмерный круг отворачивается от зрителя, эллипс, представляющий его, будет сужаться, пока, наконец, не достигнет степени 0, когда эллипс обращен в сторону.

      Градусное смещение

      Имейте в виду, что, поскольку это основано на угле между направлением, в котором смотрит круг, и направлением, в котором смотрит зритель, градус фактически изменится, просто перемещая круг в пространстве, не обязательно вращать его.

      На этой диаграмме показано, как чем дальше вправо перемещается круг по отношению к зрителю, тем больше становится видна его грань, в результате чего на странице его представляет более широкий эллипс, даже если этот круг не вращается в пространстве.

      На протяжении всего курса мы будем называть это понятие «градусным сдвигом» — в основном это идея о том, что градус нашего эллипса будет сдвигаться вширь или уже в зависимости от того, как он перемещается в пространстве.

      Малая ось

      Мы называем линию, которая проходит через самый узкий отрезок эллипса и через его центр, его малая ось . Эта линия малой оси разделит эллипс на две равные симметричные половины, поэтому, если его вырезать из страницы и сложить пополам по этой линии, он будет идеально совпадать.

      Также есть большая ось , которая проходит перпендикулярно ей (по самому широкому пролету), но на самом деле полезным компонентом является малая ось.

      Вектор нормали

      Так же, как 2D-эллипс представляет собой 3D-круг, малая ось равна чрезвычайно полезен для нас из-за того, как эта линия малой оси совпадает и выравнивается с вектором нормали – 3D-линии, которая выходит прямо из поверхности 3D-круга, полностью перпендикулярно этой поверхности.

      Это означает, что у нас есть два способа установить ориентацию нашего круга в 3D-пространстве, когда мы рисуем его на нашей 2D-странице:

      Если нам нужно, чтобы наш круг был ориентирован определенным образом в более сложной сцене , мы фактически сможем начать с обычной векторной линии, а затем использовать ее в качестве малой оси для нашего эллипса, рисуя эллипс вокруг нее так, чтобы линия разделяла его на две равные симметричные половины по самому узкому промежутку.

      Цилиндры

      Продолжая, малая ось/вектор нормали также чрезвычайно полезна, когда мы получаем цилиндрические формы. Здесь он служит «позвоночником» нашей формы.

      Концы цилиндра имеют один и тот же вектор нормали (в 3D) и малую ось (в 2D). также выравниваются по той же малой оси/вектору нормали.

      К счастью для вас, нам не нужно беспокоиться об этом прямо сейчас — они не вступят в игру до Урока 2. Просто полезно увидеть, насколько полезной может быть малая ось эллипса, особенно когда мы пытаемся выяснить все способы, которыми мы можем представить различные свойства круга в трехмерном пространстве.

      Домашнее задание и упражнения

      Домашнее задание по этому разделу следующее:

      • 2 заполненные страницы упражнения «Таблицы эллипсов»

      • 2 заполненные страницы упражнения «Эллипсы в плоскостях»

      • 1 заполненная страница упражнения «Воронки»

      Вся работа, назначенная для этого раздела, должна быть выполнена тушью с использованием маркеров/фломастеров, как описано здесь . В крайнем случае я соглашусь на работу, выполненную шариковой ручкой, но только в крайнем случае. Это исключение только для этого урока, когда ученики начинают.

      <<< Строки: Домашнее задание

      Ящики >>>

      Matplotlib.axes.Axes.draw() в Python — GeeksforGeeks

      Улучшить статью

      Сохранить статью

      • Последнее обновление: 30 апр, 2020

    • Читать
    • Обсудить

      • Улучшить статью

      Сохранить статью

      Matplotlib — это библиотека на Python, и она является числовым — математическим расширением для библиотеки NumPy. Axes Class содержит большинство элементов фигуры: Axis, Tick, Line2D, Text, Polygon и т. д., а также задает систему координат. А экземпляры Axes поддерживают обратные вызовы через атрибут callbacks.

      Функция Axes.draw() в модуле осей библиотеки matplotlib используется для рисования всего.

      Синтаксис: Axes.draw(self, renderer=None, inframe=False)

      Параметры: Этот метод принимает следующие параметры.

      • визуализатор: Этот параметр является первым параметром, и его значение по умолчанию — None.
      • внутри кадра: Этот параметр содержит логическое значение, и его значение по умолчанию равно false.

      Возвраты: Этот метод не возвращает никакого значения. Пример 10199 mpl_toolkits.mplot3d import axes3d 

      import matplotlib. pyplot as plt 

           

         

      fig, ax = plt.subplots() 

      DEF Tellme (S):

      AX.Set_TITL

           fig.canvas.draw()

           renderer = fig.canvas.renderer

           ax.draw(renderer)

         

      tellme ( 'matplotlib.axes.axes.draw () Пример функции' )

      PLT. Show ()

      : 9

      : 9

      9696969699699699699699699699699699699699699699699699699699696996969н .0007

      from mpl_toolkits.mplot3d import axes3d 

      import matplotlib.pyplot as plt 

           

         

      fig = plt.figure()

      ax = 9 ) 

           

      X, Y, Z = axes3d. get_test_data( 0.1 ) 

      ax.plot_wireframe(X, Y, Z, rstride = 5 ,  

                         cstride = 5 ) 

           

      for angle in range ( 0 , 90 ): 

           ax.view_init( 30 , angle)

           fig.canvas.draw()

           renderer = fig.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *