ГОСТ Р 50577-93 Знаки государственные регистрационные
ГОСТ Р 50577-93 Знаки государственные регистрационныеВыписка: http://sklad-zakonov.narod.ru/gost/Gr50577-93.htm
Приложение И (обязательное)
И.1 На каждом транспортном средстве должны быть предусмотрены места установки следующих регистрационных знаков (кроме знаков типов 16-18):
– одного переднего и одного заднего – на легковых, грузовых, грузопассажирских автомобилях и автобусах;
– одного заднего – на прочих транспортных средствах.
И.2 Место для установки регистрационного знака должно представлять собой плоскую вертикальную прямоугольную поверхность и выбираться таким образом, чтобы исключалось загораживание знака элементами конструкции транспортного средства, загрязнение при эксплуатации транспортного средства и затруднение прочтения. При этом регистрационные знаки не должны уменьшать углы переднего и заднего свесов транспортного средства, закрывать внешние световые и светосигнальные приборы, выступать за боковой габарит транспортного средства.
И.3 Передний регистрационный знак должен устанавливаться, как правило, по оси симметрии транспортного средства. Допускается установка переднего регистрационного знака слева от оси симметрии транспортного средства по направлению движения транспортного средства.
И.4 Место установки заднего регистрационного знака должно обеспечивать выполнение следующих условий.
И.4.1 Регистрационный знак должен устанавливаться по оси симметрии транспортного средства или слева от нее по направлению движения.
И.4.2 Регистрационный знак должен устанавливаться перпендикулярно продольной плоскости симметрии транспортного средства с отклонением не более 3°.
И.4.3 Регистрационный знак на транспортном средстве должен располагаться перпендикулярно опорной плоскости транспортного средства с отклонением не более 5°.
Примечание – Если конструкция транспортного средства не позволяет установить регистрационные знаки перпендикулярно опорной плоскости транспортного средства, то для регистрационных знаков, высота верхнего края которых не более 1200 мм, допускается этот угол увеличить до 30°, если поверхность, на которой установлен знак, обращена вверх, и до 15°, если поверхность обращена вниз.
И.4.4 Высота нижнего края заднего регистрационного знака от опорной плоскости транспортного средства должна быть не менее 300 мм, высота верхнего края знака – не более 1200 мм.
Примечания
1 В случае если конструкция транспортного средства не позволяет обеспечить высоту расположения верхнего края регистрационного знака на высоте не более 1200 мм, допускается увеличение размера до 2000 мм.
2 Измерение высоты размещения регистрационного знака от опорной плоскости транспортного средства должно проводиться на транспортном средстве снаряженной массы.
И.4.5 Регистрационный знак должен быть видимым в пространстве, ограниченном следующими четырьмя плоскостями: двумя вертикальными и двумя горизонтальными, касающимися краев знака в пределах углов видимости, указанных на рисунке 3.1.
И.4.6 Относительное расположение регистрационного знака и фонаря (фонарей) освещения регистрационного знака на транспортном средстве должно соответствовать ГОСТ Р 41.
4.
И.4.7 Регистрационный знак должен устанавливаться таким образом, чтобы в темное время суток обеспечивалось его прочтение с расстояния не менее 20 м при освещении штатным фонарем (фонарями) освещения знака транспортного средства.
Примечание – Требование не распространяется на надписи “RUS” и “ТРАНЗИТ”, а также на изображение флага Российской Федерации.
И.5 Для крепления регистрационных знаков должны применяться болты или винты с головками, имеющими цвет поля знака или светлые гальванические покрытия.
Допускается крепление знаков с помощью рамок. Болты, винты, рамки не должны загораживать или искажать имеющиеся на регистрационном знаке надпись “RUS”, изображение Государственного флага Российской Федерации, буквы, цифры или окантовку.
Рисунок И.1
Не допускается закрывать знак органическим стеклом или другими материалами.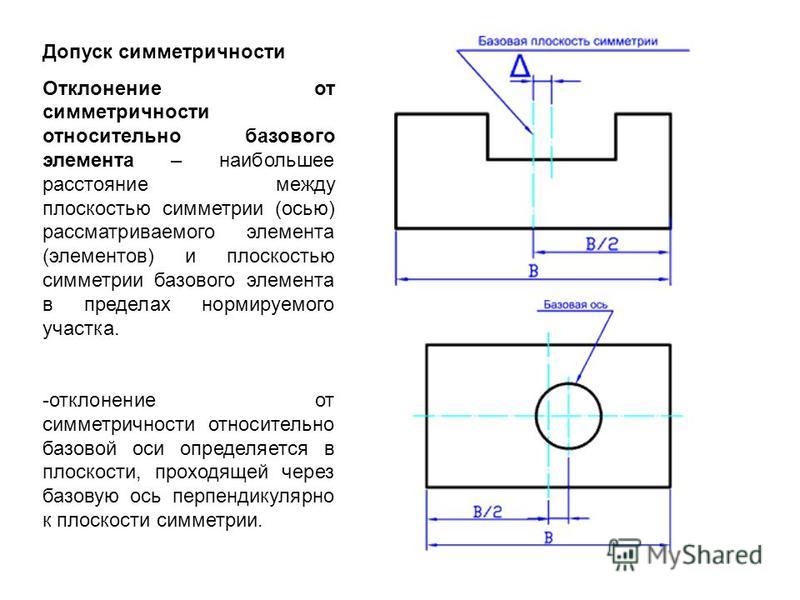
В случае несовпадения координат посадочных отверстий регистрационного знака с координатами посадочных отверстий транспортного средства крепление знаков должно осуществляться через переходные конструктивные элементы, обеспечивающие выполнение требований И.2-И.4.
И.6 Регистрационные знаки типов 16-18 должны устанавливаться:
– на легковых автомобилях и автобусах – один на переднем и один на заднем ветровых стеклах внутри салона (кабины) справа от продольной плоскости симметрии по направлению движения транспортного средства;
– на грузовых автомобилях и тракторах – один знак на переднем ветровом стекле внутри кабины справа от продольной плоскости симметрии по направлению движения транспортного средства.
Регистрационные знаки, выданные на мотоциклы и прицепы, должны находиться у водителей.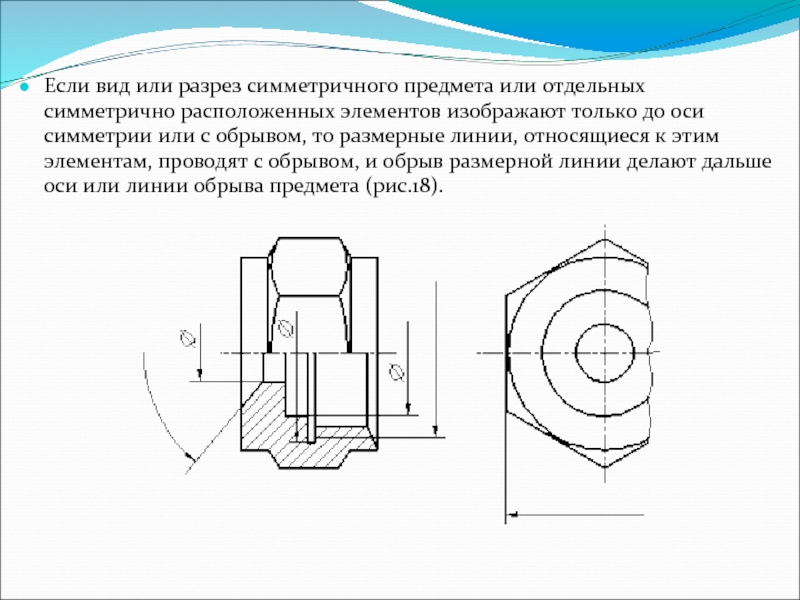
Приложение И (Введено дополнительно, Изм. N 2).
Издание (декабрь 2001 г.) с Изменениями N 1, 2, принятыми в мае 1998 г., ноябре 2001 г. (ИУС 9-98, 2-2002)
Изображения – виды, разрезы, сечения ГОСТ 2.305-68
Изображения –
виды, разрезы, сечения
ГОСТ 2.305-68
Системы расположения изображений
Европейская система
Американская система
Виды
Видом называется изображение, на
котором показана обращенная к
наблюдателю видимая часть
поверхности предмета
• Все виды на чертеже должны, по возможности,
располагаться в проекционной связи. В таких
случаях на чертеже не наносятся какие-либо
надписи, разъясняющие наименование видов.
Классификация видов
Основные виды
• ГОСТ 2.305-68 устанавливает шесть названий основных видов
• Чаще используют первые три вида. На чертеже не допускается выполнение
лишних изображений.
• Названия видов на чертежах не подписывают, если они расположены
относительно главного вида (изображения) как на рисунке выше.
Основные виды
• ГОСТом допускается располагать виды без проекционной связи, на
любом месте поля чертежа. В таких случаях вид обозначают
стрелкой в направлении взгляда, а над изображением выполняют
надпись по типу «А»
Рациональное использование
поля чертежа
* Главный вид выбирают таким образом, чтобы он давал наиболее полное
представление о форме и размерах детали
* При наименьшем количестве видов в совокупности с другими
изображениями чертеж должен полностью отображать конструкцию
изделия.
Местные виды
Местный вид – изображение отдельного,
ограниченного места поверхности
предмета.
• Местный вид может быть ограничен линией
обрыва, осью симметрии или не ограничен.
• Если местный вид выполняется в
проекционной связи по направлению взгляда,
то стрелку и надпись над местным видом не
наносят.
Местные виды
Дополнительные виды
Дополнительный вид
получается проецированием предмета на
плоскость, не параллельную ни одной из
основных плоскостей проекций.
• Если дополнительный вид располагается не в
проекционной связи (смещен), то направление взгляда
должно быть указано стрелкой А и над изображением
выполняется надпись «А»
• Дополнительный вид допускается поворачивать, тогда
к надписи «Б» добавляют справа знак
«повернуто»
Разрезы
Разрезом
называется изображение предмета, полученное при
мысленном рассечении его одной или несколькими
секущими плоскостями. При этом часть предмета,
расположенная перед секущей плоскостью, мысленно
удаляется. На плоскости проекций изображается то,
что расположено в секущей плоскости и то, что
расположено за ней. Фигура сечения штрихуется.
• Мысленное рассечение предмета относится только к данному
разрезу и не влечет за собой изменения других изображений того
же предмета
• Штриховка на всех изображениях детали выполняется, как
правило, в одном направлении.
!!! стр.61 пособия
Классификация разрезов
Разрезы
Простые
Вертикальные
Фронтальные
Горизонтальные
Профильные
Сложные
Наклонные
Ступенчатые
Местные
Ломаные
Разрезы простые
Простым разрезом называется
разрез, полученный при
применении одной секущей
плоскости.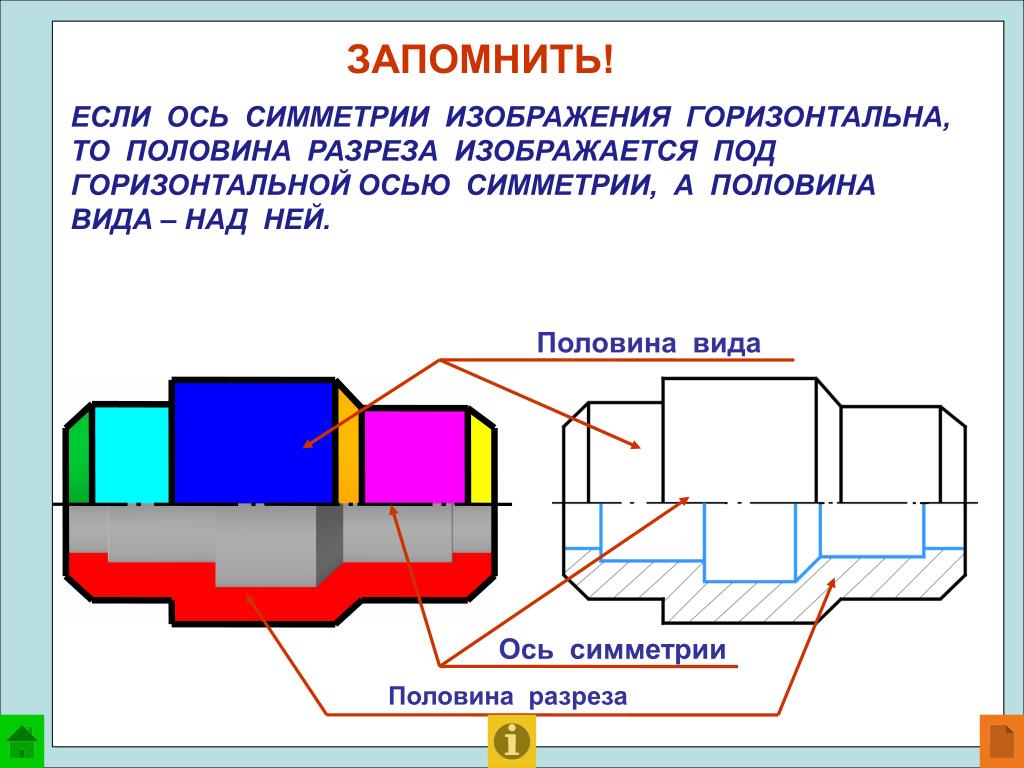
• Горизонтальные, фронтальные и
профильные разрезы могут
размещаться на месте
соответствующих видов
Фронтальный разрез
Вертикальный разрез называется фронтальным, если секущая
плоскость параллельна фронтальной плоскости проекций
Профильный разрез
Вертикальный разрез называется профильным, если секущая
плоскость параллельна профильной плоскости проекций
Обозначение разрезов
Простые разрезы не обозначают если:
• Секущая плоскость совпадает с плоскостью симметрии
детали в целом
• Разрез расположен в непосредственной проекционной
связи с видом
• Они не разделены какими-либо другими
изображениями
!!! стр.61 пособия
В остальных случаях:
• положение секущей плоскости отмечают
разомкнутой линией со стрелками,
указывающими направление взгляда и
заглавными буквами русского алфавита
• над разрезом выполняется надпись по типу
«А-А», соответствующая секущей плоскости
Соединение
части вида и части разреза
На одном изображении допускается соединять часть
вида и часть разреза.
Линии невидимого контура на соединяемых частях вида
и разреза обычно не показываются.
• Если вид и располагаемый на его месте
разрез представляют собой симметричные
фигуры, то можно соединить половину вида и
половину разреза, разделяя их
штрихпунктирной тонкой линией,
являющейся осью симметрии.
!!! стр.62 пособия
Часть разреза располагают правее или ниже оси симметрии.
• !!! Если с осью симметрии
совпадает проекция какой-либо
линии, например, ребра, то вид от
разреза отделяется тонкой
волнистой линией, проводимой
правее или левее оси симметрии.
Разрезы простые – наклонные
Наклонными называются разрезы, образованные
секущими проецирующими плоскостями.
• Наклонные разрезы должны строиться
в соответствии с направлением взгляда.
• Наклонные разрезы всегда обозначают!
Разрезы местные
Разрез, служащий для
выявления формы
предмета лишь в
отдельном ограниченном
месте, называется
местным и
ограничивается на виде
сплошной волнистой
линией.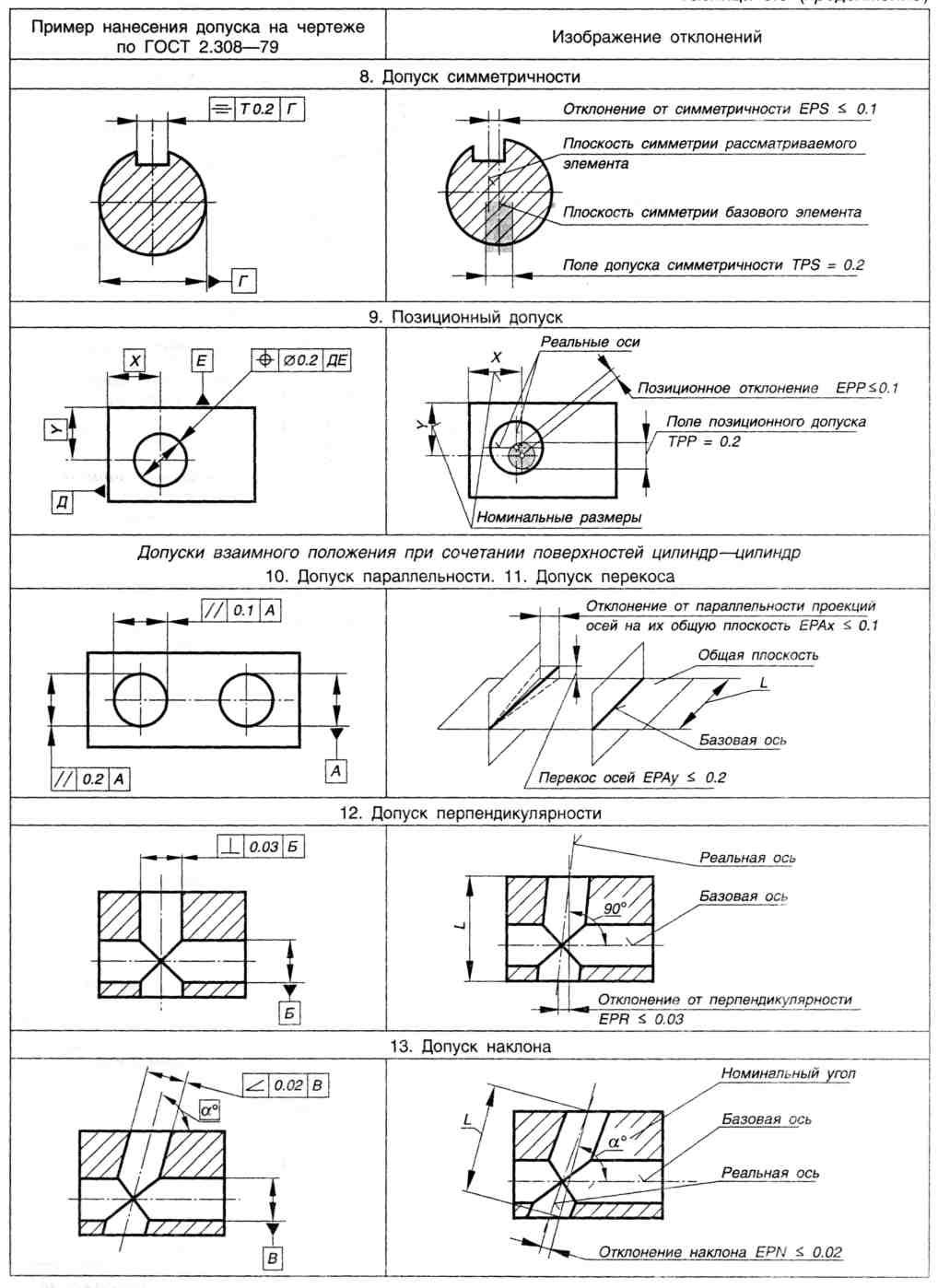
!!! Местные разрезы не обозначают!
Разрезы сложные
Сложными называются разрезы, получаемые с
помощью двух и более секущих плоскостей.
Разрезы
сложные
Горизонтальные
Ступенчатые
Ломаные
Фронтальные
Профильные
!!! Сложные разрезы всегда обозначают!
Комбинированные
Разрезы сложные ступенчатые
Ступенчатыми разрезами называются разрезы,
выполненные несколькими параллельными
секущими плоскостями.
* Все секущие плоскости совмещаются с одной (фронтальной) плоскостью.
Разрезы сложные ломаные
Ломаными называются разрезы,
полученные от рассечения предмета
не параллельными,
а пересекающимися плоскостями.
* Секущие плоскости условно поворачивают (вместе с фигурой сечения) около
линии взаимного пересечения до совмещения с плоскостью, параллельной
какой-либо из основных плоскостей проекций, поэтому ломаные разрезы могут
быть фронтальными, горизонтальными или профильными.
Перв. примен.
12.
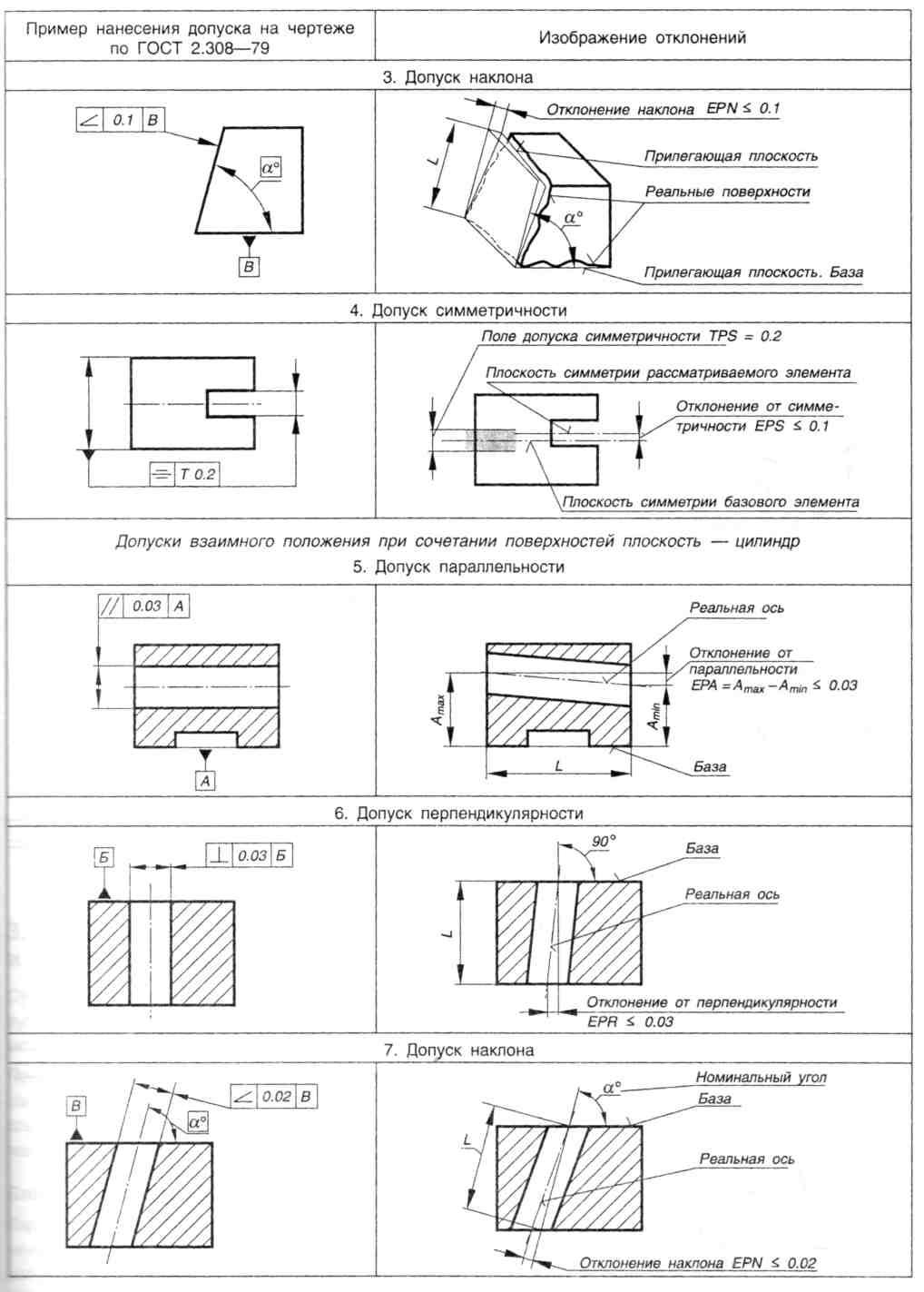1.4.05.Р6.08.00
А- А
З
40
70
Справ. №
40
16
10
З
70
2• 45Е
10
30
З
30
Инв. № подл.
Подп. и дата
А
90*
60
З
14
4 отв.
20
Взам. инв. № Инв. № дубл.
Подп. и дата
130
А
12.1.4.05.Р6.08.00
R15
30
100
Изм. Лист № докум. Подп. Дата
Разраб. Иванов В.В.
Пров.
Тихонов С.М.
Т.контр.
Н.контр.
Утв.
Корпус
Лит.
Масса Масштаб
1:1
Лист
Листов
АГТУ ИНиГ1- 1
Копировал
Формат
A3
Сечения
Сечением называется изображение
фигуры, получающееся при мысленном
рассечении предмета одной или
несколькими плоскостями.
В отличие от разреза на сечении показывается
только то, что расположено непосредственно
в секущей плоскости.
Секущие плоскости должны выбираться так,
чтобы получились нормальные поперечные
сечения.
Классификация сечений
Сечения
Симметричные
Наложенные
Несимметричные
Вынесенные
Расположенные
в разрыве
изображения
Обозначение сечений
• Не обозначают вынесенное симметричное сечение, расположенное в
непосредственной близости от изображения, если его ось симметрии
совпадает с положением секущей плоскости и пересекает контур
изображения предмета.
В остальных случаях сечение обозначают разомкнутой линией со стрелками и
заглавными буквами русского алфавита, а над самими сечениями выполняется
надпись по типу «А-А»
!!! стр.78 пособия
• Для несимметричных сечений, расположенных в разрыве
или наложенных, положение секущей плоскости указывается
линией сечения со стрелками, но буквами не обозначается.
• Если секущая плоскость проходит через некруглые
отверстия и сечение получается состоящим из отдельных
частей, то сечение должно быть заменено разрезом.
• При совпадении секущей плоскости с осью поверхности
вращения, ограничивающей отверстия или углубления,
контур отверстия или углубления в сечении
показывается полностью, т.е. сечение оформляется как
разрез.
!!! стр.79 пособия
Под ключ 24
Отв.сквозное
42. Построить сечения и нанести
размеры вала.
30
З
З
10
Ширина сегментной шпоночной канавки – 10мм.
Глубина призматической шпоночной канавки – 8 мм.
Глубина отверстия З
10 – 12 мм.
Под ключ 24
А
Отв.сквозное
19
З
З
10
Б
Б- Б
10
З
12
38
З
46
З
24
А А- А
10
З
38
8
42. Построить сечения и нанести
размеры вала.
30
Б
12
Ширина сегментной шпоночной канавки – 10мм.
Глубина призматической шпоночной канавки – 8 мм.
Глубина отверстия З
10 – 12 мм.
Выносные элементы
• Если какая-либо часть предмета требует графического
пояснения формы, размеров из-за мелкого ее
изображения, то применяют дополнительное ее
изображение, называемое выносным элементом.
Условности и упрощения,
применяемые при выполнении изображений
• Такие элементы деталей, как тонкие стенки, ребра
жесткости, ушки, спицы колес, маховиков и т.п.
показываются на разрезе незаштрихованными в том
случае, когда секущая плоскость направлена вдоль
оси или длинной стороны этих элементов детали.
• Такие детали, как винты, заклепки, шпонки,
непустотелые валы, рукоятки, шпиндели и т.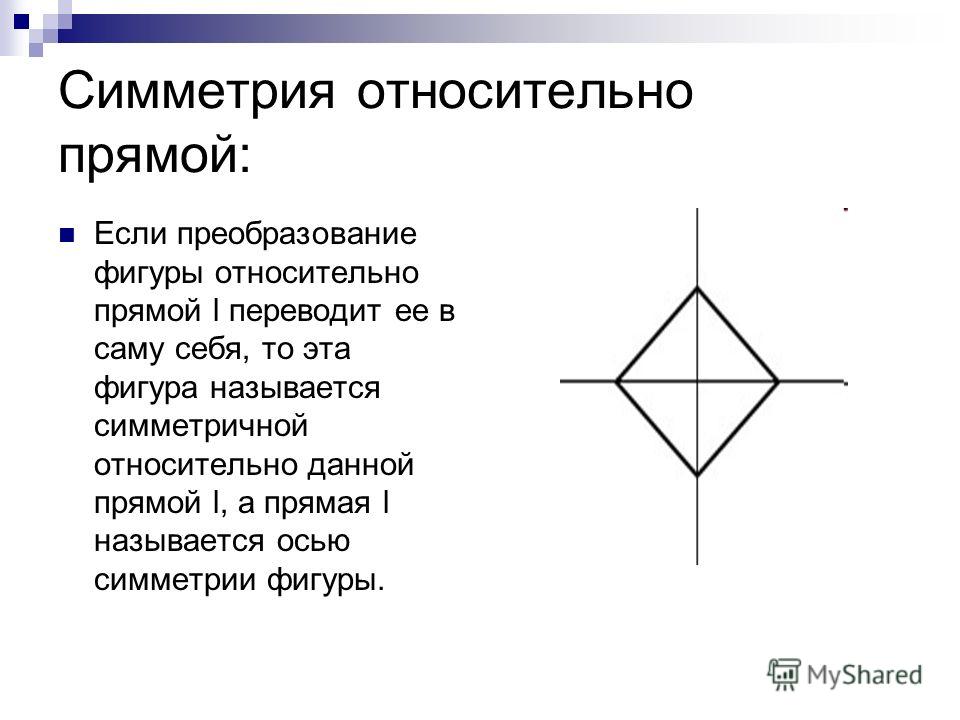
п., при
продольном разрезе показывают нерассеченными.
Шарики всегда показывают нерассеченными.
• При необходимости выделения на чертеже плоских
поверхностей предмета на них проводят диагонали
сплошными тонкими линиями.
• Длинные предметы допускается изображать с разрывом.
• Для показа отверстия в ступицах зубчатых колес,
шкивов и т.п. вместо второго изображения детали
рекомендуется давать только контур отверстий
(местный вид).
• На поверхности некоторых деталей может быть
орнамент, сетка, накатка и т.п., эти элементы
допускается изображать не полностью, а частично с
возможным упрощением.
Правила простановки размеров
Правила нанесения размеров устанавливает
ГОСТ 2.307-68.
• Общее количество размеров на чертеже должно быть
минимальным, но достаточным для изготовления
детали.
• Размеры повторять на разных изображениях не
допускается. Каждый размер проставляется только
один раз.
!!! стр.72-74 пособия
• Размеры, относящиеся к одному и тому же элементу,
рекомендуется группировать на том изображении, где
геометрическая форма элемента показана наиболее
полно.
Размерные и выносные линии предпочтительно
наносить вне контура изображения.
Необходимо избегать пересечения размерных и
выносных линий.
Категорически запрещается выносить меньший
размер за больший.
• Внешние размеры рекомендуется располагать со
стороны вида, а внутренние – со стороны разреза.
• Простановка размеров от линии невидимого контура
не рекомендуется.
З
З
З
З
З
З
З
R
Обозначения графические материалов
и правила их нанесения на чертежах.
Металлы и твердые сплавы.
Неметаллические материалы, в том числе
волокнистые, монолитные и прессованые.
Дерево.
Грунт естественный.
Стекло и светопрозрачные материалы.
Жидкости.
Аксонометрические
проекции
Аксонометрическими проекциями называют наглядные изображения объекта,
получаемые параллельным проецированием его на одну плоскость проекций П’
вместе с осями прямоугольных координат, к которым этот объект отнесен.
Прямоугольная
изометрия
Аксонометрические оси также расположены
под равными углами (120°) одна к другой,
ось z вертикальна.
Показатели искажения по всем осям равны 0,82.
Они условно приняты равными единице.
Окружности, расположенные в
координатной плоскости
или в плоскости, параллельной
ей, проецируются эллипсами
Пример построения эллипсов в трех плоскостях
z
2
2
o2
o4
o2
o4
3
3
1
o3
o1
4
4
R1
R3
o2
2
1
x
o3
x
o3
o1
1
0
y
o4
3
4
o1
y
!!! стр.75 пособия
Штриховка
в прямоугольной изометрии
В аксонометрических проекциях
спицы маховиков и шкивов,
ребра жесткости и подобные
элементы штрихуют.
Прямоугольная
диметрия
В прямоугольной диметрии ось z вертикальна,
оси х и у наклонены соответственно под углами 7°10′
и 41°25′ к горизонтальной линии чертежа.
Показатели искажения по осям х и z равны 1, по оси у – 0,5.
Окружности, расположенные в
координатной плоскости
или в плоскости, параллельной
ей, проецируются эллипсами
Фронтальная
косоугольная изометрия
Горизонтальная
косоугольная изометрия
Фронтальная
косоугольная диметрия
12.1.4.05.Р6.08.00
Перв. примен.
А- А
З
40
З
30
2• 45Е
10
30
Справ. №
70
40
16
10
З
70
130
Инв. № подл.
Подп. и дата
А
R15
90*
60
20
Взам. инв. № Инв. № дубл.
Подп. и дата
З
14
4 отв.
А
12.1.4.05.Р6.08.00
30
100
Изм. Лист № докум. Подп. Дата
Разраб. Иванов В.В.
Пров.
Тихонов С.М.
Т.контр.
Н.контр.
Утв.
Корпус
Лит.
Масса Масштаб
1:1
Лист
Листов
АГТУ ИНиГ1- 1
Копировал
Формат
A3
Ось симметрии — уравнение, формула, определение, примеры, парабола
Ось симметрии — это воображаемая прямая, которая делит фигуру на две одинаковые части, тем самым создавая одну часть как зеркальное отражение другой части.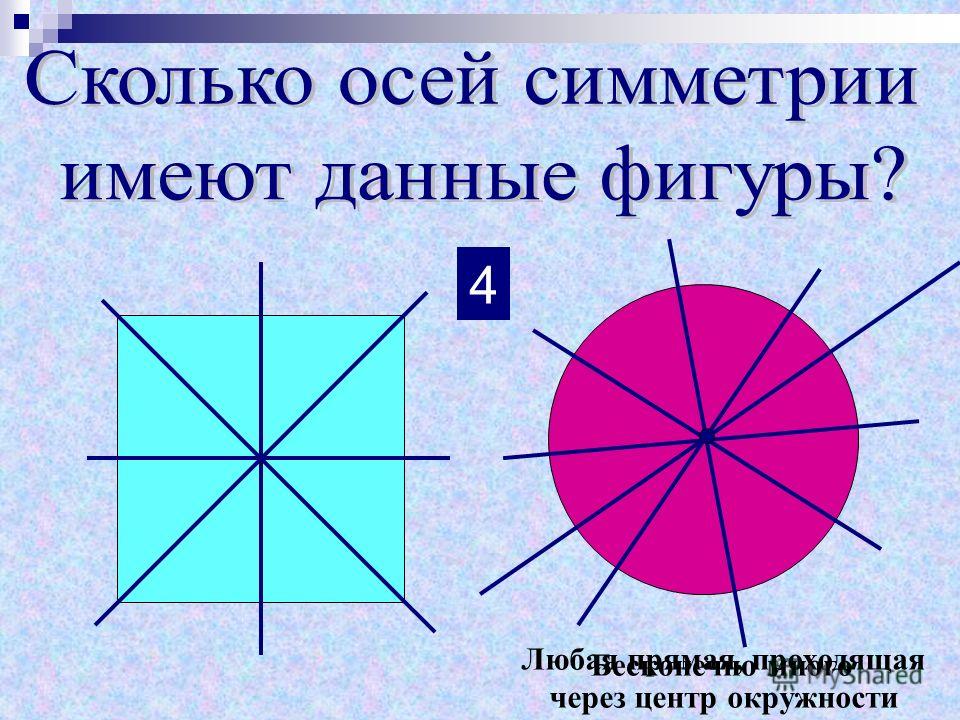
При складывании по оси симметрии две части накладываются друг на друга. Прямая линия называется линией симметрии/зеркальной линией. Эта линия может быть вертикальной, горизонтальной или наклонной.
Мы можем видеть эту ось симметрии даже в природе, такой как цветы, берега рек, здания, листья и так далее. Мы можем наблюдать это в Тадж-Махале, культовом мраморном сооружении в Индии.
| 1. | Что такое ось симметрии? |
| 2. | Ось симметрии параболы |
| 3. | Уравнение оси симметрии |
| 4. | Формула оси симметрии |
| 5. | Найти ось симметрии |
| 6. | Вывод оси симметрии |
| 7. | Идентификация оси симметрии |
| 8. | Часто задаваемые вопросы об оси симметрии |
Что такое ось симметрии?
Ось симметрии представляет собой прямую линию, делающую форму объекта симметричной.
Ось симметрии создает точные отражения на каждой из своих сторон. Он может быть горизонтальным, вертикальным или боковым. Если мы складываем и разворачиваем объект вдоль оси симметрии, две стороны идентичны. Разные фигуры имеют разные линии симметрии. У квадрата четыре оси симметрии, у прямоугольника две оси симметрии, у круга бесконечные оси симметрии, а у параллелограмма нет осей симметрии. Правильный многоугольник из n сторон имеет n осей симметрии.
Ось симметрии Определение
Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, каждая из которых является зеркальным отражением друг друга. При складывании фигуры по оси симметрии две одинаковые части накладываются друг на друга.
Ось симметрии параболы
Парабола имеет одну линию симметрии. Ось симметрии — это прямая линия, которая делит параболу на две симметричные части. Парабола может быть четырех видов. Он может быть как горизонтальным, так и вертикальным, обращенным влево или вправо.
Ось симметрии определяет форму параболы.
- Если ось симметрии вертикальна, то и парабола вертикальна (раскрывается вверх/вниз).
- Если она горизонтальна, то и парабола горизонтальна (открывается влево/вправо).
Горизонтальная ось симметрии имеет нулевой наклон, а вертикальная ось симметрии имеет неопределенный наклон.
Уравнение оси симметрии
Вершина — это точка пересечения оси симметрии с параболой. Это ключевой момент для определения его уравнения. Если парабола открывается вверх или вниз, ось симметрии вертикальна и в этом случае ее уравнением является вертикальная линия, проходящая через ее вершину. Если парабола открывается вправо или влево, ось симметрии горизонтальна, а ее уравнением является горизонтальная линия, проходящая через ее вершину. то есть
- Ось уравнения симметрии параболы, вершина которой равна (h, k) и направлена вверх/вниз, равна x = h.
- Ось уравнения симметрии параболы, вершина которой равна (h, k) и открывается влево/вправо, равна y = k.
Ось симметрии Формула
Формула оси симметрии применяется к квадратным уравнениям, где используется стандартная форма уравнения и линия симметрии. Линия, которая делит или раздваивает любой объект на две равные половины, обе половины которых являются зеркальным отражением друг друга, называется осью симметрии. Эта линия оси, разделяющая объекты, может быть любого из трех типов: горизонтальная (ось X), вертикальная (ось Y) или наклонная линия.
Уравнение оси симметрии может быть представлено, когда парабола имеет две формы:
- Стандартная форма
- Форма вершины
Стандартная форма
Квадратное уравнение в стандартной форме : y = ax 2 + b x+c
, где a, b и c — действительные числа.
Здесь формула оси симметрии: x = – b/2a.
Вершинная форма
Квадратное уравнение в вершинной форме: y = a (x-h) 2 + k
где (h, k) — вершина параболы.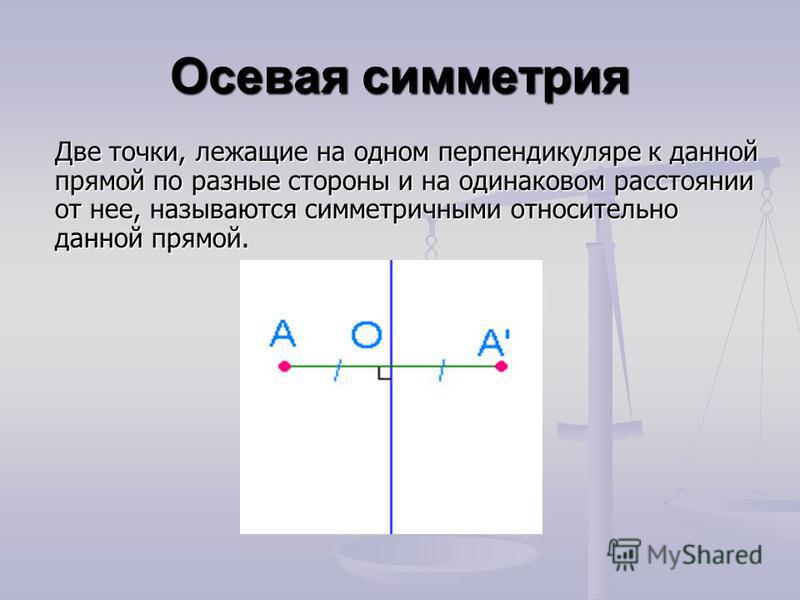
Вывод оси симметрии параболы
Ось симметрии всегда проходит через вершину параболы. Таким образом, идентификация вершины помогает нам вычислить положение оси симметрии. Формула оси симметрии параболы: x = -b/2a. Выведем уравнение оси симметрии.
Квадратное уравнение параболы: y = ax 2 + bx + c (парабола вверх/вниз).
Постоянный член ‘c’ не влияет на параболу. Поэтому рассмотрим, что y = ax 2 + bx.
Ось симметрии является средней точкой двух пересечений с х. Чтобы найти точку пересечения, подставьте y = 0.
x(ax+b)=0
x = 0 и (ax+b)=0
x = 0 и x = -b/a
формула средней точки x = (x 1 + x 2 ) / 2
x= [0 + (-b/a)] / 2
Следовательно, x = -b/2a
Примечание: Если парабола открыта слева/справа, то найдите середину y -перехватывает.
Найти ось симметрии
Пример 1: Найти ось симметрии квадратного уравнения y = x 2 – 4x + 3.
Решение:
Дано: y = x 2 – 4x + 3
Использование формула оси симметрии,
x = -b/2a
x = -(-4)/2(1)
x = 4/2
= 2
Следовательно, ось симметрии уравнения y = x 2 – 4x + 3 равно x = 2.
Пример 2: Найдите ось симметрии параболы y = 4x 2 .
Решение:
Используя формулу оси симметрии а у = 4x 2 равно x = 0,
Идентификация оси симметрии
Определим ось симметрии данной параболы, используя формулу, изученную в предыдущем разделе.
1) Рассмотрим уравнение y = x 2 – 3x + 4. Сравнивая это с уравнением стандартной формы параболы (y = ax 2 + bx + c), имеем
a = 1, b = -3 и c = 4
Это вертикальная парабола.
Таким образом, он имеет вертикальную ось симметрии.
Мы знаем, что x = -b/2a есть уравнение оси симметрии.
x = -(-3)/2(1) = 1,5
x = 1,5 – ось симметрии параболы y = x 2 – 3x + 4.
2) Рассмотрим другой пример. х = 4у 2 +5у+3.
Сравнивая со стандартной формой квадратного уравнения, получаем a = 4, b = 5 и c = 3. Эта парабола горизонтальна, и ось симметрии тоже горизонтальна.
Мы знаем, что y = -b/2a есть уравнение оси симметрии.
y = -b/2a
y = -5/2(4)
y = -0,625
3) Если даны две точки, находящиеся на одинаковом расстоянии от вершины параболы, то определяем уравнение оси симметрии путем нахождения середины этих точек. Предположим, что две точки (3, 4) и (9, 4) являются точками на параболе, тогда вершина проходит через точку пересечения, которая образует середину этих заданных точек. Таким образом, x = (3+9)/2 = 12/2 = 6. Следовательно, уравнение оси симметрии имеет вид x = 6,9.0005
Пример: Если ось симметрии уравнения y = qx 2 – 32x – 10 равна 8, то найдите значение q.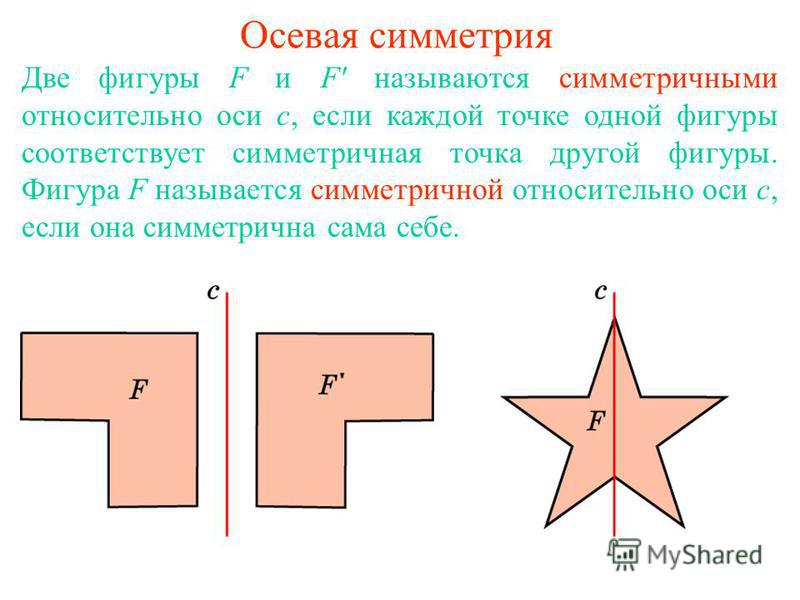
Решение: Дано,
y = qx 2 – 32x – 10
Ось симметрии x = 8
По формуле:
x = – b/2a
, где a = q, b = -32 и x = 8
8 = -(-32) / (2 × q)
8 = 32/2q
16q = 32
q = 2
Следовательно, значение q = 2
Важные замечания по оси симметрии
- Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, являющиеся зеркальным отображением друг друга.
- Для параболы y = ax 2 + b x+c ось симметрии определяется как x = -b/2a
- Правильный многоугольник с ‘n’ сторонами имеет ‘n’ осей симметрии.
☛ Статьи по теме:
- Линии симметрии в прямоугольнике
- Линии симметрии параллелограмма
Часто задаваемые вопросы об оси симметрии
Что такое ось симметрии в алгебре?
Ось симметрии — воображаемая линия, которая делит фигуру на две одинаковые части, каждая из которых является зеркальным отражением друг друга.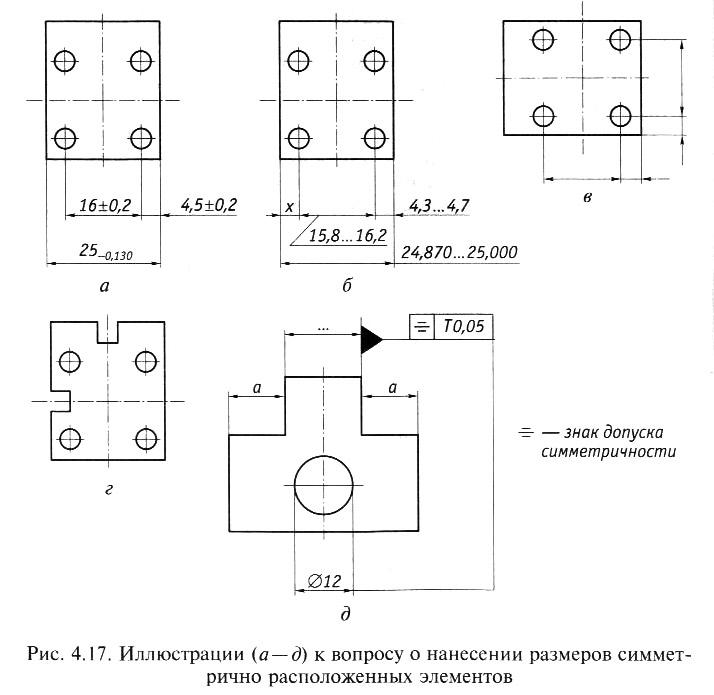
Правильный многоугольник из n сторон имеет n осей симметрии.
Что такое определение оси симметрии?
Ось симметрии — воображаемая прямая, которая делит фигуру на две одинаковые части или делает фигуру симметричной. Например, у квадрата 4, а у прямоугольника 2 оси симметрии.
Что такое формула оси симметрии?
Формула оси симметрии использует стандартную форму квадратного уравнения, а также форму вершины. Симметрия делит любую геометрическую фигуру на две равные половины. Формула оси симметрии задается как для квадратного уравнения со стандартной формой y = ax 2 + bx + c: x = -b/2a. Если парабола имеет форму вершины y = a(x-h) 2 + k, то формула будет следующей: x = h.
Какая формула используется для расчета оси симметрии стандартной формы?
Формула, используемая для нахождения оси симметрии квадратного уравнения стандартной формы y = ax 2 + bx + c, выглядит следующим образом: x = -b/2a.
Что такое формула оси симметрии для формы вершины?
Квадратное уравнение представляется в вершинной форме как: y = a(x−h) 2 + k , где (h, k) — вершина параболы. Поскольку ось симметрии и форма вершины лежат на одной линии, формула x = h.
Найдите ось симметрии квадратного уравнения y = 5x
2 – 10х + 3. Дано: у = 5х 2 – 10х + 3
Используя формулу оси симметрии,
х = -b/2а
х = -(-10)/2(5)
х = 10/10
х = 1
Следовательно, ось симметрии уравнения y = 5x 2 – 10x + 3 равна x = 1.
Что такое ось симметрии параболы?
Ось симметрии — это прямая линия, которая делит параболу на две симметричные части. Он проходит через вершину параболы. Ось симметрии параболы может быть горизонтальной или вертикальной.
Как найти ось симметрии, используя вершинную форму уравнения?
Квадратное уравнение в вершинной форме имеет вид y = a(x-h) 2 +k.
Ось симметрии находится там, где вершина пересекает параболу в точке, обозначенной вершиной (h, k). h – координата x. а в вершинной форме x = h и h = -b/2a, где b и a – коэффициенты в стандартной форме уравнения, y = ax 2 + bx + c.
Что такое ось симметрии на графике?
Горизонтальная или вертикальная линия на графике, проходящая через вершину параболы, образует ось симметрии параболы. В случае любого другого графика осью симметрии является уравнение линии, которая делит фигуру на две равные части, одна из которых является зеркальным отражением другой.
Является ли ось симметрии такой же, как и линия симметрии?
Да, линия симметрии и ось симметрии совпадают. Это воображаемые линии, которые делят фигуру на две одинаковые части, каждая из которых является зеркальным отражением друг друга. Когда фигура складывается по этой линии, две части накладываются друг на друга.
Симметрия относительно оси | Purplemath
PointGraphs
Purplemath
«Симметрия» — это определение соответствия частей формы.
Например, говорят, что человеческое тело обладает «билатеральной» (то есть двусторонней) симметрией, потому что левая и правая половины тела внешне отражают друг друга, как вы можете видеть на изображении ниже:
Содержание продолжается ниже
MathHelp.com
Симметрия
Но эта симметрия применима только к базовой структуре нашего тела; большая часть наших внутренностей, наших органов не совпадают, как вы можете видеть на изображении справа: смотрите, как печень (коричневая) и желудок (розовый) меняются сторонами, когда органы переворачиваются.:
(Рисунок выше анимирован на “живом” сайте.)
Пунктирная линия, проходящая по середине первого рисунка вверху, называется “осью симметрии”.
Если вы представляете изображение с двусторонней симметрией как нарисованное на листе прозрачного пластика с шампуром для шашлыка, пробитым через пунктирную линию, вы можете повернуть шампур (и, следовательно, лист) на 180° и в конечном итоге посмотреть на том же фото, но с другой стороны пластикового листа:
(Рисунок выше анимирован на “живом” сайте.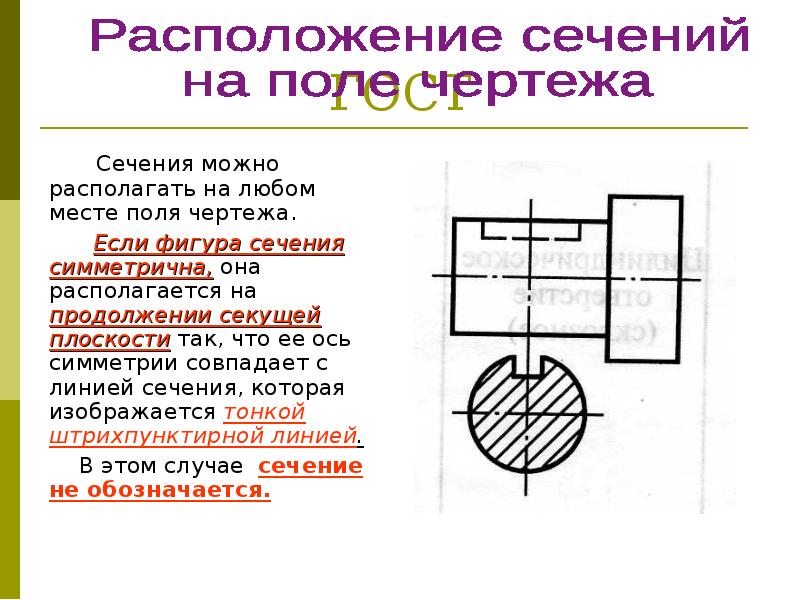
)
Фигура имеет столько симметрий, сколько шпажек может быть на ее пластиковом листе.
Например, прямоугольник можно вращать через его середину, поэтому прямоугольник имеет две симметрии.
(Рисунок выше анимирован на “живом” сайте.)
Квадрат также можно вращать по диагонали, поэтому квадрат имеет четыре симметрии.
(Рисунок выше анимирован на «живом» сайте.)
Треугольник может иметь одну или три оси симметрии, но обычно не имеет ни одной. Например:
одна линия симметрии:
три линии симметрии:
нет линий симметрии:
И круг имеет бесконечно много линий симметрии, так как любая линия, проходящая через его центр (то есть любой диаметр) также является осью симметрии.
При работе с симметрией относительно линии вас обычно спрашивают о симметрии относительно оси. С параболами (и другими кониками) вас могут спросить о симметрии около любая строка . В любом случае концепции одинаковы, потому что:
Ось x – это просто линия y = 0, а ось y – это просто линия x = 0.
Вот Некоторые примеры этих типов симметрии:
Парабола y = x 2 − 4 показана ниже:
как линия x = 0. Эта линия отмечена зеленым цветом на рисунке. Говорят, что граф «симметричен относительно y -ось”, и эту линию симметрии также называют “осью симметрии” для параболы. 4 имеет линию (или ось) симметрии, но не симметричен ни по одной из осей (то есть он не симметричен относительно оси x или y ):
Осью здесь является линия 90 119 x 90 120 = 2, как отмечено зеленым выше. Если бы вас попросили «найти ось симметрии параболы», вы бы ответили «9».0119 x = 2″.
Однако, если бы вас спросили: “Симметричен ли график относительно какой-либо из осей?”, вы бы поняли, что они спрашивают только о симметрии либо относительно x , либо y .
Иногда вас будут спрашивать о симметрии графиков, которые не соответствуют функциям, а являются отношениями (то есть графики не проходят Тест вертикальной линии.
) Нефункциональные отношения могут иметь оси симметрии.Например, график y 2 = x + 4 симметрична относительно оси x – ось. Если бы вас спросили, симметричен ли этот график относительно какой-либо из осей, вы бы ответили: «Да, относительно оси x ». Если бы вас спросили об оси симметрии (боковой) параболы, вы бы сказали: «Линия y = 0».
С другой стороны, сдвинутая парабола ( y − 2) 2 = x + 4 имеет ось симметрии, но не симметричен ни по одной из (обычных) осей:
Если бы вас спросили: «Симметричен ли этот график относительно любой оси ?», вы бы ответили: «Нет». Если бы вас спросили об оси симметрии, вы бы ответили: « y = 2» или «ось х ».
Другими словами, ваш ответ зависит от контекста. Если вы находите «четные» функции, вы будете рассматривать один вид симметрии (то есть симметрию относительно и -ось). Если вы посмотрите на графики коник, вы увидите другой вид симметрии (то есть симметрию относительно 90 119 любой прямой линии 90 120, обычно параллельной одной из 90 119 x 90 120 – и 90 119 y 90 120 -).