Высота профиля шины: что это такое?. Car tyres TD KAMA of Russia
1. Что такое высота профиля шины и как её вычислить?
2. На что влияет профиль шины?
3. Увеличение профиля шины: плюсы и минусы
4. Уменьшение профиля шины: плюсы и минусы
5. Нужно ли менять высоту профиля?
Профиль шины – один из ключевых параметров, на который нужно обращать внимание при выборе автомобильных покрышек. Для каждого автомобиля производитель, как правило, разрабатывает рекомендации касательно того, какого размера должна быть шина и какие отклонения в этих размерах допустимы. Отступления от заданного особенно часто касаются высоты профиля шины. На что влияет профиль шины, и так ли необходимо его менять? Разбираемся.
Что такое высота профиля шины и как её вычислить?
Если говорить просто, то высота профиля шины – это практически её толщина, то есть расстояние от диска до самой внешней поверхности протектора.
Загвоздка в том, что в маркировке на самой автомобильной покрышке высота профиля не указывается непосредственно в миллиметрах – она зависит от ширины покрышки.
Например, маркировка сообщает, что перед нами покрышка размерности:
215/50 R17
Ширина составляет 215 мм, высота профиля – 50% от этой ширины, а значит: 215*0,5=107,5 мм. Что важно в этой системе расчёта? Что при разной ширине покрышек с тем же значением высоты в процентах, высота на самом деле будет разной. Так, у шин 225/50 высота профиля будет составлять уже 225*0,5=112,5 мм. Так что пусть совпадение чисел после дробной черты на маркировке вас не вводит в заблуждение – при разной ширине высота тоже будет разная.
Маркировку R17 в разговорной речи нередко называют радиусом колеса, однако это не верно. R означает радиальную конструкцию (каким способом укладывается корд в шине), а цифра – посадочный или внутренний диаметр покрышки в дюймах.
Маркировка американских автомобильных шин отличается от европейских. Она представляется в виде
35×12.50 R15
Данных о высоте профиля тут нет, а все размеры измеряются в дюймах. 35 дюймов – внешний диаметр шины, 12,50 – ширина покрышки, ну а R15 – уже знакомые нам 15 дюймов посадочного диаметра. Чтобы высчитать профиль, подключаем к арифметике геометрию: из внешнего диаметра вычитаем внутренний, получаем «толщину» покрышки по обе стороны от диска, делим её на два и получаем профиль. (35-15)/2= 10 дюймов. Перевести в метры можно по схеме 1 дюйм = 2,54 см. Таким образом профиль шины – 25,4 см или 254 мм.
На что влияет профиль шины?
Как показывает практика, даже небольшое отступление от заданных производителем параметров шин может оказать влияние на то, как автомобиль поведёт себя на дороге. Так, шины с низким профилем и более крупными дисками легче управляются на поворотах, а высокий профиль шины увеличивает проходимость.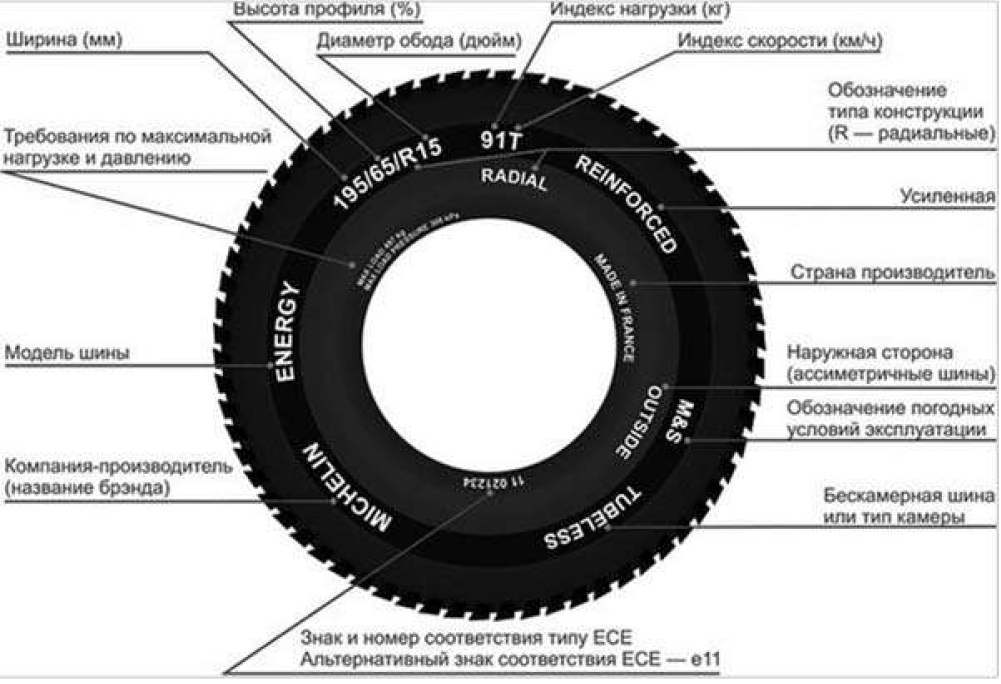
Получается, даже небольшими изменениями высоты профиля можно немного, но адаптировать автомобиль под свой стиль вождения и дорожные условия.
Насколько далеко можно отходить от оптимальной размерности – это уже другой вопрос. Уменьшать и увеличивать профиль шины можно и без изменений диаметров колеса, достаточно выбирать соответственно больший или меньший диск. Если же весь диаметр шины увеличится, то могут возникнуть проблемы: при движении покрышка будет задевать колесую арку или подкрылок, что грозит повреждениями. Да и само колесо станет ощутимо тяжелее, что ляжет дополнительной нагрузкой на подвеску. Подобные изменения хорошо выносят внедорожники, поскольку они рассчитаны на допнагрузку, а вот владельцам обычных легковых авто стоит лишний раз подумать.
Увеличение профиля шины: плюсы и минусы
Плюсы:
– при сохранении ширины покрышки, небольшое увеличение профиля сделает вождение более мягким, особенно при проезде препятствий;
– снижается риск пробоя боковины шины;
– шины с большим диаметром (на 1-2 размера) дают более высокую посадку, что повышает проходимость шины.
Минусы:
– слишком высокий профиль шины плохо скажется на показателях торможения и прохождения поворотов;
– шины с высоким профилем весят больше, что даёт дополнительную нагрузку на подвеску и сами покрышки при движении.
Уменьшение профиля шины: плюсы и минусы
К уменьшению профиля шины прибегают не так часто. Обычно это связано с желанием придать автомобилю более стильный и агрессивный вид. Шины с низким профилем и широким диском обычно удел спортивных автомобилей и автомобилей высокого класса со спортивным уклоном. И не зря.
Плюсы:
– низкопрофильные шины улучшают отзывчивость автомобиля на управление и показатели торможения;
– шины с низким профилем более устойчивы к деформации при манёврах и на поворотах;
– лучшее сцепление с ровной дорогой.
Минусы:
– низкопрофильные шины требовательны к качеству дороги, поскольку на неровной ухабистой поверхности комфорт вождения на таких покрышках резко падает;
– шины с низким профилем более шумные;
– риск деформации при длительной стоянке из-за высокого давления и увеличенного пятна контакта шины с поверхностью.
Нужно ли менять высоту профиля? Выводы
1. Низкопрофильные шины приспособлены к скоростной езде на трассах и ровных магистралях, на отечественных дорогах они вряд ли покажут себя с лучшей стороны.
2. Увеличение профиля шины с сохранением диаметра диска повышает проходимость автомобиля; увеличение профиля при соответственном уменьшении диска увеличивает комфорт вождения по неровным дорогам.
3. Производители советуют отступать от рекомендованных размеров профиля шины не более чем на 3% для легковых автомобилей.
4. Изменение профиля шины влияет на то, как поведёт себя на дороге ваш автомобиль. Изменится отзывчивость, мягкость движения, скорость разгона и торможения и многие другие характеристики, к которым придётся заново привыкать.
Маркировка шин. Как правильно определить параметры шин
Вы хотите выбрать шину для вашего авто, но плохо разбираетесь в маркировке шин? Это не проблема! В данном разделе, мы поможем вам разобраться: какие бывают параметры шины, что они означают, и какая именно покрышка подходит для вашего автомобиля.
Подобрать шины / каталог шинРасшифровка маркировки шин.
195/65 R15 91 T XL
195 — это ширина шины в мм.
65 — Пропорциональность, т.е. отношение высоты профиля к ширине. В нашем случае оно равно 65%. Проще говоря, при одинаковой ширине, чем больше этот показатель, тем шина будет выше и наоборот.
Обычно эту величину называют просто — «профиль».
Поскольку профиль шины это величина относительная, то важно учитывать при подборе резины, что если вы вместо типоразмера 195/65 R15 захотите поставить автошины с размером 205/65 R15, то увеличится не только ширина покрышки, но и высота! Что в большинстве случаев недопустимо! (за исключением случаев, когда оба этих типоразмера указаны в книжке по эксплуатации авто). Точные данные по изменению внешних размеров колеса вы можете рассчитать в специальном шинном калькуляторе.
Если это соотношение не указано (например, 185/R14С), значит оно равно 80-82% и шина называется полнопрофильной. Усиленные шины с такой маркировкой обычно применяют на микроавтобусах и легких грузовичках, где очень важна большая максимальная нагрузка на колесо.
R — означает автошину с радиальным кордом (по сути, сейчас почти все шины делаются именно так).
Многие ошибочно полагают, что R- означает радиус шины, но это именно радиальная конструкция автошины.
Бывает еще диагональная конструкция (обозначается буквой D), но в последнее время ее практически не выпускают, поскольку ее эксплуатационные характеристики заметно хуже.
15 — диаметр колеса (диска) в дюймах. (Именно диаметр, а не радиус! Это тоже распространенная ошибка). Это «посадочный» диаметр покрышки на диск, т.е. это внутренний размер шины или наружный у диска.
91 — индекс нагрузки. Это уровень предельно-допустимой нагрузки на одно колесо. Для легковых автомобилей он обычно делается с запасом и при выборе шин не является решающим значением, (в нашем случае ИН — 91 — 670 кг.). Для микроавтобусов и небольших грузовиков этот параметр очень важен и его обязательно необходимо соблюдать.
Таблица индексов нагрузки шины:
T — индекс скорости шины. Чем он больше, тем с большей скоростью вы можете ездить на данной покрышке, (в нашем случае ИС — Н — до 210 км/ч).
Говоря про индекс скорости автошины хочется отметить, что этим параметром производитель покрышек гарантирует нормальную работу резины при постоянном движении машины с указанной скоростью в течении нескольких часов.
Таблица индексов скорости:
Маркировка американских шин:
Существуют две различные маркировки американских шин. Первая очень похожа на европейскую, только перед типоразмером ставится буквы «P» (Passanger — для легковой машины) или «LT» (Light Truck — лёгкий грузовик). Например: P 195/60 R 14 или LT 235/75 R15. И другая маркировка автошины, которая принципиально отличается от европейской.
Например: 31×10.5 R15 (соответствует европейскому типоразмеру 265/75 R15)
31 — внешний диаметр шины в дюймах.
10.5 — ширина шины в дюймах.
R — автошина радиальной конструкции (более старые модели автошин были с диагональной конструкцией).
15 — внутренний диаметр шины в дюймах.
Вообще говоря, если не считать непривычных нам дюймов, то американская маркировка автошин логичная и более понятная, в отличае от европейской, где высота профиля покрышки непостоянна и зависит от ширины автошины. А тут все просто с расшифровкой: первая цифра типоразмера — внешний диаметр, вторая — ширина, третья — внутренний диаметр.
Дополнительная информация указываемая в маркировке на боковине шины:
XL или Extra Load — усиленная шина, индекс нагрузки которой выше на 3 единицы, чем у обычных автошин того же типоразмера. Другими словами если на данной шине указан индекс нагрузки 91 с пометкой XL или Extra Load, то это значит, что при данном индексе, шина способна выдержать максимальную нагрузку в 670 кг вместо 615 кг (смотреть таблицу индексов нагрузки шин).
M+S или маркировка покрышки M&S (Mud + Snow) — грязь плюс снег и означает, что шины всесезонные или зимние.
На многих летних покрышках для внедорожников указывается M&S. Однако эти шины нельзя эксплуатировать в зимнее время, т.к. зимние шины имеют совсем другой состав резины и рисунок протектора, а значок M&S указывает на хорошие показатели проходимости автошины.
All Season или AS всесезонные шины. Aw (Any Weather) — Любая погода.
Пиктограмма * (снежинка) — резина предназначена для использования её в суровых зимних условиях. Если на боковине шины нет этой маркировки, то эта автошина предназначена для использования только в летних условиях.
Aquatred, Aquacontact, Rain, Water, Aqua или пиктограмма (зонтик) — специальные дождевые шины.
Outside и Inside; ассиметричные шины, т.е. важно не перепутать какая сторона наружная, а какая внутренняя. При установке надпись Outside должна быть с наружной стороны автомобиля, а Inside — с внутренней.
RSC (RunFlat System Component) — шины RunFlat — это покрышки, на которых можно продолжать движение на автомобиле со скоростью не более 80 км/ч при ПОЛНОМ падении давления в шине (при проколе или порезе).
На этих шинах, в зависимости от рекомендаций производителя, можно проехать от 50 до 150 км. Разные производители автошин используют различные обозначения технологии RSC. Например: Bridgestone RFT, Continental SSR, Goodyear RunOnFlat, Nokian Run Flat, Michelin ZP и т. д.
Rotation или стрелка эта маркировка на боковине шины означает направленную шину. При установке покрышки нужно строго соблюдать направление вращения колеса, указанное стрелкой.
Tubeless — бескамерная шина. При отсутствии данной надписи покрышка может использоваться только с камерой. Tube Type — обозначает, что эта покрышка обязательно должна эксплуатироваться только с камерой.
Max Pressure; максимально допустимое давление в шине. Max Load — максимально допустимая нагрузка на каждое колесо автомобиля, в кг.
Reinforced или буквы RF в типоразмере (например 195/70 R15RF) означают, что это усиленная шина (6 слоёв).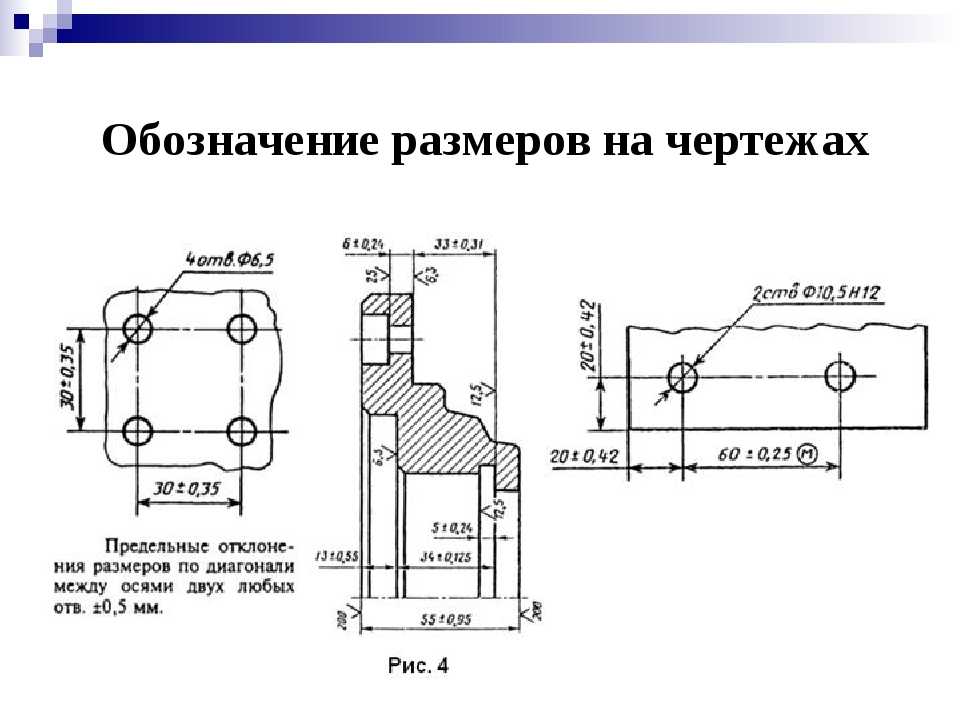
Буква С в конце типоразмера (например 195/70 R15C) обозначает грузовую шину (8 слоёв).
Radial эта маркировка на резине в типоразмере означает, что это авторезина радиальной конструкции. Steel означает, что в конструкции шины присутствует металлический корд.
Буква E (в кружочке) — шина соответствует европейским требованиям ECE (Economic Commission for Europe). DOT (Department of Transportation — Министерство транспорта США) — американский стандарт качества.
Temperature А, В или С термостойкость авторезины при высоких скоростях на испытательном стенде (А — наилучший показатель).
Traction А, В или С — способность шины к торможению на влажном дорожном полотне.
Treadwear; относительный ожидаемый километраж пробега по сравнению со специальным стандартным тестом США.
TWI (Tread Wear Indiration) — указатели индикаторов износа протектора автошины.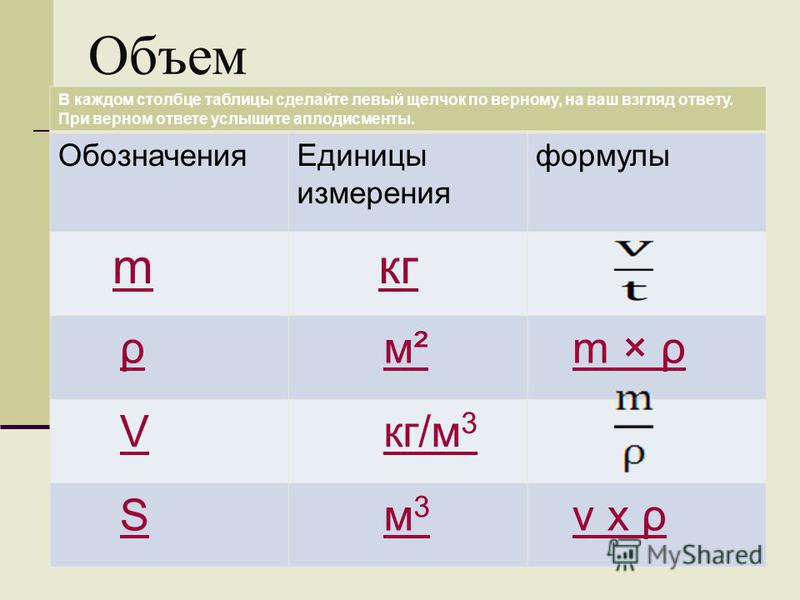
Маркировка на колесе TWI также может быть со стрелкой. Указатели располагаются равномерно в восьми или шести местах по всей окружности покрышки и показывают минимально допустимую глубину протектора. Индикатор износа выполняется в виде выступа с высотой 1.6 мм (минимальная величина протектора для легких автомобилей) и располагается в углублении протектора (как правило, в водоотводящих канавках).
DOT — Закодированный адрес производителя, код размера шины, сертификат, дата выпуска (неделя/год).
Подобрать шины / каталог шинКак записывать размеры в футах и дюймах
Изображение Public Domain из Википедии CommonsИтак, вам нужно написать что-то вроде «Высота: 5 футов» или «Длина: 9 футов», но вы не знаете правильных сокращений. Что ж, эта статья для вас!
Существует несколько различных способов написания измерений в тексте и сокращений измерений.
Содержание
Запись размеров в футах
Наиболее распространенной единицей длины в США является фут (сокращенно фут).
Один фут равен 12 дюймам.
При написании «Высота: 5 футов» вы можете сократить это до «Высота: 5 футов».
Чтобы написать «футы», вы должны использовать символ «штрих», который представляет собой одинарную кавычку « ».
Для обозначения дюймов необходимо использовать двойные кавычки «.
«Длина: 9 футов» можно было бы сократить до «Длина: 9 футов».
Футы или футы?
Давайте вспомним в этом контексте, что множественное число FOOT — это FEET.
В неформальной беседе «футы» обычно заменяют на «футы», хотя грамматически «футы» правильны, за исключением случаев, когда вы говорите о чем-то, что измеряется одним футом.
Например, несмотря на то, что «пять футов два дюйма» является грамматически правильным, вы часто слышите, как люди говорят «пять футов два дюйма», что также правильно в отношении повседневного использования. Люди, особенно в Соединенных Штатах, просто так разговаривают, хотя это и неправильно со строго грамматической точки зрения.
Запись размеров в других единицах длины
Существуют также другие единицы длины, которые обычно используются в Соединенных Штатах, например, ярд (сокращенно ярд), который равен 3 футам.
Один фут равен двенадцати дюймам, поэтому один ярд равен 36 дюймам.
Существуют также единицы длины, используемые в других странах, такие как метр (мм), километр (км).
Чтобы написать «Высота: 5 ярдов», вы должны сократить это до «Высота: 5 ярдов» или, по желанию, «Высота: 5 футов».
Когда вы пишете «Длина: 9 метров», вы должны сокращать это как «Длина: 9 метров». Чтобы сказать «Сегодня мы прошли 10 км», вы можете написать «Сегодня мы прошли 10 км.
Запись размеров в единицах площади
В дополнение к единицам длины существуют также единицы площади, такие как квадратный фут (сокращенно фут 2 ), который равен 144 дюймам. Один квадратный фут равен одному квадратному ярду, поэтому одна квадратная миля равна 640 акрам.
Для того, чтобы написать «Площадь: 1000 квадратных футов», вы должны сократить ее как «Площадь: 1000 квадратных футов» или, по желанию, «Площадь: 1000 футов 2 ».
Если вы хотите написать «Размер: 5 квадратных миль», вы можете сократить его до «Размер: 5 квадратных миль» (пробел между количеством квадратных футов и диаметром площади не является обязательным).
Единицы объема
Существуют также единицы измерения объема, такие как кварты (qt) и галлоны.
Один галлон равен 4,8 литра (жидкость США).
И одна кварта равна 32 жидким унциям.
Итак, один галлон примерно равен 128 жидким унциям.
Чтобы написать «Объем: 24 кварты», вы должны сократить его как «Объем: 24 кварты».
Если вы хотите сказать «Мы заправили наш 10-галлонный бак бензином», вы можете написать «Мы заполнили наш 10-галлонный бак бензином».
Единицы веса
Наконец, есть единицы измерения веса, такие как фунты (lbs) и килограммы (kg).
Один фунт равен 16 унциям, поэтому один килограмм равен 2,2 фунта.
Чтобы написать «Вес: 350 фунтов», вы должны сократить его до «Вес: 350 фунтов».
Вы можете переписать выражение «Масса: 10 кг», сократив его до «Масса: 10 кг».
Чтобы сказать «Я вешу 220 фунтов», вы должны написать «Я вешу 220 фунтов».
Вместо «Он весит 77 кг» можно написать «Он весит 77 кг».
Итак, теперь, когда вы знаете все сокращения, пришло время попрактиковаться в понимании измерений. Ниже приведены несколько упражнений.
Dpatel0546, CC BY-SA 4.0Упражнение 1
Запишите следующие измерения в футах и дюймах:
- Высота: 5 футов 2″
- Ширина: 10 футов 6 дюймов
- Длина: 3 фута 4 дюйма
ОТВЕТ
- Высота пять футов два дюйма. НЕОФИЦИАЛЬНО: «Его рост пять футов два дюйма».
- Ширина десять футов шесть дюймов. НЕОФИЦИАЛЬНО: «Он был шириной десять футов шесть дюймов».
- Три фута четыре дюйма в длину. НЕОФИЦИАЛЬНО: «Это три фута четыре дюйма в длину».
Упражнение 2
Запишите следующие измерения в ярдах и дюймах/сантиметрах.
- Высота: 5 ярдов 1 дюйм
- Длина: 9 ярдов 3 дюйма
ОТВЕТ
- Высота пять ярдов и один дюйм.
- Девять ярдов и три дюйма в длину.
Упражнение 3
Запишите следующие измерения в метрах и сантиметрах/миллиметрах.
- Высота: 1 м 76 см
- Длина: 7 м 21 см
ОТВЕТ
- Его высота один метр и семьдесят шесть сантиметров. ИЛИ: Его высота сто (и) семьдесят шесть сантиметров.
- Его длина семь метров и двадцать один сантиметр. ИЛИ: Его длина семьсот двадцать один сантиметр.
Упражнение 4
Запишите следующие измерения в ярдах, футах, дюймах и сантиметрах.
- 1 ярд 10 футов 3 дюйма
- 2 кварты 4 части 1 фл
- 4 км
ОТВЕТ
- Один ярд десять футов и три дюйма.
- Две кварты, четыре пинты и одна жидкая унция.
- Четыре километра.
Упражнение 5
Запишите следующие измерения в галлонах, квартах, пинтах, жидких унциях и миллилитрах.
- 1 галлон 3 кварты 12 pt 2 жидких унции
- 2 л 5 кварт 20 pt 1 мл
ОТВЕТ
- Один галлон три кварты двенадцать пинт и две унции жидкости.
- Два литра, пять кварт, двадцать пинт и один миллилитр.
В заключение
Вот и все! Теперь вы знаете все сокращения для обозначения размеров в футах, ярдах, метрах и галлонах.
РЕСУРСЫ
Как записать размеры мебели
Как правильно писать и расставлять знаки препинания
Деловой расчет
Что такое функция?
Мир природы полон взаимосвязей между изменяющимися величинами. Когда мы видим эти отношения, для нас естественно задаться вопросом: Если я знаю одну величину, могу ли я тогда определить другую?
Это устанавливает идею входной величины, или независимой переменной, и соответствующей выходной величины, или зависимой переменной. Отсюда мы получаем понятие функциональной связи, в которой выход может быть определен из входа.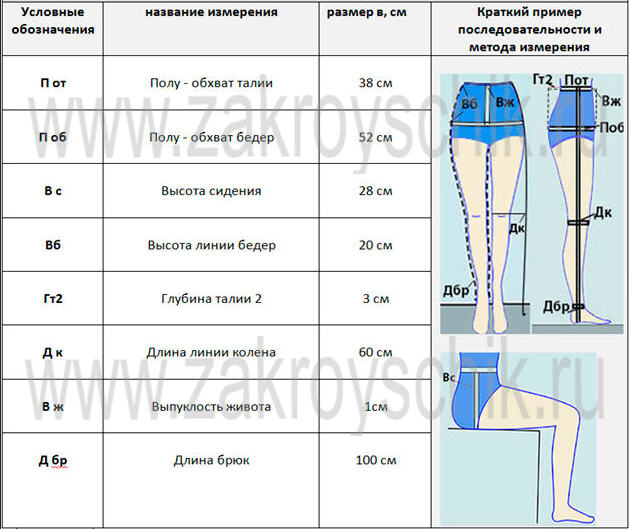
Для некоторых величин, таких как рост и возраст, между этими величинами, безусловно, существует взаимосвязь. Учитывая конкретного человека и любой возраст, достаточно легко определить его рост, но если бы мы попытались обратить эту зависимость и определить рост по заданному возрасту, это было бы проблематично, поскольку большинство людей сохраняют один и тот же рост в течение многих лет.
Функция Функция — это правило отношения между входной или независимой величиной и выходной или зависимой величиной, в которой каждое входное значение однозначно определяет одно выходное значение. Мы говорим выход является функцией входа.
Пример 1
В приведенном выше примере с ростом и возрастом является ли рост функцией возраста? Является ли возраст функцией роста?
В приведенном выше примере с ростом и возрастом было бы правильно сказать, что рост является функцией возраста, поскольку каждый возраст однозначно определяет рост.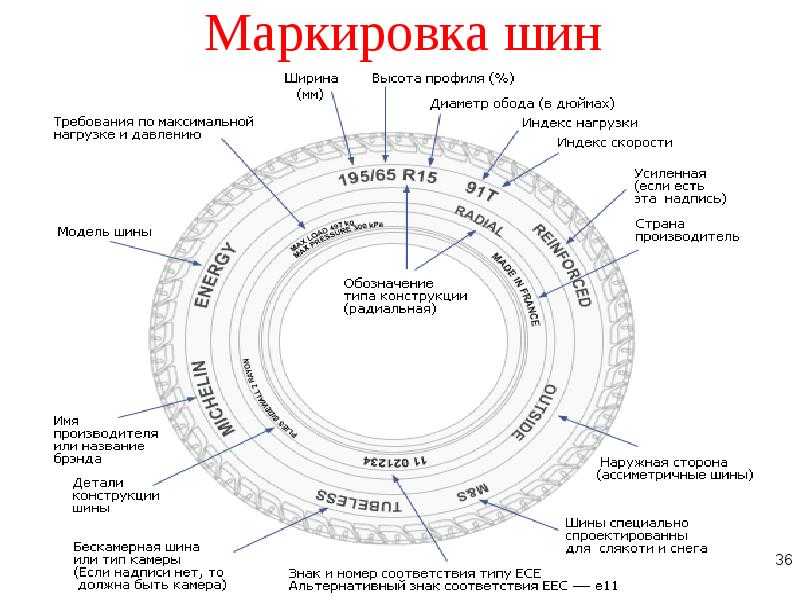
Например, на мой 18-й день рождения у меня был ровно один рост 69 дюймов.
Однако возраст не является функцией роста, поскольку один входной рост может соответствовать более чем одному выходному возрасту. Например, для ввода роста 70 дюймов имеется более одного вывода возраста, так как я был 70 дюймов в возрасте 20 и 21 года.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Обозначение функции
Для упрощения написания выражений и уравнений, содержащих функции, часто используется упрощенная запись. Мы также используем описательные переменные, чтобы помочь нам запомнить значение величин в задаче.
Вместо записи рост является функцией возраста,
мы могли бы использовать описательную переменную \(h\) для представления роста и мы могли бы использовать описательную переменную \(a\) для представления возраста.
| “рост зависит от возраста” | если мы назовем функцию \(f\), мы напишем |
| “\(h\) есть \(f\) из \(a\)” | или проще |
| \(h = f(a)\) | мы могли бы вместо этого назвать функцию \(h\) и написать |
| \(ч(а)\) | , который читается как “\(ч\) из \(а\)” |
Помните, что мы можем использовать любую переменную для имени функции; обозначение \(h(a)\) показывает нам, что \(h\) зависит от \(a\).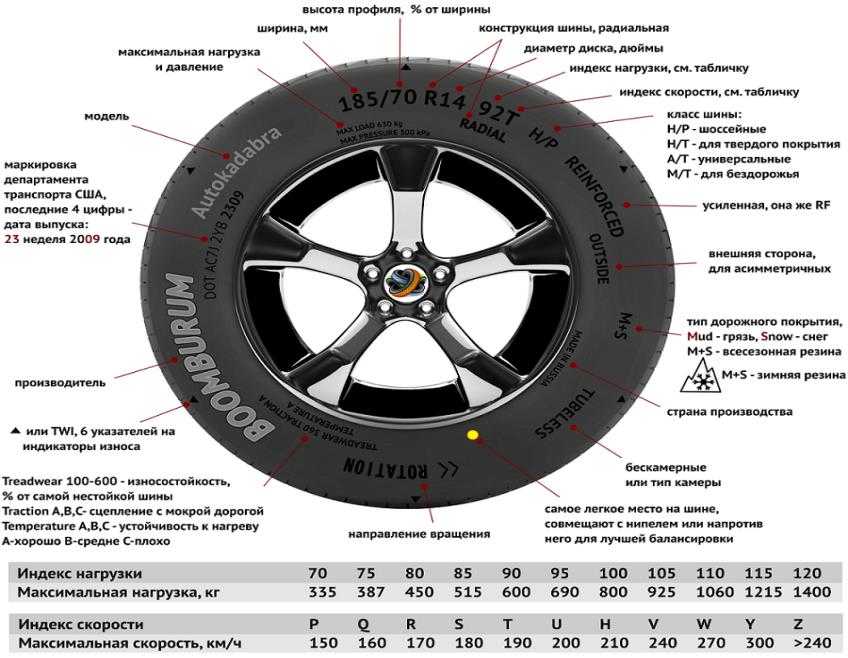
Значение \(a\)
нужно ввести в функцию \(h\)
, чтобы получить результат. Будьте внимательны – скобки указывают на то, что в функцию вводится возраст (Примечание: не путайте эти скобки с умножением!).
Обозначение функции
Обозначение output = \(f\)(input) определяет функцию с именем \(f\). Это будет читаться как вывод \(f\) ввода.
Пример 2
Функция \(N = f(y)\) дает число полицейских \(N\) в городе в год \(y\). Что нам говорит \(f(2005) = 300\)?
Когда мы читаем \(f(2005) = 300\), мы видим, что входная величина равна 2005, что является значением входной величины функции, года (\(y\)). Выходное значение равно 300, количество полицейских (\(N\)), значение выходного количества. Помните \(N=f(y)\). Это говорит нам о том, что в 2005 году в городе было 300 полицейских.
Таблицы как функции
Функции могут быть представлены разными способами: словами (как мы это делали в последних нескольких примерах), таблицами значений, графиками или формулами.
Представленный в виде таблицы, нам представлен список входных и выходных значений.
Эта таблица представляет возраст детей в годах и их соответствующий рост. В то время как некоторые таблицы показывают всю известную нам информацию о функции, эта конкретная таблица представляет лишь часть доступных данных о росте и возрасте детей.
| (ввод) \(a\), возраст в годах | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| (вывод) \(h\), высота в дюймах | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Пример 3
Какие из этих таблиц определяют функцию (если есть)?
| Вход | Выход |
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Вход | Выход |
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Вход | Выход |
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Первая и вторая таблицы определяют функции.
В обоих случаях каждый вход соответствует ровно одному выходу. Третья таблица не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Решение и оценка функций
Когда мы работаем с функциями, мы обычно делаем две вещи: вычисляем и решаю. Вычисление функции — это то, что мы делаем, когда знаем входные данные и используем функцию для определения соответствующего выхода. Вычисление всегда будет давать один результат, поскольку каждый вход функции соответствует ровно одному выходу.
Решение уравнений, включающих функцию, — это то, что мы делаем, когда знаем результат и используем функцию для определения входных данных, которые будут давать этот результат. Решение функции может привести к нескольким решениям, поскольку разные входные данные могут привести к одному и тому же результату.
Пример 4
Используя показанную таблицу, где \(Q=g(n)\)
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(Q\) | 8 | 6 | 7 | 6 | 8 |
a) Оценить \(g(3)\)
b) Решить \(g(n)=6\)
a) Оценить \(g(3)\): Оценка \(g(3)\ ) (читать: g of 3
) означает, что нам нужно определить выходное значение \(Q\) функции g при заданном входном значении \(n=3\). Глядя на таблицу, мы видим, что выход, соответствующий \(n=3\), равен \(Q=7\), что позволяет нам сделать вывод \(g(3) = 7\).
b) Решить \(g(n)=6\): Решение \(g(n) = 6\) означает, что нам нужно определить, какие входные значения \(n\) дают выходное значение 6. Глядя в таблице мы видим два решения: \(n = 2\) и \(n = 4\). Когда мы вводим 2 в функцию \(g\), наш результат равен \(Q = 6\). Когда мы вводим 4 в функцию \(g\), наш вывод также равен \(Q = 6\).
Графики как функции
Часто для определения функции можно использовать график отношения.
По соглашению графики обычно строятся с входным количеством по горизонтальной оси и выходным количеством по вертикали.
Пример 5
Какой из этих графиков определяет функцию \(y=f(x)\)?
Глядя на три приведенных выше графика, первые два определяют функцию \(y=f(x)\), поскольку каждому входному значению по горизонтальной оси соответствует ровно одно выходное значение, определяемое значением y график. Третий график не определяет функцию \(y=f(x)\), поскольку некоторые входные значения, такие как \(x=2\), соответствуют более чем одному выходному значению.
Тест вертикальной линии
Тест вертикальной линии — это удобный способ подумать о том, определяет ли график выход по вертикали как функцию входа по горизонтали. Представьте, что вы рисуете вертикальные линии на графике. Если любая вертикальная линия будет пересекать график более одного раза, то график не определяет только один вертикальный выход для каждого горизонтального входа.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Для вычисления функции с помощью графика необходимо взять заданный вход и использовать график для поиска соответствующего выхода. Для решения функционального уравнения с помощью графика необходимо взять заданный выход и посмотреть на график, чтобы определить соответствующий вход.
Пример 6
Учитывая приведенный ниже график,
а) Вычислите \(f(2)\).
б) Решите \(f(x) = 4\).
а) Чтобы оценить \(f(2)\), мы находим вход \(x=2\) на горизонтальной оси. Перемещение вверх по графику дает точку (2, 1), что дает результат \(y=1\). Итак, \(f(2) = 1\).
б) Чтобы решить \(f(x) = 4\), мы находим значение 4 на вертикальной оси, потому что если \(f(x) = 4\), то 4 является результатом. Перемещение по графику по горизонтали дает две точки с выходом 4: (-1,4) и (3,4). Они дают два решения \(f(x) = 4\): \(x = -1\) или \(x = 3\).
Это означает \(f(-1)=4\) и \(f(3)=4\), или, когда вход равен -1 или 3, выход равен 4.
Обратите внимание, что хотя график в предыдущем примере является функцией, получение двух входных значений для выходного значения 4 показывает нам, что эта функция не является однозначной.
Формулы как функции
Когда это возможно, очень удобно определять отношения с помощью формул. Если возможно выразить выход в виде формулы, включающей входную величину, то мы можем определить функцию.
Пример 7
Выразите соотношение \(2n + 6p = 12\) в виде функции \(p = f(n)\), если это возможно.
Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где \(p\) является функцией \(n\), что означает запись его как \(p =\) [что-то, включающее \ (н\)].
| \(2п + 6п = 12\) | вычесть \(2n\) с обеих сторон |
| \(6р = 12 – 2н\) | разделить обе части на 6 и упростить |
\[p=\frac{12-2n}{6}=\frac{12}{6}-\frac{2n}{6}=2-\frac{1}{3}n\]
Переписав формулу в виде \(p=\), теперь мы можем выразить \(p\) как функцию: \(p=f(n)=2-\frac{1}{3}n\)
Не каждое отношение можно выразить в виде функции с помощью формулы.
93+2\\=& -1+2\\=&1,\end{align*}\] что было желаемым результатом.
Основные функции набора инструментов
Есть несколько основных функций, имена и формы которых полезно знать. Мы называем их базовым набором функций .
Для этих определений мы будем использовать \(x\) в качестве входной переменной и \(f(x)\) в качестве выходной переменной.
Функции набора инструментов
| Константа: | \(f(x)=c\), где \(c\) – константа (число) 92}\)Квадратный корень: \(f(x)=\sqrt[2]{x}=\sqrt{x}\)Кубический корень: \(f(x)=\sqrt[3]{x}\) Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5 Одна из наших главных целей в математике — смоделировать реальный мир с помощью математических функций. При этом важно помнить об ограничениях тех моделей, которые мы создаем. В этой таблице показано соотношение между окружностью и высотой дерева по мере его роста.
Несмотря на тесную связь между ними, было бы, конечно, нелепо говорить о дереве с окружностью -3 фута или высотой 3000 футов. Когда мы определяем ограничения на входы и выходы функции, мы определяем домен и диапазон функции. Домен и диапазон Домен: Набор возможных входных значений для функции. Пример 9Используя приведенную выше древовидную таблицу, определите подходящий домен и диапазон. Мы могли бы объединить предоставленные данные с нашим собственным опытом и соображениями, чтобы аппроксимировать область определения и область значений функции \(h = f(c)\). Для домена возможные значения входной окружности c не имеют смысла иметь отрицательные значения, поэтому \(c > 0\). Точно так же для диапазона нет смысла иметь отрицательную высоту, а максимальная высота дерева может составлять 379 футов, поэтому разумный диапазон — футы. Более компактной альтернативой обозначению неравенства является обозначение интервала , в котором интервалы значений
обозначаются начальным и конечным значениями. Круглые скобки используются для
Пример 10Опишите интервалы значений, показанные на линейном графике ниже, используя построитель наборов и обозначения интервалов: Для описания значений x, лежащих в показанных выше интервалах, мы бы сказали, что |
Мы могли бы сделать обоснованное предположение о максимальном разумном значении или посмотреть, что максимальная измеренная окружность составляет около 119ноги. С этой информацией мы бы сказали, что разумный домен — ноги.