Типы рисунка – классификация обоев по типам рисунка
Типы рисунка
На обойной фабрике “ПАЛИТРА” принята классификация типов рисунка, благодаря которой все коллекции маркируются соответствующими обозначениями в каталоге.
Сюжетный рисунок
Сюжетный рисунок
[Theme]
Сюжетный рисунок превращает интерьер в роскошную арт-студию.
Портреты, города, животные, птицы и деревенские пейзажи – каждый образ состоит из множества мелких деталей, дополняющих основной тренд.
Поэтому сюжетный рисунок значит нечто большее, чем просто узор.
Обои с сюжетами
Абстракция и геометрия
Абстракция и геометрия
[Abstraction and Geometry]
Геометрические и абстрактные узоры – новая классика современного интерьера.
Притягательные сочетания прямых форм или извилистые линии создают бесконечную динамику пространства. Модные оптические эффекты дарят визуальный объем.
Геометрические элементы выбирают креативные люди, чувствующие красоту и гармонию.
Обои с геометрией
Орнамент
Орнамент
[Ornament]
Итальянские вензеля, старинные восточные орнаменты и арабские дамаски всегда считались атрибутом роскоши.
Благородные узоры на сложных фактурах обойных полотен, имитирующих бархатную или атласную ткань, подчеркивают престиж и элитарность интерьера.
Обои с орнаментами
Флористика
Флористика
[Floristic]
Цветочные и растительные узоры подчеркивают красоту природы в тропических джунглях, французском Провансе и суровых скандинавских мотивах.
Нежные букеты из лилий, архидей, лаванды, сирени приносят уют и романтику.
Крупные и мелкие цветы хорошо вписываются в разные интерьерные стили.
Обои с флористикой
Имитация
Имитация
[Imitation]
Имитация разнообразных материалов раскрывает творческую индивидуальность и свободу.
Текстуры старых деревянных досок, холодного камня, рогожки, бамбука или натуральной кожи создают гармонию в интерьере.
Рисунки в точности воспроизводят поверхности, подчеркивая связь с природой и экологичностью.
Обои с имитацией
Полоса
Полоса
[Stripe]
Обои в полоску великолепно комбинируются с классическими вензелями, нежными цветами и яркими геометрическими узорами, поэтому они остаются модным трендом уже много лет.
Вертикальные полосы помогают сгладить планировку комнаты, визуально увеличивая пространство. Ровное чередование линий расслабляет и наполняет гармонией. Полосы отлично подходят для зонирования пространства и создания акцента в любом интерьере.
Обои в полосу
Фоновые
Фон | Без рисунка
[Background]
Фоновые обои – прекрасный помощник любого обойного рисунка.
Такие обои можно использовать как в качестве компаньона, так и при отдельной оклейке, что позволяет оформить весь интерьер в едином стиле и создать в нем гармонию.
Фоновые обои
Классификация обоев
Помимо деления обоев по видам в рамках каждого вида существуют еще дополнительные классификации и характеристики обоев для стен.
1. По областям применения.
- Обои для жилых помещений ( внутри этого класса существует классификация до вида помещения в котором обои применяются, Например, для кухни,для спальни и т.п.)
- Обои для нежилых помещений ( внутри этого класса тоже существует классификация до вида помещения в котором обои применяются, Например, для кафе, для офиса и т.п.)
2. По водостойкости.
- Обои обычные – не выдерживают воздействие воды, им требуется только сухая протирка
- Обои водостойкие – выдерживают протирание влажной губкой или мягкой тряпочкой без применения моющих средств;
- Обои моющиеся – выдерживают протирание губкой или мягкой мокрой тряпкой с добавлением мягких моющих средств
- Обои супермоющиеся- можно мыть мокрой губкой или тряпкой, добавляя в воду небольшое количество ядрового мыла (сорт хозяйственного мыла, содержащий много жирных кислот), при этом обои не повреждаются.
Пятна от жира и растворителя не удаляются.
Пятна от жира и растворителя не удаляются.3. По степени выдерживаемой механической нагрузки.
- Обои обычные слабо переносят механическое воздействие
- Обои устойчивыепереносят незначительные механические нагрузки
- Обои высоко устойчивые переносят значительные нагрузки
4. По светостойкости.
- Обои обычные достаточная светостойкость
- Обои светоустойчивые хорошая светостойкость
- Обои с высокой степенью светоустойчивости очень хорошая светостойкость
5. По виду лицевой поверхности.
- Обои гладкие
- Обои с рельефным рисунком
- Обои с выдавленным рисунком
- Обои с глубоким выдавленным рисунком
- Обои легкие , их вес составляет менее 110 г/м?;
- Обои среднего веса 110-140 г/м?,
- Обои тяжелые вес более 140 г/м?.
7. По виду рисунка.
- Обои с рисунком,узором
- Обои без рисунка
8. По способу нанесения клея.
- Клей наносится на обои
- Клей наносится на стену
- Обои имеют собственный клееевой слой
9. По способу стыковки во время приклеивания.
- Обои без выравнивания не требуют совмещения рисунка
- Обои с прямым горизонтальным выравниванием (стыковкой)), одинаковый рисунок должен быть на одном уровне.
- Обои с суперточным выравниванием при наклеивании каждого последующего полотнища рисунок сдвигается на половину высоты элемента узора.
- Обои со смещенным рисунком
10. По способу удаления.
- Обои полностью удаляемые при удалении не остается ничего
- Обои не полностью удаляемые, после удаления остается нижний слой
- Обои удаляемые после замачивания
групп обоев: история
группа обоев: историякристаллографических групп и смежных тем
Людей всегда интересовали узоры, как плоскостные, так и пространственные.
Классификация узоров началась два с половиной тысячелетия назад, когда пифагорейцы открыли, что существует пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Архимед обобщил их до некоторых почти правильных тел, теперь называемых архимедовыми телами, таких как тела, состоящие из пятиугольников и шестиугольников, которые используются для футбольных мячей и мячей Buckyball.
Кеплер обнаружил другие почти правильные твердые тела и отметил правильную мозаику (замощение) плоскости. Есть только три правильных мозаики: одна из треугольников, одна из квадратов и одна из шестиугольников. Есть также несколько почти правильных мозаик, аналогичных архимедовым телам.
В семнадцатом веке Роберт Гук собрал «компанию пуль и несколько других очень простых тел», чтобы увидеть различные способы, которыми атомы могут быть расположены для построения кристаллов, в частности, кристаллов квасцов.
Классификация по двум и трем измерениям
В девятнадцатом веке началась классификация плоских и пространственных решеток и узоров.
Одна из проблем заключалась, конечно, в том, чтобы решить, когда разные паттерны демонстрируют одинаковую регулярность. Были разработаны различные методы классификации. Сначала изучались решетчатые структуры. Позже симметрии и то, как симметрии были связаны, использовались для более тонких различий. Решетки обычно анализировались с помощью квадратичных форм с использованием двух переменных в плоском случае и трех переменных в пространственном случае.
| В 1831 году Гессель впервые классифицировал 32 трехмерные точечные группы (конечные подгруппы ортогональной группы O(3), которые соответствуют классам трехмерных кристаллов. | JFC Hessel. Кристалл. Gehler’s Physikalische Wöterbuch , стр. 1023-1360. Швикерт, Лейпциг, 1830 г. Перепечатано в г. Оствальда в Klassiker der Exakten Wissenschaften. Engelmann, Leipzig, 1897. |
Все симметричные сети точек, которые могут иметь кристаллографическую симметрию, были геометрически найдены Франкенхаймом в 1835 г.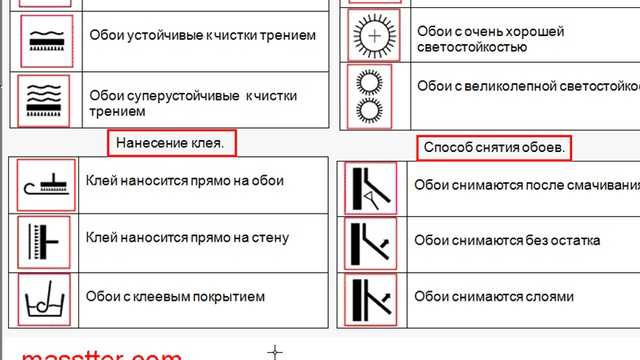 | Франкенхайм. Die Lehre von der Cohösion. Бреслау, 1835 г. |
| О. Родрикес. Des lois géométriques qui régissent les déplacements d’un systeme solide dan l’espace, et de la Variation des coordonées originant de ces deplacements рассматривает независимые причины, которые возникают при производстве. | |
| Эта теория классов кристаллов была систематизирована А. Браве, который классифицировал 14 типов пространственных решеток. См. также А. Гадолина (1871 г.) и П. Кюри (1884 г.). А. Шенфлис описал их с помощью теории групп в 189 г.1 (см. ниже). | А. Браве. Mé&moire sur les systèmes formé par des points distribués régulièrement sur un plan ou dans l’espace. Дж. Эколь Политех. 19 (1850), 1-128. Английский перевод: Мемуары 1, Кристаллографическое общество Америки, 1949 г. Также монография 4, Американская кристаллографическая ассоциация. А. Браве. Дж. Эколь Политех. 20 (1851), 102. |
| Дирихле описал то, что с тех пор известно как области Дирихле для решеток. (Нужна информация по Вороному.) | Г. Лежен Дирихле. Über die Reduction der Positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen. Journal für die reine und angewandte Mathematik 40 (1850), 209-227. |
| Г. Эйзенштейн. Tabelle der deducirten Positiven ternären quadritischen Formen, nebst den Resultaten neuer Forschungen über diese Formen, in besonderer Rücksicht auf ihre tabellarische Berechnung. Дж. Рейн Анжю. Мат. 41 (1851), 141-190. | |
| А. Ф. Мёбиус. Über das Gesetz der Symmetrie der Kristalle. Дж. Рейн Ангью. Мат. 43 (1852), 365-?. Über symmetrische Figuren. Там же. 44 (1852), 355-?. Также в собрании сочинений Мёбиуса II, стр. 349-372. | |
В общем исследовании теории групп движений Джордан описал общий метод определения всех возможных способов регулярно повторяющихся одинаковых группировок точек. | Камилла Джордан. Sur les groupes de Mouvements. ЧР Академ. науч. Париж 65 (1867), 229-232. Также Oeuvres de C. Jordan, vol. 4, стр. 113-116. Париж, Готье-Виллар, 1964 год. К. Джордан. Mémoire sur les groupes de movements. Энн. Мат. Пур. Приложение. (2) 2 (1868/1869), 167–215 и 322–345. Также Oeuvres, vol. 4, страницы 231-302. К. Джордан. Mémoire sur l’équivalence desformes. J. Ecole Polytech. 48 (1880), 112-150. Также Oeuvres, vol. 3, страницы 421-460. |
| Начиная с 1873 г. Зонке применял теорию Жордана к двух- и трехмерному пространству, но классификация была неполной. В 1879 году он описал 65 типов групп вращения в пространстве. | Леонхард Зонке. Die regelmässig ebenen Punkt systeme von unbegrenzter Ausdehnung. Borchardt J. 77, 47-102 и Berl. Монацбер. (1873), 578-583. Entwickelung einer Theorie der Krystallstruktur. Тойбнер, Лейпциг, 1879 г. Entwickelung einer Theorie der Krystallstruktur. З. Крист. Мин. 14 (1888), 417-425. |
| Е. Продам. Квадратные двойные и тройные формы. Дж. Матем. Чистый Appl. (3) 3 (1877), 21-60 и 153-207. | |
| В конце 19 века Федоров, Шенфлис и Барлоу классифицировали 17 групп обоев (групп двумерной кристаллографии) и 230 групп трехмерной кристаллографии. | |
Федоров писал в своей работе «Симметрия кристаллов », что, хотя он был знаком с работой Шенфлиса, он утверждал, что «такое совпадение в работах двух исследователей, как это, возможно, никогда прежде не наблюдалось в истории наука.” Это большое преувеличение. Они оба завершали классификацию, которая проводилась в течение некоторого времени, и поскольку классификация основывалась на одних и тех же принципах, они должны были достичь одних и тех же результатов. | Е. С. Федоров. Элементы изучения фигур. [Русский] Записки Императорского С.Петербургского Минералогического Общества [ Proc. С. Петерб. Минеральная. соц. ] (2) 21 (1885), 1-289. Симметрия конечных фигур. [Русский] (2) 28 (1891), 1-146. Симметрия в плоскости. [Русский] (2) 28 (1891), 345-390. Федоров Е.С. Симметрия кристаллов. Перевод с русского издания 1949 года. Американская кристаллографическая ассоциация, Нью-Йорк, 1971. |
| А. М. Шенфлис. Über Gruppen von Bewegungen. Матем. Анна. 28 (1886 г.), 319–342 и 29 (1887 г.), 50–80. Über Gruppen von Transformationen des Raumes in sich. там же. 34 (1889), 172-203. Кристаллическая система и кристаллическая конструкция. Тойбнер, Лейпциг, 1891 г. В. Барлоу. Über die geometrische Eigenchaften homogener starrer Strukturen. З. Крист. Мин. 23 (1894), 1-63. К. Рон. Einige Sätze über regelmässige Punktgruppen. Матем. Аннален, 53 (1900), 440-449. | |
| Х. Хилтон. Математическая кристаллография и теория групп движений. Кларендон, 1903 г. Г. Фробениус. Gruppentheoretische Ableitung der 32 Kristallklassen. С.-Б. Прейс. акад. Висс. (1911), 681-691. ( Gesammelte Abhandlungen. Springer, 1968, т. 3, стр. 519-529.) П. Ниггли. Геометрическая кристаллография дисконтинуумов. Гебрюдер Борнтрегер, 1919 г. Г. Полиа и П. Ниггли. Zeitschrift für Kristallographie und Mineralogie 69 (1924), 278-298. | |
| Стандарт для названий различных групп двумерной и трехмерной кристаллографии. | Н. Ф. М. Генри и К. Лонсдейл. International Tables for X-Ray Crystallography, vol. 1, Kynoch Press, Birmingham, England, 1952. |
там же. 25 (1896), 86-91.Классификация в высших измерениях
Проблема понимания многомерных кристаллографических групп должна была быть довольно важной, поскольку она составляла часть проблемы 18 проблем Гильберта. Давид Гильберт, ведущий математик того времени, выступил на Международном математическом конгрессе в Париже в 1919 г.00. Он предложил 23 достаточно общие проблемы, чтобы сосредоточить математические исследования. Его вопрос звучал так: «Существует ли в n -мерном евклидовом пространстве только конечное число существенно различных типов групп движений с фундаментальной областью? Двумерный и трехмерный случаи были известны, но не более многомерный случай». | Дэвид Гильберт. Гётт. Нахр. (1900), 253-297. Английский перевод: Математические задачи. Бык. амер. Мат. соц. 8 (1902), 437-479. Он-лайн html версия английского перевода. |
Бибербах решил эту проблему в 1910 году. Он доказал, что в любом измерении существует лишь конечное число групп. Он не определил фактическое число в каком-либо измерении, а только то, что их было конечно много. Бибербах показал, что эти группы были расширениями группы трансляций, которая изоморфна Z n , с помощью конечной подгруппы GL( n, Z ). Теперь группы когомологий используются для классификации расширений. Кроме того, группы, которые мы рассматриваем, часто называют группами Бибербаха. | Л. Бибербах. Über die Bewegungsgruppen des n – Dimensionsen euklidischen Raumes mit einem endlichen Fundamentalbereich. Гётт. Нахр. 1910, 75-84. Л. Бибербах. Über die Bewegungsgruppen der Euklidischen Räume, I, Math. Анна. 70 (1911), 297-336, и II, Мат. Анна. 72 (1912), 400-412. |
| В 1948 г. Зассенхаус дал алгоритм определения полного набора представителей типов n -мерных пространственных групп. | Über einen Algorithmus zur Bestimmung der Raumgruppen. Комментарий. Мат. Хелв. 21 (1948), 117-141. |
| В 1974 г. в Университете Северного Иллинойса проходил симпозиум по проблемам Гильберта, и Джон Милнор написал о проблеме 18. | Дж. Милнор. Проблема Гильберта 18: о кристаллографических группах, фундаментальных областях и упаковке сфер. Страницы 491-506 в Математические разработки, возникающие из проблем Гильберта , под редакцией Феликса Браудера. Американское математическое общество, 1976. |
| В середине 1970-х компьютеры помогли определить, что существует 4783 четырехмерных группы. | Гарольд Браун, Рольф Бюлов, Иоахим Нойбюзер, Ганс Вондрачек и Ханс Зассенхаус. Кристаллографические группы четырехмерного пространства . Wiley, New York, 1978. |
| Фактическое количество групп для размерностей больше четырех не определено, но были проведены частичные исследования. | Р. Л. Э. Шварценбергер. N-мерная кристаллография. Питман, Лондон, 1980 г. |
Арт
Ряд произведений искусства из разных культур и эпох изображают многие узоры обоев. Одним из недавних художников, извлекших пользу из их математической классификации, был М. К. Эшер. Благодаря своей дружбе с Г. С. М. Коксетером Эшер узнал о различных мозаиках, особенно о гиперболических мозаиках.
До оглавления
Назад к 17 группам обоев
К ссылкам и ссылкам
© 1997.
Дэвид Э. Джойс
Кафедра математики и информатики
Университет Кларка
Вустер, Массачусетс 01610
Эти файлы находятся по адресу http://aleph0.clarku.edu/~djoyce/wallpaper/
групп обоев: 17 групп обоев
Для справки, вот несколько таблиц и иллюстраций 17 групп обоев.
Обозначения групп обоев
Для 17 групп обоев были изобретены различные обозначения. Наиболее широко используются кристаллографические обозначения, принятые Международным союзом кристаллографов. Недавняя и более математически обоснованная система разработана Дж. Х. Конвеем и называется орбифолдной нотацией. (Идея принадлежит Уильяму Терстону)
Обозначение орбифолда
{о, 2222, **, хх, *2222, 22*, 22х, х*, 2*22, 442, *442, 4*2, 333, *333, 3*3, 632, *632}
Чтобы полностью понять орбифолд и нотацию орбифолда, требуется опыт работы в топологии.
Для тех, кто не знаком с топологией (включая автора), полезно следующее описание: можно думать, что нотация орбифолда состоит из символов, представляющих образующие группы. Целое число n указывает на наличие n-кратных поворотов. Звездочка «*» указывает на наличие отражений. Крестик «x» указывает на наличие скользящих отражений. Например, группа 442 состоит из двух отдельных наборов 4-кратных вращений и набора 2-кратных вращений. Если числа идут после звездочки, то это означает, что эти центры вращения являются пересечением зеркальных линий. Например, в группе *442 все повороты сосредоточены на зеркальных линиях. Группа 4*2 имеет только 2-кратное вращение на зеркальных линиях. Конвей подчеркивает, что думать об орбифолдных обозначениях как о генераторах на самом деле не имеет смысла. Революционная особенность орбифолдной нотации заключается в том, что она использует топологию для объяснения симметрии и приводит к более геометрическому пониманию, чем группы. (тем, кто интересуется орбифолдом, следует ознакомиться с статьей Дж.
Х. Конвея и соответствующими веб-сайтами, отсканированная статья доступна в справочном разделе)
Вот выдержка из статьи Конвея для математически продвинутых читателей.
В этой статье группа поверхностей будет дискретной группой изометрий одной из следующих трех поверхностей:
- сфера
- евклидова плоскость
- гиперболическая плоскость.
Это все односвязные поверхности постоянной гауссовой кривизны.
Приведем простую и единую нотацию, описывающую все три типа групп. Поскольку это обозначение основано на понятии орбифолда, введенном Биллом Терстоном, мы будем называть его обозначением орбифолда.
Грубо говоря, орбифолд — это фактор многообразия по дискретной группе, действующей на нем. Следовательно, у него есть одна точка для каждой орбиты группы на многообразии (орбифолд = орбитальное многообразие).
(См. также: Википедия на
[ Орбифолдная нотация Конвея ] [ https://en.
wikipedia.org/wiki/Conway’s_orbifold_notation ])
Кристаллографическая нотация
{p1, p2, pm|p1m, pg|p1g, pmm|p2mm, pmg|p2mg, pgg|p2gg, cm|c1m, cmm|c2mm, p4, p4m|p4mm, p4g|p4gm, p3, p3ml, p3lm ,6 изн,6м изн|6мм изн}
Выдержка из статьи Дорис Шаттшнайдер (Группы плоской симметрии: их распознавание и обозначение. American Math Monthly. vol 85, pp. 439-450.)
Кристаллографическая нотация состоит из четырех символов, которые обозначают условно выбранную «ячейку», высший порядок вращения и другие фундаментальные симметрии. Обычно выбирается «примитивная ячейка» (элемент решетки) с центрами вращения высшего порядка в вершинах. В двух случаях «центрированная ячейка» выбирается так, чтобы оси отражения были перпендикулярны одной или обеим сторонам ячейки. «Ось X» ячейки — левый край ячейки (вектор направлен вниз). Интерпретация полного международного символа (читается слева направо) следующая: (1) буква p или c обозначает примитивную или центрированную ячейку; (2) целое число n обозначает наивысший порядок вращения; (3) символ обозначает ось симметрии, перпендикулярную оси x: m (зеркало) указывает на ось отражения, g указывает на отсутствие отражения, но на ось скользящего отражения, l указывает на отсутствие оси симметрии; (4) символ обозначает ось симметрии под углом α к оси x, где α зависит от n, наивысший порядок вращения: α == 180 градусов для n==1 или 2, α == 45 градусов для n == 4, α == 60 градусов для n == 3 или 6; символы m, g, l интерпретируются как в (3).
Отсутствие символов в третьей и четвертой позициях указывает на то, что группа не содержит отражений или скользящих отражений…[Четыре буквенно-цифровых символа можно сократить без потери идентификации, и сокращенная форма является наиболее популярной.]
Многие сведения о группе явно указаны в орбифолдной нотации, в том числе:
- Наличие или отсутствие поворотов (указывается целыми числами, причем наивысший порядок соответствует максимальному целому числу).
- Наличие или отсутствие отражения (обозначается *).
- Наличие или отсутствие скользящего отражения (обозначается x).
| ID | Обозначение Orbifold | Обозначение IUC | Возможно Типы решеток | частное пространство | степень |
|---|---|---|---|---|---|
| 1 | или | стр.1 | ▰ , ▮ , ♦ , ■ , ▲ | тор | 2 |
| 2 | 2222 | п2 (п2ll) | ▰ , ▮ , ♦ , ■ , ▲ | закрытая наволочка | 2 |
| 3 | ** | пм (п1мл) | ▮ , ■ | цилиндр | 1 |
| 4 | хх | пг (p1gl) | ▮ , ■ | Бутыль Клейна | 1 |
| 5 | *2222 | пмм (п2мм) | ▮ , ■ | квадрат | 1 |
| 6 | 22* | пмг (п2мг) | ▮ , ■ | открытая наволочка | 1 |
| 7 | 22x | пгг (п2гг) | ▮ , ■ | неориентируемый футбольный мяч | 1 |
| 8 | х* | см (c1мл) | ♦ , ■ , ▲ | Лента Мёбиуса | 1 |
| 9 | 2*22 | см (c2 мм) | ♦ , ■ , ▲ | 4,4,2 оборот, разрез по 4,4 | 1 |
| 10 | 442 | стр. 4 | ■ | 4,4,2 оборот | 0 |
| 11 | *442 | п4м (п4мм) | ■ | 4,4,2 треугольник | 0 |
| 12 | 4*2 | п4г (п4гм) | ■ | 4,4,2 оборот, разрез по 4,2 | 0 |
| 13 | 333 | п3 | ▲ | 3,3,3 оборот | 0 |
| 14 | *333 | п3мл | ▲ | 3,3,3 треугольник | 0 |
| 15 | 3*3 | п3лм | ▲ | 6,3,2 оборот, разрез по 3,2 | 0 |
| 16 | 632 | стр. 6 | ▲ | 6,3,2 оборот | 0 |
| 17 | *632 | п6м (п6мм) | ▲ | 6,3,2 треугольник | 0 |
Визуальное представление групп обоев
Вот визуальное представление 17 групп обоев. Первый столбец содержит репрезентативные обои для каждой группы. Дизайн обоев получается путем применения всех элементов симметрии к L-образному мотиву. Сами элементы симметрии обозначены символами розового цвета, наложенными на рисунок обоев. (Стрелки, указывающие переводы, не показаны, так как их можно легко определить по расстоянию между мотивами L.) Второй столбец — это сами обои без индикаторов симметрии. Верх третьего столбца — элементы симметрии группы в элементарной ячейке. Внизу находятся его генераторы. Граница представляет собой элементарную ячейку. Серая область является его основной областью.
Генераторы выбираются так, чтобы всегда включать два непараллельных перевода. Такой набор подходит для использования алгоритмами компьютерной графики.
| 2-кратный центр вращения | |
| 3 | |
| 4 | |
| 6 | |
| ось отражения | |
| ось скользящего отражения |
| Обои и их симметрия | Обои | Симметрии и образующие |
|---|---|---|
| {1,o,p1} | ||
| {2,2222,p2} | ||
| {3,**,pm} | ||
| {4,хх,стр} | ||
| {5,*2222,пмм} | ||
| {6,22*,pmg} | ||
| {7,22x,pgg} | ||
| {8,х*,см} | ||
| {9,2*22,см} | ||
| {10 442, стр.  |