ЕГЭ. Физика. Электростатика questions & answers for quizzes and tests
Browse from millions of quizzes
QUIZ
Physics
49%
accuracy
29
plays
Юрий Никонов
2 years
New!
You can now share content with a Team.
Physics
Юрий Никонов
29
plays
10 questions
10 questions
Show Answers
See Preview
1.
 Fill-in-the-Blank
Fill-in-the-Blank5 minutes
1 pt
Два точечных заряда действуют друг на друга с силой 12 Н. Каким будет модуль силы взаимодействия между ними, если уменьшить каждый заряд в 2 раза, не меняя расстояния между ними?
2. Fill-in-the-Blank
5 minutes
1 pt
Между двумя точечными заряженными телами сила электрического взаимодействия равна 12 мН. Если заряд одного тела увеличить в 3 раза, а заряд другого тела уменьшить в 4 раза и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами? (Ответ дайте в мН.)
3. Fill-in-the-Blank
5 minutes
1 pt
С какой силой взаимодействуют в вакууме два маленьких заряженных шарика, находящихся на расстоянии 4 м друг от друга? Заряд каждого шарика 8 · 10 −8 Кл.
 Ответ выразите в мкН.
Ответ выразите в мкН.4. Fill-in-the-Blank
5 minutes
Точечные заряды q1 = 10 нКл и q2 = −30 нКл находится на некотором расстоянии друг от друга. Во сколько раз уменьшится модуль силы взаимодействия между ними, если их сначала привести в соприкосновение, а потом развести на прежнее расстояние?
5. Multiple-choice
5 minutes
1 pt
Как направлена кулоновская сила, действующая на отрицательный точечный заряд, помещенный в центр квадрата, в вершинах которого находятся заряды: +q, +q, −q, −q (см.рисунок)?
вправо
6. Multiple-choice
5 minutes
1 pt
Отрицательный заряд −q находится в поле двух неподвижных зарядов: положительного +Q и отрицательного −Q (см.
рисунок). Куда направлено относительно рисунка ускорение заряда −q в этот момент времени, если на него действуют только заряды +Q и −Q?
вправо
7. Multiple-choice
5 minutes
1 pt
На рисунке изображены два одинаковых электрометра: А и Б, шары которых имеют заряды противоположных знаков. В первом опыте электрометры соединяют проволокой, а втором – деревянной линейкой. Выберите два утверждения, соответствующие данным этим опытов.
в первом опыте показание электрометра А станет равным 1, а показание электрометра Б – равным 3
в первом опыте показания обоих электрометров станут равным 1
в первом опыте электрометр Б полностью разрядится
во втором опыте показания электрометров не изменится
во втором опыте показания электрометров станут одинаковыми
8.
 Multiple-choice
Multiple-choice5 minutes
1 pt
На рисунке изображены два одинаковых электрометра: А и Б, шары которых заряжены положительно. В первом опыте электрометры соединяют проволокой, а втором – деревянной линейкой. Выберите два утверждения, соответствующие данным этим опытов.
в первом опыте показание электрометра А станет равным 1, а показание электрометра Б – равным 3
во втором опыте показания электрометров станут одинаковыми
в первом опыте электрометр Б полностью разрядится
во втором опыте показания электрометров не изменится
в первом опыте показания обоих электрометров станут равными
9. Multiple-choice
5 minutes
1 pt
На рисунке изображены линии напряженности однородного электростатического поля, образованного равномерно заряженной протяженной пластиной.

Из приведенного ниже списка выберите два правильных утверждения
заряд пластины отрицательный
если в точку А поместить точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз
заряд пластины положительный
если в точку В поместить точечный положительный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз
электрическое поле в точке В сильнее чем в точке С
10. Multiple-choice
5 minutes
1 pt
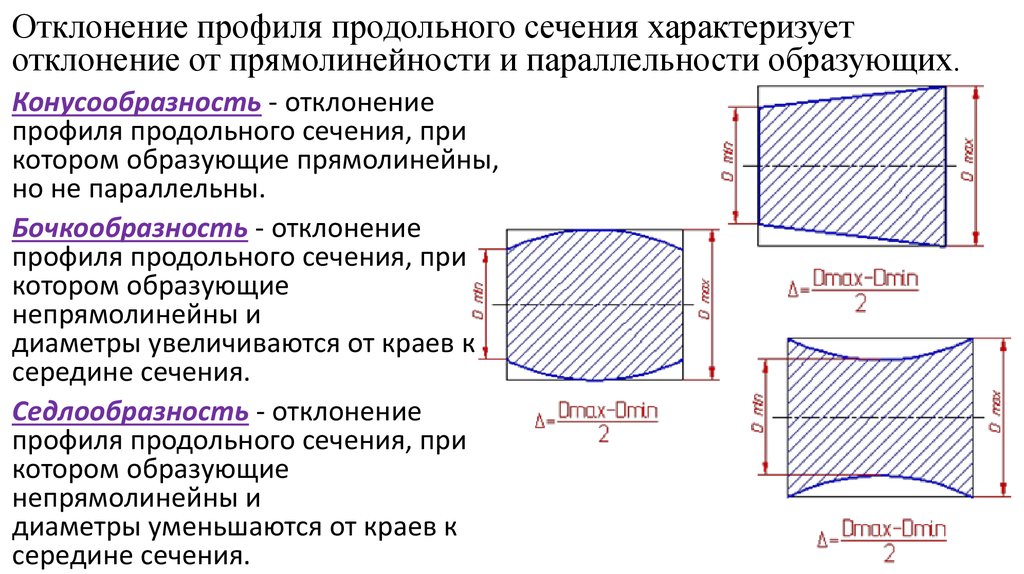
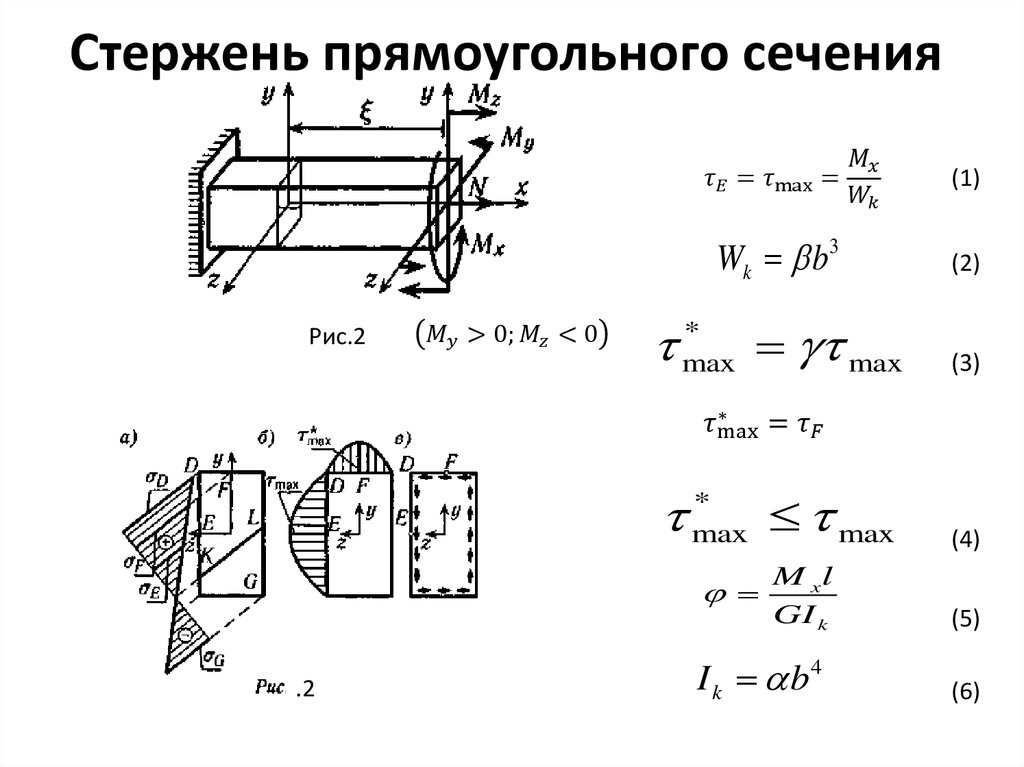
Металлическое тело, продольное сечение которого показано на рисунке, поместили в однородное электрическое поле напряженностью Е.
Из приведенных ниже списка выберите два правильных утверждения, описывающие результаты воздействия этого поля на металлическое тело.
концентрация свободных электронов в точке А наименьшая
в точке С индуцируется положительный заряд
в точке В индуцируется отрицательный заряд
положительный заряд внешнего электрического поля расположен справа
Expore all questions with a free account
Already have an account?
Методика подготовки к ЕГЭ, специфика преподавания физики.
 Примеры
ПримерыПохожие презентации:
Деятельность пришкольного лагеря с дневным пребыванием детей «Дружба» МОУ школа № 71
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Моя будущая профессия: юрист
Развитие интеллектуальной одаренности детей Новосибирской области с использованием дистанционных образовательных технологий
Творческий проект «Планирование кухни-столовой»
Моя будущая профессия – военный
Газовая хроматография
Кейсы (ситуации взаимодействия ребёнка и взрослого)
Творческий проект «мой профессиональный выбор»
Геофизические исследования скважин
1. МЕТОДИКА ПОДГОТОВКИ К ЕГЭ, СПЕЦИФИКА ПРЕПОДАВАНИЯ ФИЗИКИ Ведущий эксперт Республиканской комиссии по проверке ЕГЭ по физике
Владение понятийнымаппаратом
Пример 1
Сила гравитационного притяжения между двумя шарами,
находящимися на расстоянии 2 м друг от друга, равна 9 нН.
 Какова
Каковабудет сила притяжения между ними, если расстояние увеличить
до 6 м? Ответ выразите в наноньютонах (нН).
Ответ: 1 нН.
Пример 2
Пять одинаковых резисторов с сопротивлением 10 Ом
каждый соединены в электрическую цепь, через которую
течёт ток I = 6 А (см. рисунок). Какое напряжение
показывает идеальный вольтметр?
Ответ: 30 В
Пример 3.
Конденсатор колебательного контура длительное время подключён
к источнику постоянного напряжения (см. рисунок). В момент t = 0
переключатель К переводят из положения 1 в положение 2. Графики
А
и
Б
представляют
изменения физических
величин,
характеризующих колебания в контуре после этого (T – период
колебаний). Установите соответствие между графиками и
физическими величинами, зависимости которых от времени эти
графики могут представлять. К каждой позиции первого столбца
подберите соответствующую позицию из второго столбца и
запишите в таблицу выбранные цифры под соответствующими
буквами.

ГРАФИКИ
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) сила тока в катушке
2) энергия магнитного поля
катушки
3) энергия электрического поля
конденсатора
4)заряд правой обкладки
конденсатора
Ответ: А Б
3 4
Пример 4
На рисунке представлены направления
векторов скорости
и ускорения
мяча в инерциальной системе отсчёта. Куда
направлен в этой системе отсчёта вектор
равнодействующей всех сил, приложенных к мячу?
1)→
2)↓
3)↑
4)←
Ответ: 1
Пример 5
На рисунке изображена упрощённая диаграмма
энергетических уровней атома. Нумерованными стрелками
отмечены некоторые возможные переходы атома между
этими уровнями. Установите соответствие между
процессами поглощения света наибольшей длины волны и
испускания света наибольшей частоты и энергией
соответствующего фотона. К каждой позиции первого
столбца подберите соответствующую позицию из второго
столбца и запишите в таблицу выбранные цифры под
соответствующими буквами.

ПРОЦЕСС
А) излучение света наибольшей
частоты
Б)поглощение света наибольшей
длины волны
Ответ
А
2
Б
3
ЭНЕРГИЯ ФОТОНА
1) E1 −E0
2) E2 − E0
3) E3 −E0
4) E4 −E0
Пример 6 (процент выполнения – 54%)
Если растолочь мел в мелкую пудру, высыпать её в стакан с
водой и размешать, то, поместив каплю получившейся смеси
под окуляр микроскопа, можно увидеть, что частицы пудры
движутся в капле хаотично. Чем можно объяснить такое
движение частиц пудры?
1) диффузией молекул воды в крупинки пудры
2) хаотичными ударами со стороны молекул воды
3) притяжением крупинок пудры молекулами воды
4) сопротивлением воды движению в ней твёрдых тел
Ответ: 2
Пример 7
В закрытом сосуде под поршнем находится водяной пар
при температуре 100 °С под давлением 50 кПа. Каким
станет давление пара, если, сохраняя его температуру
неизменной, уменьшить объём пара в 3 раза?
Ответ: 100 кПа.
Пример 8
Металлическое тело, продольное сечение
которого показано на рисунке, поместили в
однородное
электрическое
поле
Под действием этого
напряжённостью.
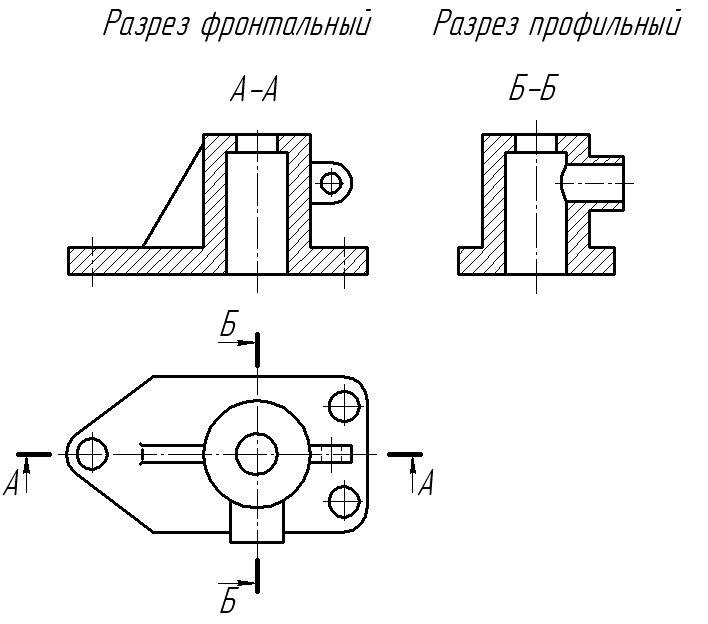
поля концентрация на поверхности
тела станет
1) самой большой в точке А
2) самой большой в точке С
3) самой большой в точке В
4) одинаковой в точках А, В и С
Ответ: 3
10. Методологические умения
Пример 9На рисунке приведена фотография
электрической цепи по измерению
сопротивления
реостата.
Погрешности измерения силы тока в
цепи и напряжения на реостате равны
половине цены деления амперметра и
вольтметра.
Чему
равна
по
результатам этих измерений сила тока
в цепи?
1) (3,2 ± 0,2) А
2) (3,2 ± 0,1) А
3) (0,50 ± 0,05) А
4) (0,500 ± 0,025) А
Ответ: 4
Пример 10
В идеальном колебательном контуре происходят свободные
электромагнитные колебания. В таблице показано, как
изменялась сила тока в контуре с течением времени.
t, 10–6 c
I, А
0
0,0
1
2,2
2
3,0
3
2,2
4
0,0
5
–2,2
6
–3,0
7
–2,2
8
0,0
9
2,2
Выберите два верных утверждения о процессе, происходящем в контуре.

1) В момент t = 2 10-6 с напряжение на конденсаторе минимально.
2) Период колебаний энергии магнитного поля катушки равен 4 10−6 с. ⋅
3) Частота колебаний равна 25 кГц.
4) В момент t = 4 10−6с заряд конденсатора равен 0.
5) В момент t = 4 10−6с
⋅ энергия магнитного поля катушки
максимальна.
Ответ: 1, 2
12. ПРИМЕР 11 (28)
13. Возможное решение:
Запишем уравнение Клапейрона-Менделеева для газа всостояниях 1 и 2:
Откуда
2. Покажем силы, приложенные к поршню, когда он уже не
опирается на выступы на стенках цилиндра. Сила тяжести
и сила давления на поршень со стороны атмосферы
постоянны. Поскольку поршень перемещается медленно,
сумму приложенных к нему сил считаем равной нулю. Отсюда
следует, что сила давления на поршень со стороны газа
тоже постоянна. Значит, её модуль
площадь горизонтального сечения поршня) при любом
положении поршня выше первоначального. Таким образом,
процесс нагревания газа изобарный
Определим температуру начала этого процесса
3.
 На отрезке температур
На отрезке температурпроцесс нагревания газа
изохорный
давление газа с ростом его температур
при нагревании увеличивается от
4. Ответ:
а) при
б) при
объем газа меняется от
по закону
График, изображающий зависимости из п. а) и б), представляет
собой ломаную линию
16. ПРИМЕР 12 (29)
17. Возможное решение:
1. Пусть скорость кубика на высоте равнав нижней точке петли потенциальная
энергия кубика равно нулю. Тогда по закону
сохранения механической энергии
2. Когда кубик находится на высоте на него действуют две силы:
сила тяжести
и сила реакции опоры
Запишем второй
закон Ньютона в проекциях на радиальное направление (Ox на
рисунке):
– центростремительное
ускорение кубика в этой точке.
По третьему закону Ньютона
Из рисунка видно, что
3. Из выражений п.1 и 2 получим:
19. ПРИМЕР 13 (30)
Возможное решение1. Так как сосуд теплоизолирован и начальные температуры газов
одинаковы, то после установления равновесия температура в
сосуде будет равна первоначальной, а гелий равномерно
распределится по всему сосуду.
 После установления равновесия в
После установления равновесия всистеме в каждой части сосуда окажется по 1 моль гелия:
В результате в сосуде с аргоном окажется 3 моль смеси:
2. Внутренняя энергия одноатомного идеального
пропорциональна температуре и количеству молей:
3. Запишем условие термодинамического равновесия:
газа
21. ПРИМЕР 14 (31)
Возможное решение:Ток в цепи до замыкания ключа К
где
– ЭДС источника
Мощность, выделяемая соответственно на резисторах
Так как после замыкание заключения ключа ток через резистор
не течет, искомая мощность, выделяемая на резисторе
замыкания ключа К,
Объединяя (1) – (4), получаем:
после
24. ПРИМЕР 15 (32)
Возможное решение1. Согласно уравнению Эйнштейна для фотоэффекта
где
– постоянная Планка, c – скорость света в вакууме,
– максимальная кинетическая энергия электронов.
где
– масса электрона,
– его максимальная скорость.
3. Объединяя 1 и 2, получим:
26. ЗАДАЧА 1 (28)
Небольшойпустой
тонкостенный
цилиндрический стакан переворачивают вверх
дном и медленно погружают в глубокий
водоем,
удерживая
ось
стакана
в
вертикальном положении.
 Над поверхностью
Над поверхностьюводоема находится воздух. Как при
погружении стакана от поверхности воды в
глубь водоема будет изменяться модуль
выталкивающей силы, действующей на
стакан? Ответ поясните, указав, какие явления
и закономерности Вы использовали для
объяснения.
Температуру
воздуха
над
поверхностью водоема, воздуха в стакане и
воды в водоеме считать одинаковой и
постоянной.
27. ЗАДАЧА 2 (29)
Небольшая шайба массой m = 10 г,начав движение из нижней точки
закрепленного вертикального гладкого
кольца радиусом R = 0,14 м, скользит
по его внутренней поверхности. На
высоте h = 0,18 м она отрывается от
кольца и свободно падает. Какую
кинетическую энергию имела шайба в
начале движения? Сделайте рисунок с
указанием сил, действующих на шайбу.
28. ЗАДАЧА 3 (30)
В вертикальном закрытом с обоих концовсосуде имеется легкоподвижный поршень (см.
рисунок), по обе стороны которого находятся
одинаковые количества воздуха.
 В равновесном
В равновесномсостоянии при температуре T объем верхней
части сосуда в 2 раза больше объема нижней
части. После того как воздух в нижней части
сосуда нагрели до 400 к, объемы верхней и
нижней частей сосуда стали равными. При
этом температура воздуха в верхней части
осталась прежней. Определите начальную
температуру воздуха в сосуде.
29. ЗАДАЧА 4 (31)
Электрическая цепь питается от батареи,имеющей ЭДС 4,5 В. Какова мощность,
выделяемая во внешней цепи при силе тока
5 А, если при силе тока 3 А она равна 9 Вт?
30. ЗАДАЧА 5 (32)
Электрон, выбиваемый из металлической пластинки с работойвыхода 2 эВ излучением с длиной волны 300 нм, попадает в
однородное магнитное поле с индукцией В = 10-3 Тл. Вектор его
скорости направлен перпендикулярно линиям индукции.
Каково максимальное возможное ускорение электрона в
магнитном поле?
English Русский Правила
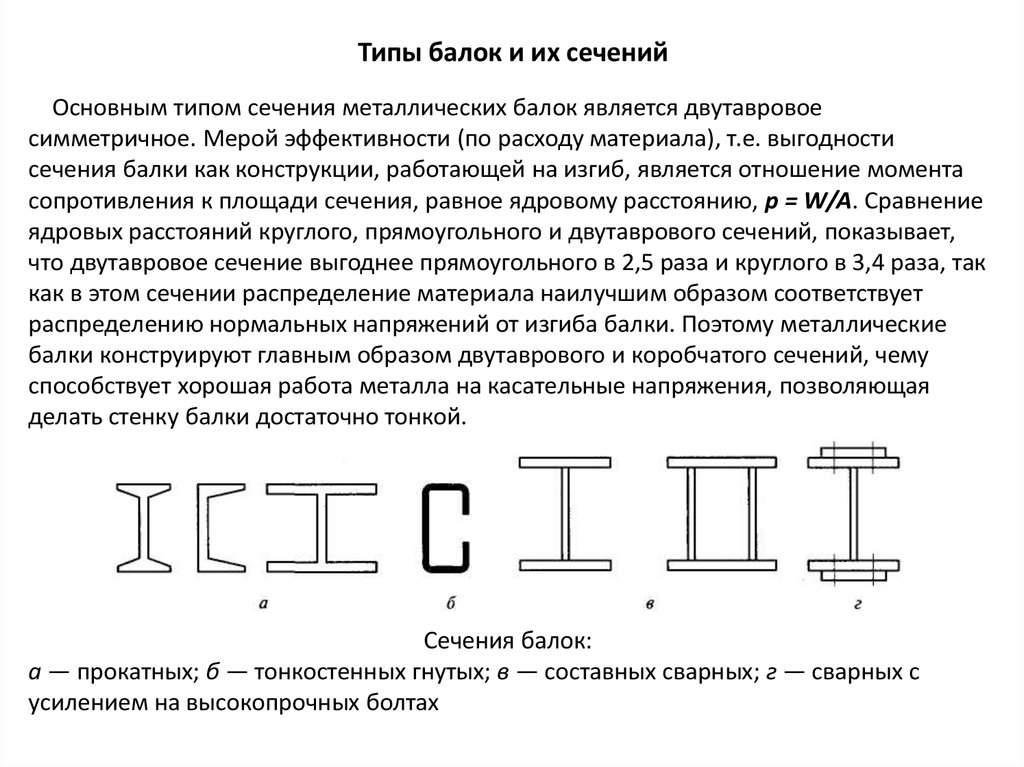
Механика материалов: изгиб – нормальное напряжение » Механика гибких конструкций
исследования
человек
курсы
блог
vimeo.com/video/87433611″ frameborder=”0″ webkitallowfullscreen=”” mozallowfullscreen=”” allowfullscreen=””> Моменты площади
Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки, и как рассчитать второй момент площади для данного поперечного сечения.
Начнем с того, что представим себе произвольное поперечное сечение — что-то не круглое, не прямоугольное и т. д.
На изображении выше произвольная форма имеет площадь, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область дА , которая существует на расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующим формулам:
Первый момент площади — это интеграл длины по площади — это означает, что он будет иметь единицы длины в кубе [L 3 ]. Это важно, потому что помогает нам найти центр тяжести объекта. Центроид определяется как «среднее 9 0023 x (или y ) позиции области”. Математически это утверждение выглядит так:
Центроид определяется как «среднее 9 0023 x (или y ) позиции области”. Математически это утверждение выглядит так:
Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она позволяет нам разбить сложную фигуру на простые формы с известными площадями и известным расположением центроидов. В большинстве инженерных сооружений есть хотя бы одна ось симметрии — и это позволяет значительно упростить нахождение центроида. Центроид должен располагаться на оси симметрии . Например:
Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно найти только центроид вдоль оси
Теперь, когда мы знаем, как найти центр тяжести, мы можем обратить внимание на второй момент площади. Как вы, возможно, помните из предыдущего раздела о кручении, это определяется как:
И, наконец, иногда нам нужно будет определить второй момент площади относительно произвольной оси x или y , которая не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс термин, который включает расстояния между двумя осями.
В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс термин, который включает расстояния между двумя осями.
Это уравнение называется теоремой о параллельных осях . Это будет очень полезно на протяжении всего курса. Как описано во вступительном видео к этому разделу, вычисление второго момента площади простой формы может быть простым. Для более сложных форм нам потребуется вычислить I путем вычисления отдельных I для каждой простой формы и объединения их вместе с использованием теоремы о параллельных осях.
Диаграммы сдвига и момента Поперечная нагрузка относится к силам, которые перпендикулярны длинной оси конструкции. Эти поперечных нагрузок вызовут изгибающий момент M , который вызывает нормальное напряжение , и поперечную силу V , которая вызывает касательное напряжение . Эти силы могут и будут варьироваться по длине балки, и мы будем использовать диаграммы сдвига и момента (диаграмма VM) для извлечения наиболее подходящих значений. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании балки с поперечной нагрузкой необходимо учитывать два важных момента:
Эти силы могут и будут варьироваться по длине балки, и мы будем использовать диаграммы сдвига и момента (диаграмма VM) для извлечения наиболее подходящих значений. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании балки с поперечной нагрузкой необходимо учитывать два важных момента:
- Как балка нагружена?
- точечная нагрузка, распределенная нагрузка (равномерная или переменная), комбинация нагрузок…
- Как балка поддерживается?
- свободно опертый, консольный, нависающий, статически неопределимый…
Знание нагрузок и опор позволит вам начертить качественную диаграмму V-M, а затем статический анализ свободного тела поможет вам определить количественное описание кривых. Начнем с того, что вспомним наши соглашений о знаках .
Эти соглашения о знаках должны быть знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает луч таким образом, что луч изгибается в «улыбку» или U-образную форму, он положительный. Лучший способ вспомнить эти диаграммы — это проработать пример. Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.
Если момент изгибает луч таким образом, что луч изгибается в «улыбку» или U-образную форму, он положительный. Лучший способ вспомнить эти диаграммы — это проработать пример. Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.
Во многих отношениях изгиб и кручение очень похожи. Изгиб возникает из-за приложенной пары или изгибающего момента M . Как и при кручении, при чистом изгибе в материале есть ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение уже не одинаково по сечению конструкции — оно меняется. Давайте начнем с того, что рассмотрим момент о z – ось изгибает конструкцию. В данном случае мы не будем ограничиваться круглыми сечениями – на рисунке ниже рассмотрим призматическое сечение.
Давайте начнем с того, что рассмотрим момент о z – ось изгибает конструкцию. В данном случае мы не будем ограничиваться круглыми сечениями – на рисунке ниже рассмотрим призматическое сечение.
Прежде чем мы углубимся в математику изгиба, давайте попробуем понять его концептуально. Возможно, лучший способ увидеть, что происходит, — наложить изогнутую балку поверх оригинальной прямой балки.
Теперь вы можете заметить, что нижняя поверхность луча стала длиннее, а верхняя поверхность луча стала короче. Также по центру луча длина вообще не изменилась – соответствует нейтральной оси. Повторяя это язык этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под сжатием. Кое-что, что является немного более тонким, но все еще можно наблюдать из наложенного выше изображения, заключается в том, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и при кручении — напряжение линейно менялось от центра к центру. Мы можем посмотреть на это распределение напряжений по поперечному сечению балки немного более явно:
Мы можем посмотреть на это распределение напряжений по поперечному сечению балки немного более явно:
Теперь мы можем найти математическую связь между приложенным моментом и напряжением внутри балки. Мы уже упоминали, что балка деформируется линейно от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием вдоль оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y=0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y=c . Мы можем записать это математически следующим образом:
Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Начнем с умножения обеих частей уравнения на E , модуль упругости Юнга. Теперь наше уравнение выглядит так:
Используя закон Гука, мы можем связать эти величины с фигурными скобками под ними с напряжением в направлении x и максимальным напряжением.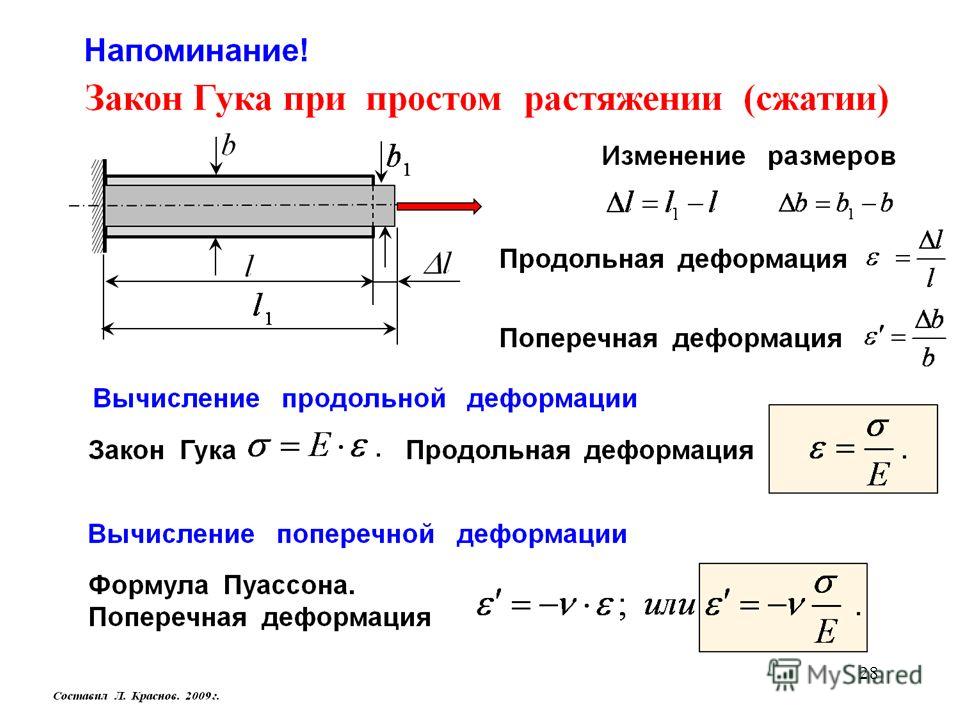 Что дает нам это уравнение для напряжения в направлении x-:
Что дает нам это уравнение для напряжения в направлении x-:
Наш последний шаг в этом процессе — понять, как изгибающий момент связан с напряжением. Для этого вспомним, что момент — это произведение силы на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в луче, дифференциальный элемент, то мы можем записать это математически как:
Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий по площади поперечного сечения балки, путем интегрирования обеих частей уравнения. И, если мы вспомним наше определение напряжения как силы на единицу площади, мы можем написать:
Последний член в последнем уравнении — интеграл по y в квадрате — представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается I (в цилиндрических координатах, помните, обозначался J ).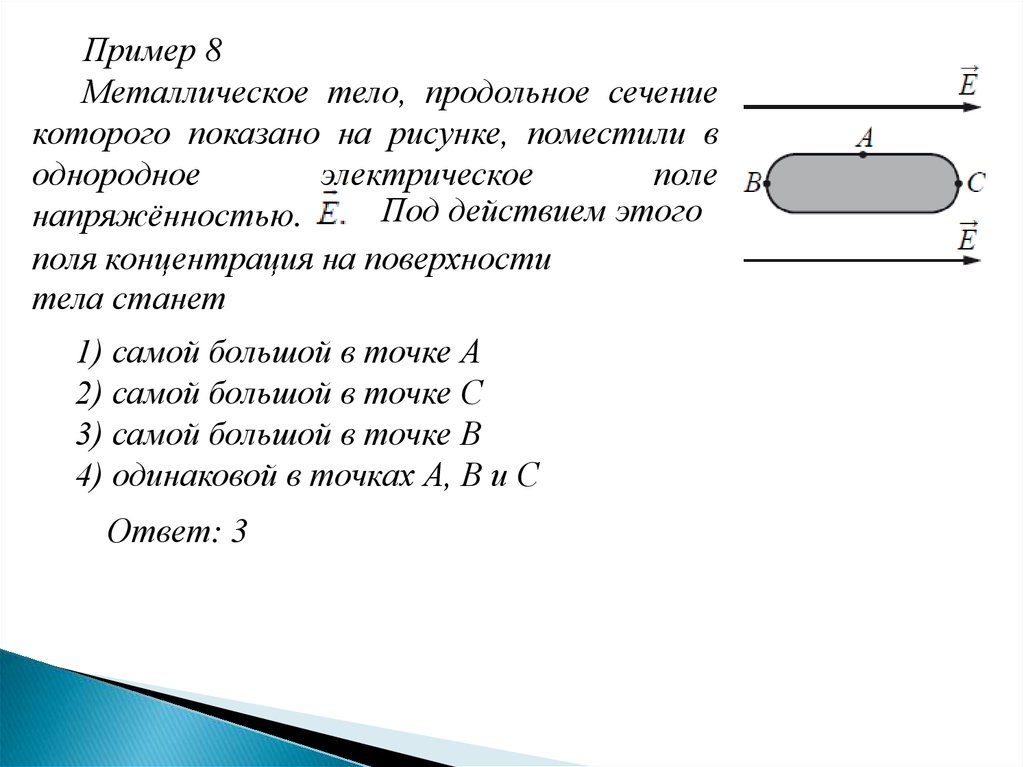 Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:
Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:
Важно отметить, что нижние индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль y ) будут меняться в зависимости от характера проблемы, то есть направления момента — по какой оси находится луч. сгибаясь? Мы основывали наши обозначения на изображении изогнутой балки на первом изображении этого урока.
Помните, в начале раздела я упомянул, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень ясно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиговое для кручения) равно пар/момент ( M для изгиба и T для кручения), умноженных на положение вдоль поперечного сечения. , , потому что напряжение неравномерно по поперечному сечению (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все делится на второй момент площади поперечного сечения.
На этом уроке мы узнали о моментах площади и диаграммах момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид . Мы узнали, как вычислить секундный момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельных осях позволяет нам вычислить второй момент площади относительно центра тяжести объекта — это полезно для разбиения сложного поперечного сечения на несколько простых фигур и объединение их вместе. Мы пересмотрели концепцию 9Диаграммы сдвига и момента 0015 из статики. Эти диаграммы будут необходимы для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, что, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении от изгиба балки. И напряжение, и деформация изменяются по поперечному сечению балки, при этом одна поверхность растягивается, а другая сжимается. Плоскость, проходящая через центр тяжести, образует нейтральную ось — вдоль нейтральной оси нет напряжений или деформаций. Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.
Плоскость, проходящая через центр тяжести, образует нейтральную ось — вдоль нейтральной оси нет напряжений или деформаций. Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.
Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы, заключения или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национальный научный фонд.
Учебник по физике: Продольная звуковая волна
В первой части Урока 1 упоминалось, что звук — это механическая волна, создаваемая вибрирующим объектом. Вибрации объекта приводят в колебательное движение частицы окружающей среды, перенося таким образом энергию через среду. Для звуковой волны, распространяющейся по воздуху, колебания частиц лучше всего описываются как продольный . Продольные волны — это волны, в которых движение отдельных частиц среды происходит в направлении, параллельном направлению переноса энергии. Продольную волну можно создать в слинке, если слинки растянуть в горизонтальном направлении, а первые витки слинки вибрировать горизонтально. В таком случае каждый отдельный виток среды приводится в колебательное движение в направлениях, параллельных направлению переноса энергии.
Продольную волну можно создать в слинке, если слинки растянуть в горизонтальном направлении, а первые витки слинки вибрировать горизонтально. В таком случае каждый отдельный виток среды приводится в колебательное движение в направлениях, параллельных направлению переноса энергии.
Звуковые волны в воздухе (и любой жидкой среде) являются продольными волнами, поскольку частицы среды, через которую распространяется звук, колеблются параллельно направлению, в котором движется звуковая волна. Вибрирующая струна может создавать продольные волны, как показано на анимации ниже. Когда вибрирующая струна движется в направлении вперед , она начинает давить на окружающие молекулы воздуха, перемещая их вправо к ближайшему соседу. Это приводит к тому, что молекулы воздуха справа от струны сжимаются в небольшую область пространства. Когда вибрирующая струна движется в обратном направлении (влево), давление воздуха сразу же понижается справа от нее, что заставляет молекулы воздуха двигаться назад влево. Более низкое давление справа от струны заставляет молекулы воздуха в этой области непосредственно справа от струны расширяться в большую область пространства. Вибрация струны вперед и назад заставляет отдельные молекулы воздуха (или слой молекул воздуха) в области непосредственно справа от струны постоянно колебаться вперед и назад по горизонтали. Молекулы движутся вправо, когда струна движется вправо, а затем влево, когда струна движется влево. Эти возвратно-поступательные колебания передаются соседним соседям за счет взаимодействия между частицами. Другие окружающие частицы начинают двигаться вправо и влево, тем самым посылая волну вправо. Поскольку молекулы воздуха (частицы среды) движутся в направлении, параллельном направлению движения волны, звуковая волна называется продольной. Результатом таких продольных колебаний является создание сжатия и разрежения в воздухе.
Более низкое давление справа от струны заставляет молекулы воздуха в этой области непосредственно справа от струны расширяться в большую область пространства. Вибрация струны вперед и назад заставляет отдельные молекулы воздуха (или слой молекул воздуха) в области непосредственно справа от струны постоянно колебаться вперед и назад по горизонтали. Молекулы движутся вправо, когда струна движется вправо, а затем влево, когда струна движется влево. Эти возвратно-поступательные колебания передаются соседним соседям за счет взаимодействия между частицами. Другие окружающие частицы начинают двигаться вправо и влево, тем самым посылая волну вправо. Поскольку молекулы воздуха (частицы среды) движутся в направлении, параллельном направлению движения волны, звуковая волна называется продольной. Результатом таких продольных колебаний является создание сжатия и разрежения в воздухе.
Независимо от источника звуковой волны — будь то вибрирующая струна или вибрирующие ножки камертона — звуковые волны, распространяющиеся по воздуху, являются продольными волнами.

 Fill-in-the-Blank
Fill-in-the-Blank Ответ выразите в мкН.
Ответ выразите в мкН.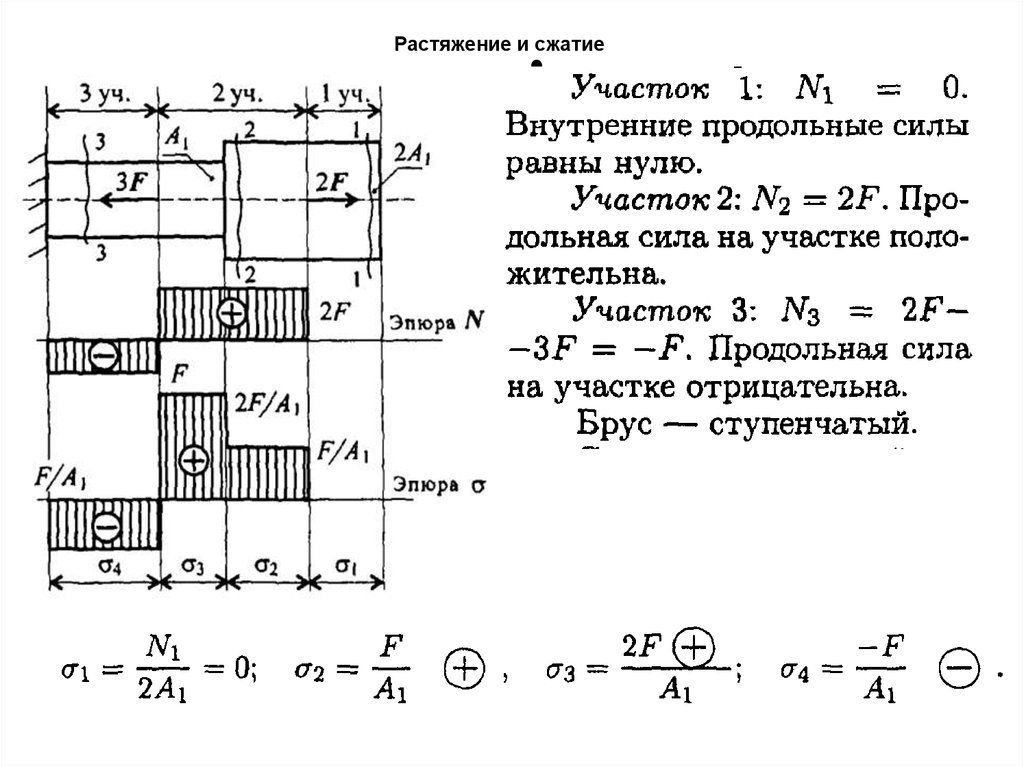
 Multiple-choice
Multiple-choice