Выбор масштаба для построений на чертеже в курсовом проекте по ТММ
После проведения метрического синтеза на листе формата А1 вычерчивается кинематическая схема механизма в масштабе. Повторим определение:
Масштаб – отношение линейных размеров изображения физической величины в виде отрезка (мм) к ее числовому значению в принятых единицах для этой величины.
Определение малоинформативно, разберем подробнее. Масштаб – это число, которое показывает, как относится длина отрезка на чертеже к той величине, которую он изображает.
Рассмотрим пример:
Нахождения масштаба по чертежу
На чертеже построен график некой функции, характеризующей зависимость между временем Т в секундах и длиной H в метрах. Необходимо определить масштаб по оси абсцисс и ординат. По определению:
$$\mu_T=\frac{10.5\;см}{1.75\;с}=\frac{105\;мм}{1.75\; с}=60\;\frac{мм}{с}$$
$$\mu_H=\frac{5\;см}{0.8\;м}=\frac{50\;мм}{0.8\;м}=62.5\;\frac{мм}{м}$$
Зная масштаб графика, можно определить, какой длины отрезок на чертеже нужно отложить, чтобы он соответствовал реальной величине.
$$l_{2м}=2\cdot\mu_H=125\;мм=12.5\;см$$
Обратной операцией можно найти, какой реальной величине соответствует отрезок чертежа.
В графической части проекта по Теории механизмов и машин
масштаб длин определяется из условия:
Длина кривошипа – первого звена на чертеже должна быть больше 50 мм.
Это значит, что для всех линейных размеров на 1 и 2 листе курсового проекта масштаб должен быть найден по формуле:
$$\mu_l=\frac{50\;мм}{l_1},$$
где \(l_1\) – длина кривошипа.
Обратите внимание, получившийся масштаб нужно округлить в большую сторону так, чтобы он соответствовал ГОСТ 2.302. В тех случаях, когда кинематическая схема не помещается на лист, возможно принятие масштабного коэффициента, округленного в меньшую сторону.
Масштабы, применяемые на инженерных чертежах, обязательно должны соответствовать ЕСКД!
Наиболее внимательные заметили, что масштабный коэффициент \(\mu_H=62.
5\;\frac{мм}{м}\) не соответствует ЕСКД, следует выбрать наиболее близкий подходящий коэффициент из таблицы. Например, 50 или 75.
Действующие масштабы
| Наименование | Значения |
| Масштабы уменьшения | 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000 |
| Натуральная величина | 1:1 | Масштабы увеличения | 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1 |
В проекте по ТММ этому моменту не уделяется достаточно внимания, однако в будущих проектах это будет считаться грубой ошибкой, цена которой – снижение оценки на балл. Следует помнить, что пунктом 4 ГОСТ 2.302 допускается применение масштабных коэффициентов на увеличение (100
Наиболее частая ошибка – применение масштабных коэффициентов кратных 3.
Такие коэффициенты в большинстве случаев приводят к образованию иррациональных длин отрезков.
Например, масштабный коэффициент 3. При делении длины отрезка 10 мм на этот коэффициент получается иррациональный результат 3,(3). Округляя и откладывая по оси единичные отрезки 3; 6; 9; 12 имеем погрешность 0,33; 0,66; 0,99; 1,2, а это недопустимо!
Погрешность подписи единичных отрезков
Такие ошибки очень распространены. Консультант физически не может сосредоточить внимание на такие мелкие моменты в работе каждого студента, и, зачастую, это становится причиной снижения оценки на защите. Будьте внимательны к выбору масштаба в данном курсовом проекте, а тем более в дальнейших инженерных задачах.
Если масштабный коэффициент был выбран успешно, следует приступить к построению кинематической схемы рычажного механизма на чертеже.
Геометрические фигуры в элементарной математике ｜ Хацуди
Иногда мы делаем фигуру больше или меньше. Хотя форма одинаковая, размер фигуры и длина сторон разные.
Есть два типа таких фигур: увеличение и уменьшение.
Когда вы увеличиваете фигуру, это увеличение. С другой стороны, когда фигура уменьшается, это сокращение. Если форма одинаковая, но длина сторон разная, то форму либо увеличивают, либо уменьшают.
Если вы узнаете об увеличении и уменьшении, вы сможете понять масштаб. Масштаб — это то, что используется в картах. Есть много моментов, когда вам нужно прочитать карту. Если вы не понимаете масштаба, вы не сможете читать карту и заблудитесь.
Итак, давайте изучим понятия увеличения и уменьшения. Это поможет вам понять размер фигур.
Содержание
- 1 Изменение длины сторон при увеличении или уменьшении
- 1.1 Длина соответствующей стороны меняется
- 1.2 Углы не меняются при увеличении и уменьшении
- 2 Найдите соответствующие стороны и вычислите длины
- 3 На карте масштаб значительно уменьшает длину
- 400 Изучение концепции1 увеличения и уменьшения
Изменение длины сторон при увеличении или уменьшении
Что такое увеличение? Увеличением называется фигура, у которой длина сторон увеличена без изменения формы.
Например, ниже показано увеличение, в котором все стороны удвоены.
Как видите, длины всех сторон удвоены. Кроме того, форма фигуры одинакова.
Размер фигуры зависит от того, во сколько раз увеличена длина сторон. Если одну сторону увеличить в три раза, то все стороны увеличатся втрое. Кроме того, если одну сторону увеличить в 5 раз, то все длины сторон увеличатся в 5 раз.
С другой стороны, уменьшение противоположно увеличению. Другими словами, длины сторон не увеличиваются, а уменьшаются. Далее идет сокращение.
Если одна сторона имеет длину в $\displaystyle\frac{1}{2}$ раз, все стороны будут иметь длину в $\displaystyle\frac{1}{2}$ раз. Кроме того, если одна сторона имеет длину в $\displaystyle\frac{1}{3}$ раз, все стороны будут иметь длину в $\displaystyle\frac{1}{3}$ раз. Это свойство редукции.
Длина соответствующей стороны меняется
Важно помнить, что длина соответствующей стороны варьируется. В конгруэнтных фигурах мы можем найти длины сторон, используя соответствующие стороны.
Точно так же соответствующие стороны важны для увеличения и уменьшения.
Форма фигуры такая же. Следовательно, есть соответствующие стороны в увеличении и уменьшении. Итак, давайте поймем, что длина соответствующих сторон меняется. Например, если длина стороны удваивается, соответствующая сторона удваивается.
Соотношение длин сторон одинаковое при увеличении и уменьшении.
Форма фигуры такая же, потому что отношение длин сторон не меняется.
Углы не меняются при увеличении и уменьшении
Как упоминалось выше, форма фигуры одинакова в увеличении и уменьшении. Следовательно, в то время как длина соответствующей стороны увеличивается или уменьшается, все соответствующие углы остаются неизменными.
Кстати, разные углы будут менять форму. Следовательно, следующие формы не одинаковы по форме.
При увеличении и уменьшении формы должны быть одинаковыми. Поэтому углы должны быть одинаковыми. Важно понимать, что при увеличении и уменьшении изменяется только длина соответствующей стороны, а не углы.
Найдите соответствующие стороны и вычислите длины
При увеличении и уменьшении найдите соответствующие стороны. Если вы это сделаете, вы можете рассчитать длину. Например, если B является расширением A, каковы угол $a$ и длина $b$?
Величины соответствующих углов одинаковы при увеличении и уменьшении. Следовательно, $a$ равно 70°. Кроме того, отношения соответствующих сторон одинаковы; если вы посмотрите на A и B, вы увидите, что удвоение стороны A дает сторону B. Следовательно, длина $b$ равна 4 см.
Найдя соответствующие стороны и углы, мы можем найти длины сторон и размеры углов.
На карте масштаб значительно уменьшает длину
Если вы узнаете об увеличении и уменьшении, вы сможете понять масштаб. В картах масштаб используется для значительного уменьшения фактического размера карты. Например, ниже представлена карта Нью-Йорка, США.
Если вы посмотрите на эту карту, вы увидите, что оранжевая рамка отмечена как 1 км.
Другими словами, длина оранжевой рамки на карте фактически соответствует 1 км. Карта должна отображать реальный мир в меньшем размере. Вот почему мы используем шкалу, чтобы показать мир в гораздо меньшем размере.
Масштаб — это коэффициент, показывающий, насколько была уменьшена фактическая длина. Например, если масштаб «1:20000», сколько километров будет составлять 10 см на карте?
Когда мы делаем карту, мы устанавливаем длину в $\displaystyle\frac{1}{20000}$ раз. Таким образом, чтобы получить реальную длину, мы должны умножить ее на 20000. Результат будет следующим.
- 10 см × 20000 = 200000 см
Затем давайте изменим единицу измерения с см на км. 1 метр это 100 см. Следовательно, 200000 см это 2000 м. Кроме того, 1 км равен 1000 м. Следовательно, 2000 м — это 2 км. Таким образом, мы видим, что 2 км и есть ответ.
Вы можете составить карту, уменьшив фактическую длину земли на тот же процент.
Изучение концепции увеличения и уменьшения
В начальной школе учащиеся узнают об увеличении и уменьшении.
Фигура той же формы, но увеличенная, является увеличением. Когда фигуру уменьшают, это уменьшение.
Отношение длин соответствующих сторон одинаково при увеличении и уменьшении. Поэтому в увеличении и уменьшении можно найти длины сторон, сравнив цифры. Кроме того, соответствующие углы равны. Это потому, что если угол меняется, форма меняется. Следовательно, если вы знаете соответствующий угол, вы можете найти угол.
Кроме того, если вы изучите увеличение и уменьшение, вы поймете масштаб. На картах используется масштаб. Чтобы узнать, какова на самом деле длина расстояния, показанного на карте, нам нужно узнать о концепции масштаба.
Увеличение или уменьшение формы — это то, что мы часто используем в нашей повседневной жизни. Один из примеров — карты. Итак, давайте попробуем понять взаимосвязь между увеличением и уменьшением и концепцией масштаба.
Рейтинг
Потребности, желания и требования: три основных понятия в маркетинге (с примерами)
ЯМР-связывание бензольных колец: орто-мета-пик и химические сдвиги
Тонкослойная хроматография (ТСХ): принципы, Rf значения и проявляющий растворитель
Ориентация и реакционная способность ароматических соединений: орто, мета, пара
Одновременные уравнения: метод сложения и метод замещения
Уменьшение масштаба | Проблемы и решения | Общественное питание | Коммерческая очистка воды | Продукты
Коммерческая фильтрация и общественное питание
Удаление накипи
Поделиться
- Поделиться по электронной почте
- Поделиться через Twitter
- Поделиться через Facebook
- Поделиться через Linkedin
- Распечатать
Что такое шкала?
Когда идет дождь, он поглощает CO2, что делает воду слегка кислой.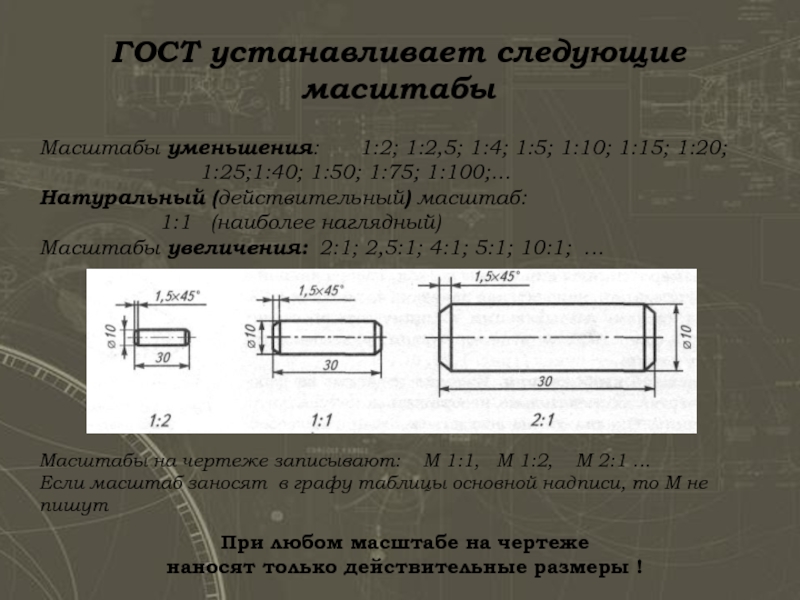
Как образуется накипь?
При воздействии энергии на жесткую воду минералы могут выпадать из раствора и оседать на поверхности. Это называется накипью, наиболее распространенной из которых является известковый налет. Эти минералы могут образовывать твердую корку, которая может вызвать множество проблем с оборудованием, от засорения до повышенного потребления энергии.
Чтобы понять процесс, который позволяет растворенным минералам восстанавливать твердую породу, важно понять состояние pH.
Шкала pH измеряется от 0,0 до 14,0, где 7,0 соответствует абсолютной нейтральности. В общих чертах, источники воды с pH ниже 7,0 имеют более высокое содержание кислоты и, как правило, растворяют горные породы в минералы. Водоснабжение с pH выше 7,0 имеет более низкое содержание кислоты и склонно к образованию минеральных отложений.
Есть два ключевых условия образования накипи:
- Уровень pH должен быть нейтральным или выше
- Должен быть перенос энергии, охлаждение или нагрев, чтобы действовать как катализатор.
Как накипь влияет на оборудование, использующее воду?
Минеральные отложения, такие как известковый налет, создают серьезные проблемы для предприятий общественного питания, использующих лед, кофе, эспрессо, пар и оборудование для мытья посуды. Минеральные отложения могут забивать трубки и небольшие отверстия, покрывать нагревательные и охлаждающие элементы и приводить к повышенному расходу моющих средств.
Многие приборы, использующие воду, от кофеварок до льдогенераторов, подвержены образованию известкового налета. Пароварки и пароконвектоматы являются одними из наиболее уязвимых. Когда вода кипит и испаряется, минералы остаются и концентрируются. Из-за этих высоких концентраций в парогенераторах может потребоваться частое обеззоливание — процесс кислотной очистки, удаляющий минеральные отложения. Этот процесс суров к поверхностям оборудования и сокращает срок службы оборудования.
Замерзающая вода также может вызвать образование накипи. Коммерческие льдогенераторы куберного типа требуют больше обслуживания для устранения образования накипи, чем любое другое оборудование, обычно используемое в сфере общественного питания. Как и пароходы, коммерческие льдогенераторы оставляют высокую концентрацию минералов, поскольку большая часть воды превращается в лед.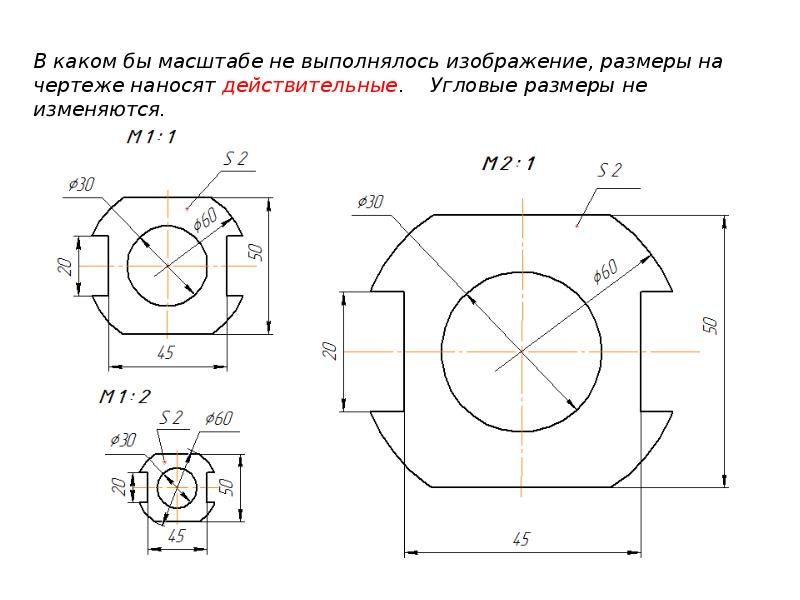
Полученный осадок представляет собой мутную смесь, полную осадка и растущих кристаллов, которые сужают трубы, засоряют насосы, закупоривают отверстия, забивают клапаны и заставляют лед свисать комками.
К счастью, рост чешуи можно уменьшить, добавив в воду небольшое количество полифосфатов. Полифосфаты абсолютно безопасны и нетоксичны, и многие из них естественным образом встречаются в пищевых продуктах или добавляются в процессе их обработки. Они также используются при очистке питьевой воды для борьбы с коррозией и образованием накипи. Большинство ситуаций, связанных с образованием накипи, могут быть решены более эффективно с помощью системы очистки воды на месте использования, которая сочетает в себе тонкую фильтрацию и подачу полифосфатов. Тонкая фильтрация уменьшает количество частиц, которые служат местами зародышеобразования для образования накипи. Эти частицы ускоряют процесс образования накипи и могут увеличивать вес накипи на 60% в зависимости от содержания частиц в исходной воде.