Прекционное черчение – Стр 4
29
Рассмотрим изображения конуса вращения на комплексном чертеже (рис. 28).
Рис. 28. Комплексный чертеж прямого кругового конуса
Чтение комплексного чертежа конуса
1. Ось вращения i перпендикулярна горизонтальной плоскости проекций и на П1 изобразится в виде точки (центр окружности основания).
2.Основание конуса – круг, расположенный в горизонтальной плоскости
уровня, поэтому на П1 изобразится в виде окружности в натуральную величину, а на П2 в виде отрезка, длина которого равна диаметру окружности основания.
3.Все образующие конуса проходят через вершину и являются прямыми общего положения, кроме S1 и S3 – фронтальных прямых уровня, S2 и S4 – профильных прямых.
4.Боковая поверхность конуса не обладает проецирующими свойствами.
5.Горизонтальный очерк – окружность основания.
6.Фронтальный очерк – треугольник, образованный проекцией основания в виде отрезка и образующими S1 и S3 – фронтальными меридианами.
30
7. Видимость поверхности. На плоскости П1 видима вершина и боковая поверхность конуса. При проецировании на П2 граница видимости проходит через фронтальный меридиан 1S3, поэтому видимой на П2 является ближняя к наблюдателю боковая поверхность конуса.
Построение профильной проекции конуса
1. Построение профильной проекции оси вращения i3, совпадающей с осью z.
2.Проецирование по горизонтальным линиям связи вершины S3 на ось i3 и основания в виде отрезка, длина которого равна диаметру окружности основания (центр окружности – на оси вращения).
3.Из вершины к крайним точкам основания проходят профильные очерковые образующие (прямые).
4.Профильный очерк – треугольник, образованный проекцией основания в виде отрезка и образующими S2 и S4 – профильными меридианами.
5.Видимой на П3 является левая половина боковой поверхности конуса.
Построение точки на поверхности конуса
1. Пусть точка А задана своей фронтальной проекцией. По условию принадлежности точки конусу, проведем через вершину и точку А образующую.
Порядок построения:
1) l2 = S2A2.
2)l2 ∩ основание = N2.
3)N1 на горизонтальной проекции окружности основания.
4)S1 N1 = l1.
5)А1 # l1 (вертикальная линия связи).
6)А3: А2А3 – горизонтальная линия связи (А3Аz = AxA1 = yA). А3 видима.
2.Пусть точка В невидима на фронтальной плоскости проекций. Построим
еегоризонтальную проекцию по принадлежности окружности конической поверхности. Окружность m для точки В лежит в плоскости, перпендикулярной оси
вращения i, значит на П2 она изобразится в виде отрезка m2 & i2 (B2 # m2). Центр окружности m лежит на оси i, диаметр окружности равен длине отрезка m2 в пределах фронтальных очерковых образующих, т. е. радиус – расстояние от оси до очерковой образующей. На П1 окружность m изобразится в натуральную величину (Om1 # i1, Rm). Находим В1 # m1 по вертикальной линии связи. В1 лежит на дальней
от наблюдателя половине конуса и является видимой. В3 строим по двум известным проекциям (В1 и В2).
В3 невидима, так как лежит за границей видимости на П3.
3. Точка С принадлежит образующей S2. Поэтому строим сначала профильную проекцию С3 # S323, а затем по двум известным (С2 и С3) строим С1
(СхС1 = СzС3 = yC).
31
Линия на конической поверхности
При пересечении поверхности конуса плоскостью можно получить следующие линии:
1) две образующие (рис. 29 а), S # α;
2)окружность (О, R) (рис. 29 б), β & і;
3)эллипс (рис. 29 в) (АВ – большая ось эллипса, СD – малая ось эллипса). Угол наклона плоскости γ к оси і больше, чем угол наклона образующей к оси і;
4)парабола (рис. 29 г) (А – вершина параболы). Плоскость τ параллельна одной из образующих;
5)гипербола. Плоскость σ наклонена к оси i под углом меньшим, чем угол наклона образующих конуса к его оси (рис. 29 д), т. е. параллельна двум образую-
щим конуса, в частном случае плоскость ( || i (рис. 29 е).
Рис. 29. Линии на поверхности конуса
32
Рис. 29. (Продолжение)
Пример построения линии на конусе
Дано: Ф – конус, боковая поверхность которого является поверхностью общего вида.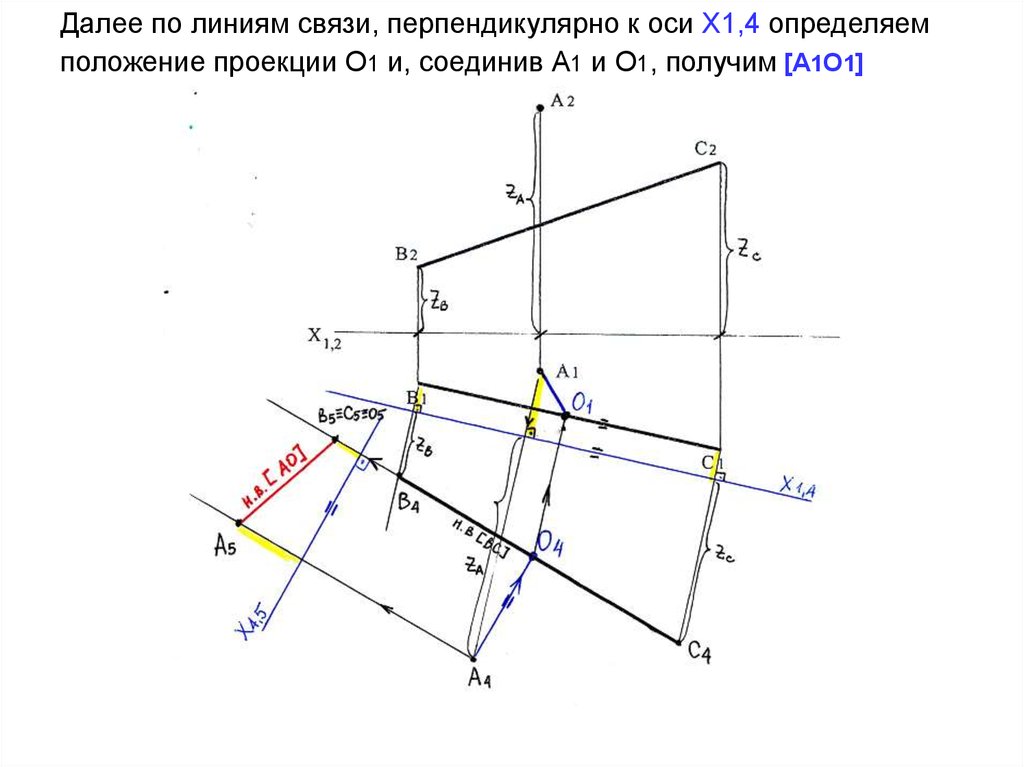
————————
l (l2) – ?
Анализ условия (рис. 30)
Линия l лежит в плоскости γ, наклоненной к оси і и пересекающей все образующие конуса. l – эллипс.
l2 – известна (γ – проецирующая на П2).
—————————
l1 и l3 – ?
Рис. 30. Построение линии на конусе
33
Порядок решения:
1. Опорные точки: АВ – большая ось эллипса, СD – малая ось эллипса. А и В принадлежат образующим конуса. С и D строятся, исходя из условия принадлежности окружности поверхности конуса.
Точки видимости на П3: точки 1 и 2 (на профильном меридиане).
2.Промежуточные точки строятся, исходя из условия принадлежности параллелям (окружностям) на поверхности конуса (см. «Построение точки на поверхности конуса», стр. 30).
Соединяем полученные точки плавной кривой по лекалам тонкой линией, следя за тем, чтобы проекции эллипса были симметричны относительно большой
ималой осей эллипса.
3.Видимость эллипса. На П1 все точки на конической поверхности видимы, поэтому обводим эллипс как видимый.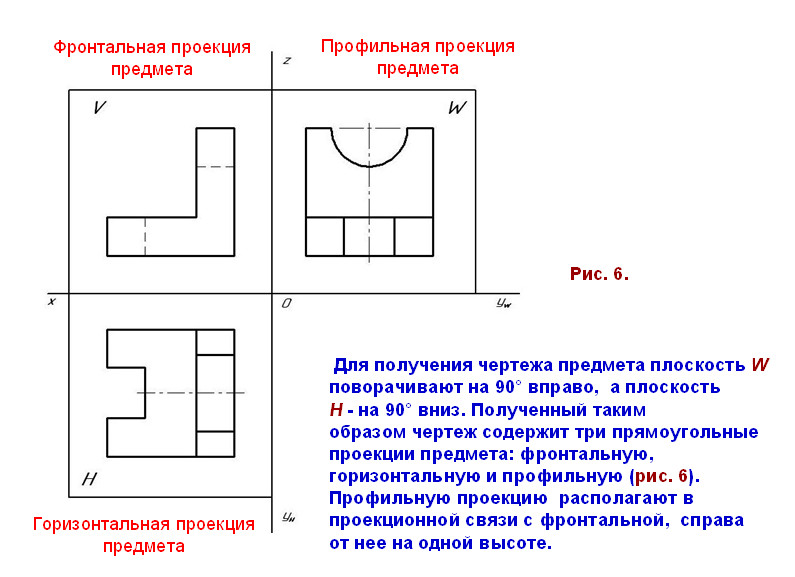
На П3 видима часть эллипса ближе границы видимости до точек видимости 13 и 23. К точке В3 уходит невидимая часть эллипса.
Пример построения выреза в конусе
Анализ условия (чтение исходного чертежа) (рис. 31)
Дано: 1. Конус, боковая поверхность которого – поверхность общего вида.
2. Сквозное призматическое отверстие, образованное тремя плоскостями, занимающими проецирующее положение по отношению к П2 (собирательное свойство фронтальной проекции отверстия).
Вывод: фронтальные проекции линий пересечения известны, необходимо построить их горизонтальные и профильные проекции.
Рис. 31. Задание для построения выреза в конусе
Порядок решения:
1. Строим изображения конуса (рис. 32) без учета отверстия, пользуясь введенными внутренними координатными осями (ось z совпадает с осью вращения конуса i) и линиями проекционной связи.
34
Рис. 32. Построение выреза в конусе
2. Строим проекции линий пересечения каждой плоскости, ограничивающей отверстие, с конической поверхностью на плоскостях проекций П1 и П3.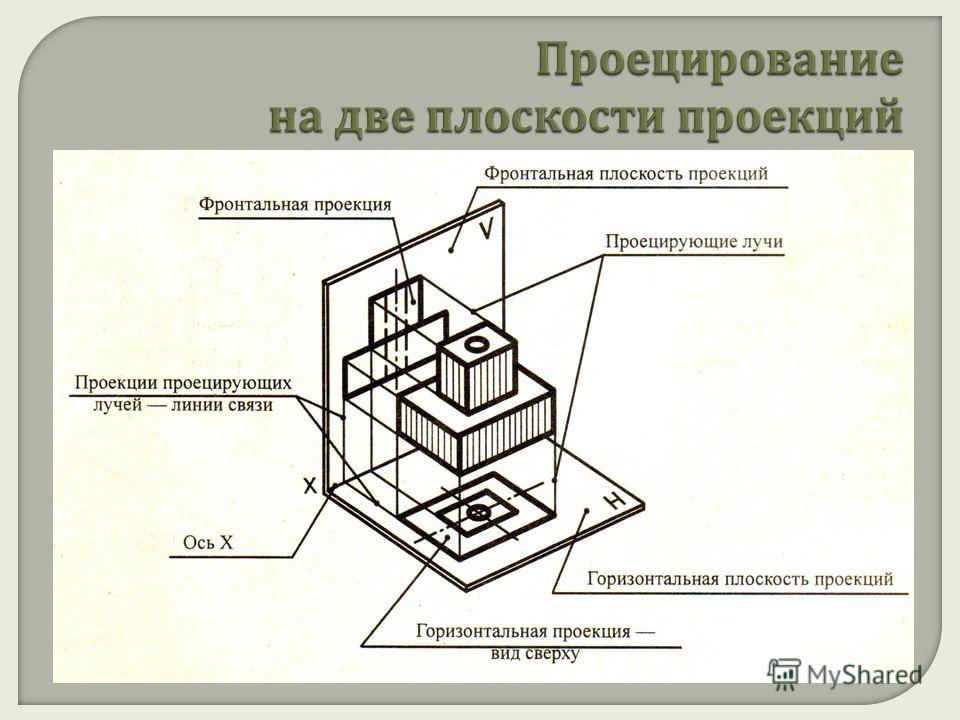
Рассмотрим, как пересекается коническая поверхность каждой плоскостью отверстия.
а) Нижняя плоскость отверстия лежит в плоскости α, которая является горизонтальной плоскостью уровня. Плоскость α перпендикулярна i и пересекает коническую поверхность по окружности, горизонтальная проекция которой – окружность радиуса R, а профильная проекция – отрезок. Но в вырез попадает не вся окружность, а две дуги между точками 1, 2 и точками 1′, 2′. Находим горизонтальные проекции точек 1, 2, 1′, 2′ на построенной горизонтальной проекции окружности, а затем их профильные проекции.
б) Плоскость выреза β пересекает коническую поверхность по эллипсу. Построение эллипса на конусе рассмотрено на стр. 32.
Эллипс строится полностью, а затем выделяются участки, попадающие в вырез, с учетом видимости.
Опорные точки: АВ – большая ось эллипса; СD – малая ось эллипса;
5 и 5′ – точки видимости на П3.
Промежуточные точки строятся из условия принадлежности конической поверхности (вспомогательные окружности в плоскостях, перпендикулярных оси вращения).
35
Соединяем полученные горизонтальные и профильные проекции точек плавными кривыми с учетом видимости, следя за симметричностью их относительно большой и малой осей эллипса.
в) Плоскость выреза γ пересекает коническую поверхность по гиперболе. Строим гиперболу полностью, а затем выделяем участки, попадающие в вырез. Плоскость γ – профильная плоскость уровня, поэтому она перпендикулярна П1, а значит, горизонтальная проекция гиперболы – прямая (собирательное свойство γ1). Следовательно, необходимо построить профильную проекцию гиперболы по двум известным.
Опорные точки: М – вершина гиперболы;
N и N′ – точки на основании конуса. Промежуточные точки строятся, исходя из условия принадлежности
точки конической поверхности (вспомогательные окружности в плоскостях, перпендикулярных оси вращения).
Соединяем полученные проекции точек плавной кривой. Гипербола на П3 невидима, так как лежит за границей видимости.
3.Строим проекции линий пересечения плоскостей призматического отверстия: прямая 11′ – пересечение плоскостей α и β, прямая 22′ – пересечение плоскостей α и γ, прямая 33′ – пересечение плоскостей β и γ.
4.Удаляем участки конуса, вырезанные отверстием. Это части образующих
45 и 4′5′, а также части конуса, заключенные между плоскостями выреза. Части гиперболы от точек 23 и 2$3 до эллипса ничем не закрыты, а, значит, видимы на П3.
5.Обводим проекции конуса и полученные линии выреза.
2.2.3. Сфера и шар
Сферическая поверхность образуется вращением окружности вокруг своего диаметра, который является осью вращения (рис. 33 а). Сферическая поверхность нелинейчатая.
Рис. 33. Образование сферической поверхности и шара
36
Шар – геометрическое тело, ограниченное сферической поверхностью. Экватор и все меридианы сферы (шара) имеют одинаковые диаметры
(рис. 33 б). Параллели имеют разные диаметры: чем ближе к экватору, тем больше диаметр параллели.
Условие принадлежности точки сфере
Если точка принадлежит сфере, то она принадлежит окружности на сфере
(рис. 34).
Для построения точки на сфере необходимо выбирать окружности в плоскостях, параллельных плоскостям проекций.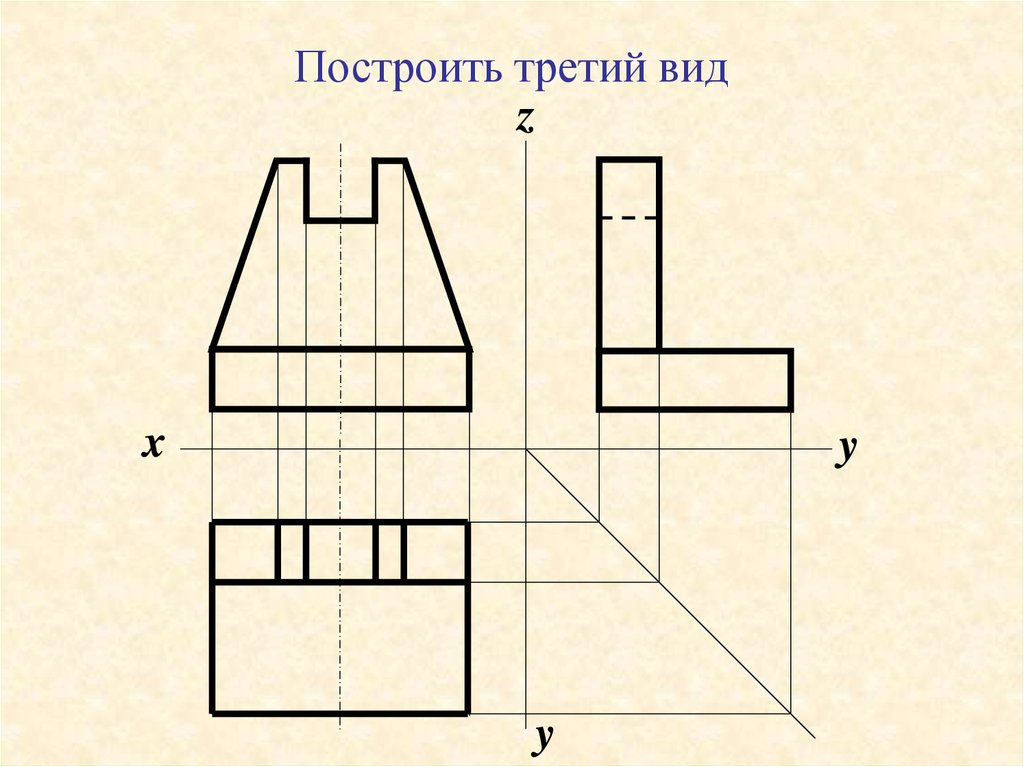
Рис. 34. Принадлежность точки сфере
Рассмотрим изображение сферы на комплексном чертеже (рис. 35).
Рис. 35. Комплексный чертеж сферы
37
Чтение комплексного чертежа сферы
1. Центр сферы – точка О – на плоскостях проекций изобразится в виде проекций О1, О2, О3. Ось вращения сферы – любой из ее диаметров; удобнее брать ось, совпадающую с осью z.
2.Горизонтальный очерк сферы – экватор.
3.Фронтальный очерк – фронтальный меридиан.
4.Профильный очерк – профильный меридиан.
5.Видимость сферы. При проецировании на П1 граница видимости проходит через экватор, поэтому видимой на П1 является верхняя половина сферы. При проецировании на П2 граница видимости проходит через фронтальный меридиан, поэтому видима на П2 ближняя к наблюдателю половина сферы.
Построение точек на поверхности сферы
1. Пусть точка А задана фронтальной проекцией. Она лежит на экваторе сферы, поэтому горизонтальную проекцию находим без дополнительных построений по вертикальной линии связи.
А3 строим по двум известным проекциям А1 и А2: АzA3 = AxA1 = yA. A3 видима.
2.Точка В принадлежит профильному меридиану сферы. Поэтому находим
сначала профильную проекцию В3, а затем по двум известным проекциям В2 и В3 строим В1. Горизонтальная проекция точки В невидима, так как лежит ниже границы видимости на П1.
3.Для построения проекций точки С, заданной фронтальной невидимой
проекцией, проводим окружность в плоскости, параллельной П1. Диаметр окружности равен длине отрезка m2. Окружность изобразится на П1 в виде окружности, центр которой совпадает с центром сферы, радиус окружности равен
половине m2. С1 # m1 и лежит за границей видимости на П2, проходящей через фронтальный меридиан. Горизонтальная проекция точки С видима, так как лежит выше границы видимости на П1, проходящей через экватор сферы. С3 строим стандартным образом по двум известным С1 и С2. С3 невидима, так как лежит за границей видимости на П3, проходящей через профильный меридиан.
Линия на сфере
При пересечении сферы с плоскостью на сферической поверхности можно получить только о к руж н о с т ь .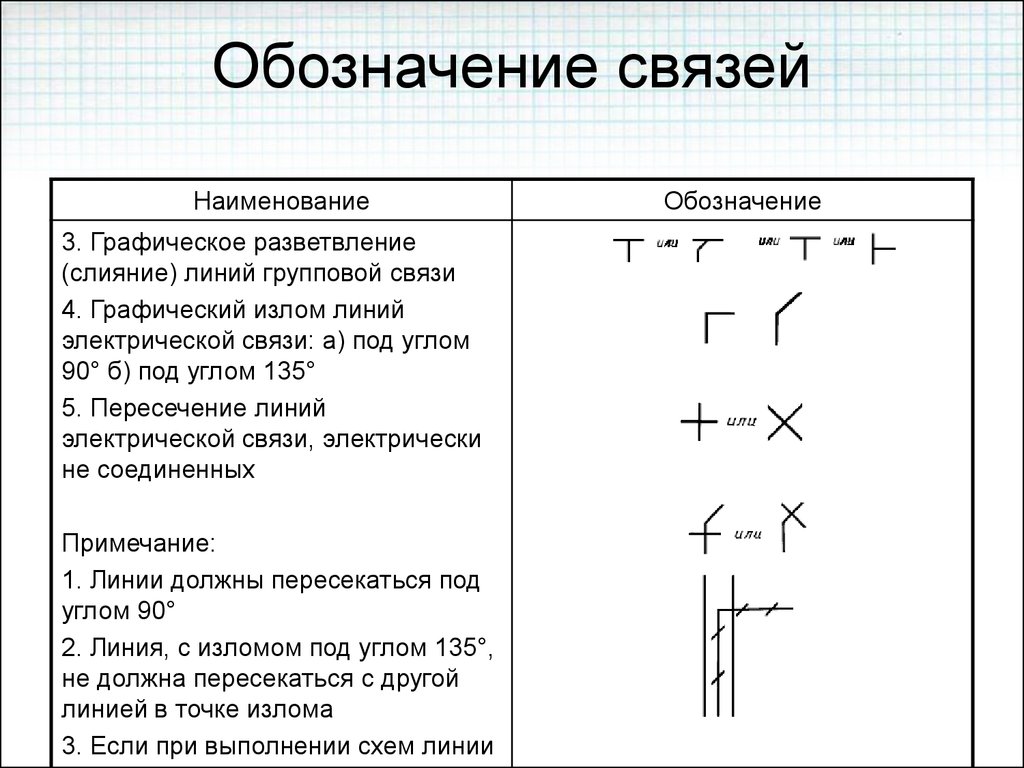
В зависимости от положения секущей плоскости α относительно плоскостей проекций (рис. 36 а – г) окружность может изобразиться:
а) окружностью, если плоскость α параллельна плоскости проекций; б) отрезком, если плоскость α перпендикулярна плоскости проекций;
в) эллипсом, если плоскость α расположена под углом к плоскости проекций.
38
) || Ï1 | ) || Ï2 |
m1 – окружность | m1 è m3 – отрезки |
m2 è m3 – отрезки | m2 – окружность |
à | á |
) || Ï3 | ) & Ï2 , ) ! Ï1 , ) ! Ï3 |
m1 è m2 – отрезки | m2 – отрезок |
m3 – окружность | m1 è m3 – эллипсы |
â | ã |
Рис. 36. Проекции окружности на сфере
Комплексный (ассоциативный) чертеж цилиндра и конуса, проекции точек
11 декабря, 2013 Анна Веселова
Здравствуйте! Мы продолжаем учиться создавать ассоциативный чертеж по 3d модели и находить недостающие проекции точек на нем.
Сегодня мы построим чертежи цилиндра и конуса.
Процесс создания ассоциативных чертежей цилиндра и конуса, такой же как и призмы, и пирамиды. Поэтому детали я опущу, подробнее о построении можете прочитать здесь — Как создать ассоциативный чертеж по 3d модели и найти проекции точек на пирамиде и призме?
Хочу только отметить следующее. Вы уже успели заметить, что созданные виды на чертеже, находятся в проекционной связи, т. е. перемещать их можно только вдоль границ главного вида. И только, начав перемещение главного вида, можно сдвинуть вверх или вниз и остальные.
комплексный (ассоциативный) чертеж цилиндра
Для того чтобы получить возможность перемещать каждый вид по отдельности нужно отменить проекционную связь. Для этого нажимаем левой кнопкой мыши по габаритному прямоугольнику вида (при этом, он подсветится зеленым), затем правой кнопкой вызываем контекстное меню и снимаем выделение с команды «Проекционная связь».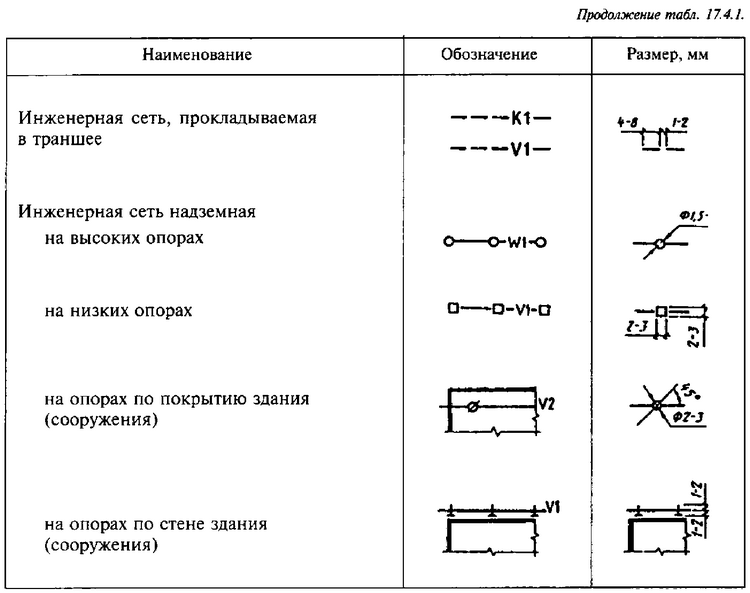
Ассоциативные чертежи в «Инженерной графике» называют комплексными.
Как найти
недостающие проекции точек на комплексном чертеже цилиндра?находим недостающие проекции точки m цилиндре
Построение недостающих проекций точек на цилиндре аналогично нахождению их на призме. Принцип тот же, только вместо граней, здесь окружность. Для нашего цилиндра недостающие проекции точек К и М находятся, как показано на рисунке при помощи вертикальных и горизонтальных линий связи.
Подробнее о процессе построения смотрите на уроке как найти проекции точек на пирамиде и призме
Как найти недостающие проекции точек на комплексном чертеже конуса?
находим проекции точек на конусе
Необходимо построить недостающие проекции точек К и М на комплексном чертеже конуса.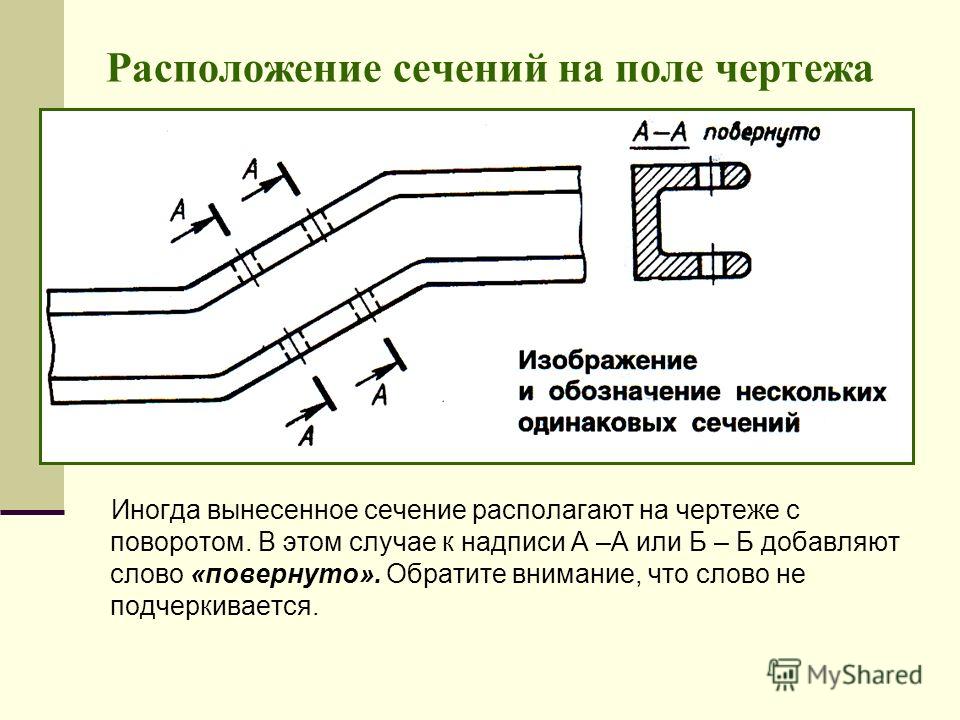
Точка М задана фронтальной проекцией m’, точка К – горизонтальной проекцией k.
построения при нахождении горизонтальной проекции точки
Построим горизонтальную проекцию m. Для этого:
- через точку m’ и вершину конуса s проводим вспомогательную прямую до пересечения ее с основанием в точке a.
- Затем через полученную точку а проводим вертикальную линию связи до пересечения с окружностью основания конуса в точке b.
- Через полученную точку b и вершину конуса s проводим прямую.
- Опускаем вертикальную линию связи из точки m’ до пересечения с прямой bs.
- Горизонтальная проекция m найдена.
Профильная проекция m’’ находится обычным образом по линиям связи.
Фронтальная проекция (k’) находится таким же, вышеописанным образом. Вот рисунок
строим фронтальную проекцию точки k
Профильную проекцию (k’’) находим по линиям связи.
Окончательно комплексные чертежи цилиндра и конуса выглядят так.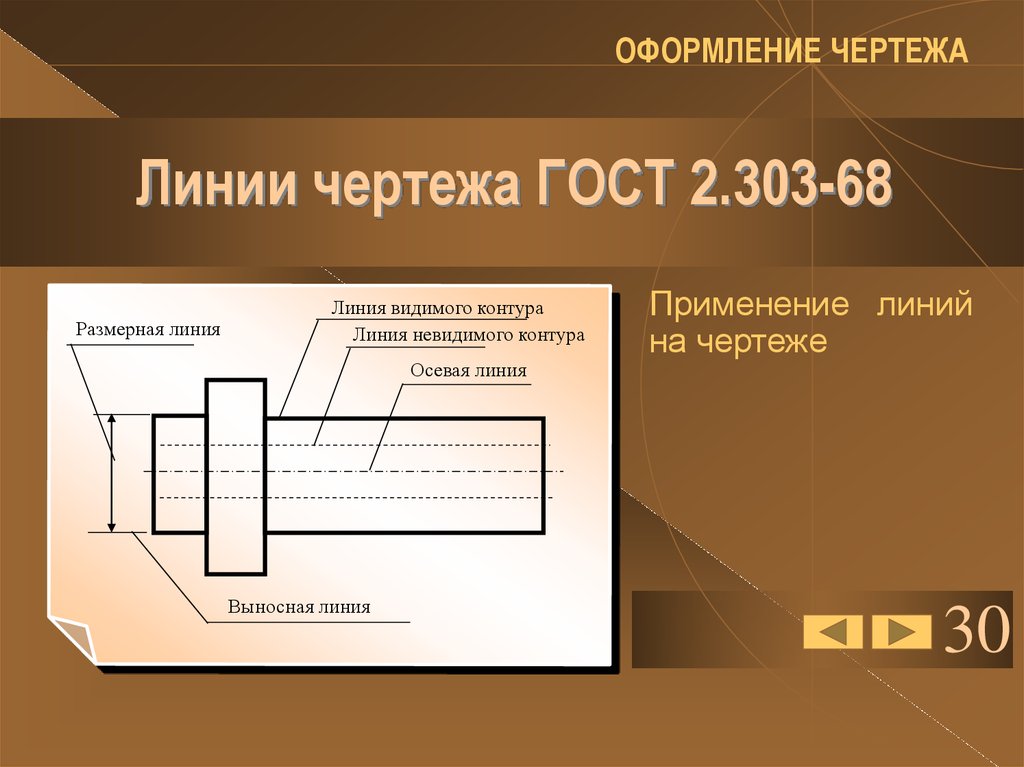
готовый комплексный чертеж конуса
готовый комплексный чертеж цилиндра
Для лучшего понимания материала рекомендую посмотреть видеоурок.
Скачать чертежи бесплатно можно здесь
Надеюсь урок “Строим ассоциативные чертежи цилиндра и конуса, находим на них недостающие проекции точек” был вам полезен.
The following two tabs change content below.
- Bio
- Latest Posts
Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок.
Присоединяйтесь!
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
21 способ общения линий
Линии — универсальный элемент визуального языка. Они передают широкий спектр значений, которые сильно зависят от контекста, в котором они появляются, и характеристик линии.
Мы учимся интерпретировать и понимать язык линий через опыт жизни в визуально грамотной культуре, а также через образование. Некоторые значения могут быть даже естественными для познания, например, использование меток для подсчета. Количество способов, которыми линии общаются, поражает. Вот 21 из них.
1. Линии изолируют и разделяют
Когда линия помещается между двумя элементами, это означает, что элементы разделены. Например, столбцы газетного текста часто разделяются вертикальными линиями, чтобы указать, что каждый столбец представляет собой отдельную статью.
Журналы часто используют разделительные линии, чтобы отделить рекламу от контента. Комиксы используют линии панели для определения каждого кадра в последовательности.
2. Линии обозначают группы
Частичная или полная линия, проведенная вокруг объектов, подразумевает, что объекты являются частью аналогичной категории или группы. Этот метод также используется в абстрактной графике, где линия, проведенная вокруг объектов на диаграмме, показывает, что элементы связаны между собой.
3. Линии обозначают единицы времени
На циферблате часов линии обозначают единицы времени. По соглашению 12 коротких линий, расположенных по окружности, представляют собой пятиминутные интервалы, хотя некоторые часы сокращают количество линий до четырех с 15-минутными интервалами. Линии также представляют временные интервалы на временных шкалах.
4. Линии обозначают единицы длины
Связь между временем и пространством переносится на визуальный язык. Линии разграничивают единицы длины, а также времени.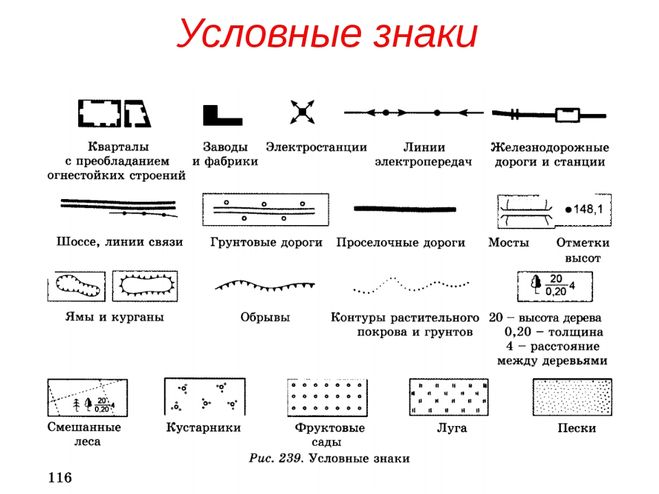
Даже без цифр деревянная, металлическая или пластиковая палочка с линиями через равные промежутки передает идею измерительного инструмента.
5. Линии передают яркость
Линии, исходящие от объекта, обозначают его яркость. Это может означать яркий, как солнце, или блестящий, как золотая монета. Поскольку лампочка также относится к «новой идее», эти линии также можно интерпретировать как обозначающие блестящую новую идею.
6. Линии передают звук
Линии, окружающие динамик, наушники или музыкальный инструмент, сообщают, что объект издает звук. Звуковые линии бывают разных стилей. Они могут быть нарисованы в виде расходящихся линий или в виде клиньев на иллюстрациях мультяшного типа, показанных здесь. Звуковые линии также изображаются в виде зубчатой линии звуковой волны или в виде концентрических полукругов.
7. Линии передают счет
С детства и во взрослом возрасте люди используют линии для счета. В системе подсчета каждая строка имеет однозначное соответствие с определенным элементом, например, одна строка для каждого балла оценки.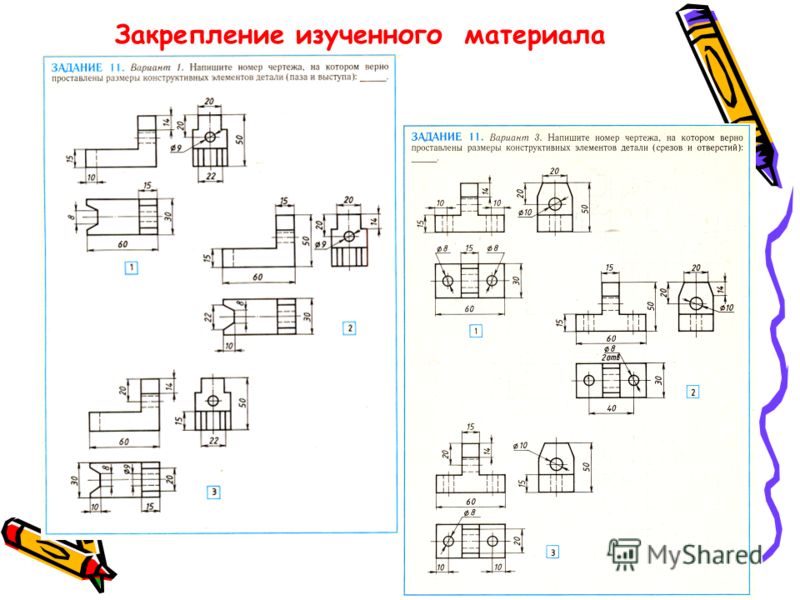
Использование линий для счета распространено во многих культурах, хотя линии могут составлять разные формы.
8. Линии представляют собой числовые данные
Линии представляют количество данных на линейных, гистограммах и других графиках. На линейных графиках линии отображают тренды. В гистограмме отдельные линии указывают суммы. Мы также считываем пики и впадины линий на машинных показаниях, таких как электрокардиограммы.
9. Линии представляют машинные данные
Таинственные линии штрих-кодовой бирки передают данные, которые не может понять никто, кроме машины. Эти линии передают эффективность и автоматизацию. Мы верим в их точность каждый раз, когда покупаем товар со штрих-кодом.
10. Линии отображают информацию о карте
Линии передают множество значений на картах. Они обозначают дороги, улицы, железнодорожные и велосипедные дорожки региона. Они колеблются на карте, изображая реки и пешеходные тропы. Линии также определяют политические и географические границы карты.
11. Линии сообщают о соединении
Линия, которая касается двух объектов, указывает на то, что объекты соединены. На диаграммах и диаграммах поля или значки соединены линиями, чтобы показать, какие из них связаны друг с другом. В информационной графике метка часто связана линией с элементом, который она называет. Круговые линии изображают соединения на сферах. При движении вокруг Земли связи происходят в глобальном масштабе.
12. Линии передают эмоции
Простите смайлик, но даже это упрощенное и схематизированное лицо выражает эмоции. Простой изгиб бровей и рта в соответствующем направлении указывает на гнев.
13. Линии сообщают о движении
Несколько горизонтальных линий движения позади объекта означают, что он движется вперед. Короткие изогнутые линии вокруг хвоста собаки говорят о том, что она виляет; те же самые линии, нанесенные вокруг человека на снегу, передают дрожь. Контекст — это основа для интерпретации.
14. Линии обозначают перфорацию
Ряд коротких отрезков в правильном контексте сообщает о перфорации для отрыва формы.
Когда показано с ножницами, он указывает, где резать. Он также может указывать, куда складывать, как при использовании в поделках из бумаги, таких как оригами.
15. Линии обозначают важность
Линия, проведенная вокруг объекта, указывает на его важность. Цель линии — привлечь внимание к выделенному объекту, выделить его из окружения.
16. Линии сообщают о передаче
Набор концентрических изогнутых линий почти всегда означает передачу какого-либо вида. Линии, используемые таким образом, стали повсеместным символом беспроводной связи.
17. Линии представляют статику
Старомодным символом помех на телевидении является зубчатая линия. Более интересная, чем плоская картина снега, зубчатая линия изображает плохой прием или сломанный телевизор.
18. Линии изображают физический мир
Бесконечное количество объектов можно нарисовать прямыми, изогнутыми или зигзагообразными линиями. Благодаря своим визуальным характеристикам и формам, которые они создают, простые линии могут быть организованы так, чтобы обозначать объекты.
Ум заполняет все остальное.
19. Линии представляют текст
Горизонтальные линии, распространенные в клипах и значках, обычно обозначают текст. В приложениях значки, начиная от кнопки вставки маркера и заканчивая инструментом вертикального межстрочного интервала, используют линии для изображения текста. Группы горизонтальных линий стали сокращением для визуального изображения абзаца. Это может быть не так для языков с вертикально ориентированным текстом.
20. Линии представляют отрицание
Линия, пересекающая объект, указывает на отрицание. Когда зачеркнутая линия пересекает текст, слово удаляется, но остается видимым. Линия, пересекающая день в календаре, означает, что этот день больше не существует. Диагональная косая черта поперек круга отрицает объект, на который она ссылается. Помните охотников за привидениями?
21. Линии обозначают ссылки
В языке Интернета подчеркивание слова или фразы означает, что это гиперссылка. По соглашению пользователи узнали, что строка под текстом означает, что щелчок по ней приведет их к соответствующему URL-адресу.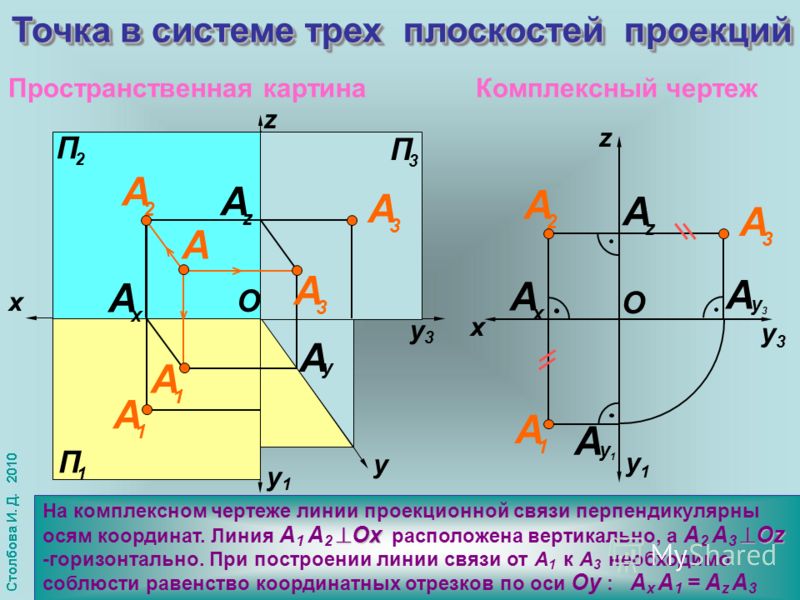
Хотя подчеркивание можно удалить с помощью стилей, оно остается одним из лучших способов сообщить читателю о потенциале связывания.
Если у вас есть дополнения к этому списку, пожалуйста, добавьте их в Комментарии. Спасибо!
900+ линий связи картинки | Без лицензионных отчислений
1–75 из 274 758 изображений
Линии Связи Стоковые фотографии Линии связи стоковые иллюстрации
Ориентиры:чистый Горизонтальный Панорамный Горизонтальный Панорамный вертикальный Площадь Вертикальный
Переключить субтитры
Макет
GridTitles
Результаты
5075100150250500
html” data-next=”/vector-clip-art/communication-lines_2.html”>Линии связи Spheres Ball
Бесшовная топографическая карта.
Телефон с сенсорным экраном правит миром
Промышленные линии связи
Азия и Австралия, глобальный
Фон общения
Европа Глобальная коммуникационная планета
Логотип изображения карты точек и линий Франции
Изображение карты точек и линий Испании.
Связной
Европа и Африка, глобальный
Высоковольтные линии электропередач
Connect Business People Network Connections
Lines – связь
Говорящий пузырь
Молекула и коммуникационный фон
Волна
Группа связи
Южная Латинская Америка Глобальный
Нидерланды Карта точек и линий Изображение
Северная и Южная Америка Global
Интернет-трафик данных
Голубая молекула и коммуникационный фон
Медиа и коммуникационные плоские цветные иконки
Мировой телефон
Северная, Южная Америка, Европа, Африка
Абстрактный фон
Абстрактные линии
Абстрактные линии
Карта мира со связью
Коммуникационный баннер
Концепция связи
Глобальный бизнес.
Новости о смартфоне
Концепция Интернета
Концепция детского общения Illustra
IT-коммуникация – База знаний
Технология сетевого цвета Фон
Рукопожатие Люди в бизнесе Логотип
Глобальная связь
Карта Андорры Светящийся силуэт Очертания из звезд, линий, точек, треугольников, низких многоугольных форм.
Изображение карты точек и линий Флориды.
Набор векторных баннеров, сетевое общение на синем фоне.
Командный цветок с логотипом листьев
Абстрактные линии
Дом
Свяжитесь с нами Дизайн иллюстрации
Связной
Общение в социальной сети.
Абстрактные линии
Медиа и коммуникационные плоские иконки
Векторный телефонный оператор
Набор иконок тонкой линии
Концепция облачных вычислений — Интернет
Молекула и коммуникационный фон
значок планеты глобус высокое качество
Векторная абстрактная футуристическая печатная плата и линия сетки
Молекула и коммуникационный фон
Логотип Family Heart Hands
Телефон
Набор плоских икон современного бизнеса и технологий
Бизнесмен Технология
Карта Нидерландов Светящийся силуэт Очертания из звезд, линий, точек, треугольников, низких многоугольных форм.
Геометрическая карта мира, вектор
Пузыри речи и мыслей
Связной
Концепция подключения к глобальной сети
Элементы дизайна технологий и коммуникаций
Фон для общения в 3D Word
Всемирная глобальная коммерческая коммуникация
Иллюстрация современных коммуникационных технологий с планшетом.