|
Навигация: Для одноэтажных зданий. Геометрические оси сечения колонн средних рядов, кроме колонн, расположенных в торцах, у температурных швов и перепадов высот зданий, следует совмещать с координационными осями здания. При устройстве проходов вдоль подкрановых путей с одной стороны колонны привязку колонн среднего ряда к координационным осям принимают по сечению подкрановой части колонны. Привязку колонн крайнего продольного ряда к координационным осям следует осуществлять таким образом, чтобы внешняя грань колонны совмещалась с координационной осью здания или была смещена наружу соси продольного ряда на 250 или 500 мм в зависимости от шага колонн, грузоподъемности, режима и вида кранового оборудования. Ось поперечного температурного шва на парных колоннах с пролетами равной высоты следует совмещать с поперечной координационной осью. Допускается осуществлять шов в пределах вставки с размером, кратным 50 мм, между двумя поперечными координационными осями. Для выполнения продольного температурного шва на парных колоннах в зданиях с пролетами одинаковой высоты следует предусматривать две продольные координационные оси со вставкой между ними. Размер вставки должен равняться сумме размеров привязки к координационным осям граней колонн, обращенных в сторону шва, и расстоянию между этими гранями, равному 500 мм, а при большем размере — кратному 250. При устройстве дует предусмотреть две поперечные координационные оси со вставкой, равной не менее. Привязку колонн к продольным координационным осям следует принимать в зависимости от шага колонн, грузоподъемности, режима работы и вида кранового оборудования. Размер вставки с равняется округленной сумме следующих размеров: привязки к продольным координационным осям граней колонн, обращенных в сторону перепада, зазора с между наружной гранью колонн повышенного пролета и внутренней плоскостью стены, толщины стены и зазора не продольного температурного шва в зданиях с покрытиями по подстропильным конструкциям грани колонн, обращенные в сторону шва, необходимо смещать с координационных осей в сторону шва на 250 мм. Рис. 1. Привязка колонн к координационным осям: Рис. Примыкание взаимно перпендикулярных пролетов осуществляется на парных колоннах со вставкой между крайней продольной и торцевой поперечной координационными осями размером, кратным 50, но не менее а — при устройстве продопьного. Продольный температурный шов между параллельными пролетами, примыкающими к перпендикулярному пролету, продлевается в перпендикулярный пролет, где он является поперечным температурным швом со вставкой между координационными осями, равной как в продольном, так и в поперечном швах. Рис. 3. Привязка колонн к координационным осям: Для многоэтажных зданий. Привязку колонн средних рядов для этих зданий надо выполнять таким образом, чтобы геометрические оси сечения колонн совмещались с продольными и поперечными координационными осями здания. Парные колонны у поперечного деформационного шва и перепада высот следует привязывать к двум координационным осям с расстоянием между осями, равным 1000 мм или более, кратным 250 мм, или к одной координационной оси, совмещенной с осью шва. Парные колонны в местах продольных деформационных швов следует привязывать к двум координационным осям. Расстояние между осями принимать кратным 50 мм, но не менее 300 мм при совмещении внешних граней колонн с продольными координационными осями и не менее 1000 мм при совмещении геометрических осей колонн с координационными осями здания. Рис. 4. Привязка колонн к координационным осям при устройстве продольного температурного шва в зданиях с проектами одинаковой высоты со вставкой размером: Рис. Рис. 6. Варианты (а, б, в, г) привязки колонн к координационным осям при примыкании взаимно перпендикулярных пролетов разных высот: Похожие статьи: Навигация:
Главная → Справочник → Статьи → Блог → Форум |
300, а при большем размере — кратной 50. При перепаде высот параллельных пролетов на парных колоннах следует предусмотреть две продольные координационные оси со вставкой с, равной не менее 300, а при большем размере — кратной 50.
2. Привязка колонн среднего ряда к координационным осям:
Колонны крайних рядов следует привязывать к продольным координационным осям так, чтобы внешние грани колонн совмещались с продольными координационными осями или были смещены наружу на 200 или 250 мм.
5. Варианты (а, б, в, г) привязки колонн к продольным координационным осям при перепаде высот параллельных пролетов: 1 — эаэор; 2 — толщина стены; с — вставкаКоординационные оси здания (сооружения)
⇐ Предыдущая3456789101112Следующая ⇒
Планы этажей зданий
Рабочие чертежи архитектурных решений
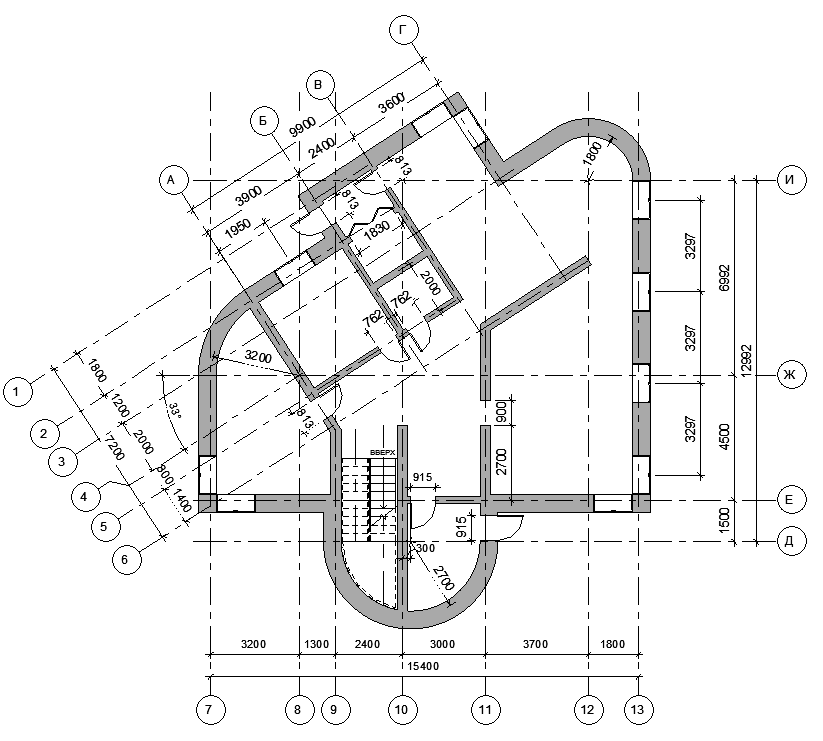
План этажа здания – это изображение разреза здания, выполненного мнимой горизонтальной секущей плоскостью, проходящей на уровне оконных и дверных проемов или на высоте 1/3 высоты изображаемого этажа здания.
План этажа дает представление о конфигурации и размерах здания, выявляет форму и расположение отдельных помещений, оконных и дверных проемов, капитальных стен, колонн, лестниц, перегородок. На план наносят контуры элементов здания (стены, простенки, столбы, перегородки и т.п.), попавших в разрез и расположенных за секущей плоскостью.
Если планы этажей многоэтажного здания имеют небольшие отличия друг от друга, то полностью выполняют план одного из этажей, для других этажей выполняют только части плана, необходимые для показа отличия от плана, изображенного полностью.
Чертежи планов здания рекомендуется вычерчивать в определенной последовательности согласно рисунку 11.
Координационные (разбивочные) оси – это координационные линии, определяющие членение здания или сооружения на модульные шаги и высоты этажей. Они определяют положение основных несущих конструкций здания и проходят по его капитальным стенам и колоннам.
Эти оси, которые могут быть продольными и поперечными, расчленяют здание на ряд элементов.
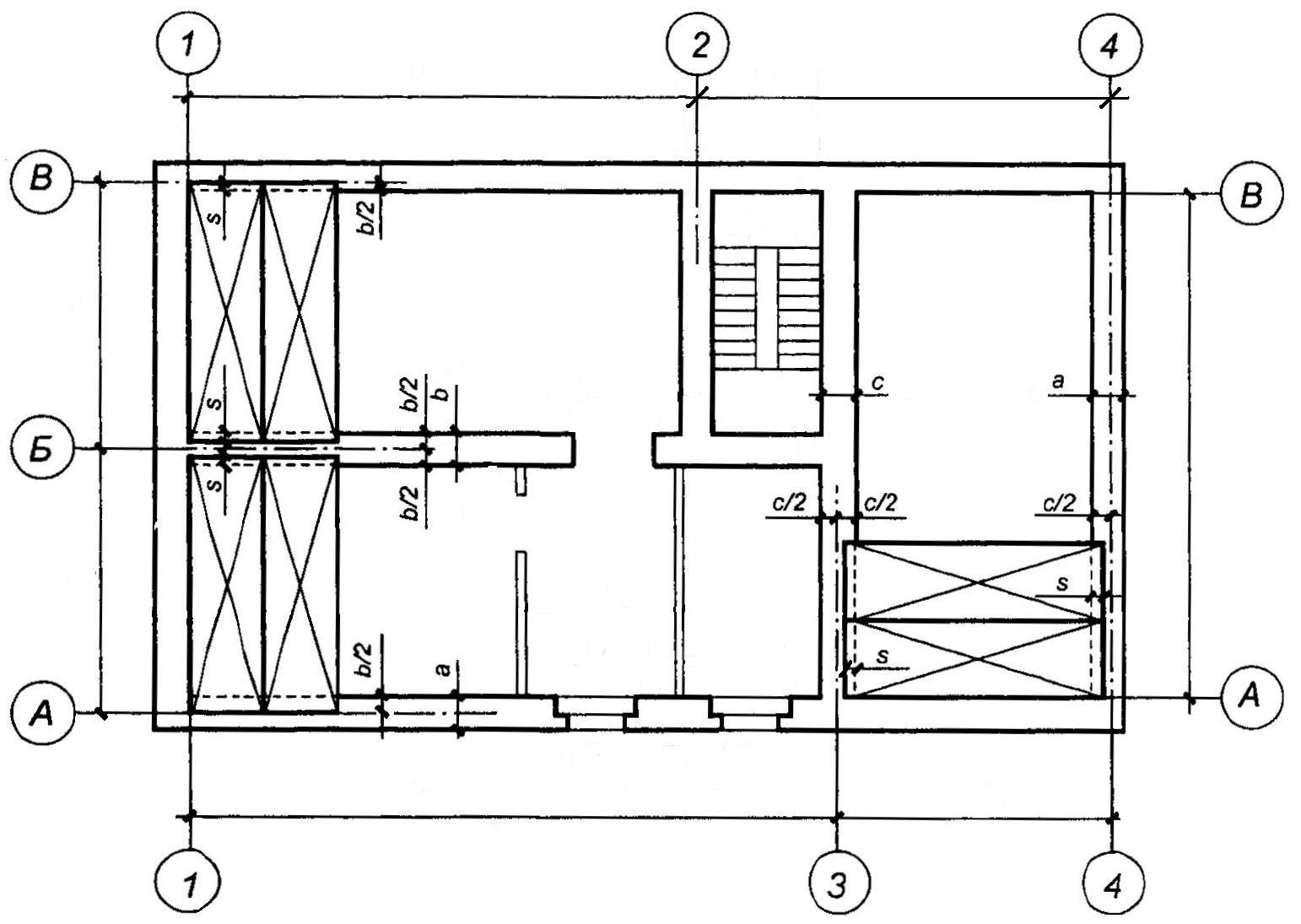
На изображениях каждого здания и сооружения указывают координационные оси, которым присваивают самостоятельную систему обозначений. Координационные оси наносят штрихпунктирными линиями с длинными штрихами в соответствии с рисунком 5. На планах разбивочные оси выводят за контур стен и обозначают прописными буквами русского алфавита и арабскими цифрами (числами), которые записывают в маркировочных окружностях диаметром 6-12мм. Маркировочные кружки координационных осей располагают на расстоянии 4мм от последней размерной линии.
Для маркировки на стороне здания с большим числом осей используют цифры, а с меньшим числом осей – буквы, за исключением букв Ё, З, Й, О, Х, Ц, Ч, Щ, Ъ, Ы, Ь. Буквами маркируют, как правило, оси, идущие вдоль здания.
Последовательность цифровых и буквенных обозначений координационных осей принимают по плану слева направо и снизу вверх, располагая маркировочные окружности с левой и нижней сторон здания (рис.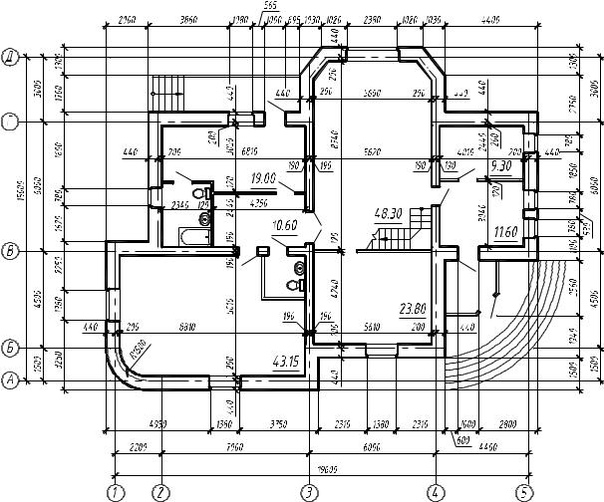
12, 20).
Обозначение координационных осей, как правило, наносят по левой и нижней сторонам плана здания и сооружения. При несовпадении координационных осей противоположных сторон плана, в местах расположения дополнительно наносят обозначения указанных осей по верхней и/или правой сторонам. Пропуски букв и чисел при маркировке осей не допускаются.
Для отдельных элементов, расположенных между координационными осями основных несущих конструкций, наносят дополнительные оси и обозначают их в виде дроби, в числителе которой указывают обозначение предшествующей координационной оси, а в знаменателе – дополнительный порядковый номер в пределах участка между координационными осями (рис 11а).
⇐ Предыдущая3456789101112Следующая ⇒ |
Дата добавления: 2015-06-29; Просмотров: 4868; Нарушение авторских прав?; Мы поможем в написании вашей работы!
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
25.
1: Системы координат – Физика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19563
- Howard Martin пересмотрено Аланом Нг
- University of Wisconsin-Madison
Системы координат используются для описания положения объекта в пространстве. Система координат — это искусственный математический инструмент, который мы строим для описания положения реального объекта.
Одномерные системы координат
Самая простая для построения система координат — та, которую мы можем использовать для описания местоположения объектов в одномерном пространстве. Например, мы можем захотеть описать местоположение поезда на прямом участке пути, идущем в направлении восток-запад.
Для этого мы должны сначала определить «начало», которое является точкой отсчета нашей системы координат. Например, отправной точкой нашего железнодорожного пути может быть вокзал Кингстона (рис. A1.1.1).
Мы можем описать положение поезда, указав, как далеко он находится от железнодорожной станции (отправной точки), используя одно действительное число, скажем, \(x\). Если поезд находится в точке \(x=0\), то мы знаем, что он находится на станции Кингстон. Если объект не находится в начале координат, то нам нужно указать, с какой стороны (на востоке или западе в нашем примере с поездом) от начала координат находится объект. Мы делаем это, выбирая направление для нашей одномерной координаты \(x\). Например, мы можем выбрать, чтобы восточная сторона дорожки соответствовала положительным значениям \(x\), а западная сторона дорожки соответствовала отрицательным значениям \(x\). Таким образом, чтобы полностью задать одномерную систему координат, нам нужно выбрать:
- место отправления.
- направление увеличения координаты \(x\).
- единиц, в которых мы хотим выразить \(x\).
В одном измерении обычно используется переменная \(x\) для определения положения вдоль “\(x\)-оси”. Ось \(х\) – это наша система координат в одном измерении, и мы представляем ее, рисуя линию со стрелкой в направлении увеличения \(х\) и указываем, где находится начало координат (как на рис. А1.1.1).
Рисунок A1.1.1 : Одномерная система координат, описывающая положение поезда. Железнодорожная станция Кингстона является отправной точкой, а восточная сторона пути соответствует положительным значениям \(x\). Поезд находится в позиции \(x_{1}\).2D системы координат
Рисунок A1.1.2 : Пример декартовой системы координат и точки \(P\) с координатами \((x_{p}, y_{p})\). Чтобы описать положение объекта в двух измерениях (например, шарик, катящийся по столу), нам нужно указать два числа. Самый простой способ сделать это — определить две оси, \(x\) и \(y\), начало и направление которых мы должны определить.
На рисунке A1.1.2 показан пример такой системы координат. Хотя в этом нет необходимости, мы выбрали оси \(x\) и \(y\), перпендикулярные друг другу. Начало системы координат находится там, где пересекаются две оси. Можно выбрать любые два направления для осей (при условии, что они не параллельны). Однако выбор осей, которые перпендикулярны (декартова система координат), обычно является наиболее удобным.
Чтобы полностью описать положение объекта, мы должны указать его положение по осям \(x\) и \(y\). Например, точка \(P\) на рисунке A1.1.2 имеет две координаты , \(x_p\) и \(y_p\), которые определяют ее положение. Координата \(x\) находится путем проведения через \(P\) линии, параллельной оси \(y\) и задаваемой пересечением этой линии с осью \(x\). Координата \(y\) находится путем проведения линии через точку \(P\), которая параллельна оси \(x\) и задается пересечением этой линии с осью \(y\).
Упражнение \(\PageIndex{1}\)
На рисунке A1.1.3 показана неортогональная система координат (где оси \(x\) и \(y\) не перпендикулярны).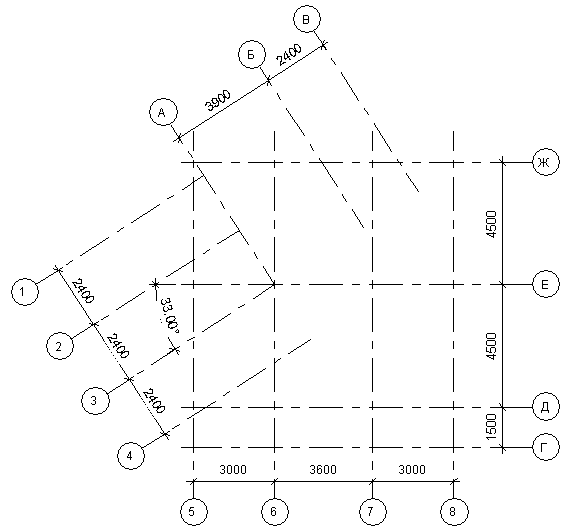
Какое значение на рисунке правильно указывает координату \(y\) точки \(P\)?
- \(у_1\)
- \(у_2\)
- \(у_3\)
- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Наиболее распространенным выбором системы координат в двух измерениях является декартова система координат, которую мы только что описали, где оси \(x\) и \(y\) перпендикулярны и имеют общее начало, как показано на рисунке A1. 1.2. Когда это применимо, по соглашению мы обычно выбираем ось \(y\), чтобы она соответствовала вертикальному направлению.
Другим распространенным выбором является «полярная» система координат, в которой положение объекта определяется расстоянием до начала координат \(r\) и углом \(\theta\) относительно заданного направления , как показано на рисунке A1.
1.4. Часто наряду с декартовой системой определяется полярная система координат, так что \(r\) — это расстояние до начала декартовой системы, а \(\theta\) — угол относительно оси \(x\). . 92}\\ \tan(\theta) &= \frac{y}{x}\end{aligned}\] Полярные координаты часто используются для описания движения объекта, движущегося по окружности, так как это означает, что только один координат (\(\theta\)) меняется со временем (если начало системы координат выбрано так, чтобы оно совпадало с центром окружности).
Трехмерные системы координат
В трех измерениях нам нужно указать три числа, чтобы описать положение объекта (например, птицы, летящей в воздухе). В трехмерной декартовой системе координат мы просто добавляем третью ось \(z\), которая взаимно перпендикулярна как \(x\), так и \(y\). Затем положение объекта можно указать с помощью трех координат: \(x\), \(y\) и \(z\). По соглашению мы используем ось \(z\) как вертикальное направление в трех измерениях.
В трех измерениях распространены две дополнительные системы координат: «цилиндрическая» и «сферическая» координаты.
Все три системы показаны на рисунке A1.1.5 в сочетании с декартовой системой.
Цилиндрические координаты можно рассматривать как расширение полярных координат. Мы сохраняем ту же декартову координату \(z\), чтобы указать высоту над плоскостью \(xy\), однако мы используем азимутальный угол , \(\phi\) и радиус, \(\rho\), для описания положения проекции точки на плоскость \(xy\). \(\phi\) — угол между осью \(x\) и линией от начала координат до проекции точки на плоскость \(xy\), а \(\rho\) — расстояние между точкой и ось \(z\). Таким образом, цилиндрические координаты очень похожи на полярную систему координат, введенную в двух измерениях, за исключением добавления координаты \(z\). Цилиндрические координаты полезны для описания ситуаций с азимутальной симметрией, таких как движение по поверхности цилиндра.
Например, рассмотрим точку \(P\) на рисунке A1.1.6. Точка \(P\) расположена на расстоянии \(\rho\) от оси \(z\), так как расположена на поверхности цилиндра (круглый конец цилиндра имеет радиус \(\rho\ )). Точка \(P\) — это высота \(z\) над плоскостью \(xy\), а прямая из оси \(z\) в точку \(P\) образует угол \(\phi\) с осью \(х\). 92}\\ \tan(\phi) &= \frac{y}{x}\\ z&=z\end{aligned}\] В сферических координатах точка \(P\) описывается радиусом, \ (r\), полярный угол \(\theta\) и азимутальный угол , \(\phi\). Радиус – это расстояние между точкой и началом координат. Полярный угол – это угол с осью \(z\), который составляет линия от начала координат до точки. Азимутальный угол определяется так же, как и в полярных координатах. Обратите внимание, что значение \(\phi\) должно быть между \(0\) и \(2\pi\), тогда как значение \(\theta\) должно быть между \(0\) и \(\ Пи\).
Сферические координаты полезны для описания ситуаций, имеющих сферическую симметрию, например, человека, идущего по поверхности Земли, поскольку радиальная координата не изменится.
2}}\\ \tan(\phi) &= \frac{y}{x}\\\ конец {выровнено}\]
Эта страница под названием 25.1: Системы координат распространяется по лицензии CC BY-SA, ее автор, ремикширование и/или куратор — Говард Мартин, редакция Алана Нг.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Райан Мартин и др.
- Лицензия
- CC BY-SA
- Показать оглавление
- нет
- Теги
Системы координат — смешанная реальность
- Статья
По своей сути приложения смешанной реальности размещают в вашем мире голограммы, которые выглядят и звучат как настоящие объекты. Это включает в себя точное позиционирование и ориентацию этих голограмм в значимых местах в мире, будь то мир их физической комнатой или созданным вами виртуальным царством. Windows предоставляет различные системы координат реального мира для выражения геометрии — они известны как 9.0060 системы пространственных координат . Вы можете использовать эти системы для определения положения голограммы, ориентации, луча взгляда или положения рук.
Опора устройства
| Функция | HoloLens (1-го поколения) | ХолоЛенс 2 | Иммерсивные гарнитуры |
| Стационарная система отсчета | ✔️ | ✔️ | ✔️ |
| Прикрепленная система координат | ✔️ | ✔️ | ✔️ |
| Система координат сцены | Пока не поддерживается | Пока не поддерживается | ✔️ |
| Пространственные анкеры | ✔️ | ✔️ | ✔️ |
| Пространственное картографирование | ✔️ | ✔️ | ❌ |
| Понимание сцены | ❌ | ✔️ | ❌ |
Масштабы возможностей смешанной реальности
Вы можете разрабатывать приложения смешанной реальности для широкого спектра пользовательских возможностей, от средств просмотра 360-градусного видео с ориентацией гарнитуры до полномасштабных приложений и игр мирового масштаба с использованием пространственного картографирования и пространственных привязок:
| Шкала опыта | Требования | Пример опыта |
|---|---|---|
| Только для ориентации | Ориентация гарнитуры (по гравитации) | Средство просмотра видео 360° |
| Сидячие весы | Выше плюс положение гарнитуры на основе нулевого положения | Гоночная игра или космический симулятор |
| Весы | Выше плюс начало пола сцены | Экшн-игра, в которой вы пригибаетесь и уклоняетесь на месте |
| Комнатные весы | Выше плюс полигон границ сцены | Игра-головоломка, в которой вы ходите вокруг головоломки |
| Мировой масштаб | Пространственные привязки (и обычно пространственное картографирование) | Игра с врагами, исходящими из ваших настоящих стен, например RoboRaid |
Приведенные выше шкалы опыта соответствуют модели «матрешки».
Ключевой принцип разработки Windows Mixed Reality заключается в следующем: данная гарнитура поддерживает приложения, созданные для целевого масштаба опыта и всех меньших масштабов.
| Отслеживание 6 степеней свободы | Этаж определен | Отслеживание на 360° | Границы определены | Пространственные анкеры | Максимальный опыт |
|---|---|---|---|---|---|
| № | – | – | – | – | Только ориентация |
| Да | № | – | – | – | Сидячий |
| Да | Да | № | – | – | Стоя – вперед |
| Да | Да | Да | № | – | Стоя – 360° |
| Да | Да | Да | Да | № | Помещение |
| Да | Да | Да | Да | Да | Мир |
Система отсчета Stage еще не поддерживается в HoloLens.
Приложение масштаба комнаты в HoloLens в настоящее время должно использовать пространственное сопоставление или понимание сцены, чтобы найти пол и стены пользователя.
Пространственные системы координат
Все приложения для трехмерной графики используют декартовы системы координат для определения положения и ориентации виртуальных объектов. Эти системы координат устанавливают три перпендикулярные оси: X, Y и Z. Каждый объект, который вы добавляете в сцену, будет иметь положение XYZ в своей системе координат. Windows называет систему координат, которая имеет реальное значение в физическом мире, пространственная система координат, которая выражает свои значения координат в метрах. Это означает, что объекты, расположенные на расстоянии двух единиц друг от друга по осям X, Y или Z, будут отображаться на расстоянии двух метров друг от друга при визуализации в смешанной реальности. Зная это, вы можете легко визуализировать объекты и окружение в реальном масштабе.
Обычно декартовы системы координат называются “правосторонними” или “левосторонними”, поскольку вы можете использовать положения рук для указания направления осей XYZ.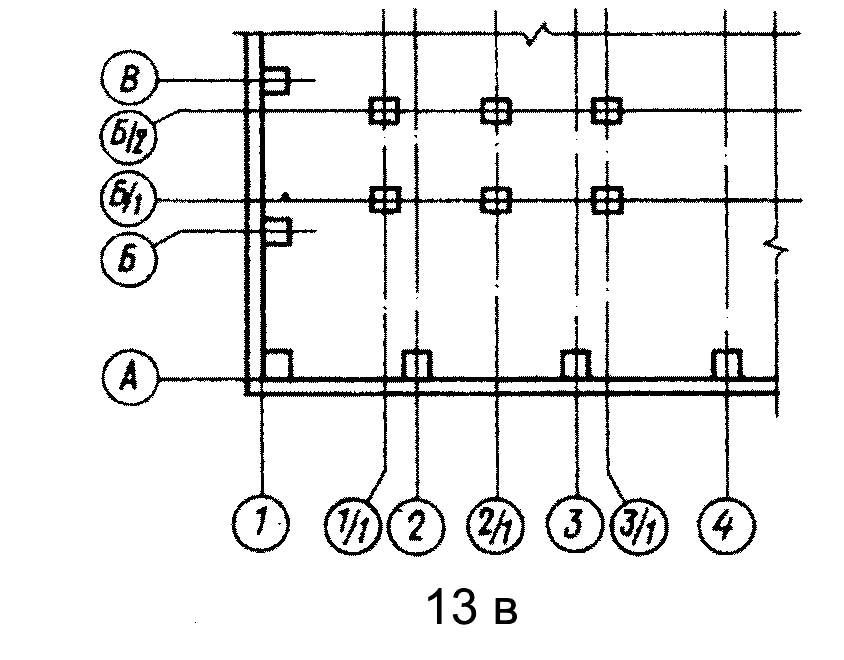
В обеих системах координат положительная ось X направлена вправо, а положительная ось Y направлена вверх. Разница между ними в том, что в правосторонней системе координат ось Z указывает на 9.0048 по направлению к от вас, а в левой системе координат ось Z указывает на от вас на .
Пространственные системы координат в Windows (и, следовательно, в Windows Mixed Reality) всегда правосторонние.
[!ПРИМЕЧАНИЯ]
- Unity и Unreal используют левостороннюю систему координат.
- Хотя левосторонние и правосторонние координаты являются наиболее распространенными системами, в 3D-программном обеспечении используются и другие системы координат. Например, приложения для 3D-моделирования нередко используют систему координат, в которой ось Y направлена к наблюдателю или от него, а ось Z направлена вверх.
Создание опыта, ориентированного только на ориентацию или сидящего в масштабе
Ключом к голографическому рендерингу является изменение представления вашего приложения о своих голограммах в каждом кадре, когда пользователь перемещается, чтобы соответствовать прогнозируемому движению его головы.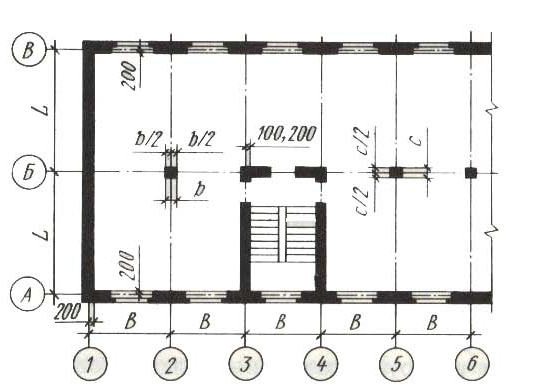
Вы можете создать сидячих представлений , учитывающих изменения положения и ориентации головы пользователя, используя стационарную систему отсчета .
Некоторый контент должен игнорировать обновления положения головы, всегда оставаясь фиксированным на выбранном заголовке и расстоянии от пользователя. Основным примером является 360-градусное видео: поскольку видео записывается с одной фиксированной точки зрения, это разрушит иллюзию перемещения позиции просмотра в зависимости от контента, даже если ориентация просмотра меняется, когда пользователь смотрит вокруг. Таких можно построить только ориентация воспринимает с использованием присоединенной системы отсчета .
Стационарная система отсчета
Система координат, обеспечиваемая стационарной системой отсчета, обеспечивает максимально стабильное положение объектов рядом с пользователем в зависимости от окружающего мира с учетом изменений положения головы пользователя.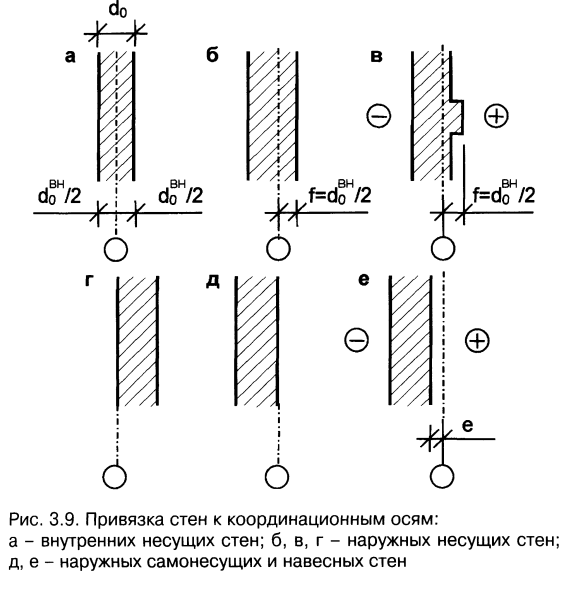
Для сидячих игр в таком игровом движке, как Unity, стационарная система отсчета — это то, что определяет «происхождение мира» движка. Объекты, размещенные в определенных мировых координатах, используют стационарную систему отсчета для определения своего положения в реальном мире с использованием тех же координат. Контент, который остается в мире, даже когда пользователь ходит по нему, называется 9.0060 заблокированный во всем мире контент .
Приложение обычно создает одну стационарную систему отсчета при запуске и использует ее систему координат на протяжении всего жизненного цикла приложения. Как разработчик приложений в Unity, вы можете просто начать размещать контент на основе источника, который будет находиться в исходном положении и ориентации головы пользователя. Если пользователь переезжает в новое место и хочет продолжить работу в масштабе сидя, вы можете отцентрировать начало мира в этом месте.
Со временем, по мере того как система узнает больше о среде пользователя, она может определить, что расстояния между различными точками в реальном мире короче или длиннее, чем система считала ранее.
Если вы визуализируете голограммы в стационарной системе отсчета для приложения на HoloLens, когда пользователи выходят за пределы области шириной около 5 метров, ваше приложение может наблюдать смещение наблюдаемого местоположения этих голограмм. Если в вашем опыте пользователи блуждают дальше 5 метров, вы создаете опыт мирового масштаба, для которого потребуются другие методы для поддержания стабильности голограмм, как описано ниже.
Прикрепленная система отсчета
Присоединенная система отсчета перемещается вместе с пользователем, когда он ходит, с фиксированным заголовком, определяемым при первом создании кадра приложением. Это позволяет пользователю удобно просматривать контент, размещенный в этой системе отсчета. Содержимое, визуализируемое таким образом, относительно пользователя, называется содержимым с блокировкой тела .
Когда гарнитура не может определить, где она находится в мире, прикрепленная система отсчета обеспечивает единственную систему координат, которую можно использовать для визуализации голограмм.
Это делает его идеальным для отображения резервного пользовательского интерфейса, чтобы сообщить пользователю, что его устройство не может найти его в мире. Приложения с масштабом для сидячих мест или выше должны включать резервный вариант только для ориентации, чтобы помочь пользователю снова начать работу, с пользовательским интерфейсом, аналогичным тому, который показан на домашней странице Mixed Reality.
Создание модели в масштабе стоя или в масштабе комнаты
Чтобы выйти за рамки сидячей работы с иммерсивной гарнитурой и создать модель в масштабе стоя , вы можете использовать систему координат сцены .
Чтобы обеспечить масштаб комнаты, позволяя пользователям ходить в пределах 5-метровой границы, которую они заранее определили, вы также можете проверить границ сцены .
Система координат сцены
При первой настройке иммерсивной гарнитуры пользователь определяет stage , который представляет собой комнату, в которой они будут испытывать смешанную реальность.
Сцена минимально определяет начало координат , систему пространственных координат с центром в выбранной пользователем позиции на полу и ориентацией вперед, где они намереваются использовать устройство. Размещая контент в этой системе координат сцены в плоскости пола Y=0, вы можете гарантировать, что ваши голограммы будут удобно отображаться на полу, когда пользователь стоит, предоставляя пользователям возможность просмотра в масштабе 90 060.0061 .
Границы сцены
Пользователь также может дополнительно определить границ сцены , область в комнате, которую он очистил для перемещения в смешанной реальности. Если это так, приложение может создать комнатный опыт , используя эти границы, чтобы голограммы всегда размещались там, где пользователь может до них дотянуться.
Поскольку система отсчета сцены обеспечивает единую фиксированную систему координат, в которой можно размещать контент, относящийся к этажам, это самый простой путь для переноса приложений в масштабе стоя и масштаба комнаты, разработанных для гарнитур виртуальной реальности.
Однако, как и в случае с этими платформами виртуальной реальности, единая система координат может стабилизировать контент только в диаметре около 5 метров (16 футов), прежде чем эффекты рычага заставят контент, находящийся далеко от центра, заметно сместиться по мере настройки системы. Чтобы выйти за пределы 5 метров, необходимы пространственные анкеры.
Создание впечатлений мирового масштаба
HoloLens позволяет создавать настоящие впечатления мирового масштаба , которые позволяют пользователям перемещаться дальше 5 метров. Чтобы создать приложение мирового масштаба, вам потребуются новые методы, помимо тех, которые используются для работы в масштабе комнаты.
Почему единая жесткая система координат не может использоваться на расстоянии более 5 метров
Сегодня при написании игр, приложений для визуализации данных или приложений виртуальной реальности типичным подходом является создание одной абсолютной мировой системы координат, которую все остальные координаты могут надежно отображать.
к. В этой среде вы всегда можете найти стабильное преобразование, определяющее отношения между любыми двумя объектами в этом мире. Если бы вы не перемещали эти объекты, их относительные преобразования всегда оставались бы неизменными. Такая глобальная система координат хорошо работает при рендеринге чисто виртуального мира, где вы заранее знаете всю геометрию. Современные приложения виртуальной реальности в масштабе комнаты обычно устанавливают такую абсолютную систему координат в масштабе комнаты с началом на полу.
Напротив, непривязанное устройство смешанной реальности, такое как HoloLens, обладает динамическим пониманием мира, управляемым датчиками, постоянно корректируя свои знания с течением времени об окружении пользователя, когда он проходит много метров по всему этажу здания. В мировом масштабе, если вы поместите все свои голограммы в единую жесткую систему координат, эти голограммы обязательно будут дрейфовать во времени либо в зависимости от мира, либо друг к другу.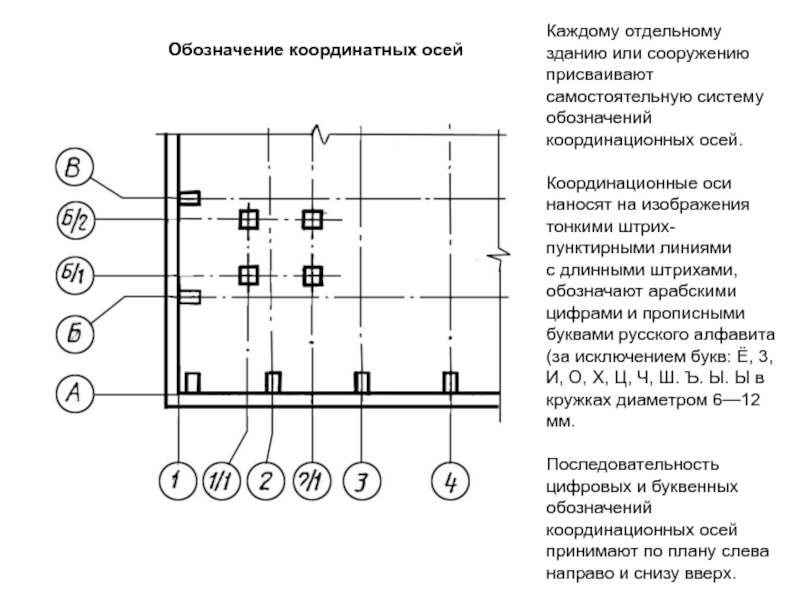
Например, в настоящее время гарнитура может считать, что два места в мире находятся на расстоянии 4 метров друг от друга, а затем уточнить это понимание, узнав, что на самом деле места находятся на расстоянии 3,9метров друг от друга. Если эти голограммы изначально были размещены на расстоянии 4 метров друг от друга в единой жесткой системе координат, одна из них всегда будет отображаться на расстоянии 0,1 метра от реального мира.
Пространственные привязки
Windows Mixed Reality решает проблему, описанную в предыдущем разделе, позволяя создавать пространственные привязки для отметки важных точек мира, в которые пользователь поместил голограммы. Пространственная привязка представляет собой важную точку в мире, которую система должна отслеживать с течением времени.
По мере того, как устройство изучает мир, эти пространственные привязки могут корректировать свое положение в зависимости друг от друга по мере необходимости, чтобы каждая привязка оставалась точно там, где она была размещена в реальном мире.
Размещая пространственную привязку в том месте, где пользователь помещает голограмму, а затем размещая эту голограмму на основе ее пространственной привязки, вы можете обеспечить оптимальную стабильность голограммы, даже когда пользователь перемещается на десятки метров.
Эта непрерывная корректировка пространственных привязок относительно друг друга является ключевым отличием систем координат от пространственных привязок и стационарных систем отсчета:
Голограммы, помещенные в стационарную систему отсчета, сохраняют жесткую связь друг с другом. Однако, когда пользователь проходит большие расстояния, система координат этого кадра может дрейфовать в зависимости от мира, чтобы голограммы рядом с пользователем выглядели стабильно.
Голограммы, помещенные в систему отсчета сцены, также сохраняют жесткую связь друг с другом. В отличие от стационарной рамы, сценическая рама всегда остается фиксированной на месте в зависимости от ее определенного физического происхождения.
Однако содержимое, отображаемое в системе координат сцены за ее 5-метровой границей, будет выглядеть стабильным только тогда, когда пользователь находится в пределах этой границы.Голограммы, размещенные с использованием одной пространственной привязки, могут смещаться в зависимости от голограмм, размещенных с использованием другой пространственной привязки. Это позволяет Windows лучше понимать положение каждой пространственной привязки, даже если, например, одна привязка должна быть скорректирована влево, а другая — вправо.
Однако содержимое, отображаемое в системе координат сцены за ее 5-метровой границей, будет выглядеть стабильным только тогда, когда пользователь находится в пределах этой границы. В отличие от стационарной системы отсчета, которая всегда оптимизируется для обеспечения стабильности рядом с пользователем, система отсчета сцены и пространственные привязки обеспечивают стабильность вблизи их исходных точек. Это помогает этим голограммам оставаться точно на месте с течением времени, но это также означает, что голограммы, визуализированные слишком далеко от источника их системы координат, будут испытывать все более серьезные эффекты рычага.
Это связано с тем, что небольшие корректировки положения и ориентации сцены или якоря увеличиваются пропорционально расстоянию от этого якоря.
Хорошее эмпирическое правило состоит в том, чтобы убедиться, что все, что вы визуализируете на основе системы координат удаленной пространственной привязки, находится в пределах примерно 3 метров от своего источника. Для близлежащего источника сцены рендеринг удаленного контента допустим, так как любая повышенная ошибка позиционирования повлияет только на небольшие голограммы, которые не будут сильно смещаться в поле зрения пользователя.
Постоянство пространственной привязки
Пространственные привязки также могут позволить вашему приложению запомнить важное местоположение даже после приостановки приложения или выключения устройства.
Вы можете сохранить на диск пространственные привязки, созданные вашим приложением, а затем снова загрузить их позже, сохранив их в хранилище пространственных привязок вашего приложения .
При сохранении или загрузке привязки вы предоставляете строковый ключ, который имеет значение для вашего приложения, чтобы позже идентифицировать привязку. Думайте об этом ключе как об имени файла для вашего якоря. Если вы хотите связать с этой привязкой другие данные, например 3D-модель, которую пользователь разместил в этом месте, сохраните ее в локальном хранилище вашего приложения и свяжите с выбранным ключом.
Сохраняя привязки к магазину, ваши пользователи могут размещать отдельные голограммы или размещать рабочую область, вокруг которой приложение будет размещать свои различные голограммы, а затем находить эти голограммы там, где они ожидают их, при многократном использовании вашего приложения.
Вы также можете использовать Пространственные привязки Azure для сохранения асинхронной голограммы на устройствах HoloLens, iOS и Android. Благодаря совместному использованию прочной облачной пространственной привязки несколько устройств могут наблюдать одну и ту же постоянную голограмму с течением времени, даже если эти устройства не присутствуют вместе в одно и то же время.
Совместное использование пространственной привязки
Ваше приложение также может совместно использовать пространственную привязку в режиме реального времени с другими устройствами, что позволяет обмениваться опытом в реальном времени.
С помощью Пространственных привязок Azure ваше приложение может совместно использовать пространственную привязку на нескольких устройствах HoloLens, iOS и Android. Благодаря тому, что каждое устройство отображает голограмму с использованием одной и той же пространственной привязки, все пользователи увидят, что голограмма появляется в одном и том же месте в реальном мире.
Избегайте контента, привязанного к голове
Мы настоятельно не рекомендуем отображать контент, привязанный к голове, который остается в фиксированном месте на дисплее (например, HUD). В целом контент, привязанный к голове, неудобен для пользователей и не кажется естественной частью их мира.
Контент с блокировкой головы обычно следует заменять голограммами, которые прикрепляются к пользователю или размещаются в самом мире.
Например, курсоры, как правило, должны выталкиваться в мир, естественно масштабируясь, чтобы отражать положение и расстояние до объекта под взглядом пользователя.
Обработка ошибок отслеживания
В некоторых условиях, например в темных коридорах, гарнитура, использующая отслеживание наизнанку, может оказаться не в состоянии правильно определить свое местоположение в мире. Это может привести к тому, что голограммы либо не будут отображаться, либо появятся в неправильных местах при неправильном обращении. Теперь мы обсудим условия, в которых это может произойти, их влияние на пользовательский опыт и советы, как лучше всего справиться с этой ситуацией.
Гарнитура не может отслеживать из-за недостатка данных датчика
Иногда датчики гарнитуры не могут определить, где находится гарнитура. Это может произойти, если:
- В комнате темно
- Если датчики закрыты волосами или руками
- Если в окружении недостаточно текстуры.
Когда это произойдет, гарнитура не сможет отслеживать свое положение с достаточной точностью для воспроизведения голограмм с привязкой к миру.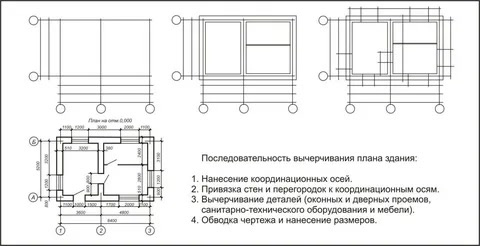
Вы не можете понять, где находится пространственный якорь, стационарный каркас или каркас сцены на устройстве. Однако вы по-прежнему можете отображать заблокированное содержимое в присоединенной системе отсчета.
Ваше приложение должно сообщать пользователю, как восстановить позиционное отслеживание, отображая некоторый запасной заблокированный контент с описанием некоторых советов, таких как раскрытие датчиков и включение большего количества источников света.
Гарнитура неправильно отслеживает из-за динамических изменений в окружающей среде
Устройство не может правильно отслеживать, если в окружающей среде много динамических изменений, например, в комнате ходит много людей. В этом случае может показаться, что голограммы прыгают или дрейфуют, когда устройство пытается отслеживать себя в этой динамичной среде. Мы рекомендуем использовать устройство в менее динамичной среде, если вы столкнулись с этим сценарием.
Гарнитура отслеживает неправильно, потому что окружающая среда значительно изменилась с течением времени
Когда вы начинаете использовать гарнитуру в среде, где мебель, настенные ковры и т.
д. были перемещены, возможно, что некоторые голограммы могут оказаться смещенными относительно их исходного положения. . Более ранние голограммы также могут прыгать, когда пользователь перемещается в новом пространстве, потому что понимание системой вашего пространства больше не соответствует действительности. Затем система пытается переназначить окружающую среду, одновременно пытаясь согласовать особенности комнаты. В этом сценарии рекомендуется поощрять пользователей заменять голограммы, которые они прикрепили к миру, если они не появляются там, где ожидалось.
Неправильно отслеживает гарнитура из-за одинаковых пространств в окружающей среде
Иногда в доме или другом помещении могут быть две одинаковые области. Например, два одинаковых конференц-зала, два одинаковых уголка, два одинаковых больших плаката, закрывающих поле зрения устройства. В таких сценариях устройство может время от времени путаться между идентичными частями и помечать их как одинаковые в своем внутреннем представлении.