Классификация сечений: 4.2 Сечения, классификация сечений

4.2 Сечения, классификация сечений

Сечение – изображение фигуры, получающейся при мысленном рассечении предмета плоскостью (рис. 12). На сечении показывается только то, что получается непосредственно в секущей плоскости.

Рисунок 12 – Примеры выполнения сечений фигур.

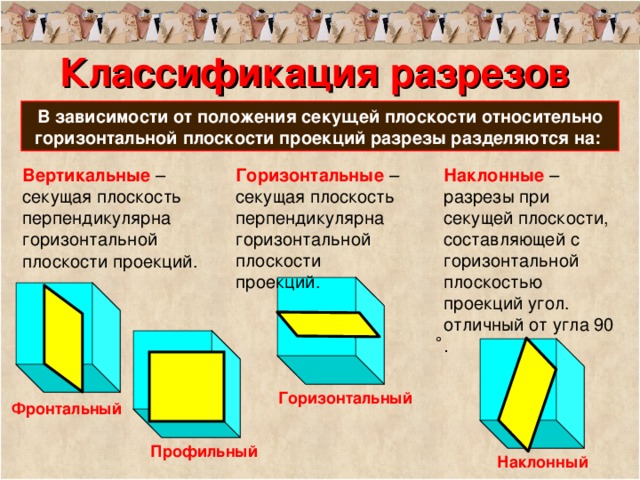
4.3 Разрезы, классификация разрезов

Pазрезом называется изобpажение пpедмета, мысленно pассеченного одной или несколькими плоскостями, при этом на pазpезе показывают и то, что pасположено за сечением (рис. 13).

Рисунок 13 – Примеры изображений сечения и разреза, получаемых при рассечении предмета плоскостью.

Примеры выполнения горизонтального и вертикального (фронтального и профильного) разрезов предмета приведены на рис. 14.

Рисунок 14 – Изображение горизонтального и вертикального разрезов.

Ниже приведены примеры различных разрезов и пояснения к ним (рис.15-17).

Рисунок 15 – Примеры простого и местного разрезов.

Рисунок 16 – Пример сложного ломаного разреза.

Рисунок 17 – Примеры половинного и наклонного разреза.

4.4 Выносные элементы

Выносной элемент – дополнительное изображение (обычно увеличенное) какой-либо части предмета, требующей графического и других пояснений в отношении формы, размеров и других данных.

Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и может отличаться от него по содержанию (например, изображение может быть видом, а выносной элемент – разрезом).

При применении выносного элемента соответствующее место отмечают на виде, разрезе или сечении замкнутой сплошной тонкой линией – окружностью с обозначением выносного элемента прописной буквой русского алфавита на полке линии-выноски.

Над изображением выносного элемента указывают обозначение и масштаб (рис. 18).

Рисунок 18 – Примеры выносных элементов.

5 Стандартные аксонометрические проекции

В технических проектах, как дополнение к рабочим чертежам, используют чертежи, полученные методом аксонометрического проецирования, которые обладают большей наглядностью.

Сущность метода заключается в том, что предмет проецируется вместе с пространственной системой координат (O, x, y, z) на аксонометрическую плоскость проекций (рис. 19).

Рисунок 19 – Образование аксонометрического изображения предмета.

ГОСТ 2.317-69 устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства.

В инженерной графике чаще используют следующие аксонометрические проекции: прямоугольную изометрическую и прямоугольную диметрическую.

Прямоугольной изометрией называется аксонометрическая проекция, в которой коэффициенты искажения по всем трем осям равны 0,82, а углы между аксонометрическими осями равны 120⁰ (рис. 20).

Рисунок 20 – Построение изображений в прямоугольной изометрии.

Для упрощения построения коэффициенты искажения по осям x, y, z принимают равным 1, тогда аксонометрическое изображение получается увеличенным в m=(1/0,82)=1,22 раза по сравнению с теоретическим изображением и называется приведенным, а масштабный коэффициент называется коэффициентом приведения.

Прямоугольной диметрией называется аксонометрическая проекция, в которой коэффициент искажения по оси

y равен 0,47, а по осям x и z – 0,94, а углы между осями равны 97⁰10΄ и 131⁰25΄ (рис. 21).

Рисунок 21 – Построение изображений в прямоугольной диметрии.

Для упрощения построения диметрическую проекцию выполняют без искажения по осям x и z и с коэффициентом искажения 0,5 по оси y. Тогда изображение получается увеличенным в m=(1/0,94)=1,06 раза.

Построение точек в аксонометрии.

Принцип построения аксонометрического изображения фигуры не зависит от вида аксонометрии.

Аксонометрия обычно строится по ортогональному чертежу.

В качестве примера рассмотрим построение точек А и Б.

На рисунке 22, а представлен комплексный чертеж точек А и Б с проекциями на трех основных плоскостях проекций (П₁ , П₂ , П₃).

Рисунок 22 – Комплексный чертеж точек А и Б и их аксонометрические проекции в прямоугольной изометрии.

Построим приведенную прямоугольную изометрию точки А. При этом, искажения по осям равны 1, т. е. координаты не изменяются.

Проведем аксонометрические оси x΄, y΄, z ΄.

Коэффициенты искажения по всем трем осям равны 1.

На аксонометрической оси x΄ отложим координату x, равную 65 и обозначим ее а΄. Через точку а΄ проведем прямую, параллельную оси

y΄ (прямые линии, параллельные в пространстве, изображаются параллельными и в аксонометрии) и на ней отложим координату y , т.е. размер 10. Далее, через полученную точку проводим прямую, параллельную оси z ΄ и на ней отложим координату z , равную 0. Получаем точку А в прямоугольной изометрии.

Приведенная прямоугольная изометрия точки Б строится аналогично.

Для построения прямоугольной диметрии точек А и Б сначала проводим аксонометрические оси, как указано выше.

Коэффициенты искажения по осям x΄ и z ΄ равны 1, т. е. соответствующие координаты не изменяются, а по оси y΄ – 0,5, т.е. координата уменьшается в два раза.

Все остальные построения аналогичны построению точки в прямоугольной изометрии.

Построение окружностей диаметром d в прямоугольной изометрии) и диметрии показано на рисунках рис. 23 и 24.

Рисунок 23 – Изображение окружности в прямоугольной изометрии.

Рисунок 24 – Изображение окружности в прямоугольной диметрии.

Классификация сечений по норме EN 1999-1-1

С помощью классификации сечений устанавливаются пределы прочности и вращательной способности частей сечения при местном выпучивании. В EN 1999‑1‑1, 6.1.4.2 (1) установлены четыре класса сечения.

• Сечения класса 1 могут образовывать пластические шарниры или зоны текучести с достаточным пластическим моментом сопротивления и вращательной способностью для пластического расчета конструкций.
• Сечения класса 2 могут развивать пластический момент сопротивления, но имеют лишь ограниченную вращательную способность вследствие местного выпучивания.
• Сечения класса 3 достигают предела текучести во внешнем, нагруженном сжатием волокне алюминиевого элемента, но не могут развить пластический момент сопротивления вследствие местного выпучивания.
• Сечения класса 4 – это сечения, в которых местное выпучивание возникает в одной или нескольких частях сечения до достижения предела текучести.

Основные типы части сечения

Классификация сечения зависит от отношения ширины к толщине b/t его сжатых частей. По норме EN 1999-1-1 [1], 6.1.4.2 (6), тонкостенные части подразделяются на следующие основные типы.

• Плоскостные выступающие части сечения
• Плоскостные внутренние части сечения, поддерживаемые с обеих сторон
• Изогнутые внутренние части сечения, поддерживаемые с обеих сторон

Данные части сечения могут быть не усиленными либо усилены продольными ребрами жесткости, отогнутыми кромками или выступами (рисунок 01).

• Основные типы части сечения

• Размеры сечения в мм

• Конструктивная система и нагрузки

• Окно 1.3 Сечения

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Классификация сечений – чистый изгиб

• Классификация сечений – чистое сжатие

• Диалоговое окно «Части c/t»

параметры гибкости

Восприимчивость неусиленных плоскостных частей к местному боковому выпучиванию определяется параметром β. По норме EN 1999-1-1, 6.1.4.3 (1), он имеет следующие значения.

• плоскостные внутренние части, поддерживаемые с обеих сторон, с постоянным распределением напряжений или плоскостные выступающие части с постоянным распределением напряжений либо максимальным напряжением сжатия на внешнем крае
  β = b / t | EN 1999-1-1, (6. 1)
• плоскостные внутренние части с переходом распределения напряжений через нулевое значение в центре
  β = 0,40 · b / t | EN 1999-1-1, (6.2)
• плоскостные внутренние части с линейно-изменяющимся распределением напряжений либо плоскостные выступающие части с максимальным напряжением сжатия на внутреннем крае
  β = η · b / t | EN 1999-1-1, (6.3)

Где:
b … ширина части сечения
t … толщина сечения
η … коэффициент распределения напряжений, который определяется по следующим формулам:
η = 0,70 + 0,30 · ψ при 1 ≥ ψ ≥ -1 | EN 1999-1-1, (6.4)
η = 0,80 / (1 – ψ) при ψ < -1 | EN 1999-1-1, (6.5)
ψ … отношение напряжений на контурах рассматриваемой плиты к максимальному напряжению при сжатии. Обычно нейтральной осью считается нейтральная ось упругих напряжений, но в случае, если сечение относится к классу 1 или 2, допустимо применение нейтральной оси пластических напряжений.

Параметры гибкости для плоскостных усиленных частей сечения указаны в EN 1999-1-1, 6.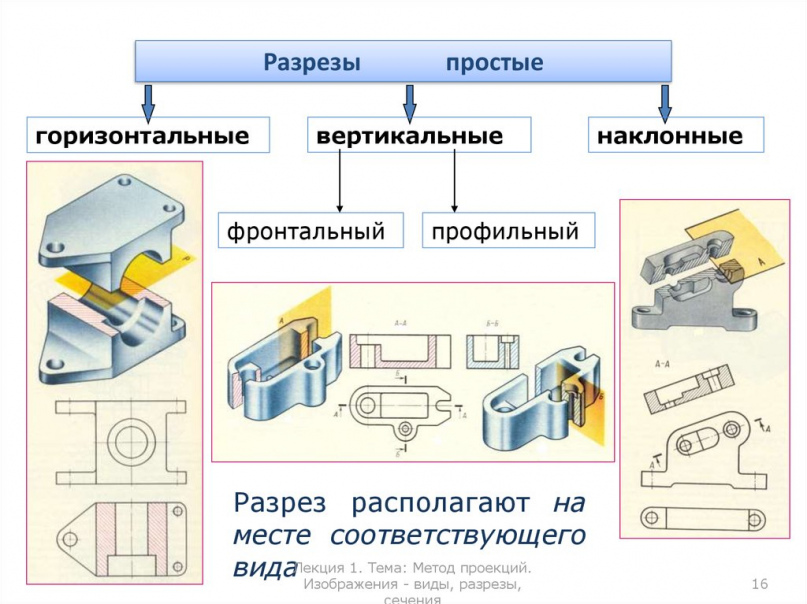 1.4.3 (3).

Норма EN 1999-1-1, п. 6.1.4.3 (4) содержит данные о параметрах гибкости для плоскостных неусиленных внутренней частей малой кривизны, поддерживаемых с обеих сторон. В EN 1999-1-1, п. 6.1.4.3 (5) рассмотрены параметры гибкости тонкостенных трубчатых профилей.

Классификация частей сечения

Для выполнения классификации рассчитанные параметры гибкости β необходимо сравнить с предельными значениями β₁ – β₃, которые определяются согласно EN 1999-1-1 по таблице 6.2 (см. ниже).
ε = √(250 / f_o)
f_o в Н/мм²

Классификация материала по таблице 3.2	Внутренняя часть			Выступающая часть
	β1 / ε	β2 / ε	β3 / ε	β1 / ε	β2 / ε	β3 / ε
Класс А, без сварных швов	11	16	22	3	4. 5	6
Класс А, со сварными швами	9	13	18	2,5	4	5
Класс B, без сварных швов	13	16,5	18	3,5	4.5	5
Класс B, со сварными швами	10	13,5	15	3	3,5	4

В данной классификации различают изгибаемые балки и сжатые стержни. В EN 1999-1-1, 6.1.4.4 (1) установлены следующие пределы.

Части сечения изгибаемых балок
β ≤ β₁ → класс 1
β₁ < β ≤ β₂ → класс 2
β₂ < β ≤ β₃ → класс 3
β₃ < β → класс 4

Части сечения сжатых стержней
β ≤ β₂ → класс 1 или 2
β₂ < β ≤ β₃ → класс 3
β₃ < β → класс 4

Каждой части сечения, которая полностью или частично подвергается сжатию, необходимо присвоить определенный класс сечения. Часть сечения с наименее благоприятным классом сечения определяет класс целого сечения. Классификация сечений конструктивных элементов, подверженных действию одновременно изгибающих и продольных сил, должна выполняться отдельно для каждой составляющей нагрузки по норме EN 1999-1-1, 6.3.3, комментарий 1. Для комбинированного напряженного состояния классификация не требуется.

Пример

Выполним классификацию у двутавра, показанного на рисунке 02, при чистом изгибе и чистом сжатии.

• Размеры сечения в мм

• Основные типы части сечения

• Конструктивная система и нагрузки

• Окно 1.3 Сечения

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Классификация сечений – чистый изгиб

• Классификация сечений – чистое сжатие

• Диалоговое окно «Части c/t»

Конструкция и нагружение показаны на рисунке 03.

• Конструктивная система и нагрузки

• Основные типы части сечения

• Размеры сечения в мм

• Окно 1.3 Сечения

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Классификация сечений – чистый изгиб

• Классификация сечений – чистое сжатие

• Диалоговое окно «Части c/t»

Материал и размеры
EN-AW 6082 (EP, ET, ER/B) T4 | EN 1999-1-1, таблица 3.2b
f_o = 110 Н/мм²
f_u = 205 Н/мм²
Класс бокового выпучивания B
ε = √(250 / f_o) = √(250 / 110) = 1,508 | EN 1999-1-1, таблица 6.2
b_w = h – 2 ∙ (t_f + r) = 220 – 2 ∙ (8 + 12) = 180 мм
b_f = 0,5 ∙ (b – t_w – 2 ∙ r) = 0,5 ∙ (100 – 6 – 2 ∙ 12) = 35 мм

Классификация сечения – чистый изгиб
Стенка (внутренняя, без сварных швов, класс бокового выпучивания B)
β_w = 0,4 ∙ b_w / t_w = 0,4 ∙ 180 / 6 = 12 | EN 1999-1-1, (6. 2)
β₁ = 13 ∙ ε = 13 ∙ 1,508 = 19,6 | EN 1999-1-1, таблица 6.2
β_w = 12 < β₁ = 19,6
Стенке присвоен класс сечения 1.

Полка (выступающая, без сварных швов, класс бокового выпучивания B)
β_f = b_f / t_f = 35 / 8 = 4,38 | EN 1999-1-1, (6.1)
β₁ = 3,5 ∙ ε = 3,5 ∙ 1,508 = 5,28 | EN 1999-1-1, таблица 6.2
β_f = 4,38 < β₁ = 5,28
Полке нужно присвоить класс сечения 1.
Целое сечение имеет класс сечения 1 при чистом изгибе.

Классификация сечения – чистое сжатие
Стенка (внутренняя, без сварных швов, класс бокового выпучивания B)
β_w = b_w / t_w = 180 / 6 = 30 | EN 1999-1-1, (6.1)
β₃ = 18 ∙ ε = 18 ∙ 1,508 = 27,14 | EN 1999-1-1, таблица 6.2
β_w = 30 > β₃ = 27,14
Стенка отнесена к классу сечения 4.
Полка (выступающая, без сварных швов, класс бокового выпучивания B)
β_f = b_f / t_f = 35 / 8 = 4,38 | EN 1999-1-1, (6. 1)
β₂ = 4,5 ∙ ε = 4,5 ∙ 1,508 = 6,79 | EN 1999-1-1, таблица 6.2
β_f = 4,38 < β₂ = 6,79
Полке нужно присвоить класс сечения 1 или 2.
Целое сечение имеет класс сечения 4 при чистом сжатии.

RF-/ALUMINIUM

Модуль RF-/ALUMINUM определяет соотношение ширины и толщины частей сечения, подвергаемых сжатию, и выполняет классификацию автоматически. Также можно определить класс сечения индивидуально в списке «Классификация сечений» в окне «1.3 Сечения» (рисунок 04). Сечения, которые не полностью включены в нормативные требования, классифицируются в RF-/ALUMINUM как «общие» и распределяются только по классам сечений 3 или 4.

• Окно 1.3 Сечения

• Основные типы части сечения

• Размеры сечения в мм

• Конструктивная система и нагрузки

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Классификация сечений – чистый изгиб

• Классификация сечений – чистое сжатие

• Диалоговое окно «Части c/t»

RF-/ALUMINUM учитывает только неусиленные части сечения по EN 1999-1-1, рисунок 6. 1 (a), а также тонкостенные трубчатые профили по EN 1999-1-1, 6.1.4.3 (5). Слегка изогнутые, неусиленные, внутренние части сечения, защемленные с обеих сторон согласно EN 1999-1-1, 6.1.4.3 (4), могут быть учтены только в расчете, выполняемом упрощенным аналитическим методом. Влияние элементов жесткости по EN 1999-1-1, 6.1.4.3 (3) не учитывается.

Классификация сечений конструктивных элементов, подвергаемых одновременно действию изгибающих и продольных сил выполняется в модуле RF-/ALUMINUM отдельно для каждого компонента нагрузки согласно EN 1999-1-1, 6.3.3, комментарий 1. При этом можно выполнить классификацию также для комбинированного напряженного состояния. Для этого деактивируйте флажок «Отдельно классифицировать составляющие нагрузки согласно 6.3.3 Примечание 1 и Примечание 2» во вкладке «Несущая способность» диалогового окна «Подробности» (рисунок 05).

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Основные типы части сечения

• Размеры сечения в мм

• Конструктивная система и нагрузки

• Окно 1. 3 Сечения

• Классификация сечений – чистый изгиб

• Классификация сечений – чистое сжатие

• Диалоговое окно «Части c/t»

Классификация сечений в модуле RF-/ALUMINUM подробно отображается для каждой сжатой части сечения в промежуточных значениях. Классификация сечений данного примера при чистом изгибе и чистом сжатии показана на рисунках 06 и 07.

• Классификация сечений – чистый изгиб

• Основные типы части сечения

• Размеры сечения в мм

• Конструктивная система и нагрузки

• Окно 1.3 Сечения

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Классификация сечений – чистое сжатие

• Диалоговое окно «Части c/t»

• Классификация сечений – чистое сжатие

• Основные типы части сечения

• Размеры сечения в мм

• Конструктивная система и нагрузки

• Окно 1. 3 Сечения

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Классификация сечений – чистый изгиб

• Диалоговое окно «Части c/t»

Нумерация частей сечения содержится в диалоговом окне «части c/t» (рисунок 08).

• Диалоговое окно «Части c/t»

• Основные типы части сечения

• Размеры сечения в мм

• Конструктивная система и нагрузки

• Окно 1.3 Сечения

• Диалоговое окно «Подробности», вкладка «Предельное состояние 1-й группы»

• Классификация сечений – чистый изгиб

• Классификация сечений – чистое сжатие

[1]	EN 1999-1-1: Bemessung und Konstruktion von Aluminiumtragwerken – Teil 1-1: Allgemeine Bemessungsregeln.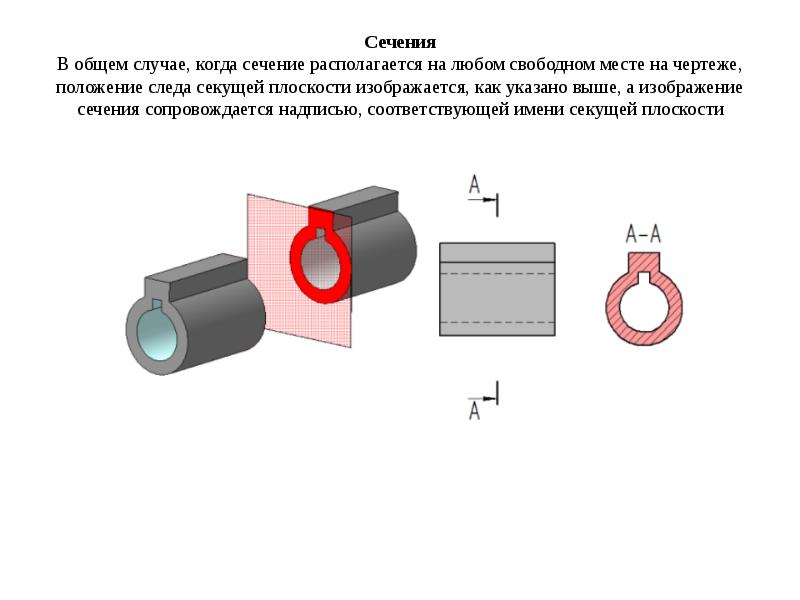 CEN, Brüssel, 05, 2007.

Классификация поперечных сечений Согласно EN 1999-1-1

Классификация поперечных сечений должна определять пределы сопротивления и способности к вращению из-за местного коробления частей поперечного сечения. В EN 1999-1-1, 6.1.4.2 (1) определены четыре класса.

• Поперечные сечения класса 1 — это сечения, которые могут образовывать пластический шарнир с возможностью вращения, необходимой для пластического анализа, без снижения сопротивления.
• Поперечные сечения класса 2 — это сечения, которые могут развивать сопротивление пластическому моменту, но имеют ограниченную вращательную способность из-за местной потери устойчивости.
• Поперечные сечения класса 3 — это сечения, в которых расчетное напряжение в волокне алюминиевого элемента при предельном сжатии может достигать условной прочности, но локальное коробление способно предотвратить развитие сопротивления полному пластическому моменту.
• Поперечные сечения класса 4 представляют собой сечения, в которых локальная потеря устойчивости возникает до достижения условного напряжения в одной или нескольких частях поперечного сечения.

Основные типы деталей поперечного сечения

Классификация поперечного сечения зависит от отношения ширины к толщине b/t его частей, подвергаемых сжатию. Согласно EN 1999-1-1 [1], 6.1.4.2 (6), тонкостенные детали классифицируют на следующие основные типы.

• плоские выступающие детали
• плоские внутренние детали
• изогнутые внутренние детали

Эти детали могут быть неармированными или усиленными продольными ребрами жесткости, краевыми выступами или утолщениями (рис. 1).

• Основные типы деталей поперечного сечения

• Размеры поперечного сечения в мм

• Структурная система и нагрузка

• Окно 1.3 Поперечные сечения

• Диалоговое окно «Подробности», вкладка «Конечное предельное состояние»

• Классификация поперечного сечения — чистый изгиб

• Классификация поперечного сечения — чистое сжатие

• Диалоговое окно c/t-Parts

Параметры гибкости

Склонность неармированной плоской детали к местному выпучиванию определяется параметром β. Согласно EN 1999-1-1, 6.1.4.3 (1), он имеет следующие значения.

• плоские внутренние части без градиента напряжения или плоские выступы без градиента напряжения или пикового сжатия в зацепе
  β = b / t | EN 1999-1-1, (6.1)
• внутренние детали с градиентом напряжения, который приводит к нейтральной оси в центре
  β = 0,40 · b / t | EN 1999-1-1, (6.2)
• внутренние части с градиентом напряжения и выступающие части с максимальным сжатием у корня
  β = η · б/т | EN 1999-1-1, (6.3)

Где:
b … Ширина части поперечного сечения
t … Толщина поперечного сечения
η … Коэффициент градиента напряжения, определяемый следующими выражениями :
η = 0,70 + 0,30 · ψ для 1 ≥ ψ ≥ -1 | EN 1999-1-1, (6.4)
η = 0,80/(1 – ψ) для ψ < -1 | EN 1999-1-1, (6.5)
ψ … отношение напряжений на краях рассматриваемой пластины к максимальному сжимающему напряжению. Как правило, нейтральная ось должна быть эластичной нейтральной осью, но при проверке того, относится ли сечение к классу 1 или 2, вам разрешено использовать пластическую нейтральную ось.

Параметры гибкости для плоских усиленных частей поперечного сечения приведены в EN 1999-1-1, 6.1.4.3 (3).

EN 1999-1-1, 6.1.4.3 (4) содержит информацию о параметрах гибкости для плоскоизогнутых, неподкрепленных деталей внутреннего поперечного сечения, защемленных с обеих сторон. В EN 1999-1-1, 6.1.4.3 (5) рассматриваются параметры гибкости тонкостенных трубчатых профилей.

Классификация деталей поперечного сечения

Расчетные параметры гибкости β необходимо сравнить с предельными значениями β 9от 0092 1 до β ₃ , которые определяются согласно EN 1999-1-1, таблица 6.2 (см. ниже).
ε = √(250 / f _o )
f _o в Н/мм²

Классификация материалов согласно таблице 3.2	Внутренняя часть			Выступающая часть
	β 1 / ε	β 2 / ε	β 3 / ε	β 1 / ε	β 2 / ε	β 3 / ε
Класс А, без сварных швов	11	16	22	3 9014 3	4,5	6
Класс А, со сваркой	9	13	18	2,5	4	5
Класс B, без сварных швов	13	16,5	18	3,5	4,5	5
Класс B, со сваркой 9Классификация Различают изгибающиеся балки и сжимаемые элементы. Следующие пределы определены в EN 1999-1-1, 6.1.4.4 (1). Детали поперечного сечения в изгибаемых балках β ≤ β 1 → класс 1 β 1 < β ≤ β 2 → класс 2 β 2 < β ≤ β 3 → класс 3 β 3 < β → класс 4 Части поперечного сечения в сжатых элементах β ≤ β 2 → класс 1 или 2 β 2 < β ≤ β 3 → класс 3 β 3 < β → класс 4 Каждый крест – часть сечения, полностью или частично подвергающаяся сжатию, должна быть отнесена к классу сечения. Часть сечения с наиболее неблагоприятным классом сечения определяет класс всего сечения. Классификация поперечных сечений элементов конструкции с изгибающими и продольными усилиями должна выполняться отдельно для каждого элемента нагрузки в соответствии с EN 19.99-1-1, 6.3.3. Для комбинированного напряженного состояния классификация не требуется. Пример Классификация выполняется для двутаврового сечения, показанного на рис. 02, для чистого изгиба и чистого усилия сжатия. Размеры поперечного сечения в мм Основные типы деталей поперечного сечения Структурная система и нагрузка Окно 1.3 Поперечные сечения Диалоговое окно «Подробности», вкладка «Конечное предельное состояние» Классификация поперечного сечения — чистый изгиб Классификация поперечного сечения — чистое сжатие Диалоговое окно c/t-Parts Система и загрузка показаны на рисунке 03. Структурная система и нагрузка Основные типы деталей поперечного сечения Размеры поперечного сечения в мм Окно 1.3 Поперечные сечения Диалоговое окно «Подробности», вкладка «Конечное предельное состояние» Классификация поперечного сечения — чистый изгиб Класс поперечного сечения — чистое сжатие Диалоговое окно c/t-Parts Материал и размеры EN-AW 6082 (EP,ET,ER/B) T4 | EN 1999-1-1, таблица 3. 2b f o = 110 Н/мм² f u = 205 Н/мм² Класс потери устойчивости B ε = √(250 / f o ) = √(250 / 110) = 1,508 | EN 1999-1-1, таблица 6.2 b w = h – 2 ∙ (t f + r) = 220 – 2 ∙ (8 + 12) = 180 мм b f = 0,5 ∙ (b – t w – 2∙r) = 0,5∙(100 – 6 – 2∙12) = 35 мм Класс поперечного сечения – чистый изгиб Стенка (внутренняя, без сварных швов, класс потери устойчивости B) β w = 0,4 ∙ b w / t w = 0,4 ∙ 180 / 6 = 1 2 | EN 1999-1-1, (6.2) β 1 = 13 ∙ ε = 13 ∙ 1,508 = 19,6 | EN 1999-1-1, таблица 6.2 β w = 12 < β 1 = 19,6 Стенка относится к классу поперечного сечения 1. ф = б ф / т f = 35 / 8 = 4,38 | EN 1999-1-1, (6.1) β 1 = 3,5 ∙ ε = 3,5 ∙ 1,508 = 5,28 | EN 1999-1-1, таблица 6.2 β f = 4,38 < β 1 = 5,28 Стенка должна быть отнесена к классу поперечного сечения 1. Все поперечное сечение должно быть отнесено к чистому изгибу в поперечном сечении класса 1. Класс поперечного сечения – чистая сила сжатия Стенка (внутренняя, без сварных швов, класс потери устойчивости B) β w = b w / t w = 180 / 6 = 30 | EN 1999-1-1, (6.1) β 3 = 18 ∙ ε = 18 ∙ 1,508 = 27,14 | EN 1999-1-1, таблица 6.2 β w = 30 > β 3 = 27,14 Стенка относится к классу поперечного сечения 4. f = b f / t f = 35 / 8 = 4,38 | EN 1999-1-1, (6.1) β 2 = 4,5 ∙ ε = 4,5 ∙ 1,508 = 6,79 | EN 1999-1-1, таблица 6.2 β f = 4,38 < β 2 = 6,79 Фланец должен быть отнесен к классу поперечного сечения 1 или 2. Все поперечное сечение должно быть отнесено к чистому сжимающему усилию к классу поперечного сечения 4. RF-/ALUMINUM RF-/ALUMINUM определяет соотношение ширины и толщины частей поперечного сечения, подвергаемых сжатию, и автоматически выполняет классификацию. Кроме того, класс поперечного сечения может быть определен индивидуально в списке «Классификация поперечного сечения» окна «1.3 Сечения» (Изображение 04). Сечения, которые не полностью охвачены стандартными спецификациями, классифицируются как «Общие» в RF-/ALUMINUM и относятся только к классам поперечного сечения 3 или 4. Окно 1.3 Поперечные сечения Основные типы деталей поперечного сечения Размеры поперечного сечения в мм Структурная система и нагрузка Диалоговое окно «Подробности», вкладка «Конечное предельное состояние» Классификация поперечного сечения — чистый изгиб Классификация поперечного сечения — чистое сжатие Диалоговое окно c/t-Parts RF-/ALUMINUM рассматривает только неподкрепленные части поперечного сечения в соответствии с EN 1999-1-1, рисунок 6. 1 (a), а также тонкостенные трубчатые секции в соответствии с EN 1999-1-1, 6.1.4.3 (5) . Слегка изогнутые, неподкрепленные части внутреннего поперечного сечения, защемленные с обеих сторон в соответствии с EN 1999-1-1, 6.1.4.3 (4), могут учитываться только при расчете, выполненном с помощью упрощенного аналитического метода. Влияние ребер жесткости согласно EN 1999-1-1, 6.1.4.3 (3) не считается. Классификация поперечных сечений элементов конструкции с изгибающими и продольными усилиями выполняется отдельно для каждого элемента нагрузки в RF-/ALUMINUM в соответствии с EN 1999-1-1, 6.3.3. Однако также возможно выполнить классификацию комбинированного напряженного состояния. Для этого снимите флажок «Отдельно классифицировать компоненты нагрузки в соответствии с 6.3.3 ПРИМЕЧАНИЕ 1 и ПРИМЕЧАНИЕ 2» на вкладке «Предельное состояние» диалогового окна «Подробности» (Изображение 05). Диалоговое окно «Подробности», вкладка «Конечное предельное состояние» Основные типы деталей поперечного сечения Размеры поперечного сечения в мм Структурная система и нагрузка Окно 1. 3 Поперечные сечения Классификация поперечного сечения — чистый изгиб Классификация поперечного сечения — чистое сжатие Диалоговое окно c/t-Parts Классификация поперечного сечения в RF-/ALUMINUM подробно отображается для каждой детали поперечного сечения, нагруженной на сжатие, среди промежуточных значений. Классификация поперечного сечения этого примера для чистого изгиба и чистого сжатия показана на изображениях 06 и 07. Класс поперечного сечения — чистый изгиб Основные типы деталей поперечного сечения Размеры поперечного сечения в мм Структурная система и нагрузка Окно 1.3 Поперечные сечения Диалоговое окно «Подробности», вкладка «Конечное предельное состояние» Класс поперечного сечения — чистое сжатие Диалоговое окно c/t-Parts Классификация поперечного сечения — чистое сжатие Основные типы деталей поперечного сечения Размеры поперечного сечения в мм Структурная система и нагрузка Окно 1. 3 Поперечные сечения Диалоговое окно «Подробности», вкладка «Конечное предельное состояние» Классификация поперечного сечения — чистый изгиб Диалоговое окно c/t-Parts Нумерацию частей поперечного сечения можно найти в диалоговом окне “c/t-Parts” (Изображение 08). Диалоговое окно c/t-Parts Основные типы деталей поперечного сечения Размеры поперечного сечения в мм Структурная система и нагрузка Окно 1.3 Поперечные сечения Диалоговое окно «Подробности», вкладка «Конечное предельное состояние» Классификация поперечного сечения — чистый изгиб Класс поперечного сечения — чистое сжатие [1]   EN 1999-1-1: Bemessung und Construktion von Aluminiumtragwerken – Часть 1-1: Allgemeine Bemessungsregeln. CEN, Брюссель, 05, 2007. Классификация стальных профилей | Медиа-центр 11 авг Еще раз добро пожаловать обратно к чертежной доске со мной, Стивен Ллойд, вы, возможно, помните, что недавно мы говорили о конструкции ригельной балки с комбинированными эффектами, мы рассмотрели напряжения фон Мизеса, мы подумали о пластике и упругие свойства балки. Теперь, что определяет, считаете ли вы балку пластичной или эластичной, это классификация, и сегодня мы рассмотрим классификацию стальных профилей. Это относится только к конструкционной стали; нержавеющая сталь и алюминий имеют разные свойства материалов, поэтому используемые критерии немного отличаются. Таким образом, это относится к конструкционной стали марок s235, s355 и т. д., к которым относится часть 3 Еврокода. сравните это с его толщиной. В случае круглого полого сечения мы сравниваем глубину с толщиной круга. Получив это отношение, мы сравниваем его и убеждаемся, что оно меньше определенного числа этих эпсилонов. Теперь эпсилон 4s235 равен 1, и значение эпсилон уменьшается, чем выше предел текучести материала. Причина этого становится ясна, когда вы начинаете говорить о формировании пластиковых петель. А пока мы просто примем это как должное. Если у вас очень низкое отношение глубины к толщине или выдающейся части к толщине, то вы пластик или секция класса 1. Например, если у вас немного меньшая толщина или немного больший диаметр, вы постепенно подниметесь по этой лестнице от пластика к компактному, от полукомпактного к тонкому в британских стандартных терминах. На языке Еврокода это класс 1, класс 2, класс 3 и класс 4 — там не такая захватывающая терминология. Итак, поговорим о пластиковых петлях. Секция класса 1, секция класса 2, класс 3 и класс 4, а также распределение напряжения при разрушении каждый раз немного отличаются. Теперь секция класса 1 или пластиковая секция, вы можете начать сгибать эту балку, и вы можете сгибать ее, и она образует петлю, и вы можете продолжать сгибать ее, и продолжать сгибать ее, и продолжать сгибать ее, и эта петля будет поддерживать определенную уровень силы, даже если вы продолжаете вызывать большее вращение. Если вы сможете добраться до края света с этим вращением, это пластиковая секция, она будет продолжать оставаться пластиковой по всему периметру. За исключением того, что у вас есть класс 2, вы также должны использовать свойства пластика с этим. Теперь, как только вы доберетесь до этой точки текучести, и ваше распределение напряжения будет выглядеть так, что оно сформирует пластичный шарнир и позволит себе вращаться, но у вас есть ограниченное количество поворотов, прежде чем эта область прогнется. Вот почему мы сравниваем толщину с длиной, все дело в локальном изгибе, потому что то, что происходит с сечением класса 3, заключается в том, что оно может достичь своего предела упругости, а может быть, и немного больше. Если ваша секция находится на границе между классами 2 и 3, вы можете получить довольно много пластика где-то между здесь и здесь. Если вы находитесь прямо на границе между классом 3 и классом 4, вы едва сможете достичь полного распределения эластичности, прежде чем что-то прогнется. Так что, если у вас очень тонкая, очень длинная выступающая кромка, к тому времени, когда у вас возникнет напряжение в верхней и нижней кромке, ваши кромки готовы прогнуться. Если у вас очень высокая и очень тонкая паутина, к тому времени, как вы начнете ее сгибать, ваша паутина уже готова рухнуть. Секция класса 4, как правило, находится в собственном маленьком мире. Секция класса 4 является аутсайдером, она не может даже выполнить полное упругое распределение напряжения до того, как ее части начнут изгибаться. Это мой любимый тип раздела, потому что к нему нужно применять специальные правила. Дополнительные специальные правила всегда забавны, когда вы занимаетесь дизайном. Я хочу взглянуть на нашу секцию Class 4, которая представляет собой SuperTube 1220 на 16 мм. На стальной опоре вы обычно получаете сильное сжатие, у вас есть земля с обеих сторон, и она хочет сжать эту трубу. Собственный вес этого также хочет, чтобы он провисал, поэтому у вас есть небольшой изгиб. Немного изгиба, немного сжатия, вы получаете распределение напряжения, выглядящее вот так. Здесь я говорю только об изгибе, и критерии немного отличаются, если вы говорите о сжатии, поскольку они относятся к изгибу, что имеет смысл, если вы думаете о локальном изгибе. Итак, давайте посмотрим на эту область здесь. При сжатии все, что не находится близко к стыку или суставу, например, в I-образной секции, может деформироваться. Если вы находитесь прямо в этом углу, вы находитесь в зоне силы. Все, что состоит из двух пересекающихся кусков стали, вряд ли согнется. Как только вы выберетесь на эту ничейную землю, на очень длинную тонкую паутину, эта часть прогнется, это часть, которая не даст вам той силы, на которую вы надеетесь. Или вы используете этот небольшой раздел канала здесь как еще один пример; в поворотах у вас, вероятно, есть некоторая сила, и вы не будете прогибаться, в этих местах здесь, где не так много стабильности, это область, в которой вы, вероятно, прогнетесь. 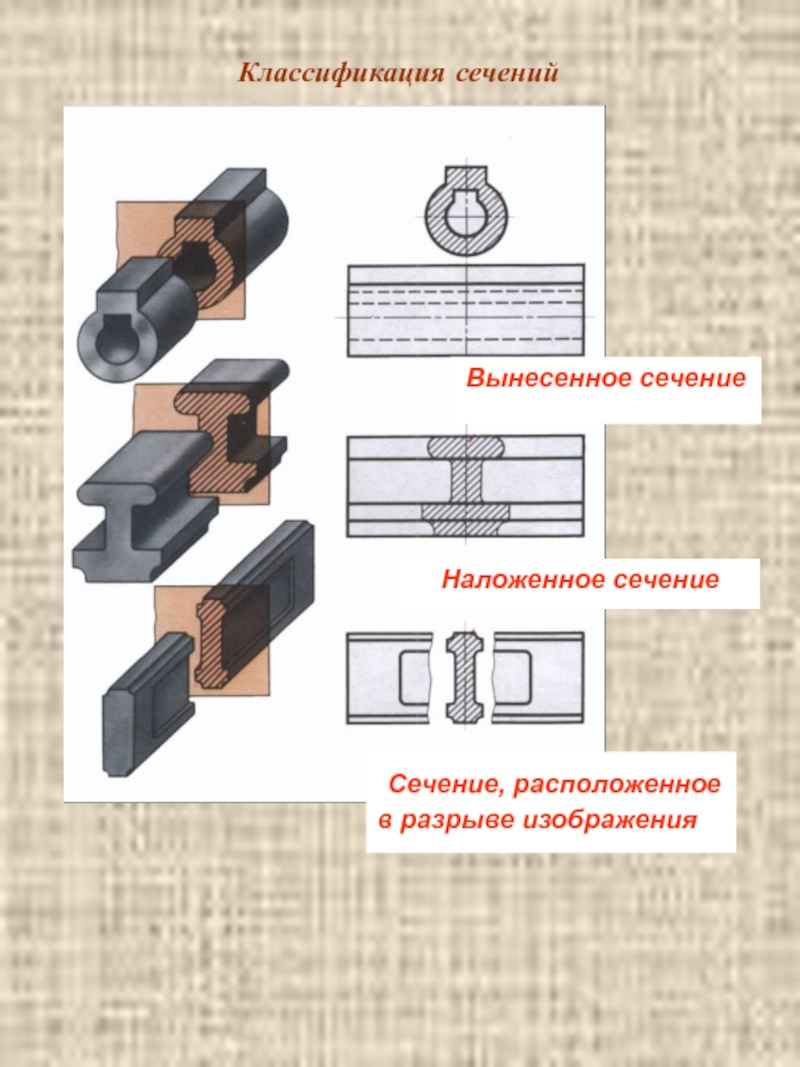Когда вы сгибаете, это другая область, потому что, если у вас есть напряжение с одной стороны и сжатие с другой, вы тянете секцию, вы не можете согнуть что-то в напряжении, поэтому нет смысла игнорировать эту область в напряжении. зона, которая не деформируется, так как не сжимается. Та область, которая не собирается прогибаться, вероятно, поможет поддерживать область рядом с ней, которая будет. Таким образом, вы можете понять, почему существуют немного другие критерии изгиба, немного другие критерии сжатия, у вас не было бы никаких критериев, если бы это был растянутый элемент, потому что вы не получаете потери устойчивости при растяжении. Ну да, но не в этом случае. Итак, что нам делать с разделом класса 4? Об этом и заговорил. Вы используете эффективную площадь, поэтому не учитываете полное распределение напряжения по всей площади, и вы говорите себе: «Ну, какие части могут деформироваться?» Если вы посмотрите, например, на Еврокод 3, часть 1, часть 5, он даст вам инструкции по металлическим конструкциям, и это то, что определяет эти области и то, сколько стали вы считаете причиной убытков. В случае наших круглых полых профилей класса 4, очень больших труб, мы рассматриваем область, которая больше всего сжимается, этот кусок вверху – тот кусок, который, как мы думаем, изогнется первым, поэтому, если он собирается изогнуться, давайте просто напишем выключить и сделать вид, что его нет. Итак, в конечном итоге вы проектируете вокруг секции, которая, хотя и является круглой, вы фактически рассматриваете ее как форму подковы. Теперь у меня есть небольшая записка, в которой я советую вам взглянуть на техническое примечание 7 Groundforce, это отличный небольшой документ, объясняющий наши идеи, лежащие в основе круглого полого профиля класса 4. Это происходит из небольшого исследования, проведенного кем-то другим об эллиптических полых сечениях, и оно объясняет, почему мы обращаемся с нашими сечениями так, как мы это делаем. Зона поражения, вообще говоря, представляет собой площадь, умноженную на коэффициент уменьшения, и это объясняет, какой коэффициент сокращения мы используем и откуда мы его получаем. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт