Какие бывают линии: Виды линий / Справочник по математике для начальной школы

Виды и особенности линий розлива

Линии розлива широко используются в самых различных отраслях промышленности — фармацевтической, ветеринарной, косметической, химической, пищевой. Завод «АВРОРА» проектирует и изготавливает обширную линейку линий для розлива жидких, вязких, густых, кремообразных и многокомпонентных продуктов. Данные установки представлены в большом разнообразии, разобраться в котором не так легко без помощи специалиста. Расскажем подробнее, какие типы линий розлива бывают, чем отличаются, что на них фасуют и как выбрать оптимальное комплексное оборудование для розлива Вашего продукта.

Комплектация линии розлива определяется исходя из ТЗ заказчика. В состав классической установки входят:

    • Дозатор

    • Укупорочная система

    • Этикетировщик

    • Конвейер

В соответствии с потребностями производства в линию могут быть включены и другие участки:

    • Установка выдува ПЭТ-тары

    • Система мойки, ополаскивания и сушки флаконов

    • Ориентатор колпаков

    • Стерилизатор тары и колпачков

    • Маркиратор

    • Машина для упаковки продукции в термопленку

    • Накопительные столы для подачи пустой тары и выгрузки готовой продукции

    • Полностью автоматические. Данный вид линий не предполагает участия персонала непосредственно в рабочем процессе.

    • Полуавтоматические. В таких линиях одна или несколько операций выполняются вручную, например, подача и установка крышек на тару. 

Линии розлива разрабатывают на базе различных типов дозирующих систем. Данный параметр зависит от консистенции, агрессивности и других особенностей фасуемого продукта, а также используемой технологии розлива. Основные типы дозаторов, используемых для фасовки продукта на линиях:

    • Перистальтический. Этот вид фасовщика представляет собой перекачивающий насос и отлично подходит для розлива жидких и слабовязких продуктов.

    • Гравитационный. Продукт разливается под действием собственной силы тяжести, равномерно наполняя тару по уровню.

    • Весовой. Данные установки выполняют фасовку различных, в том числе пастообразных продуктов, по объему (заранее установленному весу).

    • Поршневой. Продукт подается под давлением поршня, который отлично справляется с работой с густыми и пенящимися массами.

Системы розлива, используемые в линиях, могут иметь линейное или роторное (карусельное) исполнение. В первом случае группа тары наполняется одновременно после поступления заданного количества емкостей. В роторных автоматах последовательно осуществляется подача и наполнение флаконов (друг за другом). В зависимости от требуемой производительности устанавливается оптимальное количество разливочных головок в линии (от 2 до 16). 

Требования к дозирующим системам линий определяются следующими особенностями продукта:

    • Консистенция. Продукт может быть жидким, густым, склонным к вспениванию, имеющим повышенную вязкость и другие свойства, которые влияют не только на выбор типа дозатора, но и на необходимость в установке дополнительных устройств. Например, для фасовки масс, склонных к загустеванию при остывании, добавляются системы подогрева продукта в бункере, а для высоко пенящихся жидкостей могут быть установлены специальные пеногасительные устройства и системы розлива на нескольких скоростях для минимизации вспенивания.

    • Назначение. В каждой отрасли есть свои требования, предъявляемые к розливу продукции. Так, для фасовки лекарственных препаратов важно, чтобы конструкция оборудования соответствовала требованиям GMP. Асептические продукты разливают посредством стерильного розлива, который также имеет свои особенности. На пищевых производствах особенно важно при розливе обеспечить сохранность вкусовых, ароматических и других важных для пищевого продукта свойств. Специальные дозирующие системы позволяют обеспечить надлежащий розлив и минимизировать риски.

    • Уровень опасности. Классические системы розлива адаптированы к розливу спокойных жидкостей. Для фасовки продуктов, в составе которых присутствуют хлор, кислоты и другие агрессивные компоненты, потребуется особенное исполнение. Неправильно подобранный дозатор в линии в данном случае может повлечь за собой неприятные последствия, например, продукт вызовет коррозию элементов оборудования и быстрый его выход из строя. Применение тефлоновых сопел, защитных покрытий и спецматериалов позволяет избежать нежелательных эффектов. Для розлива спиртосодержащих, летучих и склонных к возгоранию продуктов выпускаются линии с взрывозащитным исполнением элементов исполнения, что обеспечивает полную безопасность работы.

Получите быстрый подбор линии розлива для Вашего производства от специалистов завода «АВРОРА»! Менеджеры компании подберут наиболее выгодные варианты под Ваши задачи и предоставят подробное коммерческое предложение! 

Линии тренда | Qlik Sense Enterprise на Kubernetes Help

Линия тренда — это визуальное представление изменения направления величины с течением времени. Линии тренда отражают характер изменения тенденций с течением времени и показывают направление и динамику изменения величин.

В каких визуализациях используются линии тренда

Визуализация	Internal”>Линии тренда
Линейчатая диаграмма	Да
Линейный график	Да

Когда используются линии тренда

Добавьте одну линию тренда в диаграмму, чтобы сгладить флуктуации данных или выделить какие-либо тенденции в изменении данных.

Если нужно показать разные виды тенденций или изменение разных величин, в диаграмму можно добавить несколько линий тренда.

Типы линий тренда

Среднее

Средняя линия тренда соответствует среднему значению данных в течение анализируемого периода времени.

 

Линейчатая диаграмма, демонстрирующая распределение продаж по месяцам. Средняя линия тренда показана штриховой линией красного цвета.

Линейная

Линейная линия тренда используется, когда величины меняются (увеличиваются или уменьшаются) с постоянным коэффициентом. Линейные линии тренда обычно строятся по простым линейным наборам данных.

 

Линейчатая диаграмма, демонстрирующая распределение продаж по месяцам. Линейная линия тренда показана штриховой линией красного цвета.

Полиноминальная (второй, третьей и четвертой степени)

Полиноминальная линия тренда представляет собой кривую, которая используется на данных, подверженных флуктуациям.

От числа флуктуаций зависит порядок полиномиальной кривой. Полиномиальная линия тренда второй степени имеет только один экстремум (вершину или впадину), третьей степени — не более двух экстремумов, четвертой степени — три экстремума.

 

Линейчатая диаграмма, демонстрирующая распределение продаж по месяцам. Полиномиальные линии трендов второй, третьей и четвертой степени показаны штриховыми линиями соответственно красного, желтого и зеленого цвета.

Экспоненциальная

Экспоненциальная линия тренда — это кривая, которая используется, если значения величин подвержены очень резким изменениям.

 

Линейчатая диаграмма, демонстрирующая распределение продаж по месяцам. Экспоненциальная линия тренда показана штриховой линией красного цвета.

Логарифмическая

Логарифмическая линия тренда — это кривая, хорошо отражающая зависимость, при которой коэффициенты изменения данных меняются очень быстро и в конце концов стабилизируются.

 

Линейчатая диаграмма, демонстрирующая распределение продаж по месяцам. Логарифмическая линия тренда показана штриховой линией красного цвета.

Степенная (Power)

Степенная линия тренда является кривой, которая подходит для наборов данных, в которых сравниваются результаты измерений, увеличивающиеся с постоянными коэффициентами .

 

Линейчатая диаграмма, демонстрирующая распределение продаж по месяцам.

Степенная линия тренда показана штриховой линией красного цвета.

Подробнее

 

• Создание детализированного измерения

линий и углов — определения, свойства, типы, практические вопросы

7 минут чтения

Древние математики ввели понятие линий для представления прямых объектов, ширина и глубина которых пренебрежимо малы. Линии, рассматриваемые Евклидом как ширина за вычетом длины, составляют основу евклидовой геометрии.

Когда два луча (часть прямой) пересекаются в одной плоскости, они образуют угол. Точка пересечения называется вершиной.

В этой статье мы рассмотрим основные свойства, определения и типы линий и углов, связанных с геометрией. Мы также рассмотрим несколько примеров, чтобы вы лучше поняли свойства линий и углов. Прежде чем мы двинемся дальше, взгляните на план подготовки к GMAT из пяти шагов, чтобы набрать 700+ баллов по GMAT:

Ниже приведен краткий обзор тем, которые мы рассмотрим в этой статье

 [скрыть]

Определение строки

Линия не имеет конечных точек. Он имеет бесконечную длину.

Определение сегмента линии

Сегмент линии — это сегмент линии, или, другими словами, мы можем сказать, что сегмент линии — это линия с двумя концами.

Например, , На диаграмме показана линия L, и один сегмент этой линии — AB.

На плоскости может быть много линий или отрезков.

Эти линии можно разделить на несколько типов в зависимости от относительного расположения одной строки по отношению к другой.

Типы линий

Пересекающиеся линии

Две линии являются пересекающимися, если они пересекаются в одной точке.

Например, L ₁ и L ₂ являются пересекающимися линиями на диаграмме ниже.

Параллельные линии

Пара прямых параллельна, если они никогда не пересекаются.

Например, L ₁ , L ₂ и L ₃ являются параллельными линиями на приведенной ниже диаграмме.

Поперечная линия

Поперечная линия пересекает две или более линий в разных точках.

Например, линия L ₃ является поперечной линией на приведенной ниже диаграмме.

Далее мы рассмотрим углы и их свойства.

Набрав Q50-51 на GMAT, вы получите 700+ баллов GMAT. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта. Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:

Угол – что это такое?

Угол образуется при пересечении двух прямых. Обозначим угол символом ∠.

Угол состоит из двух катетов и одной общей вершины, в которой сходятся две прямые.

Например, ∠AOD образуется при пересечении линий AB и CD.

Кроме того, ∠AOD образуется между ветвями AO и OD, поэтому мы включаем A, O и D в название угла.

Знаете ли вы, что положение точек катетов не имеет значения, если общей вершиной является средняя буква в названии угла

Измерение угла

Угол измеряется в градусах.

Угол может измеряться от нуля (0) градусов до 360 градусов. Основываясь на измерении угла, они делятся на четыре типа:

1. Острый угол
2. Прямой угол
3. Тупой угол
4. Угол рефлектора

Острый угол

Когда измерение угла находится между 0 градусов и 90 градусов.

Прямой угол

Когда измерение угла равно 90 градусов.

• Если между двумя прямыми имеется прямой угол, то говорят, что эти две прямые перпендикулярны друг другу .

Тупой угол

При измерении угла между 90 и 180 градусами.

Прямая линия имеет угол 180 градусов.

Угол отражения

При измерении угла между 180 и 360 градусами.

Мы обсудили основные типы углов.

Теперь обсудим углы, образованные при пересечении двух прямых.

Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. Мы являемся наиболее проверенной компанией GMAT Prep на GmatClub с более чем 2200+ обзорами, по состоянию на 4 октября 2021 года.

Углы, образованные две интерселирующие линейки

. пересекаются друг с другом, то образуются 4 угла.

• И углы , которые противоположны друг другу в точке пересечения , известны как вертикально противоположные углы .
• Вертикально противоположные углы всегда равны.

Теперь обсудим углы, образованные при пересечении двух прямых третьей прямой, т. е. поперечной линией.

Углы, образованные поперечной линией

Когда поперечная линия пересекает две прямые, образуются восемь углов, как показано на рисунке.

Теперь из этой диаграммы получается несколько специальных пар углов.

Например: если вы заметили , что (∠1, ∠3), (∠2, ∠4), (∠5, ∠7) и (∠6, ∠8) являются вертикально противоположными углами.

Аналогично получаем несколько других видов углов. Давайте обсудим их.

Другие типы углов

Внутренние и внешние углы

Внутренние углы — это углы, находящиеся внутри области между двумя линиями.

• И внешние углы – это те, которые равны , а не присутствует в этом регионе.

Например:

• ∠2, ∠3, ∠5 и ∠8 — внутренние углы.
• А, ∠1, ∠4, ∠6 и ∠7 — внешние углы.

Соответствующие углы

Два угла называются соответствующими, если они лежат по одну сторону от поперечной линии так, что:

• Один угол является внутренним, а
• Другой является внешним Например:

  (∠4, ∠8), (∠3, ∠7), (∠1, ∠5) и (∠2, ∠6) — 4 пары соответствующих углов

  Чередующиеся внутренние углы

  Два внутренних угла , лежащие на противоположной стороне поперечной линии, называются параллельными внутренними углами.

  Например:

  • (∠2, ∠8) и (∠3, ∠5) — альтернативные внутренние углы.

  Альтернативные внешние углы

  Два внешних угла, лежащих на противоположной стороне поперечной линии, называются альтернативными внешними углами.

  Например:

  • (∠1, ∠7) и (∠4, ∠6) — альтернативные внешние углы.

  Примечание: Если поперечная линия пересекает две параллельные прямые, то соответствующие углы, альтернативные внутренние углы и альтернативные внешние углы равны.

  Итак, мы рассмотрели все типы углов.

  Давайте теперь узнаем о некоторых свойствах углов.

  Свойства углов

  Сумма углов на одной стороне прямой

  Сумма всех углов по одну сторону прямой всегда равна 180 градусам.

  Например, сумма ∠1, ∠2 и ∠3 составляет 180 градусов.

  Сумма углов вокруг точки

  Сумма всех углов вокруг точки всегда равна 360 градусам.

  Например, сумма углов (∠1, ∠2 и ∠3) вокруг точки O составляет 360 градусов.

  Если вам понравилась эта статья, вот еще несколько статей, которые могут вам понравиться:

  • Свойства четырехугольника
  • Свойства окружности
  • Свойства треугольников
  • GMAT Геометрические формулы и понятия треугольников

  Применение свойств линий и углов в вопросах

  Линии и углы – вопрос 1

  параллельна прямой EF. Если ∠AHD и ∠JIE равны 118° и 30° соответственно, то какова мера угла GIB?

  1. 30
  2. 32
  3. 34
  4. 40
  5. 62

  Решение

  Шаг 1: Дана

  • линия CD параллельна линии EF.
  • ↑AHD = 118 °
  • секрет = 30 °

  Шаг 2: Найти

  • Мера угла retgib

  Шаг 3: Подход и работа

  . мера угла GIB.

  • Итак, по заданной информации мы знаем, что прямая CD параллельна прямой EF, а прямая AB им перпендикулярна.
    • Следовательно, ∠DHI = ∠FIB, так как оба угла являются соответствующими.
      • Мы можем найти грытиную или omfib AS
        • ↑AHD + ↑DHI = 180 °
        • 118 ° + грыти ∠GIB
          • Судя по диаграмме, ∠FIG = ∠JIE, так как это вертикально противоположные углы между EF и JG.
          • ∠FIB = ∠FIG + ∠GIB
          • 62° = ∠JIE + ∠GIB
          • 62° = 30° + ∠GIB
          • ∠GIB = 32° 9017
          9014 9014

        Следовательно, правильный ответ – вариант B.

        Линии и углы – вопрос 2

        На приведенной выше диаграмме угол DFE и угол BFC представлены X и Y соответственно. Если ∠AFC = 100° и ∠BFE = 45°, то каково значение Y-X?

        1. 20
        2. 25
        3. 30
        4. 35
        5. 40
        . 0094
      • ∠BFE = 45°

      Шаг 2: найти

      • значение Y-X

      .

      Мера угла Y:

      • Нам дано ∠AFC = 100° и,
        • ∠AFC + ∠BFC = 180°, так как сумма углов на одной стороне прямой равна 9093 180°. 100° + ∠BFC = 180°
          • ∠BFC = Y = 80°

      Измерение угла x:

      • Мы приведены грыти боковая прямая равна 180°.
      • X + 45° +80°= 180°
        • X = 55°

    Следовательно, Y – X = 80° – 55° = 25°.

    Таким образом, правильный ответ — вариант B.

    Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. Мы являемся самой популярной компанией по подготовке к GMAT на gmatclub с более чем 2200 отзывами по состоянию на 4 октября 2021 года.

     

    Основные определения, типы и уравнения

    Все в мире, от маленького цветка до области на карте, состоит из набора точек, сложенных вместе в различных формах. Самая основная и элементарная форма геометрии — это линия.

     

    Это одномерная фигура, не имеющая толщины и бесконечно простирающаяся от крайних концов. Ее еще называют прямой линией или правильно подчеркивают тот факт, что она не имеет никаких кривых нигде по своей длине. У них есть возможность встраиваться в многомерные пространства.

    В древности математики ввели понятие линии с единственной целью обозначения объектов, которые не имели кривых или были прямыми с незначительной глубиной и шириной. Известный математик определил линию как «длину без ширины».

    Линия имеет начальную и конечную точки. Предположим, что это точки A и B. 

    Мы представляем линию, помещая две стрелки в обе конечные точки, указывающие в противоположных направлениях. Это символизирует тот факт, что линия простирается в обоих направлениях.

    Типы линий

    Существуют различные типы линий. Давайте обсудим формулы, цифры и определения каждого из них.

    There are five types of lines, they are:

    1. Vertical line

    2. Horizontal line

    3. Parallel line

    4. Skew line

    5. Perpendicular lines 

    Vertical Line 

    • Вертикальная линия — это прямая линия, или, говоря простым языком, стоячая линия. Этот тип линии имеет неопределенный наклон.

    • Мы можем нарисовать график для вертикальной линии, изобразив x = n. Здесь n эквивалентно любому вещественному числу. Все точки на вертикальной линии имеют одинаковую координату x. Он параллелен оси Y координатной плоскости.

    • Уравнение вертикальной линии x = a. Здесь x — любая точка на линии с координатой x, a — точка пересечения с x.

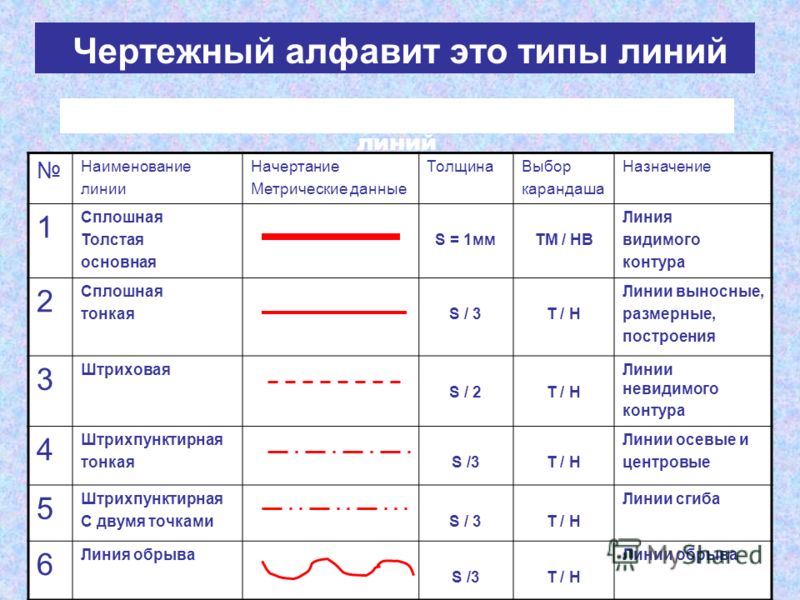
    Горизонтальная линия

    Горизонтальная линия — это один из типов линий, в котором все точки имеют одинаковую координату y. Ее еще называют спальной линией. Он параллелен оси x плоскости. Наклон горизонтальной линии равен нулю.

    Уравнение горизонтальной линии: y = b. Здесь y — любая точка на линии координат x, а b — точка пересечения с осью y. Он не зависит от х.

    Параллельная линия

    Две прямые называются параллельными, если расстояние между двумя прямыми одинаково во всех точках. Эти две линии не пересекаются ни в одной точке пространства. Они никогда и нигде не встречаются.

    Перпендикулярная линия

    Перпендикулярные линии образуются, когда горизонтальная и вертикальная линии встречаются в одной точке. Это две прямые, которые образуют конгруэнтный смежный угол друг к другу. Угол, образованный между вертикалью и горизонталью, составляет девяносто градусов.

    Некоторые основные определения 

    Отрезок линии. Отрезок линии имеет две конечные точки фиксированной длины.

    Луч: у луча есть одна конечная точка, а другой конец бесконечно простирается в одном направлении.

    Прямая линия: Прямая линия не имеет ни начала, ни конца и имеет бесконечную длину.

    Уравнение прямой

    Стандартная форма уравнения прямой: Ax + By = C, где A, B и C — действительные числа, A > 0, а x, y — переменные. Стандартную форму уравнения линии также можно записать как Ax + By – C = 0,9.0003

    Стандартная форма уравнения линии

    Стандартная форма линии представлена ​​в виде Ax + By = C, где A, B и C — целые числа. Она дает ту же информацию, что и форма с пересечением наклона. , у = тх + с.