Определение натуральной величины фигуры сечения — Студопедия
Поделись с друзьями
Нередко практический интерес представляет задача определения натуральной величины фигуры сечения.
Определим натуральную величину сечения (четырехугольника), полученного на рис. 3.11. Так как четырехугольник 1234 занимает общее положение в пространстве, то его натуральную величину можно определить двумя переменами плоскостей проекций, сначала построив плоскость, перпендикулярную четырехугольнику 1234, а затем – параллельную ему. Чтобы не загромождать чертеж (рис. 3.11), вынесем построения на отдельный рисунок 3.12. Для построения плоскости, перпендикулярной плоскости четырехугольника 1234, необходимо начертить одну из главных линий, например, горизонталь. Ее фронтальная проекция h2 должна быть параллельна оси П1/П2. По точкам пересечения 2 и 4 с четырехугольником 1234 находим и горизонтальную проекцию h1 горизонтали.
Новая ось П4/П1, разделяющая П1 и новую плоскость П4, должна быть перпендикулярна h1. Затем получаем проекцию 14243444 в виде прямой. И наконец, вычертив вторую новую ось П5/П4, параллельно 1434, построим проекцию 15253545 четырехугольника в плоскости П5. Это и есть натуральная величина четырехугольника 1234. Сечение заштрихуем под углом 45° к горизонтальной прямой.
Чаще приходится решать более простую задачу – определение натуральной величины сечения многогранника плоскостью частного положения. В этом случае достаточно сделать всего одну замену плоскостей проекций. Рассмотрим на примере сечения пирамиды горизонтально–проецирующей плоскостью S (рис 3.13). Пусть задана горизонтальная проекция S 1.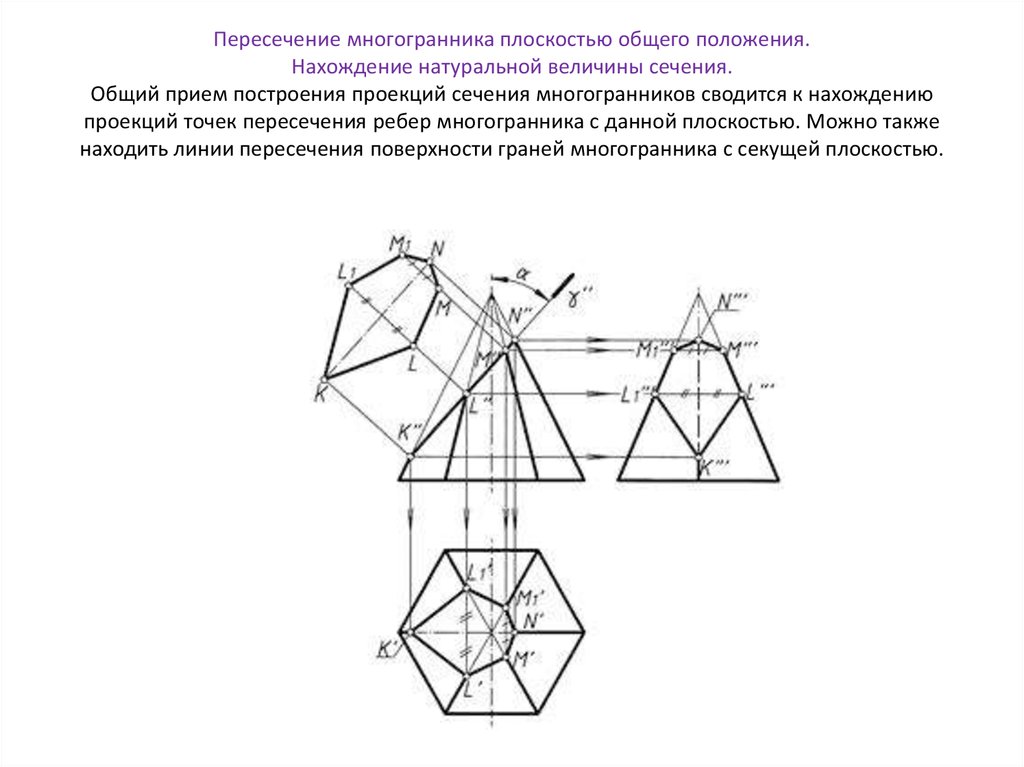 Необходимо найти линию пересечения плоскости S с пирамидой и определить натуральную величину сечения. Таким образом, задача разбивается на две части: сначала надо построить сечение в плоскостях П1и П2, а затем определить его натуральную величину.
Необходимо найти линию пересечения плоскости S с пирамидой и определить натуральную величину сечения. Таким образом, задача разбивается на две части: сначала надо построить сечение в плоскостях П1и П2, а затем определить его натуральную величину.
Рис. 3.13. Построение линии пересечения и определение натуральной величины сечения пирамиды плоскостью.
Чтобы решить первую часть задачи нужно найти все точки пересечения плоскости S с ребрами пирамиды и соединить их отрезками прямой. Горизонтальная проекция S1 пересекает ребра пирамиды в точках 11, 21, 31, 41 (рис. 3.13, а). По линиям связи находим их фронтальные проекции 12, 22, 32, 42 на фронтальных проекциях соответствующих ребер. Соединяя найденные точки, получаем линию пересечения 1 Плоская фигура, ограниченная полученной линией (на рис. 5.9, а заштрихована), и является сечением пирамиды плоскостью. В нашем примере это четырехугольник 1234.
Плоская фигура, ограниченная полученной линией (на рис. 5.9, а заштрихована), и является сечением пирамиды плоскостью. В нашем примере это четырехугольник 1234.
Для определения натуральной величины четырехугольника 1234 способом замены плоскостей проекций не обязательно строить новую ось параллельно S1 (или 11214131), ввиду ограниченности площади чертежа. Достаточно соблюдать основные принципы построения. Начертим новую ось на свободном поле чертежа. Перенесем на нее точки 11,21
,41,31, не меняя расстояния между ними. Проведем через них перпендикуляры к оси. Затем отложим на построенных перпендикулярах отрезки, равные расстояниям от оси П2/П1, которую считаем расположенной на основании А2В2С2 пирамиды, до соответствующих проекций 12, 22, 42, 32. Соединив указанные точки, получим натуральную величину сечения пирамиды заданной плоскостью S (рис. 3.13, б).
Соединив указанные точки, получим натуральную величину сечения пирамиды заданной плоскостью S (рис. 3.13, б).Как видим, сечение в натуральную величину отличается от 12223242 лишь тем, что оно вытянуто вдоль S1.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Сечение многогранников плоскостью
Плоская фигура, полученная при пересечении любого многогранника плоскостью, представляет собой некоторый многоугольник. Вершины этого многоугольника находятся как точки пересечения ребер многогранника с секущей плоскостью, а стороны многоугольника строятся как линии пересечения граней многогранника с секущей плоскостью.
Сечение призмы проектирующей плоскостью (фиг. 302).
I, а. Пятиугольная прямая призма поставлена основанием на плоскость П1 и рассечена фронтально-проектирующей плоскостью δ.
Требуется:
а) построить проекции сечения;
б) найти натуральную величину фигуры сечения;
в) построить развертку поверхности усеченной призмы;
г) построить аксонометрическую проекцию усеченной призмы.
I, б. Нахождение проекций сечений. Фронтальная проекция В 2С2А2D2Е2 фигуры сечения совпадает с фронтальной проекцией δ2 плоскости δ, так как вершины фигуры сечения являются точками пересечения ребер призмы с плоскостью δ. Горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы, так как призма прямая и ее ребра и грани перпендикулярны плоскости П1. Профильная проекция фигуры сечения выявится многоугольником, полученным путем построения третьей проекции по двум данным.
I, в. Нахождение натуральной величины фигуры сечения.
а) Метод совмещения. Совместим плоскость δ с плоскостью П1. За ось вращения принимаем горизонтальный след плоскости δ. Проекция δ2 совместится с осью х12. Пользуясь правилом совмещения, находим натуральную величину фигуры сечения ¯A¯B¯C¯D¯E.
Проекция δ2 совместится с осью х12. Пользуясь правилом совмещения, находим натуральную величину фигуры сечения ¯A¯B¯C¯D¯E.
Фигуру сечения и ее проекции на чертеже выделяют штриховкой под углом 45° к оси х12.
Штриховка может быть наклонена как вправо, так и влево, но для всех проекций и фигуры сечения штриховку следует выполнять в одну сторону.
II.
 Построение развертки поверхности усеченной призмы. Строим развертку боковой поверхности данной призмы. Затем на соответствующих боковых ребрах откладываем размеры оставшихся после отсечения плоскостью частей ребер H, Н1, Н2, H3 и Н4, которые берем с фронтальной и профильной проекций. Соединив последовательно прямыми точки DO, ЕO, АO, ВO, СO, DO, получим линию сечения, по которой плоскость δ рассекает призму на две части. Для получения развертки поверхности усеченной призмы к соответствующим боковым граням пристраиваем фигуру сечения и нижнее основание.
Построение развертки поверхности усеченной призмы. Строим развертку боковой поверхности данной призмы. Затем на соответствующих боковых ребрах откладываем размеры оставшихся после отсечения плоскостью частей ребер H, Н1, Н2, H3 и Н4, которые берем с фронтальной и профильной проекций. Соединив последовательно прямыми точки DO, ЕO, АO, ВO, СO, DO, получим линию сечения, по которой плоскость δ рассекает призму на две части. Для получения развертки поверхности усеченной призмы к соответствующим боковым граням пристраиваем фигуру сечения и нижнее основание.III. Построение аксонометрических проекций усеченной призмы.
III, а. Строим аксонометрическую проекцию призмы, пользуясь координатами на (фиг.302, I, а).
III, б. На соответствующих ребрах боковых граней откладываем от нижнего основания оставшиеся части ребер, используя для этого размеры Н, Н

Полученные точки А’, В’, С, D’, Е’ и А’ соединяем прямыми. Определяем невидимые и видимые элементы и обводим их соответствующими линиями.
Сечение призмы плоскостью общего положения (фиг.303).
I, а. Треугольная прямая призма поставлена основанием на плоскость П1 и рассечена плоскостью а общего положения.
Требуется:
а) построить проекции сечения;
б) найти натуральную величину фигуры сечения;
в) построить развертку поверхности усеченной призмы;
г) построить аксонометрическую проекцию усеченной призмы.
В этом случае горизонтальная проекция фигуры сечения сливается с горизонтальной проекцией призмы, так как боковые ребра и грани призмы перпендикулярны плоскости П 1. Для построения фронтальной проекции воспользуемся горизонталями. Через точку А1 – горизонтальную проекцию ребра – проводим прямую, параллельную проекции следа k1 – горизонтальную проекцию h1 горизонтали. Затем найдем ее фронтальную проекцию h2, которая, пересекаясь с фронтальной проекцией ребра D2E2 в точке А2 определит фронтальную проекцию точки пересечения ребра призмы с плоскостью а.
Затем найдем ее фронтальную проекцию h2, которая, пересекаясь с фронтальной проекцией ребра D2E2 в точке А2 определит фронтальную проекцию точки пересечения ребра призмы с плоскостью а.
I, б. Аналогичным построением находим остальные точки пересечения ребер призмы плоскостью а (В2, С2), после чего соединим последовательно прямыми точки А2, В2, С2 и А2 и получим фронтальную проекцию А2В2С2 фигуры сечения – треугольника.
I, в. Натуральную величину фигуры сечения находим путем совмещения плоскости а с плоскостью П
II и III. Построение развертки поверхности усеченной призмы и аксонометрических проекций аналогично соответствующим построениям для пятиугольной призмы (фиг.302).
Сечение пирамиды фронтально – проектирующей плоскостью (фиг. 304).
1, а. Правильная четырехугольная пирамида поставлена основанием на плоскость П1 и рассечена фронтально-проектирующей плоскостью б.
Правильная четырехугольная пирамида поставлена основанием на плоскость П1 и рассечена фронтально-проектирующей плоскостью б.
Требуется:
а) построить проекции сечения;
б) найти натуральную величину фигуры сечения;
в) построить развертку поверхности усеченной пирамиды;
г) построить аксонометрическую проекцию усеченной пирамиды (фиг.304, а).
I. б. Фронтальная проекция фигуры сечения – отрезок E2F2К2М2 – совпадает с фронтальной проекцией δ2 так как точки пересечения ребер пирамиды с секущей плоскостью лежат в плоскости δ.
Горизонтальные проекции точек пересечения находят при помощи вертикальных линий связи на горизонтальных проекциях соответствующих ребер, например: точку Е1 на горизонтальной проекции ребра S1A1, точку F1 на S1B1 и т.д.
Соединив последовательно прямыми точки Къ Ei, &i, JWi и Кг, получим горизонтальную проекцию фигуры сечения.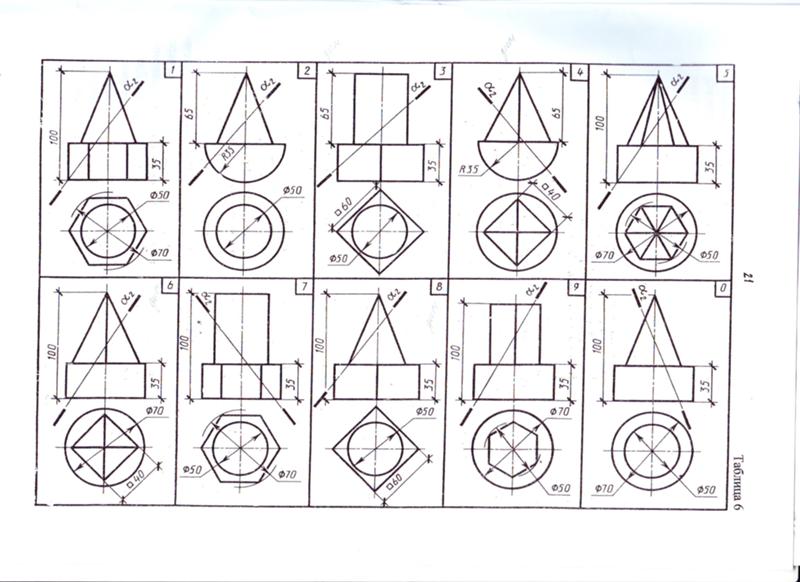
Профильная проекция фигуры сечения – четырехугольник E3F3M3K3 находится, как третья проекция, по двум данным (фиг.304,б).
I. в. Натуральная величина фигуры сечения находится способом совмещения плоскости δ с плоскостью П1 и способом перемены плоскостей проекций, где за новую плоскость П4 принята плоскость δ, а за новую ось проекций S24 – проекция δ2 (фиг.304,в).
II. Для построения развертки боковой поверхности находим натуральную величину ребра пирамиды путем построения прямоугольного треугольника S2O2¯D2, у которого S2O2 = H, a O2¯D2 = S1¯D1; гипотенуза S2D2 является натуральной величиной ребра. Зто равносильно повороту ребра до параллельности плоскости П2. Затем строим развертку боковой поверхности нерассеченной пирамиды – фигуру, состоящую из четырех равнобедренных треугольников, основания которых равны сторонам квадрата основания, а боковые стороны – натуральным величинам ребер.
Для определения величины отсеченных частей ребер, вместо поворота их, переносим с профильной проекции на натуральную величину ребра точки E3,F3,M3 и К3, получаем размеры R1,R2,R3,R4 Равные отсеченным частям ребер размер R1 равен отсеченной части S2¯E2, R2 равен S2¯F2 и т. д. (фиг.304, I, б).
Перенеся на развертку при помощи этих размеров на соответствующие ребра точки Ео, Fo, Мо, Ко и Ео и соединив их последовательно прямыми, получим ломаную линию, по которой пирамида рассечена фронтально-проектирующей плоскостью δ. Для получения развертки поверхности усеченной пирамиды к линии сечения присоединяем соответствующей стороной фигуру сечения, а к линии основания — основание пирамиды.
III, а. Для изображения изометрической проекции усеченной пирамиды, пользуясь координатами с (фиг.304, I, б), сначала строим основание и вершину пирамиды, а затем вторичную проекцию фигуры сечения (горизонтальную проекцию фигуры сечения) E’1F’1M’1K’1.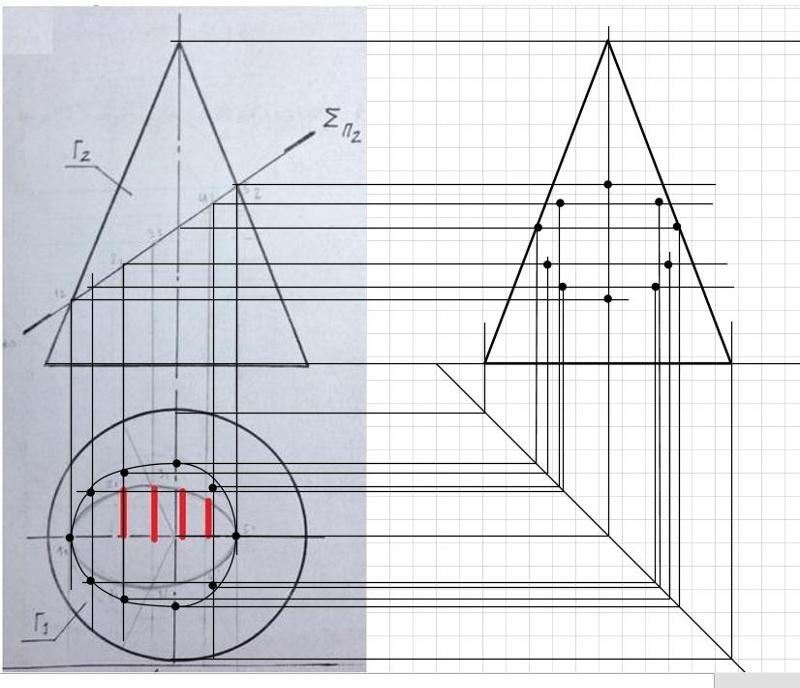
III, б. Соединяем прямыми точку S’ (вершину пирамиды) с точками А’, В’, С и D’ (вершинами основания) – получаем изометрическую проекцию пирамиды.
Из точек Е’1, F’1, M’1 и К’1 параллельно оси z проводим прямые до пересечения с соответствующими ребрами пирамиды. Точки Е’1, F’1, M’1 и К’1 явятся вершинами фигуры сечения, соединив которые прямыми, получим изометрическую проекцию фигуры сечения.
III, в. Определив видимые и невидимые элементы усеченной призмы, обводим их соответствующими линиями и заштриховываем фигуру сечения. Над усеченной частью пирамиды изображена отсеченная ее часть.
Сечение тел вращения плоскостью…..
Как сделать секцию героя Divi в полный рост
Этот быстрый совет покажет вам, как легко настроить секцию героя Divi на полную высоту на настольном компьютере, планшете и телефоне.
Раздел Divi Hero в полный рост
Производим хорошее первое впечатление
Все мы знаем, насколько важно первое впечатление, и это утверждение верно и для наших веб-сайтов и целевых страниц. Первый раздел на домашней или целевой странице известен как «главный раздел», , и многие пользователи хотят сделать его полной высотой, чтобы создать эффект погружения. Это легко сделать в Divi с помощью небольшой подсказки, и я собираюсь показать вам, как сделать раздел героя Divi полной высоты.
Первый раздел на домашней или целевой странице известен как «главный раздел», , и многие пользователи хотят сделать его полной высотой, чтобы создать эффект погружения. Это легко сделать в Divi с помощью небольшой подсказки, и я собираюсь показать вам, как сделать раздел героя Divi полной высоты.
В Divi можно создать секцию полной высоты двумя способами. Раньше единственным методом был простой фрагмент CSS, но теперь есть способ сделать это непосредственно в Divi Builder. Этот учебник покажет вам оба метода на случай, если вам понадобится тот или иной, в зависимости от ситуации.
Сделать секцию Divi полной высоты с помощью настроек размера
Перейдите к любым настройкам секции Divi Builder на вкладку Дизайн . Перейдите к переключателю Sizing и найдите Минимальная высота настройка. Установите значение минимальной высоты на «100vh» и сохраните изменения.
Перейдите к переключателю Sizing и найдите Минимальная высота настройка. Установите значение минимальной высоты на «100vh» и сохраните изменения.
Это было просто! Теперь ваш главный раздел будет такой же высоты, как и любое устройство, которое используют посетители вашего сайта, будь то настольный компьютер, планшет или телефон.
Сделать раздел Divi полной высоты с помощью CSS
Альтернативный вариант включает всего одну строку кода, которую нужно добавить в раздел, который вы хотите сделать полноразмерным.
Перейти в раздел настройки на Вкладка «Дополнительно» . Перейдите к переключателю Custom CSS и найдите Main Element . Скопируйте и вставьте следующий фрагмент кода ниже в эту область ввода.
мин-высота: 100вх;
Итак, вот два способа создать раздел героя в полный рост в Divi. Надеюсь, вам понравилось, и вы сможете использовать его на своих веб-сайтах Divi!
Последнее обновление: 15 ноября 2022 г. , 19:20
, 19:20
Вот и все!
Надеюсь, вам понравилось изучение раздела «Как сделать полноростового героя Divi». Пожалуйста, поделитесь своими мыслями в комментариях ниже. Если вы найдете ценность в этом типе публикации, пожалуйста, подпишитесь , потому что у нас есть тонн обучающих материалов, которые нужно опубликовать !Подписаться
Каждый месяц мы рассылаем по электронной почте бюллетень с последними учебными пособиями, обновлениями продуктов, полезными ресурсами и любыми другими отраслевыми или личными новостями. Иногда мы отправляем дополнительное отдельное электронное письмо здесь и там, если просто не можем ждать! Вот что вы получите, если подпишетесь, и вы всегда сможете отказаться от подписки в любое время, если просто больше не можете этого терпеть 🙂
Публикация в блоге OptinИмя
Фамилия
Пожалуйста, поделитесь этой публикацией!
Фейсбук
Твиттер
Пинтерест
Нельсон — владелец компании Pee-Aye Creative в прекрасном штате Пенсильвания. Он любит помогать малому бизнесу, исследовать природу, создавать веб-сайты с помощью Divi и учить других.
Он любит помогать малому бизнесу, исследовать природу, создавать веб-сайты с помощью Divi и учить других.
Календарь событий Divi
Рейтинг 5.00 из 5
Легко интегрируйте плагин «Календарь событий» с Divi и отображайте и настраивайте свои события с помощью красивых модулей Divi!
От: 45,00 $ / годКурс Divi для начинающих
С рейтингом 5,00 из 5
Начните создавать удивительные веб-сайты Divi с помощью нашего полного учебного курса для начинающих с 4,5 часами видео и письменных материалов!
От: 47,00 $ / годDivi Carousel Maker
Рейтинг 5.00 из 5
Создавайте красивые карусели из любых модулей Divi, включив переключатель и изменив настройки дизайна!
От: 25,00 $ / годDivi Contact Form Helper
Рейтинг 5,00 из 5
Обновите контактную форму Divi с множеством новых настроек и премиальных функций, таких как загрузка файлов, выбор даты и времени, настраиваемая строка темы, электронные письма с подтверждением, интеграция с Zapier, сохранение отправленных материалов.
От: 25,00 $ / год к базе данных, SMTP, значкам, новым тегам слияния, статистике панели мониторинга и многому другому!
к базе данных, SMTP, значкам, новым тегам слияния, статистике панели мониторинга и многому другому!
У наших видео есть просмотры! Присоединяйтесь к подписчикам и наслаждайтесь видео-уроками!
Посетите наш канал
Оставьте отзыв!
Оставляя комментарий, вы соглашаетесь с нашей Политикой в отношении комментариев к блогу и YouTube
Раздел | Университет Webflow
В этом видео используется старый пользовательский интерфейс. Скоро будет обновленная версия!
Раздел — это элемент макета шириной 100 %, занимающий всю ширину окна браузера. Разделы играют важную роль в структуре и макете страницы. Разделы позволяют создавать отдельные блоки контента и делить страницу на значимые сегменты.
На этом уроке:
- Добавить раздел
- Стиль A Раздел
- Минимальная высота
- Высота видового порта
- Добавить 3D -перспективу
Добавить раздел
. Вы можете добавить Секция
Вы можете добавить Секция
Добавить раздел
. страница из панели Elements (A). По умолчанию Раздел будет охватывать всю ширину тела.
Также по умолчанию разделы не имеют отступов внутри. Если вы не хотите, чтобы ваш контент занимал всю ширину тела, перетащите контейнер, чтобы элементы располагались по центру страницы.
Совет для профессионалов: Чтобы иметь хорошую, согласованную структуру веб-сайта, добавьте разделы в элемент body, а затем организуйте содержимое в контейнерах, размещенных внутри этих разделов.
Стиль раздела
Высота раздела автоматически подстраивается под его содержимое — по мере добавления элементов раздел становится выше. Вы также можете установить определенную высоту на панели «Стиль».
Комбинированные классы
Комбинированные классы позволяют добавлять комбинированные стили и основаны на исходном классе раздела — вы можете переопределять стили и добавлять стиль поверх комбинированного класса.
Если вы внесете изменения в исходный раздел, вы увидите, что это изменение передается всем экземплярам этого раздела (если оно не переопределено в комбинированном классе).
Вы также можете переопределить комбинированный класс. Когда вы проектируете и разрабатываете другой раздел, вы можете добавить исходный класс раздела.
Автоматическая высота
Когда вы добавляете текст и мультимедиа в раздел, высота изменяется, чтобы определить высоту. Независимо от того, сколько контента вы добавляете, высота раздела соответствует содержимому внутри.
Заполнение секции также влияет на ее высоту. Лучше всего установить верхнее и нижнее заполнение раздела и добавить содержимое, чтобы оно могло соответствующим образом измениться.
Минимальная высота
Чтобы установить определенную высоту для раздела, рекомендуется установить минимальную высоту (например, 500 пикселей), чтобы раздел мог расширяться вместе со своим содержимым.
Если вы установите нормальную высоту, содержимое в конечном итоге будет выливаться или обрезаться.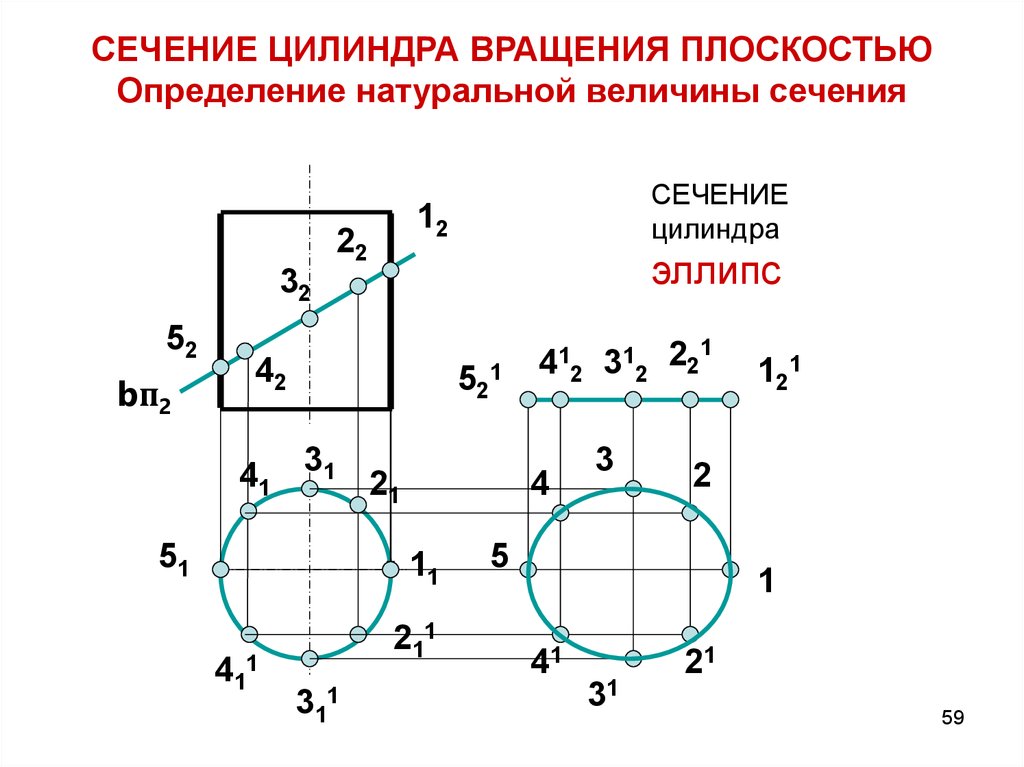
Использование flexbox для центрирования содержимого
С вашим контейнером в Разделе выберите Раздел и установите для него значение гибкий . Затем вы можете вертикально центрировать его дочерние элементы (вертикально центрируя Контейнер).
Высота области просмотра (vh)
В некоторых случаях, например, при создании основных разделов, вы можете задать разделу определенную высоту. В этом случае используйте единицу высоты области просмотра (vh), чтобы указать высоту сечения.
Например, 100vh заполнит 100% высоты области просмотра. Установка его на 50vh заполнит 50% высоты области просмотра и так далее.
Узнайте больше о различных единицах измерения ширины и высоты, которые можно установить для элементов.
Совет профессионала : Установите настройку отображения раздела на изгиб, чтобы центрировать контейнер и его содержимое вертикально внутри раздела.
Добавить трехмерную перспективу
Если у вас есть дочерние элементы секции (любые элементы внутри секции, даже если они находятся внутри других элементов внутри секции), вы можете добавить поворот или движение в трехмерном пространстве. Если к каждому элементу применен один и тот же класс, вы будете стилизовать их все сразу.
И вы добавляете 3D-преобразование, любой тип 3D-перемещения выглядит плоским (это потому, что это изометрическая проекция, а эффект, который нам может понадобиться, — это перспективная проекция).0003
Чтобы продемонстрировать перспективную проекцию, оставьте вращение как есть и включите эффект 3D-камеры.
Выбрав «Раздел», щелкните в настройках «Преобразование» и добавьте дочернюю проекцию (перспективу, влияющую на дочерние элементы).
Более высокое значение параметра «Перспектива для детей» дает более плоский эффект, например, если камера направлена на удаленные объекты с помощью телеобъектива, а более низкое значение соответствует приближению к объектам с помощью широкоугольного объектива.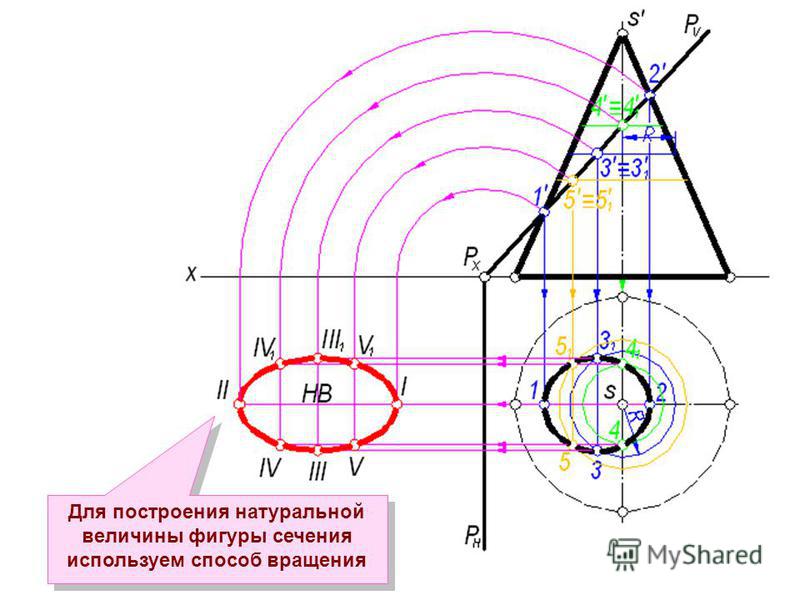

 к базе данных, SMTP, значкам, новым тегам слияния, статистике панели мониторинга и многому другому!
к базе данных, SMTP, значкам, новым тегам слияния, статистике панели мониторинга и многому другому!