Как правильно строить сечения: построить сечение пирамиды

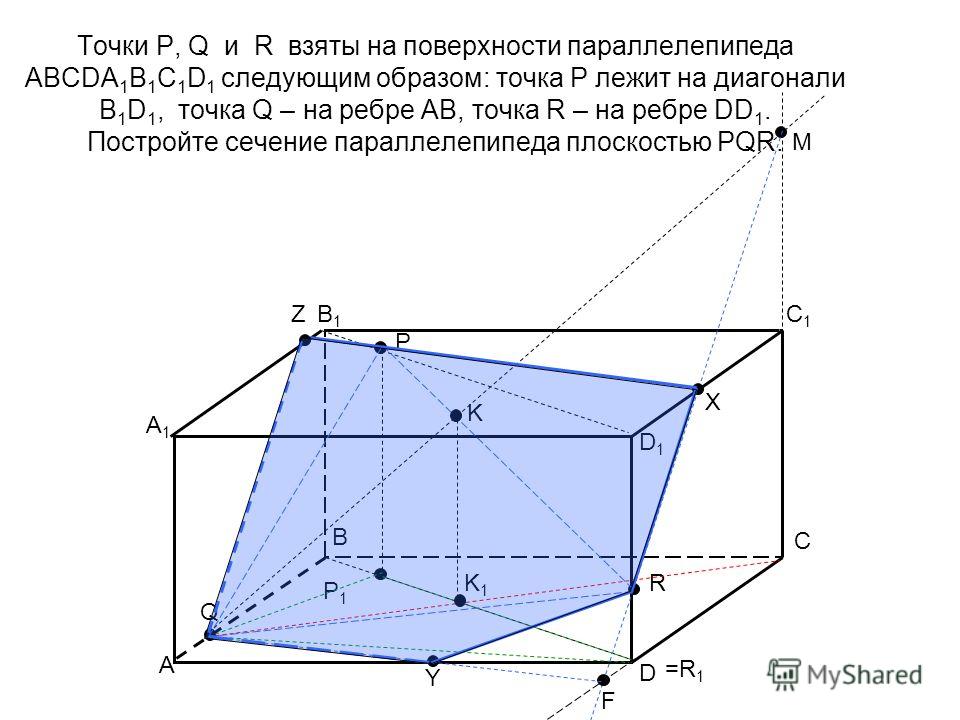
построить сечение пирамиды

Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.

В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.

Пример.

Построить сечение плоскостью (MNP)

 

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

 

 

 

 

 

 

Треугольник MNP — сечение пирамиды

Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.

Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом.

Аналогично строим след PN.

 

Треугольник MNP — искомое сечение.

 

Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.

Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.

Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.

Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.

Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.

 

 

 

Треугольник BKL — искомое сечение.

 

 

 

Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.

Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.

 

 

 

 

Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.

Продолжим прямую NP.

Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.

Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.

Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.

Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).

Через H и точку M, лежащую в этой же плоскости, можем провести прямую.

Получим след MT.

T — точка пересечения прямых MH и AC.

Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).

 

4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.

 

 

 

Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.

Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.

Значит, продлевая MN, ищем точку пересечения ее с  прямой AS. Назовем эту точку R.

 

Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), которой принадлежит прямая AS.

Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.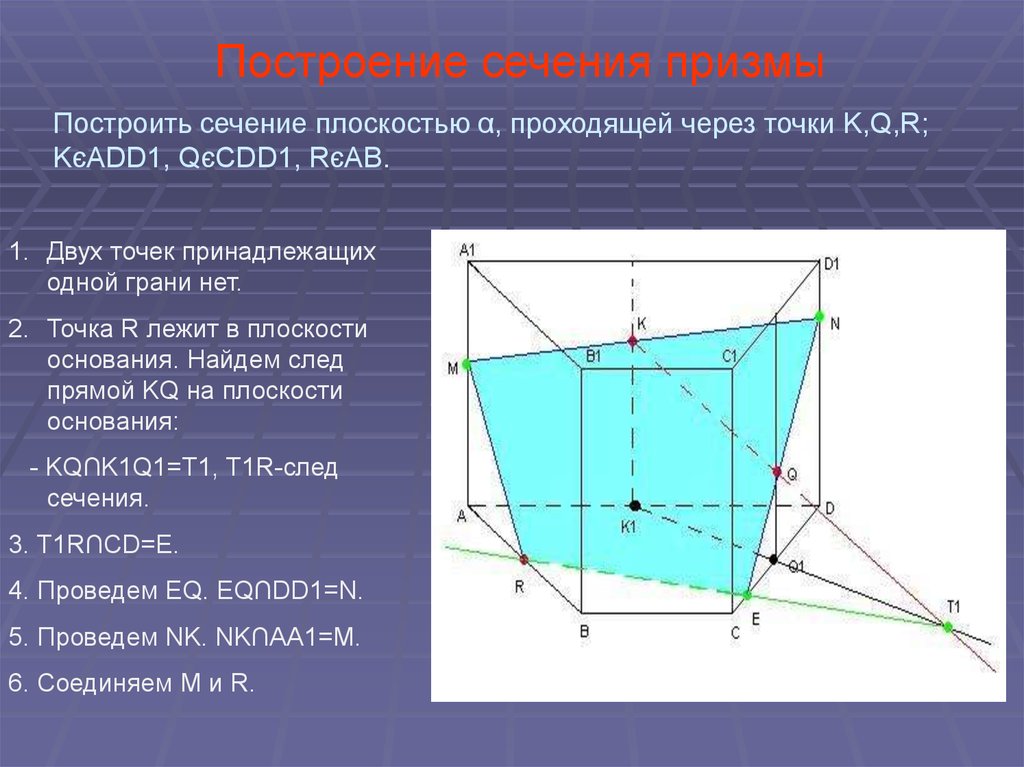

Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.

 

 

 

 

Таким образом, получили все то же сечение MNPT.

 

 

 

 

Рассмотрим еще один пример такого рода.

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

 

Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).

Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).

 

 

Через точки M и P прямую провести не можем.

1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.

 

 

Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую.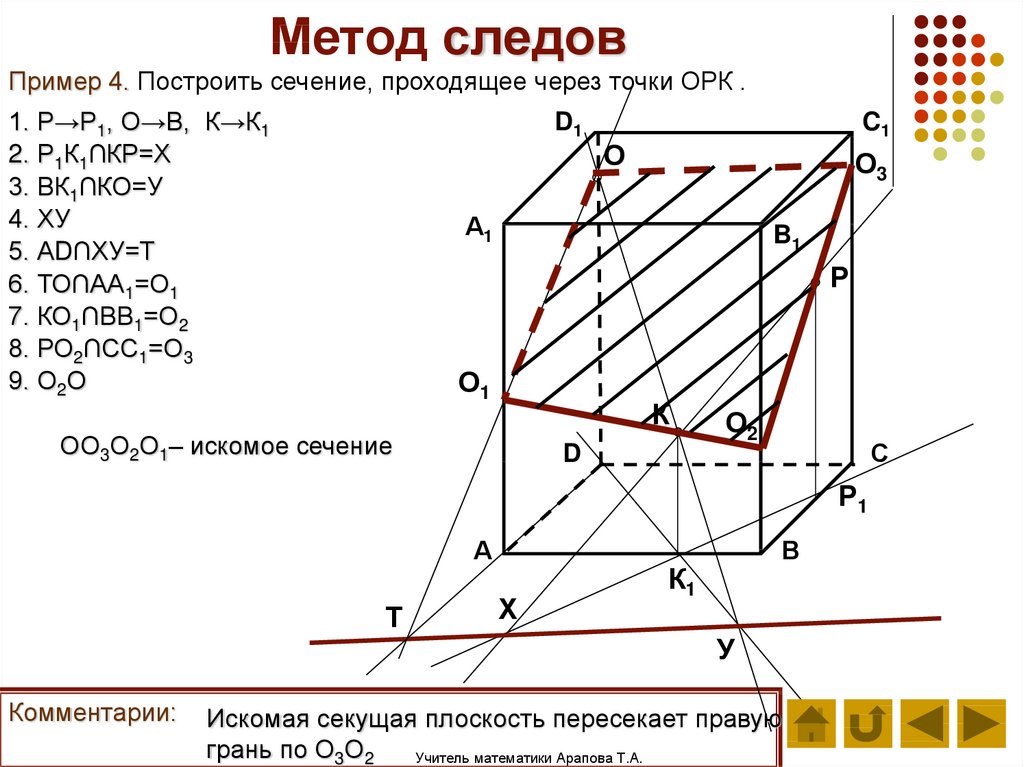 Ее след — PF.

F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.

 

2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.

Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).

Простая физика – EASY-PHYSIC

Построение сечения методом следов – это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению.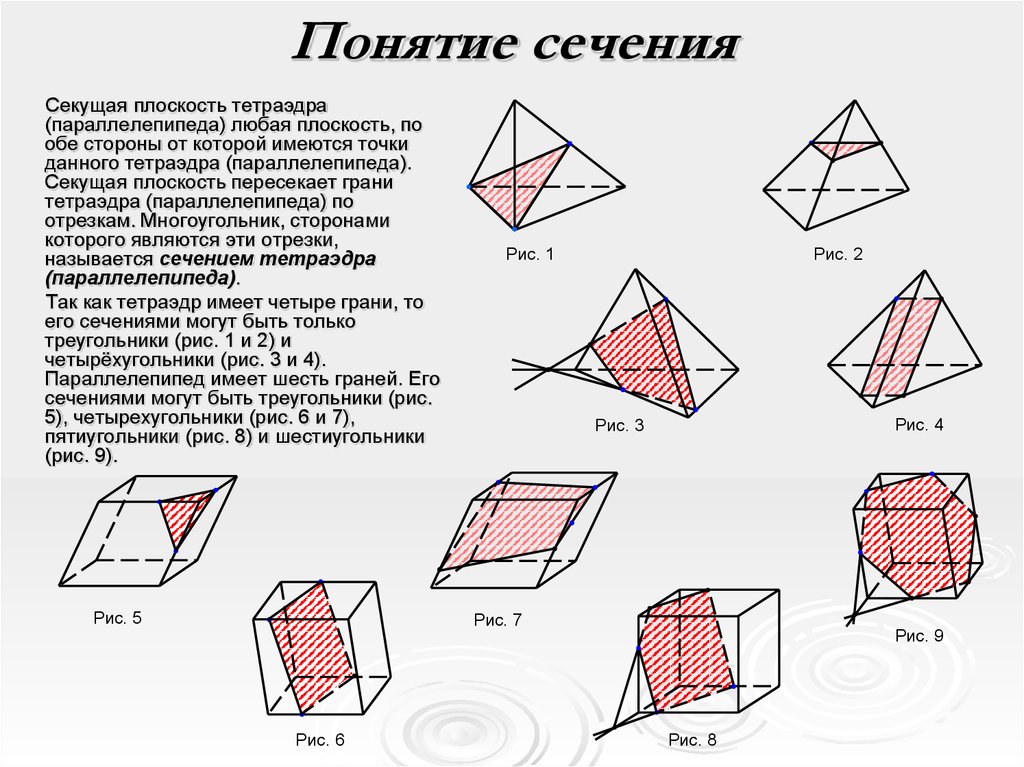 Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.

Задача 1.

Построить сечение параллелепипеда плоскостью, проходящей через точки  .

Задача 1. Дано

Шаг 1. Чезез точки и , которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой , которая также принадлежала бы основанию. Для этого проводим прямую , и находим точку ее пересечения с прямой – .

Задача 1. Шаг 1.

Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра – .

Задача 1. Шаг 2.

Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой , которая принадлежала бы плоскости задней грани.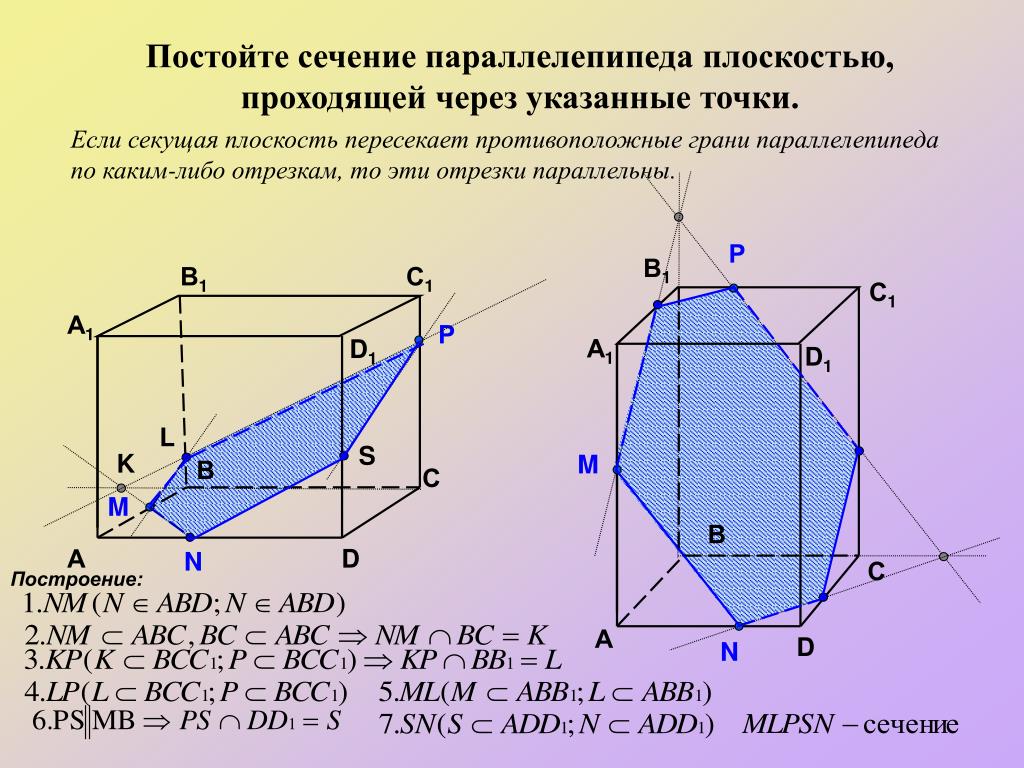 Для этого проведем прямую , которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой – . Через две точки задней грани проводим прямую , и находим место пересечения этой прямой с ребром – .

Задача 1. Шаг 3.

Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.

Задача 1. Шаг 4.

 

Задача 2.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Задача 2. Дано.

Шаг 1. Точки и лежат в одной плоскости, можно соединить их прямой. Прямая пересечет ребро в точке .

Задача 2. Шаг 1.

Шаг 2. Точки и также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра – .

Задача 2. Шаг 2

Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости.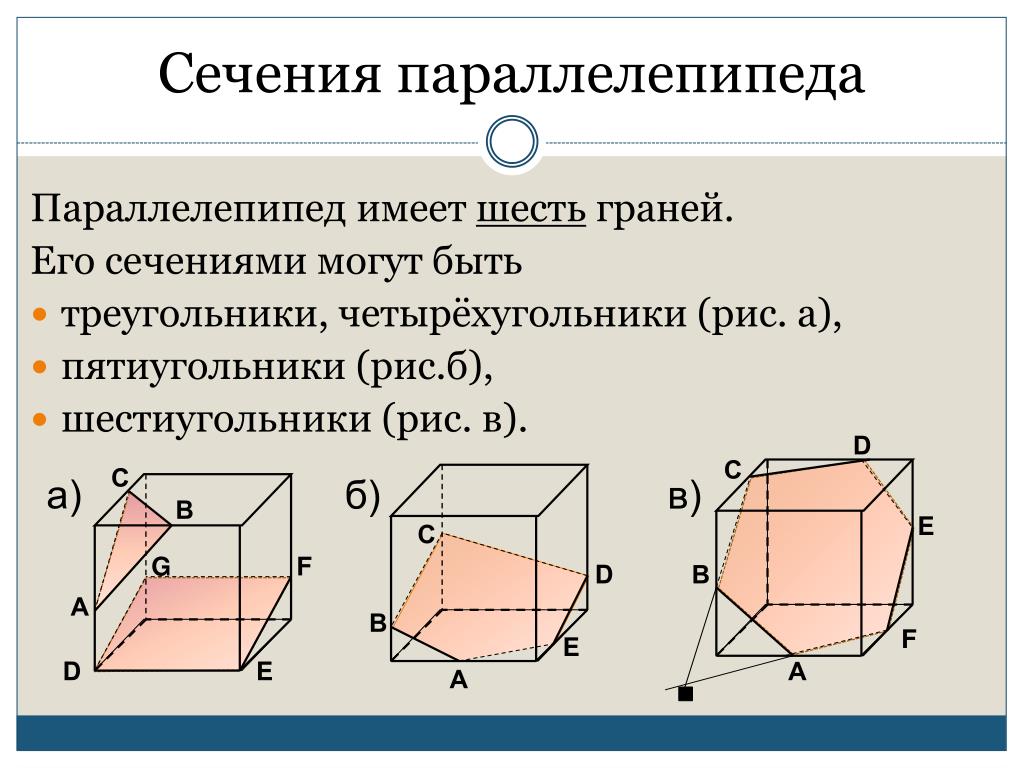 Для того, чтобы найти такую точку, проведем луч и найдем его пересечение с прямой – ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения – точка . Точки и можно соединить отрезком.

Задача 2. Шаг 3.

Шаг 4. Находим точку пересечения отрезком ребра – точку .

Задача 2. Шаг 4

Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.

Задача 2. Шаг 5

Задача 3.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Задача 3. Дано.

Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка принадлежит грани основания, поэтому нужна точка в этой плоскости.

Задача 3. Шаг 1

Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой – .

Задача 3. Шаг 2.

Шаг 3.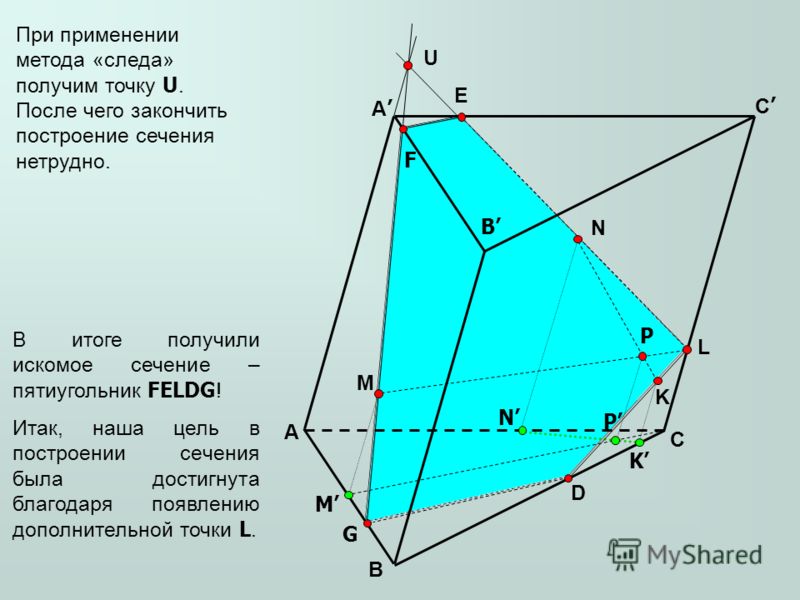 Проводим прямую и находим точку пересечения этой прямой с ребром – точка .

Задача 3. Шаг 3.

Шаг 4. Теперь надо найти точку в плоскости передней  грани, потому что в этой плоскости у нас уже есть точка – точка . Для того, чтобы найти такую точку, продлим прямую  и найдем пересечение этой прямой с прямой – точка .

Задача 3. Шаг 4

Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер – точку , и ребра – точку .

Задача 3. Шаг 5.

Шаг 6. Соединяем точки и получаем многоугольник сечения.

Задача 3. Шаг 6

Окончательный вид сечения с другого ракурса:

Окончательный вид

Задача 4.

Построить сечение параллелепипеда плоскостью, проходящей через точки  . Точка в задней грани.

Задача 4. Дано

Шаг 1.  Проводим прямую через две точки одной плоскости – и .  Определяем точку пересечения данной прямой ребра – .

Задача 4. Шаг 1.

Шаг 2. Продолжение прямой пересечется с продолжением прямой – так как обе прямые принадлежат плоскости задней грани. Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .

Задача 4. Шаг 2.

Шаг 3. Точка – точка пересечения прямой ребра . Продлим также ребро и найдем пересечение прямой и прямой – точку , которая принадлежит плоскости основания.

Задача 4. Шаг 3

Шаг 4. Соединяем Точки и плоскости основания, определяем точку пересечения данной прямой с ребром – точку . Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.

Задача 4. Шаг 4.

Окончательный вид сечения с другого ракурса:

Окончание построения

КАК ПОКАЗАТЬ РАЗРЕЗ ПО ТОПОГРАФИЧЕСКОЙ КАРТЕ | by Amidu Edson

Поперечное сечение представляет собой профиль обсуждаемой области. Это диаграмма, показывающая изменение высоты вдоль линии, проведенной между двумя точками на карте .

На экзамене всегда будет указан вертикальный масштаб — менять его нельзя.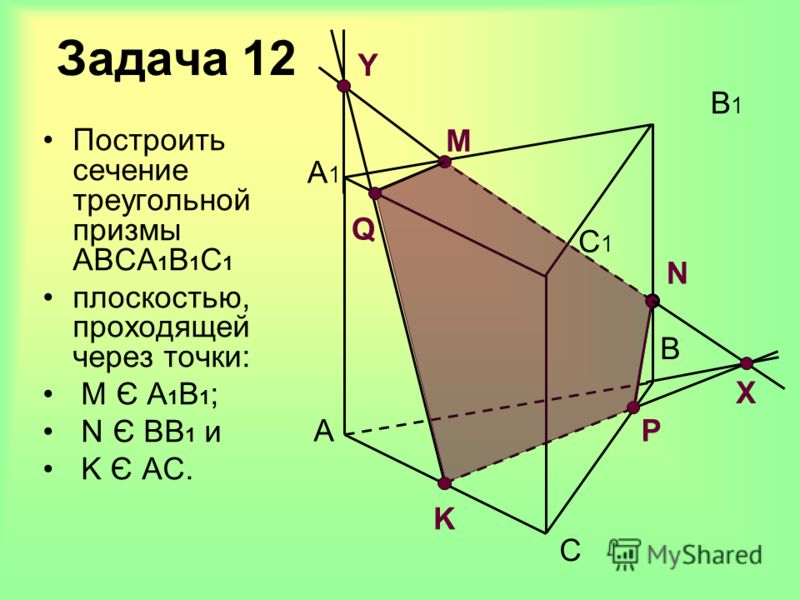 например 1 см соответствует 50 метрам по оси Y (вертикальная ось) Помните: Горизонтальный масштаб остается 1:50 000 (это будет масштаб карты)

ПЕРЕД стартом изучите площадь поперечного сечения до общей формы или лжи земли, то есть всегда имел представление о форме ДО того, как вы начнете наносить высоты или рисовать сечение.

• На «волшебном» листе бумаги обозначьте сечение на карте и сопоставьте его с «заданным» графиком. Отметьте на графике правую крайнюю точку и проведите вертикальную линию, чтобы разграничить ее.
• Положите на карту лист бумаги и (удерживая его неподвижно) отметьте КАЖДЫЙ контур, который его пересекает, ТОЧНО пронумеровав каждую отметку по вертикали. Например. 2 2 2 2 0 2 4 6 0 0 0 0
• Теперь поместите «волшебный» лист бумаги вдоль базовой линии графика — убедитесь, что две крайние точки точно выровнены. Сопоставив вертикальную шкалу с отмеченной высотой контура, отметьте маленький «x», чтобы показать положение каждого контура на графике.
• ВАШИ КРАЯ ГРАФИКА ДОЛЖНЫ СОВПАДАТЬ С ГРАНИЦАМИ ГРАФИКА — нигде на земле кусок земли не заканчивается в воздухе!!!
• Соедините эти точки произвольно, стараясь показать долины или холмы, где 2 или 3 соседние точки находятся на одной высоте.
• Напишите ПОЛНЫЙ заголовок на поперечном разрезе, например. Поперечный разрез от * 96 до r 281 на 3326 г. до н.э. Выдержка из карты города Грэма 1: 50 000 Топографическая серия
• Отметка в горизонтальном масштабе, Отметка в вертикальном масштабе с указанием единиц измерения Обозначьте края поперечного сечения, используя обозначенные точки (НЕ только A и B

Преувеличение по вертикали Используется, поскольку вертикальный масштаб должен быть преувеличен, потому что, если бы горизонтальный масштаб использовался для вертикали, рельеф выглядел бы как почти плоская линия на поперечном сечении. Формула:

Преувеличение по вертикали = Масштаб по вертикали (дан на поперечном сечении)/ Масштаб по горизонтали (1 см соответствует 50000 см)

Например, масштаб по вертикали = 1 см соответствует 20 метрам ) путем умножения на 100, т. е. 1 : 2 000 VE = 1:2000/1:50000 VE = 50000/2000/ VE = 25, умноженное на 9.0007

Интер видимость Это концепция того, можно ли увидеть одно место на карте из другого. Это решается путем изучения высот между двумя местами. Любая земля, которую нельзя увидеть за большей высотой, известна как МЕРТВАЯ ЗЕМЛЯ.

Если выпуклый склон находится между двумя точками, вторая не видна. Грубый набросок поперечного сечения показывает это легче. На интервидимость также может влиять наличие зданий или растительности.

Первоначально опубликовано по адресу https://geographypoint.com 3 июля 2015 г.

Рисование поперечного сечения на топографической карте

Как проводить этот урок дома:

Иногда

нас просят нарисовать поперечное сечение или профиль между двумя точками или двумя конкретными привязками сетки на топографической карте. Мы можем сделать это с помощью контурных линий.

Поперечный разрез представляет собой вид сбоку на область или местность. Поперечное сечение помогает нам визуализировать область.

Вот как это делается.

Шаг 1 : Допустим, нас попросили провести поперечное сечение между двумя точками A и B на диаграмме ниже. Нарисуйте линию, чтобы соединить две точки A и B, как показано на рисунке ниже.

Шаг 2: Положите лист бумаги вдоль линии, соединяющей А и В, то есть начальной и конечной точек.
Шаг 3: Отметьте каждое место на бумаге, где каждая контурная линия пересекает край бумаги, и запишите значение каждой контурной линии, как показано на рисунке 2 ниже.

Шаг 4: На отдельном листе бумаги нарисуйте горизонтальную линию того же размера, что и линия A – B. Это будет горизонтальная ось вашего графика.
Шаг 5: На вертикальной оси нашего графика вам нужно выбрать масштаб, который начинается немного ниже самого низкого значения высоты вдоль поперечного сечения и немного выходит за самое высокое значение высоты, как показано на рисунке 3 ниже.
Шаг 6: Положите размеченный край бумаги вдоль горизонтальной линии и отметьте высоту каждой контурной линии точкой.

Шаг 7 : Соедините точки сечения плавной линией. Завершите поперечное сечение, пометив его и заштриховав область под графиками.

В следующих двух видеороликах объясняется, как построить поперечное сечение на топографической карте.

Ваша задача сейчас построить собственное поперечное сечение. Воспользуйтесь контурной картой под названием I mage 4 Rock Mountain , доступной в разделе ресурсов.

а. Начертите поперечный разрез по линии А – В, отмеченной на карте.
б. Начертите поперечное сечение по линии C – D, отмеченной также на той же карте.

Иногда нас также просят указать, видно место или нет из определенной точки на карте. Это известно как intervisibility . Взаимовидимость на карте — это когда одна точка видна из другой и наоборот, то есть являются ли две точки на карте взаимовидимыми.