Угол наклона рельефа на местности: как измерить
Те пользователи, которые работают с рельефом в программе Наш Сад и используют для этого редактор Рельефа, знают: чтобы наклонить поверхность нужно задать угол ее наклона в градусах. Как же определить угол наклона рельефа подручными средствами, если в «кустах», случайно нет теодолита или тахеометра?
Метод вешек
Нам понадобятся: 3 колышка, шнур, рейка жесткая, уровень.
Вбиваем две вешки (колышка) по краям на перепаде высот (см. схему). Забиваем гвоздь или вкручиваем шуруп в произвольной точке С одной из вешек. Замеряем расстояние d от поверхности земли. Привязываем в этом месте шнур и с натяжением закрепляем его к другой вешке в точке А на том же, одинаковом расстоянии d от земли. Берем жесткую рейку, такую, чтобы не прогибалась и закрепляем на ней уровень. Устанавливаем рейку так, чтобы один ее конец находился в точке С, а другой лежал на еще одной вешке. Эту вешку забиваем в землю таким образом, чтобы она касалась натянутого шнура. Рейка на ней должна лежать горизонтально по уровню. Измеряем расстояние DE от шнура до рейки по вертикали и расстояние DС по горизонтали. Согласно схеме это длина рейки. Нам нужно найти значение угла β в градусах. Это и будет искомый угол наклона.
Рейка на ней должна лежать горизонтально по уровню. Измеряем расстояние DE от шнура до рейки по вертикали и расстояние DС по горизонтали. Согласно схеме это длина рейки. Нам нужно найти значение угла β в градусах. Это и будет искомый угол наклона.
Мы легко можем измерить и вычислить соотношение DE/DC. В тригонометрии это тангенс угла — число, которое определяется соотношением противолежащего и прилежащего к этому углу катетов треугольника CDE. Зная это соотношение можно вычислить величину угла, например, воспользовавшись тригонометрической функцией, обратной тангенсу — арктангенсом.
Вычисляем угол наклона на калькуляторе Windows
Значение арктангенса вычисляем, используя стандартный калькулятор из состава Windows. Щелкаем кнопку «Пуск», переходим в раздел «Все программы», находим «Стандартные» и жмем «Калькулятор». Этот же результат достигнем, нажав сочетание клавиш WIN + R, набрав в строке «Выполнить» команду calc и щелкнув кнопку «OK».
Переключаем калькулятор в режим вычисления тригонометрических функций.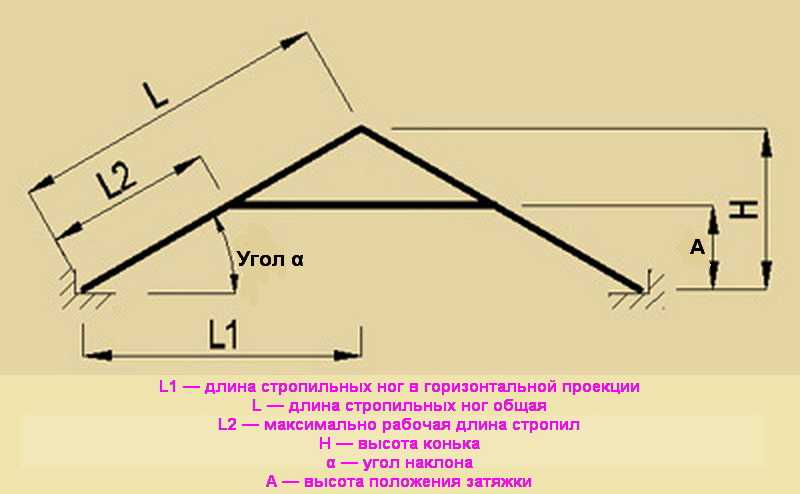 Для этого открываем меню «Вид» и находим пункт «Инженерный» или «Научный» (в зависимости от версии используемой операционной системы).
Для этого открываем меню «Вид» и находим пункт «Инженерный» или «Научный» (в зависимости от версии используемой операционной системы).
Вводим известное значение тангенса. Это делаем с клавиатуры или щелкая нужные кнопки интерфейса калькулятора.
При этом выбираем единицу измерения «Градусы» — DEG, чтобы получить результат вычисления именно в градусах, а не в радианах или градах. Ставим метку в checkbox (пустом квадратике) с надписью Inv. Так инвертируем значения вычисляемых функций, обозначенные на кнопках калькулятора. Если такого «квадратика» нет, зажимаем кнопку Shift или «↑». На рисунке слева нужные нам параметры подчеркнуты красной линией.
Щелкаем кнопку с надписью tg или tan (тангенс) и далее « = ». Калькулятор вычисляет значение функции обратной тангенсу — арктангенс. Это значение и будет искомым углом.
Вместо Win-калькулятора можно использовать, например, онлайн-калькуляторы тригонометрических функций. Найти такие сервисы в интернете достаточно легко, задав поиск в браузере.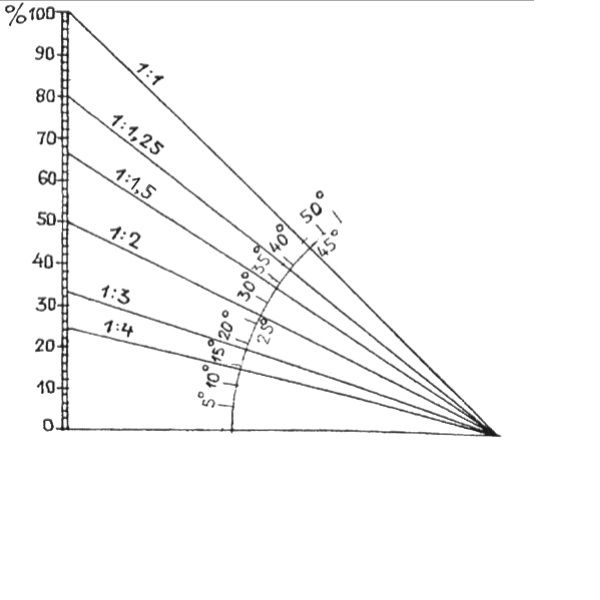
Важно помнить!
Измерения на местности проводим как можно точнее и рейку устанавливаем точно по уровню. Имейте в виду, что если длина рейки пусть даже полтора-два метра, а длина отрезка АВ метров 15-20, то даже незначительное отклонение уровня от горизонтали дает существенную погрешность. Тем не менее это разумный способ. Он позволяет, пусть и не совсем точно, определить угол наклона рельефа местности.
Используя подобие треугольников АВС и СDЕ можно вычислить также перепад высот: h=АВ*DE/ DС.
самостоятельное определение угла в градусах
Проекты загородных домов должны соответствовать многим требованиям, пожеланиям и даже причудам каждого владельца. Но в большинстве случаев их объединяет одна особенность — без надёжной крыши не может обойтись никакое здание. В этом случае на первый план ставится не только архитектурная задумка здания, но также специфические требования к показателю угла наклона крыши.
- Особенности конструкции крыши
- Для чего необходимо подкровельное пространство
- Уклон угла в градусах
- Скатная и плоская крыша — особенности
- Минимальный показатель уклона
- Самостоятельное определение уклона крыши
- Величина нагрузок внешней среды
Особенности конструкции крыши
Проектировка конструкции крыши — это довольно непростой процесс, который требует от владельца большой ответственности, особенно это относится сложной конфигурации зданий.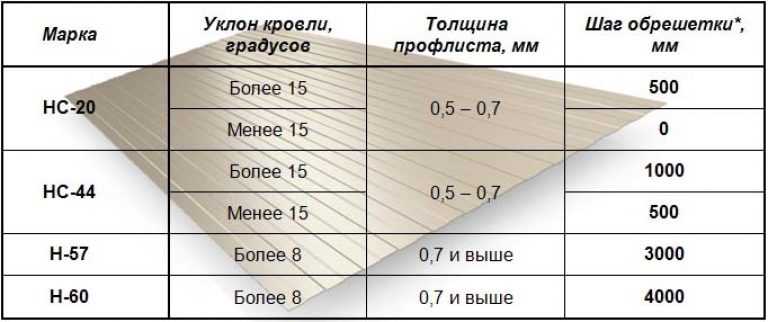 Лучше всего будет доверить такое дело мастеру, который опытен и обладает навыком в таких делах, у него есть соответствующие программы и инструменты, с помощью которых он сможет произвести более точные расчёты. Но владелец дома также может заинтересоваться некоторыми моментами установки скатов, с теоретической точки зрения. К примеру, очень важно точно знать, как рассчитать общий угол уклона крыши самостоятельно, для начала хотя бы приблизительно.
Лучше всего будет доверить такое дело мастеру, который опытен и обладает навыком в таких делах, у него есть соответствующие программы и инструменты, с помощью которых он сможет произвести более точные расчёты. Но владелец дома также может заинтересоваться некоторыми моментами установки скатов, с теоретической точки зрения. К примеру, очень важно точно знать, как рассчитать общий угол уклона крыши самостоятельно, для начала хотя бы приблизительно.
Это поможет сразу же спроектировать необходимый вам результат работы, который будет соответствовать реальным условиям региона, по конструкции самой крыши, по планируемому материалу, а также по назначению чердака. В некоторой степени показатель угла ската крыши поможет провести предварительный расчёт всех параметров и числа пиломатериалов для стропильной системы и общей площади кровли.
Для чего необходимо подкровельное пространство
Перед расчётом угла наклона крыши очень важно точно определить, в каких целях будет использоваться в доме чердак.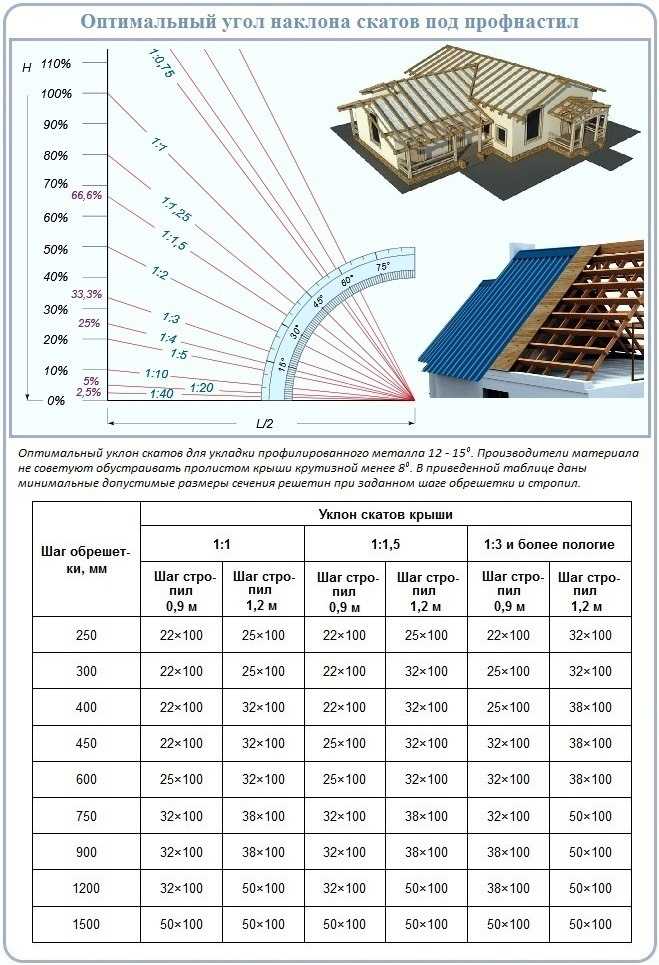 Если вы хотите сделать его жилого типа, то угол наклона потребуется большой — чтобы помещение было более просторным, а также высоким. Второй выход — провести ломанную установку — мансардную кровлю. В большинстве случаев данный тип крыши создаётся двускатным, но в конструкции может быть и четыре ската. Во втором случае вариант считается более сложным, поэтому без опытного проектировщика обойтись будет невозможно, но многие предпочитают проводить такую процедуру самостоятельно.
Если вы хотите сделать его жилого типа, то угол наклона потребуется большой — чтобы помещение было более просторным, а также высоким. Второй выход — провести ломанную установку — мансардную кровлю. В большинстве случаев данный тип крыши создаётся двускатным, но в конструкции может быть и четыре ската. Во втором случае вариант считается более сложным, поэтому без опытного проектировщика обойтись будет невозможно, но многие предпочитают проводить такую процедуру самостоятельно.
При увеличении показателя уклона крыши нужно помнить о следующем:
- Владельцу придётся затратить намного больше финансовых средств на кровельные материалы, так как площадь скатов возрастёт.
- На большие скаты происходит сильная нагрузка со стороны ветра. Если сравнивать общую нагрузку на одном и том же доме с углом ската в одиннадцать градусов и сорок пять, то во втором случае она будет в пять раз больше. Чтобы кровля могла выдерживать такие нагрузки и активно подавлять их, стропильную систему делают усиленного типа — возводятся балки и стропила с большим сечением и меньшим шагом.
 А это ведёт к увеличению стоимости работы.
А это ведёт к увеличению стоимости работы. - Если угол наклона ската превышает 60 градусов, то снеговые нагрузки значительно увеличиваются — осадки скатываются и не успевают задержаться на поверхности крыши. Но при создании мансарды ломанного типа снеговые нагрузки учитываются при расчёте верхней части крыши — в этом месте плоскость обладает уклоном меньше 60 градусов.
- Не все кровельные материалы разрешено применять для устройства крутых скатов, так что во внимание нужно брать максимальный угол наклона, с которым могут использоваться такие виды крыш.
Это совсем не значит, что крыши с небольшим уклоном чем-то лучше. Они обходятся по стоимости материалов намного дешевле кровли, но обладают и своими недостатками:
- Требуют установки снегозадержателей, чтобы не дать возникнуть лавинообразному сходу снега.
- На месте снегозадержателей нужно устанавливать обогрев кровли и водосточной трубы — это обеспечит таяние снега и своевременный отвод воды с крыш.

- При небольшом уклоне велик шанс того, что влага начнёт затекать в сами стыки. В результате это приведёт к необходимости дополнительной гидроизоляции.
Кровли с малым уклоном также не считаются хорошим решением для дома. Рассчитывать уклон крыши следует таким образом, чтобы найти общее соотношение между внешним видом (дом должен выглядеть красиво и изящно), практической стороной (при наличии используемого чердака), а также материалом (стоимость всей работы должна быть оптимальной).
Уклон угла в градусах
Наклонный угол, как и другие фигуры по геометрическим законам, измеряется в градусах. Но во многих документах, включая СНИПы, такой показатель величины будет отражён в процентах, именно поэтому не нужно предъявлять слишком строгих требований, чтобы использовать лишь одну общую единицу измерения.
В этом случае главное — высчитать пропорции для соотношения, если владельцу потребуется перевести проценты в градусы и, наоборот. Это очень важно для удобства при проведении вычислительных работ.
Это очень важно для удобства при проведении вычислительных работ.
Сам коэффициент пересчёта градусов варьируется с 1,7 (для одного градуса) до 2 (до 45 градусов). В том случае, когда очень важно использовать показатели, выраженные не целыми процентами, а в виде цифрового изображения, используют промилле — сотые доли %.
Если следовать теории, то показатель наклонности может варьироваться от 60 до 70 градусов, но в действительности делать этого не будет смысла. Да и на внешний вид такая конструкция будет выглядеть непривлекательно, конечно же, если только ваш дом не находится в горной местности.
Скатная и плоская крыша — особенности
Плоские перекрытия представляют собой исключительно горизонтальную поверхность, как бы ни казалось странным название. Строительный азимут в этом случае также обладает наклоном, хоть и не таким большим — его минимальный показатель должен доходить до трёх градусов.
Владелец при установке плоской поверхности должен понять, что в этом случае требуется создать водоотводный воронок, стенки которого будут наклонены на 1,5 градуса.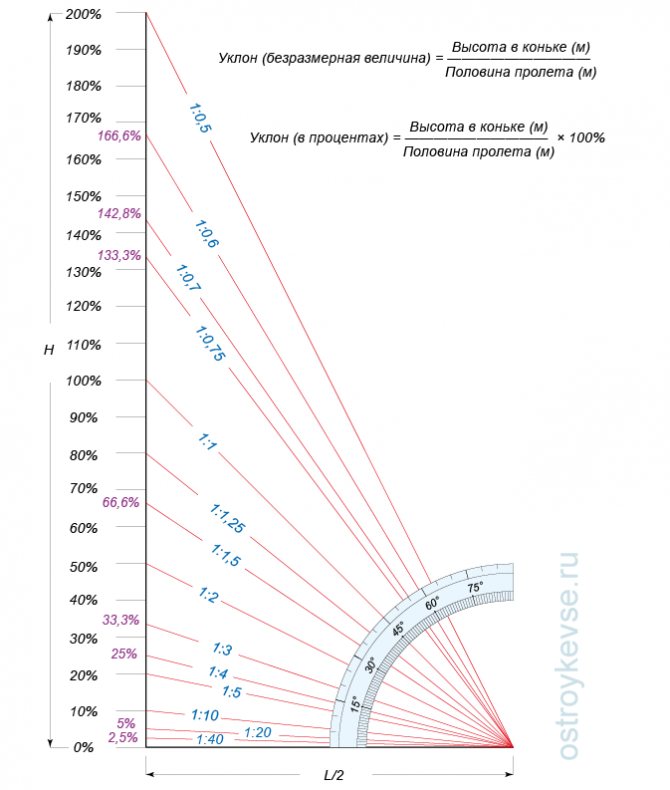
Если же говорить о величинах плоской поверхности, то уклон в таком типе кровли должен варьироваться от 5 до 7 градусов. Это обусловлено тем, что крыши с углом, превышающим 10 градусов, сложно отнести к плоским. При всём этом 12−15 градусов чаше всего уже относится к минимальному порогу для скатной поверхности. Оптимальная величина считается довольно широкоформатной.
Оптимальный наклон для схода снега в этом случае будет варьироваться от 40 до 50 градусов.
Например, для односкатного навеса лучше всего использовать диапазон от 20 до 30 градусов, а при двускатных конструкциях показатель возрастает до 45 градусов. Данный объёмный интервал покажет на индивидуальные показатели и тип кровли.
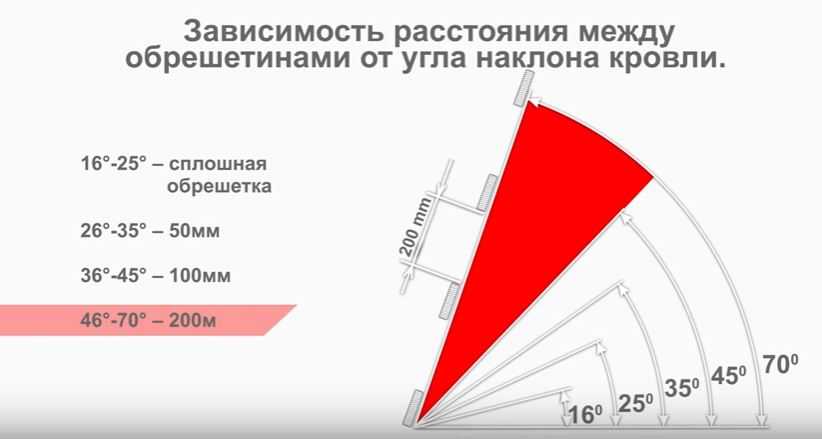
При небольшом азимуте стыки проходят обработку водостойким и морозостойким герметикам в обязательном порядке. Если показатель ската крыши доходит до 15 градусов либо превышает его, то настилание профнастила должно проходить при нахлесте в 200 миллиметров, если же уклон крыши меньше пятнадцати градусов — нахлест увеличивается сразу на несколько «волн».
Минимальный показатель уклона
Кровля считается главным материалом при устройстве верхней поверхности крыши, она также требует соблюдения определённых правил уклона в зависимости от её вида.
- Если с профнастилом используется угол с показателем в 12 градусов, то для металлочерепицы такой показатель нужно увеличить до пятнадцати градусов.
- Мягкая черепица может быть уложена на крышу с уклоном в одиннадцать градусов. В этом случае нужно учитывать особенности сплошной облицовки.
- При укладке керамической черепицы показатель наклона должен доходить до 22 градусов.
- Также нужно учитывать и то, что стропильная система подаётся большой нагрузке в случае ската с небольшой наклонностью. Чтобы избежать перегрузки ската во время строительства, нужно обязательно помнить о рекомендуемом наклоне.
- Минимальный показатель уклона кровли из сэндвич-панелей доходит до пяти градусов, если в панелях конструкции в дальнейшем будут находиться окна, то такой показатель возрастает до семи градусов.

Самостоятельное определение уклона крыши
Чтобы изменить общий угол ската, можно применить специальный прибор, который поможет не тратить вам своё свободное время. Название такого инструмента — уклономер.
Также можно воспользоваться механическим угломером — более бюджетный вариант, но при этом не исключены длительная морока с таким устройством, особенно в том случае, если владелец использует инструмент первый раз.
Перед началом измерения необходимо понять общую специфику устройства:
- Стандартный тип угломера без электронных функций выглядит как рейка с зафиксированной рамой. На стыке планок расположена ось, на который закреплён маятник. В его комплект входит пара колец, грузик, указатель, а также пластина. В дополнение к такому прибору идёт шкала с делениями, которая расположена на внутренней части выреза. Если расположить рейку по горизонтали, то указатель будет совпадать с нулевым делением шкалы.

- Теперь следует рассмотреть главный процесс измерения, для которого и был создан данный прибор. Для начала рейку угломера следует выставить перпендикулярно по отношению к коньку. После на шкале маятника будет указана нужная величина в градусном показателе.
- Способ, который основан на самостоятельном расчёте здания для изменения наклона с помощью проведения математический вычислений, не так эффективен. Чтобы измерить наклон крыши самостоятельно, для начала нужно определить длину катетов и гипотенузы. Если же говорить об измерении наклона кровли, то в этом случае прямая ската и станет гипотенузой.
- После рассчитывается длина противолежащего и прилежащего катетов. Первым катетом является расстояние, которое разделяет конёк и перекрытие, а размер второго нужно принимать в виде расстояния между серединой перекрытия и карнизным свесом на одном из скате.
- В этом случае после получения двух значений для нахождения третьего используется правило тригонометрии.

Сам алгоритм расчёта наклонности крыши можно разделить на четыре шага. Для начала необходимо учесть все природные особенности, которые будут влиять на будущую поверхность, сверяем свои строительные планы с ценой на нужные материалы в интернет-магазине, определяем тип применяемого в работе материала и продолжаем находить больше полезной информации о строительной работе и по возможности спрашиваем все интересующие вопросы у специалистов.
Если говорить о нагрузке, то лучше не выбирать минимальный показатель наклона, так как это может отрицательно повлиять на новую крышу. Если же кровля плоская, и изменить её не получится, то нужно обязательно использовать укрепительные редуты.
В общем расчёте цены не нужно забывать о массе общей конструкции дома и помнить о нагрузке от осадков — это поможет выявить не только правильный, но также и более экономичный метод для вас и вашего бюджета.
Если уклон ската доходит до 10 градусов, то лучше всего подойдёт отделка из гравия, до 20 градусов — шифер, а также профнастил. Стальные и медные листки лучше всего использовать в больших конструкциях, когда показатель верхнего румба варьируется от 50 до 60 градусов.
Величина нагрузок внешней среды
Ещё одним важным фактором в этом случае считается значение угла наклона кровли при воздействии на него внешних нагрузок, которые выпадают на конструкцию крыши.
В это случае можно заметить определённую связь. Можно заранее вычислить все линейные размеры и углы, но в итоге всё равно придётся провести деталировку. Нужно чётко определить, из какого материала будут создаваться узлы стропильной системы и детали, какова длина их сечения, шаг расположения, а также максимальная длина между двумя точками опоры, метод крепления элементов и их установка на несущие стены дома. Кроме собственного веса, на уклон большое влияние оказывает воздействие из внешней среды.
youtube.com/embed/lksTdWQWs-Y”>4.3 Наклон линии | Аналитическая геометрия
4.3 Наклон линии (EMBGD)
На диаграмме показано, что прямая образует угол \(\theta\) с положительной осью \(x\). Это называется угол наклона прямой.
Мы замечаем, что если градиент изменяется, то значение \(\theta\) также изменяется, поэтому угол наклон линии связан с ее градиентом. Мы знаем, что градиент – это отношение изменения \(y\)-направление на изменение \(x\)-направления:
Из тригонометрии мы знаем, что функция тангенса определяется как отношение:
\[\tan \theta = \frac{\text{противоположная сторона}}{\text{прилегающая сторона}}\]
А из схемы мы видим, что
\начать{выровнять*} \tan \theta &= \dfrac{\Delta y}{\Delta x} \\ \поэтому m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \текст{180}\текст{°} \end{выравнивание*}
Следовательно, градиент прямой линии равен тангенсу угла, образованного между прямой и
положительное направление оси \(х\).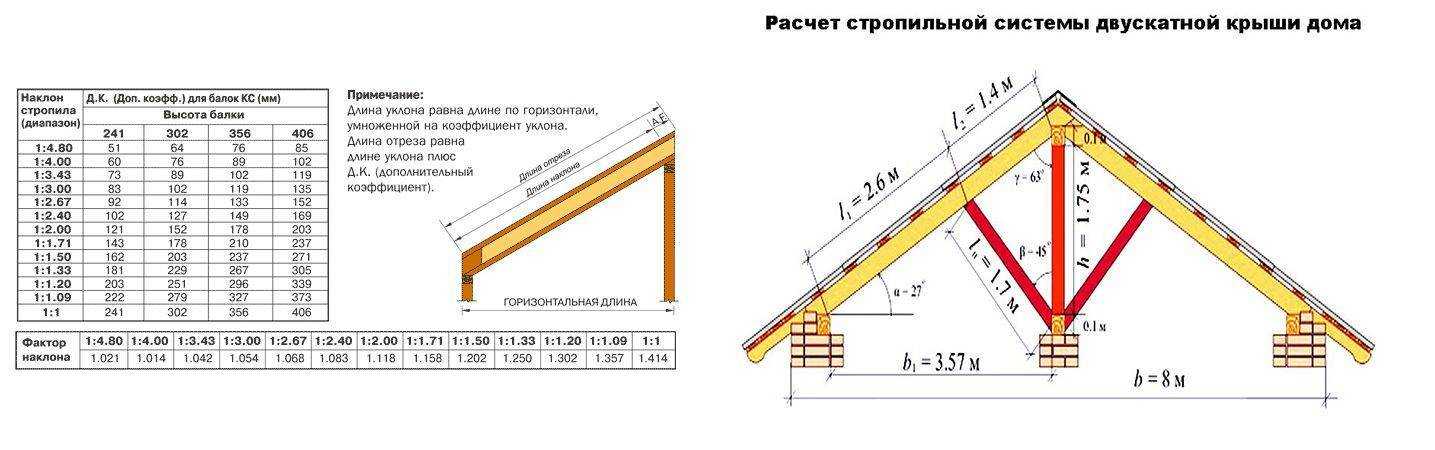
Вертикальные линии
- \(\тета = \текст{90}\текст{°}\)
- Градиент не определен, поскольку значения \(x\) не изменились (\(\Delta x = 0\)).
- Следовательно, \(\tan \theta\) также не определено (график \(\tan \theta\) имеет асимптоту в \(\theta = \текст{90}\текст{°}\)).
Горизонтальные линии
- \(\тета = \текст{0}\текст{°}\)
- Градиент равен \(\text{0}\), поскольку значения \(y\) не изменяются (\(\Delta y = 0\)).
- Следовательно, \(\tan \theta\) также равно \(\text{0}\) (график \(\tan \theta\) проходит через происхождение \((\text{0}\text{°};0))\).
Линии с отрицательным уклоном
Если прямая имеет отрицательный наклон (\(m < 0\), \(\tan \theta < 0\)), то угол, образованный
между прямой и положительным направлением оси \(х\) тупая.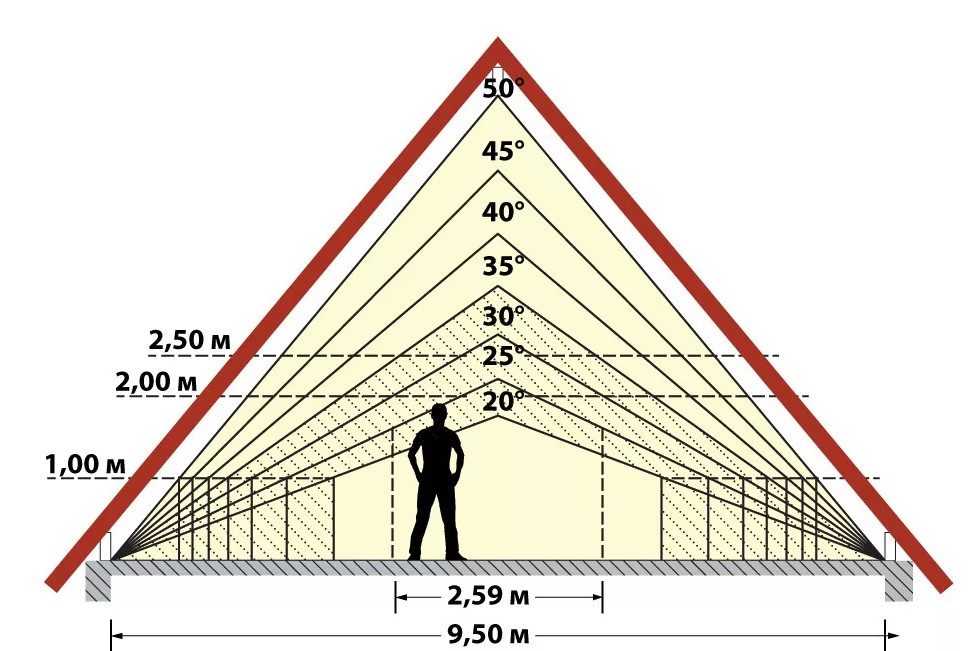
Из диаграммы CAST в тригонометрии мы знаем, что функция тангенса отрицательна во втором и четвертом квадрант. Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить \(\text{180}\text{°}\), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол в второй квадрант: 9{-1}(-\текст{0,7}) \\ &= -\текст{35,0}\текст{°} \конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой угол во втором квадранте:
\начать{выровнять*} \тета &= -\текст{35,0}\текст{°} + \текст{180}\текст{°} \\ &= \текст{145}\текст{°} \конец{выравнивание*}
И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \(\theta = \text{145}\text{°}\) дает градиент \(m = -\text{0,7}\).
Угол наклона
Учебник Упражнение 4. 5
5
\(\text{60}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{60}\text{°} \\ \поэтому m &= \text{1,7} \end{align*}
\(\text{135}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -\text{1} \end{выравнивание*}
\(\text{0}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{0}\text{°} \\ \поэтому m &= \text{0} \end{align*}
\(\text{54}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{54}\текст{°} \\ \поэтому m &= \text{1,4} \end{выравнивание*}
\(\text{90}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{90}\текст{°} \\ \поэтому m & \text{ не определено} \end{align*}
\(\text{45}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{45}\text{°} \\ \поэтому m &= \text{1} \end{выравнивание*}
\(\text{140}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{140}\text{°} \\ \поэтому m &= -\text{0,8} \end{align*}
\(\text{180}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{180}\text{°} \\ \поэтому m &= \text{0} \end{выравнивание*} 9{-1} \влево( \text{0,75} \вправо) \\ \поэтому \тета &= \text{36,8}\text{°} \end{align*}
\(2y – x = 6\)
\begin{align*} 2у – х&=6\ 2у &= х + 6 \\ y &= \frac{1}{2}x + 3 \\ \загар \тета &= м \\ &= \фракция{1}{2} \\ \theta &= \tan^{-1} \left( \text{0,5} \right) \\ \поэтому \тета &= \текст{26,6}\текст{°} \end{выравнивание*} 9{-1} \влево( \текст{1} \вправо) \\ \поэтому \тета &= \text{45}\text{°} \end{align*}
\(y=4\)
Горизонтальная линия
\(x = 3y + \frac{1}{2}\)
\begin{align*} х &= 3y + \frac{1}{2} \\ x – \frac{1}{2} &= 3y \\ \frac{1}{3}x – \frac{1}{6} &= y \\ \поэтому m &= \frac{1}{3} \\ \theta &= \tan^{-1} \left( \frac{1}{3} \right) \\ \поэтому \тета &= \text{18,4}\text{°} \end{выравнивание*} 9{-1} \влево( \текст{0,577} \вправо) \\ \поэтому \тета &= \text{30}\text{°} \конец{выравнивание*}
Рабочий пример 8: Наклон прямой линии
Определить угол наклона (с точностью до \(\text{1}\) десятичного знака) прямой линии
проходящей через точки \((2;1)\) и \((-3;-9)\). {-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
{-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусы).
Напишите окончательный ответ
Угол наклона прямой равен \(\text{63,4}\)\(\text{°}\).
temp textРабочий пример 9: Наклон прямой линии
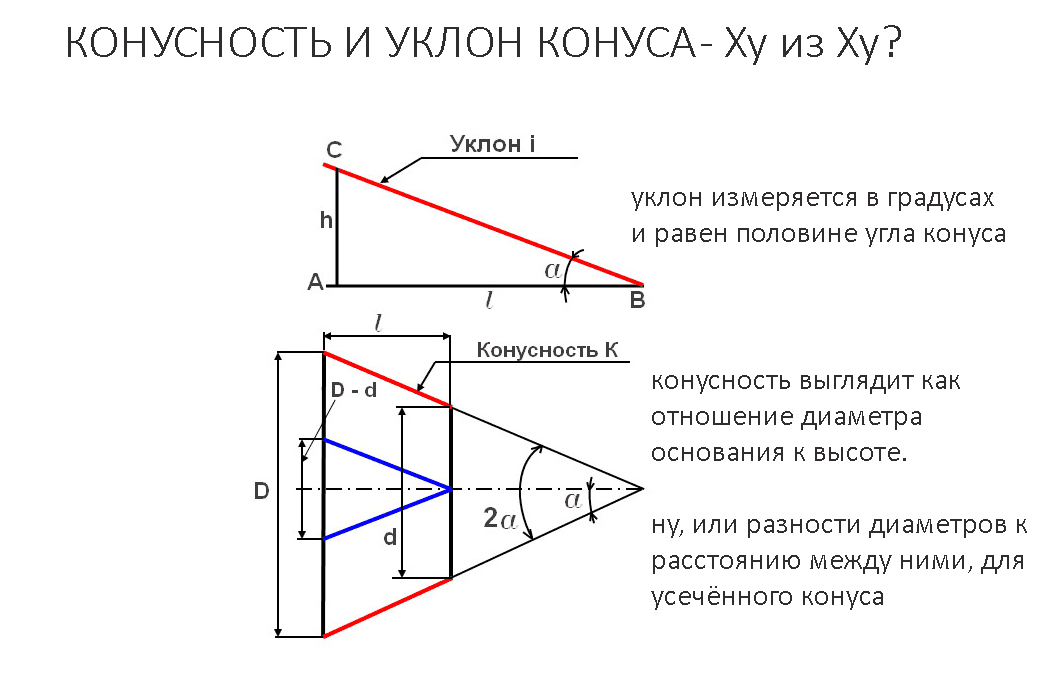
Определите уравнение прямой, проходящей через точку \((3;1)\) и с углом наклон \(\text{135}\text{°}\).
Используйте угол наклона для определения градиента линии
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -1 \конец{выравнивание*}
Запишите уравнение прямой линии в форме точки градиента. x – x_1)\]
Подставить заданную точку \((3;1)\)
\begin{выравнивание*} у – 1 & = -(х – 3) \\ у&=-х+3+1\ &= -х + 4 \конец{выравнивание*}
Напишите окончательный ответ
Уравнение прямой линии \(y = -x + 4\).
Рабочий пример 10: Наклон прямой линии
Определить острый угол (с точностью до \(\text{1}\) десятичного разряда) между прямой, проходящей через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямая \(y = – \frac{3}{2}x + 4\).
Начертить эскиз
Начертить прямую через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямую \(y = – \ дробь{3}{2}x + 4\) в подходящей системе координат. Обозначьте \(\alpha\) и \(\beta\) углы наклона две линии. Обозначьте \(\theta\) острый угол между двумя прямыми.
Обратите внимание, что \(\alpha\) и \(\theta\) — острые углы, а \(\beta\) — тупой угол.
\[\begin{массив}{rll}
\hat{B}_1 &= \text{180}\text{°} – \beta & (\angle \text{на строке}) \\
\text{and} \theta &= \alpha + \hat{B}_1 \quad & (\text{ext.} \angle \text{ of } \triangle =
\text{ сумма внутр.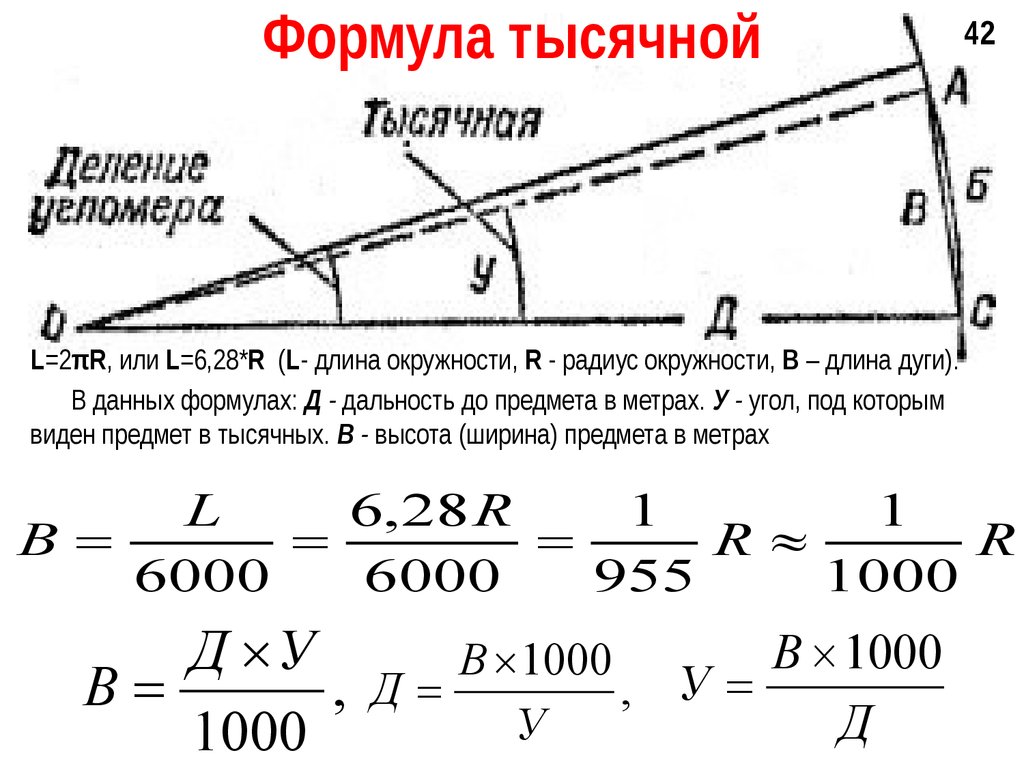 опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} – \бета) \\
&= \text{180}\text{°} + \alpha – \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} – \бета) \\
&= \text{180}\text{°} + \alpha – \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \(\beta\) равен тупой угол, лежащий во второй четверти, поэтому
\начать{выравнивать*} \beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\ &= \текст{123,7}\текст{°} \конец{выравнивание*}
Определить градиент и угол наклона линии через \(M\) и \(N\)
Определение градиента \начать{выравнивать*} m & = \frac{y_2 – y_1}{x_2 – x_1} \\ & = \dfrac{3 – \frac{7}{4}}{4-(-1)} \\ & = \dfrac{\frac{5}{4}}{5} \\ &= \фракция{1}{4} \end{align*}
Определить угол наклона \начать{выравнивать*} \загар \альфа & = м\\ & = \фракция{1}{4} \\ \поэтому \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\ &= \текст{14,0}\текст{°} \end{выравнивание*}
Напишите окончательный ответ
\begin{align*} \тета & = \текст{180}\текст{°} + \альфа – \бета\\ & = \text{180}\text{°} + \text{14,0}\text{°} – \text{123,7}\text{°} \\ & = \текст{70,3}\текст{°} \end{align*}
Острый угол между двумя прямыми равен \(\text{70,3}\)\(\text{°}\).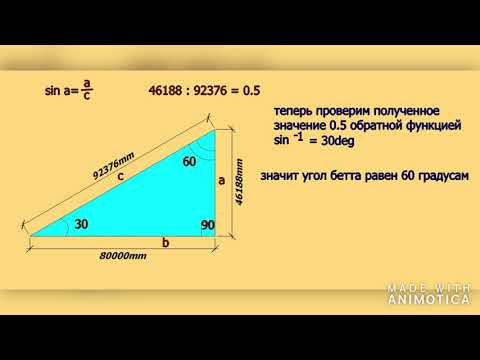 {-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} – \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} – \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
{-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} – \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} – \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
линия, проходящая через \((-1;-6)\) и \((-\frac{1}{2};-\frac{11}{2})\)
\begin{выравнивание*} m &= \frac{y_2 -y_1}{x_2 – x_1} \\ &= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\ &= \ гидроразрыва {\ гидроразрыва {1} {2}} {\ гидроразрыва {1} {2}} \\ \поэтому m &= 1 \\ \theta &= \tan^{-1} \left( 1 \right) \\ \поэтому \тета &= \text{45}\text{°} \end{выравнивание*} 9{-1} \влево(-\frac{1}{3} \вправо) \\ \поэтому \тета &= -\текст{18,4}\текст{°} \\ \поэтому \тета &= \text{180}\text{°} – \text{18,4}\text{°} \\ \поэтому \тета &= \текст{161,6}\текст{°} \end{align*}
Градиент undefined
Определить острый угол между линией, проходящей через точки \(A(-2;\frac{1}{5})\)
и \(B(0;1)\) и прямой, проходящей через точки \(C(1;0)\) и \(D(-2;6)\). {-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} – \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} – \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} –
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
{-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} – \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} – \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} –
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
Определить угол между прямой \(y + x = 3\) и прямой \(x = y + \frac{1}{2}\).
Пусть угол наклона линии \(y + x = 3\) равен \(\alpha\), а угол наклона наклон линии \(x = y + \frac{1}{2}\) равен \(\beta\). Пусть угол между двумя строки будут \(\тета\):
\начать{выравнивать*}
у &= – х + 3 \\
\поэтому m &= – 1 \\
\alpha &= \tan^{-1} \left(-1\right) \\
\поэтому \alpha &= -\text{45}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} – \text{45}\text{°} \\
\поэтому \alpha &= \text{135}\text{°} \\
х &= у + \ гидроразрыва {1} {2} \\
х – \фракция{1}{2} &= у \\
\поэтому m &= 1 \\
\beta &= \tan^{-1} \left(1 \right) \\
\поэтому \бета &= \text{45}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} – \alpha) \quad (\text{ext. {-1} \left( 2 \right) \\
\поэтому \бета &= \text{63,4}\text{°} \\
m &= \frac{y_2 -y_1}{x_2 – x_1} \\
&= \frac{2 – \frac{7}{3}}{0 + 1} \\
&= \frac{-\frac{1}{3}}{1} \\
\поэтому m &= -\frac{1}{3} \\
\поэтому \alpha &= -\text{18,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} – \text{18,4}\text{°} \\
\поэтому \alpha &= \text{161,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} – \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{63,4}\text{°} + (\text{180}\text{°} –
\текст{161,6}\текст{°} ) \\
&= \текст{81,8}\текст{°}
\конец{выравнивание*}
{-1} \left( 2 \right) \\
\поэтому \бета &= \text{63,4}\text{°} \\
m &= \frac{y_2 -y_1}{x_2 – x_1} \\
&= \frac{2 – \frac{7}{3}}{0 + 1} \\
&= \frac{-\frac{1}{3}}{1} \\
\поэтому m &= -\frac{1}{3} \\
\поэтому \alpha &= -\text{18,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} – \text{18,4}\text{°} \\
\поэтому \alpha &= \text{161,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} – \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{63,4}\text{°} + (\text{180}\text{°} –
\текст{161,6}\текст{°} ) \\
&= \текст{81,8}\текст{°}
\конец{выравнивание*}
Что мне делать с вдавленными углами?
Purplemath
Что такое угол возвышения/наклона?
Угол подъема/наклона — это угол, который идет над горизонталью с любой точки обзора. Например, предположим, что вы стоите на тротуаре и смотрите на верхнюю часть дымохода дома через улицу.
Например, предположим, что вы стоите на тротуаре и смотрите на верхнюю часть дымохода дома через улицу.
Содержание продолжается ниже
MathHelp.com
Углы возвышения и депрессии
Угол, который отражает вашу линию обзора над улицей между вами и этим домом, будет углом наклона / возвышения.
Что такое угол депрессии/склонения?
Угол склонения/депрессии – это угол, который идет ниже горизонтали с любой точки обзора. Например, предположим, что вы стоите на балконе своей квартиры на третьем этаже и задаетесь вопросом, как далеко находится тротуар. Угол между горизонталью (когда вы смотрите через парковку на свою подругу на ее террасе третьего этажа в соседнем здании) и тротуаром будет углом депрессии / склонения.
Всякий раз, когда у вас есть один из этих углов, вы должны немедленно начать представлять себе, как прямоугольный треугольник впишется в описание.
- Проезжая по прямому ровному участку Аризонского шоссе, вы замечаете особенно высокий кактус сагуаро («сух-ВАХР-о») прямо рядом с указателем мили.
 Следя за одометром, вы останавливаетесь ровно на две десятых мили по дороге. Достав теодолит вашего сына из багажника, вы измеряете угол подъема от вашего положения до вершины сагуаро, равный 2,4°. С точностью до фута, какой высоты кактус?
Следя за одометром, вы останавливаетесь ровно на две десятых мили по дороге. Достав теодолит вашего сына из багажника, вы измеряете угол подъема от вашего положения до вершины сагуаро, равный 2,4°. С точностью до фута, какой высоты кактус?
Две десятых мили составляют 0,2 × 5280 футов = 1056 футов, так что это мое горизонтальное расстояние. Мне нужно найти высоту х кактуса. Итак, я рисую прямоугольный треугольник и маркирую все, что знаю:
Масштаб не важен; Я не утруждаю себя точно рисовать углы или расстояния. Я просто использую рисунок в качестве заполнителя, то есть как способ отслеживать информацию; конкретный размер значения не имеет.
Что такое актуально то, что у меня есть «противоположное» и «прилегающее» и мера угла. Это означает, что я могу составить и решить уравнение, используя отношение тангенсов:
h / 1056 = тангенс (2,4°)
h = 1056 × tan(2,4°) = 44,25951345. ..
..
Проверяя условие упражнения, я вспоминаю, что моя единица измерения — футы и что я должен округлить. Затем с точностью до фута сагуаро составляет:
44 фута в высоту
- Вы запускали воздушного змея с вершины обрыва, но каким-то образом ухитрились сбросить его в озеро внизу. Вы знаете, что выдали 325 футов веревки. Сюрвейер во время обеденного перерыва подходит и говорит вам, что угол склонения от вашей позиции к кайту составляет 15°. Насколько высок обрыв, на котором стоите вы и геодезист? (Округлите ответ до ближайшего целого числа.)
Сначала я рисую свой треугольник:
Горизонтальная линия сверху — это линия, от которой отмеряется угол наклона. Но по природе параллельных линий такой же угол находится и в нижнем треугольнике. Я могу легче увидеть коэффициенты срабатывания в нижнем треугольнике, а высота немного более очевидна. Поэтому я буду использовать эту часть рисунка.
У меня есть противоположная сторона, гипотенуза и угол, поэтому я буду использовать отношение синусов, чтобы найти высоту.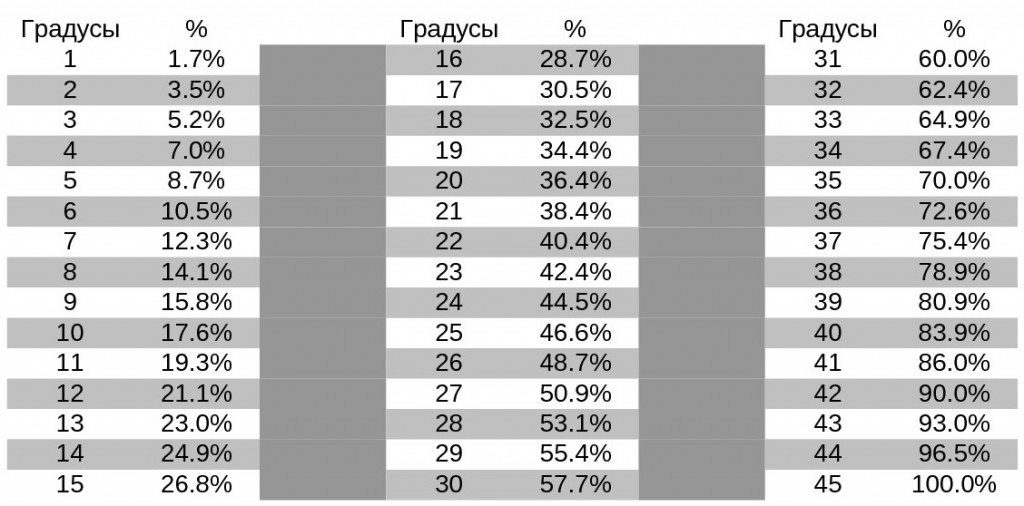
h /325 = sin(15°)
h = 325×sin(15°) = 84,11618966…
Проверяя оператор упражнения, я вспомнил, что мои единицы измерения – футы и что я Должен округлить. Затем обрыв стоит над озером на высоте:
около 84 футов
- Маяк стоит на холме на высоте 100 м над уровнем моря, как показано на рисунке ниже. Если ∠ACD составляет 60°, а ∠BCD равно 30°, найдите высоту маяка с точностью до целого метра.
Первое, что я замечаю, это то, что даже без округления мой ответ может быть только приблизительным, потому что маяки немного сужаются по мере подъема. Таким образом, внешняя точка основания маяка не находится прямо под внешней точкой вершины.
(Но это математика, а не реальная жизнь, поэтому можно игнорировать это и просто работать с картинкой, которую мне дали.)
Второе, что я замечаю, это то, что мне придется работать над этим упражнением. шагами.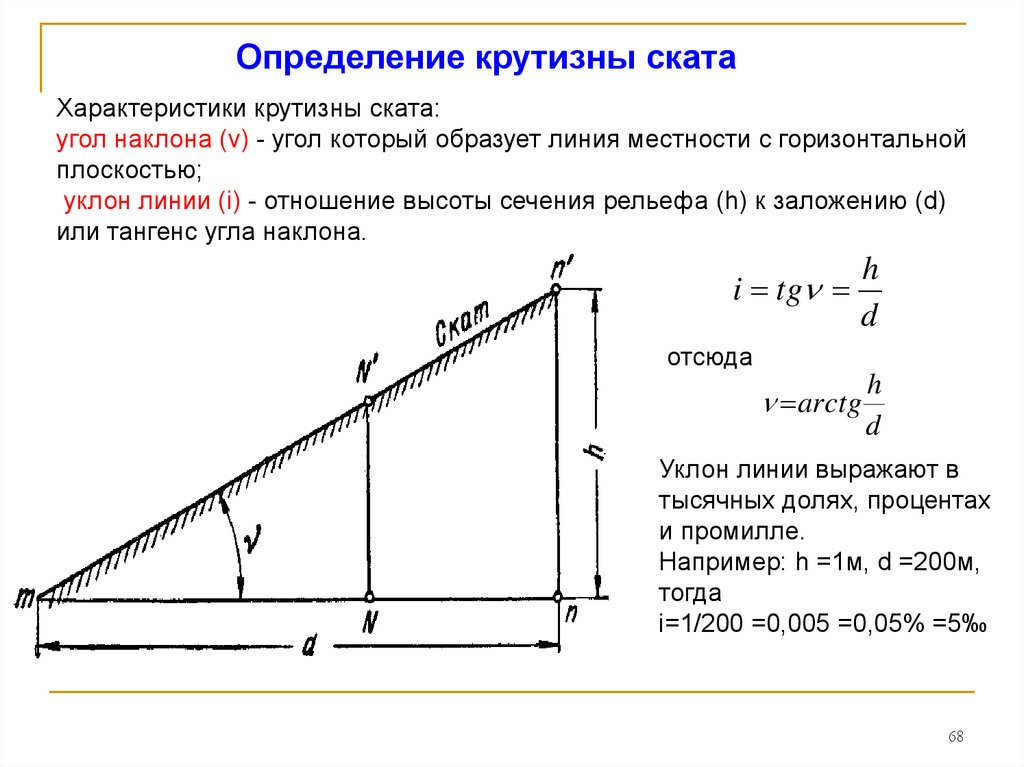 Я не могу найти высоту башни AB, пока не получу длину основания CD. Думайте о D как о перемещенном вправо, чтобы встретить продолжение вниз линии высоты AB, образуя прямоугольный треугольник, как показано на моем отредактированном рисунке ниже:
Я не могу найти высоту башни AB, пока не получу длину основания CD. Думайте о D как о перемещенном вправо, чтобы встретить продолжение вниз линии высоты AB, образуя прямоугольный треугольник, как показано на моем отредактированном рисунке ниже:
В моем первом вычислении длины стороны CD я использую высоту холма как длину противоположной стороны треугольника BCD.
100/|CD| = тангенс (30°)
100/тангенс(30°) = |CD| = 173.2050808…
Чтобы свести к минимуму ошибку округления, я буду использовать все цифры из своего калькулятора в своих вычислениях и постараюсь выполнять вычисления в своем калькуляторе полностью.
Теперь, когда у меня есть длина основания, я могу найти общую высоту, используя угол, измеряющий высоту от уровня моря до вершины башни.
h /173,2050808 = tan(60°)
h = 173,2050808×tan(60°) = 300
Отлично! Сохранив все цифры и проведя вычисления в своем калькуляторе, я получил точный ответ.

 А это ведёт к увеличению стоимости работы.
А это ведёт к увеличению стоимости работы.

 Следя за одометром, вы останавливаетесь ровно на две десятых мили по дороге. Достав теодолит вашего сына из багажника, вы измеряете угол подъема от вашего положения до вершины сагуаро, равный 2,4°. С точностью до фута, какой высоты кактус?
Следя за одометром, вы останавливаетесь ровно на две десятых мили по дороге. Достав теодолит вашего сына из багажника, вы измеряете угол подъема от вашего положения до вершины сагуаро, равный 2,4°. С точностью до фута, какой высоты кактус?