Угол. Обозначение углов / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Угол. Обозначение углов
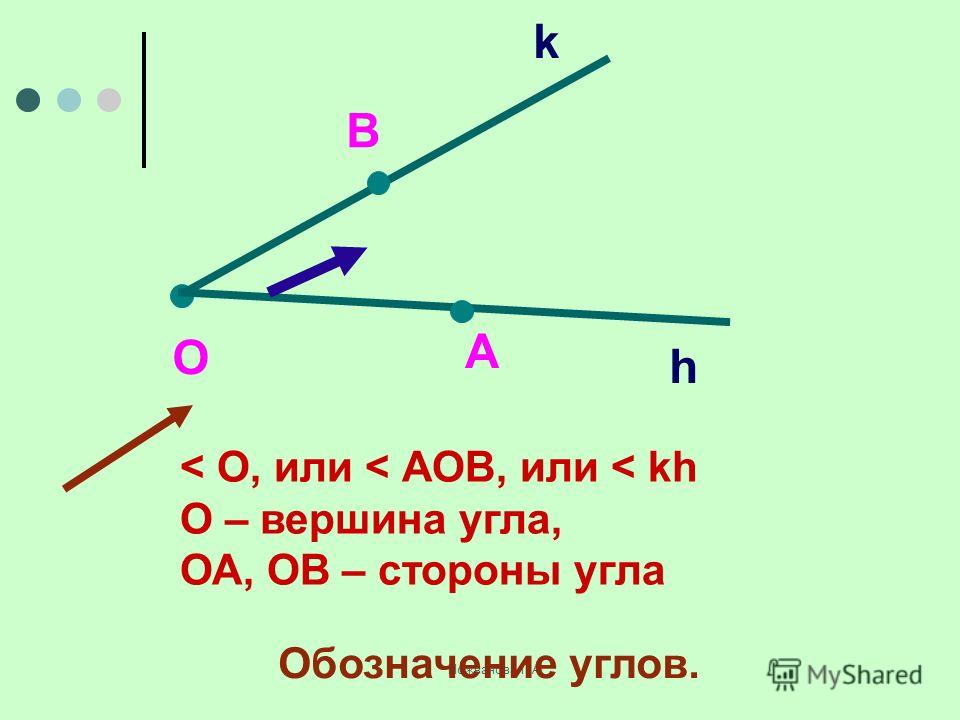
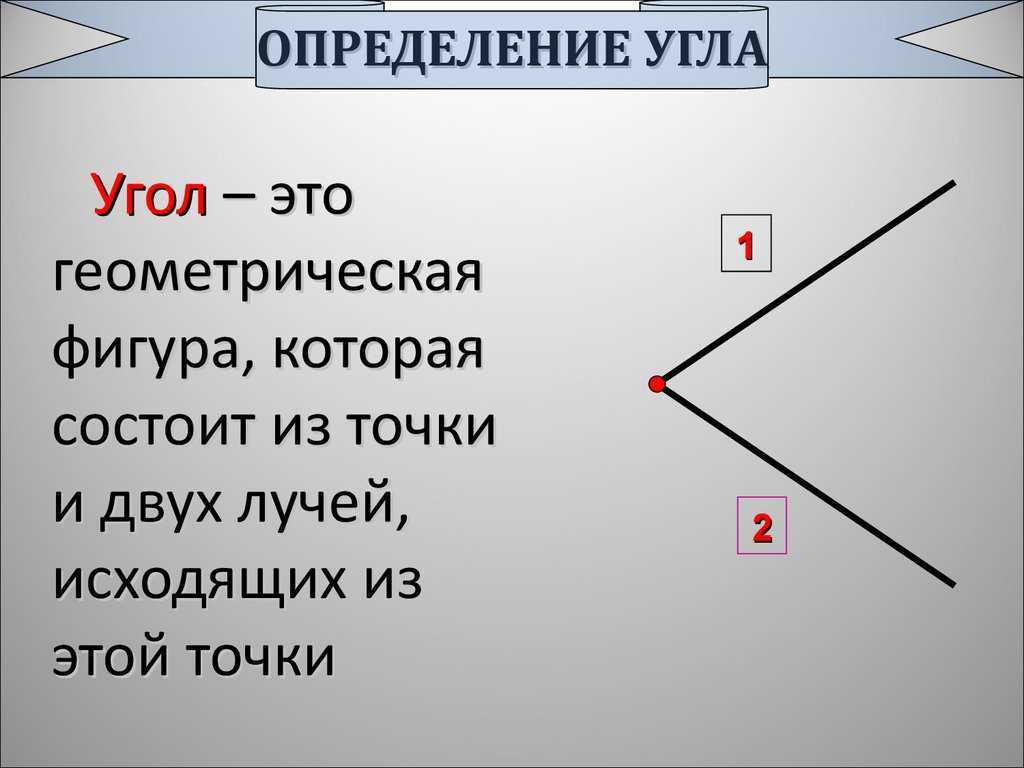
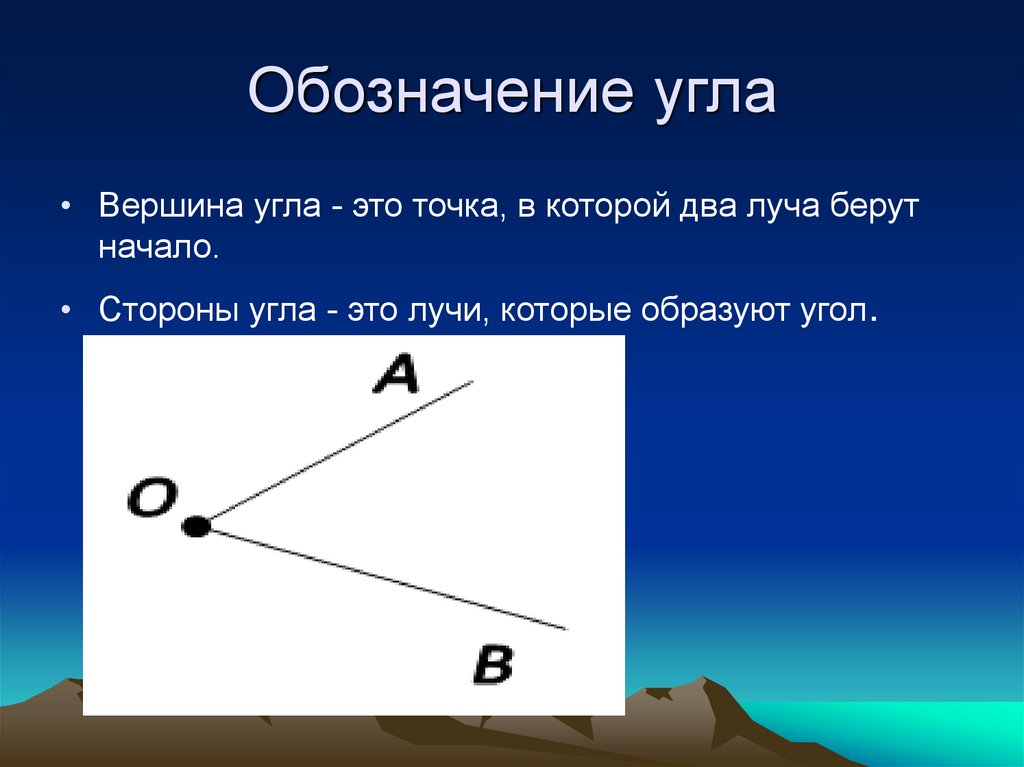
Угол – геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
На рис. 1 лучи АВ и АС – стороны угла, точка А – вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т.к. точки В и С не являются вершинами данного угла).
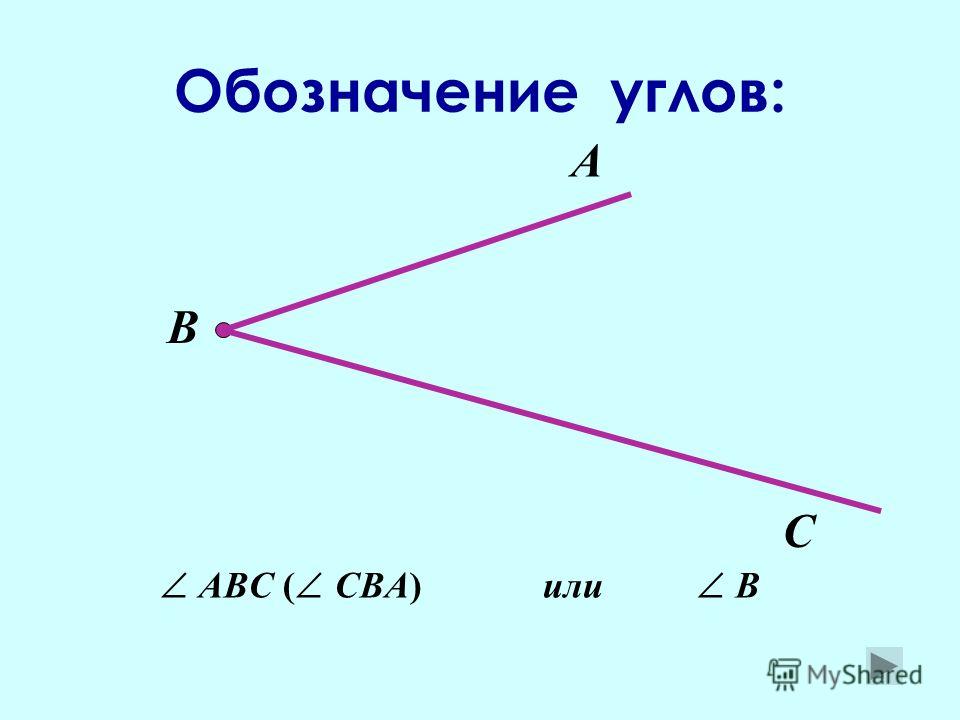
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой.
Биссектриса – луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ – биссектриса угла НОD.
Прямой угол – угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На рис. 6 АОВ и ВОС – прямые, АОС – развернутый.
Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.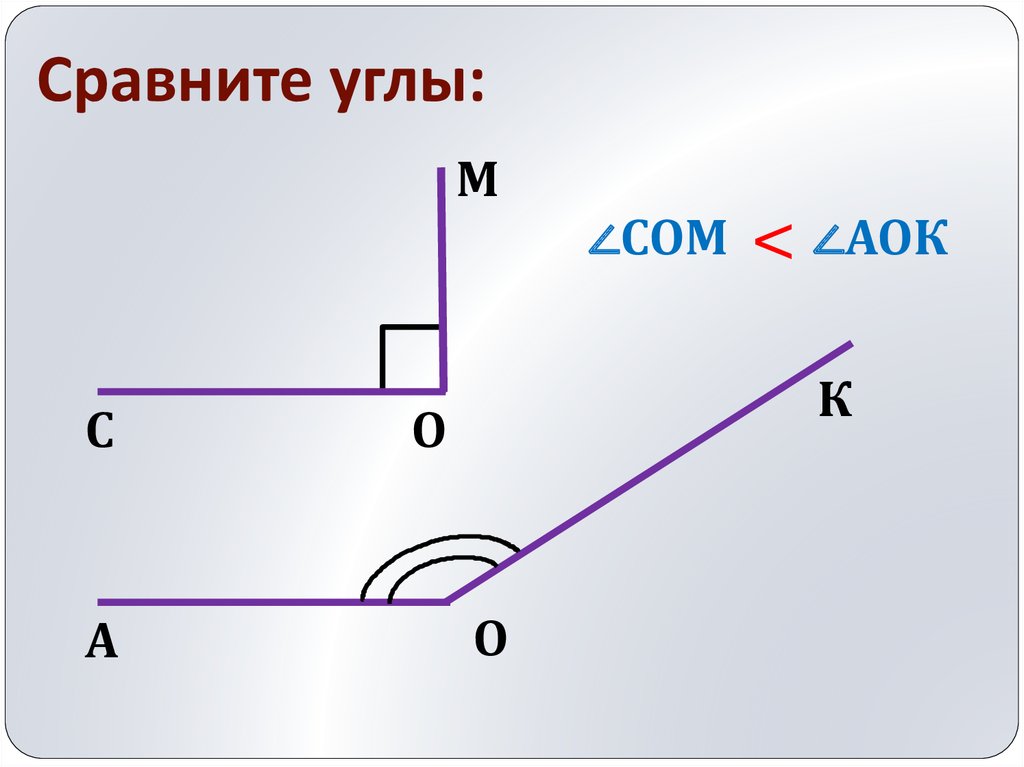
Острый угол – угол, который меньше прямого угла. На рис. 7 МОN – острый.
Тупой угол – угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК – тупой.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1622, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1639, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1641, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1775, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 298, Мерзляк, Полонский, Якир, Учебник
Номер 315, Мерзляк, Полонский, Якир, Учебник
Номер 1029, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 219, Мерзляк, Полонский, Якир, Учебник
Номер 391, Мерзляк, Полонский, Якир, Учебник
Номер 495, Мерзляк, Полонский, Якир, Учебник
Номер 714, Мерзляк, Полонский, Якир, Учебник
Номер 1226, Мерзляк, Полонский, Якир, Учебник
Номер 1234, Мерзляк, Полонский, Якир, Учебник
Номер 1236, Мерзляк, Полонский, Якир, Учебник
Задание 247, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 773, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1571, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759, Мерзляк, Полонский, Якир, Учебник
Задание 81, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
как обозначить и измерить углы, правила
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений.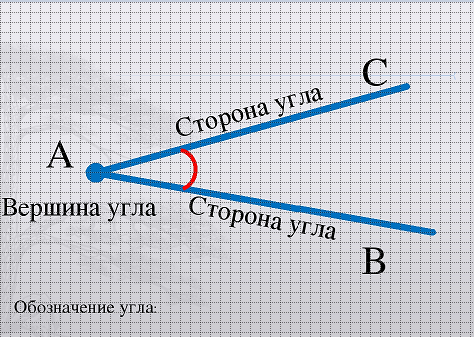 Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла
– точка, из которой выходят лучи (О).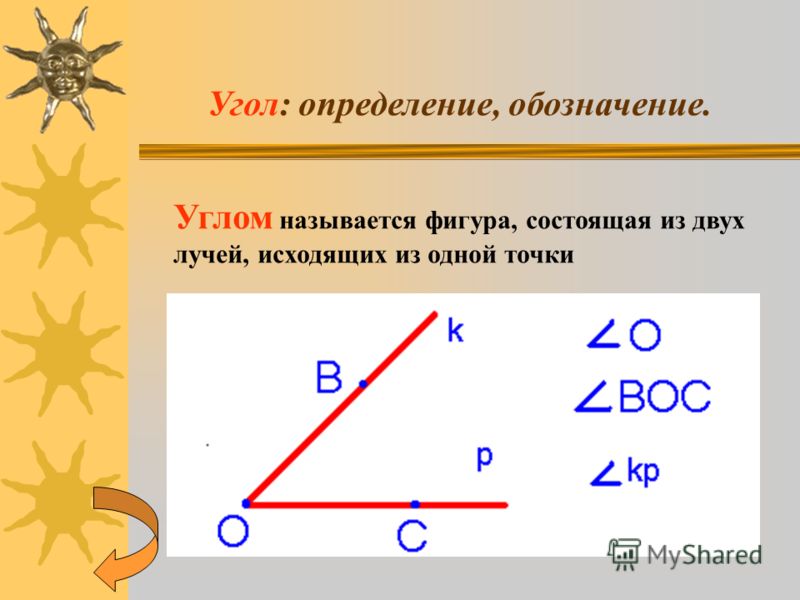
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
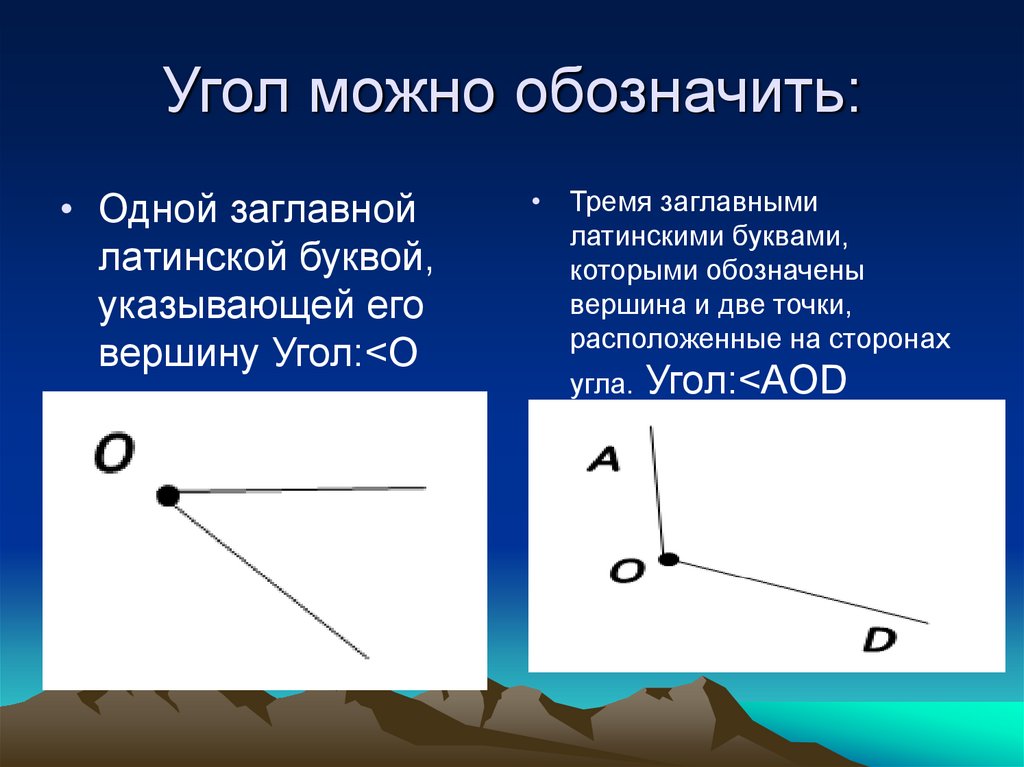
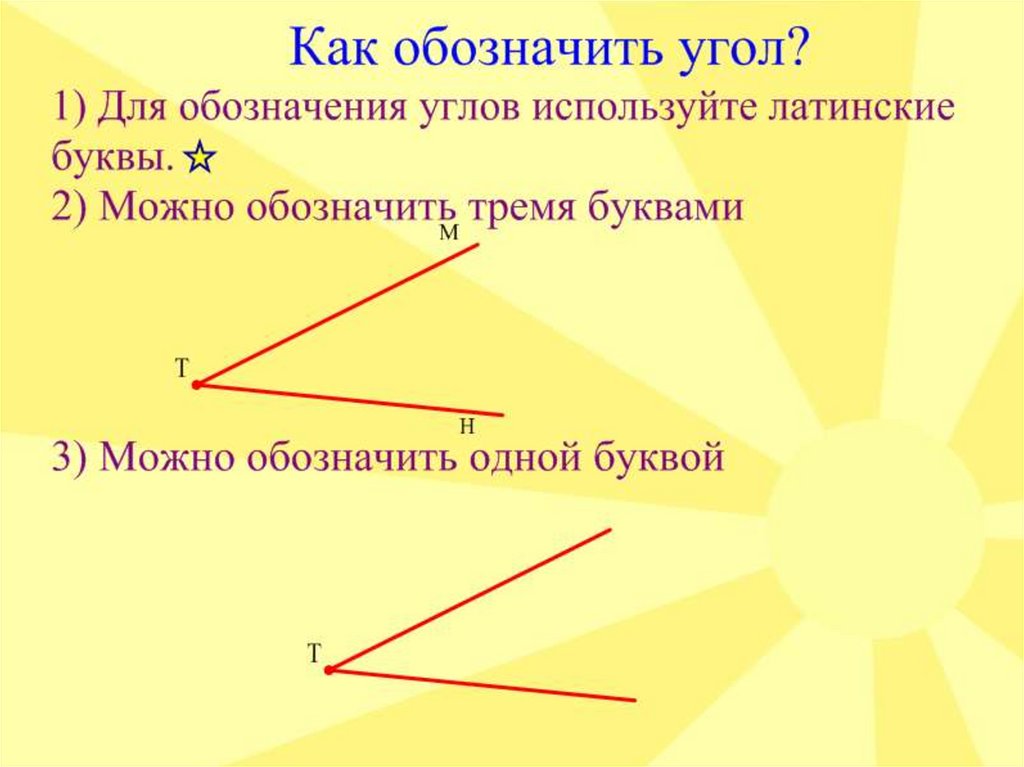
Как обозначить углы?
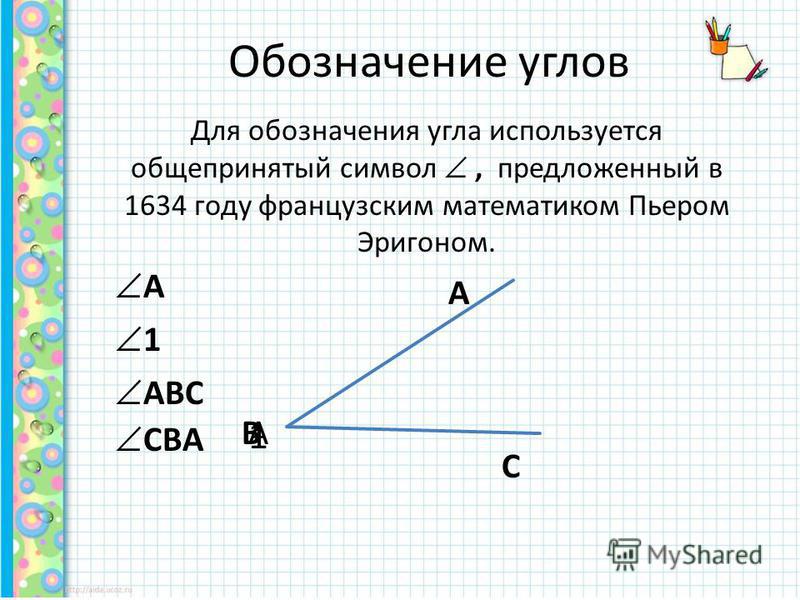
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.
д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. - Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
Типы углов
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. - Развернутый угол — угол, образованный прямой линией, называется прямым углом.
 Это
Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
Смежные углы
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми.
 {\circ}\]
{\circ}\]
Разница между смежными и вертикальными угламиСмежные углы Вертикальные углы Два угла с общей стороной и вершиной называются смежными. Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. Имеют общую сторону и общую вершину. Имеют общую вершину, но не имеют общую сторону Смежные углы не всегда равны по величине Вертикально противоположные углы равны по величине Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
\[\angle A_{1} O_{1} B_{1}\] и \[\angle A_{2} O_{2} B_{2}\] полностью совмещаются при наложении следовательно: \[\angle A_{1} O_{1} B_{1}=\angle A_{2} O_{2} B_{2}\]
\[\angle A_{1} O_{1} B_{1}\] и \[ \angle A_{2} O_{2} B_{2}\] не совмещаются при наложении: \[\angle A_{1} O_{1} B_{1} \neq \angle A_{2} O_{2} B_{2}\]
Причем: \[\angle A_{1} O_{1} B_{1}<\angle A_{2} O_{2} B_{2}\]
При этом развернутые углы всегда являются равными.

Совмещение углов \[\angle A B C\] и \[\angle M N K\] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые.
 Линии могут быть как параллельными, так и непараллельными.
Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет \[\left(\frac{1}{360}\right)\] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
Радианная мера
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица.
 Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:Вот еще несколько примеров углов: -1 радиан, радиан, \[1 \frac{1}{2}\] радиан, \[-1 \frac{1}{2}\] радиан.
Длина окружности = \[2 \pi r \ldots\] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна \[2 \pi\]. Следовательно, один полный оборот начальной стороны образует в центре угол \[2 \pi\] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = \[\frac{l}{r}\] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
\[\theta=\frac{l}{r}\]
\[l=r \theta\]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- \[2 \pi\] радиан — в радианах
Следовательно, \[2 \pi\] радиан = 360° ⇒ \[\pi\] радиан = 180°.
 {\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
{\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как измерить угол
Для измерения углов используется транспортир:
ТранспортирПопробуем измерить угол \[\angle A O B\]
Шаги для измерения угла \[\angle \mathrm{AOB}\].
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
Далее попробуем измерить этот ∠AOC:
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC.
 Таким образом, ∠ AOC = 143°
Таким образом, ∠ AOC = 143°Как построить углы
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.
Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
Обозначение углов на чертеже
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.

На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.
Угол – Определение и типы с примерами
После того, как вы узнали о точках, прямых, отрезках и плоскости, следующее, что нужно знать, это то, что происходит, когда две прямые пересекаются в одной точке. То есть когда образуется угол.
Углы — одно из основных понятий геометрии. Мы не можем думать об определении какой-либо формы, будь то треугольники, четырехугольники или многоугольники, без их углов. Таким образом, угол образует часть каждой геометрической формы.

Что такое угол
Математически угол определяется как фигура, которая образуется, когда два луча встречаются в одной точке. Обозначается символом ∠. Угол обычно измеряется в градусах, обозначаемых знаком «°». Термин «угол» происходит от латинского слова «angulus», что означает «угол».
УголГрадус — это мера поворота. Полный оборот вокруг точки дает нам полный круг, равный 360°, половинный оборот дает нам полукруг, равный 180°, а четверть оборота дает нам прямой угол, равный 90°.
Части угла
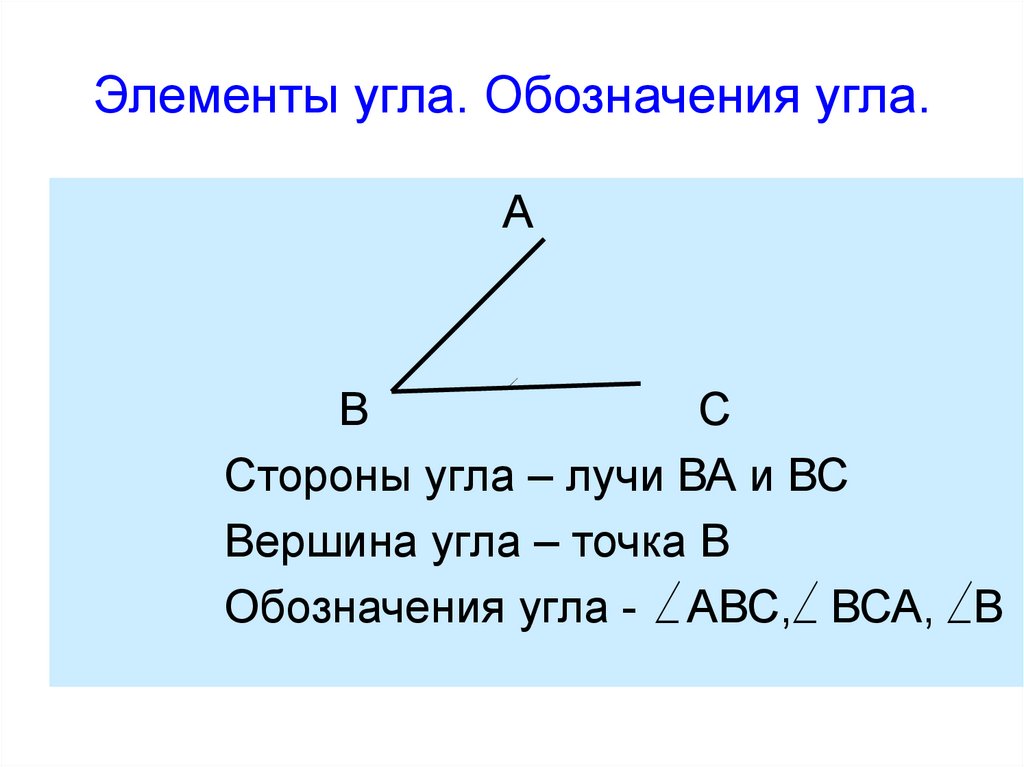
Части угла- Плечи : Две прямые или изогнутые стороны, соединяющиеся в угол, называются плечами. Здесь OX и OY — стороны угла ∠XOY.
- Вершина : Общая конечная точка, где два луча встречаются, образуя угол. Здесь точка «О» является вершиной.
Угол может быть назван двумя способами:
Метод – 1 : Символ угла, за которым следуют три точки, определяющие угол.
 Средняя буква – вершина. Таким образом, приведенную выше цифру можно записать как ∠XOY или ∠YOX.
Средняя буква – вершина. Таким образом, приведенную выше цифру можно записать как ∠XOY или ∠YOX.Метод – 2 : Просто запишите вершину. Пишется как ∠O.
Иногда греческие буквы, такие как α, β, γ, θ и φ, или строчные латинские буквы, такие как a, b, c, x, y и z, также используются для обозначения угла или его размера.
Как найти меру угла
Величина угла измеряется с помощью транспортира, который обычно имеет полукруглую форму и прозрачен.
Измерение углов с помощью транспортираТипы углов
Все углы обычно классифицируются в зависимости от их величины или степени вращения на шесть основных типов:
Типы углов- Острый угол : Угол, измеренный меньше 90° называется острым углом. Другими словами, он лежит в пределах от 0° до 9°.0°.
- Прямой угол : Угол, равный ровно 90°, называется прямым углом. Он образуется, когда две стороны угла перпендикулярны друг другу.
 Знак прямого угла также можно показать с помощью четверти круга вместе со стандартным знаком, как показано на рисунке.
Знак прямого угла также можно показать с помощью четверти круга вместе со стандартным знаком, как показано на рисунке. - Тупой угол : Тупой угол называется угол, величина которого больше 90° и меньше 180°.
- Прямой угол : Угол, который составляет ровно 180°, называется прямым углом. Он похож на прямую линию, отсюда и название прямого угла.
- Угол рефлекса : Угол, величина которого больше 180° и меньше 360°, называется углом рефлекса.
- Полный угол : Угол, градусная мера которого равна 360°, называется полным углом. Он образован одним полным оборотом одного из его рычагов.
Другие типы углов
Углы также иногда классифицируют по их положению, направлению вращения, сумме их пар или их поперечной на следующие типы:
- Interior Angles
- Exterior Angles
- Positive Angles
- Negative Angles
- Complementary Angles
- Supplementary Angles
- Vertically Opposite Angles
- Adjacent Angles
- Alternate Interior Angles
- Alternate Exterior Angles
- Corresponding Angles
- Последовательные внутренние углы
Примеры из реальной жизни
В нашей повседневной жизни мы видим углы почти повсюду вокруг нас.
 Некоторые из примеров приведены ниже:
Некоторые из примеров приведены ниже:- Углы, образованные стрелками часов.
- Алфавиты A, K, M, N, V, W, X, Y и Z содержат острые углы, а E, F, H, L и T — прямые углы.
- Предметы повседневного использования, такие как вешалки для одежды, ножницы, края столов, лопасти вентилятора, велосипедные спицы и колеса, имеют углы.
- Учебные принадлежности, такие как линейка, открытый циркуль и квадраты, содержат углы.
- Углы используются в навигации самолетов и кораблей.
- Инженеры и архитекторы используют углы для проектирования дорог, зданий и спортивных комплексов.
- Художники используют свои знания ракурсов для создания набросков и картин.
- Подробнее ресурсы
- Острый угол
- ПРАВИЛЬНЫЙ КОНГ
- Тупой угол
- Прямой угол
- Угол рефлекса
- Полный угол
- СООБЩЕНИЯ И СПАЗВЛЕНИЕ.0018
- Внутренние и внешние углы
- Положительные и отрицательные углы
- Альтернативные внутренние углы
- Альтернативные углы.
 Угол
Угол - Угол 45 градусов
Типы углов, определение, свойства, примеры
Углы образуются при пересечении двух прямых в одной точке. Мера «расстояния» между этими двумя лучами называется «углом». Обозначается символом ∠. Углы обычно измеряются в градусах и радианах, что является мерой округлости или вращения. Углы являются частью нашей повседневной жизни. Инженеры и архитекторы используют углы для проектирования дорог, зданий и спортивных сооружений.
1. Что такое углы? 2. Типы углов и их свойства 3. Углы на основе поворота 4. Как измерить угол? 5. Как построить углы? 6. Часто задаваемые вопросы об углах Что такое углы?
В геометрии угол образуется при соединении двух лучей в их концах.
 Эти лучи называются сторонами или плечами угла. Давайте прочитаем о различных частях угла.
Эти лучи называются сторонами или плечами угла. Давайте прочитаем о различных частях угла.Части угла
С углом связаны две основные части: стороны и вершина.
Плечи угла
Два луча, соединяющиеся в одной точке и образующие угол, называются плечами угла . Обратите внимание на приведенный ниже рисунок, на котором показано, что ОА и ОВ являются сторонами угла АОВ.
Вершина угла
Вершина является общей конечной точкой, общей для двух лучей. Обратите внимание на рисунок, на котором вершина O отмечена как точка соединения двух плеч.
Мера угла
Угол измеряется в градусах. Один полный оборот вокруг точки образует полный угол в 360°.
Углы лучше всего измерять с помощью транспортира. Транспортир представляет собой измерительный инструмент, имеющий форму полукруга. Это полупрозрачный инструмент, который помогает нам измерять углы в градусах.
 Он имеет градусы, отмеченные по часовой стрелке от 0° до 180° на внешней шкале и против часовой стрелки от 0° до 180° на внутренней шкале.
Он имеет градусы, отмеченные по часовой стрелке от 0° до 180° на внешней шкале и против часовой стрелки от 0° до 180° на внутренней шкале.Типы углов и их свойства
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла. Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
Острый угол
Острый угол — это угол, градусная мера которого больше 0° и меньше 90°.
Прямой угол
Когда угол равен 90°, он называется прямым углом. Прямой угол легко заметить, так как он образует форму буквы L.
Тупой угол
Когда измерение угла меньше 180°, но больше 90°, это тупой угол.
Прямой угол
Угол, образованный прямой линией, называется прямым углом. Другими словами, прямой угол — это прямая линия, а угол, образованный между двумя лучами, равен 180°. Под прямым углом два луча противоположны друг другу. Два прямых угла составляют прямой угол.
 Поскольку мера прямого угла равна 180°, он составляет половину полного оборота окружности.
Поскольку мера прямого угла равна 180°, он составляет половину полного оборота окружности.Угол рефлекса
Угол рефлекса — это угол, величина которого больше 180°, но меньше 360°.
Полный угол
Когда измерение угла равно 360°, это полный угол.
Угол, основанный на вращении
В зависимости от направления измерения или направления вращения углы бывают двух типов:
- Положительные углы
- Отрицательные углы
Положительные углы
Угол, измеренный в направлении против часовой стрелки (против часовой стрелки), является положительным углом. Другими словами, положительные углы — это те углы, которые повернуты от основания в направлении против часовой стрелки.Отрицательные углы
Отрицательные углы — это те углы, которые измеряются по часовой стрелке от основания. Другими словами, отрицательные углы — это те углы, которые представляют собой углы, повернутые от основания по часовой стрелке.
Как измерить угол?
Мы используем транспортиры для измерения углов. Обратите внимание на приведенный ниже рисунок, на котором показано ∠AOB. Давайте попробуем и посмотрим, сможем ли мы выяснить, к какому типу относится угол ∠AOB. Разве это не похоже на острый угол? Это означает, что его мера больше 0° и меньше 90°. Давайте научимся измерять этот угол с помощью транспортира.
Как измерить острый угол?
Попробуем измерить заданную ∠AOB.
- Шаг 1: Совместите транспортир с лучом OB, как показано ниже. Начните считывать внутреннюю шкалу с отметки 0 ° в правом нижнем углу транспортира.
- Шаг 2: Число на транспортире, которое совпадает со вторым лучом , является мерой угла. Измерьте угол, используя внутреннюю шкалу транспортира. Таким образом, ∠AOB = 37°
Как измерить тупой угол?
Теперь попробуем измерить заданный ∠AOC.

- Шаг 1: Измерьте угол по внешней шкале транспортира от отметки 0° в нижнем левом углу .
- Шаг 2: Число на внешней шкале транспортира, совпадающее с OA, является мерой ∠AOC. Таким образом, ∠AOC = 143°
Как построить углы?
Транспортиром строим углы. Начертим угол 50°.
- Шаг 1: Сначала нарисуйте луч OB и совместите транспортир с OB , как показано.
- Шаг 2: Используя внутреннюю шкалу транспортира, отметьте точку A над отметкой на транспортире, которая соответствует 50°.
- Шаг 3: Снимите транспортир и проведите луч, начинающийся в точке O и проходящий через эту точку A. Таким образом, ∠AOB — искомый угол, то есть ∠AOB = 50°.
Примечание.
 Если луч идет в другом направлении, мы измеряем угол по внешней шкале от отметки 0° внизу слева.
Если луч идет в другом направлении, мы измеряем угол по внешней шкале от отметки 0° внизу слева. На приведенном ниже рисунке показано, как нарисовать угол 50°, когда луч направлен в другую сторону.
После размещения транспортира на OB мы используем внешнюю шкалу и отмечаем 50°, как показано. Затем мы отмечаем эту точку как A и соединяем ее с точкой O. Это образует угол AOB = 50°
Важные замечания по углам
- 0°< Острый угол < 90°
- 90°< Тупой угол < 180°
- 180° < угол отражения < 360°
- Прямой угол равен 90°
- Прямой угол равен 180°.
☛ Связанные статьи
- Пары уголков
- Секущие и смежные углы
- Внутренние уголки
Углы Примеры
Пример 1: Обратите внимание на размер углов и определите тип углов для каждой фигуры.
Решение:
а) Заданный угол равен 40°.
 Это острый угол, потому что его градусная мера меньше 90°.
Это острый угол, потому что его градусная мера меньше 90°.
б) данный угол равен 117°. Это тупой угол, потому что его градусная мера больше 90°, но меньше 180°.
в) данный угол равен 121°. Это тупой угол, потому что его градусная мера больше 90°, но менее 180°.
г) данный угол равен 185°. Это рефлекторный угол, потому что его величина больше 180°, но меньше 360°.Пример 2:
Классифицируйте следующие углы на острые, тупые, прямые и отраженные.
а) 24°
б) 150°
в) 90°
г) 270°Решение:
(а) 24° лежит между 0° и 90°, значит угол острый.
(b) 154° лежит между 90° и 180°, поэтому это тупой угол.
(c) 90° известен как прямой угол.
(d) 270° находится между 180° и 360°, поэтому это рефлекторный угол.Пример 3: Запишите верно или неверно следующие утверждения:
a.) 180° < угол отражения < 360°
b.
 ) 0°< тупой угол < 90°
) 0°< тупой угол < 90° 2 9 c. ) Два луча, соединяющиеся в одной точке и образующие угол, называются сторонами угла.
Решение:
a.) Верно, 180° < угол отражения < 360°
b.) Неверно, 0°< острый угол < 90°
c.) Верно, два луча, которые соединяются в общие точки, образующие угол, называются плечами угла.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об углах
Что такое угол в математике?
Углы образуются при пересечении двух лучей в одной точке. «Отверстие» между этими двумя лучами называется «углом», который обозначается символом ∠.
 Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.
Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.Каковы 6 типов углов?
6 типов углов: прямые углы, острые углы, тупые углы, прямые углы, отраженные углы и полные углы.
Как вы описываете углы?
Угол можно описать как фигуру, образованную двумя лучами, встречающимися в общей конечной точке, называемой вершиной угла.
☛ Также проверьте:
- Рабочие листы углов
- Углы в четырехугольнике Рабочие листы
- Геометрические углы Рабочие листы
Какие бывают типы углов, основанные на вращении?
В зависимости от направления измерения или направления вращения углы можно разделить на два типа:
- Положительные углы: Положительные углы — это углы, которые измеряются и поворачиваются от основания в направлении против часовой стрелки.
- Отрицательные углы: Отрицательные углы — это те углы, которые измеряются и поворачиваются от основания по часовой стрелке.

В чем разница между прямым углом и рефлекторным углом?
Прямой угол – это прямая линия, а угол между двумя лучами равен 180°. Его можно образовать путем совмещения двух смежных прямых углов. Другими словами, два прямых угла составляют прямой угол. Принимая во внимание, что угол рефлекса больше 180°, но меньше 360°.
Какие бывают виды углов, образованных при прохождении секущей через параллельные прямые?
Когда секущая проходит через параллельные прямые, образуется множество пар углов, таких как соответствующие углы, вертикально противоположные углы, чередующиеся внутренние углы и чередующиеся внешние углы.
Какие типы углов меньше 180°?
Существует два типа углов, мера которых меньше 180°, т. е. острые и тупые углы. Мера острых углов всегда меньше 90°, а тупых углов больше 90°, но всегда меньше 180°. Примеры острых углов: 50°, 60°, тупые углы: 170°, 165°.
Какова сумма всех трех углов треугольника?
Сумма трех углов треугольника равна 180°.


 д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.
д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.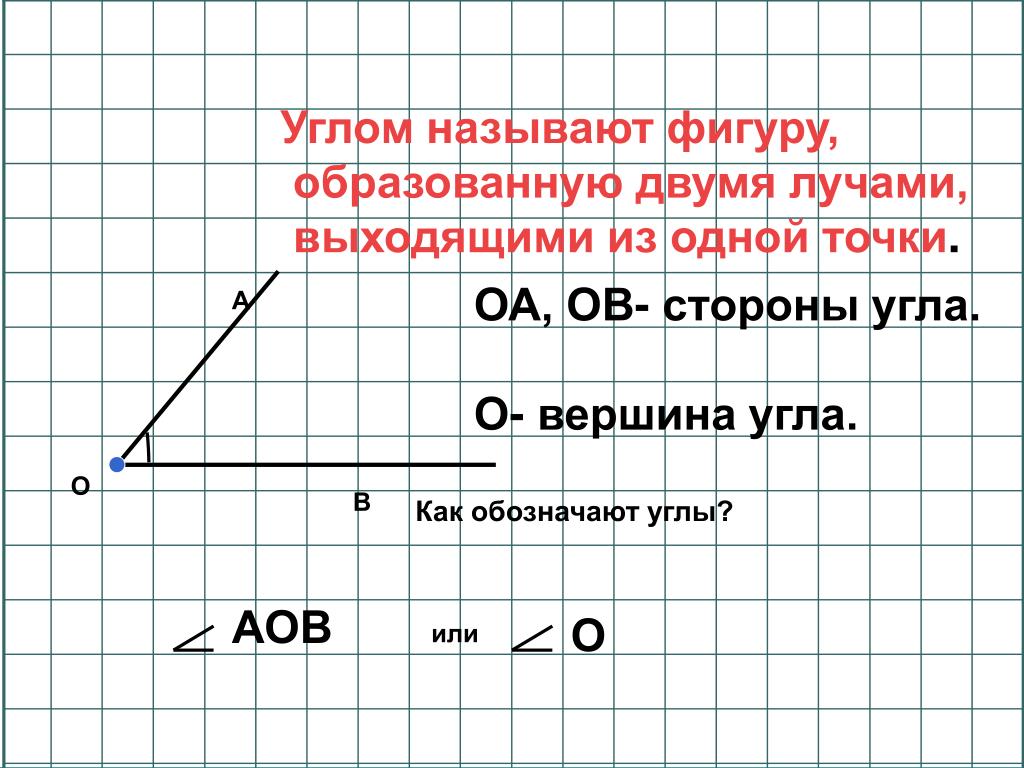 Это
Это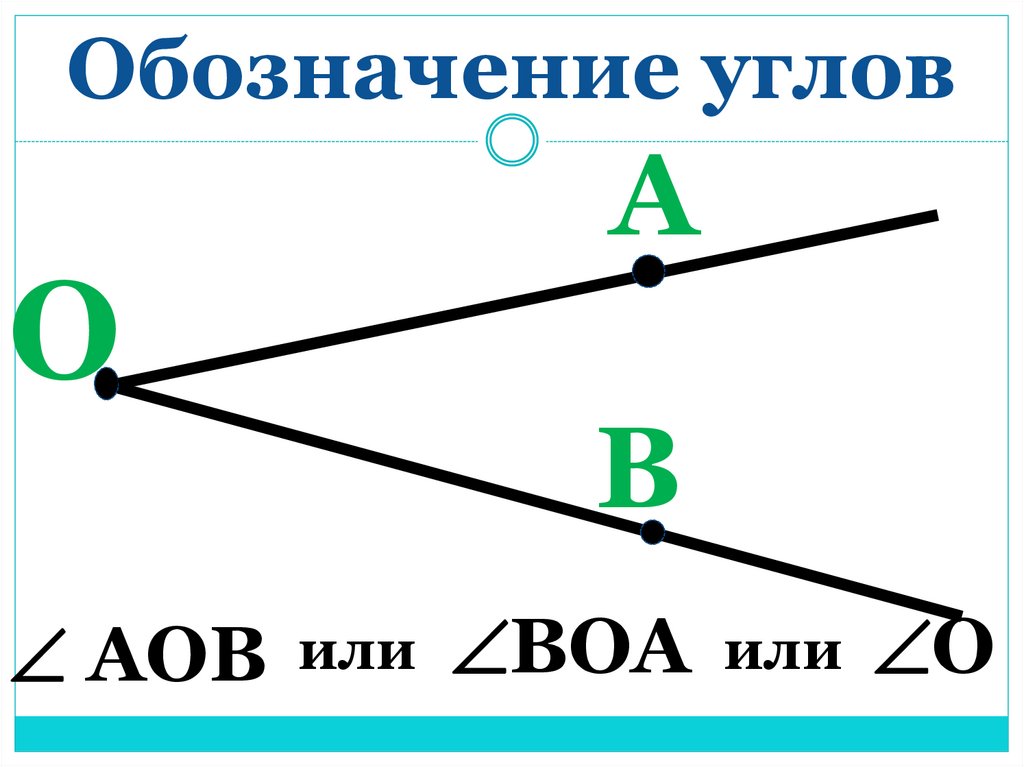 {\circ}\]
{\circ}\]
 Линии могут быть как параллельными, так и непараллельными.
Линии могут быть как параллельными, так и непараллельными.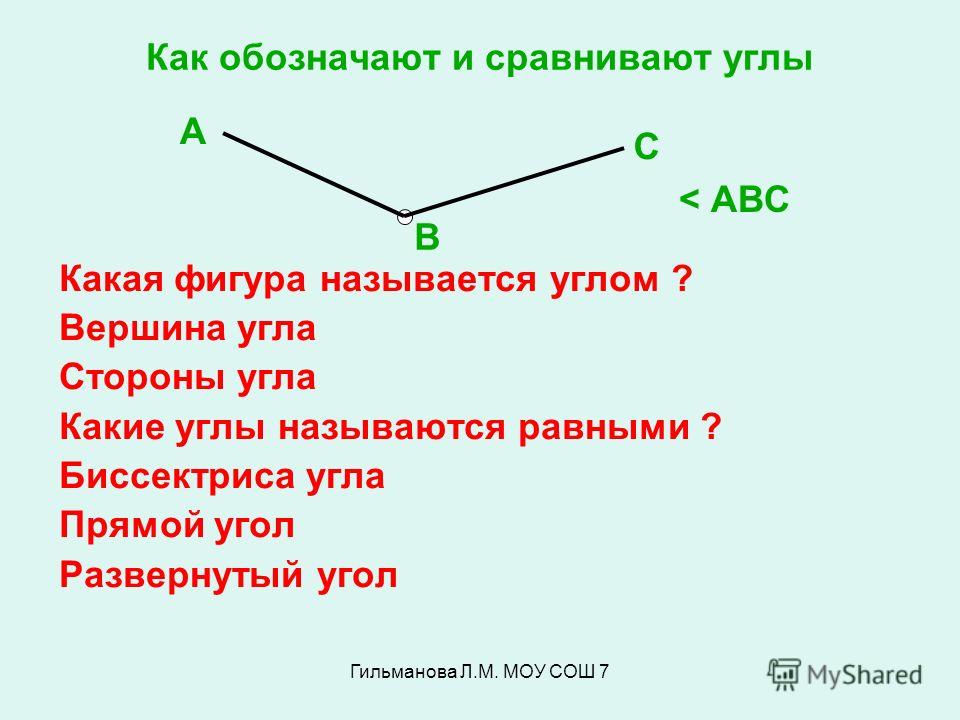 Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит: {\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
{\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.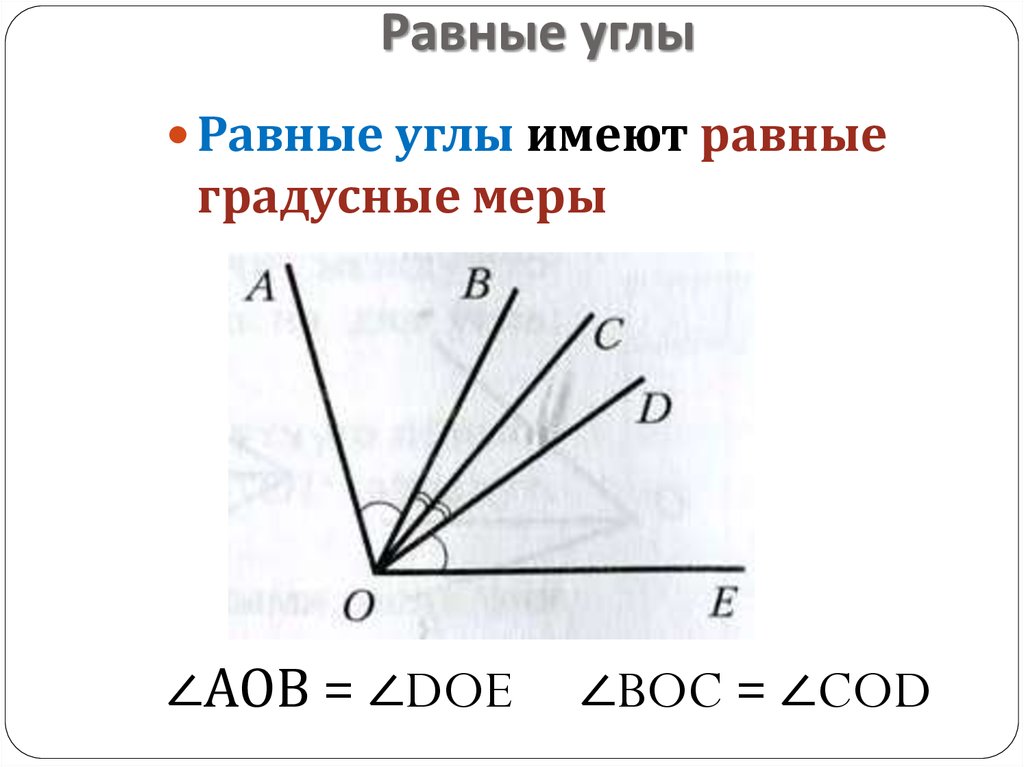 Таким образом, ∠ AOC = 143°
Таким образом, ∠ AOC = 143°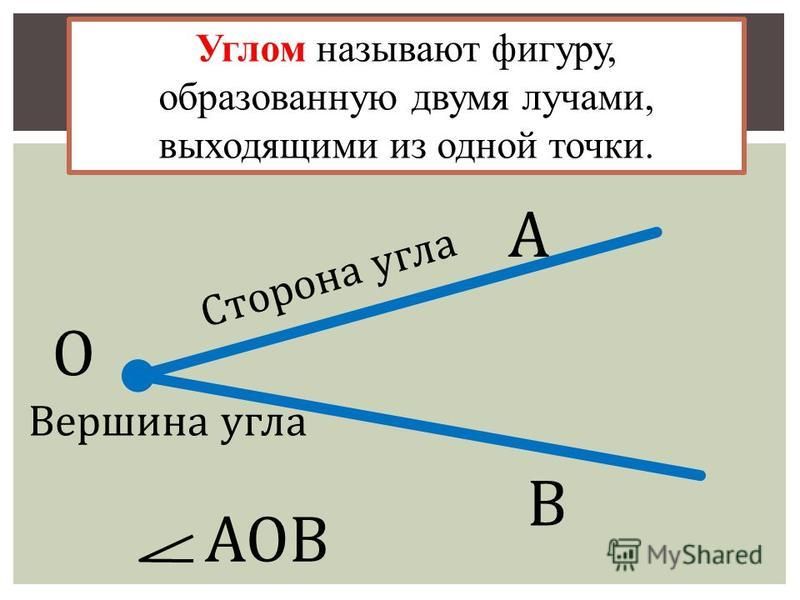
 Средняя буква – вершина. Таким образом, приведенную выше цифру можно записать как ∠XOY или ∠YOX.
Средняя буква – вершина. Таким образом, приведенную выше цифру можно записать как ∠XOY или ∠YOX.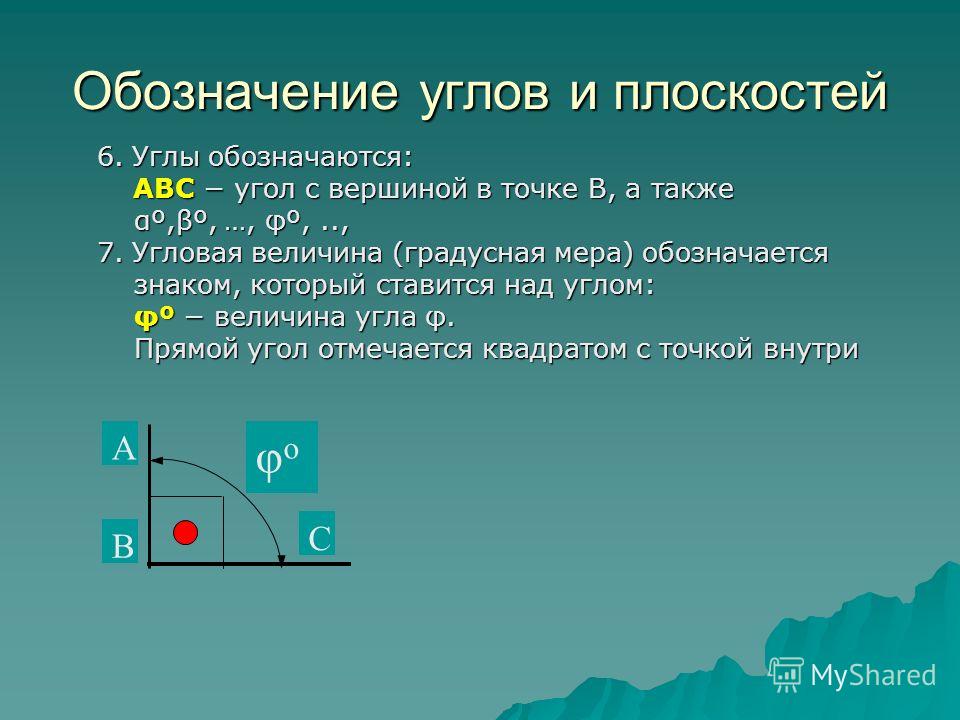 Знак прямого угла также можно показать с помощью четверти круга вместе со стандартным знаком, как показано на рисунке.
Знак прямого угла также можно показать с помощью четверти круга вместе со стандартным знаком, как показано на рисунке. Некоторые из примеров приведены ниже:
Некоторые из примеров приведены ниже: Угол
Угол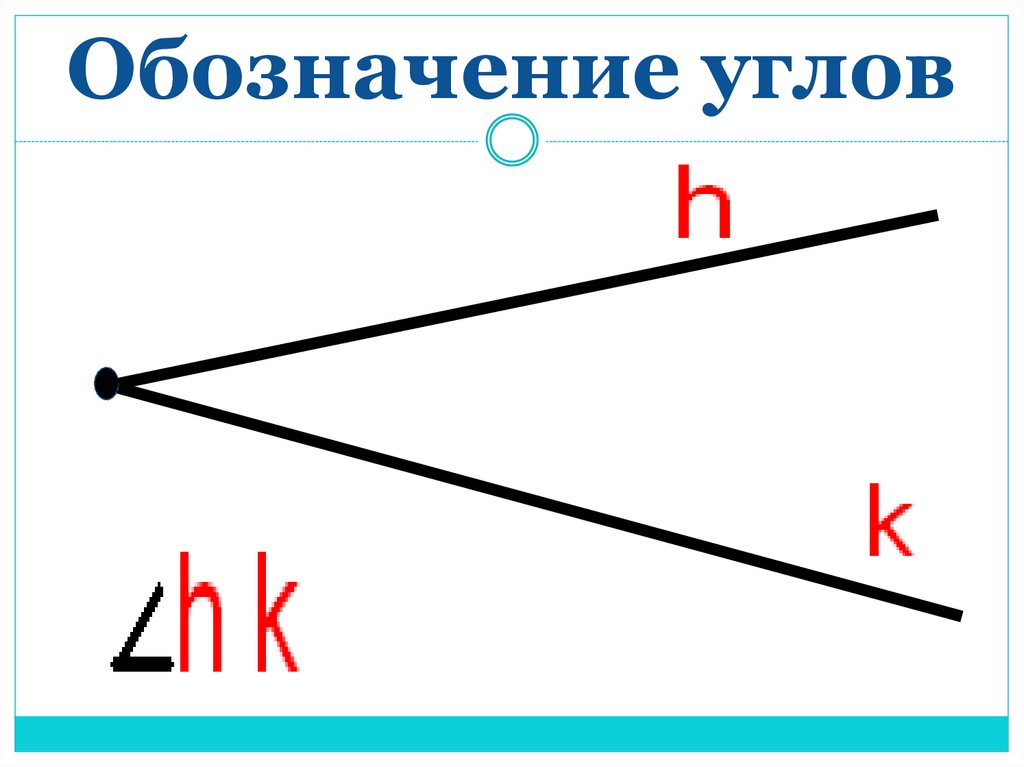 Эти лучи называются сторонами или плечами угла. Давайте прочитаем о различных частях угла.
Эти лучи называются сторонами или плечами угла. Давайте прочитаем о различных частях угла.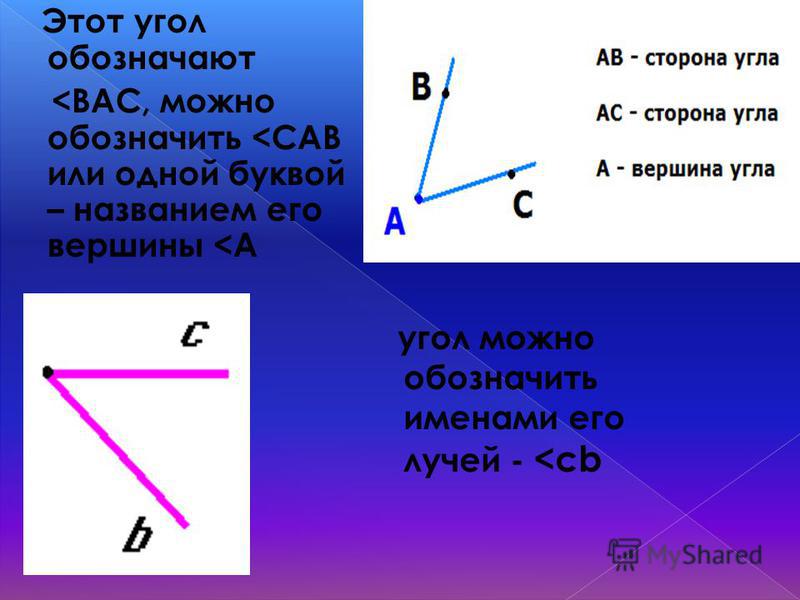 Он имеет градусы, отмеченные по часовой стрелке от 0° до 180° на внешней шкале и против часовой стрелки от 0° до 180° на внутренней шкале.
Он имеет градусы, отмеченные по часовой стрелке от 0° до 180° на внешней шкале и против часовой стрелки от 0° до 180° на внутренней шкале.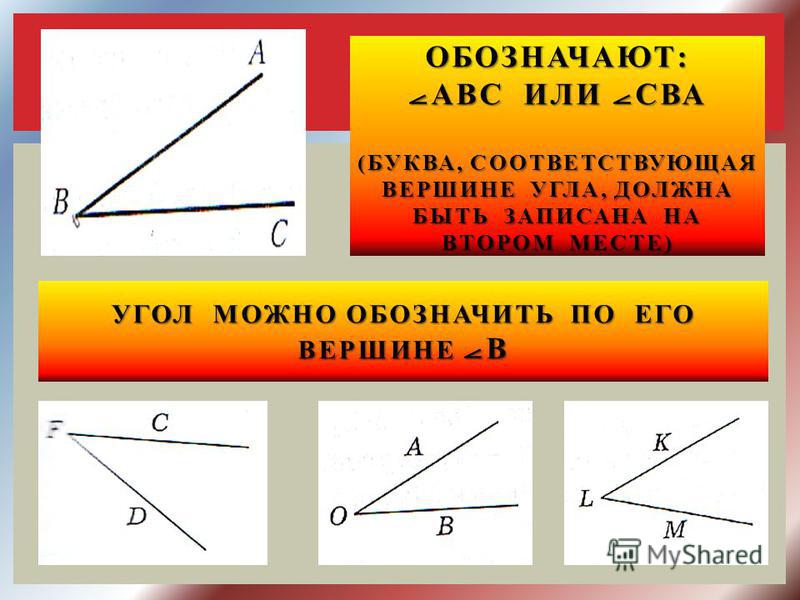 Поскольку мера прямого угла равна 180°, он составляет половину полного оборота окружности.
Поскольку мера прямого угла равна 180°, он составляет половину полного оборота окружности.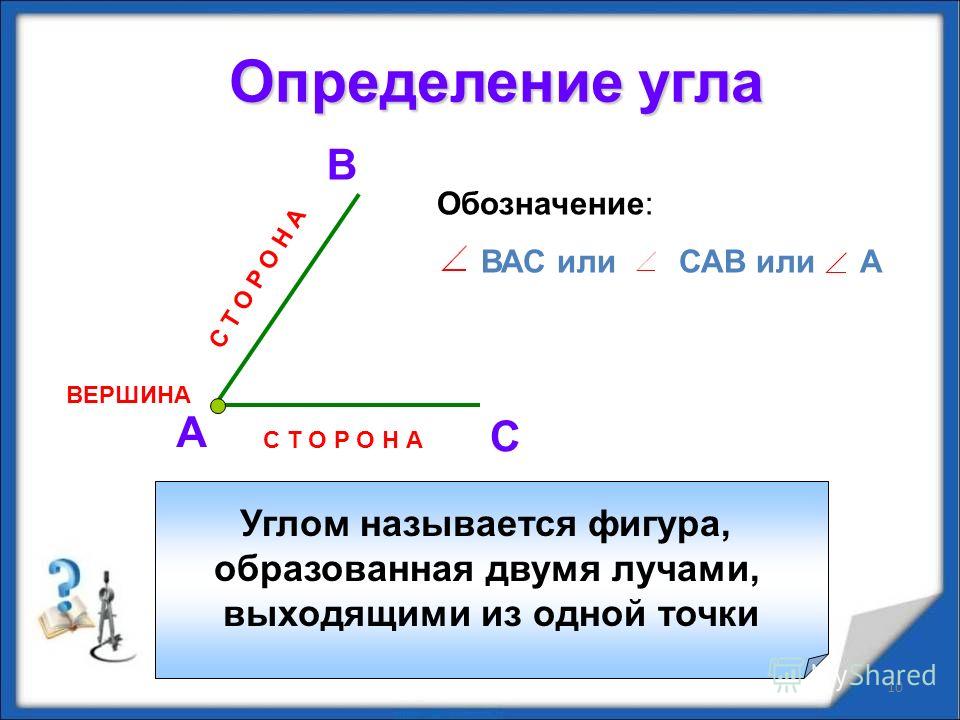
 Если луч идет в другом направлении, мы измеряем угол по внешней шкале от отметки 0° внизу слева.
Если луч идет в другом направлении, мы измеряем угол по внешней шкале от отметки 0° внизу слева. 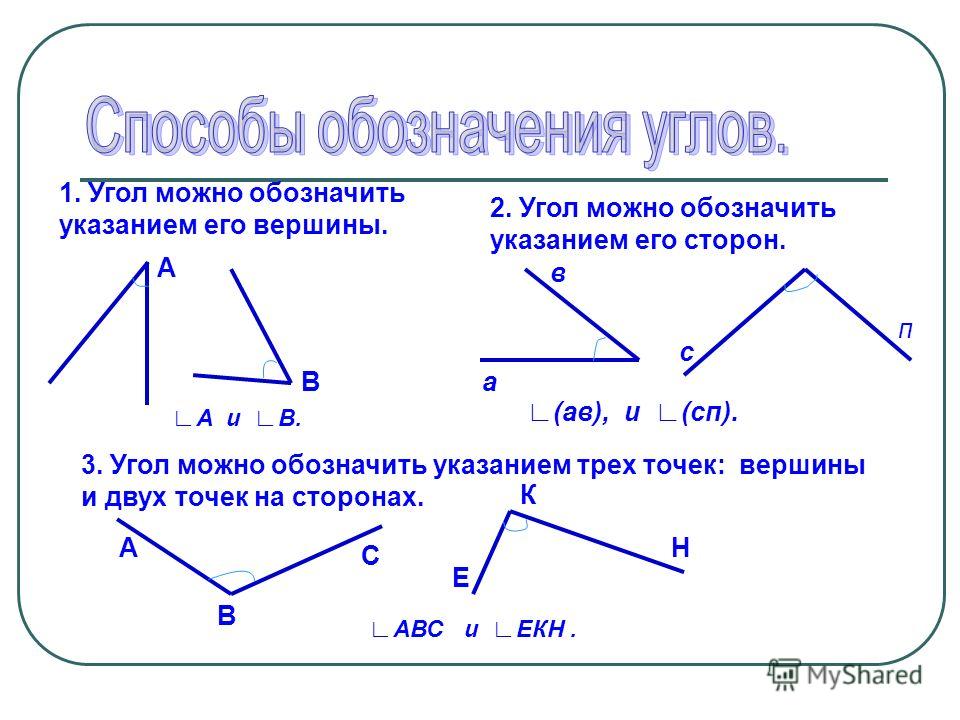 Это острый угол, потому что его градусная мера меньше 90°.
Это острый угол, потому что его градусная мера меньше 90°.  ) 0°< тупой угол < 90°
) 0°< тупой угол < 90°  Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.
Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.