Угол. Обозначение углов / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Угол. Обозначение углов
Угол – геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
На рис. 1 лучи АВ и АС – стороны угла, точка А – вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т.к. точки В и С не являются вершинами данного угла).
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР).
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1.
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой.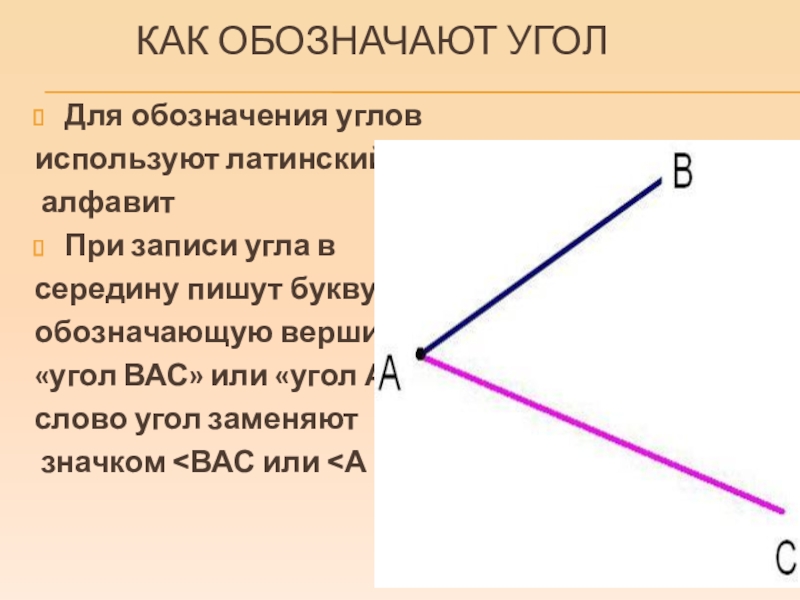
Биссектриса – луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ – биссектриса угла НОD.
Прямой угол – угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На
Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
Острый угол – угол, который меньше прямого угла. На рис. 7 МОN – острый.
Тупой угол – угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК – тупой.
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1660, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1703, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1842, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 288, Мерзляк, Полонский, Якир, Учебник
Номер 303, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 8, Мерзляк, Полонский, Якир, Учебник
Номер 14, Мерзляк, Полонский, Якир, Учебник
Номер 10, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 219, Мерзляк, Полонский, Якир, Учебник
Номер 391, Мерзляк, Полонский, Якир, Учебник
Номер 392, Мерзляк, Полонский, Якир, Учебник
Номер 1220, Мерзляк, Полонский, Якир, Учебник
Номер 1234, Мерзляк, Полонский, Якир, Учебник
Номер 1236, Мерзляк, Полонский, Якир, Учебник
Номер 1237, Мерзляк, Полонский, Якир, Учебник
Задание 1385, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1546, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759, Мерзляк, Полонский, Якир, Учебник
Задание 81, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 422, Мерзляк, Полонский, Якир, Учебник
Угол.
 Обозначение углов
Обозначение угловПредставим себе такую историю.
– Саша, а ты знаешь, что листья на ветке растения всегда располагаются в строгом порядке? – спросил Паша.
– Что значит в строгом порядке? – удивился Саша. – Как числа в натуральном ряду что ли?
– Нет, Саша, листья на ветке растения отстоят друг от друга на определённый угол по или против часовой стрелки – продолжил Паша. – Величина этого угла разная для разных растений.
– Ого! – удивился Саша. – И ведь правда, а я даже и не замечал такого раньше! Но ведь угол – это геометрическое понятие. Зачем растениям углы?
– Такое расположение позволяет листьям растений наиболее эффективно получать влагу и солнечный свет.
– Паша, а ты знаешь, как в математике строят углы? – решил спросить Саша.
– Да, – ответил Паша, – если мы на листе бумаги из одной точки проведём два луча, то получим фигуру, которая называется углом.
– А углы в математике тоже имеют свои
названия? – спросил Саша.
– Да, но об этом лучше спросить у Электроши – сказал Паша.
– Ребята, прежде чем я вам расскажу об углах и их обозначениях, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– Ну а теперь поговорим об углах, – продолжил Электроша. – Давайте проведём на листе бумаги два луча ВА и ВС с общим началом в точке В.
Запомните!
– Значит, угол – это два луча с общим началом? – спросил Саша.
– Всё верно! – подтвердил Электроша.
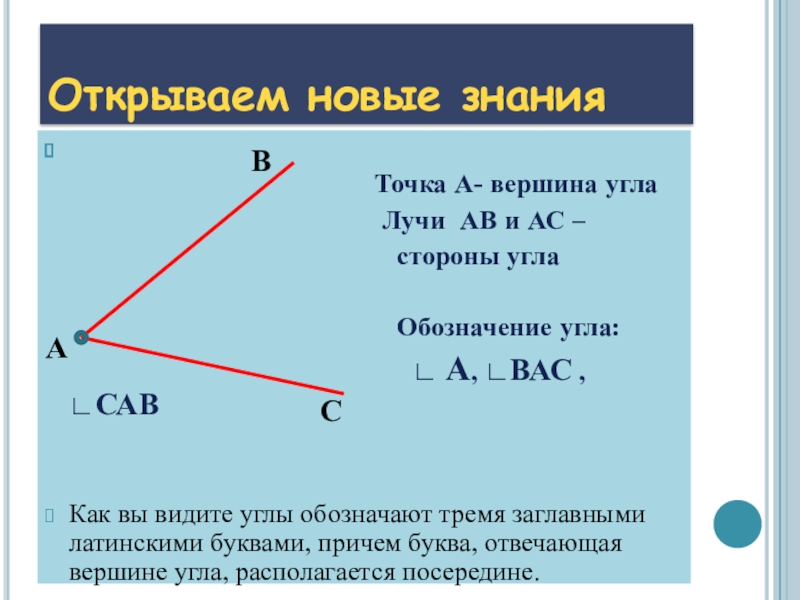
Лучи называют сторонами угла, а их общее начало – вершиной угла.
Так, например, в угле, который мы с вами построили, лучи ВА и ВС – это стороны угла, а точка В – его вершина.
– Визуально углы делят на «внешний» и «внутренний».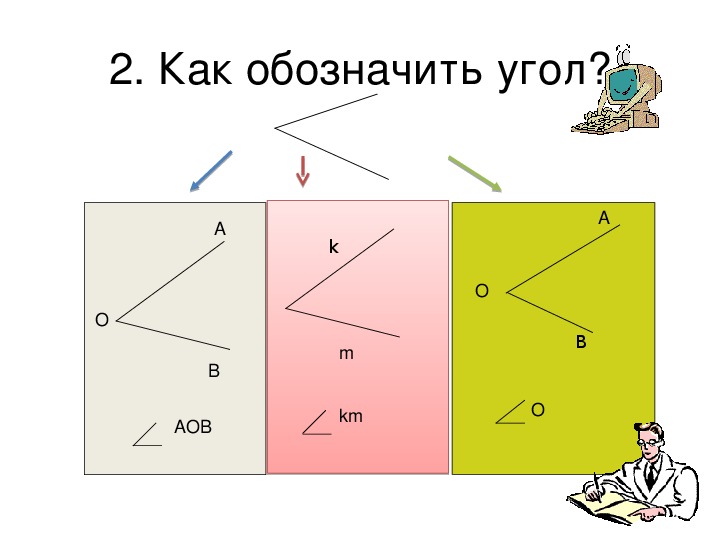 Мы же чаще будем работать именно с внутренними углами.
Мы же чаще будем работать именно с внутренними углами.
– А как обозначают углы? – спросил Паша.
– Для обозначения углов используют следующий символ: . Тогда наш угол можно обозначить так: ∠АВС или ∠СВА. Обратите внимание: называть угол можно с любого края, но не с вершины. Буква, которая соответствует вершине угла, должна всегда находиться в середине названия.
Также этот же угол можно обозначить и короче, одной заглавной латинской буквой, указывающей его вершину. Тогда наш угол можно обозначить так: угол В.
– Посмотрите, я построил три различных угла – продолжил Электроша. – Может, вы сможете их назвать? – спросил он у ребят.
– Первый угол можно обозначить, как ∠PQR – начал Саша, – второй ∠EFT, а третий – ∠KOZ.
– Ещё эти углы можно обозначить так, – продолжил Паша, – ∠Q, ∠F и ∠O.
– Молодцы! – похвалил ребят Электроша. – А
теперь посмотрите на следующие углы. Попробуйте сосчитать и назвать все углы на
рисунке.
Попробуйте сосчитать и назвать все углы на
рисунке.
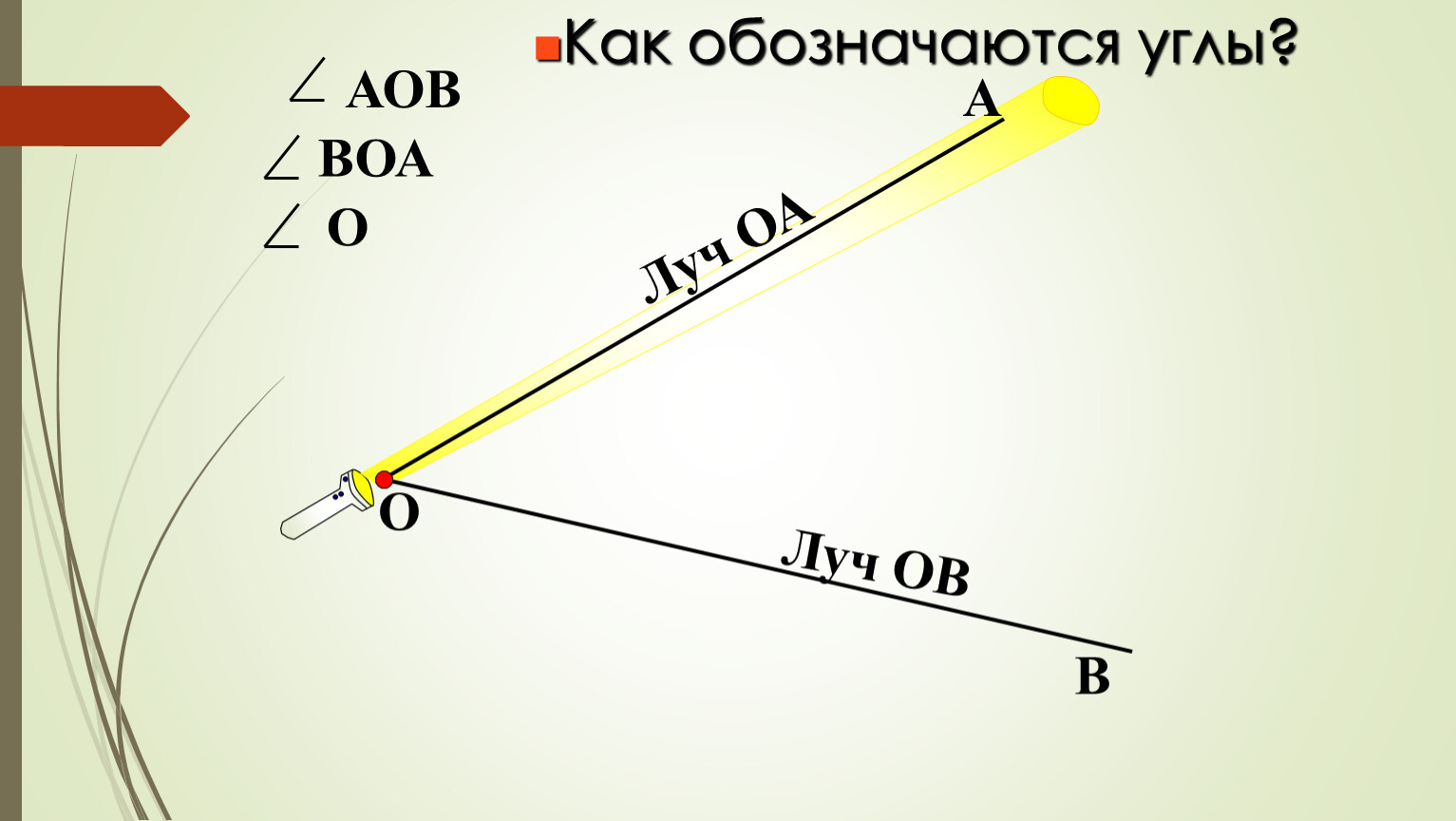
– Угол AOB, – начал Паша, – угол BOC и угол AOC.
– Всё верно! – сказал Электроша. – На нашем рисунке изображены три угла.
– А как же угол О? – спросил Саша.
– Ни один из трёх углов на рисунке нельзя обозначить только одной буквой. У них одна и та же вершина – точка О, но сами углы разные.
– Два угла могут иметь одну общую сторону, – продолжил Электроша. – На нашем рисунке углы AOB и BOC имеют общую сторону ОB. Также в этом случае говорят, что луч ОB проходит между сторонами угла АОC и делит его на два угла: АОB и BОC.
– А теперь давайте проведём небольшой
эксперимент. Возьмём лист бумаги, отметим на нём точки M, О, N таким образом, как показано на рисунке. Перегнём лист так, чтобы его две
соседние стороны совместились. Затем по линии сгиба проведём луч, например, ОP. Обратите внимание, мы получили два угла:
угол MОP и угол NОP, которые совпадают.
Запомните! Два угла называют равными, если они совпадают при наложении.
– То есть углы MОP и NОP равны? – решили спросить ребята.
– Да! – ответил Электроша. – Угол MОP равен углу NОP, а записывают это так: . На рисунке равные углы, как правило, отмечают равным количеством дужек.
– Луч ОP имеет своё название. Такой луч называют биссектрисой угла.
Запомните! Биссектриса делит угол на два равных угла.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: отметьте в тетради точку О и проведите через неё две прямые. На прямых отметьте точки А, B, C и D по разные стороны от точки О. Сколько всего углов у вас получилось? Назовите их.
Решение: на рисунке получилось шесть углов: угол АОB, угол BОC, угол CОD, угол DОА, угол АОC и угол BОD.
Следующее задание: на рисунке угол АОC равен углу BОD. Есть ли ещё на рисунке равные углы? Если есть, то
назовите их.
Есть ли ещё на рисунке равные углы? Если есть, то
назовите их.
Решение: угол АОC состоит из двух углов: угла АОB и угла BОC. Аналогично и угол BОD состоит из углов BОC и CОD. Видим, что угол BОC общий угол углов АОC и BОD. Значит, углы АОB и CОD равны тоже.
– Ребята, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.
Итак, масса 4 персиков и 3 яблок вместе 425 г. А 3 персика и 4 яблока (вместе) имеют общую массу 345 г. Все персики имеют одинаковую массу. Яблоки тоже весят одинаково. Какова общая масса одного персика и одного яблока (вместе)?
Решение: так как по условию задачи 4 персика
и 3 яблока вместе весят 425 г, а также 3 персика и 4 яблока вместе весят 345 г,
то можем узнать, сколько будут весить 7 персиков и 7 яблок вместе, то есть к 425
прибавим 345, получим 770 г. А теперь можем найти вес одного персика и одного
яблока вместе: 770 разделим на 7 и получим 110 г.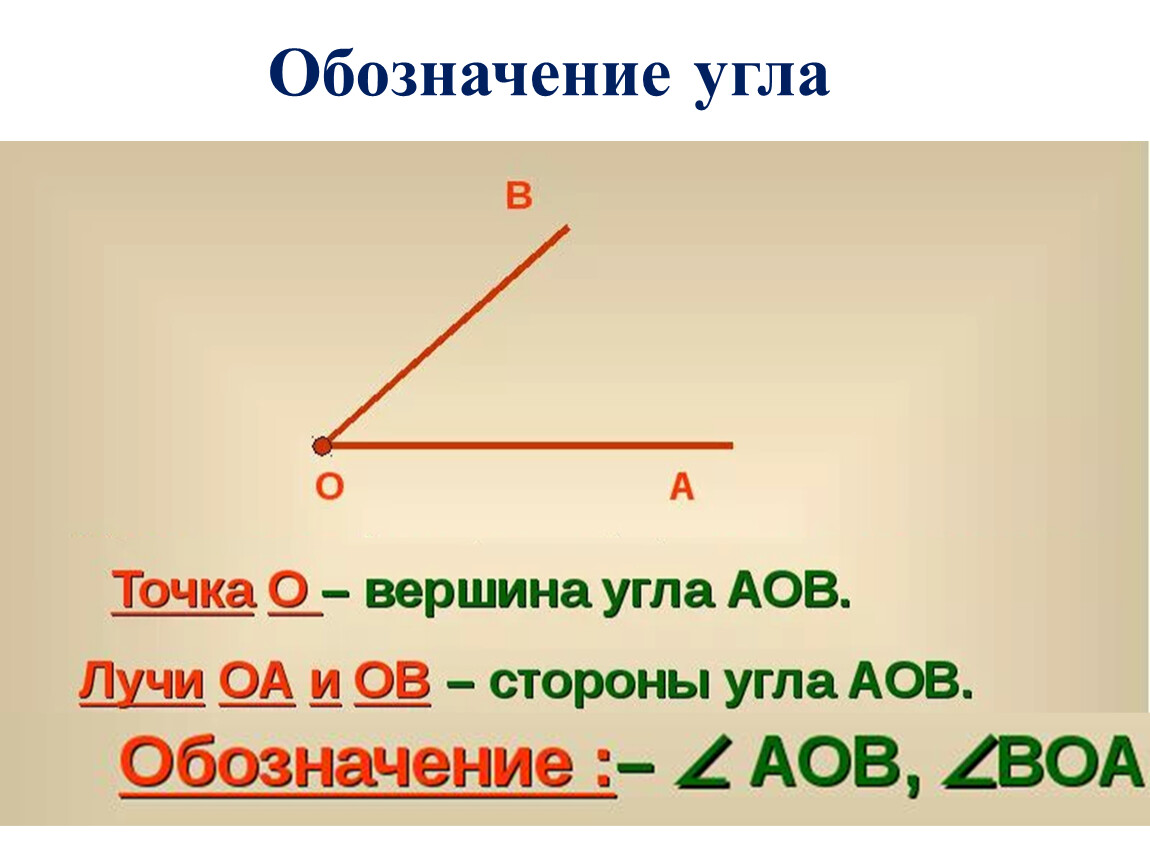
Ответ: 110 грамм общая масса одного персика и одного яблока.
Определение углов (типы углов с примерами)
Геометрия — это раздел математики, который занимается изучением форм и их измерениями. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах. Мы знаем, что геометрия подразделяется на 2D-геометрию и 3D-геометрию. Прежде чем разделить все геометрические фигуры, они состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется «углом». В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Содержание:
- Угол Значение
- Типы углов
- Свойства
- Примеры
- Часто задаваемые вопросы
Определение угла в математике
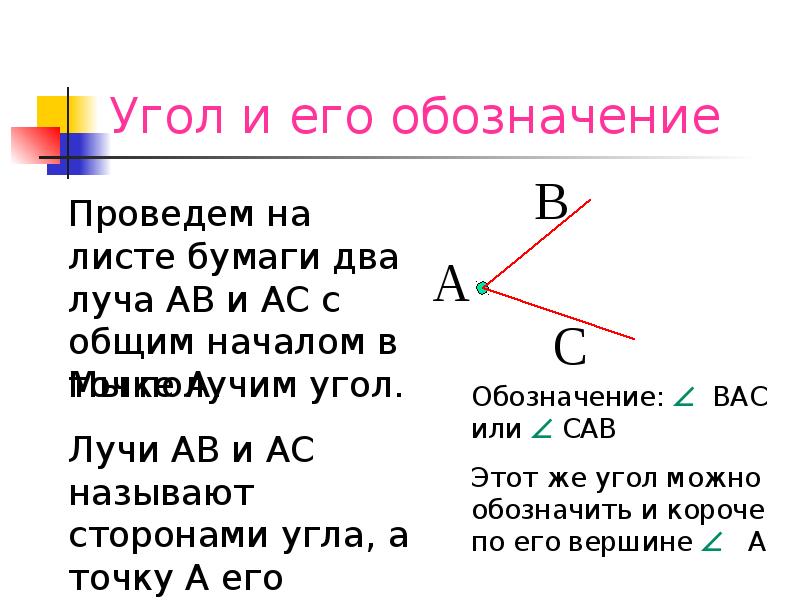
Что такое угол? В плоской геометрии фигура, образованная двумя лучами или линиями, имеющими общую конечную точку, называется углом. Слово «угол» происходит от латинского слова «angulus», что означает «угол». Два луча называются сторонами угла, а их общий конец называется вершиной. Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными. Угол обозначается символом «∠». Измерение угла между двумя лучами можно обозначить греческой буквой θ, α, β и т. д. Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
Слово «угол» происходит от латинского слова «angulus», что означает «угол». Два луча называются сторонами угла, а их общий конец называется вершиной. Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными. Угол обозначается символом «∠». Измерение угла между двумя лучами можно обозначить греческой буквой θ, α, β и т. д. Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
Положительный угол: Если угол идет против часовой стрелки, то он называется положительным углом.
Отрицательный угол: Если угол направлен по часовой стрелке, то он называется отрицательным углом.
Как пометить углы?
Существует два разных способа обозначения углов. Они:
Метод 1: Дайте имя углу. Как правило, угол обозначается строчной буквой, такой как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тета (θ) и т. д.
д., или греческими буквами альфа (α), бета (β), тета (θ) и т. д.
Метод 2: Используя три буквы на фигурах, мы можем определить угол. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60°
.Как измерить угол?
Углы обычно измеряются в градусах (°). Важным геометрическим инструментом, помогающим измерять углы в градусах, является транспортир. Транспортир состоит из двух наборов чисел, идущих в противоположных направлениях. Один набор идет от 0 до 180 градусов на внешнем ободе, а другой набор идет от 180 до 0 градусов на внутреннем ободе.
Для получения дополнительной информации о частях угла посмотрите видео ниже:
Типы уголков
Уголки подразделяются на следующие типы:
- Острый угол – угловая мера меньше 90 градусов
- Прямой угол – угол ровно 90 градусов
- Тупой угол – угол, градусная мера которого больше 90 градусов, но меньше 180 градусов
- Прямой угол – угол, равный точно 180 градусам
- Угол рефлекса – угол, величина которого больше 180 градусов и меньше 360 градусов
- Полный угол – угол, градусная мера которого точно равна 360 градусам
На основе этих углов и линий он далее классифицируется по различным типам, таким как дополнительные углы, дополнительные углы, смежные углы, вертикальные углы, альтернативные внутренние углы, альтернативные внешние углы и так далее.
Ряд углов образуется при пересечении секущей двух или более линий. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными. Некоторые из важных пар углов:
- Соответствующие углы
- Альтернативные внутренние углы
- Альтернативные внешние углы
- Внутренние углы на одной стороне поперечной
- Дополнительные уголки
- Смежные углы
- Вертикальные углы
Теперь давайте обсудим некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то параллельные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей дополнительные.

- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными
Свойства углов
Ниже приведены важные свойства углов:
- Сумма всех углов по одну сторону прямой всегда равна 180 градусам,
- Сумма всех углов вокруг точки всегда равна 360 градусам.
Примеры углов
Вопрос 1:
Найдите неизвестный угол x для данного треугольника ABC, где ∠A = 28° и ∠B = 91°
Решение:
Учитывая, что ∠A = 28° и ∠B = 91°
Пусть ∠C = x
Мы знаем, что сумма внутренних углов треугольника равна 180°
Следовательно,
∠А + ∠В + ∠С = 180°
28°+ 91° + х = 180°
119° + х = 180°
х = 180° – 119°
х = 61°
Следовательно, значение неизвестного угла равно 61°
Вопрос 2:
Найдите неизвестный угол в четырехугольнике ABCD, где ∠A = 120°, ∠B = 60°, ∠C = 45°.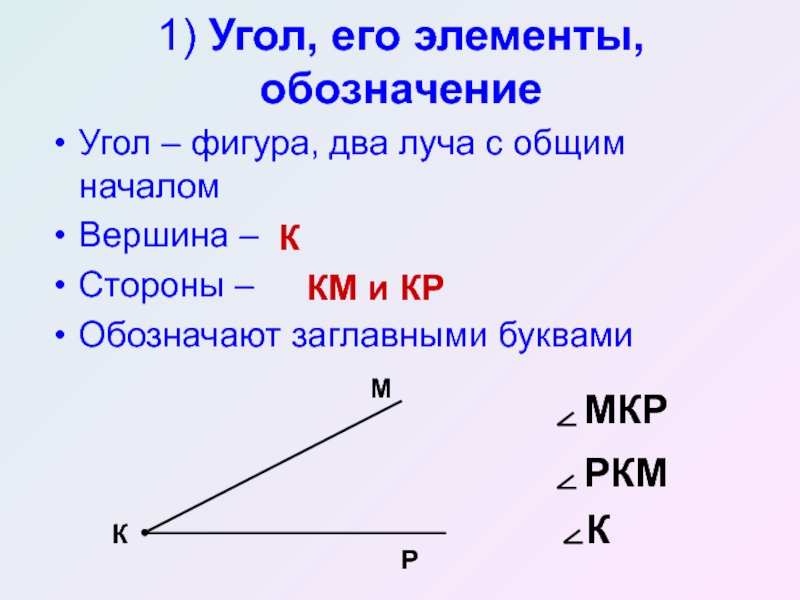 Найдите неизвестный угол D.
Найдите неизвестный угол D.
Дано:
∠А = 120°
∠В = 60°
∠С = 45°
Чтобы найти ∠D.
Мы знаем, что сумма внутренних углов четырехугольника равна 360°.
Следовательно,
∠А + ∠В + ∠С + ∠D = 360° ….(1)
Теперь подставляем известные значения в уравнение (1), получаем
120° + 60°+ 45° + ∠D = 360°
225° + ∠D = 360°
∠D = 360° – 225°
∠D = 135°
Следовательно, неизвестный угол ∠D равен 135°
Часто задаваемые вопросы об углах
Q1
Определение угла в геометрии
Угол определяется как фигура, в которой два луча встречаются в общей точке, называемой вершиной. Угол обозначается символом «∠».
Q2
Какие существуют типы углов?
Различные типы углов:
Острый угол
Тупой угол
Прямой угол
Рефлекторный угол
Прямой угол
Полный угол
Q3
Назовите свойства углов
Два основных важных свойства углов:
Сумма всех углов на одной стороне прямой линии всегда составляет 180 градусов.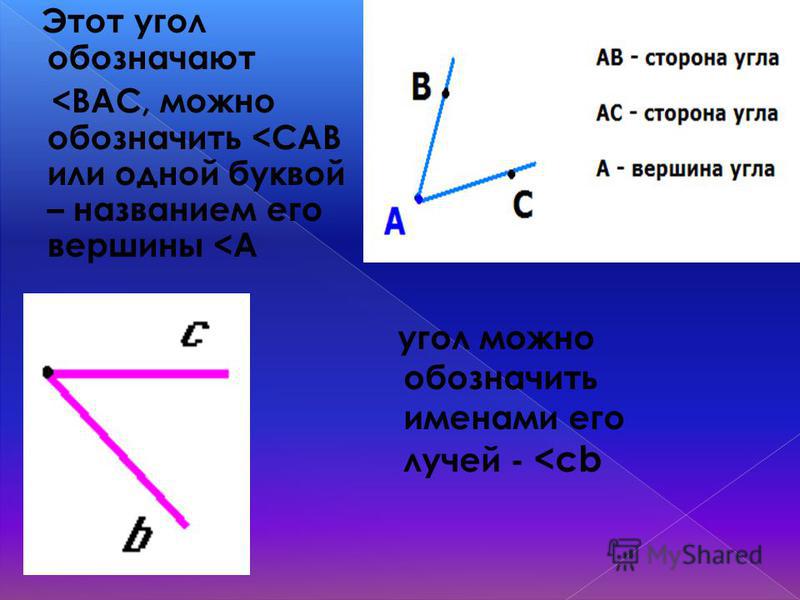
Сумма всех углов вокруг точки всегда составляет 360 градусов.
Q4
Что понимают под внутренними и внешними углами?
Угол, образованный внутри фигуры, называется внутренним углом, а угол, образованный снаружи фигуры, называется внешним углом.
Q5
Что понимают под смежным и вертикальным углами?
Если два угла имеют общую вершину и общее плечо, то такие углы называются смежными. Вертикальные углы — это углы, противоположные друг другу при пересечении двух прямых.
Загрузите BYJU’S — приложение для обучения сегодня и подпишитесь на канал BYJU на YouTube, чтобы учиться в увлекательной форме.
углов – Значение | Определение | Примеры
Углы образуются при пересечении двух прямых в одной точке. Мера «расстояния» между этими двумя лучами называется «углом». Обозначается символом ∠. Углы обычно измеряются в градусах и радианах, что является мерой округлости или вращения. Углы являются частью нашей повседневной жизни. Инженеры и архитекторы используют углы для проектирования дорог, зданий и спортивных сооружений. Давайте узнаем больше о определение углов в математике , значение углов, различные свойства углов, а также некоторые примеры углов.
Углы являются частью нашей повседневной жизни. Инженеры и архитекторы используют углы для проектирования дорог, зданий и спортивных сооружений. Давайте узнаем больше о определение углов в математике , значение углов, различные свойства углов, а также некоторые примеры углов.
| 1. | Что такое углы? |
| 2. | Типы углов и их свойства |
| 3. | Углы на основе поворота |
| 4. | Как измерить угол? |
| 5. | Как построить углы? |
| 6. | Часто задаваемые вопросы об углах |
Что такое углы?
В геометрии угол образуется при соединении двух лучей в их концах. Эти лучи называются сторонами или плечами угла. Давайте прочитаем о различных частях угла.
Части угла
С углом связаны две основные части: стороны и вершина.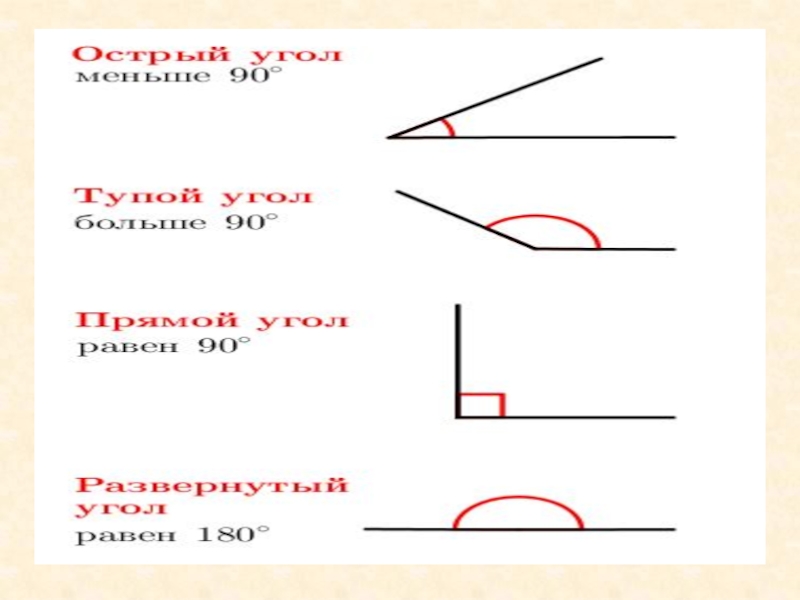
Плечи угла
Два луча, которые соединяются в одной точке, образуя угол, называются плечами угла . Обратите внимание на приведенный ниже рисунок, на котором показано, что ОА и ОВ являются сторонами угла АОВ.
Вершина угла
Вершина является общей конечной точкой, общей для двух лучей. Обратите внимание на рисунок, на котором вершина O отмечена как точка соединения двух плеч.
Мера угла
Угол измеряется в градусах. Один полный оборот вокруг точки образует полный угол в 360°.
Углы лучше всего измерять с помощью транспортира. Транспортир представляет собой измерительный инструмент, имеющий форму полукруга. Это полупрозрачный инструмент, который помогает нам измерять углы в градусах. Он имеет градусы, отмеченные по часовой стрелке от 0° до 180° на внешней шкале и против часовой стрелки от 0° до 180° на внутренней шкале.
Типы углов и их свойства
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла. Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
Каждый тип угла имеет уникальную идентификацию на основе измерения угла. Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
Острый угол
Острый угол — это угол, который больше 0° и меньше 90°.
Прямой угол
Когда угол равен 90°, он называется прямым углом. Прямой угол легко заметить, так как он образует форму буквы L.
Тупой угол
Если угол больше 90°, но меньше 180°, это тупой угол.
Прямой угол
Угол, образованный прямой линией, называется прямым углом. Другими словами, прямой угол — это прямая линия, а угол, образованный между двумя лучами, равен 180°. Под прямым углом два луча противоположны друг другу. Два прямых угла составляют прямой угол. Поскольку мера прямого угла равна 180°, он составляет половину полного оборота окружности.
Угол рефлекса
Угол рефлекса — это угол, величина которого больше 180°, но меньше 360°.
Полный угол
Когда измерение угла равно 360°, это полный угол.
Угол на основе поворота
В зависимости от направления измерения или направления вращения углы бывают двух типов:
- Положительные углы
- Отрицательные углы
Положительные углы
Угол, измеренный в направлении против часовой стрелки (против часовой стрелки), является положительным углом. Другими словами, положительные углы — это те углы, которые повернуты от основания в направлении против часовой стрелки.
Отрицательные углы
Отрицательные углы — это углы, которые измеряются по часовой стрелке от основания. Другими словами, отрицательные углы — это те углы, которые представляют собой углы, повернутые от основания по часовой стрелке.
Как измерить угол?
Мы используем транспортиры для измерения углов. Обратите внимание на приведенный ниже рисунок, на котором показано ∠AOB. Давайте попробуем и посмотрим, сможем ли мы выяснить, к какому типу относится угол ∠AOB.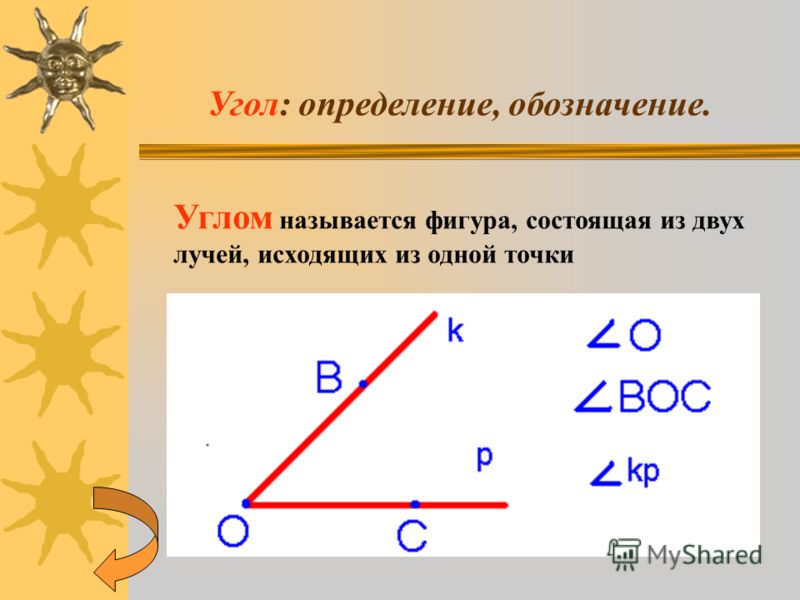 Разве это не похоже на острый угол? Это означает, что его мера больше 0° и меньше 90°. Давайте научимся измерять этот угол с помощью транспортира.
Разве это не похоже на острый угол? Это означает, что его мера больше 0° и меньше 90°. Давайте научимся измерять этот угол с помощью транспортира.
Как измерить острый угол?
Попробуем измерить заданный ∠AOB.
- Шаг 1: Совместите транспортир с лучом OB, как показано ниже. Начните считывать внутреннюю шкалу с отметки 0 ° в правом нижнем углу транспортира.
- Шаг 2: Число на транспортире, которое совпадает со вторым лучом , является мерой угла. Измерьте угол, используя внутреннюю шкалу транспортира. Таким образом, ∠AOB = 37°
Как измерить тупой угол?
Теперь попробуем измерить заданный ∠AOC.
- Шаг 1: Измерьте угол по внешней шкале транспортира от отметки 0° в левом нижнем углу .
- Шаг 2: Число на внешней шкале транспортира, совпадающее с OA, является мерой ∠AOC.
 Таким образом, ∠AOC = 143°
Таким образом, ∠AOC = 143°
Как построить углы?
Мы можем строить углы, используя такие инструменты, как транспортир или циркуль. Здесь воспользуемся транспортиром для построения углов. Начертим угол 50°.
- Шаг 1: Сначала нарисуйте луч OB и совместите транспортир с OB , как показано.
- Шаг 2: Используя внутреннюю шкалу транспортира, отметьте точку А над отметкой на транспортире, которая соответствует 50°.
- Шаг 3: Снимите транспортир и проведите луч, начинающийся в точке O и проходящий через эту точку A. Таким образом, ∠AOB — искомый угол, то есть ∠AOB = 50°.
Примечание. Если луч идет в другом направлении, мы измеряем угол по внешней шкале от отметки 0° внизу слева.
На приведенном ниже рисунке показано, как нарисовать угол 50°, когда луч направлен в другую сторону.
После размещения транспортира на ВО мы используем внешнюю шкалу и отмечаем 50°, как показано. Затем мы отмечаем эту точку как A и соединяем ее с точкой O. Это образует угол AOB = 50°
Важные замечания по углам
- 0°< Острый угол < 90°
- 90°< Тупой угол < 180°
- 180° < угол отражения < 360°
- Прямой угол равен 90°
- Прямой угол равен 180°.
☛ Связанные статьи
- Пары уголков
- Секущие и смежные углы
- Внутренние уголки
Углы Примеры
Пример 1: Обратите внимание на размер углов и определите тип углов для каждой фигуры.
Решение:
а) Данный угол равен 40°. Это острый угол, потому что его градусная мера меньше 90°.
б) Данный угол равен 117°. Это тупой угол, потому что его градусная мера больше 90°, но меньше 180°.

в) Данный угол равен 121°. Это тупой угол, потому что его градусная мера больше 90°, но менее 180°.
г) данный угол равен 185°. Это рефлекторный угол, потому что его величина больше 180°, но меньше 360°.
Пример 2:
Классифицируйте следующие углы на острые, тупые, прямые и рефлекторные.
а) 24°
б) 150°
в) 90°
г) 270°
Решение:
(а) 24° лежит в от 0° до 90°, значит угол острый.
(b) 154° лежит между 90° и 180°, поэтому это тупой угол.
(c) 90° известен как прямой угол.
(d) 270° находится между 180° и 360°, поэтому это рефлекторный угол.
Пример 3: Напишите верно или неверно следующие утверждения:
a.) 180° < угол отражения < 360°
b.) 0°< тупой угол < 90°
c.) два луча, которые соединяющиеся в одной точке и образующие угол, называются сторонами угла.
Решение:
a.
 ) Верно, 180° < угол отражения < 360°
) Верно, 180° < угол отражения < 360°b.) Неверно, 0°< острый угол < 90°
c.) Верно, два луча, которые соединяются в общие точки, образующие угол, называются плечами угла.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об углах
Что такое угол в математике?
Углы образуются при пересечении двух лучей в одной точке. «Отверстие» между этими двумя лучами называется «углом», который обозначается символом ∠. Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.
Какие бывают 6 типов углов?
6 типов углов: прямые углы, острые углы, тупые углы, прямые углы, отраженные углы и полные углы.
Как вы описываете углы?
Угол можно описать как фигуру, образованную двумя лучами, встречающимися в общей конечной точке, называемой вершиной угла.
☛ Также проверьте:
- Рабочие листы углов
- Углы в четырехугольнике Рабочие листы
- Геометрические углы Рабочие листы
Какие бывают типы углов, основанные на вращении?
В зависимости от направления измерения или направления вращения углы можно разделить на два типа:
- Положительные углы: Положительные углы — это углы, которые измеряются и поворачиваются от основания в направлении против часовой стрелки.
- Отрицательные углы: Отрицательные углы — это те углы, которые измеряются и поворачиваются от основания по часовой стрелке.
В чем разница между прямым углом и рефлекторным углом?
Прямой угол – это прямая линия, а угол между двумя лучами равен 180°. Его можно образовать путем совмещения двух смежных прямых углов. Другими словами, два прямых угла составляют прямой угол. Принимая во внимание, что угол рефлекса больше 180°, но меньше 360°.
Другими словами, два прямых угла составляют прямой угол. Принимая во внимание, что угол рефлекса больше 180°, но меньше 360°.
Какие бывают виды углов, образованных при прохождении секущей через параллельные прямые?
Когда секущая проходит через параллельные прямые, образуется много пар углов, таких как соответствующие углы, вертикально противоположные углы, чередующиеся внутренние углы и чередующиеся внешние углы.
Какие типы углов меньше 180°?
Существует два типа углов, мера которых меньше 180°, т. е. острые и тупые углы. Мера острых углов всегда меньше 90°, а тупых углов больше 90°, но всегда меньше 180°. Примеры острых углов: 50°, 60°, тупые углы: 170°, 165°.
Какова сумма всех трех углов треугольника?
Сумма трех углов треугольника равна 180°.
☛ Проверить сейчас:
- Углы треугольника Рабочие листы
- Калькулятор углов треугольника
Сколько углов по 90 градусов в прямом угле?
В 180-градусном угле или прямом углу есть два угла 90°.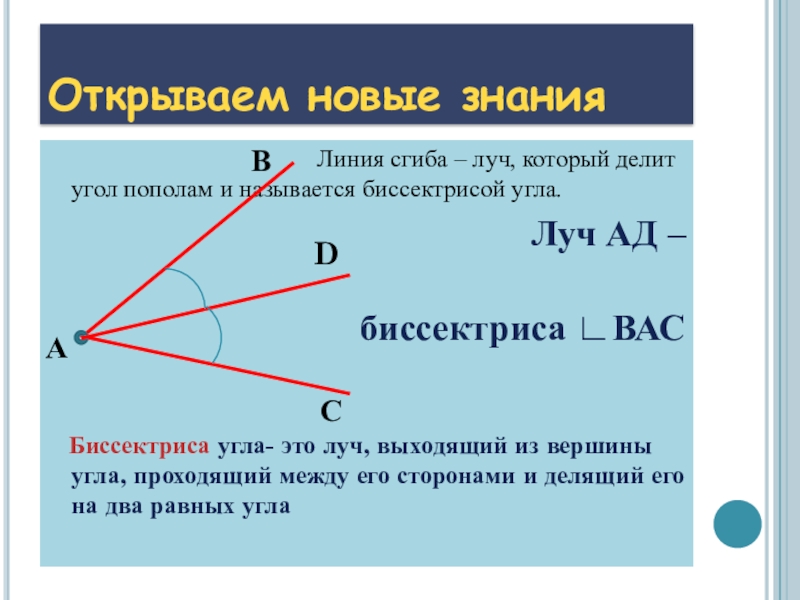 Так как 90° + 90° = 180°, то в прямом углу два угла по 90°.
Так как 90° + 90° = 180°, то в прямом углу два угла по 90°.
Перечислите типы парных углов.
Типы уголков попарно перечислены ниже:
- Смежные углы
- Дополнительные уголки
- Дополнительные уголки
- Альтернативные внутренние углы
- Альтернативные внешние углы
- Соответствующие углы
- Вертикальные уголки
- Последовательные внутренние углы
Что такое полный угол?
Когда угол завершает свой полный оборот, начиная с 0° и заканчивая 360°, он называется полным углом. Другими словами, полный угол равен 360°.
Как вы измеряете углы?
Углы можно легко измерить с помощью простого измерительного инструмента, известного как транспортир. Этот инструмент имеет форму полукруга, который имеет внутреннюю шкалу и внешнюю шкалу с отметками от 0° до 180°. Подробное объяснение измерения углов с помощью транспортира приведено выше на этой странице.
Как углы используются в реальной жизни?
Есть много мест, где используются углы.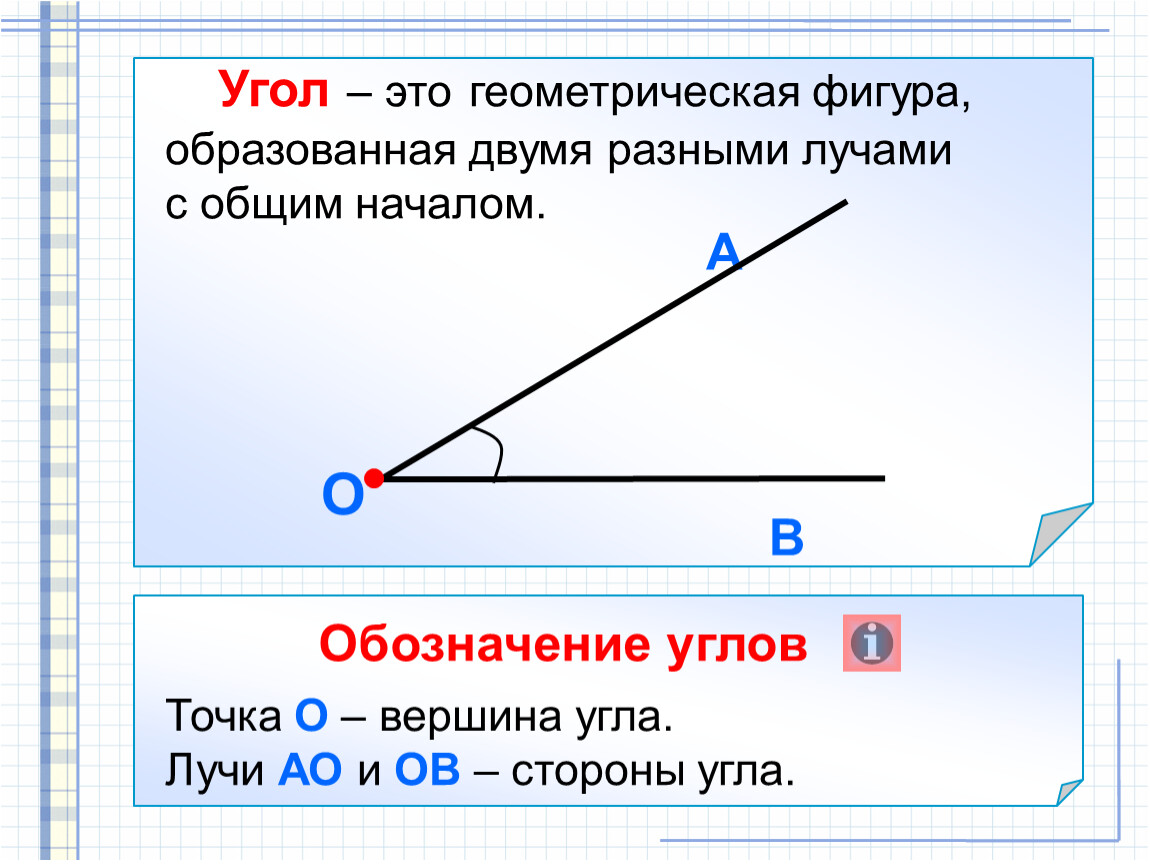

 Таким образом, ∠AOC = 143°
Таким образом, ∠AOC = 143°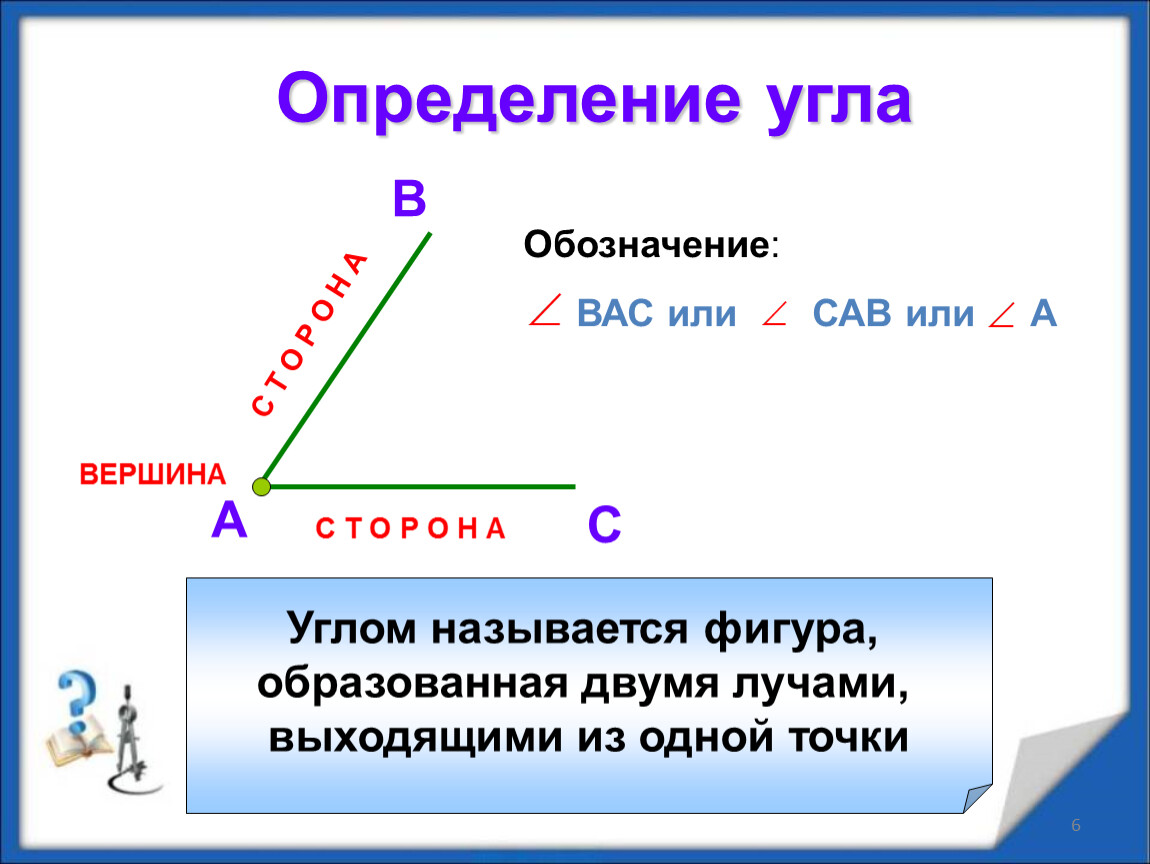
 ) Верно, 180° < угол отражения < 360°
) Верно, 180° < угол отражения < 360°