Как обозначается уклон: Обозначение уклона на чертежах

Уклон и конусность – презентация онлайн

Похожие презентации:

Основы архитектуры и строительных конструкций. Основы проектирования

Конструктивные схемы многоэтажных зданий

Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)

Правила выполнения архитектурно-строительных чертежей

ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)

задачи на построение (геометрия 7 класс)

Выполненный вариант контрольной работы по разделу “Техническое черчение”. (Приложение 3)

Параллельность в пространстве. (Графическая работа 2)

Строительное черчение. Графическое оформление и чтение строительных чертежей

Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты

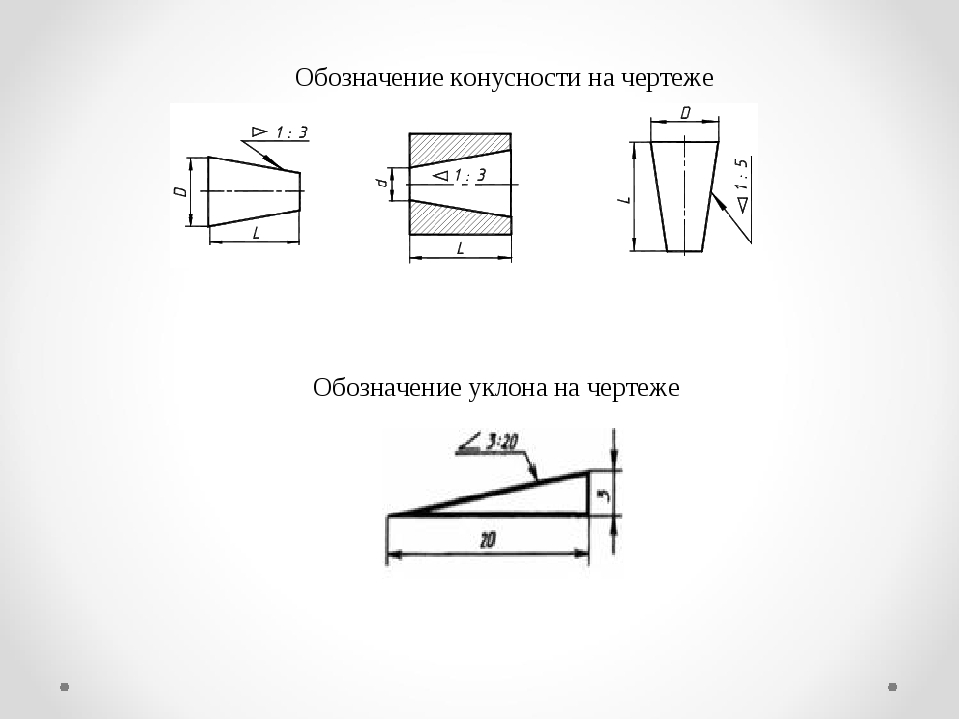
1. УКЛОН И КОНУСНОСТЬ

• Во многих деталях машин используются
уклон и конусность.
• Уклон встречается в профилях прокатной
стали, в крановых рельсах, в косых шайбах
и прочих деталях.
• Конусность встречается в каждом
токарном, фрезерном или сверлильном
станке, в режущем инструменте, которые
имеют конусные хвостовики и в ряде
других деталей.

3. УКЛОН – это величина, которая характеризует наклон одной прямой относительно другой.

4. Где встречается уклон?

В технологии машиностроения!

5. Где встречается уклон?

В автомобильном транспорте!

6. Обозначается уклон знаком  . На чертеже уклон выражается отношением двух чисел или в процентах.

Обозначается уклон знаком .
На чертеже уклон выражается
отношением двух чисел или в
процентах.

7. Знак ставится перед числовым значением уклона над полкой линии-выноски. Острый угол знака должен быть направлен в ту же

сторону, что и
острый угол уклона.

8. Поэтапное построение уклона  1:3

Поэтапное построение
уклона 1:3

9. Поэтапное построение уклона 15%

10. Примеры выполнения уклона

11. Примеры выполнения уклона

12. КОНУСНОСТЬ – это отношение диаметра основания конуса к его высоте.

13. Где встречается конусность?

14. Где встречается конусность?

15. Конусность обозначается знаком  , вершина знака должна быть направлена в сторону вершины конуса.

Конусность может быть заданаКонусность обозначается
знаком , вершина знака должна быть
направлена в сторону вершины конуса.
Конусность может быть задана
отношением двух чисел
или в процентах.

16. Конусность C определяется по формуле где D – диаметр конуса, мм; L – высота конуса, мм.

Конусность C определяется по формуле
C=D:L,
где D – диаметр конуса, мм;
L – высота конуса, мм.

17. Поэтапное построение полного конуса

18. Конусность усеченного конуса C определяется по формуле где D – диаметр большего основания конуса, мм; d – диаметр меньшего

Конусность усеченного конуса C
определяется по формуле
C = (D – d): L ,
где D – диаметр большего
основания конуса, мм;
d – диаметр меньшего
основания конуса, мм;
L – высота конуса, мм.

19. Поэтапное построение усеченного конуса

20. Формулы для определения D, d и L

Диаметр большего основания конуса определяется по формуле
D = d+ C L
Диаметр меньшего основания конуса определяется по формуле
d = D – C L
Высота конуса определяется по формуле
L = (D – d): C

21.

Контрольные вопросы1. Что называется уклоном?
2. В чем выражается уклон?
3. Какой знак ставится перед
числовым значением уклона?
4. Что называется конусностью?
5. Какой знак ставится перед
числовым значением конусности?

22. Рассчитайте

•D=100, d=50,
уклон 1:2, L=?
• L=100

23. Рассчитайте

•D=?, d=10,
уклон 1:4, L=250
• D=72,5

24. Рассчитайте

•D=30, d=?,
уклон 1:7, L=70
• d=20

English     Русский Правила

Методические указания для лабораторной работы 4 по дисциплине «Инженерная графика» (по разделу «Геометрическое черчение») 2 курс

Лабораторная работа

Нанесение размеров на чертежах.

Определение, построение по заданной величине и обозначение уклона и конусности.

Цель работы:

– изучить виды размеров, правила и приемы нанесения их на чертежах;

– научиться определять и строить уклон и конусность;

– научиться наносить размеры на чертежах по ГОСТу.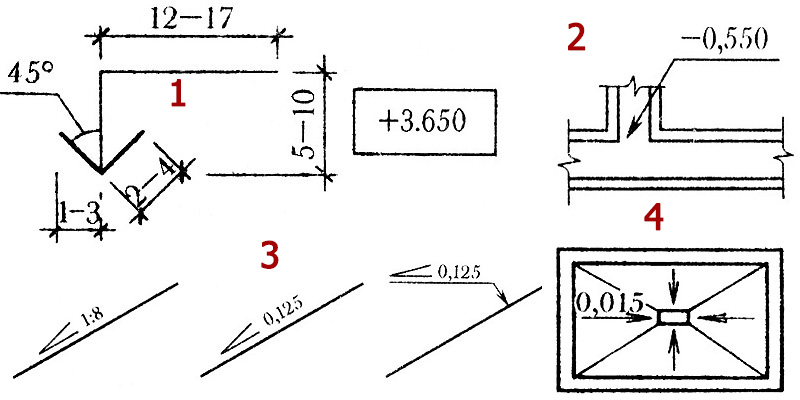

Пояснение к работе.

Лабораторная работа выполняется в рабочей тетради формата А4 с помощью набора чертежных инструментов и при­надлежностей.

При выполнении задания студент должен:

– изучить правила и приемы нанесения размеров на чертежах;

– научиться наносить размеры их на чертежах;

– научиться определять и строить уклон и конусность.

По окончанию работы студент должен иметь представление о размерах, уклоне и конусности; должен научиться проставлять размеры на чертежах и строить уклон и конусность.

Предварительная подготовка.

Ознакомиться с теоретической частью работы. Ознакомиться с заданием.

Выполнение работы.

На выполнение работы отводится не менее 1 часа. Работа выполняется каждым студентом индивидуально.

Содержание отчета.

Отчетом по лабораторной работе служит выполненное задание в рабочей тетради формата А4.

Задание.

1. Определить, на каком из трех чертежей рис. 1 правильно нанесены размерные числа по отношению к размерным линиям. Какие ошибки допущены на остальных чертежах?

Рисунок 1

2. В рабочей тетради вычертить изображение контура детали по размерам и проставить размеры, исправив ошибки, допущенные в примере при нанесении размерных линий и размерных чисел.

3. Построить в рабочей тетради линии, уклоны которых к горизонтальной прямой составляют 1:7 и 20 %. Нанести на построенных линиях обозначение уклона.

4. Определить конусность усеченного конуса, если диаметр его меньшего основания равен 50 мм, большего — 80 мм, а высо­та — 90 мм.

Контрольные вопросы

1. Каковы форма стрелок на концах размерной линии и при­мерное соотношение ее элементов?

2. Каковы минимально допустимые расстояния между параллельными размерными линиями и между размерной линией и линией видимого контура?

3. В каких случаях линейные и угловые размеры наносятся на полке линии-выноски?

4. В каком месте размерной линии наносится размерное число?

5. Допускается ли пересечение размерных чисел и стрелок размерных линий какими-либо линиями чертежа?

6. В каких единицах измерения задают линейные размеры на чертежах и в каком случае эти единицы указывают на чертеже?

7. Как рекомендуется располагать размерные числа на несколь­ких параллельных или концентрических размерных линиях?

8. Каковы единицы измерения угловых размеров и указывают ли эти единицы на чертежах?

9. Какие знаки наносятся при обозначении диаметра, радиуса, сферы, квадрата, уклона, конусности и каковы их размеры по отношению к размерным числам?

10. Как обозначаются, вычисляются, строятся уклон и конусность?

Литература:

1. Бродский А.М. Инженерная графика (металлообработка): учебник для студ. учреждений сред. проф. образования / Бродский А.М., Фазлулин Э.М., Халдинов В.А.- 7-е издание – М.: Издательский центр «Академия», 2011. – 400 с.

2. Бродский А.М. Практикум по инженерной графике: учеб. пособие для студ. учреждений сред. проф. образования / Бродский А.М., Фазлулин Э.М., Халдинов В.А. – 6-е издание – М.: Издательский центр «Академия», 2011. – 192 с.

3. Боголюбов С.К. Индивидуальные задания по курсу черчения Учебное пособие для средних специальных учебных заведений. 3-е изд. – М.: ООО ИД “Альянс”, 2007. – 368 с.

Теоретическая часть

НАНЕСЕНИЕ РАЗМЕРОВ НА ЧЕРТЕЖАХ

Правила нанесения размеров и предельных отклоне­ний на чертежах и других технических документах устанавливает ГОСТ 2.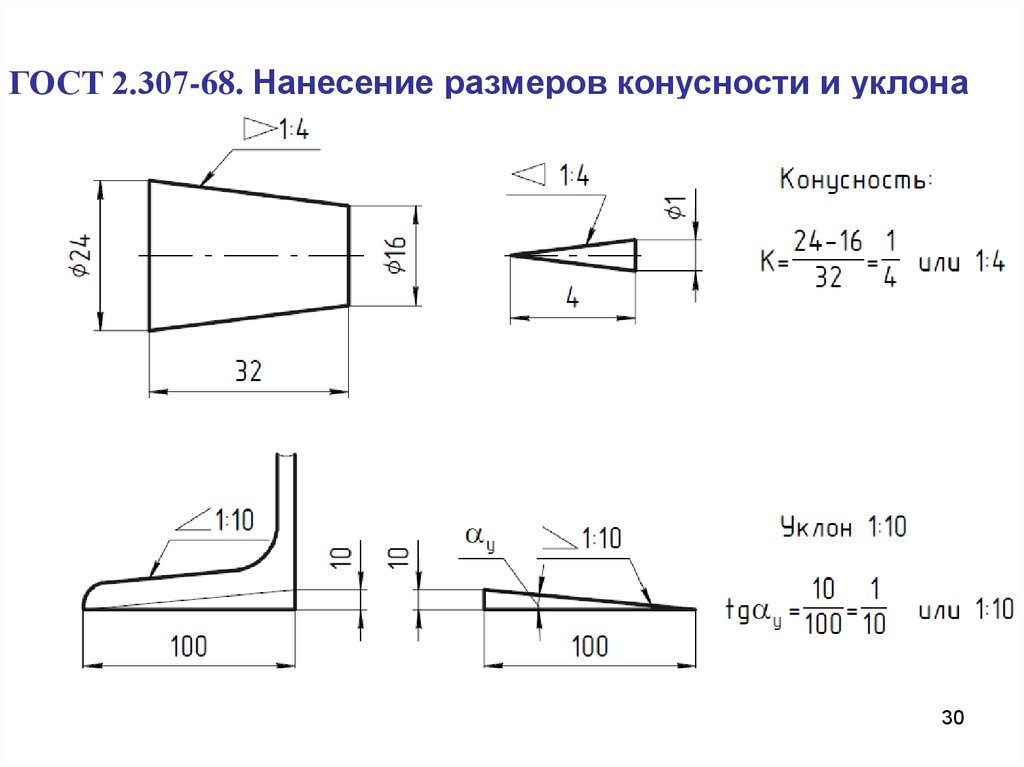 307—68.

Размеры на чертежах указывают размерными чи­слами и размерными линиями. Размерные числа должны соответствовать действительным размерам изображаемого предмета, независимо от того, в каком масштабе и с какой точностью выполнен чертеж.

Размеры бывают линейные — длина, ширина, высо­та, величина диаметра, радиуса, дуги и угловые — раз­меры углов.

Линейные размеры указывают на чертеже в милли­метрах, единицу измерения на чертеже не указывают.

Стрелки, ограничивающие размерные линии, должны упираться острием в соответствующие линии контура или в выносные и осевые линии (рис. 1, а). Выносные линии должны выходить за концы стрелок размерной линии на 1…5 мм (рис. 1, а).

Величина стрелки выбирается в зависимости от тол­щины (s) линий видимого контура и должна быть одина­кова для всех размерных линий чертежа. Форма стрелки и примерное соотношение ее элементов пока­заны на рис. 1, б. Размерные и выносные линии вы­полняют сплошными тонкими линиями. В пределах од­ного чертежа размерные числа выполняют цифрами одного шрифта (чаще применяют шрифт размером 3,5). Размерные числа ставят над размерной линией, параллельно ей и возможно ближе к середине.

Минимальное расстояние между параллельными размерными линиями должно быть 7 мм, а между раз­мерной линией и линией контура — 10 мм.

Рисунок 1

Необходимо избегать пересечения размерных и вы­носных линий.

При нанесении нескольких параллельных или кон­центричных размерных линий на небольшом рассто­янии друг от друга размерные числа над ними рекомен­дуется располагать в шахматном порядке (рис.2).

При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки допус­кается заменять засечками (размеры 2; 1; 2 на рис. 2), наносимыми под углом 45° к размерным линиям, или четкими точками (размеры 6; 4; 2 на рис.2). В местах нанесения размерного числа осевые, центровые линии и линии штриховки прерывают (размер 50 на рис.2).

Рисунок 2

При изображении изделия с разрывом размерную линию не прерывают и наносят действительный раз­мер (рис.3, а). Если стрелки размерных линий пере­секают расположенные близко друг к другу контурные линии, то эти линии допускается прерывать (рис.3, б). В случае, показанном на рис.3, в, размерную и выносные линии проводят так, чтобы они вместе с измеряемым отрезком образовали параллелограмм.

Рисунок 3

Если наклон размерной линии к вертикали менее 30°, то размерное число наносят на полке линии-выноски (рис. 4, а).

Способ нанесения размерного числа при различных положениях размерных линий на чертеже определяют наибольшим удобством чтения чертежа.

Размерные числа не допускается пересекать какими-либо ли­ниями чертежа, т.е. в месте нанесения размерного числа осевые, центровые линии и линии штриховки прерываются. Не допускается разрывать линии контуров для нанесения размер­ных чисел и наносить их в местах пересечения размерных, вынос­ных и центровых линий. Стрелка размерной линии также не мо­жет пересекаться никакой линией чертежа. Любая линия при пе­ресечении со стрелкой прерывается.

При нанесении нескольких параллельных или концентричес­ких размерных линий на небольшом расстоянии друг от друга раз­мерные числа над ними рекомендуется располагать в шахматном порядке относительно их середины. Причем меньшие размеры располагаются ближе к контуру изображения, а большие — даль­ше, во избежание пересечения размерных и выносных линий.

Число размеров, определяющих форму отдельных элементов детали и их взаимное расположение, должно быть достаточным для обеспечения возможности изготовления детали.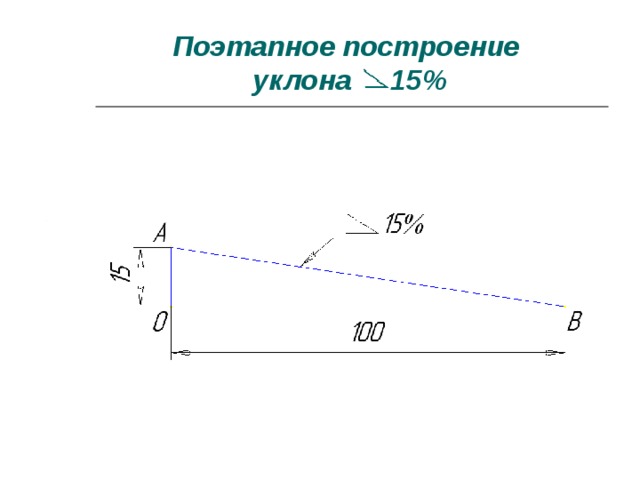 Не допуска­ется повторять размеры одного и того же элемента на изображе­ниях, а также в технических требованиях.

Размеры, не обязательные для данного вида чертежа, но кото­рые указываются для большего удобства пользования, называют­ся справочными и отмечаются на чертежах звездочкой, а в технических требованиях к чертежу делается надпись «*Размер для справок».

На изображении с разрывом размерная линия не прерывается.

При совмещении вида с разрезом следует отдельно группиро­вать размеры, относящиеся к внешним и внутренним очертаниям

Если для нанесения размерного числа недостаточно места над размерной линией, то размеры наносят, как показано на рис. 4, б; если недостаточно места для нанесения стрелок, то их наносят, как показано на рис. 4, в.

Рисунок 4

При указании размера радиуса перед размерным числом ставят прописную букву R. На рис. 5, а пока­заны примеры нанесения размеров радиусов.

При большой величине радиуса допускается центр приближать к дуге, в этом случае размерную линию радиуса показывают с изломом под углом 90° (R 90 на рис.5, а). Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать ее относительно центра (R 250 на рис.5, а).

Перед размерным числом диаметра ставят знак Ø (рис.5, б), высота которого равна высоте цифр раз­мерных чисел. Знак представляет собой окружность, пересеченную косой чертой под углом 45° к размерной линии.

При указании размера диаметра окружности размер­ную линию можно проводить с обрывом, при этом обрыв размерной линии следует делать несколько дальше центра окружности (Ø50, на рис. 5, б).

Если недостаточно места для нанесения стрелок или размерного числа над размерной линией, то размеры диаметров наносят, как показано на рис. 5, б, Ø15; Ø12.

При указании радиуса или диаметра сферы также пользуются знаками R и Ø. В случаях, когда на чер­теже трудно отличить сферу от других поверхностей, допускается надпись «Сфера» или знак О, напри­мер, «Сфера О 30» или О R12».

Размеры квадрата наносят, как показано на рис.5, в. Высота знака □ должна быть равна высоте раз­мерных чисел на чертеже (ГОСТ 2.307—68).

Угловые размеры наносят так, как показано на рис.5, г. Для указания размера угла размерная линия про­водится в виде дуги с центром в его вершине, а вынос­ные линии — радиально. В зоне, расположенной выше горизонтальной осевой линии, размерные числа поме­щают над размерными линиями со стороны их выпу­клости; в зоне, расположенной ниже горизонтальной осевой линии, — со стороны вогнутости размерных ли­ний (рис.5, г).

Рисунок 5

В заштрихованной зоне наносить размерные числа не рекомендуется.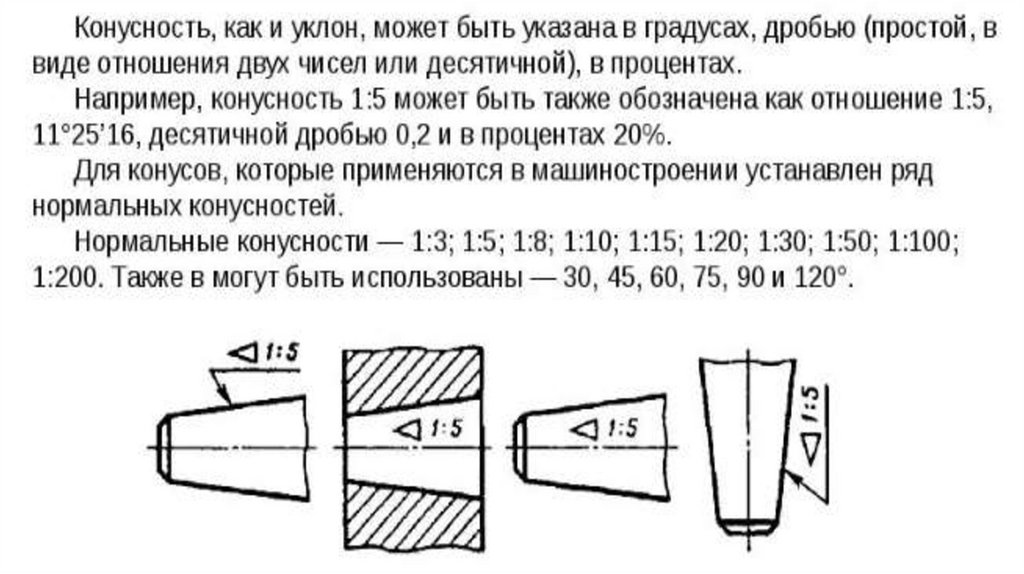 В этом случае размерные числа должны расположиться на горизонтально нанесенных полках (рис.5, г, размеры 30 и 40°).

В случаях, когда надо показать координаты вер­шины скругляемого угла или центра дуги, выносные линии проводят от точки пересечения сторон скругля­емого угла (размер 45 на рис.6, а) или от центра дуги скругления (размер 17 на рис.6, а).

Размеры контура криволинейного профиля наносят, как показано на рис.6, б.

Рисунок 6

ПОСТРОЕНИЕ И ОБОЗНАЧЕНИЕ УКЛОНА

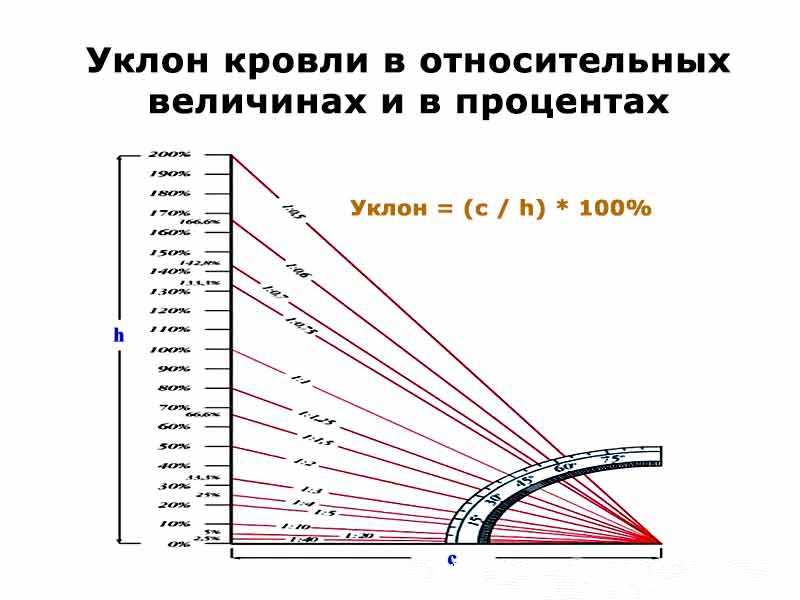
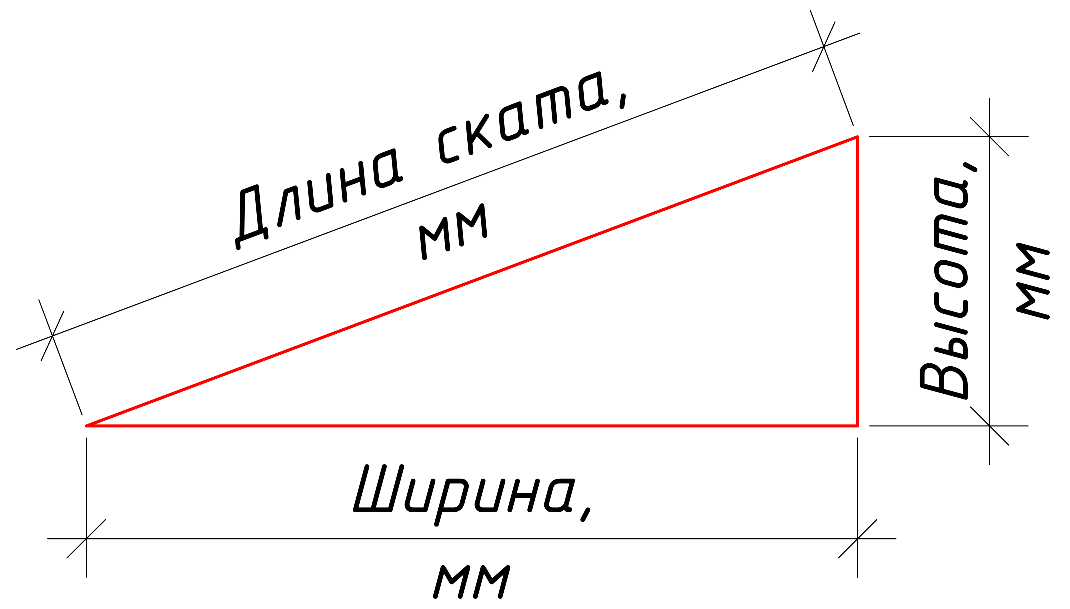
Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой. Уклон выражают дробью или в процентах.

Уклон i отрезка ВС относительно отрезка ВА опре­деляют отношением катетов прямоугольного тре­угольника ABC (рис.7, а), т. е.

Для построения прямой ВС (рис.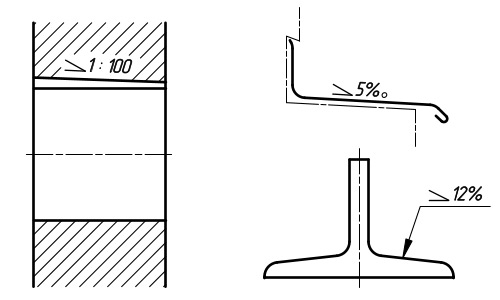 7, а) с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки А влево отложить отрезок AB, равный четырем единицам длины, а вверх отрезок AC, равный одной единице длины. Точки С и В соединяют прямой, которая дает направление искомого уклона.

Уклоны применяются при вычерчивании деталей, например, стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготов­ленных литьем (рис.7, д).

При вычерчивании контура детали с уклоном сна­чала строится линия уклона (рис.7, в и г), а затем контур.

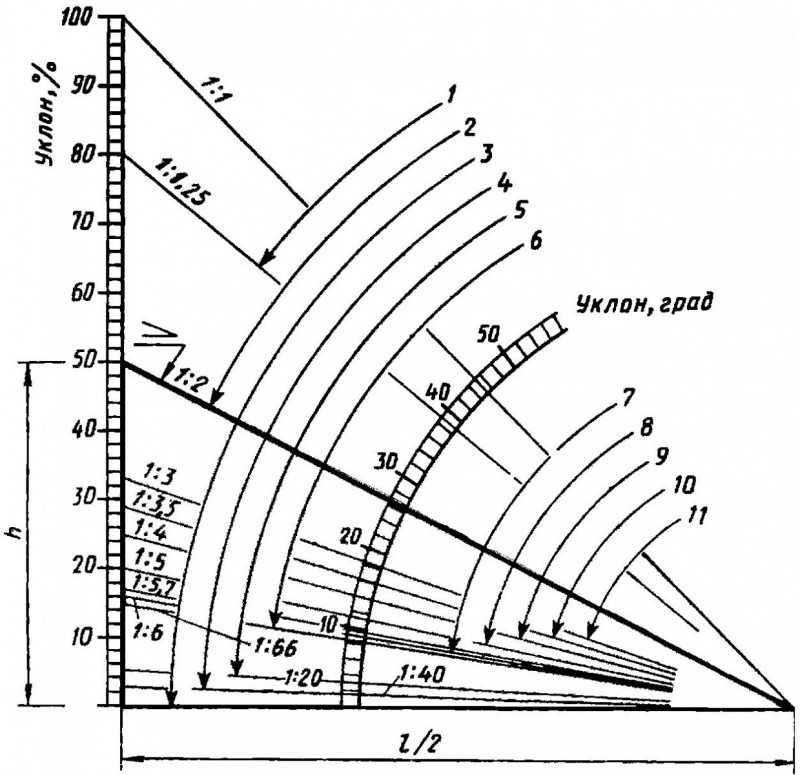
Если уклон задается в процентах, например, 20% (рис.7, б), то линия уклона строится так же, как гипо­тенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100%, а другого — 20%. Очевидно, что уклон 20% есть иначе уклон 1:5.

По ГОСТ 2.307—68 перед размерным числом, опре­деляющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рис. 7, в и г).

Рисунок 7 Рисунок 8

ПОСТРОЕНИЕ И ОБОЗНАЧЕНИЕ КОНУСНОСТИ

На рис.8, а даны для примера детали: оправка, ко­нус и сверло, которые имеют конусность.

Конусностью называется отношение диаметра осно­вания конуса к его высоте (рис.8, б), обозначается конусность буквой С. Если конус усеченный (рис.8, в) с диаметрами оснований D и d и длиной L, то конус­ность определяется по формуле

Например (рис. 70, в), если известны размеры D=30 мм, d=20 мм и L=70 мм, то

Если известны конусность С, диаметр одного из оснований конуса d и длина конуса L, можно опреде­лить второй диаметр конуса. Например, C=l:7, d=20 мм и L=70 mm; D находят по формуле D=CL+d= 1/7x70+20=30 мм (рис.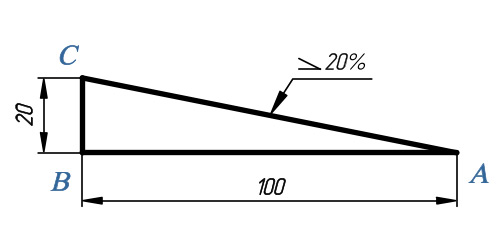 8, г).

По ГОСТ 2.307—68 перед размерным числом, харак­теризующим конусность, необходимо наносить услов­ный знак конусности, который имеет вид равнобедрен­ного треугольника с вершиной, направленной в сто­рону вершины конуса (рис.8, в и г).

Обычно на чертеже конуса дается диаметр большего основания конуса, так как при изготовлении коничес­кой детали этот диаметр можно измерить значительно легче и точнее.

Нормальные конусности и углы конусов устанавли­вает ГОСТ 8593—81.

ГОСТ 25548— 82 устанавливает термины и опре­деления.

Наклон линии — определение, формулы и примеры

В геометрии мы видели линии, проведенные на координатной плоскости. Чтобы предсказать, являются ли линии параллельными или перпендикулярными, или под любым углом, без использования какого-либо геометрического инструмента, лучший способ определить это — измерить наклон. В этой статье мы подробно обсудим, что такое наклон, формулу наклона для параллельных линий, перпендикулярных линий, уклон для коллинеарности со многими решенными примерами.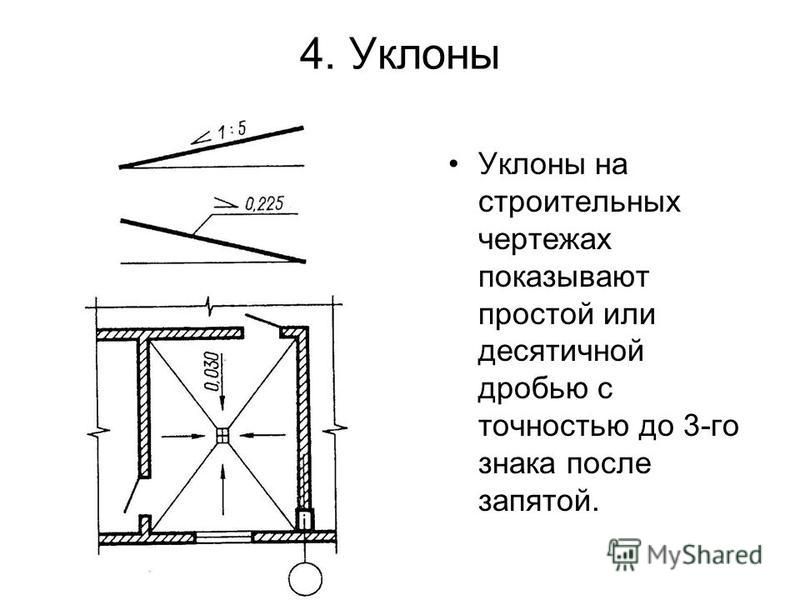

Что такое уклон?

В математике наклоном линии называется изменение координаты y по отношению к изменению координаты x.

Чистое изменение координаты y представлено Δy, а чистое изменение координаты x представлено Δx.

Следовательно, изменение координаты y по отношению к изменению координаты x определяется выражением,

m = изменение y/изменение x = Δy/Δx

Где «м» — наклон линии.

Наклон линии также может быть представлен цифрой 9.0003

тангенс θ = Δy/Δx

Итак, тангенс θ – наклон линии.

Обычно наклон линии определяет ее крутизну и направление. Наклон прямой между двумя точками (x

1 , y ₁ ) и (x ₂ , y ₂ ) можно легко определить, найдя разницу между координатами точек. Уклон обычно обозначается буквой «м».

Формула уклона

Если P(x ₁ ,y ₁ ) и Q(x ₂ ,y ₂ ) являются двумя точками на прямой линии, тогда формула наклона определяется как:

Уклон, м = Изменение координаты y/Изменение координаты x м = (у 2 – у 1 )/(х 2 – х 1 )

Таким образом, на основе приведенной выше формулы мы можем легко вычислить наклон линии между двумя точками.

Другими словами, наклон линии между двумя точками также называется подъемом линии от одной точки к другой (по оси Y) по ходу (по оси X). Следовательно,

Уклон, м = Подъем/Прогон

Уравнение наклона линии

Уравнение для наклона линии и точек, также называемых точечным наклоном, форма уравнения прямой линии определяется как:

у – у 1 = м(х – х 1 )

Принимая во внимание, что наклон-пересечение образует уравнение линии:

у = мх + б

Где b — точка пересечения с осью y.

Как найти наклон линии на графике?

На данном рисунке, если угол наклона данной линии с осью x равен θ, то наклон линии определяется тангенсом θ. Следовательно, существует связь между линиями и углами. В этой статье вы узнаете различные формулы, связанные с углами и линиями.

Наклон линии задается как m = tan θ. Если две точки A (x ₁ , y ₁₎ и B(x ₂ , y ₂ ) лежат на прямой с x ₁ ≠ x ₂  тогда наклон линии AB определяется как:

\(\begin{array}{l} m = tan\ \theta =\frac{y_2~-~y_1}{x_2~-~x_1}\end{массив} \)

Где θ — угол, который линия AB образует с положительным направлением оси x.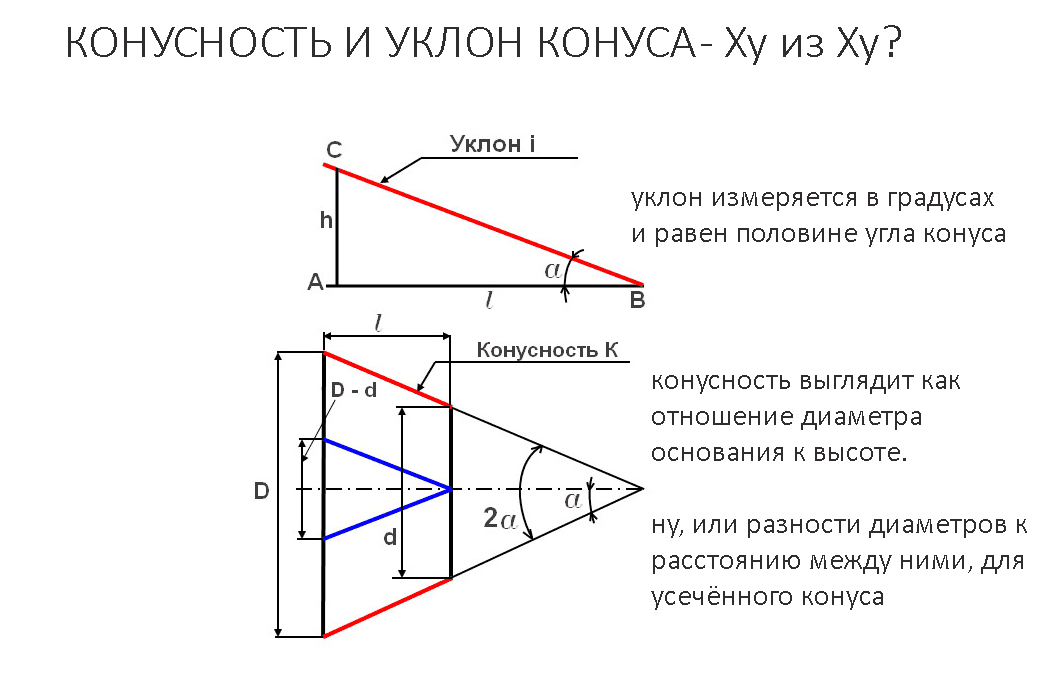 θ лежит между 0° и 180°.

Следует отметить, что θ = 90° возможно только тогда, когда линия параллельна оси Y, т.е. при x ₁ = x ₂  при этом конкретном угле наклон линии не определен.

Условия перпендикулярности, параллельности и коллинеарности прямых приведены ниже:

Уклон для параллельных линий

Рассмотрим две параллельные прямые, заданные l ₁ и l ₂  с наклоном α и β соответственно. Чтобы две прямые были параллельны, их наклон также должен быть равен, т.е. α=β. Это приводит к тому, что тангенс α = тангенс β. Следовательно, условие параллельности двух прямых с наклонами α, β: tan α = tan β.

Следовательно, если наклоны двух прямых на декартовой плоскости равны, то эти прямые параллельны друг другу.

Таким образом, если две прямые параллельны, то m ₁ = m ₂ .

Обобщая это для n линий, они параллельны только тогда, когда наклоны всех линий равны.

Если уравнение двух прямых задано как ax + by + c = 0 и a’ x + b’ y + c’= 0, то они параллельны, когда ab’ = a’b. (Как? Вы можете прийти к этому результату, если найдете наклоны каждой прямой и приравняете их.)

Уклон для перпендикулярных линий

На рисунке две строки l ₁ и l ₂  с наклоном α, β. Если они перпендикулярны, мы можем сказать, что β = α + 90°. (Используя свойства углов)

Их наклоны могут быть указаны как:

м ₁ = тангенс (α + 90°) и м ₂ = тангенс α.

\(\begin{array}{l}\Rightarrow m_1 = – кроватка\ \alpha = -~ \frac{1}{tan~\alpha} = -~\frac {1}{m_2}\end{array} \)

\(\begin{array}{l}\Rightarrow m_1 = -\frac {1}{m_2} \end{array} \)

\(\begin{array}{l}\Rightarrow m_1 ~\times ~m_2 = -1\end{array} \)

Таким образом, чтобы две прямые были перпендикулярны, произведение их наклона должно быть равно -1.

Если уравнения двух прямых задаются как ax + by + c = 0 и a’ x + b’ y + c’ = 0, то они перпендикулярны, если aa’ + bb’ = 0. (Опять вы можно прийти к этому результату, если найти наклоны каждой прямой и приравнять их произведение к -1.)

Также читайте: Перпендикулярные линии

Наклон для коллинеарности

Чтобы две прямые AB и BC лежали на одной прямой, наклон обеих прямых должен быть одинаковым и должна быть хотя бы одна общая точка, через которую они должны проходить. Таким образом, чтобы три точки A, B и C лежали на одной прямой, наклоны AB и BC должны быть равны.

Если уравнение двух прямых задается как ax + by + c = 0 и a’ x+b’ y+c’ = 0, то они коллинеарны, когда ab’ c’ = a’ b’ c = a’ c’b.

Угол между двумя линиями

Когда две прямые пересекаются в одной точке, угол между ними может быть выражен через их наклоны и определяется по следующей формуле:

\(\begin{array}{l}tan\ \theta = | \frac{ m_2~-~m_1}{1~+~m_1~ m_2}|\end{array} \)

где м ₁ и м ₂ — наклоны линий AB и CD соответственно.

\(\begin{array}{l}\text{Если } \frac{ m_2~-~m_1}{1~+~m_1~ m_2} \text{ положительно, то угол между прямыми острый. }\ конец {массив} \)

\(\begin{array}{l}\text{Если } \frac{ m_2~-~m_1}{1~+~m_1~ m_2} \text{ отрицательно, то угол между линиями тупой.}\ конец {массив} \)

Наклон вертикальных линий

Вертикальные линии не имеют наклона, так как не имеют крутизны. Или можно сказать, что мы не можем определить крутизну вертикальных линий.

Вертикальная линия не будет иметь значений координат x. Итак, согласно формуле наклона линии,

Уклон, м = (y ₂ – y ₁ )/(x ₂ – x ₁ ) 

Но для вертикальных линий х ₂ = х ₁ = 0

Следовательно,

м = (у ₂ – у ₁ )/0 = не определено

Точно так же наклон горизонтальной линии равен 0, так как координаты y равны нулю.

м = 0/(x ₂ – x ₁ ) = 0 [для горизонтальной линии]

Положительный и отрицательный наклон

Если значение наклона линии положительное, это показывает, что линия поднимается вверх по мере нашего движения или положительное значение подъема над бегом.

Если значение наклона отрицательное, то линия на графике прокручивается, когда мы движемся вдоль оси x.

Решенные примеры наклона линии

Пример 1:

Найдите наклон прямой между точками P = (0, –1) и Q = (4,1).

Решение:

Даны точки P = (0, –1) и Q = (4,1).

Из формулы наклона мы знаем, что

Наклон линии, м = (y ₂ – y ₁ )/(x ₂ – x ₁ )

м = (1-(-1))/(4-0) = 2/4 = ½

Пример 2:

Найдите наклон линии между P(–2, 3) и Q(0, –1).

Решение:

Даны две точки P(–2, 3) и Q(0, –1).

Следовательно, наклон линии

м = (-1-3)/0-(-2) = -4/2 = -2

Пример 3:

Рамья проверяла график и поняла, что рейз составил 10 единиц, а пробег — 5 единиц. Каким должен быть наклон линии?

Решение:

Учитывая, что повышение = 10 единиц

Пробег = 5 ед.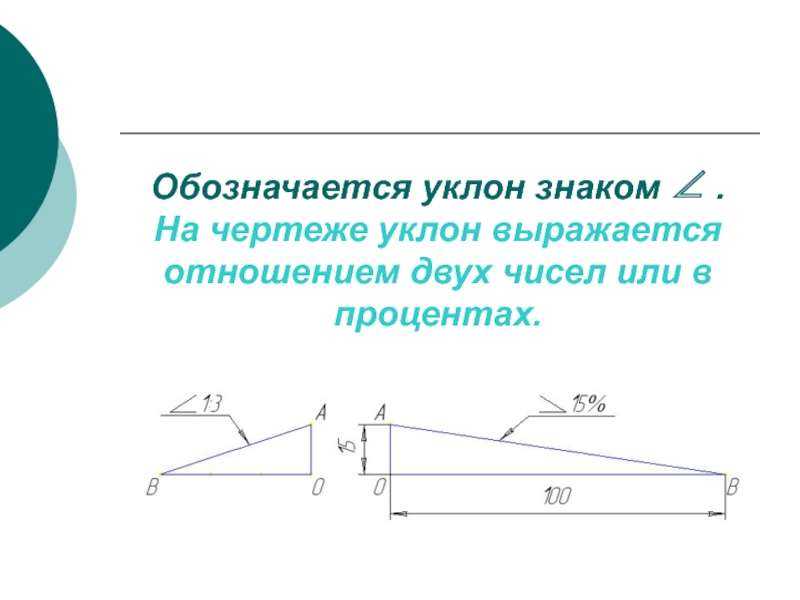

Мы знаем, что наклон линии определяется как отношение подъема к пробегу.

т.е. уклон, м = подъем/прогон

Следовательно, наклон = 10/5 = 2 единицы.

Следовательно, наклон линии равен 2 единицам.

Оставайтесь с нами с BYJU’S — приложением для обучения и загрузите приложение, чтобы легко изучать все понятия, связанные с математикой, просматривая больше видео.

Часто задаваемые вопросы о наклоне прямой

Q1

Что такое наклон прямой линии?

Наклон выражает крутизну и направление линии. Он показывает, насколько крута линия.

Q2

Какими тремя способами можно найти уклон?

Наклон можно найти с помощью различных методов, таких как стандартная форма, форма пересечения наклона и форма точки пересечения.

Q3

Что такое уравнение точки-наклона прямой?

Точечно-наклонная форма уравнения прямой определяется формулой:
y − y ₁ = m(x − x ₁ )

Q4

Как найти наклон прямой?

Нам нужно найти отношение разницы между координатами y и x двух точек, образующих линию. Полученное значение представляет собой наклон линии. Он показывает подъем линии по оси Y по сравнению с линией по оси X.

Q5

Каков наклон между двумя точками?

Наклон между двумя точками вычисляется путем оценки изменения значений координаты Y и координаты X. Например, уклон между точками (4,8) и (-7,1) равен:
м = (1-8)/(-7-4) = -7/-11 = 7/11

Q6

Каков наклон линии: y = −2x + 7?

Наклон линии, уравнение которой y = -2x + 7, равен -2.
м = -2

Определение уклона – Концепция

Одной из самых важных идей, которые вы
увидите во всем своем изучении
алгебры, является идея наклона.
А наклон просто относится к
насколько крута линия.
Это основное определение.
Это то, что я помогаю
или помогает мне вспомнить, что означает наклон.

С ним связано множество причудливых обозначений
.
И мы поговорим об этом через секунду.

Но если вы можете просто вспомнить
затылком, что наклон означает, насколько крутой
линия есть, она
вам очень поможет.

Итак, вы видите, что каждый раз, когда я
рисую прямую линию, коэффициент наклона
остается одинаковым для всей этой линии.
И вот что я имею в виду.

Допустим, это мои оси X и Y
, и у меня есть вот эта линия.
Линия имеет одинаковую крутизну
все время.
Имеет тот же коэффициент наклона.
И мы собираемся получить во втором
то, что я имею в виду под соотношением.
И вот о чем я.
Когда мы говорим об уклоне или крутизне,
определяется как изменение
Y по сравнению с изменением X. Как
в дроби.
Изменение Y сверх изменения X.
Вот почему мы называем это отношением.

Помните, что соотношение похоже на дробь.
Итак, если бы я нарисовал здесь маленький треугольник
, который показывает, насколько крута моя линия
, это было бы изменением в части Y
, потому что Y вверх и вниз.
Это будет мое изменение в части X,
, потому что X расположен горизонтально.
И какими бы ни были эти числа на графике
, я бы написал дробью.
Это одна вещь, которую вы хотите, чтобы
помнил.
Изменение Y поверх изменения X.

Иногда мы пишем это, используя этот маленький треугольник
.
Этот треугольник представляет собой греческую букву
дельта, что довольно сложно.
Вы не только должны выучить математику
, но теперь вы должны выучить греческий язык.
Это означает изменение Y поверх изменения
X. Эта дельта представляет собой
изменение слова.

И третий способ написать это, используя
букву М. М означает уклон,
и если бы у меня было две точки,
я использовал бы их здесь.
Допустим, у меня была эта точка. Я собираюсь
назвать ее X из моей первой точки, а затем
Y из моей первой точки.
Вот мое второе замечание.
X из моей второй точки. Я собираюсь использовать
, эту маленькую цифру 2, чтобы показать, что это моя вторая точка
. Y для моего второго пункта.

Тогда есть формула, которую я мог бы использовать, используя
эти числа X и Y, чтобы найти M, или
склон.
И так я бы написал, что Y на
убери Y1 поверх X2 убери X1.
Это то же самое, только
написано по-другому.
Я выясняю, насколько изменились мои значения Y
, и добавляю это к тому, насколько
сильно изменились мои значения X
в дробной части.

Таким образом, эта формула действительно важна каждый раз, когда
у вас есть две точки, подобные этой.
Эти маленькие числа здесь хитрые.
Это не означает, что нужно взять значение Y и 9.0315 умножьте его на 2 или возьмите значение Y
и умножьте его на 1.
означает, что мы просто записываем с помощью
то, что называется индексом.
Это мое второе значение Y.
Я вычитаю свое первое значение Y.
И мы вернемся к этому позже, когда вы,
, ребята, приступите к домашним заданиям.

Несколько других вещей, которые я хочу, чтобы вы помнили о
с наклоном, а это
, иногда наклоны – это положительные числа
, а иногда наклоны – отрицательные числа
. И вот как вы можете сказать.

Каждый раз, когда вам дают график,
там есть моя ось и моя линия.
Подумайте о том, если бы вы катались на скейтборде
, и вы шли бы вместе, и вы
врезались бы в эту рампу.
Это пандус в гору.
Мы называем это положительным наклоном.
В отличие от того, если вы нажмете на эту линию здесь,
здесь вы идете на скейтборде,
Я не знаю, почему это шум скейтбординга.
Я только что это придумал. Ты катаешься на скейтборде.
Если вы ударите эту штуку, вы упадете.
Вот почему мы называем это отрицательным наклоном.
Каждый раз, когда линия увеличивается слева
вправо, это называется положительным.
Уменьшается слева направо,
называется минусом.

Об этом нужно помнить, когда
вы, ребята, подходите к своим проблемам.
Это все математические обозначения, которые
вы будете видеть снова и снова и
снова и снова.
Так что привыкнешь.

Последнее, что я хочу оставить вам,
, это размышления о задачах со словами,
потому что много раз графики, как мы
знаю, представляют реальный мир.